A simple hypoplastic model for overconsolidated clays

Abstract

This paper presents a simple hypoplastic constitutive model for overconsolidated clays. The model needs five independent parameters and is as simple as the modified Cam Clay model but with better performance. A structure tensor is introduced to account for the history dependence. Simulations of various elementary tests show that the model is capable of capturing the salient behavior of overconsolidated clays.

1 Introduction

The effect of overconsolidation on the mechanical behavior of clays is well documented in the literature. Unlike normally consolidated clays, overconsolidated (OC) clays show peak strength along with dilatancy and postpeak strain softening under shearing. Accurate characterization of the behavior of OC clays is of great importance for many engineering applications, such as foundation design [1], slope stabilization [4], and embankment construction [36].

During the last four decades, great effort has been devoted to the development of constitutive models for predicting the mechanical behaviors of OC clays [2, 10, 17, 19, 25, 28, 52, among others]. Most of these works were based on the critical state concept [31, 32], and developed from the original or modified Cam Clay (MCC) models. The capacity of the models has been largely enhanced by introducing various concepts, such as bounding surface [6] and subloading surface [12]. While these approaches have achieved certain success, some fundamental issues still remain unsolved, particularly the model complexity and the numerous model parameters. Often, the models make use of the evolution of the yield surfaces, and switch functions to differentiate between loading and unloading, which hamper the numerical implementation of the models [34].

Recently, there is growing interest in the use of hypoplasticity to model the mechanical behaviors of soils [3, 7,8,9, 11, 13, 14, 18, 20, 26, 29, 30, 37,38,39,40,41, 43, 48]. Hypoplastic models were developed without recourse to the concept in elastoplasticity theory such as yield surface, plastic potential and decomposition of the strain into elastic and plastic parts. Therefore, hypoplastic models are usually characterized by simple formulations and few parameters. Moreover, hypoplastic model possesses a single formulation for the incrementally nonlinear behavior without using a predefined criterion for loading and unloading. These features make the numerical implementation of hypoplastic models, in comparison to elastoplastic models, easier and more straightforward [35, 40].

The early hypoplastic models [18, 45], containing four tensor polynomial terms with four material parameters, are as simple as the MCC model. The stress tensor is considered as the only state variable in such basic models. As a consequence, these basic models are not able to account for the complex history dependence. Later, the critical state concept was incorporated in hypoplasticity by introducing the void ratio as an additional state variable to account for the effect of density. The first hypoplastic model with critical state by Wu et al. [44] represents an important development of hypoplasticity in this regard. This extension leads to a number of critical state hypoplastic models for sand [3, 11, 15, 39, 46, 47].

The first attempt to extend hypoplastic model to clay was made by Niemunis [26, 27], who combined the critical state concept of clay with hypoplasticity to describe the behavior of OC clays. Based on this model, Mašín [21, 23, 24] proposed several hypoplastic models for OC clays. While these models can capture some features of OC clays, their performance in undrained condition is rather poor. Huang et al. [16] proposed a hypoplastic model for normally consolidated soils, emphasising the undrained behavior. However, this model made use of a loading criterion, which is at the sacrifice of the model simplicity. More recently, Shi et al. [33] introduced a nonlinear Hvorslev surface into the Cam–Clay hypoplastic model [23] for heavily OC clays. This model, however, inherits the shortcomings of the basic model. Moreover, the capacity of the aforementioned models is frequently gained at the cost of their simplicity. Therefore, further extensions based on these models will inevitably increase the complexity of the model and the number of the parameters.

The primacy of this work is to develop a hypoplastic constitutive model that is capable of describing the salient behaviors of OC clay, while still keeping the model simplicity. Our development is based on a basic constitutive model proposed recently by Wu et al. [48]. First, the background of hypoplasticity and the basic idea for overconsolidation are introduced. Next, a simple hypoplastic model is developed and some numerical tests are performed to show the model performance. In the following, except where specified otherwise, effective stress is used.

2 General framework for OC clays

2.1 Constitutive equation

To gain perspective, let us start with the following hypoplastic constitutive framework proposed by Wu and Kolymbas [43].

$$\begin{aligned} \mathring{\mathbf{T}}={\varvec{\mathcal{L}}}(\mathbf{T} ):\mathbf{D} +\mathbf{N} (\mathbf{T} )\Vert \mathbf{D} \Vert \end{aligned}$$

(1)

where $\mathbf{T}$ is the Cauchy stress tensor; $\mathbf{D}$ is the strain rate (stretching) tensor. The tensorial functions ${\varvec{\mathcal{L}}}$ and $\mathbf{N}$ are of the 4th and 2nd order, respectively. The colon : denotes an inner product between two tensors. $\Vert \mathbf{D} \Vert$ stands for the Euclidean norm of the stretching tensor. The Jaumann stress rate tensor $\mathring{\mathbf{T}}$ is defined in terms of the material time-derivative of the Cauchy stress tensor $\dot{\mathbf{T }}$ and the spin tensor $\mathbf{W}$:

$$\begin{aligned} \mathring{\mathbf{T}}=\dot{\mathbf{T}}+\mathbf{T} \mathbf{W} -\mathbf{W} \mathbf{T} \end{aligned}$$

(2)

The stretching and spin tensors are related to the velocity gradient tensor through

$$\begin{aligned} \mathbf{D} =\frac{1}{2}\Big[\varvec{{\nabla}v}+(\varvec{{\nabla v}})^{T}\Big],\quad \mathbf{W} =\frac{1}{2}\Big[\varvec{{\nabla}v}-(\varvec{{\nabla v}})^{T}\Big] \end{aligned}$$

(3)

where $\varvec{v}$ is the velocity and $\varvec{\nabla}$ is the gradient operator.

The functions ${\varvec{\mathcal{L}}}$ and $\mathbf{N}$ must be isotropic to remain invariant under rigid body rotations. Since ${\varvec{\mathcal{L}}}$ is independent of $\mathbf{D}$, constitutive equations in the form of Eq. (1) are necessarily rate independent. This can be easily ascertained by the fact that Eq. (1) is positively homogeneous of the first degree in strain rate $\mathbf{D}$. To show this, we can write Eq. (1) in the following form by making use of Euler’s theorem for homogeneous functions.

$$\begin{aligned} \mathring{\mathbf{T}}=[{\varvec{\mathcal{L}}}+\mathbf{N} \otimes {\vec {\mathbf{D}}}]:\mathbf{D} \end{aligned}$$

(4)

where ${\vec {\mathbf{D}}}=\mathbf{D} /\Vert \mathbf{D} \Vert$ is the direction of strain rate and $\otimes$ stands for the dyadic product. The term in the square brackets in Eq. (4) is the directional stiffness tensor, which can be viewed as the counterpart of the tangential stiffness of elastoplastic models. Obviously, the directional stiffness tensor depends on the direction of strain rate ${\vec {\mathbf{D}}}$. Therefore, loading and unloading in the hypoplastic model (4) are implicitly stated without additional loading criterion. This is different from elastoplastic models, where two stiffness tensors, one for loading and the other for unloading, are used. Furthermore, elastoplastic models need explicit loading criterion to decide which stiffness shall be used.

2.2 Basic idea for overconsolidation

We propose to consider the effect of overconsolidation by manipulating the nonlinear term in constitutive Eq. (1). This idea can be best explained by examining the effective stress paths in undrained triaxial test with the help of the so-called response envelope for the case of isochoric deformation.

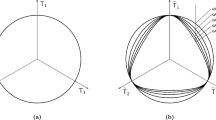
Staring from a stress state, a stress rate (stress increment) can be obtained for a strain rate from constitutive Eq. (1). In other words, a response is obtained for a strain rate. For a rosette of strain rates with a constant magnitude, we obtain a rosette of stress increments, which can be represented in the stress space graphically (response envelope). Obviously, the distance from the initial stress $\mathbf{T} _0$ to any point on the response envelope represents the stiffness along certain strain rate. The response envelope at a given initial stress state $\mathbf{T} _0$ is the surface spanned by all stresses $\mathbf{T} =\mathbf{T} _0+\Delta \mathbf{T}$. The response envelopes can be best visualized by considering the Rendulic plane for strain rate and stress, e.g., the $p-q$ plane, where the stress increments can be represented by vectors.

Let us consider an isotropic stress state, with $T_{11} = T_{22}=T_{33}$. The response envelope of constitutive Eq. (1) consists of the contributions from the linear and nonlinear terms, which is shown in Fig. 1. The response envelope of the linear term, which is incrementally linear, represents an ellipse with the initial stress in the center [43]. The nonlinear term remains independent of the direction of strain rate and represents a translation along the p-axis. As a result of the translation, the initial stress is not at the center of the ellipse as shown in Fig. 1 for the case of N_p > 0. Obviously, the initial stress is shifted to the right, which gives rise to smaller stiffness for loading (smaller distance to the right) and larger stiffness for unloading (larger distance to the left).

Fig. 1

Visualization of the idea of overconsolidation by the response envelope in the $p-q$ plane. N_p denotes the projection of N at the p-axis

We proceed to consider the effective stress path during undrained triaxial compression test starting from an isotropic stress state. For an isochoric strain rate, the linear term gives rise a pure deviatoric stress increment, i.e., $\Delta p =0$. The nonlinear term gives rise to a vector pointed to the origin along the p-axis (see the vector for N_p > 0 in Fig. 1). The overall response of constitutive Eq. (1) consists of the contributions of the linear and nonlinear parts. The vector sum of the two parts leads to a stress increment pointed toward left. Therefore, the initial effective stress path starting from an isotropic stress state is directed to the left. This agrees in principle with the experimental observations for normally consolidated soils.

For OC clays, however, the shape of the effective stress paths is known to depend on OCR. The stress path becomes steeper for light overconsolidation and turns toward right for heavy overconsolidation. As shown in Fig. 1, the initial stress path can be manipulated by the nonlinear term. For N_p = 0, the stress path is vertical. For N_p < 0, the stress path turns toward right. The idea is to introduce a structure tensor into the nonlinear term, which represents the history dependence.

2.3 Constitutive framework

Following the above reasoning, we seek to establish a framework to incorporate the consolidation history by introducing a structure tensor in the following way:

$$\begin{aligned} \mathring{\mathbf{T}}={\varvec{\mathcal{L}}}(\mathbf{T} +\mathbf{S} ) :\mathbf{D} +\mathbf{N} (\mathbf{T} -\mathbf{S} )\Vert \mathbf{D} \Vert \end{aligned}$$

(5)

where $\mathbf{S}$ is a second-order symmetric tensor representing the overconsolidation.

Bearing in mind that the structure tensor shall vanish for normal consolidation $(\hbox{OCR} = 1)$, we proceed to introduce the following simple expression for the structure tensor:

$$\begin{aligned} \mathbf{S} =\alpha \text{ln}\left( \frac{1}{R}\right) \mathbf{T} \quad (0<R\leqslant 1) \end{aligned}$$

(6)

where $\alpha$ is a model parameter; R is the stress ratio representing the overconsolidation defined as:

$$\begin{aligned} R =\frac{p_e^+}{p_e} \end{aligned}$$

(7)

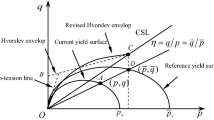
in which $p_e^+$ and $p_e$ are the pre-consolidation pressure in MCC model and the Hvorslev equivalent pressure, respectively. Their definitions are shown in Fig. 2 with the formulations given as follows:

$$\begin{aligned} p_e^+=p\left[ 1+(\frac{q}{Mp})^2 \right] , \quad p_e = \text{exp}\left[ \frac{N-\text{ln} (1+e)}{\lambda ^*}\right] \end{aligned}$$

(8)

where the inclination M corresponds to the stress ratio at the critical state by $M= 6\text{sin}\phi _c/(3-\text{sin}\phi _c)$ with $\phi _c$ being the critical state friction angle; the index $\lambda ^*$ is the slope of the normal compression line in the double logarithmic ${\text{ln}}(1+e)-{\text{ln}} p$ plane; N denotes the logarithmic value of the specific volume at the reference stress $p_r=1$ kPa. Note that the parameter N is different from the tensorial function $\textbf{N}$ in Eq. (1).

Fig. 2

The definition of a Hvorslev equivalent pressure $p_e$ [5] and b stress ratio R

The stress ratio R is widely used for overconsolidation in some elastoplastic models [50, 51]. Note that R has a different physical meaning from the conventional overconsolidation ratio OCR. A smaller value of R corresponds to a larger OCR. Obviously, the structure tensor vanishes for normal consolidation and critical state with $R = 1$. In these cases, the model (5) degenerates to the basic Eq. (1).

2.4 Improvement for undrained tests

Many undrained tests on sand and normally consolidated clay in the literature show an initially vertical effective stress path starting from an isotropic stress state. This behavior suggests an initially elastic behavior. However, as illustrated in Fig. 1, the hypoplastic model (1) predicts an effective stress path directed toward left from an isotropic stress state. Some attempts have been made to remedy this shortcoming [16, 22, 26, 49]. We proceed to multiply the nonlinear term in model (1) with a function $f_u$, which vanishes for isochoric strain rate to give

$$\begin{aligned} \mathring{\mathbf{T}}={\varvec{\mathcal{L}}}(\mathbf{T} +\mathbf{S} ):\mathbf{D} +f_u\mathbf{N} (\mathbf{T} -\mathbf{S} )\Vert \mathbf{D} \Vert \end{aligned}$$

(9)

where the multiplier $f_u$ is defined by

$$\begin{aligned} f_u=\frac{\Vert \mathbf{B} :\mathbf{D} \Vert }{\Vert \mathbf{B} \Vert \;\Vert \mathbf{D} \Vert } \end{aligned}$$

(10)

with $\mathbf{B }=-{{\varvec{\mathcal{L}}}}^{-1}:\mathbf{N}$ denoting the flow rule of the model. The multiplier $f_u$ can be viewed as the cosine of the angle between the strain rate direction ${\vec {\mathbf{D}}}$ and the flow direction ${\vec {\mathbf{B}}}$.

Figure 3 shows the mechanism of the function $f_u$ on the improvement of an undrained triaxial test. Compared to typical experimental results, the original prediction (dashed line) bends significantly toward the left at the onset of shearing. This unrealistic prediction, however, can be largely improved by the function $f_u$. Note that the function $f_u$ does not influence the shear strength at the critical state since $f_u=1$ at the critical state. To show this, let us first consider the stress states (a) and (b) at the beginning of shearing and at the critical state, respectively. For an undrained test with isochoric deformation, a purely deviatoric strain direction is expected. Therefore, the flow direction ${\vec {\mathbf{B}}}$ and the strain direction ${\vec {\mathbf{D}}}$ are perpendicular at the onset of the shearing while coincide at the critical state. Obviously, the variations of ${\vec {\mathbf{B}}}$ and ${\vec {\mathbf{D}}}$ give rise to a monotonic increase of $f_u$ from 0 to 1 ($0\leqslant f_u \leqslant 1$) in an undrained shear test starting from an isotropic stress state. This leads to an initially vertical effective stress path from an isotropic stress state. On the other hand, the function $f_u$ cannot change the isotropic stress state of the proposed model. As shown by the isotropic stress state (c) in Fig. 3, ${\vec {\mathbf{B}}}$ and ${\vec {\mathbf{D}}}$ with the same direction lead to the function $f_u =1$.

Fig. 3

Mechanism of $f_u$ on the improvement of an undrained triaxial test. $\Vert\vec{\textbf{D}}\Vert=\textbf{D}/\Vert\textbf{D}\Vert$ and $\Vert\vec{\textbf{B}}\Vert=\textbf{B}/\Vert\textbf{B}\Vert$ are the strain rate direction and flow direction, respectively

3 Hypoplastic constitutive model for OC clay

Having established the framework to incorporate the consolidation history, we proceed to consider the following specific constitutive model proposed by Wu et al. [48]. This model consists of three linear terms and one nonlinear term.

$$\begin{aligned} \mathring{\mathbf{T}}=C_1(\text{tr}{} \mathbf{T} )\mathbf{D} + C_2(\text{tr}{} \mathbf{D} )\mathbf{T} + C_3\frac{\text{tr}(\mathbf{T} {} \mathbf{D} )}{\text{tr}{} \mathbf{T} }{} \mathbf{T} + C_4(\mathbf{T} +\mathbf{T} ^{*})\Vert \mathbf{D} \Vert \end{aligned}$$

(11)

in which $C_i\,(i=1,2,3,4)$ are dimensionless material constants. $\mathbf{T} ^*$ is the deviatoric part of $\mathbf{T}$. The performance of the above constitutive equation is well documented in the literature [48]. For the numerical implementation of the model we refer to Wang et al. [40].

Combining Eq. (9) with the constitutive model (11), we obtain a simple hypoplastic model as follows for OC clays:

$$\begin{aligned} \mathring{\mathbf{T}}&=C_1\text{tr}(\mathbf{T} +\mathbf{S} )\mathbf{D} + C_2\text{tr}{} \mathbf{D} (\mathbf{T} +\mathbf{S} )+ C_3\frac{\text{tr}(\mathbf{T} {} \mathbf{D} +\mathbf{S} {} \mathbf{D} )}{\text{tr}(\mathbf{T} +\mathbf{S} )}(\mathbf{T} +\mathbf{S} )\\ &\quad +f_uC_4(\mathbf{T} -\mathbf{S} +\mathbf{T} ^{*}-\mathbf{S} ^{*})\Vert \mathbf{D} \Vert \end{aligned}$$

(12)

Since the above equation is written in tensorial notation, the essential features of the model can be hardly perceived without detailing it in component form. For details of the component form of hypoplastic models, the reader are referred to [45]. The complete formulations of the constitutive equation are given in the "Appendix".

4 Model performance

We consider several element tests, including oedometer tests and triaxial compression tests, to show the model performance. The material constants listed in Table 1 are used to obtain the numerical results throughout the paper.

Table 1 Model parameters for numerical simulations

Note that the material constants $C_i\,(i=1,2,3,4)$ can be related to some well-established parameters in soil mechanics, such as the initial tangential modulus $E_i$, the initial Poisson’s ratio $\nu _i$, the critical friction angle $\phi _c$. These parameters can be readily determined with a single triaxial compression test [45]. Moreover, the constitutive equation is homogenous in stress, which means that the parameter $E_i$ can be scaled by $\lambda ^*$ for clays. We are then left with five independent parameters for the constitutive Eq. (12). A detailed procedure to calibrate the model parameters can be found in our forthcoming paper.

4.1 Oedometer test

The oedometer test is commonly used to determine the consolidation history of OC clays. The ratio of the radial stress to the vertical stress $K_0$, called earth pressure coefficient at rest, is important for a variety of engineering problems.

The predicted $K_0$ using the basic model (11) and the proposed model (12) is shown in Fig. 4a. It shows that $K_0$ decreases with increasing critical friction angle $\phi _c$. The predicted $K_0$ by the proposed model is slightly larger than that obtained from the basic model. The results are compared to Jáky’s empirical relation: $K_0=1-\text{sin}\phi _c$. Obviously, the model predictions agree well with the empirical relationship by Jáky. Unlike Jáky’s formula, the models show nonlinear relationship particularly for high friction angle.

Fig. 4

a Critical friction angle $\phi _c-K_0$ relation, b model performance in oedometer and isotropic compression tests

The predicted $e-\text{ln} p$ curves from oedometer tests are compared to those obtained from isotropic compression tests. Figure 4b shows that the same loading index $\lambda ^*$ can be obtained from both tests, while the two tests predict slightly different unloading behaviors. Usually, a larger unloading index can be obtained from the isotropic test. Since the oedometer tests predict similar consolidation behavior as the isotropic compression test, the parameters N and $\lambda ^*$ can be determined from an oedometer test as well. It is noteworthy that some hypoplastic models [16, 26, 39] predict different normal compression lines in isotropic and in oedometer conditions.

Unlike some existing hypoplastic models for clays [16, 21, 24, 42], the unloading index, i.e., $\kappa ^*$, is not used in the proposed model. In fact, the unloading index facilitates the predictions of unloading behavior of one loading cycle, while it has little contribution in capturing the cyclic behavior with a large number of loading cycles [24]. Although the unloading index is not included in the model, the unloading behavior can be predicted fairly well. This is different from the MCC model, in which the elastic behaviors are solely controlled by the unloading index. In hypoplastic model, however, we do not differentiate between the elastic and the plastic deformation. Therefore, it is not necessary to include the unloading index.

4.2 Triaxial compression test

We now consider the model performance in triaxial compression tests. Both drained and undrained triaxial compression tests are simulated to show the model capacity for describing the deformation and strength behavior of OC clays. A wide range of overconsolidation ratios from 1 to 10 is considered. The initial OCR is specified by defining different initial void ratios, which are obtained by performing isotropic loading–unloading tests with different pre-consolidation pressures. In all simulations, a constant confining pressure of 100 kPa is used.

The numerical simulation of drained triaxial tests with various OCRs is shown in Fig. 5. The stress–strain curves in Fig. 5a show that the strength behavior changes from strain hardening to strain softening with the increase of the OCRs. At large strain, all stress–strain curves approach asymptomatically to the critical state, characterized by the critical friction angle. Correspondingly, the volumetric responses change from contraction to dilatancy with the increase of the OCRs. With further increasing the deformation, the volumetric strain rate vanished at the critical state, as shown in Fig. 5b. The effective stress path in the $p-q$ plane can be normalized by the Hvorslev equivalent pressure $p_e$, defined as a mean stress at the isotropic normal compression line at the current void ratio. As may be seen from Fig. 5c all normalized effective stress paths eventually converge to the critical state regardless of the initial OCRs.

Fig. 5

Model prediction of drained triaxial compression tests with different OCRs

The numerical results of undrained triaxial tests with various OCRs are shown in Fig. 6. The result of the stress ratio (q/p) is shown in Fig. 6a. For tests with high OCRs, along with the deformation, the stress ratios (q/p) first increase to reach a peak and then decrease to approach the critical state. As shown in Fig. 6b that the initial OCR significantly influences the shear strength in the undrained test. The shear strength increases with the increase of the OCRs. Besides, the undrained effective stress paths are predominately governed by the OCRs. As shown in Fig. 6c, reasonable predictions of the normalized stress paths can be obtained by the proposed model. Particularly, the normalized stress paths form an envelope resembling a state bound surface. The shape of the surface is close to the elliptic shape of the yield surface of the MCC model on the wet side ($\hbox{OCR} \leqslant 2$), while similar to the nonlinear Hvorslev surface on the dry side ($\hbox{OCR} > 2$). This enables the constitutive model to predict a reasonable peak shear strength for heavily OC clays. These characteristics of the simulation are corroborated qualitatively by numerous laboratory tests.

Fig. 6

Model prediction of undrained triaxial compression tests with different OCRs

5 Conclusions

Our mission is to develop a constitutive model, which is as simple as the MCC model but with better performance particularly for overconsolidated clays. We venture a formal comparison between our model and the MCC model in terms of formulation, number of parameters and model performance. Both MCC and our model possess simple formulation. However, the formulation of the hypoplastic model is even simpler than MCC model, since our model does not assume the separation of strain rate into elastic and plastic parts. Both model requires five model parameters, which can be easily determined from oedometer and triaxial tests.

The MCC model captures the salient features of normally and overconsolidated clays. Whereas the MCC model provides fairly decent prediction for normally consolidated clays, the prediction for heavily over-consolidated soil is rather crude. The stress-strain curve is characterized by an initially linear relationship until the yield surface is reached. Afterwards, the stress experiences strain softening toward the critical state. Similar observation can be made for the development of pore water pressure over strain, which decreases linearly (suction) until yielding. Upon yielding the pore water pressure changes abruptly to approach the pore pressure of the critical state. The effective stress path for heavily over-consolidated soils is discontinuous consisting a strain line under the yield surface and a subsequent segment leading to the critical state. Our model shows improvements across the board. The stress–strain, pore pressure–strain and the effective stress path are smooth. The hypoplastic model does not make use of the yield surface nor the hardening rule, which might be an advantage for numerical implementation.

Appendix

The constitutive model is formulated as:

$$\begin{aligned} \mathring{\mathbf{T}}&=C_1\text{tr}(\mathbf{T} +\mathbf{S} )\mathbf{D} + C_2\text{tr}{} \mathbf{D} (\mathbf{T} +\mathbf{S} )+ C_3\frac{\text{tr}(\mathbf{T} {} \mathbf{D} +\mathbf{S} {} \mathbf{D} )}{\text{tr}(\mathbf{T} +\mathbf{S} )}(\mathbf{T} +\mathbf{S} )\\&\quad +f_uC_4(\mathbf{T} -\mathbf{S} +\mathbf{T} ^{*}-\mathbf{S} ^{*})\Vert \mathbf{D} \Vert \end{aligned}$$

(A1)

where the structure tensor $\mathbf{S}$ is expressed as:

$$\begin{aligned} \mathbf{S} =\alpha \text{ln}\left( \frac{1}{R}\right) \mathbf{T} \end{aligned}$$

(A2)

with the stress ratio R defined as

$$\begin{aligned} R= \left( p+\frac{q^2}{M^2p}\right) \text{exp}\left[ \frac{\text{ln} (1+e)-N}{\lambda ^*}\right] \end{aligned}$$

(A3)

The multiplier $f_u$ is expressed as:

$$\begin{aligned} f_u=\frac{\Vert \mathbf{B} :\mathbf{D} \Vert }{\Vert \mathbf{B} \Vert \;\Vert \mathbf{D} \Vert } \end{aligned}$$

(A4)

In the proposed model, the material constants $C_i\,(i=1,2,3,4)$ can be determined by $E_i$, $\nu _i$, and $\phi _c$. The parameters N, $\lambda ^*$, and $\alpha$ are used to describe consolidation history. Since $E_i$ can be scaled by $\lambda ^*$, only five independent parameters are required.