1 Background, aim, and scope

In a seminal paper on uncertainty analysis in life cycle assessment (LCA), Heijungs (1996) discussed the issue of combining lower and upper values of LCA parameters to obtain an idea of the uncertainty range of LCA results. In fact, it was concluded that this was not a feasible approach for LCA systems of a sufficiently large size. The argument was that it cannot be predicted a priori if for a certain LCA parameter the lower or the upper value will produce the lowest LCA result. “This would imply that all combinations of upper and lower values must be tried in order to find the upper and lower values of the result. If there are 10,000 figures used as input data—a typical number for a mediocre LCI—the number of combinations is 210000, a number which amounts to a 1 with 3000 zeroes. A hopeless task: even for a computer that performs l09 operations per second, this would mean a calculation time that is considerably longer than the estimated age of the universe!” (Heijungs 1996, p. 160).

Although computers have shown a tremendous increase in performance since 1996, the argument of computation time still holds. The widely used ecoinvent (v2.0) has a technology matrix that contains 39,723 non-zero coefficients, and an intervention matrix with 85,317 non-zero coefficients. So, a gain of computation speed is offset by an increase in the size and complexity of the inventory system.

Since Heijungs' argument against using all combinations of upper and lower values, several developments can be seen:

  • Whenever uncertainty calculations are made in an LCA study, parameter variation for a restricted number of parameters and Monte Carlo analysis are the most popular approaches (see Lloyd and Ries 2007 for a review).

  • Analytical approaches, e.g., involving Taylor series expansion, are gaining ground (Heijungs 1996; Ciroth 2004; Hong et al. 2010).

  • Approaches using fuzzy uncertainty calculus have been made operational (Chevalier 1996; Ardente et al. 2004; Tan 2008).

The first two developments obviate the combination of all possibilities. Sampling approaches, of which the Monte Carlo is the most primitive example, are based on a probabilistic view of constructing an output distribution by means of repeated stochastic calculations. The number of runs typically taken is between 100 and 10,000, so far less than 210000. Moreover, the number of runs required does not necessarily depend on the number of input parameters; furthermore, Monte-Carlo-based approaches can be implemented relatively easily even with different probability distributions, or when probabilistic parameters exhibit correlations. The analytical approach is based on a formula by Gauss for the propagation of uncertainties in a first order Taylor approximation. Such an approximation is good enough for errors that are not excessive (Heijungs et al. 2005). Hong et al. (2010) state that the analytical approach is needed because the Monte Carlo approach is too demanding. Such claims are on the other hand denied by Peters (2007). But still, even with Peters' efficient algorithm, 210000 computations would be impossible.

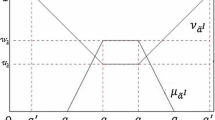
The third approach, using fuzzy uncertainty propagation, is based on the use of intervals, containing a lower and an upper value for so-called α-cuts (Tan 2008). A fuzzy number may be viewed as a family of nested intervals, each with a corresponding level of plausibility (denoted by Π) ranging from 0 to 1. For example, Fig. 1 shows a triangular fuzzy number with lower and upper limits of 5 and 20, respectively, and with most plausible value of 10. A horizontal slice through the fuzzy distribution at any Π = α gives an interval known as an α-cut. For example, it can be seen in this particular case that the intervals corresponding to α = 0, 0.4 and 1 are (5, 20), (7, 16), and (10, 10), respectively. For α = 0, the resulting α-cut is known as the support, while for α = 1 it is known as the core. Fuzzy arithmetic may be implemented by decomposing fuzzy arguments into α-cuts, performing interval arithmetic on corresponding α-cuts, and subsequently combining the resulting intervals into the final fuzzy result (Kaufmann and Gupta 1991). The accuracy of this procedure depends on the number of α-cuts used; a larger number of α-cuts give better resolution at the expense of increased computational effort.

Fig. 1
figure 1

Core, support, and α-cut of a triangular fuzzy number (Tan 2008)

Full size image

Fuzzy uncertainty calculations have the advantage that they require far less runs than a Monte Carlo approach. Tan's example uses 11 α-cuts, so with just 11 runs (or 22, if we want to make sure resource extractions are included properly as well), we can create a fairly good picture of the output uncertainty (see Tan 2008, Fig. 3). This is in stark contrast to the Monte Carlo approach, where it is for sure that a study with 11 or 22 runs will never be accepted.

In principle, in the fuzzy approach, one would still have to try all combinations of lower and upper values of the input parameters to compute the lower and upper values of the results as described by Heijungs (1996). However, Tan (2008, p. 588) bases his method on the implicit assumption that lower values in the technology matrix propagate as upper values of the LCI result, and vice versa.

This paper will address the question if this implicit assumption is valid. It will discuss the conditions under which we can be confident that lower values for the technology matrix combine to upper values for the inverse of the technology matrix, and vice versa.

2 Materials and methods

A brief description of the matrix-based LCI model is given here. More detailed discussion can be found in Heijungs and Suh (2002).

The flow of economic goods within the life cycle system is balanced such that the net system output corresponds to the functional unit:

$$ {\mathbf{As}} = {\mathbf{f}} $$
(1)

where A is the technology matrix, s is the scaling vector, and f is the functional unit vector. Rearranging Eq. (1) gives:

$$ {\mathbf{s}} = {{\mathbf{A}}^{ - 1}}{\mathbf{f}} $$
(2)

Likewise, the equation for balances of flows of resources and emissions of the life cycle is:

$$ {\mathbf{Bs}} = {\mathbf{g}} $$
(3)

where B is the intervention matrix and g is the inventory vector. Eqs. (2) and (3) may then be combined to give the generalized LCI model:

$$ {\mathbf{g}} = {\mathbf{B}}{{\mathbf{A}}^{ - 1}}{\mathbf{f}} $$
(4)

Every column in A or B represents a process within the life cycle system, each with a corresponding scaling factor in s. The elements of f and g correspond to specific economic goods (i.e., products and services) or environmental streams (i.e., emissions and resources). The convention used is that positive values in A, B, f, or g represent outflows, while negative values denote inflows (Heijungs and Suh 2002).

This basic model was then extended by Tan (2008) based on the work of Buckley (1989) to allow for computation with upper and lower limits of interval valued parameters. Assuming that the functional unit is specified precisely by a unique value, Eq. (2) can be modified to give:

$$ {{\mathbf{s}}_{L,\alpha }} = {\left( {{{\mathbf{A}}_{U,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(5)

and

$$ {{\mathbf{s}}_{U,\alpha }} = {\left( {{{\mathbf{A}}_{L,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(6)

where s U,α and s L,α are the upper and lower bounds of the scaling vector, respectively, and A U,α and A L,α are the upper and lower bounds of the technology matrix, respectively. These bounds represent the extreme values of the fuzzy parameters at any given α-cut. The fuzzy inventory results for emissions can then be found using:

$$ {{\mathbf{g}}_{E,L,\alpha }} = {{\mathbf{B}}_{E,L,\alpha }}{\left( {{{\mathbf{A}}_{U,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(7)

and

$$ {{\mathbf{g}}_{E,U,\alpha }} = {{\mathbf{B}}_{E,U,\alpha }}{\left( {{{\mathbf{A}}_{L,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(8)

where g E,U,α and g E,L,α are the upper and lower bounds of the emissions inventory vector, respectively, and B E,U,α and B E,L,α are the upper and lower bounds of the emissions intervention matrix, respectively. The fuzzy results for resource inputs need to be calculated separately using:

$$ {{\mathbf{g}}_{R,L,\alpha }} = {{\mathbf{B}}_{R,L,\alpha }}{\left( {{{\mathbf{A}}_{L,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(9)

and

$$ {{\mathbf{g}}_{R,U,\alpha }} = {{\mathbf{B}}_{R,U,\alpha }}{\left( {{{\mathbf{A}}_{U,\alpha }}} \right)^{ - 1}}{\mathbf{f}} $$
(10)

where g R,U,α and g R,L,α are the upper and lower bounds of the resources inventory vector, respectively, and B R,U,α and B R,L,α are the upper and lower bounds of the resources intervention matrix, respectively. Note that Eqs. (9) and (10) differ in structure from Eqs. (7) and (8). This change is due to the convention used where negative numbers indicate inflows of resources (Heijungs and Suh 2002; Tan 2008), so that the lower bounds actually indicate the larger flow magnitudes than the upper bounds. Since any given fuzzy LCI model can be decomposed into a family of nested interval models using α-cuts, the above equations need only to be repeated for the required resolution level. The final fuzzy inventory results can be determined by combining the interval results found using Eqs. (7–10).

Note that the validity of the fuzzy LCI model rests on Eqs. (5) and (6). The major question we now face is: can we prove that s L,α is obtained by inserting (a i,j ) U,α for all i, j, and likewise that s u,α is obtained by inserting (a i,j ) L,α ? This sounds trivial, as matrix inversion is a sort of division, and you get a low result when you divide by a high number and the other way around. But matrix inversion is not exactly the same as a simple division. It can be considered as a generalization of a division by a number to a division by a tableau of numbers simultaneously, and it is not a priori clear if indeed any higher coefficient in the technology matrix leads to a lower value of the scaling factors. To answer this question, we go to a formula that was proposed by Sherman and Morrison (1950). This formula gives the inverse of a matrix in case you have it for a matrix with one element different. So, suppose you have a matrix A with inverse A −1, and you change one element of A (say, a i,j ) by an amount \( \delta \). In other words, suppose A′ is given by

$$ {a\prime_{kl}} = \left\{ {\begin{array}{*{20}{c}} {{a_{kl}} + \delta } \hfill & {{\hbox{if }}i = k{\hbox{ and }}j = l} \hfill \\{{a_{kl}}} \hfill & {\hbox{otherwise}} \hfill \\\end{array} } \right. $$
(11)

Then the new (A)−1 becomes according to Sherman and Morrison

$$ {\left( {{{\left( {{\mathbf{A\prime}}} \right)}^{ - 1}}} \right)_{kl}} = {\left( {{{\mathbf{A}}^{ - 1}}} \right)_{kl}} - \frac{{{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ki}}{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{jl}}\delta }}{{1 + {{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ji}}\delta }} $$
(12)

The formula by Sherman and Morrison is valid for a change of one coefficient in a matrix, and there is no rule for what happens if two or more coefficients change at the same time. However, we can apply it successively in that case; see below.

How can we connect this formula to our problem? Suppose we have constructed the full matrix A and calculated its inverse A −1. Now, we concentrate on a certain parameter, say α ij , and take the upper value for a certain α-cut, (a ij ) U,α . This can be translated as setting \( {a\prime_{ij}} = {a_{ij}} + \delta \) with \( \delta \geqslant 0 \).

Now, Eq. (12) can be expressed as

$$ {\left( {{{\left( {{\mathbf{A\prime}}} \right)}^{ - 1}}} \right)_{kl}} = {\left( {{{\mathbf{A}}^{ - 1}}} \right)_{kl}} + \varepsilon $$
(13)

with

$$ \varepsilon = - \frac{{{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ki}}{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{jl}}\delta }}{{1 + {{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ji}}\delta }} $$
(14)

As \( \delta \geqslant 0 \), we find that \( \varepsilon \leqslant 0 \) whenever (A −1) rs   ≥  0 for all elements r, s. This condition is also known as that A −1 is a non-negative matrix, and it may be symbolized as A −1 ≥ 0. Note that it is a sufficient condition, but not a necessary one: we may think of a matrix A −1 with some elements negative, and still with \( \varepsilon \leqslant 0 \). The argument holds also true if we look at the lower value of a ij , (a ij ) L,α , in which case we find \( \varepsilon \geqslant 0 \).

A final issue to address is what happens if not just one element α ij of A changes into \( {a\prime_{ij}} = {a_{ij}} + \delta \), but when several or all elements change simultaneously. Let us consider what happens when we change α ij into \( {a\prime_{ij}} = {a_{ij}} + {\delta_{ij}} \) and α pq into \( {a\prime_{pq}} = {a_{pq}} + {\delta_{pq}} \). Recursive application of Eq. (13) gives

$$ {\left( {{{\left( {{\mathbf{A \prime\prime}}} \right)}^{ - 1}}} \right)_{kl}} = {\left( {{{\left( {{\mathbf{A \prime}}} \right)}^{ - 1}}} \right)_{kl}} + {\varepsilon_{pq}} = {\left( {{{\mathbf{A}}^{ - 1}}} \right)_{kl}} + {\varepsilon_{pq}} + {\varepsilon_{ij}} $$
(15)

with

$$ {\varepsilon_{ij}} = - \frac{{{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ki}}{{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{jl}}{\delta_{ij}}}}{{1 + {{\left( {{{\mathbf{A}}^{ - 1}}} \right)}_{ji}}{\delta_{ij}}}} $$
(16)

and

$$ {\varepsilon_{pq}} = - \frac{{{{\left( {{{\left( {{\mathbf{A\prime}}} \right)}^{ - 1}}} \right)}_{kp}}{{\left( {{{\left( {{\mathbf{A\prime}}} \right)}^{ - 1}}} \right)}_{ql}}{\delta_{pq}}}}{{1 + {{\left( {{{\left( {{\mathbf{A\prime}}} \right)}^{ - 1}}} \right)}_{qp}}{\delta_{pq}}}} $$
(17)

In other words, the argument and conditions apply equally well to a successive application of the formula by Sherman and Morrison.

3 Results

What does this mean? It means that we have found a condition (namely, A −1 ≥ 0) for which the lower value of any coefficient a ij leads to an upper value for A −1. In other words, Tan's (2008) Eqs. (5) and (6) are correct, provided A −1 ≥ 0.

4 Discussion

At this point, it is relevant to discuss the question if indeed A −1 ≥ 0, or the conditions in which it is or is not. In doing so, we have to explore the literature of the so-called inverse-positive matrices (Schröder 1961). An inverse-positive matrix A is a square invertible matrix that satisfies the above condition that all elements of the inverse are non-negative. Intuitively, inverse-positive matrices play an important role in many real-world systems (Fujimoto and Ranade 2004), as production volumes in an economic system and chemical concentrations in a chemical system are necessarily non-negative. So let us consider the case of LCA.

When the matrix A has a non-negative inverse, it means that for every conceivable (positive) functional unit vector f the scaling vector s is positive. In other words, it is not possible to obtain an s with one or more negative elements provided f ≥ 0. Like in input–output economics, where the Hawkins–Simon condition specifies a “feasible” economy (Hawkins and Simon 1949), we could interpret this as a “feasible” technology in the LCA case (Suh and Heijungs 2007). However, that is a step too fast for process-based LCA, where the data structure is crucially different from IOA. We mention the following issues:

  • IO tables are square by definition, while the technology matrix in LCA may be rectangular. Three important reasons are cut-off of remote processes, the presence of multifunctional processes, and the presence of products that are produced by two or more processes (Heijungs and Suh 2002, pp. 33–73).

  • One of the ways of dealing with multifunctional processes is by substitution (or system expansion), where “avoided processes” are introduced. Such processes will have negative scaling factors, a practice that is quite accepted in the LCA community. As a matter of fact, an avoided process can be interpreted as a case of a second process producing the same product which is displaced or made redundant by a multifunctional process (Heijungs and Suh 2002).

  • IO tables are symmetric, in the sense that the ordering of rows and columns is consistent. If row 5 represents steel production in an industry-by-industry table, so does column 5, and if row 5 represents steel in a product-by-product table, so does column 5. In a product-by-industry LCA table, this need not be the case; for instance, row 5 may well represent steel, while steel production is in column 17. Hence, unlike in IOA, the diagonal of the technology matrix has no special meaning in LCA (Heijungs et al. 2006).

  • In monetary IO tables, a positive number means a purchase of a product or service, even if the product itself has a negative price. In a physical set-up, as in most LCA tables, the production of waste can be represented as a physical output, along with the product. Thus, a required waste-processing for an activity is not necessarily represented as an input (negative in the I–A), but may show up as an output (positive) as well, keeping in mind that this is not a case of coproduction (Suh 2004).

Altogether, we come to formulate a number of transformation steps that will safeguard A for having the property of being inverse-positive, and hence suitable for efficient manipulation with fuzzy techniques:

  • The matrix must be made square, by removing cut-off flows, redefining products that are produced by more than one process, and allocating processes that produce more than one product. Avoided processes cannot be used to deal with multifunctionality, as these will by definition have negative scaling factors.

  • Physical waste flows, i.e., products with a negative economic value, must be converted into corresponding flows (in the opposite direction) of waste treatment services with a positive economic value. Hence a positive coefficient for a process producing waste turns into a negative coefficient for this process requiring a waste treatment service as an input. This service becomes the economic output of a waste treatment facility that receives the physical waste stream. In some databases (ecoinvent), this convention has already been adopted.

Observe that there is no need to make the table symmetric, and no need to normalize the output of each process to unity. Although Suh and Heijungs (2007) mention such requirements for the application of structural path analysis, they are for the present purpose of suitability for fuzzy methods sufficient, but not necessary.

A last nagging problem is that of the failure to use the approach in combination with avoided processes, in the context of the substitution method for dealing with multifunctional processes. As stated, the rigorous proof presumes that all processes operate in the “forward” direction, producing valuable output, not in the “reverse” direction, avoiding valuable output. This means that the efficient algorithm employing fuzzy uncertainty propagation is restricted to LCA studies that do not employ substitution. Is this a serious restriction, also given the upcoming consequential LCA? We think it is not. One main reason is that we should differentiate between substitution and system expansion, even though the two terms are often considered to be equivalent, and are sometimes even used as synonyms. As pointed out by Heijungs and Guineé (2007), system expansion adds functions to the system, so that in the alternatives with which it is compared, these functions are to be added as well. Therefore, the alternative systems contain extra processes that produce in the “forward” mode extra functions, with positive scaling factors. In contrast, substitution removes the extra function by introducing “avoided” processes, effectively adding processes in the “reverse” mode, with negative scaling factors for the “avoided” processes. The rigorous proof given does not work for LCA studies with substitution, but it works for LCA studies with system expansion. As a consequential LCA will relax certain ceteris paribus assumptions of standard LCA, we will always have a case where more functions are affected, and where scenarios of final demand and scenarios of processes are involved. This is compatible with the system expansion approach, and hence compliant with the conditions for efficient fuzzy error propagation stated in this paper.

5 Conclusions

This paper provides rigorous proof that the underlying assumptions used in the fuzzy matrix-based LCI approach of Tan (2008) are valid provided that A −1 ≥ 0. The argument is based on Sherman and Morrison's (1950) formula for calculating the value of the element of an inverted matrix, given a perturbation of the corresponding element in the original matrix. This proof thus allows for the computationally efficient propagation of parametric uncertainties in fuzzy matrix-based LCI models using decomposition with α-cuts for feasible life cycle systems without avoided processes, which by definition have negative scaling factors. We also provide guidelines for transformation of matrix A into a form that ensures that the LCI model is suited for rigorous fuzzy uncertainty propagation.