Quantifying the Uncertainty of Critical Resolved Shear Stress Values Derived from Nano-Indentation in Hexagonal Ti Alloys

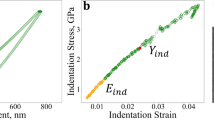
Abstract

Background

Inverse indentation analysis (IIA) optimizes the adjustable parameters in a chosen constitutive description of crystal plasticity until the load–depth response and the residual surface topography match between real and simulated nanoindentation into one (or multiple) grains. Based on synthetic data, past work demonstrated that initial critical resolved shear stress (CRSS) values of hexagonal crystals could be extracted with good reproducibility from indenting a single strategically chosen crystal orientation.

Objective

The goal of the present contribution is to more deeply assess the IIA method using measured (instead of synthetic) topography and load–depth data sets that were acquired for three different Ti alloys at ambient and elevated temperature, and fitted based on a size-independent phenomenological power-law constitutive description of crystal plasticity.

Methods

The uncertainties in measuring surface topography and load–depth response and the uncertainties resulting from choices made in the setup of the finite element indentation simulation are quantified and linked to the reliability of the ultimately identified CRSS values.

Results

Surface topography uncertainties largely outweigh those of the load–depth response. Optimization can be accelerated by upscaling of shallower indentation simulations but only to a limited degree, i.e., to about an upscaling factor of 2 to 3. The physical interpretation of identified CRSS values needs careful consideration of the effect of limited indentation depth.

Conclusions

The present work demonstrates that reliable identification of CRSS values is possible when the combined relative deviations in topography and load–depth response inherent in the actual indentation experiment and in the practical constraints of the corresponding simulations stay below around 20 %. Consequently, the applicability of the IIA method requires pre-assessment of the uncertainties outlined in this work to determine the feasibility of extracting constitutive parameters and their expected validity.

Appendices

Simulation Framework and Constitutive Model

Deformation Kinematics

The current model is formulated within a finite-strain framework and uses the multiplicative decomposition [23] of the total deformation gradient

$$\begin{aligned} \mathbf {F}&= \mathbf {F}_\text {e}\mathbf {F}_\text {p}\end{aligned}$$

(3)

into an elastic deformation gradient $\mathbf {F}_\text {e}$ and a plastic deformation gradient $\mathbf {F}_\text {p}$. The plastic deformation rate

$$\begin{aligned} \dot{\mathbf {F}}_\text {p}&= \mathbf {L}_\text {p}\mathbf {F}_\text {p}\end{aligned}$$

(4)

is related to plastic velocity gradient $\mathbf {L}_\text {p}$, which, in turn, is additively composed from slip rates on individual slip systems,

$$\begin{aligned} \mathbf {L}_\text {p}&= \sum _\alpha \dot{\gamma }^{\alpha } \mathbf {s}^\alpha \otimes \mathbf {n}^\alpha , \end{aligned}$$

(5)

where the unit vectors $\mathbf {s}^\alpha$ and $\mathbf {n}^\alpha$ are the slip direction and slip plane normal for slip system $\alpha = 1,2,3,\ldots ,N$. The shear stress resolved on a particular slip system $\alpha$ follows from Hooke’s law as

$$\begin{aligned} \tau ^\alpha&= \mathbb {C}\left( {\mathbf {F}_\text {e}}^{\text{ T }} \mathbf {F}_\text {e}-\mathbf {I}\right) /2 :\mathbf {s}^\alpha \otimes \mathbf {n}^\alpha . \end{aligned}$$

(6)

Phenomenological Power-Law Description

The shear rate

$$\begin{aligned} \dot{\gamma }^{\alpha }&= \dot{\gamma }^{}_0 \left| {\frac{\tau ^{\alpha }}{\xi ^{\alpha }}}\right| ^n \, {\text {sgn}} \left( \tau ^{\alpha } \right) \end{aligned}$$

(7)

is governed by the ratio between the corresponding resolved shear stress $\tau ^{\alpha }$ and slip resistance $\xi ^{\alpha }$ raised to a power $n$ (stress exponent). The slip resistance

$$\begin{aligned} \dot{\xi }^{\alpha }&= h_0\,\sum _{\beta } \left( 1 - \frac{\xi ^{\beta }}{\xi _\infty ^{\beta }} \right) ^a q^{\alpha \beta }\left| {\dot{\gamma }^{\beta }}\right| \end{aligned}$$

(8)

evolves from an initial value $\xi _0^{\alpha }$ asymptotically with shear accumulating on all slip systems, where $h_0$ is a prefactor, $a$ a fitting parameter, $q^{\alpha \beta }$ the cross-hardening matrix, and $\xi _\infty ^{\beta }$ reflects the asymptotic slip resistance of the family containing slip system $\beta$.

Experimental Data

Figures 7 and 8 collect the surface topography and load–depth response, respectively, of all indentations separated by material and indentation temperature.

Fig. 7

Surface topographies resulting from indentations at ambient temperature (left) and elevated temperature (right) for the three investigated Ti alloys (rows). Location of each topography on the inverse pole figure indicates the crystallographic indentation direction; in-plane rotation follows the convention of [24]. For each material–temperature combination, all indents labeled in color were individually subjected to inverse indentation analysis to establish CRSS values of basal, prismatic, and pyramidal $\langle {c+a}\rangle$ slip families. Samples are named according to their column and row in the performed indentation grid

Fig. 8

Increase of indenter force with depth up to maximum load (4, 6, or 10 mN) for all crystallographic indentation directions shown in Fig. 7. Corresponding simulations for IIA were performed up to indicated indentation depth and upscaled to colored target range (compare Fig. 3(b) and (e))