Inferring the Number of Attributes for the Exploratory DINA Model

Abstract

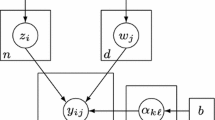
Diagnostic classification models (DCMs) are widely used for providing fine-grained classification of a multidimensional collection of discrete attributes. The application of DCMs requires the specification of the latent structure in what is known as the ${\varvec{Q}}$ matrix. Expert-specified ${\varvec{Q}}$ matrices might be biased and result in incorrect diagnostic classifications, so a critical issue is developing methods to estimate ${\varvec{Q}}$ in order to infer the relationship between latent attributes and items. Existing exploratory methods for estimating ${\varvec{Q}}$ must pre-specify the number of attributes, K. We present a Bayesian framework to jointly infer the number of attributes K and the elements of ${\varvec{Q}}$. We propose the crimp sampling algorithm to transit between different dimensions of K and estimate the underlying ${\varvec{Q}}$ and model parameters while enforcing model identifiability constraints. We also adapt the Indian buffet process and reversible-jump Markov chain Monte Carlo methods to estimate ${\varvec{Q}}$. We report evidence that the crimp sampler performs the best among the three methods. We apply the developed methodology to two data sets and discuss the implications of the findings for future research.

Appendices

Appendix A

Reversible Jump MCMC Algorithm

We use reversible jump MCMC to move between ${\varvec{Q}}$ matrices of different numbers of columns. With the probabilities for “birth” and “death” steps $b_K+d_K=1$, we have two possible moves:

• 1. Birth move: We propose $K\rightarrow K+1$ with probability $b_K$.

  To make our algorithm more efficient, we apply the collapsed Gibbs sampling (Liu 1994) by integrating ${\varvec{\alpha }}_i$ out:

  $$\begin{aligned} P({\varvec{Y}} \vert {\varvec{g}},{\varvec{s}},{\mathbf {Q}},{\varvec{\pi }},K)=\prod _{i=1}^{N} \sum _{{\varvec{\alpha }}_c \in \lbrace 0,1 \rbrace ^K}^{} \pi _c \prod _{j=1}^{J} P(Y_{ij}\vert s_j,g_j,{\varvec{\alpha }}_c, {\varvec{q}}_j), \end{aligned}$$

  so that we can skip the step of sampling ${\varvec{\alpha }}_i$. Following the steps described in Algorithm 4, let ${\varvec{Q}}_K=({\varvec{q}}_1,\ldots ,{\varvec{q}}_K)$, we propose the move from $\lbrace {\varvec{Q}}_K , {\varvec{\pi }},K \rbrace \rightarrow \lbrace {\varvec{Q}}_{K+1} , {\varvec{\pi }}^{*}, K+1\rbrace$, which is

  $$\begin{aligned} \left[ \begin{matrix} {\varvec{q}}_1 \\ \vdots \\ {\varvec{q}}_K \\ {\varvec{q}}_{K+1}\\ \pi _1\\ \vdots \\ \pi _C\\ u_1\\ \vdots \\ u_C\\ \end{matrix} \right] \rightarrow \left[ \begin{matrix} {\varvec{q}}_1 \\ \vdots \\ {\varvec{q}}_K \\ {\varvec{q}}_{K+1}\\ \pi _1^{*}\\ \vdots \\ \pi _C^{*}\\ \pi _{C+1}^{*}\\ \vdots \\ \pi _{2C}^{*}\\ \end{matrix} \right] . \end{aligned}$$

  (31)

  The RJ-MCMC acceptance ratio is

  $$\begin{aligned} A&=\dfrac{P({\varvec{Y}} \vert {\varvec{g}},{\varvec{s}},{\varvec{Q}}_{K+1},{\varvec{\pi }}^{*},K+1)}{P({\varvec{Y}} \vert {\varvec{g}},{\varvec{s}},{\varvec{Q}}_{K},{\varvec{\pi }},K)}\times \dfrac{P(K+1)P({\varvec{\pi }}^{*}\vert {\varvec{\delta }}_0^{*},K+1)P({\varvec{Q}}_{K+1}\vert K+1)}{P(K)P({\varvec{\pi }}\vert {\varvec{\delta }}_0,K)P({\varvec{Q}}_{K}\vert K)}\nonumber \\&\quad \times \dfrac{d_{K+1}\dfrac{1}{K+1}}{b_K \prod _{j=1}^{J}p(q_{j,K+1}|q_{1,K+1},\ldots ,q_{j-1,K+1})\prod _{i=1}^{C}p (u_i^{*})}\times \vert J\vert , \end{aligned}$$

  (32)

  where

  $$\begin{aligned} \dfrac{P({\varvec{\pi }}^{*}\vert {\varvec{\delta }}_0^{*},K+1)}{P({\varvec{\pi }}\vert {\varvec{\delta }}_0 ,K)}=\dfrac{\Gamma (2^{K+1})}{\Gamma (2^{K})}, \qquad ({\varvec{\delta }}_0={\varvec{1}}_{2^K}, {\varvec{\delta }}_0^{*}={\varvec{1}}_{2^{K+1}}), \end{aligned}$$

  and the Jacobian matrix J is

  $$\begin{aligned} \begin{aligned} \vert J \vert&= \left| \dfrac{\partial {\varvec{\pi }}^{*}}{\partial ({\varvec{\pi }},{\varvec{u}}^{*})} \right| \\ \\&= \begin{vmatrix}&\begin{pmatrix} u_1 &{} &{} &{} \\ &{} u_2 &{} &{} \\ &{} &{} \ddots &{}\\ &{} &{} &{} u_C\\ \end{pmatrix}&\begin{pmatrix} \pi _1 &{} &{} &{} \\ &{} \pi _2 &{} &{} \\ &{} &{} \ddots &{}\\ &{} &{} &{} \pi _C\\ \end{pmatrix}\\&\begin{pmatrix} 1-u_1 &{} &{} &{} \\ &{} 1-u_2 &{} &{} \\ &{} &{} \ddots &{}\\ &{} &{} &{} 1-u_C\\ \end{pmatrix}&\begin{pmatrix} -\pi _1 &{} &{} &{} \\ &{} -\pi _2 &{} &{} \\ &{} &{} \ddots &{}\\ &{} &{} &{} -\pi _C\\ \end{pmatrix}\\ \end{vmatrix}\\ \\&= \prod _{i=1}^{C}\pi _i. \end{aligned} \end{aligned}$$

  (33)

  The acceptance probability for the proposed birth move is min(1, A).

• 2. Death move: We propose $K\rightarrow K-1$ with probability $d_K$.

  We randomly select a column in ${\varvec{Q}}_K$ to delete. The acceptance probability is min$(1,A^{-1})$, where $A^{-1}$ can be computed in a similar way as Eq. 32.

Appendix B

Acceptance Ratio of Crimp Sampler

The crimp sampler moves between identifiable spaces with deterministic transformations of the model parameters. The posterior distribution of ${\varvec{\xi }}^{K}=({\varvec{Q}}_K,{\varvec{\pi }}_K,{\varvec{A}}_K,K)$ and ${\varvec{\Omega }}$ is

$$\begin{aligned} p({\varvec{A}}_K,{\varvec{\pi }}_K,{\varvec{Q}}_K,K,{\varvec{\Omega }}|{\varvec{Y}})\propto p({\varvec{A}}_K,{\varvec{\pi }}_K,{\varvec{Q}}_K,K|{\varvec{Y}},{\varvec{\Omega }})p({\varvec{\Omega }}), \end{aligned}$$

(34)

where

$$\begin{aligned} p({\varvec{A}}_K,{\varvec{\pi }}_K,{\varvec{Q}}_K,K|{\varvec{Y}},{\varvec{\Omega }})&\propto p({\varvec{Y}}|{\varvec{A}}_K, {\varvec{\Omega }},{\varvec{Q}}_K)p({\varvec{A}}_K|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)p({\varvec{Q}}_K,K)\nonumber \\&\propto p({\varvec{A}}_K,{\varvec{\pi }}|{\varvec{Y}},{\varvec{\Omega }},{\varvec{Q}}_K)p({\varvec{Q}}_K,K). \end{aligned}$$

(35)

Let ${\varvec{u}}=(u_0,\ldots ,u_{2^K-1})$ be a vector of independent random variables. The conditional posterior of ${\varvec{\xi }}^K$ and ${\varvec{u}}$ is

$$\begin{aligned} p({\varvec{A}}_K,{\varvec{\pi }}_K,{\varvec{u}},{\varvec{Q}}_K,K|{\varvec{Y}},{\varvec{\Omega }})\propto p({\varvec{A}}_K,{\varvec{\pi }}_K|{\varvec{Y}},{\varvec{\Omega }},{\varvec{Q}}_K)p({\varvec{Q}}_K,K)p({\varvec{u}}). \end{aligned}$$

(36)

Note that for ${\varvec{\pi }}_K\sim \text {Dirichlet}({\varvec{d}}_K)$ where ${\varvec{d}}_K=(d_0,\ldots ,d_{2^K-1})$,

$$\begin{aligned} p({\varvec{A}}_K|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)=C_K \prod _{c=0}^{2^K-1}\pi _{c}^{n_c+d_c-1}, \end{aligned}$$

(37)

where $n_c$ is the number of respondents in class c and the normalizing constant is

$$\begin{aligned} C_K=\frac{\Gamma (\sum _{c=0}^{2^K-1}d_c)}{\prod _{c=0}^{2^K-1}\Gamma (d_c)}. \end{aligned}$$

(38)

Moves from $K\rightarrow K+1$ involve transiting from ${\varvec{\xi }}^K=({\varvec{A}}_K,{\varvec{\pi }}_K,{\varvec{Q}}_K,K,{\varvec{u}})\rightarrow$ ${\varvec{\xi }}^{K+1}=({\varvec{A}}_{K+1},{\varvec{\pi }}_{K+1},{\varvec{Q}}_{K+1},K+1)$. That is, the move to a higher dimension involves a transformation of ${\varvec{\pi }}_K$ and ${\varvec{u}}$ into ${\varvec{\pi }}_{K+1}$. Specifically, let

$$\begin{aligned} \pi _{c0}&= \pi _c(1-u_c),\nonumber \\ \pi _{c1}&= \pi _c u_c, \end{aligned}$$

(39)

where $\pi _{c0}$ and $\pi _{c1}$ are elements of ${\varvec{\pi }}_{K+1}$ for $c=0,\ldots ,2^K-1$. Note the Jacobian of transformation equals $|J|=\prod _{c=0}^{2^K-1} (\pi _{c0}+\pi _{c1})^{-1}$.

Let ${\varvec{a}}_{K+1}=(\alpha _{1,K+1},\ldots ,\alpha _{N,K+1})^\top$ be an N vector of the proposed $K+1$ binary attributes. The full conditional distribution for the proposed $K+1$ state prior to transformation is

$$\begin{aligned} p&({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}},{\varvec{Q}}_{K+1},K+1|{\varvec{Y}},{\varvec{\Omega }})\nonumber \\&\propto p({\varvec{Y}}|{\varvec{A}}_K,{\varvec{a}}_{K+1},{\varvec{\Omega }},{\varvec{Q}}_{K+1})p({\varvec{a}}_{K+1}|{\varvec{A}}_K,{\varvec{u}})p({\varvec{A}}_K|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)p({\varvec{u}})p({\varvec{Q}}_{K+1},K+1), \end{aligned}$$

(40)

where $p({\varvec{a}}_{K+1}|{\varvec{A}}_K,{\varvec{u}})=\prod _{i=1}^n\sum _{c=0}^{2^K-1}{\mathcal {I}}({\varvec{\alpha }}_i^\top {\varvec{v}}=c)\left( u_c^{\alpha _{i,K+1}}(1-u_c)^{1-\alpha _{i,K+1}}\right)$.

Let $u_c\sim \text {Beta}(1,1)$ for $c=0,\ldots ,2^K-1$ and consider ${\varvec{d}}={\varvec{1}}_{2^K}$. The conditional prior distribution of ${\varvec{a}}_{K+1}$, ${\varvec{A}}_K$, ${\varvec{\pi }}_K$, and ${\varvec{u}}$ given ${\varvec{Q}}_{K+1}$ is

$$\begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}})\propto \left( \prod _{c=0}^{2^K-1} u_c^{n_{c1}}(1-u_c)^{n_{c0}}\right) C_K \prod _{c=0}^{2^K-1}\pi _{c}^{n_c+d_c-1}, \end{aligned}$$

(41)

where $n_{c0}+n_{c1}=n_{c}$, $n_{c0}$ is the number of individuals in class c (for attributes 1 to K) with attribute $K+1$ equal to 0, and $n_{c1}$ corresponds to the number of individuals in class c with attribute $K+1$ equal to 1. Applying the transformation implies

$$\begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_{K+1})&\propto C_K \prod _{c=0}^{2^K-1} \left( \frac{\pi _{c1}}{\pi _{c0}+\pi _{c1}}\right) ^{n_{c1}} \left( \frac{\pi _{c0}}{\pi _{c0}+\pi _{c1}}\right) ^{n_{c0}} \left( \pi _{c0}+\pi _{c1}\right) ^{n_c} \times |J_c|\nonumber \\&= C_K \prod _{c=0}^{2^K-1} \pi _{c1}^{n_{c1}}\pi _{c0}^{n_{c0}} \left( \pi _{c0}+\pi _{c1}\right) ^{-1}. \end{aligned}$$

(42)

The transformed conditional posterior distribution is therefore

$$\begin{aligned} p&({\varvec{A}}_{K+1},{\varvec{\pi }}_{K+1},{\varvec{Q}}_{K+1},K+1|{\varvec{Y}},{\varvec{\Omega }})\nonumber \\&\propto p({\varvec{Y}}|{\varvec{A}}_{K+1},{\varvec{\Omega }},{\varvec{Q}}_{K+1})p({\varvec{A}}_{K+1},{\varvec{\pi }}_{K+1})p({\varvec{Q}}_{K+1},K+1), \end{aligned}$$

(43)

where ${\varvec{A}}_{K+1}=({\varvec{A}}_{K},{\varvec{a}}_{K+1})$.

The transformed posterior for ${\varvec{\xi }}^{K+1}$ requires we propose values for ${\varvec{a}}_{K+1}$ and the $2^K$ ${\varvec{u}}$, which form the additional elements of ${\varvec{\pi }}_{K+1}$ (in fact, RJ-MCMC transitions between spaces this way). Proposals for these parameters must be carefully constructed to ensure proper mixing and acceptance rates. Rather than proposing values we integrate out ${\varvec{a}}_{K+1}$ and ${\varvec{u}}$. That is, we implement the inverse transformations

$$\begin{aligned} \pi _c&=\pi _{c0}+\pi _{c1},\nonumber \\ u_c&=\frac{\pi _{c1}}{\pi _{c0}+\pi _{c1}}, \end{aligned}$$

(44)

sum over ${\varvec{a}}_{K+1}$, and integrate out ${\varvec{u}}$ to find,

$$\begin{aligned}&p({\varvec{A}}_{K},{\varvec{\pi }}_K,{\varvec{Q}}_{K+1},K+1|{\varvec{Y}},{\varvec{\Omega }})\nonumber \\ \propto&\int \sum _{\alpha _{1,K+1}=0}^1\cdots \sum _{\alpha _{N,K+1}=0}^1 p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}},{\varvec{Q}}_{K+1},K+1|{\varvec{Y}},{\varvec{\Omega }}) {\varvec{d}}{\varvec{u}}\nonumber \\ =&\left\{ \int \left[ \prod _{i=1}^N \sum _{\alpha _{i,K+1}=0}^1 p({\varvec{Y}}_i|{\varvec{\alpha }}_i,\alpha _{i,K+1},{\varvec{\Omega }},{\varvec{Q}}_{K+1})p(\alpha _{i,K+1}|{\varvec{u}}, {\varvec{\alpha }}_i)\right] p({\varvec{u}}){\varvec{d}}{\varvec{u}}\right\} \nonumber \\&\times p({\varvec{A}}_{K}|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)p({\varvec{Q}}_{K+1},K+1) \nonumber \\ =&p({\varvec{Y}}|{\varvec{A}}_K,{\varvec{\Omega }},{\varvec{Q}}_{K+1})p({\varvec{A}}_{K}|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)p({\varvec{Q}}_{K+1},K+1). \end{aligned}$$

(45)

Therefore, for $K\rightarrow K+1$, with the uniform prior for ${\varvec{Q}}_K$ and K, all terms but the likelihood functions will cancel out in the MH acceptance ratio, i.e.,

$$\begin{aligned} \frac{p({\varvec{Q}}^*_{K+1}|{\varvec{A}}_{K},{\varvec{\pi }}_K,{\varvec{\Omega }},{\varvec{Y}})}{ p({\varvec{Q}}_K|{\varvec{A}}_{K},{\varvec{\pi }}_K,{\varvec{\Omega }},{\varvec{Y}})}=\frac{p({\varvec{Y}}|{\varvec{A}}_{K},{\varvec{\Omega }},{\varvec{Q}}^*_{K+1})}{ p({\varvec{Y}}|{\varvec{A}}_{K},{\varvec{\Omega }},{\varvec{Q}}_K)}. \end{aligned}$$

(46)

Transitions to lower dimensions involve a move from ${\varvec{\xi }}^K\rightarrow$ ${\varvec{\xi }}^{K-1}=({\varvec{A}}_{K-1},{\varvec{\pi }}_{K-1},{\varvec{Q}}_{K-1},K-1)$. Without loss of generality, suppose the Kth attribute is proposed to be deleted. Therefore, ${\varvec{\alpha }}_i=(\tilde{{\varvec{\alpha }}}_i^\top ,\alpha _{iK})^\top$ and ${\varvec{A}}_{K-1}=(\tilde{{\varvec{\alpha }}}_1,\ldots ,\tilde{{\varvec{\alpha }}}_N)^\top$.

An important observation is that deleting a column of ${\varvec{Q}}$ implies an attribute is no longer related to observed responses, which implies

$$\begin{aligned} p({\varvec{Y}}_i|\tilde{{\varvec{\alpha }}}_i,\alpha _{iK}=0,{\varvec{\Omega }},Q_{K-1})=p({\varvec{Y}}_i|\tilde{{\varvec{\alpha }}}_i,\alpha _{iK}=1,{\varvec{\Omega }},Q_{K-1}). \end{aligned}$$

(47)

The conditional posterior after summing over ${\varvec{a}}_K$ is

$$\begin{aligned} p&({\varvec{A}}_{K-1},{\varvec{\pi }}_K,{\varvec{Q}}_{K-1},K-1|{\varvec{Y}},{\varvec{\Omega }})\nonumber \\&\propto \left[ \prod _{i=1}^N \sum _{\alpha _{iK}=0}^1 p({\varvec{Y}}_i| \tilde{{\varvec{\alpha }}}_i,\alpha _{iK},{\varvec{\Omega }},{\varvec{Q}}_{K-1})p({\varvec{\alpha }}_i| {\varvec{\pi }}_K)\right] p({\varvec{\pi }}_K)p({\varvec{Q}}_{K-1},K-1) \nonumber \\&= \left[ \prod _{i=1}^N p({\varvec{Y}}_i|{\varvec{\alpha }}_i,{\varvec{\Omega }},{\varvec{Q}}_{K-1}) \sum _{\alpha _{iK}=0}^1 p({\varvec{\alpha }}_i|{\varvec{\pi }}_K)\right] p({\varvec{\pi }}_K)p({\varvec{Q}}_{K-1},K-1) \nonumber \\&=p({\varvec{Y}}|{\varvec{A}}_{K-1},{\varvec{\Omega }},{\varvec{Q}}_{K-1})p({\varvec{A}}_{K-1}|{\varvec{\pi }}_K)p({\varvec{\pi }}_K)p({\varvec{Q}}_{K-1},K-1), \end{aligned}$$

(48)

where

$$\begin{aligned} p({\varvec{A}}_{K-1}|{\varvec{\pi }}_K)=\prod _{c=0}^{2^{K-1}-1}\left( \pi _{c0}+\pi _{c1}\right) ^{n_c} \end{aligned}$$

(49)

and $n_c$ is the number of individuals in the collapsed class c. The joint conditional prior for ${\varvec{A}}_{K-1}$ and ${\varvec{\pi }}_K$ is

$$\begin{aligned} p({\varvec{A}}_{K-1},{\varvec{\pi }}_{K})=p({\varvec{A}}_{K-1}|{\varvec{\pi }}_{K})p({\varvec{\pi }}_{K})=\left( \prod _{c=0}^{2^{K-1}-1}(\pi _{c0}+\pi _{c1})^{n_c}\right) \left( C_K \prod _{c=0}^{2^{K-1}-1}\pi _{c0}^{d_{c0}-1}\pi _{c1}^{d_{c1}-1}\right) .\nonumber \\ \end{aligned}$$

(50)

We then transform ${\varvec{\pi }}_K$ by defining

$$\begin{aligned} \pi _c&=\pi _{c0}+\pi _{c1},\nonumber \\ u_c&=\frac{\pi _{c1}}{\pi _{c0}+\pi _{c1}}, \end{aligned}$$

(51)

for $c=0,\ldots ,2^{K-1}-1$ where $\pi _c$ is an element of ${\varvec{\pi }}_{K-1}$. The transformation implies

$$\begin{aligned} p({\varvec{A}}_{K-1},{\varvec{u}},{\varvec{\pi }}_{K-1})&=\left( \prod _{c=0}^{2^{K-1}-1}\pi _{c}^{n_c}\right) \left( C_K \prod _{c=0}^{2^{K-1}-1} \pi _c^{d_{c1}+d_{c0}-2}u_c^{d_{c1}-1}(1-u_c)^{d_{c0}-1}\right) |J|^{-1}\nonumber \\&=C_K\left( \prod _{c=0}^{2^{K-1}-1}\pi _{c}^{n_c+d_{c0}+d_{c1}-1}\right) \left( \prod _{c=0}^{2^{K-1}-1}u_c^{d_{c1}-1}(1-u_c)^{d_{c0}-1}\right) \nonumber \\&=p({\varvec{A}}_{K-1}|{\varvec{\pi }}_{K-1})p({\varvec{\pi }}_{K-1})p({\varvec{u}}). \end{aligned}$$

(52)

Therefore, integrating over ${\varvec{u}}$ yields

$$\begin{aligned}&p({\varvec{A}}_{K-1},{\varvec{\pi }}_{K-1},{\varvec{Q}}_{K-1},K-1|{\varvec{Y}},{\varvec{\Omega }})\nonumber \\ \propto&\int p({\varvec{A}}_{K-1},{\varvec{\pi }}_{K-1},{\varvec{u}},{\varvec{Q}}_{K-1},K-1|{\varvec{Y}},{\varvec{\Omega }}) {\varvec{d}}{\varvec{u}}\nonumber \\ =&p({\varvec{Y}}|{\varvec{A}}_{K-1},{\varvec{\Omega }},{\varvec{Q}}_{K-1})p({\varvec{A}}_{K-1}|{\varvec{\pi }}_{K-1}) p({\varvec{\pi }}_{K-1})p({\varvec{Q}}_{K-1},K-1) \int p({\varvec{u}}) {\varvec{d}}{\varvec{u}}, \end{aligned}$$

(53)

where

$$\begin{aligned} \int p({\varvec{u}}) {\varvec{d}}{\varvec{u}} =\prod _{c=0}^{2^{K-1}-1}\int u_c^{d_{c1}-1}(1-u_c)^{d_{c0}-1} d u_c=\prod _{c=0}^{2^{K-1}-1} \text {Beta}(d_{c0},d_{c1}). \end{aligned}$$

(54)

If the prior for ${\varvec{\pi }}_K\sim \text {Dirichlet}({\varvec{1}}_{2^K})$, then the integral is one. Since we use the uniform prior of $p({\varvec{Q}},K)$, the acceptance ratio becomes

$$\begin{aligned} \frac{p({\varvec{Q}}^*_{K-1}|{\varvec{A}}_{K},{\varvec{\pi }}_K,{\varvec{\Omega }},{\varvec{Y}})}{ p({\varvec{Q}}_K|{\varvec{A}}_{K},{\varvec{\pi }}_K,{\varvec{\Omega }},{\varvec{Y}})}=\frac{p({\varvec{Y}}|{\varvec{A}}_{K-1},{\varvec{\Omega }},{\varvec{Q}}^*_{K-1})\left( \prod _{c=0}^{2^{K-1}-1}{\pi _{c}}^{n_{c}+1}\right) }{ p({\varvec{Y}}|{\varvec{A}}_{K},{\varvec{\Omega }},{\varvec{Q}}_K)\left( \prod _{c=0}^{2^{K-1}-1}\pi _{c1}^{n_{c1}}\pi _{c0}^{n_{c0}}\right) }. \end{aligned}$$

(55)

Appendix C

Gibbs Sampling Step for Updating ${\varvec{\alpha }}$ in Crimp Sampler

The conditional posterior distribution of ${\varvec{a}}_{K+1}$, ${\varvec{A}}_K$, ${\varvec{\pi }}_K$, and ${\varvec{u}}$ is

$$\begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}}\vert {\varvec{Y}},{\varvec{\Omega }},{\varvec{Q}}_{K+1})\propto p({\varvec{Y}} \vert {\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\Omega }},{\varvec{Q}}_{K+1})\cdot p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}}); \end{aligned}$$

(56)

then, the marginal posterior of ${\varvec{a}}_{K+1}$ and ${\varvec{A}}_K$ is

$$\begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1}\vert {\varvec{Y}},{\varvec{\Omega }},{\varvec{Q}}_{K+1})\propto p({\varvec{Y}} \vert {\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\Omega }},{\varvec{Q}}_{K+1})\cdot \int \int p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}})d{\varvec{\pi }}_K d{\varvec{u}}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1},{\varvec{\pi }}_K,{\varvec{u}})&=p({\varvec{A}}_{K} \vert {\varvec{\pi }}_K)\cdot p({\varvec{\pi }}_K)\cdot p({\varvec{u}})\cdot p({\varvec{a}}_{K+1} \vert {\varvec{A}}_K,{\varvec{u}})\\&\propto \left( \prod _{c=0}^{2^K-1} u_c^{n_{c1}}(1-u_c)^{n_{c0}}\right) \prod _{c=0}^{2^K-1}\pi _{c}^{n_c+d_c-1}. \end{aligned} \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{aligned} p({\varvec{A}}_{K},{\varvec{a}}_{K+1})&\propto \int \left( \prod _{c=0}^{2^K-1} u_c^{n_{c1}}(1-u_c)^{n_{c0}}\right) d {\varvec{u}} \int \left( \prod _{c=0}^{2^K-1}\pi _{c}^{n_c+d_c-1}\right) d{\varvec{\pi }}_K\\&\propto \left( \prod _{c=0}^{2^K-1} B(n_{c1}+1,n_{c0}+1 ) \right) \cdot \dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_c+1)}{\Gamma (N+2^K)}. \end{aligned} \end{aligned}$$

(57)

Let $n_c^{\prime }$ be the number of individuals other than i with K attributes equal to ${\varvec{\alpha }}_c$, and let $n_{c0}^{\prime }$ and $n_{c1}^{\prime }$ be the number of such individuals with $\alpha _{c,K+1}=0$ and $\alpha _{c,K+1}=1$, respectively. So $n_c^{\prime }=n_{c0}^{\prime } + n_{c1}^{\prime }$. That is,

$$\begin{aligned} \begin{aligned} n_c&=n_c^{\prime }+{\mathcal {I}} ({\varvec{\alpha }}_i^\top {\varvec{v}}=c), \\ n_{c0}&=n_{c0}^{\prime }+(1-\alpha _{i,K+1}) {\mathcal {I}} ({\varvec{\alpha }}_i^\top {\varvec{v}}=c), \\ n_{c1}&=n_{c1}^{\prime }+\alpha _{i,K+1} {\mathcal {I}} ({\varvec{\alpha }}_i^\top {\varvec{v}}=c). \end{aligned} \end{aligned}$$

Recall the following properties for the beta and gamma functions:

$$\begin{aligned} \begin{aligned} B(x+1,y)&=B(x,y)\cdot \dfrac{x}{x+y},\\ B(x,y+1)&=B(x,y)\cdot \dfrac{y}{x+y},\\ \Gamma (x+1)&=x\cdot \Gamma (x). \end{aligned} \end{aligned}$$

Then, Eq. 57 can be written as:

$$\begin{aligned}&p( {\varvec{\alpha }}_1,\ldots , {\varvec{\alpha }}_N, \alpha _{1,K+1},\ldots ,\alpha _{N,K+1})\propto \nonumber \\&\Bigg (\prod _{c=0}^{2^K-1} B(n_{c1}^{\prime }+\alpha _{i,K+1} {\mathcal {I}} ({\varvec{\alpha }}_i^\top {\varvec{v}}=c)+1,\Bigg .\Bigg .n_{c0}^{\prime }+(1-\alpha _{i,K+1}) {\mathcal {I}} ({\varvec{\alpha }}_i^\top {\varvec{v}}=c)+1 ) \Bigg ) \cdot \dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_c+1)}{\Gamma (N+2^K)}. \end{aligned}$$

(58)

Let ${\varvec{A}}_{(i)}=({\varvec{\alpha }}_1,\ldots , {\varvec{\alpha }}_{i-1},{\varvec{\alpha }}_{i+1},\ldots ,{\varvec{\alpha }}_N)$ and ${\varvec{\alpha }}_{(i),K+1}=(a_{1,K+1},\ldots ,\alpha _{i-1,K+1},\alpha _{i+1,K+1}, \cdots ,a_{N,K+1})$. By integrating out ${\varvec{\alpha }}_i$ and $\alpha _{i,K+1}$, we have

$$\begin{aligned}&p({\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1})=\nonumber \\&\sum _{c=0}^{2^K-1} \left[ p({\varvec{\alpha }}_i^\top {\varvec{v}}=c,\alpha _{i,K+1}=0, {\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1} ) +p(\alpha _i^\top {\varvec{v}}=c, \alpha _{i,K+1}=1, {\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1} ) \right] . \end{aligned}$$

(59)

Note that

$$\begin{aligned} B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+2 )&=\dfrac{n_{c0}^{\prime }+1}{n_{c}^{\prime } +2}B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1 ),\\ B(n_{c1}^{\prime }+2,n_{c0}^{\prime }+1 )&=\dfrac{n_{c1}^{\prime }+1}{n_{c}^{\prime } +2}B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1 ),\\ \Gamma (n_c^{\prime }+2)&=(n_c'+1)\Gamma (n_c^{\prime }+1), \end{aligned}$$

which implies

$$\begin{aligned}&p(\alpha _i^\top {\varvec{v}}=c,\alpha _{i,K+1}=0, {\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1} ) \nonumber \\ =&\dfrac{n_{c0}^{\prime }+1}{n_{c}^{\prime }+2} \left( \prod _{c=0}^{2^K-1} B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1 ) \right) \cdot \dfrac{(n_c^{\prime }+1) \prod _{c=0}^{2^K-1} \Gamma (n_c^{\prime }+1)}{\Gamma (N+2^K)}, \end{aligned}$$

and

$$\begin{aligned}&p(\alpha _i^\top {\varvec{v}}=c,\alpha _{i,K+1}=1, {\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1} ) \nonumber \\ =&\dfrac{n_{c1}^{\prime }+1}{n_{c}^{\prime }+2} \left( \prod _{c=0}^{2^K-1} B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1 ) \right) \cdot \dfrac{(n_c^{\prime }+1) \prod _{c=0}^{2^K-1} \Gamma (n_c^{\prime }+1)}{\Gamma (N+2^K)}. \end{aligned}$$

Then, Eq. 59 should be

$$\begin{aligned} \begin{aligned} p({\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1})&=\left( \prod _{c=0}^{2^K-1} B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1) \right) \cdot \dfrac{ \prod _{c=0}^{2^K-1} \Gamma (n_c^{\prime }+1)}{\Gamma (N+2^K)} \left( \sum _{c=0}^{2^K-1}(n_c^{\prime }+1) \right) \\&=\left( \prod _{c=0}^{2^K-1} B(n_{c1}^{\prime }+1,n_{c0}^{\prime }+1 ) \right) \cdot \dfrac{ \prod _{c=0}^{2^K-1} \Gamma (n_c^{\prime }+1)}{\Gamma (N+2^K-1)}. \end{aligned} \end{aligned}$$

(60)

Therefore, the full conditional distribution for ${\varvec{\alpha }}_i^\top {\varvec{v}}=c$ and $\alpha _{i,K+1}=1$ is

$$\begin{aligned} \begin{aligned} p({\varvec{\alpha }}_i^\top {\varvec{v}}=c,\alpha _{i,K+1}+1\vert {\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1} )&=\dfrac{p({\varvec{\alpha }}_i^\top {\varvec{v}}=c,\alpha _{i,K+1}+1,{\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1})}{p({\varvec{A}}_{(i)},{\varvec{\alpha }}_{(i),K+1})}\\&=\dfrac{n_{c1}^{\prime }+1}{n_{c}^{\prime }+2}\cdot \dfrac{n_{c}^{\prime }+1}{N+2^K-1}. \end{aligned} \end{aligned}$$

(61)

In order to update $\alpha _{i,K+1}$ sequentially, we need to find

$$\begin{aligned} p({\varvec{\alpha }}_i,\alpha _{i,K+1}\vert {\varvec{A}}_{(i)},\alpha _{1,K+1},\ldots ,\alpha _{i-1,K+1}) =\dfrac{p({\varvec{A}}_{K}, \alpha _{1,K+1},\ldots ,\alpha _{i,K+1})}{p({\varvec{A}}_{(i)},\alpha _{1,K+1},\ldots ,\alpha _{i-1,K+1})}. \end{aligned}$$

(62)

The probability in the numerator is calculated by summing Eq. 57 over $\alpha _{i+1,K+1},\ldots ,\alpha _{N,K+1}$:

$$\begin{aligned}&p({\varvec{A}}_K, a_{1,K+1},\ldots ,a_{i,K+1})\nonumber \\ =&\sum _{\alpha _{i+1,K+1}=0}^1 \ldots \sum _{\alpha _{N,K+1}=0}^1 p({\varvec{A}}_{K}, {\varvec{a}}_{K+1})\nonumber \\ =&\dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_{c,N}+1)}{\Gamma (N+2^K)} \cdot \sum _{\alpha _{i+1,K+1}=0}^1 \ldots \sum _{\alpha _{N,K+1}=0}^1 \left( \prod _{c=0}^{2^K-1} B(n_{c1,N}+1,n_{c0,N}+1 )\right) . \end{aligned}$$

(63)

Given that

$$\begin{aligned} n_{c,N}=&n_{c,N-1}+{\mathcal {I}}({\varvec{\alpha }}_N^\top {\varvec{v}}=c), \\ n_{c1,N}=&n_{c1,N-1}+\alpha _{N,K+1} \cdot {\mathcal {I}} ({\varvec{\alpha }}_N^\top {\varvec{v}}=c),\\ n_{c0,N}=&n_{c0,N-1}+(1-\alpha _{N,K+1}) \cdot {\mathcal {I}}({\varvec{\alpha }}_N^\top {\varvec{v}}=c), \end{aligned}$$

we have

$$\begin{aligned}&\sum _{\alpha _{N,K+1}=0}^1 \left( \prod _{c=0}^{2^K-1} B(n_{c1,N}+1,n_{c0,N}+1 ) \right) \\&=\prod _{c=0}^{2^K-1} B(n_{c1,N-1}+1,n_{c0,N-1}+{\mathcal {I}} ({\varvec{\alpha }}_N^\top {\varvec{v}}=c)+1 ) +\prod _{c=0}^{2^K-1} B(n_{c1,N-1}+{\mathcal {I}} ({\varvec{\alpha }}_N^\top {\varvec{v}}=c)+1,n_{c0,N-1}+1 ) \\&=\left[ \prod _{c=0}^{2^K-1} B(n_{c1,N-1}+1,n_{c0,N-1}+1 )\right] \left( \frac{n_{c0,N-1} +1}{n_{c1,N-1}+n_{c0,N-1}+2}+\frac{n_{c1,N-1}+1}{n_{c1,N-1}+n_{c0,N-1}+2}\right) \\&=\prod _{c=0}^{2^K-1} B(n_{c1,N-1}+1,n_{c0,N-1}+1 ). \end{aligned}$$

Therefore, Eq. 63 can be written as:

$$\begin{aligned} p({\varvec{A}}_K, \alpha _{1,K+1},\ldots ,\alpha _{i,K+1})=\dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_{c,N}+1)}{\Gamma (N+2^K)} \cdot \prod _{c=0}^{2^K-1} B(n_{c1,i}+1,n_{c0,i}+1 ). \end{aligned}$$

(64)

For the probability in the denominator,

$$\begin{aligned}&p({\varvec{A}}_{(i)},\alpha _{1,K+1},\ldots ,\alpha _{i-1,K+1})\nonumber \\ =&\sum _{{\varvec{\alpha }}_i^\top {\varvec{v}}=c^*=0}^{2^K-1}\sum _{\alpha _{i-1,K+1}=0}^1 p({\varvec{A}}_K, \alpha _{1,K+1},\ldots ,\alpha _{i,K+1})\nonumber \\ =&\sum _{c^*=0}^{2^K-1} \left[ \dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_{c,N}+1)}{\Gamma (N+2^K)} \cdot \prod _{c=0}^{2^K-1} B(n_{c1,i-1}+1,n_{c0,i-1}+1 ) \right] \nonumber \\ =&\dfrac{ \prod _{c=0}^{2^K-1} B(n_{c1,i-1}+1,n_{c0,i-1}+1 )}{\Gamma (N+2^K)} \cdot \sum _{c^*=0}^{2^K-1} (n_{c^*,N}^{\prime }+1) \cdot \prod _{c=0}^{2^K-1} \Gamma (n_{c,N}^{\prime }+1)\nonumber \\ =&\left( \prod _{c=0}^{2^K-1} B(n_{c1,i-1}+1,n_{c0,i-1}+1 )\right) \cdot \dfrac{\prod _{c=0}^{2^K-1}\Gamma (n_{c,N}^{\prime }+1)}{\Gamma (N+2^K-1)}. \end{aligned}$$

(65)

Combining Eqs. 64 and 65, Eq. 62 is

$$\begin{aligned}&p({\varvec{\alpha }}_i^\top {\varvec{v}},\alpha _{i,K+1}\vert {\varvec{A}}_{(i)},\alpha _{1,K+1}, \cdots ,\alpha _{i-1,K+1})\nonumber \\ =&\dfrac{\dfrac{\prod _{c=0}^{2^K-1} \Gamma (n_{c,N}+1)}{\Gamma (N+2^K)} \cdot \prod _{c=0}^{2^K-1} B(n_{c1,i}+1,n_{c0,i}+1 )}{\left( \prod _{c=0}^{2^K-1} B(n_{c1,i-1}+1,n_{c0,i-1}+1 )\right) \cdot \dfrac{\prod _{c=0}^{2^K-1}\Gamma (n_{c,N}^{\prime }+1)}{\Gamma (N+2^K-1)}}\nonumber \\ =&\dfrac{1}{N+2^K-1} \cdot \left( \prod _{c=0}^{2^K-1} \dfrac{B(n_{c1,i}+1,n_{c0,i}+1 )\Gamma (n_{c,N}+1)}{B(n_{c1,i-1}+1,n_{c0,i-1}+1)\Gamma (n_{c,N}^{\prime }+1)} \right) . \end{aligned}$$

(66)

If ${\varvec{\alpha }}_i^\top {\varvec{v}}=c$ and $\alpha _{i,K+1}=1$, then Eq. 66 can be simplified as

$$\dfrac{n_{c1,i-1}+1 }{n_{c,i-1}+2} \cdot \dfrac{n_{c}^{\prime }+1}{N+2^K-1},$$

and if ${\varvec{\alpha }}_i^\top {\varvec{v}}=c$ and $\alpha _{i,K+1}=0$, Eq. 66 is

$$\begin{aligned} \dfrac{n_{c0,i-1}+1 }{n_{c,i-1}+2} \cdot \dfrac{n_{c}^{\prime }+1}{N+2^K-1}. \end{aligned}$$

Therefore, we can update $({\varvec{\alpha }}_{i}, \alpha _{i,K+1})$ sequentially to $({\varvec{\alpha }}_c,\alpha ^*)$ with probability proportional to $p({\varvec{Y}}_i \vert {\varvec{\alpha }}_i^\top {\varvec{v}}=c,\alpha _{i,K+1}=1,{\varvec{\Omega }},{\varvec{Q}}_{K+1}) \cdot \left( \dfrac{n_{c\alpha ^*,i-1}+1 }{n_{c,i-1}+2} \cdot \dfrac{n_{c}^{\prime }+1}{N+2^K-1}\right)$, $c=0,\ldots ,2^K,\alpha ^*=0,1$.

Appendix D

Posterior Distribution of $\lambda$ in Indian Buffet Process Algorithm

Assume $\lambda \sim Gamma(a,b)$, and $\lambda$ is only related to ${\varvec{Q}}$, so its posterior can be updated by

$$\begin{aligned} p(\lambda ^{(t)}|{\varvec{Q}}^{(t)})&\propto p({\varvec{Q}}^{(t)}|\lambda )p(\lambda ) \nonumber \\&\propto \lambda ^{K}\text {exp}\left\{ -\lambda H_N \right\} \lambda ^{a-1}\text {exp}\left\{ -\lambda b\right\} \nonumber \\&\propto \lambda ^{K + a-1}\text {exp}\left\{ -\lambda (H_N+b) \right\} , \end{aligned}$$

(67)

then $\lambda ^{(t)}$ can be sampled from Gamma$(K +a, H_N+b)$, where K is the number of features in current ${\varvec{Q}}^{(t)}$ and $H_N$ the Nth harmonic number.

Appendix E

Problem set of Elementary Probability Theory

Table 8 Summary of RMSE of estimated item parameters for $K=3, \rho =0$ by sample size N.

Table 9 Summary of RMSE of estimated item parameters for $K=4, \rho =0$ by sample size N.

Table 10 Summary of RMSE of estimated item parameters for $K=5, \rho =0$ by sample size N.

Table 11 Summary of the frequency of estimated ${\hat{K}}$ by sample size N, number of true attributes K, and attribute dependence $\rho$ using DIC selection.

The twelve questions from R package pks (Heller and Wickelmaier 2013) are

• 1. A box contains 30 marbles in the following colors: 8 red, 10 black, 12 yellow. What is the probability that a randomly drawn marble is yellow?

• 2. A bag contains 5-cent, 10-cent, and 20-cent coins. The probability of drawing a 5-cent coin is 0.35, that of drawing a 10-cent coin is 0.25, and that of drawing a 20-cent coin is 0.40. What is the probability that the coin randomly drawn is not a 5-cent coin?

• 3. A bag contains 5-cent, 10-cent, and 20-cent coins. The probability of drawing a 5-cent coin is 0.20, that of drawing a 10-cent coin is 0.45, and that of drawing a 20-cent coin is 0.35. What is the probability that the coin randomly drawn is a 5-cent coin or a 20-cent coin?

• 4. In a school, 40% of the pupils are boys and 80% of the pupils are right-handed. Suppose that gender and handedness are independent. What is the probability of randomly selecting a right-handed boy?

• 5. Given a standard deck containing 32 different cards, what is the probability of not drawing a heart?

• 6. A box contains 20 marbles in the following colors: 4 white, 14 green, 2 red. What is the probability that a randomly drawn marble is not white?

• 7. A box contains 10 marbles in the following colors: 2 yellow, 5 blue, 3 red. What is the probability that a randomly drawn marble is yellow or blue?

• 8. What is the probability of obtaining an even number by throwing a dice?

• 9. Given a standard deck containing 32 different cards, what is the probability of drawing a 4 in a black suit?

• 10. A box contains marbles that are red or yellow, small or large. The probability of drawing a red marble is 0.70, the probability of drawing a small marble is 0.40. Suppose that the color of the marbles is independent of their size. What is the probability of randomly drawing a small marble that is not red?

• 11. In a garage there are 50 cars. 20 are black and 10 are diesel powered. Suppose that the color of the cars is independent of the kind of fuel. What is the probability that a randomly selected car is not black and it is diesel powered?

• 12. A box contains 20 marbles. 10 marbles are red, 6 are yellow and 4 are black. 12 marbles are small and 8 are large. Suppose that the color of the marbles is independent of their size. What is the probability of randomly drawing a small marble that is yellow or red?

Appendix F

Supplementary Simulation Results

Tables 8, 9 and 10 report comparison on the root-mean-squared error (RMSE) of the estimated item parameters for $\rho =0$ for the cases where K was correctly estimated. The tables show that both the crimp sampler and RJ-MCMC give a smaller RMSEs on item parameter estimation than IBP across different sample sizes and K, and the crimp sampler is slightly better than RJ-MCMC for the $K=5$ case. The results for $\rho =0.25$ are omitted here because the performance was similar. Table 11 reports the performance of inferring K using DIC selection.