1 Introduction

Rainfall is a complex atmospheric process, which is space and time dependent and it is not easy to predict. Due to the apparent random characteristics of rainfall series, they are often described by a stochastic process (Chinchorkar et al. 2012). For water resources planning purposes, a long-term rainfall series is required in hydrological and simulation models (Tantanee et al. 2005). There have been many attempts to find the most appropriate method for rainfall prediction for example, coupling physical, marine, and meteorological or satellite data with a forecasting model, or even applying several techniques such as the artificial neural network or fuzzy logic as a forecasting approach (Hsu et al. 1995; Dawson and Wilby 2001; Hettiarachchi et al. 2005). In recent years, several numerical weather forecasts have been proposed for weather prediction but most of these models are limited to short period forecasts. This paper introduces a new approach for prediction of rainfall series.

Several time series models have been proposed for modeling monthly rainfall series (Bhakar et al. 2006) and annual rainfall series such as the autoregressive model (AR) (Yevjevich 1972), the fractional Guassian noise model (Matalas and Wallis 1971), autoregressive moving-average models (ARMA) (Carlson et al. 1970) and the disaggregation multivariate model (Valencia and Schaake 1973). Moustris et al. (2011) examine the possibility of long term precipitation forecast (four consecutive months) by the application of ANNs, using long monthly precipitation time series of four meteorological stations in Greece.

In the past decade, wavelet theory has been introduced to signal processing analysis. In recent years, the wavelet transform has been successfully applied to wave data analysis and other ocean engineering applications (Massel 2001; Teisseire et al. 2002; Huang 2004). The time-frequency character of long-term climatic data is investigated using the continuous wavelet transform technique (Lau and Weng 1995; Torrence and Compo 1997; Mallat 1998) and wavelet analysis of wind wave measurements obtained from a coastal observation tower (Huang 2004). Chou (2011) used wavelet denoising method in linear perturbation models (LPMs) and simple linear models (SLMs) for rainfall and runoff time series data. Wang and Li (2011) used a new wavelet transform method for developing the synthetic generation of daily stream flow sequences. Wu et al. (2004) used a combination of neural networks and wavelet methods to predict underground water levels.

Dynamical Recurrent Neural Network (DRNN) on each resolution scale of the sunspot time series resulting from the wavelet decomposed series with the Temporal Recurrent Back propagation (TRBP) algorithm (Aussem and Murtagh 1997). There are some appreciable studies of wavelet transform based neural network models (Wang and Ding 2003; Anctil and Tape 2004; Cannas et al. 2006; Kisi 2008; Wang et al. 2009). The wavelet transform is also integrated with multiple linear regression (Kucuk and Agiralioğlu 2006; Kisi 2009, 2010) and support vector machine approach (Kisi and Cimen 2011). Adamowski and Sun (2010) compared the relative performance of the coupled wavelet-neural network models (WA–ANN) and regular artificial neural networks (ANN) for flow forecasting at lead times of 1 and 3 days for two different non-perennial rivers in semiarid watersheds of Cyprus. Kisi (2011) investigated the performance of the wavelet regression (WR) technique in daily river stage forecasting and determined the WR model was improved combining two methods, discrete wavelet transform and a linear regression model. Sang (2013), developed a method for discrete wavelet decomposition and an improved wavelet modeling framework, WMF for short was proposed for hydrologic time series forecasting. By coupling the wavelet method with the traditional AR model, the Wavelet-Autoregressive model (WARM) is developed for annual rainfall prediction (Tantanee et al. 2005). Partal and Kisi (2007) used a conjunction model (wavelet-neuro-fuzzy) to forecast the Turkey daily precipitation. The observed daily precipitations are decomposed to some sub series by using Discrete Wavelet Transform (DWT) and then appropriate sub series are used as inputs to neuro-fuzzy models for forecasting of daily precipitations. Each of these studies showed that different black box models trained or calibrated with decomposed data resulted in higher accuracy than the single models that were calibrated with an undecomposed and noisy time series. In this paper, a Wavelet Neural Network (WNN) model, which is the combination of wavelet analysis and ANN, has been proposed for rainfall forecast Darjeeling station, India.

2 Wavelet Analysis

The wavelet analysis is an advanced tool in signal processing that has attracted much attention since its theoretical development (Grossmann and Morlet 1984). Its use has increased rapidly in communications, image processing and optical engineering applications as an alternative to the Fourier transform in preserving local, non-periodic and multiscaled phenomena. The difference between wavelets and Fourier transforms is that wavelets can provide the exact locality of any changes in the dynamical patterns of the sequence, whereas the Fourier transforms concentrate mainly on their frequency. Moreover, Fourier transform assume infinite length signals, whereas wavelet transforms can be applied to any kind and any size of time series, even when these sequences are not homogeneously sampled in time (Antonios and Constantine 2003). In general, wavelet transforms can be used to explore, denoise and smoothen time series which aid in forecasting and other empirical analysis.

Wavelet analysis is the breaking up of a signal into shifted and scaled versions of the original (or mother) wavelet. In wavelet analysis, the use of a fully scalable modulated window solves the signal-cutting problem. The window is shifted along the signal and for every position the spectrum is calculated. Then this process is repeated many times with a slightly shorter (or longer) window for every new cycle. In the end, the result will be a collection of time-frequency representations of the signal, all with different resolutions. Because of this collection of representations we can speak of a multiresolution analysis. By decomposing a time series into time-frequency-space, one is able to determine both the dominant modes of variability and how those modes vary in time. Wavelets have proven to be a powerful tool for the analysis and synthesis of data from long memory processes. Wavelets are strongly connected to such processes in that the same shapes repeat at different orders of magnitude. The ability of the wavelets to simultaneously localize a process in time and scale domain results in representing many dense matrices in a sparse form.

2.1 Discrete Wavelet Transform (DWT)

The basic aim of wavelet analysis is to determine the frequency (or scale) content of a signal and then it assess and determine the temporal variation of this frequency content. This property is in complete contrast to the Fourier analysis, which allows for the determination of the frequency content of a signal but fails to determine frequency-time dependence. Therefore, the wavelet transform is the tool of choice when signals are characterized by localized high frequency events or when signals are characterized by a large numbers of scale variable processes. Because of its localization properties in both time and scale, the wavelet transform allows for tracking the time evolution of processes at different scales in the signal.

The wavelet transform of a time series f(t) is defined as

$$ f\left(a,b\right)=\frac{1}{\sqrt{a}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f(t)\varphi \left(\frac{t-b}{a}\right) dt} $$
(1)

where φ (t) is the basic wavelet with effective length (t) that is usually much shorter than the target time series f(t). The variables ‘a’ is the scale or dilation factor that determines the characteristic frequency so that its variation gives rise to a spectrum and ‘b’ is the translation in time so that its variation represents the ‘sliding’ of the wavelet over f(t). The wavelet spectrum is thus customarily displayed in time-frequency domain. For low scales i.e. when |a| < <1, the wavelet function is highly concentrated (shrunken compressed) with frequency contents mostly in the higher frequency bands. Inversely, when |a|> > 1, the wavelet is stretched and contains mostly low frequencies. For small scales, we obtain thus a more detailed view of the signal (also known as a “higher resolution”) whereas for larger scales we obtain a more general view of the signal structure.

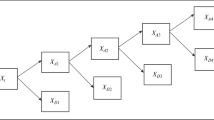
The original signal X(n) (Fig. 1) passes through two complementary filters (low pass and high pass filters) and emerges as two signals as Approximations (A) and Details (D). The approximations are the high-scale, low frequency components of the signal. The details are the low-scale, high frequency components. Normally, the low frequency content of the signal (approximation, A) is the most important part. It demonstrates the signal identity. The high-frequency component (detail, D) is nuance. The decomposition process can be iterated, with successive approximations being decomposed in turn, so that one signal is broken down into many lower resolution components (Fig. 1).

Fig. 1
figure 1

Diagram of multiresolution analysis of signal

Full size image

2.2 Mother Wavelet

The choice of the mother wavelet depends on the data to be analyzed. The Daubechies and Morlet wavelet transforms are the commonly used “Mother” wavelets. Daubechies wavelets exhibit good trade-off between parsimony and information richness, it produces the identical events across the observed time series and appears in so many different fashions that most prediction models are unable to recognize them well (Benaouda et al. 2006). Morlet wavelets, on the other hand, have a more consistent response to similar events but have the weakness of generating many more inputs than the Daubechies wavelets for the prediction models.

3 Artificial Neural Networks

An ANN, can be defined as a system or mathematical model consisting of many nonlinear artificial neurons running in parallel, which can be generated, as one or multiple layered. Although the concept of artificial neurons was first introduced by McCulloch and Pitts, the major applications of ANN’s have arisen only since the development of the back-propagation method of training by Rumelhart (Rumelhart et al. 1986). Following this development, ANN research has resulted in the successful solution of some complicated problems not easily solved by traditional modeling methods when the quality/quantity of data is very limited. ANN models are ‘black box’ models with particular properties, which are greatly suited to dynamic nonlinear system modeling. The main advantage of this approach over traditional methods is that it does not require the complex nature of the underlying process under consideration to be explicitly described in mathematical form. ANN applications in hydrology vary, from real time to event based modeling.

The most popular ANN architecture in hydrologic modeling is the multilayer perceptron (MLP) trained with BP algorithm (ASCE(2000a, b)). A multilayer perceptron network consists of an input layer, one or more hidden layers of computation nodes, and an output layer. The number of input and output nodes is determined by the nature of the actual input and output variables. The number of hidden nodes, however, depends on the complexity of the mathematical nature of the problem, and is determined by the modeler, often by trial and error. The input signal propagates through the network in a forward direction, layer by layer. Each hidden and output node processes its input by multiplying each of its input values by a weight, summing the product and then passing the sum through a nonlinear transfer function to produce a result. For the training process, where weights are selected, the neural network uses the gradient descent method to modify the randomly selected weights of the nodes in response to the errors between the actual output values and the target values. This process is referred to as training or learning. It stops when the errors are minimized or another stopping criterion is met. The Back Propagation Neural Network (BPNN) can be expressed as

$$ Y=f\left({\displaystyle \sum WX-\theta}\right) $$
(2)

where X = input or hidden node value; Y = output value of the hidden or output node; f (.) = transfer function; W = weights connecting the input to hidden, or hidden to output nodes; and θ = bias (or threshold) for each node.

3.1 Method of Network Training

Levenberg-Marquardt method (LM) was used for training of the given network. It is a modification of the classic Newton algorithm for finding an optimum solution to a minimization problem. In practice, LM is faster and finds better optima for a variety of problems than most other methods (Hagan and Menhaj 1994). The method also takes advantage of the internal recurrence to dynamically incorporate past experience in the training process (Coulibaly et al. 2000).

The Levenberg-Marquardt Algorithm (LMA) is given by

$$ {X}_{k+1}={X}_k-{\left({J}^TJ+\mu I\right)}^{-1}{J}^te $$
(3)

where, X is the weights of neural network, J are the Jacobian matrix of the performance criteria to be minimized, ‘μ’ is a learning rate that controls the learning process and ‘e’ is residual error vector. If scalar μ is very large, the above expression approximates gradient descent with a small step size, while if it is very small; the above expression becomes Gauss-Newton method using the approximate Hessian matrix. The Gauss-Newton method is faster and more accurate near an error minimum. Hence we decrease μ after each successful step and increase only when a step increases the error. LMA has great computational and memory requirements, and thus it can only be used in small networks. It is faster and less easily trapped in local minima than other optimization algorithms.

3.2 Selection of Network Architecture

Increasing the number of training patterns provide more information about the shape of the solution surface, and thus increases the potential level of accuracy that can be achieved by the network. A large training pattern set, however can sometimes overwhelm certain training algorithms, thereby increasing the likelihood of an algorithm becoming stuck in a local error minimum. Consequently, there is no guarantee that adding more training patterns leads to improve solution. Moreover, there is a limit to the amount of information that can be modeled by a network that comprises a fixed number of hidden neurons. The time required to train a network increases with the number of patterns in the training set. The critical aspect is the choice of the number of nodes in the hidden layer and hence the number of connection weights.

Based on the physical knowledge of the problem and statistical analysis, different combinations of antecedent values of the time series were considered as input nodes. The output node is the time series data to be predicted in one step ahead. Time series data was standardized for zero mean and unit variation, and then normalized into 0 to 1. The activation function used for the hidden and output layer was logarithmic sigmoidal and pure linear function respectively. For deciding the optimal hidden neurons, a trial and error procedure started with two hidden neurons initially, and the number of hidden neurons was increased up to 10 with a step size of 1 in each trial. For each set of hidden neurons, the network was trained in batch mode to minimize the mean square error at the output layer. In order to check any over fitting during training, a cross validation was performed by keeping track of the efficiency of the fitted model. The training was stopped when there was no significant improvement in the efficiency, and the model was then tested for its generalization properties. Figure 2 shows the multilayer perceptron (MLP) neural network architecture when the original signal taken as input of the neural network architecture.

Fig. 2
figure 2

Signal data based multilayer perceptron (MLP) neural network structure

Full size image

3.3 Method of Combining Wavelet Analysis with ANN

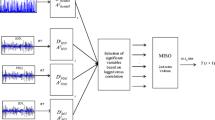
The decomposed details (D) and approximation (A) were taken as inputs to neural network structure as shown in Fig. 3, where ‘i’ is the level of decomposition varying from 1 to I and j is the number of antecedent values varying from 0 to J and N is the length of the time series. To obtain the optimal weights (parameters) of the neural network structure, LM back propagation algorithm was used to train the network. A standard MLP with a logarithmic sigmoidal transfer function for the hiddenlayer and linear transfer function for the output layer were used in the analysis. The number of hidden nodes was determined by trial and error procedure. The output node will be the original value at one step ahead.

Fig. 3
figure 3

Wavelet based multilayer perceptron (MLP) neural network structure

Full size image

4 Linear Auto-Regressive (AR) Modeling

A common approach for modeling univariate time series is the autoregressive (AR) model:

$$ {X}_t=\delta +{\phi}_1{X}_{t-1}+{\phi}_2{X}_{2-1}+\cdots \cdots +{\phi}_2{X}_{2-1}+{A}_t $$
(4)

where X t is the time series, A t is white noise, and

$$ \delta =\left(1-{\displaystyle \sum_{i-1}^p{\phi}_i}\right)\mu $$
(5)

where ‘μ’ is the mean of the time series. An autoregressive model is simply a linear regression of the current value of the series against one or more prior values. AR models can be analyzed with linear least squares technique. They also have a straightforward interpretation. The determination of the model order can be estimated by examining the plots of Auto Correlation Function (ACF) and Partial Auto Correlation Function (PACF). The number of non-zero terms (i.e. outside confidence bands) in PACF suggests the order of the AR model. An AR (k) model will be implied by a sample PACF with k non-zero terms, and the terms in the sample ACF will decay slowly towards zero. From ACF and PACF analysis for rainfall, the order of the AR model is selected as 1.

5 Performance Criteria

The performance of various models during calibration and validation were evaluated by using the statistical indices: the Root Mean Squared Error (RMSE), Correlation Coefficient (R) and Coefficient of Efficiency (COE).

The definitions of different statistical indices are presented below:

$$ \mathrm{RMSE}=\sqrt{\frac{\left[{\displaystyle \sum_{t=1}^N{\left({y}_t^o-{y}_t^c\right)}^2}\right]}{N}} $$
(6)
$$ \mathrm{R}=\frac{{\displaystyle \sum_{i=1}^N\left({y}_t^o-\overline{y^o}\right)\left({y}_t^c-\overline{y^c}\right)}}{\sqrt{\left[{\displaystyle \sum_{t=1}^N{\left({y}_t^o-\overline{y^o}\right)}^2}\right]\left[{\displaystyle \sum_{t=1}^N{\left({y}_t^c-\overline{y^c}\right)}^2}\right]}} $$
(7)
$$ \mathrm{COE}=1-\frac{\left[{\displaystyle \sum_{t=1}^N{\left({y}_t^o-{y}_t^c\right)}^2}\right]}{\left[{\displaystyle \sum_{i=1}^N{\left({y}_t^o-\overline{y^o}\right)}^2}\right]} $$
(8)

where y o t and y c t are the observed and calculated values at time t respectively, \( \overline{y^o} \) and \( \overline{y^c} \) are the mean of the observed and calculated values.

6 Study Area and Data Collection

Darjeeling is a small town in the Himalayan foot hills (Fig. 4), lying at an altitude of 2,130 m above mean sea level and known as the Queen of the Hills. It is located in Darjeeling District in the extreme north of West Bengal State in the east of India. The district extends from tropical plains at about 91 m above sea level to an altitude of 3,658 m on the Sandakfu-Phalut ridge. The hills of Darjeeling are part of the Mahabharat Range or Lesser Himalaya. Kanchenjunga, the world’s third-highest peak, 8,598 m (28,209 ft) high, is the most prominent mountain visible from Darjeeling.

Fig. 4
figure 4

Location of the study area

Full size image

To forecast the rainfall at Darjeeling rain gauge station (Fig. 4), monthly rainfall, minimum and maximum temperature data of 74 years from 01 January 1901 to 01 September 1975 was used. The first 44 years (60 % data) from 01 January 1901 to 01 November 1945 was used for calibration of the model, and the remaining 26 years (40 % data) from 01 December 1945 to 01 September 1975 data were used for validation. The annual mean maximum temperature is 14.9 °C while the mean minimum temperature is 8.9 °C, with monthly mean temperatures range from 5–17 °C. The lowest temperature recorded was −3.7 °C in the month of February 1905. The average annual precipitation is 3,092 mm, with an average of 126 days of rain in a year. The highest rainfall occurs in July.

Table 1 shows the statistics of the calibration, validation and total data for monthly rainfall, minimum temperature and maximum temperature. The recorded monthly maximum rainfall is 1,401 mm, while the mean monthly rainfall was 2,350 mm. The observed monthly rainfall shows low positive skewness (1.2) and indicates that the data has less scattered distribution. The minimum of the maximum temperature is 5.5 °C, while the maximum of the maximum temperature is 21.5 °C.

Table 1 Statistical properties of rainfall, minimum and maximum temperatures
Full size table

6.1 Development of Wavelet Neural Network Model

The original time series was decomposed into Details and Approximations to certain number of sub-time series {D 1, D 2…. D p , A p } by wavelet transform algorithm. These play different role in the original time series and the behavior of each sub-time series is distinct (Wang and Ding 2003). So the contribution to original time series varies from each successive approximations being decomposed in turn, so that one signal is broken down into many lower resolution components, tested using different scales from 1 to 10 with different sliding window amplitudes. In this context, dealing with a very irregular signal shape, an irregular wavelet, the Daubechies wavelet of order 5 (DB5), has been used at level 3. Consequently, D 1, D 2, D 3 were detail time series, and A 3 was the approximation time series. The decomposed sub series of details and approximations along with original series for rainfall was shown in Fig. 5.

Fig. 5
figure 5

Decomposed wavelet sub-time series of rainfall from 1901 to 1974

Full size image

An ANN was constructed in which the sub-series {D 1, D 2, D 3, A 3} at time t are input of ANN and the original time series at t + T time are output of ANN, where T is the length of time to forecast. The input nodes for the WNN are the decomposed subsets of antecedent values of the rainfall, minimum and maximum temperatures and were presented in Table 2. The Wavelet Neural Network model (WNN) was formed in which the weights are learned with Feed forward neural network with Back Propagation algorithm. The number of hidden neurons for BPNN was determined by trial and error procedure.

Table 2 Model Inputs for ANN
Full size table

7 Results and Discussion

To forecast the rainfall at Darjeeling rain gauge station, the monthly rainfall, is minimum temperature and maximum temperature data of 74 years was used. The first 44 years data were used for calibration of the model, and the remaining 26 years data were used for validation. The model inputs (Table 2) were decomposed by wavelets and decomposed sub-series were taken as input to ANN. ANN was trained using back propagation with LM algorithm. The optimal number of hidden neurons for WNN and ANN was determined as six by trial and error procedure. The final structure of the WNN model is the number of inputs used in ANN Multiplied by 4 sub-series for every input neuron as obtained by wavelet decomposition, 6 hidden neurons and 1 output neuron. Whereas, the final structure of the ANN model is the number of inputs used in ANN, 6 hidden neurons and 1 output neuron. The performance of various models estimated to forecast the rainfall was presented in Table 3.

Table 3 Goodness of fit statistics of the calibration and validation for the forecasted rainfall
Full size table

From Table 3, it is found that low RMSE values (63.01 to 117.39 mm) for WNN models when compared to ANN and AR models. It has been observed that WNN models estimated the peak values of rainfall to a reasonable accuracy (peak rainfall in the data series is 1401.80 mm). Further, it is observed that the WNN model having two antecedent values of the rainfall, one minimum temperature and maximum temperature estimated minimum RMSE (63.01 mm), high correlation coefficient (0.9736) and highest efficiency (>94 %) during the validation period. The model IV (Bold) of WNN was selected as the best fit model to forecast the rainfall in 1 month advance.

Figures 6 and 7, shows the observed and modeled graphs for ANN and WNN models during calibration and validation respectively. It is found that values modeled from WNN model properly matched with the observed values, whereas ANN model underestimated the observed values. From this analysis, it is evident that the performance of WNN was much better than ANN and AR models in forecasting the rainfall.

Fig. 6
figure 6

Plot of observed and modeled rainfall for ANN model during (a) calibration and (b) validation

Full size image
Fig. 7
figure 7

Plot of observed and modeled rainfall for WNN model during (a) calibration, and (b) validation

Full size image

The distribution of error along the magnitude of rainfall computed by WNN and ANN models during the validation period has been presented in Fig. 8. From Fig. 8, it was observed that the estimation of peak rainfall was very good as the error is minimum when compared with ANN model. Figure 9 shows the scatter plot between the observed and modeled rainfall by WNN and ANN. It was observed that the rainfall forecasted by WNN models were very much close to the 45° line. From this analysis, it was worth to mention that the performance of WNN was much better than the standard ANN and AR models in forecasting the rainfall in 1-month advance.

Fig. 8
figure 8

Distribution of error plots along the magnitude of monthly rainfall for (a) ANN model and (b) WNN model during validation period

Full size image
Fig. 9
figure 9

Scatter plot between observed and modeled monthly rainfall for (a) ANN model and (b) WNN model during validation period

Full size image

8 Conclusions

This paper reports a hybrid model called wavelet neural network model (WNN) for time series modeling of monthly rainfall. The proposed model is a combination of wavelet analysis and artificial neural network. Wavelet decomposes the time series into multilevel of details and it can adopt multiresolution analysis and effectively diagnose the main frequency component of the signal and abstract local information of the time series. The proposed WNN model has been applied to monthly rainfall of Darjeeling rain gauge station. The time series data of rainfall was decomposed into sub series by DWT. Appropriate sub-series of the variable used as inputs to the ANN model and original time series of the variable as output. Model parameters are calibrated using 44 years of data and rest of the data is used for model validation. From this analysis, it was found that efficiency index is more than 94 % for WNN models whereas it is 64 % for ANN models respectively.

Overall analysis indicates that the performance of ANN are relatively lower compared to that of WNN models; this may be plausibly due to the variation in nonlinear dynamics of temperature which plays a predominant role in hilly areas included in rainfall process that mapped effectively by Wavelet based models. It may be noted that hydrological data used in the WNN model has been decomposed in details and approximation, which may lead to better capturing the rainfall processes. The study only used data from one rain gauge station and further studies using more rain gauges data from various areas may be required to strengthen these conclusions.