Abstract
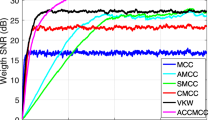
In this paper, we propose a new kernel correlation coefficient (KECC), with an emphasis on its robustness against impulsive noise and/or monotonic nonlinear transformations. To gain further insight, we compared KECC with other four correlation coefficients, namely, Pearson’s product moment correlation coefficient (PPMCC), Kendall’s tau (KT), Spearman’s rho (SR) and order statistics correlation coefficient (OSCC). Extensive simulation experiments were conducted under linear, nonlinear, normal and contaminated Gaussian models (CGM) based on seven means of performance evaluation. Theoretical analysis showed that KECC satisfies various desired properties. Numerical results suggest that KECC performs equally well with the optimal PPMCC under the bivariate normal model, and outperforms the others when impulsive noise and/or nonlinearity exist in the data. Moreover, KECC can detect accurately the time delay of signals corrupted by impulsive noise. Last but not least, KECC runs in linearithmic time, only slightly slower than the fastest PPMCC. The advantages of KECC revealed in this work might shed new light on the topic of correlation analysis, which is important in many areas including signal processing.









Similar content being viewed by others
References
Dougherty, E.R., Kim, S., & Chen, Y. (2000). Coefficient of determination in nonlinear signal processing. Signal Processing, 80(10), 2219–2235.
Lian, J., Garner, G., Muessig, D., & Lang, V. (2010). A simple method to quantify the morphological similarity between signals. Signal Processing, 90(2), 684–688.
Delmas, J.P., & Abeida, H. (2009). Asymptotic distribution of circularity coefficients estimate of complex random variables. Signal Processing, 89(12), 2670–2675. Special Section: Visual Information Analysis for Security.
He, Y., Gan, T., Chen, W., & Wang, H. (2012). Multi-stage image denoising based on correlation coefficient matching and sparse dictionary pruning. Signal Processing, 92(1), 139–149.
Xu, W., Chang, C., Hung, Y.S., Kwan, S.K., & Fung, P.C.W. (2006). Order statistic correlation coefficient and its application to association measurement of biosignals. In 2006 IEEE International Conference on Acoustics, Speech and Signal Processing, 2006. ICASSP 2006 Proceedings, volume 2 (pp. II–II).
Xu, W., Chang, C., Hung, Y.S., Kwan, S.K., & Chin Wan Fung, P. (2007). Order statistics correlation coefficient as a novel association measurement with applications to biosignal analysis. IEEE Transactions on Signal Processing, 55(12), 5552–5563.
Xu, W., Chang, C., Hung, Y.S., & Chin Wan Fung, P. (2008). Asymptotic properties of order statistics correlation coefficient in the normal cases. IEEE Transactions on Signal Processing, 56(6), 2239–2248.
Xu, W., Hung, Y.S., Niranjan, M., & Shen, M. (2010). Asymptotic mean and variance of gini correlation for bivariate normal samples. IEEE Transactions on Signal Processing, 58(2), 522–534.
Xu, W., Hou, Y., Hung, Y.S., & Zou, Y. (2013). A comparative analysis of spearman’s rho and kendall’s tau in normal and contaminated normal models. Signal Processing, 93(1), 261–276.
Gibbons, J.D., & Chakraborti, S. (1992). Nonparametric Statistical Inference, 3rd edn. New York: Dekker, M.
Mari, D.D., & Kotz, S. (2001). Correlation and dependence, volume 518 World Scientific.
Fisher, R.A. (1990). Statistical methods, Experimental Design, and Scientific Inference. New York: Oxford university press.
Fisher, R.A. (1921). On the ’probable error’ of a coefficient of correlation deduced from a small sample. Metron, 1, 3–32.
Fieller, E.C., Hartley, H.O., & Pearson, E.S. (1957). Test for rank correlation coefficients.i. Biometrika, 44, 470–481.
Kendall, M., & Gibbons, J.D. (1990). Rank Correlation Methods, 5th edn. New York: Oxford University Press.
Ma, R., Xu, W., Wang, Q., & Chen, W. (2014). Robustness analysis of three classical correlation coefficients under contaminated gaussian model. Signal Processing, 104, 51–58.
Pearson, K. (1914). On an extension of the method of correlation by grades or ranks. Biometrika, 10(2/3), 416–418.
Schechtman, E., & Yitzhaki, S. (1987). A measure of association base on Gini’s mean difference. Communications in Statistics-Theory Methods, 16(1), 207–231.
Ma, R., Xu, W., Zhang, Y., & Ye, Z. (2014). On an extension of the method of correlation by grades or ranks. PLos ONE, 9(11), e112215.
Xu, W., Ma, R., Zhou, Y., Peng, S., & Hou, Y. (2016). Asymptotic properties of pearsons rank-variate correlation coefficient in bivariate normal model. Signal Processing, 119, 190–202.
Stuart, A., & Ord, J.K. (1991). Kendall’s Advanced Theory of Statistics Volume 2 Classical Inference and Relationship, 5th edn. London: Edward Arnold.
Epanechnikov, V.A. (1969). Non-parametric estimation of a multivariate probability density. Theory of Probability & Its Applications, 14(1), 153–158.
Cleveland, W.S., & Devlin, S.J. (1988). Locally weighted regression: an approach to regression analysis by local fitting. Journal of the American Statistical Association, 83(403), 596–610.
Reznic, Z., Zamir, R., & Feder, M. (2002). Joint source-channel coding of a gaussian mixture source over the gaussian broadcast channel. IEEE Transaction on Information Theory, 48(3), 776–781.
Chen, R., Wang, X., & Liu, J.S. (2000). Adaptive joint detection and decoding in flat-fading channels via mixture Kalman filtering. IEEE Transaction on Information Theory, 46(6), 2079–2094.
David, H.A., & Nagaraja, H.N. (2003). Order Statistics, 3rd edn: Wiley-Interscience, Hoboken.
Balakrishnan, N., & Rao, C.R. (1998). OrderStatistics: Applications Vol. 17. New York: Elsevier.
Balakrishnan, N., & Radhakrishna Rao, C. (1998). Order Statistics: Theory and Methods Vol. 16. New York: Elsevier.
Stuart, A., & Ord, J.K. (1994). Kendall’s Advanced Theory of Statistics Volume 1 Distribution Theory, 6th edn. London: Edward Arnold.
Fieller, E.C., Hartley, H.O., & Pearson, E.S. (1957). Test for rank correlation coefficients.i. Biometrika, 44, 470–481.
Serfling, R.J. (2009). Approximation theorems of mathematical statistics Vol. 162. Wiley.
Acknowledgment
This work was jointly supported in part by National Natural Science Foundation of China (Projects 61271380 and U1501251), in part by Guangdong Natural Science Foundation (Project 2014A030313515), and in part by Guangzhou Science and Technology Plan (Project 201607010290).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof Proof of Theorem 2
Let \(\nu _{\mathcal {X}}\) and \(\nu _{\mathcal {Y}}\) be the population medians of \(\mathcal {X}\) and \(\mathcal {Y}\), respectively. Then, from [31], we have
Define
When the sample size \(N\to \infty \), it follows that
□
Therefore, we need to work out all the three expectation terms in Eq. 35.
For the bivariate normal distribution \(\phi _{1}(\mathcal {X},\mathcal {Y})\) in Eq. 32, the pdf
where
with
For the bivariate normal distribution \(\phi _{2}(\mathcal {X},\mathcal {Y})\) in Eq. 33, the pdf is
where
with
From Eqs. 30–41, the numerator in Eq. 35 becomes
where
with
and
with
Now we need to evaluate H 1 and H 2. It follows that
where
Then, from Eqs. 38, 50 and 51, we have
and hence
where
Write
where
Then
In a parallel manner, we have
where
Write
where
A substitution of Eq. 60 into Eq. 47 gives
Similarly we can also obtain
Given Eqs. 42, 59, 65–67 along with the fact that ρ∈[−1,+1], we arrive at
where S and T are defined in Eqs. 9 and 10, respectively.
To show that the last term in Eq. 68 is approximately equal to ρ, we need to evaluate \(\eta _{\mathcal {X}}\) and \(\eta _{\mathcal {Y}}\) contained in S and T. Let Φ1(⋅) and Φ2(⋅) be the cdf of \(\mathcal {N}(\mu _{\mathcal {X}},\sigma ^{2}_{\mathcal {X}})\) and \(\mathcal {N}(\mu _{\mathcal {X}},\sigma ^{\prime 2}_{\mathcal {X}})\), respectively. Let q U and q L be the upper and lower quartiles of \(\mathcal {X}\), respectively. Since the marginal distribution of \(\mathcal {X}\) is
we have
By the assumption of \(\sigma ^{\prime }_{\mathcal {X}}\gg \sigma _{\mathcal {X}}\), it follows that 0<Φ2(q U )<Φ1(q U ), and hence, from Eq. 69,
Let \({\Phi }_{1}^{-1}(\cdot )\) be the inversion function of Φ1(⋅). Due to the monotonic property of \({\Phi }_{1}^{-1}\), we have, after imposing the transform \({\Phi }_{1}^{-1}\) to Eq. 70,
An application of Taylor’s theorem to the leftmost term in Eq. 71 gives
where β lies in between (1−ε)Φ1(q U ) and Φ1(q U ). This means that
which along with Eq. 71 leads to
Similarly, we also have
Then
and
In a similar way, we can also obtain
Substituting Eqs. 72 and 73 into Eqs. 10 and 9, respectively, we have
and
Applying these results to the last term in (68) with the assumption of ε being small, we finally have
thus completing the proof.
Rights and permissions
About this article
Cite this article
Xu, W., Li, B., Ma, R. et al. A Novel Kernel Correlation Coefficient with Robustness Against Nonlinear Attenuation and Impulsive Noise. J Sign Process Syst 89, 395–413 (2017). https://doi.org/10.1007/s11265-016-1212-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11265-016-1212-8