Dimensionality, Coordinate System and Reference Frame for Analysis of In-Situ Space Plasma and Field Data

Abstract

In the analysis of in-situ space plasma and field data, an establishment of the coordinate system and the frame of reference, helps us greatly simplify a given problem and provides the framework that enables a clear understanding of physical processes by ordering the experimental data. For example, one of the most important tasks of space data analysis is to compare the data with simulations and theory, which is facilitated by an appropriate choice of coordinate system and reference frame. While in simulations and theoretical work the establishment of the coordinate system (generally based on the dimensionality or dimension number of the field quantities being studied) and the reference frame (normally moving with the structure of interest) is often straightforward, in space data analysis these are not defined a priori, and need to be deduced from an analysis of the data itself. Although various ways of building a dimensionality-based (D-based) coordinate system (i.e., one that takes account of the dimensionality, e.g., 1-D, 2-D, or 3-D, of the observed system/field), and a reference frame moving along with the structure have been used in space plasma data analysis for several decades, in recent years some noteworthy approaches have been proposed. In this paper, we will review the past and recent approaches in space data analysis for the determination of a structure’s dimensionality and the building of D-based coordinate system and a proper moving frame, from which one can directly compare with simulations and theory. Along with the determination of such coordinate systems and proper frame, the variant axis/normal of 1-D (or planar) structures, and the invariant axis of 2-D structures are determined and the proper frame velocity for moving structures is found. These are found either directly or indirectly through the definition of dimensionality. We therefore emphasize that the determination of dimensionality of a structure is crucial for choosing the most appropriate analysis approach, and failure to do so might lead to misinterpretation of the data. Ways of building various kinds of coordinate systems and reference frames are summarized and compared here, to provide a comprehensive understanding of these analysis tools. In addition, the method of building these systems and frames is shown not only to be useful in space data analysis, but also may have the potential ability for simulation/laboratory data analysis and some practical applications.

1 Introduction

In physics studies, the establishment of two systems is fundamental: one is the reference frame of a system relative to the observer and another is the coordinate system. A coordinate system establishes the orientation of an observed object/field in space, and a reference frame (with defined velocity) establishes its motion. An appropriate reference frame and coordinate system may help us greatly simplify a given problem, perform calculations more easily, make experimental data more ordered and enable a clearer understanding of physical processes. This is especially vital in space plasma theory, simulation and data analysis.

In both theoretical analysis and numerical simulations, the coordinate system and the reference frame are chosen a priori. For example, in the theoretical analyses of Kelvin-Helmholtz waves (e.g., Pu and Kivelson 1983), or tearing mode configurations (e.g., Terasawa 1983), the physical fields are set to be 2-D and then the coordinate system is naturally based on the dimensionality (dimension number, number of spatial degrees of freedom required to describe a field, i.e., whether it is 1-D, 2-D or 3-D) based coordinate system (hereafter we refer to as a ‘D-based coordinate system’). Examples in simulation work include 2-D simulations of magnetic reconnection (e.g., Lin and Swift 1996; Birn and Hesse 2001; Daughton et al. 2009) or 1-D simulations of plasma processes (e.g., Dawson 1983), which have all used a D-based coordinate system. In these studies, the reference frame is just the frame moving along with the structure, e.g., the current sheet or a flux rope.

For the discussion of coordinate systems, in this article we mainly focus on a local Cartesian coordinate system which varies with position. Global coordinate systems can be seen in the review papers by Song and Russell (1999) and Kivelson and Russell (1995). As we have mentioned, in most simulation and theoretical analysis, the natural coordinate system choice is D-based. We should emphasize the definition of dimensionality (dimension number) here. Dimensionality is a basic concept in plasma physics and ordinary fluid dynamics. In most physical problems we only care about the variation of physical fields, and therefore we use the spatial variation of field quantities instead of the field quantity itself to define the dimensionality. For example, say we have a (scalar or vector) field quantity with a given structure in 3 dimensional Cartesian space $\varphi =\varphi ( x,y,z )$. If the field quantity varies in only one direction (say, $x$), such that $\partial \varphi /\partial y = \partial \varphi /\partial z = 0$ (for each Cartesian component, if it is a vector), then we have $\varphi = \varphi (x)$ and the structure is one-dimensional (1-D). If there is no change along only one direction (say $z$), such that $\partial \varphi / \partial z = 0$, then $\varphi = \varphi (x,y)$ (i.e., the physical field varies in the $x$–$y$ plane) and the field/structure is two-dimensional (2-D). In this case the $z$-direction is known as the invariant axis of the structure. If one cannot find any invariant directions, the field/structure is three dimensional (3-D). For both 1-D and 2-D cases, we allow the existence of all three components of a field quantity. Based on dimensionality, we can establish a local Cartesian coordinate system. This D-based coordinate system has a very clear physical meaning. For example, a flux rope or a flux transfer event (e.g., Russell 1995) is often a 2-D structure and all fields vary little along its axis. Then, if we can determine its dimension number, the invariant axis, which corresponds to the axis of the flux rope, can be found. Another example is a 1-D current sheet (often seen at the magnetopause and the magnetotail or in a shock front) in which all field quantities vary only along its normal direction. If we have determined its dimension number, then the only variation direction is found and it corresponds to just the normal of the current sheet.

After we have obtained data from space instruments, we often hope to interpret it through some theoretical work or numerical simulations that are expressed in a D-based coordinate system. However, the data are obtained initially in the spacecraft frame. For example, for a spin-stabilized satellite, one axis is the spin axis and the other two axes are in the plane perpendicular to the spin axis. Then, if we know the direction of the spin axis in the Earth’s frame we can transform the data to a global coordinate system such as the Geocentric Solar Ecliptic (GSE) or Geocentric Solar Magnetospheric (GSM) coordinates. This step of axis transformation is usually not very difficult and normally is provided in the scientific data of the satellite mission. However, if we intend to analyze the data in a D-based coordinate system, it is not very straight forward. We require a general method to identify this coordinate system through analyzing the data itself.

For a 1-D structure such as a current sheet, finding its normal forms the basis of building a D-based coordinate system, because the normal is the only variation direction of the 1-D structure. To completely build a Cartesian coordinate system, we need the other two axes, which can be any two orthogonal directions that are in the plane perpendicular to the normal. Over the past years of space data analysis, various attempts to define such coordinates have been made. The first systematic and quantitative method for establishing a Cartesian coordinate system was the minimum variance analysis (MVA) method proposed by Sonnerup and Cahill (1967). It is undoubted that the coordinate system established by using the method of MVA (Sonnerup and Cahill 1967) has played, and will continue to play, a key role in single and multiple satellite data analysis. Methods like the Timing (e.g., Russell et al. 1983) or coplanarity (e.g., Schwartz 1998) can also be used to find the normal for building a D-based coordinate system for 1-D cases. For a 2-D structure such as a flux rope, because its axis is the invariant direction, finding the flux rope axis is the first step to build a D-based coordinate system. After we have determined the axis, the other two axes can be any two orthogonal directions that are in the plane perpendicular to the axis, and we can choose one direction as the projection of the spacecraft path in this plane and the last axis of this D-based coordinate system completes the right hand orthogonal set. D-based coordinate systems are a kind of local coordinate system. Other kinds of local coordinate systems such as the local field aligned coordinate system, used when studying some waves in the magnetosphere (e.g., Hartinger et al. 2011; Shi et al. 2013, 2014) will not be discussed in detail in this article.

For the description of processes taking place in space, one must use a reference frame. A good frame of reference is often the frame that is moving along with the structure in space, within which one can analyze the physical processes (note that the “structure” of interest, e.g. a magnetic flux rope, may not be simply moving with the plasma flow). In theory/simulation work, for example, to study a flux tube, reconnection point, or current sheet characteristics, we often need to study the electromagnetic fields and plasma/particle dynamics in the reference frame moving along with the structure. Then the mass, momentum and energy conservation equations can more easily be solved in this structure rest-frame. When we intend to link the data to the physical parameters obtained from theory/simulation, or to give the observed phenomena a physical explanation, if we do not use the same frame, the explanation will be very difficult. However, the measured plasma and electromagnetic field data are gathered in the spacecraft frame, and in most cases of interest the structure moves with respect to the spacecraft. One simple and direct consideration is that if we could find the structure velocity, we then will be able to obtain the reference frame.

When the velocity of the structure is determined, one kind of reference frame is established. So, as a first step, it is important to determine the proper motion speed of the structure. In the non-relativistic approach (in which the magnetic field is independent of the observational frame of reference, but the electric field and plasma velocity are different in different frames), the time variation of a physical field quantity, $\varphi$ (which can be the density, temperature, pressure or magnetic field magnitude etc., or one component of a vector field), in the observer frame (normally this can be either the spacecraft or the instrument frame), is

$$\frac{\partial \phi }{\partial t}{|}_{\mathrm{obs}}=\frac{\partial \phi }{\partial t}{|}_{\mathrm{str}}-{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}\cdot \mathrm{\nabla }\phi$$

(1.1)

where we use the subscript ‘obs’ to indicate a partial-derivative in the observer frame (or spacecraft frame), and ‘str’ to indicate variation in the frame moving along with the structure. $V$_str in (1.1) is the structure velocity relative to the observer. This equation means that the time variation of the observed $\varphi$ can be caused either by the temporal variation (first term on the right) or the spatial variation (second term on the right), or both. In fact equation (1.1) can be derived from the material derivative expanded in the Euler description of a fluid, $\frac{\mathrm{d}\phi }{\mathrm{d}t}=\frac{\partial \phi }{\partial t}+\stackrel{\rightharpoonup }{V}\cdot \mathrm{\nabla }\phi$, where $\frac{\mathrm{d}\varphi }{ \mathrm{d}t}$ is the material derivative (also called substantial derivative or particle derivative) that describes the time variation in the frame moving with the material particle, $\frac{\partial \varphi }{ \partial t}$ is the local derivative representing the time variation in the observer frame and $\stackrel{\rightharpoonup }{V}\cdot \mathrm{\nabla }\phi$ is the convective derivative. Because the local derivative and the convective derivative are much easier to measure/observe than the material derivative, in practice we normally use the former two to describe the physical processes, although many physical laws like momentum conservation are more conveniently described under a Lagrangian description using material derivatives. In space, the structure can be analogous to the material particle and then we obtain equation (1.1). For all these time derivatives, we use partial derivative with subscripts indicating the frame instead of using partial derivative or total derivative, because the only difference between partial derivative or total derivative here is the frame difference and in different points of view the partial derivative and total derivative can be changed into each other. For example, the position of the symbol ‘$d$’ and ‘$\partial$’ we used in this equation $\frac{\mathrm{d}\phi }{\mathrm{d}t}=\frac{\partial \phi }{\partial t}+{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}\cdot \mathrm{\nabla }\phi$ are opposite to that in (1.1) in Song and Russell (1999) but the equation we are using is the same, which means the symbol ‘$d$’ and ‘$\partial$’ themselves have no physical difference here. Therefore to state clearly and avoid unnecessary confusions, we use the ‘$\partial$’ to replace the ‘$d$’ and use different subscripts (‘obs’ or ‘str’) to distinguish temporal variations in different reference frames. Then, when we intend to use a theory or simulation which is described in the ‘str’ frame to interpret observations that are measured in the spacecraft ‘sc’ frame, equation (1.1) provides a way of frame transformation.

In summary, while in simulations and theoretical work the establishment of the coordinate system and the reference frame is straightforward, the determination of these from space data needs some more analysis. In this article, we will review the methods of establishing the D-based coordinate system and ways of constructing the proper frame of reference that are used in the space data analysis, and their application in the analysis on structures measured in space. Over the past twenty years, especially following the launch of the ESA Cluster constellation, many multi-point methods have been developed and applied to study space physics processes. Applications of these techniques are critically dependent on correct determination of structure dimensionality, principle axis and velocity. Nevertheless, we find that in some cases some techniques were not quite appropriately applied and may have affected their conclusions. Now that the new NASA constellation Magnetospheric Multiscale (MMS) is operational; it is necessary and timely to clarify these problems and further develop new multi spacecraft data analysis techniques.

In this review paper, the determination of dimensionality analysis, principle axis and velocity determination will be discussed, and also other related methods, such as some single satellite methods will be summarized and compared. Applications on reconstruction techniques for magnetic flux ropes, current sheets and other magnetic structures will be introduced, and, we will review the conditions under-which each method should be most appropriately and effectively used. In both Sects. 2 and 3 we will first review single spacecraft-based methods, and then multi-point methods, including some traditional methods and their continuing development, and novel approaches developed very recently. In Sect. 2, we will review six methods for building D-based coordinate systems. While all of these methods can build a D-based coordinate system for 1-D structures, some methods may no longer be D-based when applied to higher dimensional structures. In some of these (but not all) cases, this may be rectified by a simple axis rotation. In Sect. 3 we will review the frame of reference in which the observer resides. We make the argument that finding the observational frame is dependent upon/closely related to finding the D-based coordinate system. For example, the application of the traditional Triangulation/Timing methods (Russell et al. 1983) to 2-D structures obtains both the reference frame and a D-based coordinate system together. In Sect. 4 we discuss some uncertainties and cautions in using some important methods. Since in data analysis different field quantities might have different features, we also discuss the dimensionality for different field quantities. Then we compare all the methods discussed, and show where they can be best applied. We emphasize that different methods will have their best application in different circumstances. Therefore, we advise in many cases to use different methods for the same event to compare and obtain a more reliable coordinate system and reference frame. Lastly we show some potential applications of some gradient methods in simulation and other circumstances.

2 D-Based Coordinate Systems

As we have mentioned Sect. 1, dimensionality based coordinate system is very commonly used in the numerical simulation and theoretical analysis of 1-D or 2-D problems. In the data analysis of in situ observations, 2-D or 1-D problem is often much easier to study and compare with numerical or theoretical analysis than a three dimensional (3-D) one. It is important, therefore, to pre-determine the dimensionality (dimension number) and characteristic directions of observed space structures before proceeding with further data analysis. In addition, a reduced dimension number is an assumption of many analysis methods. For example, the widely used MVA method (Sonnerup and Scheible 1998), the multi-spacecraft-timing method and its later revision (e.g., Russell et al. 1983; Zhou et al. 2006a, 2006b; Zhou et al. 2009), and Grad–Shafranov (GS) reconstruction methods (Hau and Sonnerup 1999; Hu and Sonnerup 2002; Sonnerup et al. 2006; Tian et al. 2010, 2014) are all set up for 1-D or 2-D structures. However, even for commonly identified structures the dimension number is not always as expected. For example, the magnetopause current sheet sometimes is not 1-D but has some small 2-D structures embedded (e.g., Sonnerup and Guo 1996). Magnetic flux ropes, which are generally regarded as 2-D, may actually be 3-D. In such situations the GS method is not applicable. Therefore, the examination of the structure dimension number with multi-points data is desirable.

In the past and recent years, the dimensionality based coordinated system in data analysis has been established in various cases. In this Section first we will introduce some traditional and new single spacecraft methods, followed by a review of some multi spacecraft approaches including a method directly through the definition of dimensionality (dimension number). The comparison of the methods will be made in Sect. 4.3.

2.1 Sonnerup-Cahill Minimum/Maximum Variance Analysis (MVA) Based Coordinate System

The first systematic and quantitative method for establishing a Cartesian coordinate system is the minimum variance analysis (MVA) method proposed by Sonnerup and Cahill (1967). The MVA based coordinate system is a kind of principle-axes coordinate system. It is the most commonly used method to analyze current layers (e.g., magnetopause, shock, or tail current sheet) and was developed using magnetic field measurements in near-Earth space (Sonnerup and Cahill 1967). This method is easy to understand and implement, and it can always provide a Cartesian coordinate system, which makes it very powerful and useful in the space data analysis community. There is no doubt that coordinate systems established by using the method of MVA (Sonnerup and Cahill 1967) have played and will continue to play an indispensable role in single satellite data analysis and still in multi-satellite data analysis.

For 1-D cases such as a current sheet, there is only a single variation direction (the normal direction) and this can be found using MVA analysis, leading directly to the construction of a D-based coordinate system. For 2-D cases, the construction of a D-based coordinate system is indirect. Here is one approach (see details in Sect. 2.2): first we build a coordinate system using the three eigenvectors, $L$, $M$ and $N$, which indicate maximum, intermediate and minimum variance directions from the MVA method. Then we can rotate any of them to obtain the invariant axis using the method mentioned in Hu and Sonnerup (2002). In principle we do not need these $L$, $M$ or $N$—we can just use an arbitrary direction as an initial guess and then rotate it to obtain the invariant axis using a minimization procedure. Once we have determined the invariant axis, the construction of the D-based coordinate system is almost complete.

When it was first introduced, the MVA method was based on the assumption that the boundary is 1-D (Sonnerup and Scheible 1998), such that the magnetic field along the normal of the 1-D structure does not vary either temporally or spatially (this requires that both the magnetic and electric fields should be 1-D, i.e., they only vary along one direction). For many 2D or 3D structures it is also very useful to provide a local coordinate system (not D-based), although sometimes the physical interpretation of the original axes may not be very clear. This method gives three orthogonal axes based on the magnetic field measurements not at one time moment, but a time interval between two observational time points, which are selected arbitrarily but sufficiently far apart to use enough sampled data. Then in some cases using different time intervals one may obtain different axes, indicating finer scale structure; for example, when there are some sublayers within a current sheet.

A detailed introduction of the method can be found in (Sonnerup and Scheible 1998). The starting point of the MVA method is this: for a 1-D magnetic structure, the condition that $\nabla \cdot \vec{B} =0$ implies, for a suitably rotated set of coordinate unit vectors $( \vec{n}_{1}, \vec{n}_{2}, \vec{n}_{3} )$, that ${\partial B_{n1}} / \partial n_{1} = {\partial B_{n2}} / {\partial n_{2}} = {\partial B_{n3}} / {\partial n_{3}} = 0$. This is because, for a 1-D structure, variations in all components of $\vec{B}$ must already be zero in two of the three directions (e.g. $\vec{n}_{1}$ and $\vec{n}_{2}$; $\partial / \partial n_{1} = \partial / \partial n_{2} = 0$), therefore $\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}=\partial B_{n3}/\partial n_3=0$ for the third direction (Actually this is the coordinate system which can be determined by the three eigenvectors of the minimum directional derivative (MDD) method described in Sect. 2.4). This means that $B_{n3}$ does not change along the direction ${\stackrel{\rightharpoonup }{n}}_3$. Similarly, $\nabla \times \vec{E} =0$ in the direction of ${\stackrel{\rightharpoonup }{n}}_3$, if $\vec{E}$ is also 1-D (Note that when $\vec{B}$ is 1-D, it is not always guaranteed that $\vec{E}$ is also 1-D, as discussed in Sect. 4.2). According to Faraday’s law $\partial \stackrel{\rightharpoonup }{B}/\partial t=-\mathrm{\nabla }\times \stackrel{\rightharpoonup }{E}$, we obtain that $\partial B_{n3}/\partial t = 0$, namely $B_{n3}$ does not change with time. Then, for a 1-D structure, $B_{n3}$ does not vary either in time or space, that is, it is always constant. To find the direction of ${\stackrel{\rightharpoonup }{n}}_3$ which makes $B_{n3}$ nearly constant, we can use a set of ($N$) magnetic field measurements over a given time interval to calculate the variance of the magnetic field in a direction $\vec{n}$, given by: $\sigma _{n}^{2} = \frac{1}{N} \sum_{i=1}^{N} ( B_{n} ( i ) - \langle B_{n} ( i ) \rangle ) ^{2}$ (where $B_{n} ( i ) = \vec{B} ( i ) \cdot \vec{n}$) and find the direction $\vec{n}$ that minimizes $\sigma _{n}^{2}$. In practice, as shown in detail by Sonnerup and Scheible (1998), this can be expressed as a conditional minimization/maximization problem and can be solved by calculating the eigenvalues and eigenvectors of a symmetric matrix $\overleftrightarrow{M}=〈\stackrel{\rightharpoonup }{B}\stackrel{\rightharpoonup }{B}〉-〈{\stackrel{\rightharpoonup }{B}}_i〉〈{\stackrel{\rightharpoonup }{B}}_j〉$. The three eigenvalues of $\overleftrightarrow{M}$ ($\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$) are real and the eigenvectors $L$, $M$ and $N$ are perpendicular to each other. Then the three eigenvectors build a new coordinate system. If the satellite passes through a 1-D structure this is indicated by ($\lambda _{1}$, $\lambda _{2} \gg \lambda _{3}$ (the converse of this may not be true, see Sonnerup and Scheible (1998) and the discussion below in this section). In this case the normal direction of this 1-D structure is just along the eigenvector corresponding to the minimum eigenvalue, ${\stackrel{\rightharpoonup }{n}}_3$. Then, for a 1-D case the three orthogonal eigenvectors derived from $\overleftrightarrow{M}$ build a D-based coordinate system. But if $\lambda _{1}$, $\lambda _{2} \gg \lambda _{3}$, the structure is not necessarily 1-D, see Sonnerup and Scheible (1998) and the discussion below in this section.

Note that even for 2-D or 3-D structures, as the matrix $\overleftrightarrow{M}=〈\stackrel{\rightharpoonup }{B}\stackrel{\rightharpoonup }{B}〉-〈{\stackrel{\rightharpoonup }{B}}_i〉〈{\stackrel{\rightharpoonup }{B}}_j〉$ is symmetrical, we can always obtain three eigenvalues which are real and three eigenvectors perpendicular to each other corresponding to the three eigenvalues. Therefore, even for a 2-D or 3-D structure, in practice we are still able to calculate three the eigenvectors and eigenvalues. Therefore, the MVA analysis essentially simplifies the problem, and can always help us find a new available coordinate system. It should also be noted that because in 2-D or 3-D problems, the coordinate system is not D-based any more, the meaning of each axis is not necessarily clear, and should be evaluated case by case. As described in Sonnerup and Scheible (1998), from MVA methods one cannot know whether the structure is one/two-dimensional or not. For example, for a 2-d flux tube, the three directions of the MVA methods cannot always strictly denote the axial direction of the flux tube. Using simulated flux ropes in a 3-D MHD simulation, Xiao et al. (2004) found that for different virtual satellite crossing paths, the axial direction of flux tube is close to different eigenvector directions of the MVAB method. It is suggested to use MVAJ to help determine the axial direction, because practically a flux rope has a very strong electric current along the axis (Xiao et al. 2004; Haaland et al. 2004). Then the maximum variation of the current should be along the axis. As shown in Fig. 1, we tested the ability of MVAB (Fig. 1b, c, and d) and MVAJ (Fig. 1e, f, and g) methods in determining the axial direction in a magnetic field generated from a self-consistent 2D flux rope model. In this model, the axial field $B_{z}$ can be taken as different functions of magnetic potential A, corresponding to flux ropes with different structure (e.g. Tian et al. 2019). The red lines in Fig. 1a represent 25 test paths with different impact parameter (IP), the minimum distance between the path and the axis center, in the cross section of the flux rope. The second, third and fourth rows show angles between $L$, $M$, $N$ and the true invariant $z$-axis for three flux ropes with different $B_{z}$, respectively. We find that the $M$ (minimum variation direction) and $L$ (maximum variation direction) vectors are close to the invariant axis (i.e., less than 30^∘) for MVAB and MVAJ, respectively, only when the impact parameter (IP) is close to zero for flux ropes with non-zero axial fields. Nevertheless, MVAJ has been successfully used in the analysis of data from the Cluster mission (Escoubet et al. 2001) to determine the axis of a flux rope (e.g., Pu et al. 2005) and a discontinuity (Haaland et al. 2004; Rezeau et al. 2018). The results of MVA also depend on the model of the structure (Tian et al. 2019; also see Lepping et al. 1990 for a similar experiment). For example, when the axial field is zero, $N$ from MVAB or $L$ from MVAJ can well characterize the axis direction (Fig. 1d and g).

Fig. 1

(a) The cross section of a model magnetic flux rope. Magnetic field lines are plotted with black lines and 25 paths for MVA tests are over-plotted with red lines. (b–d) shows the angles between the eigenvectors $\mathbf{L}$, $\mathbf{M}$ and $\mathbf{N}$ of MVAB analysis and the true invariant $z$ axis for three types of flux rope (i) $p= \frac{e^{-2A}}{3 \mu _{0}}$, $B _{z} = \frac{e^{-A}}{\sqrt{3}}$, representing a normal flux rope; (ii) $p=0$, $B_{z} = e^{-A}$, representing a forcefree flux rope; and (iii) $p= \frac{e^{-2A}}{2 \mu _{0}}$, $B_{z} =0$, representing a magnetic island, where $p$ denotes plasma pressure, $A$ is magnetic potential and $B_{z}$ is the axial magnetic field. (e–g) have the same format as in b–d but for MVAJ analysis (adopted from Tian et al. 2019). The vector with the smallest angle with $z$ is closest to the actual axial direction of the flux rope model

The MVA methods can not only be used to analyze magnetic field and current density, but also can be applied to the electric field (Sonnerup and Scheible 1998), mass flow $\rho \stackrel{\rightharpoonup }{V}$ (e.g., Sonnerup and Scheible 1998; Zhao et al. 2016), velocity vector $\stackrel{\rightharpoonup }{V}$ (e.g., Knetter 2005; Ling et al. 2018), and other vector fields. For a 1-D structure, as we mentioned above, the magnetic field along normal does not vary with both time and space. Theoretically, this is not valid for 2-D or 3-D structures but we can still perform the MVA on a time series of data to obtain a coordinate system which is in many cases better than the original system for the problem we need to analyze.

When one uses the GS reconstruction method (e.g., Sonnerup and Guo 1996; Sonnerup et al. 2006; Hasegawa et al. 2007; Tian et al. 2014, 2019) to reconstruct a flux tube, as it is a requirement to have a sufficiently accurate axis, the minimum or medium variation direction from MVA needs to be rotated to an angle to approach the real axial direction of the flux tube (e.g. Hu and Sonnerup 2002); then a D-based coordinate system is built. In this way, MVA can act as an indirect way to build a D-based coordinate system. A GUI interface for the MVA method can now be accessed in the Space Physics Environment Data Analysis System (SPEDAS).

2.2 D-Based Coordinate System for a 2-D Structure Based on Grad–Shafranov Reconstruction Method

The theories of series of Grad–Shafranov (GS) or MHD reconstruction methods are 2-D based in a D-based coordinate system, and the reconstructed plane is chosen to be the plane perpendicular to the invariant axis (e.g. Hau and Sonnerup 1999; Hu and Sonnerup 2002; Hasegawa et al. 2007; Teh et al. 2007; Sonnerup et al. 2006, 2016; Sonnerup and Teh 2008; Hasegawa et al. 2017). This reconstruction method has been applied to 2-D flux ropes (e.g., Hau and Sonnerup 1999; Hu and Sonnerup 2002; Hasegawa et al. 2007), the magnetopause current sheet (e.g., Hasegawa et al. 2004), reconnection structures (Teh et al. 2010), and drift mirror structures (e.g., Tian et al. 2012). The construction of a D-based coordinate as the first step is essential to the whole reconstruction.

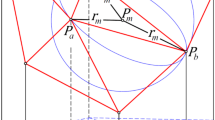
The invariant axis can be determined and then the D-based coordinate system can be established by the GS technique if the structure encountered is 2-D, time independent and magnetohydrostatic (Sonnerup et al. 2006). To obtain the axis through this technique one needs a reference frame, which can be obtained through the methods discussed in Sect. 3. For such a structure, the three quantities, thermal pressure $p$, the axial component of the magnetic field $B_{z}$ and hence the transverse pressure $P_{t} =p+ \frac{B_{z}^{2}}{2 \mu _{0}}$ are field line invariants. If the spacecraft trajectory intersects a field line in the 2D plane more than once, the field line invariant should have the same values of these quantities at each intersection point of a field line. Figure 2 shows the cross section of a Lundquist flux rope. The x axis is the trajectory of the spacecraft. The small circles and stars represent samples in the left and right half of the flux rope, respectively. $A_{l}$ and $A_{m}$ indicate the initial and maximum out-of-plane component of magnetic vector potential value. Hu and Sonnerup (2002) introduced a residue parameter $\mathrm{RES}=[ \sum_{i=1}^{m_{0}} ( P_{t,i}^{1\mathrm{st}} - P_{t,i}^{2\mathrm{nd}} )^{2} ]^{\frac{1}{2}} /| \max ( P_{t} ) - \min (P_{t} )|$ to represent the degree of scatter of $P_{t}$, where $\mathrm{m}_{0}$ is the number of points interpolated between $A_{l}$ and $A_{m}$. By testing trial axes with axis directions varying over a hemisphere, the optimal axis can be found when RES has a minimum.

Fig. 2

The top panel shows the cross section of the Lundquist flux rope model centered at $(x, y)=(0, 0.5)$. The solid line along $x$ axis is the projected spacecraft trajectory. The bottom panel shows the relationship between transverse pressure $P_{t}(x,0)$ and magnetic potential $A(x,0)$ for an incorrect $z$ axis. The small circles denote data points collected by a virtual spacecraft in the inbound trajectory. The stars denote data points in the out bound trajectory. $A_{l}$ and $A_{m}$ are the magnetic potentials at the starting point and the point of the closest approach, respectively. $A \in [A_{l}, A_{m}]$ is uniformly interpolated by $m_{0}$ points with the index of $i \in [1,m_{0}]$ for calculating the residue RES (adapted from Hu and Sonnerup 2002)

Figure 3 shows the residue map for a magnetic flux rope crossing event observed by the Magnetospheric Multiscale (MMS) spacecraft (Burch and Phan 2016). The resolution of the search grid is 10 degrees in longitude direction and 5 degrees in latitude direction. This shows that except for the axis ($L$) from MVAJ, the axis directions estimated by other methods are very consistent with each other. It should be noted that the broader area encircled by the contour line in Fig. 3 indicates some uncertainty of this method, which is 1.5 times the minimum RES. However, for events in which many field lines are encountered only once, such as the magnetopause crossings, the above method will fail.

Fig. 3

Polar map of axis directions for the magnetic flux rope event on 15 Oct. 2015, see text for detail (adapted from Tian et al. 2019). Small dots indicate the search grid points on the hemisphere of unit radius. The ‘+’ point on the pole indicates the minimum variance direction from MDD method. The direction deduced by minimum reside method of Hu and Sonnerup (2002) is marked with a triangle. An asterisk denotes the maximum variance direction from MVAJ. The square indicates medium variance direction from MVAB

If multi-satellite data are available, the invariant axis can be obtained by trial and error in another way. Hasegawa et al. (2004) used the intermediate variance direction of the MVA analysis with the constraint of $〈\stackrel{\rightharpoonup }{B}〉\cdot \stackrel{\rightharpoonup }{n}=0$ based on one satellite data, where $\stackrel{\rightharpoonup }{n}$ is the minimum variance direction in MVA acting as the initial $z$-axis to conduct a GS reconstruction. The resulting optimal axis is the one for which the correlation coefficient between the magnetic fields reconstructed in the map and the fields actually observed by other spacecraft reaches a highest value. Figure 4 shows a case of magnetopause reconstruction. A high correlation coefficient of 0.9790 (Fig. 4b) between the predicted and measured magnetic fields suggests that the invariant axis is well determined. The high correlation coefficient also indicates that the conditions, i.e. 2D and stationary, are suitable for the GS technique. For Cluster observed events, Hasegawa et al. (2005, 2006) further showed that by ingesting data from all four Cluster spacecraft, four independent field maps, one for each spacecraft, can be reconstructed and then merged into an optimized GS map.

Fig. 4

(a) Reconstructed magnetic field map for a magnetopause crossing by the Cluster 1 spacecraft on 30 June 2001 (adapted from Hasegawa et al. 2004). Contours indicate the magnetic field lines projected onto the reconstruction plane and color shows the magnetic component along the invariant axis. The measured magnetic fields from all four spacecraft are overlapped on the plane with white arrows. (b) Correlation between the measured and recovered magnetic field components

2.3 Multi-point Timing—Setting a D-Based Coordinate System for a 1-D Structure

For 1-D structures, Timing methods can help to build a D-based coordinate system after finding the normal direction. Since one can get the normal and velocity at the same time from this approach, we will discuss it in detail in Sect. 3.3. There are a number of different versions of this method that differ based on their starting assumptions. For example, assuming the velocity is constant we have the CVA (Constant Velocity Approach: e.g., Russell et al. 1982; Knetter et al. 2004), while assuming the thickness is constant we get CTA (Constant Thickness Approach: Haaland et al. 2004). Other related approaches are DA (Discontinuity Analyzer, Dunlop and Woodward 1998) and MTV (Minimum Thickness Variation, Paschmann et al. 2005). In this review we will mainly discuss the CVA.

2.4 Method of Building a D-Based Coordinate System Through Definition of Dimensionality: Minimum Directional Derivative (MDD) Analysis

Shi et al. (2005) proposed a method directly based on the definition of dimensionality. Since this analysis method is derived from looking for the minimum derivative along various directions, it was named as “Minimum Directional Derivative (or Difference)” analysis, or MDD analysis in short. Note that although other ways of building a D-based Coordinate System are not as straightforward as the MDD method from the definition of the dimension number, they are still very necessary, especially when the estimation of field gradient fails, which happens in many cases. A GUI interface for the MDD method can now be accessed in the SPEDAS.

2.4.1 Review of the Analysis Processes

First we discuss the dimension number determination for the magnetic field. For other parameters like electric field or flow field the algebraic manipulations are the same. For a 1-D or 2-D structure, if a certain direction $\stackrel{\rightharpoonup }{n}$ is along the invariant direction, i.e. along which all the parameters remain constant, from the definition of dimensionality we mentioned in Sect. 1, it will certainly satisfy that the directional derivative along $\stackrel{\rightharpoonup }{n}$ for all component of the magnetic field is equal to zero, i.e., $\partial B_{x}/\partial n=0$, $\partial B _{y}/\partial n=0$ and $\partial B_{z}/\partial n=0$, where $x$, $y$, and $z$ are the axes of a certain coordinate system such as GSE, and then one finds ${(\partial \stackrel{\rightharpoonup }{B}/\partial n)}^2={(\partial B_x/\partial n)}^2+{(\partial B_y/\partial n)}^2+{(\partial B_z/\partial n)}^2=0$. To find the invariant direction $\stackrel{\rightharpoonup }{n}$, we just need to find the minimum value of ${(\partial \stackrel{\rightharpoonup }{B}/\partial n)}^2$. Therefore we must first calculate the gradient of the magnetic field.

Using the measurements of a multi-spacecraft system with at least four spacecraft, it is not difficult to estimate all nine components of the magnetic gradient tensor $G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ at every observing moment, using various methods of estimation. For the case of four spacecraft such as Cluster or MMS, linear estimation is appropriate and identical results can be obtained from different methods including least squares methods (Harvey 1998; Chanteur and Harvey 1998), Barycentric method (Chanteur 1998), and Taylor expansion method (Pu et al. 2003), etc. The least squares method can be easily applied when there are more than four points of measurements. Here we briefly introduce the Taylor expansion scheme (Pu et al. 2003) to calculate $\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$, which can be expanded as

$$G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}=\left[\begin{array}{ccc}\frac{\partial B_x}{\partial x}& \frac{\partial B_y}{\partial x}& \frac{\partial B_z}{\partial x}\\ \frac{\partial B_x}{\partial y}& \frac{\partial B_y}{\partial y}& \frac{\partial B_z}{\partial y}\\ \frac{\partial B_x}{\partial z}& \frac{\partial B_y}{\partial z}& \frac{\partial B_z}{\partial z}\end{array}\right]$$

(2.1)

Taking the components of the first row of $\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ as an example, the Taylor expansion is accurate to first order in $\Delta r\cdot \nabla B_{x}$ measured by satellite C1, C2 and C4 in the vicinity of C3 is

$$B_{xi}=B_{x3}+\mathrm{\Delta }{\stackrel{\rightharpoonup }{r}}_{i3}\cdot \mathrm{\nabla }{B}_{x3}(i=1,2,4)$$

(2.2)

where $\mathrm{\Delta }{\stackrel{\rightharpoonup }{r}}_{i3}={\stackrel{\rightharpoonup }{r}}_i-{\stackrel{\rightharpoonup }{r}}_3$ represents the position of satellite C$i$ relative to C3, $\nabla B_{x3} = (\frac{\partial B_{x3}}{ \partial x},\frac{\partial B_{x3}}{\partial y},\frac{\partial B_{x3}}{ \partial z})$ indicates the $Bx$ gradient at the C3 position. Since the Bx components and $\mathrm{\Delta }{\stackrel{\rightharpoonup }{r}}_{i3}$ can be easily obtained from observation, it is then easy to calculate $\nabla B_{x3}$ by solving the three linear equations (2.2). For a linear approximation, $\nabla B_{x}$ is identical using different satellites, so we can use $\nabla B_{x3}$ to represent the $\nabla B _{x}$ that we need. In the same way, all the components of $\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ can be obtained, which are first-order accurate at C3.

Now we turn back to the question of finding the minimum value of ${(\partial \stackrel{\rightharpoonup }{B}/\partial n)}^2={(\partial B_x/\partial n)}^2+{(\partial B_y/\partial n)}^2+{(\partial B_z/\partial n)}^2$. The product of $\stackrel{\rightharpoonup }{n}$ and $\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ is

$$\stackrel{\rightharpoonup }{D}=\stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\stackrel{\rightharpoonup }{B}=\partial \stackrel{\rightharpoonup }{B}/\partial n=(\partial B_x/\partial n,\partial B_y/\partial n,\partial B_z/\partial n)$$

(2.3)

Then, given the estimation of matrix $\nabla \vec{B}$, the invariant axis $\stackrel{\rightharpoonup }{n}$ can be determined by minimization of $D^2={(\partial \stackrel{\rightharpoonup }{B}/\partial n)}^2={(\partial B_x/\partial n)}^2+{(\partial B_y/\partial n)}^2+{(\partial B_z/\partial n)}^2$, and this minimization is subject to the normalization constraint $\vert \vec{n} \vert ^{2} - 1 = 0$. In order to solve this problem of conditional extremum, we introduce a Lagrange multiplier $\lambda$ and seek the solution of three linear equations

$$ \left \{ \textstyle\begin{array}{l} \displaystyle\frac{\partial }{\partial n_{x}} \bigl( D^{2} - \lambda \bigl(| \vec{n} |^{2} - 1\bigr) \bigr) = 0 \\ \displaystyle\frac{\partial }{\partial n_{y}} \bigl( D^{2} - \lambda \bigl(| \vec{n} |^{2} - 1\bigr) \bigr) = 0 \\ \displaystyle\frac{\partial }{\partial n_{z}} \bigl( D^{2} - \lambda \bigl(| \vec{n} |^{2} - 1\bigr) \bigr) = 0 \end{array}\displaystyle \right ., $$

(2.4)

where ($n_{x}$, $n_{y}$, $n_{z}$) are three components of $\stackrel{\rightharpoonup }{n}$ in the original coordinate system in which the magnetic field data are given. Carrying out the differentiations, Eqs. (2.4) become

$$\{\begin{array}{l}\stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial n_x}=\lambda n_x\\ \stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial n_y}=\lambda n_y\\ \stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{D}}{\partial n_z}=\lambda n_z\end{array}.$$

(2.5)

Note that the partial derivatives $\partial /\partial n_{x}$, $\partial /\partial n_{\mathrm{y}}$, and $\partial /\partial n_{z}$ in the above equations are applied holding ($x$, $y$, $z$) constant, hence these equations simplify to

$$\{\begin{array}{l}\stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial x}=\lambda n_x\\ \stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial y}=\lambda n_y\\ \stackrel{\rightharpoonup }{n}\cdot \mathrm{\nabla }\overrightarrow{B}\cdot \frac{\partial \stackrel{\rightharpoonup }{B}}{\partial z}=\lambda n_z\end{array}.$$

(2.6)

Finally, these equations have the form of an eigenvalue problem $(\overleftrightarrow{L}-\lambda \overleftrightarrow{I})\overrightarrow{n}=0$ where $\overleftrightarrow{L}=\overleftrightarrow{G}{\overleftrightarrow{G}}^T=(\mathrm{\nabla }\overrightarrow{B}){(\mathrm{\nabla }\overrightarrow{B})}^T$ ($T$ denotes transposition) is a symmetrical matrix. Therefore the eigenvalues of $\overleftrightarrow{L}$ are all real and the corresponding eigenvectors are orthogonal. It can be demonstrated (by writing the matrix $\overleftrightarrow{L}$ in the eigenvector basis, where the matrix $\overleftrightarrow{L}$ is diagonal) that the three eigenvalues $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ represent the maximum, intermediate and minimum values of $D^{2}$. The three eigenvectors $\vec{n}_{1}$, $\vec{n}_{2}$ and $\vec{n}_{3}$ thus represent the three directions along which $D^{2}$ have the maximum, intermediate, and minimum values, which are $\vert \partial \vec{B} / \partial n_{1} \vert ^{2}$, $\vert \partial \vec{B} / \partial n_{2} \vert ^{2}$, and $\vert \partial \vec{B} / \partial n_{3} \vert ^{2}$, respectively. Thus the three eigenvalues can be viewed as the indicators for determining the dimension number of the magnetic structure, since they identify directions along which the spatial gradients are large or small. Generally, we can say that if $\lambda _{1}$, $\lambda _{2}$ and $\lambda _{3}$ are not very far from each other within a structure, we can regard it as a 3-D structure. If $\lambda _{1}$, $\lambda _{2}\gg \lambda _{3}$, we can deem it as a quasi-2-D structure with its invariant direction along $\vec{n}_{3}$, i.e., $\partial / \partial n_{3}=0$. If $\lambda _{1}\gg \lambda _{2}$, $\lambda _{3}$, then it can be regarded as a quasi-1-D structure, with the invariant axes in the plane of $\vec{n}_{2}$ and $\vec{n}_{3}$, and the only variant direction is along $\vec{n}_{1}$.

Here in data analysis we briefly summarize the practical steps of dimension number determination and D-based coordinate system setup, containing the following steps, see Fig. 5. First, estimate the field gradient tensor $G = \nabla \vec{B}$ ($\vec{B}$ can be replaced by any vector field, e.g. $\stackrel{\rightharpoonup }{V}$ or $\stackrel{\rightharpoonup }{E}$) at every moment by multi-point measurements. Second, find the eigenvalues and eigenvectors of a symmetrical matrix $L = GG^{T} = ( \nabla \vec{B} ) ( \nabla \vec{B} )^{T}$. The three eigenvalues $\lambda _{\max }$, $\lambda _{\mathrm{mid}}$, and $\lambda _{\min }$ represent the maximum, intermediate and minimum values of the field directional derivatives, and the three eigenvectors ${\stackrel{\rightharpoonup }{n}}_{max}$, ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$ and ${\stackrel{\rightharpoonup }{n}}_{min}$ represent the corresponding directions. Third, based on these calculations we determine the dimensionality and characteristic directions of the structure, as shown in Fig. 5. One special case not mentioned in Fig. 5 is when $\lambda _{1}\gg \lambda _{2}\gg \lambda _{3}$, it can be 1-D or 2-D depending on one’s point of view. Finally, the directions ${\stackrel{\rightharpoonup }{n}}_{max}$, ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$ and ${\stackrel{\rightharpoonup }{n}}_{min}$ can be used to build a D-based coordinate system.

Fig. 5

Steps of MDD tool to determine the structure dimension number and principal directions

It is worth noting here that $\stackrel{\rightharpoonup }{n}$ and $-\stackrel{\rightharpoonup }{n}$ are the same eigenvector (the same situation also appears in the MVA analysis, see the discussion in Sonnerup and Scheible (1998) when calculating eigenvectors. For an ordered visualization of the results, one way is to set arbitrarily the $x$ (or $y$, $z$) component of $\stackrel{\rightharpoonup }{n}$ to be positive so that we can get a series of directions which can be compared with each other, and one can also calculate the average direction or check for variations of the structure.

Another point we would like to mention here is the attempt of finding the quantitative index of dimension number in order to visualize the effective dimensionality more easily. Rezeau et al. (2018) recently introduced three parameters that may be used as proxies, $D_{1} = (\lambda _{\max } - \lambda _{\mathrm{mid}} )/\lambda _{\max }$, $D _{2} = (\lambda _{\mathrm{mid}} - \lambda _{\min } )/\lambda _{ \max }$ and $D_{3} = \lambda _{\min } /\lambda _{\max }$, which all vary from 0 to 1 and whose sum is 1. When $\lambda _{\max }$, $\lambda _{\mathrm{mid}}\ \mbox{and} \lambda _{\min }$ are comparable to each other, one obtains $D_{1} \approx 0$ and $D_{2} \approx 0$, while $D_{3} \approx 1$, indicating a quasi-3-D case. When $\lambda _{\max } \gg \lambda _{\mathit{mid}}, \lambda _{\min }$, one obtains $D_{1} \approx 1$, while $D_{2} \approx 0$ and $D_{3} \approx 0$, which indicates a quasi-1-D case. When $\lambda _{\max },\lambda _{\mathrm{mid}}\gg \lambda _{\min }$ one obtains $D_{1} \approx 0$, $D_{3} \approx 0$, while $D_{2} \approx 1$, which indicates a quasi-2-D case. However, the difference between these three cases are not always clear and the three proxies are not always ideal. Considering a flux rope with $\lambda _{\max } = 5$, $\lambda _{\mathrm{mid}} = 1$ and $\lambda _{\min } = 0.1$, for example, we get the dimensionality proxies $D_{1} = 0.8$, $D_{2} = 0.18$ and $D_{3} = 0.02$. The structure can be 1-D but it shows a slightly 2-D character since $D_{2}$ is not negligible (1-D but much more 2-D than 3-D). The fact that $D_{1} > D _{2}$ indicates that the tube is strongly flattened in one direction, which shows a transition between 1D (tube flattened) and 2D (circular tube). Such flux rope structures have been shown in Shi et al. (2006) from Cluster data and Tian et al. (2019) from MMS data.

Moreover, direct comparison of eigenvalues may overestimate the difference between spatial gradients, since the eigenvalues are actually the square of the spatial gradients along the corresponding eigenvectors. Since $\sqrt{\lambda }$ is equivalent to the directional derivative with the same units, we can also use $\sqrt{\lambda }$ instead of $\lambda$ in the calculations stated above. Tian et al. (2019) have also introduced some other parameters to indicate the dimension number.

Denton et al. (2010, 2012) have proposed a modified method and tested it using simulation data, which will be discussed in Sects. 4.1 and 4.4. Rezeau et al. (2018) have also proposed generalized MDD methods, which will be mentioned in Sect. 4.2.

2.4.2 Normal of a 1-D Structure and D-Based Coordinate

For a 1-D structure, as discussed in Sect. 1, all the parameters vary only in one direction, i.e., the maximum derivative direction, which is also the normal of the structure. Therefore, we can use the MDD analysis to determine the normal of a quasi-1-D discontinuity and then build a D-based coordinate system.

For a 1-D case, the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$ from the MDD analysis is along the gradient of the total magnetic field. This can be demonstrated as follows: in the MDD coordinate system, for a 1-D structure, $\nabla B = (0,0,\partial B/ \partial n_{\max})$ is just along the ${\stackrel{\rightharpoonup }{n}}_{max}$ direction. In the same way, for 2-D cases one can find that $\nabla B = (0,\partial B/\partial n_{\mathrm{mid}},\partial B/ \partial n_{\max})$ is in the plane perpendicular to ${\stackrel{\rightharpoonup }{n}}_{min}$, not solely along ${\stackrel{\rightharpoonup }{n}}_{max}$ or ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$.

Here we perform a simulation in which a cluster of spacecraft moves across a 1-D Harris current sheet (similar to the magnetotail current sheet) modelled as,

$$\overrightarrow{B}=B_{x0}tanh\left(\frac{z}{L_0}\right){\stackrel{\rightharpoonup }{e}}_x+B_{z0}{\stackrel{\rightharpoonup }{e}}_z,$$

(2.7)

from which we can easily see that the normal of the current sheet is along the $z$ direction and the physical fields along $x$ and $y$ plane do not vary. Note that the variation is still 1-D although the magnetic field components in both $x$ and $z$ directions are non-zero. We assume four virtual satellites traverse this model 1-D current sheet and plot the MDD analysis result in Fig. 6. The satellites cross the current sheet from top left to bottom right, as shown in Fig. 6h, where the field lines in the $xz$ plane are also plotted. The magnetic field components detected by one of the four virtual spacecraft are plotted in the first panel of Fig. 6. From panel 6b and c one can easily find that the results of the analysis indicate a 1-D feature of the structure, a maximum eigenvalue $\lambda _{\max }$ corresponds to the $z$ direction, and the other two eigenvalues $\lambda _{\mathrm{mid}}\ \mbox{and}\ \lambda _{ \min }$ are close to zero. Then the calculated normal direction $\mathit{Nmax}$ is clearly along $z$ direction, as set in the model. Unlike the well-determined normal direction, we cannot distinguish $\mathit{Nmid}$ and $\mathit{Nmin}$ because they are both invariant directions, and $\mathit{Nmid}$ and $\mathit{Nmin}$ can be any orthogonal directions (in the $x$–$y$ plane) perpendicular to $\mathit{Nmax}$, which is also consistent with the properties of a 1-D structure. The fluctuations in $\lambda _{\min}$ and $\lambda _{\mathrm{mid}}$ are as expected in Fig. 6b, and indicate that the variations along the $\mathit{Nmin}$ and $\mathit{Nmid}$ are so small that numerical errors are dominant. This is consistent with the configuration of the field and confirms the reliability of the calculation. Small random errors are added to avoid the construction of a singular matrix in the calculation of eigenvalues of the 1-D field gradient, considering the expectation that the $\lambda _{\mathrm{mid}}\ \mbox{and}\ \lambda _{\min }$ are close to zero. From MDD analysis, these two orthogonal directions in the $x$–$y$ plane are not constant but unstable throughout the current sheet, which means that for a pure 1-D structure the minimum and intermediate directions are not clear, although they are both in the plane perpendicular to the normal. Then for this 1-D structure, the D-based coordinate system has one definite axis, i.e., the normal of the current sheet. If we wish to prevent the other two axes from varying with time, we can set one axis along the magnetic field projected in the $\mathit{Nmid}$–$\mathit{Nmin}$ plane, whose direction is invariant. Another way is to use MVAB or the minimum gradient analysis method discussed in Sect. 2.6 to obtain one definite axis along $x$.

Fig. 6

MDD result for four virtual satellites traversing a modeled 1-D current sheet (equation (2.7) with $L_{0} = 100~\mbox{km}$, $B _{x0} = 40~\mbox{nT}$, $B _{z0} = 10~\mbox{nT}$). (a) Magnetic field observed along the trajectory; (b) square root of eigenvalues $\lambda _{ \max }$, $\lambda _{ \mathrm{mid} }$, $\lambda _{ \mathrm{min} }$ of the matrix $L$; (c) the Rezeau et al. dimensionality indices of the structure: $\mathrm{D1} = \frac{\sqrt{\lambda _{\max }} - \sqrt{ \lambda _{\mathrm{mid}}}}{\sqrt{\lambda _{\max }}}$, $\mathrm{D2} = \frac{\sqrt{ \lambda _{\mathrm{mid}}} - \sqrt{\lambda _{\min }}}{\sqrt{ \lambda _{\mathrm{max} }}}$ and $\mathrm{D3} = \frac{\sqrt{\lambda _{\mathrm{min} }}}{\sqrt{\lambda _{\mathrm{max} }}}$; (d) maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{\max }$; (e) intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (f) minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{\min }$; (g) the calculation quality indicator calculated by two methods, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ (Dunlop and Woodward 1998, blue line) and $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}$ $( i, j = x/y/z )$ (Olshevsky et al. 2015, red line). (h) The spacecraft (SC) trajectory and the magnetic field lines of the current sheet in the $x$–$z$ plane. The blue/green/red line is the $x/y/z$ component of the vector in panels a, d, e and f. Random errors on the order of $10^{-7}$ nT have been added to the background field in order to avoid singularities

Unlike the MVA method, which generally obtains results by using a series of data samples during an interval by a single satellite, using the MDD analysis we can obtain the direction at every observed moment using multipoint measurements. Therefore, MDD can in principle see the time variation of the directions. For example, in Fig. 4 of Shi et al. (2005), the maximum directions at some points in the boundary layer (shading area) have some rotations to the mean normal direction, implying that the layer may not be spatially uniform or has some temporal variations.

In data analysis, Shi et al. (2005, 2009a, 2009b), Sun et al. (2010) and Yao et al. (2016) have calculated the normal direction using Cluster data, and Yao et al. (2017, 2018) and Rezeau et al. (2018) have applied this approach to MMS data.

2.4.3 Invariant Axis and D-Based Coordinate for a 2-D Structure

If the observed flux tube is a quasi-2-D structure, we can determine its invariant axis direction using the MDD analysis method, and then we can obtain a D-based coordinate system by determining the invariant axis. Shi et al. (2005) have applied the analysis on a modeled flux rope by Elphic and Russell (1983) and a flux rope from Cluster observations. Denton et al. (2016) and Hasegawa et al. (2017) have applied the analysis on a magnetic reconnection site using MMS data.

Here we use a magnetic field model for a 2D flux rope, $\nabla ^{2}A = e^{ - 2A}$ as Hau and Sonnerup (1999) and Hu and Sonnerup (2002) have used in their benchmark of GS reconstruction, where $A$ is the out-of-plane component of the magnetic vector potential. This model has an analytical solution for $A$, given by:

$$ A(x,y) = \ln \bigl\{ \alpha \cos x + \sqrt{1 + \alpha ^{2}} \cosh y \bigr\} $$

(2.8)

where ($\tilde{x}$, $\tilde{y}$) is the axis in the plane perpendicular to the invariant axis $z$. When $\alpha > 0$, we obtain a 2D flux rope embedded in a current sheet, and when $\alpha = 0$, it is a 1-D current sheet.

Then we perform a simulation in which a cluster of four spacecraft move across this series of flux tubes, see Fig. 7. The separation is set to be 10 km, much smaller than the current sheet width, 400 km. We find that MDD can determine that it is a quasi-2-D structure because $\lambda _{\max },\lambda _{\mathit{mid}} \gg \lambda _{\min }$ (Fig. 7b), and the average invariant axis of this interval is $(0.001, -0.020, 0.999)$, very close to z which is the axis of each flux rope in the model. These structures are 2-D but close to 1-D (Fig. 7b), because they are flux ropes embedded in a current sheet. Therefore, we can still find approximately the current sheet normal direction which is along ${\sim} N_{\mathrm{max}}$. Examples of flux ropes observed by MMS will be shown in Sect. 3.4.3.

Fig. 7

Simulated MDD analysis on modeled flux ropes: (a) magnetic field observed along the trajectory; (b) square root of eigenvalues $\lambda_{\max}$, $\lambda _{\mathrm{mid}}$, and $\lambda _{\min}$ of the matrix $L$; (c) the Rezeau et al. dimensionality indices of the structure $\mathrm{D1} = \frac{\sqrt{\lambda _{\max }} - \sqrt{\lambda _{\mathrm{mid}}}}{\sqrt{\lambda _{\max }}}$, $\mathrm{D2} =\frac{\sqrt{\lambda _{\mathrm{mid}}} - \sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$, $\mathrm{D3} = \frac{\sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$; (d) maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (e) intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (f) minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (g) the calculation quality indicators calculated by two ways, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ (blue line) and $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ (red line). (h) the SC trajectory and the $B_{z}$ value of the flux rope in the $x$–$y$ plane. The blue/green/red line is the $x/y/z$ component of the vector in a and d–f. Some fluctuations in $\lambda _{\min}$ are as expected and indicate that the variation along the $\mathit{Nmin}$ is so small that numerical errors are dominant. This is consistent with the configuration of the field and confirms the reliability of the calculation

Recent studies using MMS data show that a combination of MDD and MVA provides more reasonable estimates of the $L$–$M$–$N$ coordinate systems of approximately 2-D current sheets during ongoing reconnection than MDD or MVA only. Here the $L$ axis is along the direction of the reconnecting magnetic field component, the $N$ axis is perpendicular to the current sheet, and the $M$ axis is along the reconnection line (the $X$ line) in the 2-D model. Denton et al. (2018) developed a hybrid method in which the normal ($N$) is estimated as the maximum directional derivative of the magnetic field and the $L$ axis is along the maximum variance direction of the magnetic field. Small adjustments are necessary to make the $L$–$M$–$N$ axes strictly orthogonal to each other (see Appendix of Denton et al. 2018 for details). Genestreti et al. (2018) showed that the best $L$–$M$–$N$ coordinate system for a magnetotail reconnection event can be estimated by a combined MDD and MVAVe (minimum variance analysis of the electron velocity) method. In their study, the $M$ axis is defined to be along the cross product of the $N$ axis from MDD and the maximum variance direction of the electron velocity (which turns out to be roughly along the $L$ axis), and the $L$ axis completes the right-handed orthogonal system.

For a 3-D structure, if it is not perfectly isotropic, it can still have maximum, medium and minimum derivative directions. Then we can still get its three principle axis from MDD analysis and a D-based coordinate system can still be built.

2.5 D-Based Coordinate System for a 2-D Structure Based on MVA of the Magnetic Pressure Gradient

As mentioned above it is found that the MVA on the electric current density, i.e., MVAJ is sometimes valid for finding a flux rope invariant axis. Then the D-based coordinate system can be built when studying a flux rope using MVAJ if we can obtain accurate current observations/estimations inside the flux rope.

Recently in studying some events from MMS data in the magnetopause, Zhao et al. (2016) found that because both the current and the magnetic field components along the direction of rope axis are not constant, the minimum variance analysis on either of them can not result in an accurate rope axial direction. Therefore, they suggest to perform the minimum variance analysis on the magnetic pressure gradient. The magnetic pressure gradient can be calculated using four satellites data by the way introduced in Sect. 2.4.1. Based on the assumption that the flux rope pressure profile is uniform along the axial direction in the MMS spacecraft spatial separation scale (around 10 km), the pressure gradient acts only perpendicular to the rope axis. Thus minimum variance analysis on the magnetic pressure gradient gives a good estimation of the axial direction of flux ropes using MMS data. In one of the same events, we have performed the MDD analysis (see Fig. 8). The axis direction from MDD is $[-0.336, 0.836, -0.434]$ in GSM coordinates, averaged from (2015-10-16 13:04:29.2 to 2015-10-16 13:04:29.8) and has an angular difference of 2.75 degrees from Zhao’s calculation $[-0.319, 0.861, -0.396]$ (their Fig. 3a). Based on the magnetic pressure gradient. Recently, Zhao et al. (2018, private communication) proposed a PQR system, where $R$ is the rope axial direction determined by the minimum variance of the magnetic pressure gradient, $Q$ is along the average direction of the flux rope motion in the spacecraft frame, and $P$ completes the right-hand coordinate system. This coordinate system is particularly convenient for a 2-D flux rope study since the bipolar field signature will be revealed in the $P$ component and unipolar core field will be revealed in $R$ component. Also, one can calculate the different forces in the momentum equation to study the physics in a flux rope.

Fig. 8

MDD analysis on a flux transfer event: (a) magnetic field in GSM coordinate system observed by MMS1 along the trajectory; (b) square root of eigenvalues $\lambda _{\max}$, $\lambda _{\mathrm{mid}}$, and $\lambda_{\min}$ of the matrix $L$ (dashed horizontal line indicates $\delta B/l_{\max }$, given measurement error $\delta B = 0.05$ nT and the largest separation among spacecraft $l_{\max }$, discussed in Sect. 4.1); (c) minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (d) structure velocity perpendicular to the invariant axis, i.e., in the variant plane, see discussion in Sect. 3.4.3; (e) the calculation quality indicators calculated in two ways, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ (blue line), $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ (red line). The results for the two periods within the two blue boxes have the smaller uncertainties and more stable directions

Other single or multi-point methods for building a D-based coordinate system for a flux rope have also been developed. Assuming axial symmetry, Rong et al. (2013) developed a method to obtain the invariant axis of a flux rope. Zhang et al. (2013) and Yang et al. (2014) using the methods of Shen et al. (2007)’s curvature determination methods studied some force free flux ropes.

2.6 Minimum Gradient Analysis (Local-MVA-Like Method)

Using multi-point calculations, we can also obtain a coordinate system similar to MVA at every moment. As has partially been mentioned in Shi et al. (2005), if we can calculate the spatial difference of the field using multipoint measurements, another way to build a coordinate system is to calculate the extremum value of the gradient of $B_{n}$. Considering the product of $\nabla \vec{B}$ and $\vec{n}$ we find that $\vec{D}'$ is the gradient of $B_{n}$, i.e., $\vec{D}' = \nabla \vec{B} \cdot \vec{n} = \nabla B_{n} = ( \partial B_{n} / \partial x,\partial B_{n} / \partial y,\partial B_{n} / \partial z )$. We can also calculate the extremum of $D^{\prime \,2}$ to see what happens. Following similar algebraic manipulations as used in Sect. 2.4.1, we find that the minimization of $D^{\prime \,2}$ is equivalent to solving the eigenvalues and eigenvectors of a matrix $L' = G^{T}G = ( \nabla \vec{B} )^{T} ( \nabla \vec{B} )$. This matrix is also symmetrical and has real eigenvalues and orthogonal eigenvectors. If one eigenvalue of $L$ is $\lambda$ and its eigenvector is $\stackrel{\rightharpoonup }{n}$, i.e., $G{G}^T\stackrel{\rightharpoonup }{n}=\lambda \stackrel{\rightharpoonup }{n}$, after multiplying $G^{T}$ on both sides we get $G^{T}G(G^T\stackrel{\rightharpoonup }{n})=\lambda (G^T\stackrel{\rightharpoonup }{n})$. So $\lambda$ is also an eigenvalue of $L'$ and the corresponding eigenvector should be $G^T\stackrel{\rightharpoonup }{n}$. Then the matrix $L' = G^{T}G$ here and $L = GG^{T}$ in Sect. 2.4 have the same eigenvalues but different eigenvectors. The process of minimization of $D^{\prime \,2}$ then becomes the minimization of the gradient of $B_{n}$. Then we may call this approach ‘Minimum Gradient Analysis’ (MGA). The objective of this method is similar to that of the MVAB method, because MVAB is looking for the minimum variance of $B_{n}$. If the variance of $B_{n}$ is minimum, then the gradient of $B_{n}$ should also be minimum if the magnetic field structure does not vary with time (the stationarity of magnetic field is always true for a 1-D structure as mentioned in Sect. 2.1, and is often valid for 2-D/3-D structures if the motion across the spacecraft is very fast). We can call this analysis a local-MVAB-like analysis for multi-point data (The ‘local’ means performing MVAB at every moment, which means it is performed at a local small area compared to the traditional MVAB for the whole crossing). Figure 9 shows a simulated result of this kind of calculation for a modeled current sheet given by (2.7). From the point of view of MVA, the maximum direction of $B_{n}$ should be along $x$, and one cannot distinguish the medium and minimum directions, and this is just consistent with the result shown in Fig. 9. For this case we may discuss a physical explanation of why the eigenvalues are the same while the eigenvectors are different. We can find that the three eigenvalues in Fig. 9b are exactly the same as those in Fig. 6b when we use the same set of random errors added to the magnetic field. The maximum direction of MDD is along $\stackrel{\rightharpoonup }{z}$ for this current sheet, and then from the discussion above the maximum direction of MGA should be along

$$G^T\stackrel{\rightharpoonup }{z}=\left[\begin{array}{ccc}\frac{\partial B_x}{\partial x}& \frac{\partial B_x}{\partial y}& \frac{\partial B_x}{\partial z}\\ \frac{\partial B_y}{\partial x}& \frac{\partial B_y}{\partial y}& \frac{\partial B_y}{\partial z}\\ \frac{\partial B_z}{\partial x}& \frac{\partial B_z}{\partial y}& \frac{\partial B_z}{\partial z}\end{array}\right]\stackrel{\rightharpoonup }{z}=\left[\begin{array}{ccc}0& 0& \frac{\partial B_x}{\partial z}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]=[\frac{\partial B_x}{\partial z},0,0]\propto \stackrel{\rightharpoonup }{x},$$

(2.9)

which is consistent with the calculation in Fig. 9d. For cases with $B_{y}$ or $B_{z}$ varying along $\stackrel{\rightharpoonup }{z}$ as shown in Sect. 4.3, the result may be different.

Fig. 9

Simulated local-MVA-like (MGA) analysis on the modeled current sheet (the same model, parameters, and random errors added as in Fig. 6): (a) magnetic field observed along the trajectory; (b) square root of eigenvalues $\lambda _{ \max }$, $\lambda _{ \mathrm{mid} }$, and $\lambda _{ \mathrm{min} }$ of the matrix $L'$; (c) maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (d) intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (e) minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (f) the calculation quality indicators calculated by two ways, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ (blue) and $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ (red); (g) the SC trajectory and the magnetic field line of the current sheet in the $x$–$y$ plane; The blue/green/red curve is the $x/y/z$ component of the vector in panels a, d, e and f. From panel d one can note that this method can successfully find the maximum direction as the single satellite MVAB method as shown in Table 1, although it cannot well distinguish $\mathit{Nmin}$ and $\mathit{Nmid}$ directions, which is also true for local MVA

Using this method, we cannot directly build a D-based coordinate system. However, the MVAB method can help find the $L$ direction which is difficult for the MDD analysis. Then in some 1-D cases, as described in (2.7) using the combination of MDD and MGA methods we may find different axes for the D-based coordinate system. Note that, if we use the four satellite data at every moment in time to perform the MVA, one can expect the same results with the MGA.

2.7 D-Based Coordinate System for a 2-D Structure Based on Current Density Measurements

The MMS mission has for the first time enabled sufficiently accurate measurements of the electric current density with the plasma instruments (e.g., Eastwood et al. 2016; Phan et al. 2016), and that capability allowed for the development of a new method for the invariant axis orientation of steady, 2-D structures (Hasegawa et al. 2019). The method can be used to estimate the orientation of the X line and flux rope axis from single-spacecraft measurements of the magnetic field and current density.

Here we assume that the structure is time independent and 2-D (${\partial } / {\partial t} =0$, ${\partial } / {\partial z} =0$) and that the co-moving frame velocity ${\stackrel{\rightharpoonup }{\mathbf{V}}}_{\mathrm{str}}$ is known from either of the methods to be discussed in Sect. 3. The $x$ axis is defined to be antiparallel to the projection of ${\stackrel{\rightharpoonup }{\mathbf{V}}}_{\mathrm{str}}$ onto the plane perpendicular to the $z$ axis, and the $y$ axis completes the orthogonal system. The $y$ component of Ampère’s law $\mathrm{\nabla }\times \stackrel{\rightharpoonup }{\mathbf{B}}={\mu }_0(\stackrel{\rightharpoonup }{\mathbf{j}}+{\epsilon }_0\partial \stackrel{\rightharpoonup }{\mathbf{E}}/\partial t)$ can then be reduced to $- {\partial B_{z}} / {\partial x} = \mu _{0} j_{y}$. This indicates that we can obtain the $B_{z}$ values at points along the spacecraft path from integration along $x$ of the $y$ component $j_{y}$ of the current density, which can be measured as $\stackrel{\rightharpoonup }{\mathbf{j}}=ne$ (${\stackrel{\rightharpoonup }{\mathbf{v}}}_i-{\stackrel{\rightharpoonup }{\mathbf{v}}}_e$) by the state-of-the-art plasma instruments, in addition to direct measurements by the magnetometers. For an accurate orientation of the invariant axis $\hat{\mathbf{z}}$, $B_{z}$ from the spatial integration of $j_{y}$

$$ B_{z,\mathrm{pla}} = B_{z,\mathrm{mag}} ( t=0 ) - \mu _{0} \int j_{y} dx, $$

(2.10)

where $dx=-{\stackrel{\rightharpoonup }{\mathbf{V}}}_{\mathrm{str}}\mathbf{\cdot }\hat{\mathbf{x}}dt$ and $t=0$ represents the start of the time interval under discussion, should agree with $B_{z,\mathrm{mag}}$, $B_{z}$ directly measured by the magnetometers during the corresponding interval. The optimal invariant axis can thus be estimated by minimizing the following residue $\mathrm{RES} = \sum_{m=1} ^{m=M} ( B_{z, \mathrm{mag}}^{(m)} - B_{z,\mathrm{pla}}^{(m)} ) ^{2}$, where $M$ is the total number of data points used in the reconstruction. For structures that satisfy the 2-D and steady assumptions, the correlation between the field components $B_{z, \mathrm{pla}}$ and $B_{z,\mathrm{mag}}$ along the optimal invariant axis should be sufficiently high. For an MMS magnetotail reconnection event as reported by Torbert et al. (2018) and Genestreti et al. (2018), the correlation coefficient is 0.9525 and the derived invariant axis is only 5 degrees away from the $M$ axis estimated by the combined MDD-MVAVe method, which suggests that the observed reconnection was roughly 2-D and steady. By use of the coordinate system thus obtained, reasonable magnetic field and electron streamline patterns in and around the electron diffusion region have been reconstructed from the 2-D electron MHD reconstruction (Hasegawa et al. 2019).

3 Frame of Reference

Here the frame of reference in which the observer resides is called the observational frame. If we can find a reference frame in which the observed magnetic field does not vary with time, then this is a steady magnetic or an electrostatic structure, and this reference frame (which moves with the magnetic field structure) is often called a ‘proper frame’ (e.g., Khrabrov and Sonnerup 1998b; Sonnerup et al. 2013). Obviously, in this frame ${(\frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t})}_{\mathrm{str}}=-\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$, where the subscript ‘str’ indicates the field quantities in the magnetic field structure reference frame. To find this frame in which the curl of the electric field vanishes, one easy way is to let the electric field vanish in a frame. Then we have the deHoffmann–Teller (HT) frame, which can be determined by a single satellite method, as discussed in Sect. 3.1. Other single satellite methods will be discussed in Sect. 3.2, followed by some multi spacecraft methods discussed in later subsections.

3.1 Frame in Which Electric Field Disappears: deHoffmann–Teller Frame

De Hoffmann and Teller (1950) first introduced the HT reference frame in the study of an MHD shock, where the electric field ${\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}$ disappears in this reference frame. Obviously, if ${\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$, ${(\frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t})}_{\mathrm{str}}=-\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$ must be satisfied. If the HT reference frame exists, then the magnetic field versus time observed by a satellite is only caused by the motion of a quasi static magnetic field structure relative to the satellite. The ultimate goal of the deHoffmann–Teller (HT) analysis is to find the velocity of the HT reference frame ${\stackrel{\rightharpoonup }{V}}_{\mathrm{HT}}$, using a set of discretely sampled data points in the practical analysis. This generally involves the use of the least squares method to search for the minimum value of residual electric field in the new reference frame. Details can be seen in the review by Khrabrov and Sonnerup (1998b).

A very prominent advantage of the HT analysis is that one can find some indicators that may be used to estimate the reliability of the analysis results. In short, one can compare the electric field measured by the satellite and the electric field caused by the motion of the HT frame to determine whether the resulting HT frame is reasonable. If they are very close, the electric field in the HT reference frame should be very close to zero. One specific approach is to draw a scatter plot of electric field components in the satellite frame versus the corresponding components of the field in the HT frame. If the slope of the line of best fit and the correlation coefficient is close to 1, the reliability of the HT should be good. Another way is to calculate the ratio of the mean square of the residual electric field in the HT frame and the mean square of the original electric field in the satellite frame. A measure of the reliability of the HT frame is then given by the reciprocal of this ratio. However, we should be careful when using these indicators. If the derived HT velocity is very high, as expected in the solar wind, the correlation coefficient is naturally high (i.e., the ratio is small). So they are not good proxies of a good HT frame. The correlation coefficient or ratio should be calculated not in the spacecraft frame, but in the frame in which the average plasma flow velocity is zero, as has been done in Hasegawa et al. (AG, 2015).

However, the requirement of ${\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$ is too strict (i.e., it is sufficient for a proper frame, but not necessary). In many cases, such as perpendicular shock (with a cross shock electric potential inside the ramp), some magnetic flux ropes (see discussion by Sonnerup and Hasegawa 2005) and other structures possessing a curl-free electric field in the frame moving with the structure, a proper frame can still exist, but cannot be obtained through the HT analysis. In some structures such as shocks and other discontinuities, there are often some intrinsic electric fields within the layer along the normal, which can affect the quality of the determination of the frame velocity from the direct HT analysis, and may be important for the understanding of physical processes within the layer. When performing HT analysis on these structures, we should manually exclude the data points within the layer to obtain a correct proper frame, see reviews in Khrabrov and Sonnerup (1998a, 1998b, ISSI book) and Paschmann and Sonnerup (2008, ISSI book). In these cases, the use of SH method (Sonnerup and Hasegawa 2005) or STD (Sect. 3.4) may be helpful in finding the proper frame.

A revised HT analysis can also find an estimate of the acceleration (Khrabrov and Sonnerup 1998a, 1998b, ISSI book), but this is an average (constant) acceleration over the time-domain of the sampled data. For instantaneous velocity calculations at every time sample (i.e. allowing variable acceleration) one can refer to Sect. 3.3.

3.2 Proper Frame Obtained from Single Point Data: Minimum Faraday Residue (MFR) and Sonnerup–Hasegawa (SH) Methods by Assuming a Priori the Dimensionality (Dimension Number) of a Structure

Since multi-point data sources are currently limited to the Cluster and MMS missions, finding a proper frame from a single satellite when the HT analysis fails is still very useful. Several novel attempts have been made previously. Assuming a 1-D structure, minimum Faraday residue analysis (MFR) (Terasawa et al. 1996; Khrabrov and Sonnerup 1998b) and minimum mass flux residue analysis (MMR) (Sonnerup et al. 2004) have been proposed. For a 1-D structure, Faraday’s law requires that the components of the electric field tangential to the layer are constant, and then a least squares method can be performed to obtain the normal and the velocity along the normal. Sonnerup et al. (2006, 2007) have suggested some unified approaches which can be applied to any measured quantity that follows a classical conservation law. See a detailed review in Sonnerup and Teh (2008, ISSI book).

For a time invariant structure, it is required that $\partial B/ \partial t=0$ in the proper frame we are looking for. According to Faraday’s law, $\nabla \times E = -\partial B/\partial t$, so $\nabla \times E = 0$. Further, if the structure is 2-D, the electric component Ez along the invariant axis should be constant across the structure. Note that the components perpendicular to the invariant axis are not necessarily zero, so a HT frame may not exist. Sonnerup and Hasegawa (2005) have proposed a scheme (hereafter referred to as the SH method) to derive the direction along which the electric field component has minimum variance. By this method, the orientation of the invariant direction and the velocity components of the structure perpendicular to the invariant direction can be obtained. For structures of magnetic flux rope type, the SH method can give satisfactory results, consistent with estimates from other methods, e.g., from a multi-spacecraft method based on G–S reconstruction (Hasegawa et al. 2006). However, other attempts show that the SH method does not work for most observed as well as numerically simulated reconnection events (Teh and Sonnerup 2008; Denton et al. 2010, 2012). Sonnerup et al. (2013) theoretically discussed the reasons for such shortcomings, and made clear that a significant, non-removable, non-uniform electric field in the plane transverse to the invariant direction is required for the method to work properly. It is also found that the results are sensitive to deviations from strict two-dimensionality and time stationarity.

If we can combine the MDD and MFR/SH methods for multi-point data analysis, we may obtain more reliable results. For example, we can use the MDD method to find a structure close to 1-D, and then use MFR to get the normal direction and velocity.

3.3 Triangulation for 1-D/2-D Structures: Four Spacecraft Timing

Here is another method to find the normal of a 1-D structure, and then build a D-based coordinate system and reference frame. Burlaga and Chao (1971) and Russell et al. (1983) developed and used the Triangulation method, also named Timing method, to study interplanetary discontinuities. It is used for a planar structure crossed by at least four spacecraft. A planar structure is actually a 1-D structure, in which all field quantities vary only in one direction, i.e., its normal direction. If a structure has a finite thickness rather than lying in a plane, the timing method is still valid as long as the structure is one-dimensional. So the traversal of a 1-D structure is the basic assumption of Triangulation method. The original Triangulation method also assumes that the velocity of the 1-D boundary does not vary during the crossing of all spacecraft, and then it is also called the ‘Constant Velocity Approach’ or CVA. If one assumes that the velocity can be changed but the boundary thickness is constant, the approach can be modified to a ‘Constant Thickness Approach’ or CTA, which is summarized in Haaland et al. (2004) and Sonnerup and Teh (2008).

Here we only review the CVA scheme for four-satellite crossings. Suppose a plane or 1-D structure moves across four satellites, where we know the positions of each satellite $\mathrm{\Delta }{\stackrel{\rightharpoonup }{r}}_{ij}$ ($i$, $j=1$, 2, 3, $i \neq j$) and the traversing time difference between each pair of the satellites $\Delta t_{ij}$ ($i$, $j=1$, 2, 3, $i \neq j$). We thus obtain

$$v\mathrm{\Delta }{t}_{ij}=\mathrm{\Delta }{\stackrel{\rightharpoonup }{r}}_{ij}\cdot \stackrel{\rightharpoonup }{n},$$

(3.1)

where $\vec{n}$ is the normal direction, and $v$ is the velocity magnitude. Then we get three linear equations plus ${|\stackrel{\rightharpoonup }{n}|}^2=1$, and the solution of $\stackrel{\rightharpoonup }{n}$ and $v$ are obtained by solving these four linear equations.

In addition to the 1-D assumption, the structure must be quasi-static, such that when the structure is crossed by all satellites, its normal direction does not change during the interval. Recently Plaschke et al. (2017) performed a time-varying Timing velocity determination, using 3 s long sliding intervals of high time resolution data from four MMS satellites, by computing the cross-correlation functions of each spacecraft pair to obtain $\Delta t_{ij}$. Knetter (2005), Xiao et al. (2015), and Yao et al. (2016, 2017, 2018) further considered the uncertainties of such a calculation.

In order to use the Timing method in two-dimensional cases, Zhou et al. (2006a) proposed a Multiple Triangulation Analysis method, hereafter referred to as the MTA method. If the structure is 2-D, we can use timing analysis for a series of magnetic field contour surfaces and obtain a series of velocities and directions, as shown in Fig. 10. The direction which is perpendicular to the plane, identified by the minimum variance of the series of normal vectors is the invariant direction of the two-dimensional structure. We can use a mathematical method similar to that used in the MVA and MDD analysis to get the direction, i.e., the invariant direction of this 2-D structure. Then a D-based coordinate system can also be built through MTA. From a case study, they found that the directions calculated by the MTA method and the MDD method are the same for a quasi-2-D flux tube (see Zhou et al. 2006a). In principle, the MTA approach should also have the capability to determine the dimensionality of a given structure, since the distribution of the normal directions can be characterized by three eigenvalues of the MTA matrix ($\lambda _{\max }$, $\lambda _{\mathrm{mid}}\ \mbox{and}\ \lambda _{ \min }$). In case $\lambda _{\min }$ is much smaller than the other two (which means that the series of normal directions are nearly coplanar, see Fig. 4a of Zhou et al. 2006b), the structure can be treated as 2-D and the eigenvector with the minimum eigenvalue represents the axis of the 2-D structure. If $\lambda _{\max }$ is much larger than the other two, the series of normal directions is aligned with the eigenvector with the largest eigenvalue; this is the normal direction of the 1-D structure. For 3-D structures, the three eigenvalues are not well separated. For very large separations of four satellites, when MDD is not valid because the field gradient calculation is no longer accurate, it still has the ability to give a normal for a 1-D structure. In 2-D cases, however, the MTA approach fails if the spacecraft separation is comparable to or larger than the scale size of the 2-D structure. This method does not require cylindrical symmetry assumption (although a cylindrical flux rope is used in Fig. 10 as an example), and the magnetic field vectors do not need to lie in a plane.

Fig. 10

Schematic view of MTA method of a 2-D flux rope (from Zhou et al. 2006b), showing the four satellite constellation (here they assume Cluster) passing through a flux rope. Using the Triangulation Method, the normal directions of each contour plane can be obtained, none of which have $z$ components. The set of magnetic contour planes are represented by the dashed circles and the normal directions of these planes are shown by solid arrows. Thus, the cross product of each pair of directions for each contour plane should point to the flux rope axis

Since the traditional Timing method is only applicable to the 1-D case and the MTA method can be used in 1-D or 2-D cases, one may use the MDD analysis (when the satellite separation is small enough so that the gradient calculation is valid) to determine the structure dimension number and then perform the traditional timing or MTA methods. For example, when calculating the velocity of magnetic peaks, Yao et al. (2018) first determined the dimension number of a structure with MDD analysis, found its boundary can be deemed as 1-D, and then used traditional timing methods to calculate the normal direction and propagation velocity. The velocity can also be obtained by the method introduced in Sect. 3.4, and the results from different methods can confirm each other.

The timing velocities are calculated by each magnetic field contour surface. Therefore, according to these series of timing velocities and directions, one can obtain the velocity perpendicular to the axis using similar mathematical procedures to those used in MVA and MDD. From some examples, Zhou et al. (2006b) found that there is little difference between the results of the MTA and STD method introduced in Sect. 3.4 for a 2-D structure.

3.4 Proper Frame for a (Quasi-) Stationary Structure: Spatio-Temporal Difference (STD) Frame from Multi-point Data

As mentioned in Sect. 3.1, when performing the HT analysis, we require the electric field to vanish in the frame we want to find, which is too strict because in some cases the electric field does not vanish but we only find that the curl of electric field disappears in a proper frame where ${(\frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t})}_{\mathrm{str}}=0$. In addition, the traditional timing method assumes a 1-D structures—i.e. the dimension number of a structure is assumed before performing the analysis. Trying to avoid these problems, Shi et al. (2006) developed a method of velocity calculation (or frame determination) for any structure dimension number, known as the “Spatiotemporal Difference” (STD) analysis of the magnetic field. A GUI interface for the STD method can now be accessed in the SPEDAS.

3.4.1 Introduction to the Analysis

If the structure to be analyzed does not change significantly during the interval over which the satellite system moves across it (in other words, the time scale of the structure motion is small compared with the structure variation time), it is a quasi-stationary structure. So, in the reference frame of the structure we have $\frac{\partial \phi }{\partial t} \big\vert _{\mathrm{str}}\sim 0$. Then from (1.1) we get

$$\frac{\partial \varphi }{\partial t}{|}_{\mathrm{sc}}=-{\stackrel{\rightharpoonup }{v}}_{\mathrm{str}}\cdot \mathrm{\nabla }\varphi ,$$

(3.2)

where the observation frame ‘obs’ is the spacecraft frame, here referred to as ‘sc’. Equation (3.2) means that the temporal change of the magnetic field measured by the spacecraft is only caused by the non-uniform property of the structure.

In space observation, we have measurements of various parameters, such as moments (including density, temperature, and velocity) and vector fields (electric field and magnetic field, each of which contain three components). In principle we just need to pick any three of these quantities (each component of a vector field can be used as one field quantity) to replace $\phi$ in (3.2) and obtain three linear equations. The calculation of $\nabla \phi$ needs data from at least four spacecraft (see Sect. 2.4.1 in detail). By utilizing the finite difference approximation, $\frac{\partial \phi }{\partial t} \big \vert _{\mathrm{sc}}$ at every moment can be calculated using data from one spacecraft or mean values from multi-spacecraft data. Then we can obtain the three components of the vector ${\stackrel{\rightharpoonup }{v}}_{\mathrm{str}}$ by solving the three linear equations.

The three magnetic field components are recommended in this calculation due to their higher time resolution, smaller measurement error, and easier accessibility. Thus we will take magnetic data as an example to introduce the method in detail. Using magnetic field, (3.2) can be written as

$$ \frac{\partial \vec{B}}{\partial t} \bigg\vert _{\mathrm{sc}} + \vec{V} _{\mathrm{str}} \cdot \nabla \vec{B} = 0 $$

(3.3)

The first term on the left is the temporal variation caused by the motion through spatial gradients of the magnetic field, and $\vec{V}_{\mathrm{str}}$ (to be determined) is the velocity of the structure relative to the observer, that is, the spacecraft. Equation (3.3) means that the observed temporal change of the magnetic field by the spacecraft is only caused by the motion of the structure. The main idea of this method is to solve the difference equations of (3.3) at every observed point: $\partial \vec{B}/\partial t \big\vert _{\mathrm{sc}}$ can be estimated by calculating the magnetic field time difference observed by the spacecraft at the observation time series resolution; matrix $\nabla \vec{B}$ can be estimated by many multi-point methods mentioned in Sect. 2.4.1.

Here it is worth noting that when calculating $\partial \vec{B}/\partial t\vert _{\mathrm{sc}}$ we can obtain the result with second order accuracy by using the central finite difference $(\vec{B}_{i+1}-\vec{B}_{i-1})/ (t_{i+1}-t_{i-1})= (\vec{B}_{i+1}-\vec{B}_{i-1})/2 \Delta t$. If we use the mean value measured by the four satellites, that is a linear interpolation of the measured magnetic field to the barycenter of the tetrahedron, as has been demonstrated in Harvey (1998). The time step length $\Delta t$ should be set according to the characteristic length of the observed structure, neither too short nor too long. If the step length $\Delta t$ is too short, the measurement data of the magnetic field may often have a lot of short time disturbances which will influence the calculation of $\partial \vec{B}/\partial t \vert _{\mathrm{sc}}$ and then the velocity of structure. If $\Delta t$ is too long, the accuracy of the difference will be poor. Empirically, we suggest that $\Delta t$ can be taken as ${\sim} 1/10$ of the characteristic time scale of the structure. For example, when a current sheet crossing takes ∼1 min, the $\Delta t$ can be taken as ∼6 seconds.

For a 3-D structure, the calculation is straightforward. The three components of $\vec{V}_{\mathrm{str}}$ can be directly calculated by solving (3.2), expanded as three linear equations with three unknowns.

However, for 1-D or 2-D structures, there must be at least one direction $\stackrel{\rightharpoonup }{n}$ satisfying $\partial /\partial n \sim 0$ and then the determination of the magnetic gradient tensor has $\det (\nabla \vec{B})\sim 0$. This is the reason why directly solving (3.2) will produce inaccurate solutions which may result in apparently turbulent velocity components. This can be shown in Figures in Sect. 3.4.3 and 3.4.4 for 2-D and 1-D structures: the inaccurate solution along the invariant direction will be distributed in all the three components of the velocity data in the GSE coordinate system and makes all the three components contain large uncertainties.

Therefore, we expect that from the magnetic field data, we can only obtain a reliable velocity determination along one direction for a 1-D structure, and along two directions for a 2-D structure. To solve this problem, we need to use the MDD method to find a structure’s dimension number and its characteristic (principal) directions, using multi-point magnetic field measurements, as introduced in Sect. 2.4.

Once the structure’s dimension number and the three principal directions are determined, we can solve the problem in the MDD eigenvector-based coordinate system, i.e., the D-based coordinate system. Or (3.3) can be transformed to be $\partial \overrightarrow{B}/\partial t{|}_{\mathrm{sc}}{\overleftrightarrow{T}}_r{\overleftrightarrow{T}}_r^T{(\mathrm{\nabla }\overrightarrow{B})}^T{\overleftrightarrow{T}}_r=-{\overrightarrow{V}}_{\mathrm{str}}{\overleftrightarrow{T}}_r{\overleftrightarrow{T}}_r^T(\mathrm{\nabla }\overrightarrow{B}){(\mathrm{\nabla }\overrightarrow{B})}^T{\overleftrightarrow{T}}_r$, where ${\overleftrightarrow{T}}_r=\{{\overrightarrow{n}}_1,{\overrightarrow{n}}_2,{\overrightarrow{n}}_3\}$ (here ‘,’ means different rows) is the transformation matrix from the original coordinate system (e.g., GSE) to the MDD eigenvector-based coordinate system. We get

$$\frac{\partial \overrightarrow{B}}{\partial t}{|}_{\mathrm{sc},\mathrm{MDD}}\cdot {(\mathrm{\nabla }\overrightarrow{B})}^T{|}_{\mathrm{MDD}}=-{\overrightarrow{V}}_{\mathrm{str}}{|}_{\mathrm{MDD}}\cdot \overleftrightarrow{\Lambda }$$

(3.4)

where from Sect. 2.4, we find that $\overleftrightarrow{\Lambda }={\overleftrightarrow{T}}_r^T(\mathrm{\nabla }\overrightarrow{B}){(\mathrm{\nabla }\overrightarrow{B})}^T{\overleftrightarrow{T}}_r$ is a diagonal matrix, of which the diagonal terms are the three eigenvalues $\lambda _{\max }$, $\lambda _{\mathrm{mid}}$ and $\lambda _{\min }$ of the $L$ matrix introduced above. Here ${\overrightarrow{V}}_{\mathrm{str}}{|}_{\mathrm{MDD}}={\overrightarrow{V}}_{\mathrm{str}}\cdot {\overleftrightarrow{T}}_r$ is the velocity vector in the basis formed from eigenvectors. Then we can solve the linear equations (3.4) one by one if the corresponding eigenvalue is significant. That is, for a 1-D structure, we just solve the first equation corresponding to the largest eigenvalue $\lambda _{\max }$ and then get the velocity along its direction of variation, i.e., its normal; while for a 2-D structure, we only solve the first two equations related to $\lambda _{\max }$ and $\lambda _{\mathrm{mid}}$, and obtain the velocity components along the maximum and intermediate derivative directions.

An alternative way is to first calculate the three components of the velocity by solving the difference equations of (3.3), and then project the result to the three directions ($\lambda _{\max }$, $\lambda _{\mathrm{mid}}$ and $\lambda _{\min }$). The velocities along the maximum direction (for a 1-D structure) or maximum and intermediate directions (for a 2-D structure) can have a relatively reliable accuracy, but the other direction(s) will not. Then from figures in Sect. 3.4.3 and 3.4.4, we find that the velocities along $\mathit{Nmax}$ and $\mathit{Nmid}$ are no longer turbulent and the only turbulent velocity is along $\mathit{Nmin}$ for a 2-D structure, and for a 1-D structure the velocity along $\mathit{Nmax}$ is no longer turbulent and the turbulent velocities are along $\mathit{Nmin}$ and $\mathit{Nmid}$. Since generally the variations are not exactly 1-D or 2-D, the corresponding eigenvalues are not exactly zero (then the $\mathrm{det}(\nabla \vec{B} )$ is not strictly equal to zero). This point has been shown to be the case over many years of data analysis (see e.g., Shi et al. 2006, 2009a, 2009b, 2013; Sun et al. 2010). In benchmark calculations for a pure 1-D or 2-D case when some eigenvalues are zero in a certain direction, it is found that the calculation seldom overflows because of the limited digits a computer can deal with and there will be a very small deviation from pure 1-D and 2-D. Even when we get strict zero eigenvalues at some calculating points, by adding very small random perturbations (e.g., $10^{-5}$ of the original values) to the original field, one can still get a very accurate dimension numbers and directions. This is good example that observational errors can play a positive role. This is similar to the positive effect that numerical errors can play in the numerical simulation of the fluids, where dissipation provided by the accumulated error can stabilize the numerical scheme.

The above two solutions are intrinsically identical in the analysis of real data: the transformation to the MDD coordinate system before (i.e., in the 1st way) or after (i.e., in the 2nd way) the calculation can give same results. In practice, we can use both of them and cross-check each other.

Here we summarize the practical steps needed to perform the STD analysis on actual data, as illustrated in Fig. 11:

Fig. 11

Practical steps needed to perform STD analysis on actual data

1. The MDD analysis is carried out to obtain the dimensionality (dimension number) of the structure.

2. We solve the problem by a method depending on the structure dimension number. For a 3-D structure we can calculate three components of the velocity vector after estimating the magnetic gradient tensor G at every moment and the time variation of the magnetic field, $\partial \vec{B}/\partial t \vert _{\mathrm{sc}}$; for a 2-D (1-D) structure, we can solve (3.3) in the original coordinate system (e.g., in GSE) and then project the velocity vector onto the eigenvectors calculated from the MDD method, or calculate the velocity along two or one directions (by solving (3.4)) in the coordinate system determined by the eigenvectors of the MDD analysis. We emphasize here that the setting of time step length $\Delta t$ is sometimes very important, and it should be set according to the characteristic length of the observed structure, neither too short nor too long, as discussed above.

3. Finally, the velocity can be obtained along the normal direction for a 1-D structure, or along the direction perpendicular to the invariant axis for a 2-D structure.

3.4.2 Application to a 3-D Structure

Here we perform the STD calculation for the example of a dipole field. The equations to describe its magnetic field are,

$$ \left \{ \textstyle\begin{array}{l} B_{0} = 3.12 \times 10^{4}~\mbox{nT} \qquad R = 1~\mbox{km} \qquad r = \sqrt{x^{2} + y^{2} + z^{2}} \\ \phi = \arccos (x/\sqrt{x^{2} + y^{2}} )\quad \quad \theta = \arccos (z/r) \\ B_{x} = - \frac{3}{2}B_{0}(R/r)^{3}\sin 2\theta \sin \phi \\ B_{y} = - \frac{3}{2}B_{0}(R/ r)^{3}\sin 2\theta \cos \phi \\ B_{z} = - B_{0}(R/r)^{3}(1- 3\cos ^{2}\theta ) \end{array}\displaystyle \right .. $$

(3.5)

For a bar magnet or a simple dipole field, $\partial \vec{B}/ \partial t \vert _{\mathrm{str}} = 0$ is satisfied strictly. Suppose that it moves along one direction at a velocity of $[140, -160, -120]$ in an arbitrary coordinate system, as seen in Fig. 12. We then place four virtual spacecraft within the magnetic field structure and move the structure with respect to the satellites in order to produce the satellite time-series data. From MDD we find that it is 3-D and then all three velocity components can be calculated, giving in this case $[135.35, -163.39, -123.98]$ m/s. We find that the result is very accurate. Similar results can be expected for quadruple and higher order magnetic fields. We then expect that for any magnetic field derived from a scalar potential, which therefore has no in situ current (and can be a superposition of dipole, quadruple and higher order magnetic fields) the translation velocity can be calculated by the STD method.

Fig. 12

STD results for a modeled 3-D dipole field (model given in (3.5)). (a) Magnetic field observed along a virtual satellite trajectory; (b) square root of eigenvalues $\lambda_{\max}$, $\lambda_{\mathrm{mid}}$, and $\lambda_{\min}$ of the matrix $L$; (c) velocity along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (d) velocity along the intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (e) velocity along the minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (f) velocity of the structure in 3-D

For most cases in the space, the fields contain contributions from both in-situ current generated fields and the fields generated by remote currents (i.e., the scalar potential magnetic field). Then the STD method can still be directly performed as long as it is a 3-D structure, provided that the spacecraft separation is small enough to resolve the spatial scale of the structure. Shi et al. (2006) investigated a possible 3-D structure near the polar cusp region using Cluster data, as shown in Fig. 13. Wendel and Adrian (2013) using this method gave the velocity of a structure and found the results are consistent with that obtained from the superposed epoch approach (Fig. 14). In the superposed epoch approach, the authors used a linear approximation to produce a superposed epoch snapshot of the magnetic field structure around the null at every time moment, which provides instantaneous positions of the null with respect to the spacecraft and therefore obtains the velocity of the null.

Fig. 13

STD calculation for a 3-D structure (from Shi et al. 2006)

Fig. 14

Results comparison from superposed epoch and STD method, adopted from Wendel and Adrian (2013)

If the three eigenvectors are stable during the crossing of a localized magnetic structure, we can use the three MDD directions to build a new coordinate system which can represent the principle directions of the structure and might also provide some help to analyze the structure.

3.4.3 Application to a 2-D Structure

Here we use the sequence of 2-D flux ropes described in Sect. 2.4.3, assuming that it moves along one direction at a velocity of $[-4000, -420, 40]$ in an arbitrary coordinate system. In this case the velocity perpendicular to the invariant axis is along $(0.707, 0.707, 0)$. We then put four virtual satellites at one position and let the structures pass by in order to produce the satellite time-series data, from which we calculate the structure velocity. From the MDD calculation we find that it is 2-D, and only two velocity components can be calculated. The velocity perpendicular to the invariant axis is then $[-3887.80, -420.65, -0.71]$ when we calculate the mean values over the whole interval in Fig. 15. However, the velocity along the invariant axis can be arbitrary.

Fig. 15

STD results for the modeled 2-D flux ropes (model given by (2.8) with $a=0.225$). (a) Magnetic field observed along the trajectory; (b) square root of eigenvalues $\lambda_{\max}$, $\lambda_{\mathrm{mid}}$, and $\lambda_{\min}$ of the matrix $L$; (c) velocity along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (d) velocity along the intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (e) velocity along the minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (f) calculated velocity components only perpendicular to the invariant axis, i.e., in the variant plane

For a 2-D case, the velocity can be calculated only perpendicular to the axis (invariant axis). Typically we find that $V_{ \mathrm{min} }$ fluctuates, and $V_{ \mathrm{max} }$ or $V_{ \mathrm{mid} }$ are often not stable themselves (mostly because the maximum and minimum direction are not stable), but $V_{\mathrm{2D}}$ which is a vector composed of $V_{ \mathrm{max} }$ and $V_{ \mathrm{mid} }$ is stable and represents the motion perpendicular to the axis.

For the large scale flux rope event shown in Sect. 2.5, we can calculate the velocity of the structure perpendicular to the axis, i.e., velocity in the variant plane, as shown in Fig. 8d. From the results we can see the velocity as a function of time, and then the acceleration can be derived accordingly. The average velocity for the leading edge is $({-}47.613\ {-}88.763\ {-}109.121)$ km/s, and that for the trailing edge is $({-}22.762\ {-}26.366\ {-}33.429)$ km/s. The inconsistent velocities of the two edges suggest that the flux rope is expanding. In Fig. 16 we show an STD calculation using MMS data for a small scale magnetosheath flux rope event in GSE coordinates (Yao et al. 2019). The calculation in the central part of the structure (shown in blue shaded area in Fig. 16) shows that the small scale flux rope is 2-D (Fig. 16b) and the velocity can be obtained perpendicular to the flux rope axis (Fig. 16f). In the core of the flux rope (∼14:07:56.35–14:07:56.45 UT) the structure is even more 2-D than in the outer parts if we look at the eigenvalues in Fig. 16b. Over the duration indicated by the shaded area the calculation quality indicators are well below 0.4 (Fig. 16g), which suggests the linear assumption is valid. Vstr_2D (Fig. 16f) is the resultant velocity of $V_{\max}$ (Fig. 16d) and $V_{\mathrm{mid}}$ (Fig. 16e). The axis direction appears to be very stable (Fig. 16c), and the velocity varies little (Fig. 16f), which means that the flux rope moved at a roughly constant velocity. Another 2-D example for the magnetotail current sheet can be found in Shi et al. (2006).

Fig. 16

STD analysis on a flux rope event: (a) GSM Bx observed by MMS1-4 along the trajectory; (b) square root of eigenvalues $\lambda _{\max}$, $\lambda_{\mathrm{mid}}$, and $\lambda_{\min}$ of the matrix $L$ (dashed horizontal line indicates $\delta B/l_{\max }$, given measurement error $\delta B = 0.05$ nT and the largest separation among spacecraft $l_{\max }$, discussion in Sect. 4.1); (c) minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; (d) velocity along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (e) velocity along the intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (f) velocity of 2D structure ($V_{\max}$ and $V_{\mathrm{mid}}$ combined); (g) the calculation quality indicators calculated by two ways, which shows the quality for linear assumption, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ (blue line), $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ (red line). Blue shaded region marks the interval when the SC crosse the flux rope

3.4.4 Application to a 1-D Structure

Here we use the same 1-D current sheet as in Sect. 2.4.2. We assume that it moves along one direction at a velocity of $[1200, 10, 125]$ in an arbitrary coordinate system. In this case the velocity component only along the variant ($z$) axis can be well estimated. We then put four virtual satellites at one position and let the structures pass by in order to produce the satellite time-series data, from which we calculate the structure velocity. From MDD we find that it is 1-D and only one velocity component can be calculated. The velocity along the variant axis can be calculated, which turns out to be $[0.12, 0.30, 124.89]$ when we calculate the mean values during the crossing, as shown in Fig. 17. The velocity perpendicular to the normal can be arbitrary. Figure 18 shows a calculation during a magnetopause crossing event (Russell et al. 2017) observed by MMS at the dusk flank of the magnetosphere. The normal direction during the time indicated by the shaded area is stable, while slight variations in the velocity may indicate some acceleration of the current sheet. For a 1-D case, the velocity can be calculated only along the normal (variant axis). The velocity of the magnetopause along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$, calculated by the STD method using different $\Delta t$ ranging from 0.3 s (not shown) to 2 s (here) are quite similar.

Fig. 17

STD results for a modeled 1-D current sheet (same model and parameters with Fig. 6): (a) magnetic field observed along the trajectory; (b) square root of eigenvalues $\lambda_{\max}$, $\lambda _{\mathrm{mid}}$, and $\lambda _{\min}$ of the matrix $L$; (c) velocity of the current sheet; (d) velocity along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (e) velocity along the intermediate derivative direction ${\stackrel{\rightharpoonup }{n}}_{\mathrm{mid}}$; (f) velocity along the minimum derivative direction ${\stackrel{\rightharpoonup }{n}}_{min}$; $10^{-7}$ nT has been added to the background field in order to avoid some singularities when calculating eigenvalues. Note that for this pure 1-D structure the velocity is only valid for the maximum direction, i.e., only the $\mathit{Vmax}$ is reliable, which is the reason why $\mathit{Vmid}$ and $\mathit{Vmin}$ appear to be more turbulent

Fig. 18

MDD and STD analysis on a magnetopause crossing event (Russell et al. 2017) observed by MMS at the dusk flank of the magnetosphere: (a) GSM Bz observed by MMS1-4 along the trajectory; (b) square root of eigenvalues $\lambda _{\max}$, $\lambda _{\mathrm{mid}}$, and $\lambda _{\mathrm{min}}$ of the matrix $L$; (dashed horizontal line indicates $\delta B/l_{\max }$, given measurement error $\delta B = 0.05$ nT and the largest separation among spacecraft $l_{\max }$, discussions in Sect. 4.1). (c) The Rezeau et al. dimensionality indices of the structure $D1 = \frac{\sqrt{\lambda _{\max }} - \sqrt{\lambda _{\mathrm{mid}}}}{\sqrt{\lambda _{\max }}}$, $D2 = \frac{\sqrt{\lambda _{\mathrm{mid}}} - \sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$, $D3 = \frac{\sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$; (d) maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (e) velocity of the magnetopause along the maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; (f) the calculation quality indicators calculated by two ways, $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{\mathrm{B}}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{\mathrm{B}}}|$ (blue line), $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ (red line)

3.4.5 Application to Determine a Pass-Through Spatial Structure and Enter/Retreat Structure

Shi et al. (2009a) have summarized the procedures on how to distinguish the spatial “pass through” effects (field change due to one or more structures passing through or being passed by the spacecraft) from “enter/retreat” effects (the field change is caused by a structure passing the spacecraft in one direction and then moving back over the spacecraft) empirically from field profiles measured by more than one spacecraft. This is very useful because it can help us make a quick judgement concerning these two effects just by observing the relative profiles of different satellites. If we find “interlaced” profiles of the form shown in Fig. 19e, it should be a spatial “pass through’’’ structure (for example, a surface wave with finite amplitude). If we observe “nested” field profiles (Fig. 19d), it can be interpreted as either an “enter/retreat” or spatial “pass through” effect, depending on the relative position between the spacecraft and the structure/boundary. If we have four identical spacecraft forming a tetrahedron, the possibility of distinguishing the two effects can be greatly enhanced.

Fig. 19

Illustration of pass-through spatial structure and enter/retreat structure observed by two satellites, adopted from Shi et al. (2009a). (a) “Enter/retreat” effect: the spacecraft entering one region and then moving back, crossing the same boundary; (b) spatial “pass through” effect: the two spacecraft passing through a structure along one line; (c) spatial “pass through” effect: the two spacecraft passing through a structure through different parts of it; (d) the “nested” field profiles measured by the two spacecraft; and (e) the “interlaced” field profiles

Having at least four spacecraft measurements allows us to quantitatively distinguish these two effects by calculating the boundary motion velocity and direction, either using the timing method or STD method. Shi et al. (2009a) have applied these techniques to a magnetic hole in the cusp detected by Cluster. From Fig. 20a, we can see that the total magnetic field shows “interlaced” profiles, e.g., for SC3 and SC4, which suggests a spatial structure being traversed during this time interval. Then the calculation of the boundary velocity quantitatively shows us a ‘pass through’ structure, because the leading and trailing boundaries move along almost the same direction as is evident from Fig. 20c.

Fig. 20

A pass-through spatial structure example, a magnetic hole in the cusp. From Shi et al. (2009a). (a) total magnetic field observed by the four spacecraft; (b) MDD eigenvalues (magnetic field variations) along minimum, intermediate, and maximum derivative directions; (c) maximum derivative direction, here identical to the 1-D boundary velocity direction; and (d) speed along n1 at every moment. The shaded regions are LB, leading boundary and FB, following boundary/trailing boundary. Since the sign of the eigenvector n1 is arbitrary in the MDD calculation (see the text), here we set it along the velocity direction. (e) and (f) Illustration of the Cluster tetrahedron configuration, and the boundary surface, normal direction and velocity in $\mathit{XY}$ and $\mathit{XZ}$ plane in GSE, respectively. The arrows indicate the boundary velocities. The magnetic hole is between these two boundaries. Note that in this case the tetrahedron is magnified for the reader’s convenience

Now we show an example of an enter/retreat structure for the boundaries of the cusp. From Fig. 21b we can see that these two boundaries are roughly 1-D (the intervals of rapid change in the time series indicate a boundary crossing); so we can only obtain the velocity along one direction in which the field has maximum variations, the normal. The velocity along the normal is shown in Fig. 21c. The valid results are in the two shaded intervals where all four spacecraft are in the same structure. During the traversal of each satellite for the two times in Fig. 21, we find that the velocities are stable for each of the shaded intervals when the spacecraft entered and exited the cusp. Thus, one can build a reference frame with a nearly constant velocity for each of the traversals. The mean speed of the first crossing is 21.0 km/s along $(-0.417, -0.276, -0.866)$ in GSM, while that of the velocity of the second boundary is 15.9 km/s, directing to $(0.047, 0.209, 0.977)$ in GSM, which is opposite to that of the first one, indicating an enter/retreat of the cusp. From this figure one may also find that STD may see the instantaneous velocity of the boundaries.

Fig. 21

Enter/retreat structure example, from Shi et al. (2009b). (a) Total magnetic field observed by the four spacecraft; (b) magnetic field variations along minimum, intermediate, and maximum derivative directions; and (c) boundary velocity along the normal in GSM at every moment. (d) Schematic illustration of the crossing of high-latitude boundaries

4 Discussion

4.1 Uncertainties and Cautions Concerning Various Analysis Methods

The uncertainties of MVA have been discussed by Sonnerup and Scheible (1998). Errors for the Timing method have been discussed by various authors (e.g., Zhou et al. 2009; Vogt et al. 2011; Xiao et al. 2015; Plaschke et al. 2017). Here we mainly discuss the uncertainties and cautions for the MDD and STD analysis. Since these two methods are based on the estimation of gradient of the magnetic field $G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$, just as the current estimation method does, a simple guideline is that whenever the current calculation is accurate, the MDD calculation should be accurate. The accuracy of the STD method depends not only on the accuracy of $G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ estimation, but also on two other factors: the accuracy of calculating the $( \frac{\partial \vec{B}}{\partial t} ) _{\mathrm{sc}}$ and the accuracy of the steady state assumptions $( \frac{\partial \vec{B}}{\partial t} )_{\mathrm{str}} = 0$.

Robert et al. (1998) have analyzed the current calculation uncertainties in detail. They also proposed an empirical method to measure the magnitude of the current calculation error (or the calculation quality), that is, if the magnitude of $|\nabla \cdot \vec{B}/\nabla \times \vec{B}|$ is greater than a certain value (like 0.4), we deem the current calculation error too large and not credible. We can also use an error indicator in an MDD plot as in Fig. 6 for the building of a D-based coordinate system. Considering that sometimes the magnetic gradient is large but the current is small (e.g., in the center of a magnetic hole or a magnetic mirror (Tian et al. 2019; Yao et al. 2016, 2017; Shi et al. 2009a)), we also use another index, i.e., $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$, where $\max (|\frac{ \partial B_{i}}{\partial j}|)$ is the maximum absolute value of all components of $G= \partial \vec{B}$.

Here we summarize the error sources of the MDD method, which come from the measurement error of the magnetic field, the error in determination of the satellite relative position, simultaneity of the measurements made between different spacecraft, and truncation errors in the estimation of the matrix (spacecraft tetrahedron shape parameters, c.f. Robert et al. 1998 as a source of error are included in the truncation error) $G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$, which have been discussed extensively before (e.g., Chanteur 1998; Harvey 1998; Robert et al. 1998; Denton et al. 2010, 2012).

Now we discuss the truncation errors in $G=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$. When using the gradient based method for Cluster or MMS, the four spacecraft should each be simultaneously within the same structure and the separation of the spacecraft $l_{\mathrm{sc}}$ must be much smaller than the scale of the structure $l_{\mathrm{str}}$, i.e. $l_{\mathrm{sc}}\ll l_{\mathrm{str}}$. In practice, we can look at the profiles of measured fields from different spacecraft in order to determine whether the separation is sufficiently small. An empirical way is to simply visually inspect the observed time-series in order to judge whether the profiles of fields measured by different spacecraft are near enough and bear some resemblance with each other, i.e., whether the four spacecraft lie within the same structure during the calculation interval. As illustrated in Fig. 22, two spacecraft are in the same structure and linear interpolation is valid for the measurements in Fig. 22a, but in Fig. 22b,c the two spacecraft are too far apart, and are not in the same structure, such that linear interpolation between them will fail.

Fig. 22

(a) Example that all spacecraft can be seen in a same structure and then the gradient can be calculated correctly. This is a magnetosheath flux rope event observed by Yao et al. (2018). (b–c) Examples showing that not all satellites are in the same structure and one cannot perform gradient based methods like MDD, Curlometer, STD, while Timing method can be performed

This does not always mean, however, that the smaller spacecraft separations, the better the accuracy. As pointed by Robert et al. (1998), the relative measurement errors between every spacecraft pair become large at small separations, because the field measurement errors are nearly constant, and hence there should be an optimal separation distance.

Considering the measurement error $\delta B$, the smallest gradient of magnetic field should be ${\sim }\delta B/l_{\max }$, where the $l_{\max }$ is the largest separation among spacecraft. In the panel of eigenvalues, we can add a dashed horizontal line to indicate $\delta B/l_{\max }$, given $\delta B = 0.05$ nT and $l_{\max }$ depending on the real situation. Then if the square of the eigenvalues is lower than this line, we should be careful; see examples in Figs. 8, 16 and 18.

Denton et al. (2010, 2012) discussed the MDD and STD methods and further developed them to study the magnetic reconnection point, considering various errors of the field data which may bring uncertainties in the calculation. First they tested these methods by using a magnetotail reconnection point obtained from numerical simulations assuming four virtual satellites passing through the structure. In these cases, they found that the characteristic directions of the reconnection point and the moving velocity of the reconnection point can be well determined. They considered two kinds of errors in magnetic field measurement that is worth our attention in real satellite data analysis: one is the digitization (noise) errors that randomly vary with respect to time, another is systematic inter-spacecraft calibration errors that are either constant or at least very slowly evolving in time. In general, the former is small and unlikely to be a problem, and the latter is larger and sometimes could reach 0.1 nT, in the cases of Cluster and MMS. To minimize the influence of the calibration error, Denton et al. (2010, 2012) suggested to use the gradient of the perturbed field $\delta (\mathrm{\nabla }\stackrel{\rightharpoonup }{B})=\mathrm{\nabla }\stackrel{\rightharpoonup }{B}-〈\mathrm{\nabla }\stackrel{\rightharpoonup }{B}〉$ instead of that of the total field $\mathrm{\nabla }\stackrel{\rightharpoonup }{B}$ when carrying out analysis using MDD and STD. In their simulated case, they argue that the calculation can be improved, mainly for the intermediate and minimum directions. Teh et al. (2010) reconstructed a reconnection structure by solving the steady resistive MHD equations in two dimensions, with initial inputs of field and plasma data from a single spacecraft as it passes through it, using the velocity calculation by Denton et al. (2010). However, Denton et al. (2012) also mentioned that if the background has a spatial gradient itself, removing the background may lead to a systematic deviation of the calculated results. Therefore, caution must be made when we use this modified approach.

Tian et al. (2019) have statistically tested the influence of spacecraft separation, noise/turbulence level, and tetrahedron shape on the accuracy of MDD results with the use of a 2D magnetic flux rope model. As shown in Fig. 23, the errors in characteristic directions from the MDD method are related to the noise/turbulence level, inter-spacecraft distance and spatial gradient of the structure. The noise is introduced as $\Delta B_{j}^{\mathrm{NL}} =\mathrm{NL}\boldsymbol{\cdot } \langle \vert B \vert \rangle \boldsymbol{\cdot }\mathrm{RAND}()$, where $j$ denotes the magnetic field component, the coefficient NL represents noise level and $\langle \vert B \vert \rangle$ represents averaged magnetic field strength (e.g. Hu and Sonnerup 2002). RAND () generates normally distributed random numbers. Turbulence (natural noise) is introduced as $\Delta B_{j}^{\mathrm{TL}} = \mathrm{TL} \cdot \langle \vert B \vert \rangle \cdot (0.4 R_{0} \cdot | k_{j} | ^{- \frac{5}{6}} )\cdot \cos [2 \pi \cdot \boldsymbol{k} \cdot \boldsymbol{r} _{{m}} ]$, where TL is a coefficient reflecting the ratio of the turbulence amplitude to the background value; $R_{0}$ is the half width of the model flux rope; $\boldsymbol{r}_{{m}}$ represents the position vector of the $m$th vertex ($m=1$, 2, 3, 4) relative to the tetrahedron center. $\boldsymbol{k}$ is wave vector with each component of $\vert k_{j} \vert = \frac{1}{\lambda _{j}}$; at each moment the wavelength $\lambda _{j},\ (j= x,y)$ is a random value satisfying $\lambda _{j} =0.001 R_{0} +|\mathrm{rand} '()|$, where $\mathrm{rand} '()$ generates normally distributed random numbers with mean value 0 and variance 0.2$R_{0}$. The wavelength $\lambda _{z}$ is determined by the divergence-free condition of magnetic field (Tian et al. 2019). Unlike noise, the turbulent magnetic field is divergence-free at any point, and its magnitude depends on the plasma environment but not on the accuracy of the instrument. Figure 23 shows that even with a magnetic field disturbance with level of 10%, MDD can still give robust dimensionality information as long as the length of the spacecraft tetrahedron is 0.1–1 times the structure radius. The angle of deviation from the axis predicted by MDD to the actual model axis for each operation when $\Delta R <1R _{0}$ is shown in Fig. 23f. The percentage of points less than $30^{\circ}$ (considered accurate) in the bins < 0.1, 0.1–0.3, 0.3–0.5, 0.5–0.7, 0.7–0.9, 0.9–1.1 and >1.1 are also plotted (circles connected by the curves; with values corresponding to the right-hand axis). It can be seen that the percentage is greater than 80% when $| \nabla \cdot \boldsymbol{B} |/ | \nabla \times \boldsymbol{B} |<0.4$ or $| \nabla \cdot \boldsymbol{B} |/\max(| \partial B _{i}/\partial j|) <0.6$. Therefore, for a given flux rope structure, 0.4 and 0.6 can be taken as (time independent) thresholds for these two parameters, respectively. The lower the parameters, the more accurate the MDD results when the separation is small.

Fig. 23

Influence of noise and turbulence on the MDD results for a flux rope model. (a) Cross section of the model flux rope. The black dot denotes the point where the axial direction is tested. (b–c) Distribution of $\Delta \theta$ (invariant direction error of MDD calculation) versus noise (NL) or turbulence level (TL) and separation ($\Delta R$). (d, e) The distribution of the two quality indicators $|\frac{\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}}{\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}}|$ and $\frac{|\mathrm{\nabla }\cdot \stackrel{\rightharpoonup }{B}|}{max(|\frac{\partial B_i}{\partial j}|)}(i,j=x/y/z)$ versus TL and $\Delta R$. (f) The relationship between $\Delta \theta$ and the above parameters. Adapted from Tian et al. (2019) See text for detail

One type of error in the STD method comes from our stationarity assumption, i.e., ($(\frac{\partial \vec{B}}{\partial t})_{\mathrm{str}}\sim 0$), which means we can calculate its velocity only if the structure itself changes very slowly on the time scale of the motion. When we calculate ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ from the STD analysis, if the structure is steady, we have ${(\frac{\partial \stackrel{\rightharpoonup }{B}}{\partial t})}_{\mathrm{str}}=-\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$ in the rest frame of the structure. To test this assumption of steady state, we can calculate $\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}$ in the structure frame and see if it is close to zero. Substituting ${\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}={\stackrel{\rightharpoonup }{E}}_{\mathrm{sc}}+{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}\times \stackrel{\rightharpoonup }{B}$, we get $\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{sc}}-\stackrel{\rightharpoonup }{B}(\mathrm{\nabla }\cdot {\stackrel{\rightharpoonup }{V}}_{\mathrm{str}})+\stackrel{\rightharpoonup }{B}\cdot \mathrm{\nabla }{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}-{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}\cdot \mathrm{\nabla }\stackrel{\rightharpoonup }{B}$. From $( \frac{\partial \vec{B}}{ \partial t} )_{\mathrm{sc}} + \vec{V}_{\mathrm{str}} \cdot \nabla \vec{B} = 0$ (assume this is valid here) and ${(\frac{\partial \overrightarrow{B}}{\partial t})}_{\mathrm{sc}}=-\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{sc}}$, we get $\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=-\stackrel{\rightharpoonup }{B}(\mathrm{\nabla }\cdot {\stackrel{\rightharpoonup }{V}}_{\mathrm{str}})+\stackrel{\rightharpoonup }{B}\cdot \mathrm{\nabla }{\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$. So if ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ does not vary spatially, we should get $\mathrm{\nabla }\times {\stackrel{\rightharpoonup }{E}}_{\mathrm{str}}=0$. This result is very reasonable: at a given moment if we can calculate ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ in many different positions and find it is homogeneous, then it is a coherent and steady structure. On the other hand, if ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ is inhomogeneous, we will see the expansion, compression or deformation and then it is not steady. How can we test whether ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ is spatially constant or not in practice? If we have far more than four satellites to calculate the ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ simultaneously at different places using each combination system of four satellites, it will be easy. However, if we only have one cluster of four satellites, we may need some assumptions. For example, if we observe ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ does not vary with time during the whole crossing of the structure, it is likely that the ${\stackrel{\rightharpoonup }{V}}_{\mathrm{str}}$ is also spatially constant. Another possible way is to perform a reconstruction. Reconstruction methods have been proposed and applied based mainly on single point measurements, e.g., GS reconstruction as discussed in Sect. 2.2 or on multi-point measurements, e.g., first-order expansion (Wendel and Adrian 2013; Fu et al. 2015). Higher order reconstructions based on multi-point measurements can also be possibly performed even if we only have four satellites. Assuming that the structure is stationary we can obtain its velocity, and then we can deem the whole crossing time of the structure as one time moment so that we will obtain a system with many satellites in different positions of the structure. The relative distance of different positions can be derived from the structure velocity and time difference when the satellites reach different positions. Then we can perform 2nd to 3rd order (or even higher order depending on the point number) fits to get the whole field of the structure. Chanteur (1998) has proposed to use this approach to get the higher order gradient of the field. For 2-D or 3-D cases by this way of reconstruction one may not get accurate results perpendicular to the spacecraft trajectory. However, for the 1-D case, if the variant axis is along the trajectory, we may reconstruct the field of the structure more accurately. Then if we reconstruct the structure from data of two different parts (corresponding to two different time moments) to obtain a whole picture of the structure, we may compare the reconstruction at different times. If the differences between the two results are only minor, then it can be considered stationary, provided the reconstruction is sufficiently accurate. Of course this proposed approach is too idealized. A much better way is to launch tens of satellites and then we can make better reconstruction with higher order.

Other sources of STD calculation error exist in the finite difference equations of (3.3), and generally, the truncation errors dominate, which give us two limitations of the STD method: $l_{\mathrm{sc}} \ll l_{\mathrm{str}}$ and $\Delta t V_{\mathrm{str}} \ll l_{\mathrm{str}}$ (see the analysis detail in Shi et al. 2006), where $l_{\mathrm{sc}}$ is the spacecraft separation scale, $l_{\mathrm{str}}$ is the structure’s scale, and $\Delta t$ is the time step which we used in calculating $( \frac{\partial \vec{B}}{\partial t} )_{\mathrm{sc}}$. Because the accuracy of the magnetic field, $\delta B_{i}$ (where $B_{i}$ is one component of the magnetic field), is normally dominated by systematic inter-spacecraft calibration errors, which can reach 0.1 nT for Cluster and MMS as mentioned above, the field variation during the interval $\Delta t$ should be larger than $\delta B_{i}$, that is $\delta B_{i} < \Delta t \vert ( \frac{ \partial B_{i}}{\partial t} )_{\mathrm{sc}} \vert$, so the $\Delta t$ should satisfy $\Delta t > \frac{\delta B_{i}}{ \vert ( \frac{\partial B_{i}}{\partial t} )_{\mathrm{sc}} \vert }$. Similarly, $l_{\mathrm{sc}}$ should satisfy $l_{\mathrm{sc}} > \frac{\delta B_{i}}{ \vert \frac{\partial B_{i}}{\partial l} \vert }$, where $l$ is along a certain direction. Thus, the optimal $\Delta t$ and $l_{\mathrm{sc}}$ satisfy $\frac{\delta B_{i}}{ \vert ( \frac{\partial B_{i}}{ \partial t} )_{\mathrm{sc}} \vert } < \Delta t \ll \frac{l_{\mathrm{str}}}{V _{\mathrm{str}}}$ and $\frac{\delta B_{i}}{ \vert \frac{\partial B_{i}}{ \partial l} \vert } < l_{\mathrm{sc}} \ll l_{\mathrm{str}}$. Therefore, suitable $\Delta t$ and $l_{\mathrm{sc}}$ should be taken for different cases.

4.2 Dimensionality (Dimension Number) for Different Field Quantities

In previous sections we have only considered the dimensionality of magnetic field structures. However, if we consider other fields such as current density, electric field, or velocity field, we may find that they have different dimensionalities. That is, when the magnetic field is 1D, it does not guarantee that the other parameters are also 1D.

Since the current density is $\stackrel{\rightharpoonup }{J}=\mathrm{\nabla }\times \stackrel{\rightharpoonup }{B}$, if $\partial \stackrel{\rightharpoonup }{B}/\partial n=0$, $\partial \stackrel{\rightharpoonup }{J}/\partial n=0$. So the dimension number of the current density should be equal to or smaller than that of the magnetic field. The dimension number can be smaller (e.g., 2-D for magnetic field but 1-D or constant for current density) because the current density is calculated from the spatial derivative of the magnetic field.

Rezeau et al. (2018) argue that in low beta plasmas when the magnetic field controls all the other plasma parameters, one can deem that if magnetic field is 1-D, then all the other parameters will be 1-D, while in higher beta plasma, pressure effects are important, and it is not certain that the 1-D variations of $B$ can ensure all the plasma parameters will be 1-D from the fluid momentum equations of both ions and electrons.

We suspect that the opposite may actually be the case. In low beta plasma, the force balance (MHD momentum equation) is controlled by the magnetic terms only. Then it does not matter how velocity and pressure are distributed in space (they may be 2-D or 3-D). In Fig. 24 we plot the MDD results for velocity, convection electric field and magnetic field for a magnetopause crossing. We find that there is some slight difference in the normal for different parameters from the results of $B$, $V$ and $E$ fields. When Beta is higher during the early phase, all three parameters appear to be 1-D, however when Beta is lower during the later phase, $V$ and $E$ appear to be 2-D structures, while the magnetic field appears to be 1-D. Although Rezeau et al. (2018) proposed a generalized MDD method using a combination of magnetic field and electric field to obtain the overall dimensionality of a structure, different parameters (physical quantities) could have different dimensionalities.

Fig. 24

MDD analysis on a magnetopause crossing events (Russell et al. 2017) observed by MMS at the dusk flank of the magnetosphere: first row shows the MDD analysis using magnetic field data, from top to bottom (a) GSM Bz observed by MMS1-4 along the trajectory; (b) square root of eigenvalues $\lambda_{\mathrm{max}}$, $\lambda_{\mathrm{mid}}$, and $\lambda_{\min}$ of the matrix $L$; (c) the Rezeau et al. dimensionality indices of the structure $D1 = \frac{\sqrt{\lambda _{\max }} - \sqrt{\lambda _{\mathrm{mid}}}}{\sqrt{\lambda _{\max }}}$, $D2 = \frac{\sqrt{\lambda _{\mathrm{mid}}} - \sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$, $D3 = \frac{\sqrt{\lambda _{\min }}}{\sqrt{\lambda _{\max }}}$; (d) maximum derivative direction ${\stackrel{\rightharpoonup }{n}}_{max}$; second row shows the MDD analysis using ion velocity, from top to bottom (f) GSM Vz observed by MMS1-4 along the trajectory; (g)–(i) same format as (b)–(d); third row shows the MDD analysis using electric field data ($\vec{E} = - \vec{V}_{\mathrm{ion}} \times \vec{B}$); (k) GSM Ey observed by MMS1-4 along the trajectory; (l)–(n) same format as (b)–(d). (e), (j), and (o) all show the same plasma beta

We should also note that the dimensionality may be related to the coordinate system we use. For example, for an axially symmetrical structure (like some kinds of flux ropes), in D-based Cartesian coordinates, it is 2-D as $B=B(x,y)$ if $z$ is the invariant axis. However, if we use a cylindrical coordinate system, we find that the field only varies in the r direction, i.e., $B=B(r)$. Then from this point of view, the structure turns out to be 1-D.

4.3 Comparison of Various Methods

In this section we will compare and contrast between the methods discussed in previous sections, and try to give a description of where they can be best applied. We emphasize here that there are not ‘better’ or ‘worse’ methods. Different methods will have their best application in different circumstances. In many cases we may use different methods at the same time to compare and obtain a more reliable coordinate system and reference frame.

First we discuss the difference between MVA and MDD. As emphasized by Sonnerup and Scheible (1998), $\lambda _{3}\ll \lambda _{2}$ from the MVA method does not automatically indicate that a 1-D current layer has been traversed and for a 2-D structure, one cannot necessarily conclude that the minimum variance direction is along with the invariant axis. In other words, the fact that one or two eigenvalues are equal to zero in the MVAB method is not a sufficient condition for one or two-dimensionality (also see Dunlop and Woodward 1998; Dunlop et al. 2002). This means that one may not directly use the MVA method to determine the dimension number or invariant axis orientation of a structure observed. In the MDD analysis, if we find an eigenvalue equal to zero, it follows that ${(\partial \stackrel{\rightharpoonup }{B}/\partial n)}^2={(\partial B_x/\partial n)}^2+{(\partial B_y/\partial n)}^2+{(\partial B_z/\partial n)}^2=0$, which means the derivatives of $B_{x}$, $B_{y}$, and $B_{z}$ along this eigenvector direction $\stackrel{\rightharpoonup }{n}$ should all be zero. This shows that the MDD method can provide a sufficient condition for one or two-dimensionality of a structure and then give the invariant axis directions at the same time.

Although MVAB and MDD are both looking for a coordinate system to simplify the problem, the MVA method is seeking for the extreme variation value of $B_{n}^{2}$, and the MDD approach is seeking for the extremum of $|\partial \vec{B}/\partial n|^{2}$. So the extreme values and eigenvector directions obtained by the two methods are often different.

We can schematically show the axis difference obtained by MDD and MVA analysis for the simplest 1-D case, as plotted in Fig. 25. For a current sheet in which the magnetic field on one side of the current sheet is antiparallel to the field on the other side, the magnetic field can be written as

$$\overrightarrow{B}=B_{x0}tanh\left(\frac{z}{L_0}\right){\stackrel{\rightharpoonup }{e}}_x.$$

(4.1)

In the MDD analysis for this kind of case, as also calculated in Sect. 2.4.2, ${\stackrel{\rightharpoonup }{n}}_{max}$ will be along the $z$ direction, and the other two axes can be any two orthogonal directions in the $xy$ plane. If we calculate the MVAB eigenvalues, a maximum eigenvalue $\lambda _{\max }$ will be found which corresponds to the $x$ direction, because the variation of $B_{x}$ throughout the crossing is the largest, and the other two eigenvalues $\lambda _{\mathrm{mid}}$ and $\lambda _{\min }$ are close to zero (may not be strictly zero because of numerical errors) which corresponds to any two perpendicular directions in $yz$ plane. The above conclusion is true even if we add a constant $B_{y0}$ and $B_{z0}$ in the magnetic field, such as

$$\overrightarrow{B}=B_{x0}tanh\left(\frac{z}{L_0}\right){\stackrel{\rightharpoonup }{e}}_x+B_{y0}{\stackrel{\rightharpoonup }{e}}_y+B_{z0}{\stackrel{\rightharpoonup }{e}}_z,$$

(4.2)

from which we can easily see that the normal of the current sheet is still along the z direction while the field quantities along x and y plane do not vary, still indicating a 1-D structure from the definition of dimensionality, although all three field components exist. Then the MDD results will be the same as those shown in Fig. 25, and the MVA results remain the same. In Table 1 we show the MVAB results for these two cases, which suggests that for this special 1-D current sheet MVAB may not distinguish well between the mid and min directions to find the normal. Therefore, in data analysis, we can use HMVA (hybrid MVA) as suggested by Gosling and Phan (2013) and recently used by, e.g., Hietala et al. (2018) in situations where it is hard to distinguish the $M$ and $N$ directions but $L$ is sufficiently clear.

Fig. 25

A schematic showing the right handed coordinate systems given by (a) the MVA method; (b) the MDD method for a Harris current sheet without guide field

Table 1 Summary of MVAB result of 1D current sheet of (4.2). Random errors on the order of 0.01 nT are added to the magnetic field data to resemble real data and to avoid the singularity in calculating the eigenvalues of the matrix. Three runs have been carried out for two sets of parameters of the model. We can find that in the same model the eigenvalue and eigenvector of the intermediate and minimum directions are quite different every time, while the eigenvalue and eigenvector of maximum direction remain the same

On the other hand, in many observational events, e.g., in the magnetopause current sheet, using MVA we can often find the normal direction very accurately. This could be due to the fact that the current sheets are seldom as ideal as (4.2) shows, i.e., the tangential field perpendicular to the background field direction ($L$ direction) is seldom constant and then it might still have variations, since 1-D magnetic field structures only require the field along the normal to be constant. When we slightly revise the field model, adding a non-constant $B_{y}$ across the current sheet, like

$$\overrightarrow{B}=B_{x0}tanh\left(\frac{z}{L_0}\right){\stackrel{\rightharpoonup }{e}}_x+B_{y0}sech\left(\frac{z}{L_1}\right){\stackrel{\rightharpoonup }{e}}_y+B_{z0}{\stackrel{\rightharpoonup }{e}}_z,$$

(4.3)

which is still a 1-D field, we then can separate $\lambda _{\mathrm{mid}}$ and $\lambda _{\min }$ in MVAB, even if $B_{y}$ is very small (here we set $B_{y0} = 0.1B_{x0}$). Then the minimum and medium eigenvalues can be well separated and $\mathit{Nmin}$ in MVAB is closer to the $z$ axis as we expected, see results in Table 2.

Table 2 Summary of MVAB result of 1D current sheet as in (4.3). For this current sheet which is closer to real data in the magnetopause or magnetotail current sheet, MVA can distinguish between the mid and min directions and then obtain the correct normal

In Table 3 we list the ability of various methods in solving different issues. For example, some methods need a quasi-stationary assumption while some do not; some can obtain instantaneous results to see the variation of direction or frame velocity, while some can obtain only one velocity using the data for the whole crossing; some have a presumed dimension number, some do not need this assumption.

Table 3 Capabilities and requirements of various methods in solving different issues

4.4 Potential Applications of Gradient Based Methods in Simulation Data Analysis and Other Problems

The MDD and STD methods can be effectively used in numerical simulations. In the analysis of simulated data, we can calculate dimension number, characteristic directions and velocities of simulated magnetic field structures (such as plasmoid, FTE, magnetopause current sheet, bow shock, and magnetotail current sheet). It can also be very convenient to automatically calculate the time variation of velocity and direction for the simulated structure.

Compared to satellite data analysis, it is more convenient to use the methods in analyzing numerical simulation data. Firstly, in principle it is not restricted by satellite separation and the precision of the results can be highly improved because the grid points in the numerical simulation must be close enough to meet the requirement that their spacing is much smaller than the structure scale. Second, the number of ‘satellites’ can be unlimited: one mesh point corresponds to one satellite. So we can calculate the structure’s direction and velocity distribution in the whole simulation domain. Third, unlike the situation we met in real data analysis, there are always measured points in the structure to calculate velocity and direction. Fourth, the dimension number used in the numerical simulation can be tested. As described above, the definition of dimension in MDD is exactly the same as that in numerical simulation. For example, if the structure is simulated in 3-dimensions but it is examined by the MDD analysis to be a two-dimensional structure, then we may switch to 2-D simulation for this case, greatly reducing the computer simulation time. This can be done automatically by some computer programs. The studies of Denton et al. (2010, 2012) are the first attempt to use these methods in a numerical simulation, although they used only 4 points to make calculations. Figure 26 shows a distribution of maximum eigenvalues from MDD of the magnetic field in a global MHD simulation, from which we can easily find the magnetopause and the current sheet.

Fig. 26

Spatial distribution of $\lambda _{\max}$ from MDD of the magnetic field in a global MHD simulation

In laboratory plasmas, if we have multi point magnetic probes, in principle we can also apply the same techniques to attain the proper frame and coordinate systems. This could be useful in the analysis of transient convective MHD instabilities. By the way, it is well known that many everyday objects in our world produce a magnetic field, such as vehicles, aircraft and so on. When they are moving, they carry magnetic field along with them. So using the STD method we can also measure the movement velocity of magnetic field and then we will know the speed of the object. If the magnetic field of objects does not vary with time, the first term in the right hand side of equation (1.1) is strictly equal to 0. For example, for a bar magnet as discussed in Sect. 3.4.2, its magnetic field is a dipole magnetic field, and the magnetic field on it does not vary with time. If it moves at some given velocity and we calculate the velocity using the STD method, we find our calculation is quite consistent with the given velocity (not shown here). The magnetic field of real magnetic objects may be complicated by including dipole magnetic field, quadrupole magnetic field and higher order terms. In principle, the STD method should work, and the further investigation is still ongoing. More work is required to test if this is practically useful. First we need to put a huge number of magnetometers in space (atmosphere). It might not work if magnetometers are installed on or near vehicles, because they may observe a time-independent field (in the vehicle rest frame) under a steady state condition. There may also be substantial electromagnetic radiation from the vehicle that cannot be neglected. More work should be done to investigate the feasibility of this idea.