Polynomials under Ornstein–Uhlenbeck noise and an application to inference in stochastic Hodgkin–Huxley systems

Abstract

We discuss estimation problems where a polynomial $s\rightarrow \sum _{i=0}^\ell \vartheta _i s^i$ with strictly positive leading coefficient is observed under Ornstein–Uhlenbeck noise over a long time interval. We prove local asymptotic normality (LAN) and specify asymptotically efficient estimators. We apply this to the following problem: feeding noise $dY_t$ into the classical (deterministic) Hodgkin–Huxley model in neuroscience, with $Y_t=\vartheta t + X_t$ and X some Ornstein–Uhlenbeck process with backdriving force $\tau$, we have asymptotically efficient estimators for the pair $(\vartheta ,\tau )$; based on observation of the membrane potential up to time n, the estimate for $\vartheta$ converges at rate $\sqrt{n^3\,}$.

1 Introduction

Problems of parametric inference when we observe over a long time interval a process Y of type

$$\begin{aligned} dY_t = \left( \sum _{j=1}^m \vartheta _j\, f_j(t) \;-\; \tau \, Y_t \right) dt + \sqrt{c\,} dW_t ,\quad \tau >0 \end{aligned}$$

with unknown parameters $(\vartheta _1,\ldots ,\vartheta _m)$ or $(\vartheta _1,\ldots ,\vartheta _m,\tau )$ and with $(f_1,\ldots ,f_m)$ a given set of functions have been considered in a number of papers; alternatively, such models can be written as

$$\begin{aligned} Y_t = \sum _{j=1}^m \vartheta _j\, g_j(t) + X_t ,\quad dX_t = -\tau X_t\, dt + \sqrt{c\,} dW_t \end{aligned}$$

with related functions $(g_1,\ldots ,g_m)$. Also, driving Brownian motion W in the Ornstein–Uhlenbeck type equations above has been replaced by certain Lévy processes or by fractional Brownian motion. Many papers focus on orthonormal sets of periodic functions $[0,\infty )\rightarrow \mathbb {R}$ with known periodicity. To determine estimators and limit laws for rescaled estimation errors in this case, periodicity allows to exploit ergodicity or stationarity with respect to the time grid of multiples of the periodicity. We mention Dehling et al. (2010), Franke and Kott (2013) and Dehling et al. (2017) where limit distributions for least squares estimators and maximum likelihood estimators are obtained. Rather than in asymptotic properties, Pchelintsev (2013) is interested in methods which allow to reduce squared risk—i.e. risk defined with respect to one particular loss function—uniformly over determined subsets of the parameter space, at fixed and finite sample size. Asymptotic efficiency of estimators is the topic of Höpfner and Kutoyants (2009), where sums $\sum \vartheta _j f_j$ as above are replaced by periodic functions S of known periodicity whose shape depends on parameters $(\vartheta _1,\ldots ,\vartheta _m)$. When the parametrization is smooth enough, local asymptotic normality in the sense of LeCam (see Le Cam 1969; Hajek 1970; Davies 1985; Pfanzagl 1994; Le Cam and Yang 2002; with a different notion of local neighbourhood see Ibragimov and Khasminskii (1981) and Kutoyants (2004)) allows to identify a limit experiment with the following property: risk—asymptotically as the time of observation tends to $\infty$, and with some uniformity over small neighbourhoods of the true parameter—is bounded below by a corresponding minimax risk in a limit experiment. This assertion holds with respect to a broad class of loss functions.

With a view to an estimation problem which arises in stochastic Hodgkin–Huxley models and which we explain below, the present paper deals with parameter estimation when one observes a process Y

$$\begin{aligned} Y_t = \sum _{j=0}^p \vartheta _j\, t^j + X_t ,\quad dX_t = -\tau X_t\, dt + \sqrt{c\,} dW_t ,\quad \tau >0 \end{aligned}$$

(1)

with leading coefficient $\vartheta _p>0$ so that paths of Y almost surely tend to $\infty$. Then good estimators for the parameters based on observation of Y up to time n show the following behaviour: whereas estimation of parameters $\tau$ and $\vartheta _0$ works at the ’usual’ rate $\sqrt{n\,}$, parameters $\vartheta _j$ with $1\le j\le p$ can be estimated at rate $\sqrt{n^{2j+1}\,}$ as $n\rightarrow \infty$. With rescaled time $(tn)_{t\ge 0}$, we prove local asymptotic normality as $n\rightarrow \infty$ in the sense of LeCam with local scale

$$\begin{aligned} \psi _n\, {:}{=}\, \left( \begin{array}{lllll} \frac{1}{\sqrt{n\,}} &{} 0 &{} \ldots &{} \ldots &{} 0 \\ 0 &{} \frac{1}{\sqrt{n^3\,}} &{} \ldots &{} \ldots &{} 0 \\ 0 &{} \ddots &{} \ddots &{}\ddots &{} 0 \\ 0 &{} \ldots &{} \ldots &{} \frac{1}{\sqrt{n^{2p+1}\,}} &{} 0 \\ 0 &{} \ldots &{} \ldots &{} 0 &{} \frac{1}{\sqrt{n\,}} \end{array} \right) \end{aligned}$$

and with limit information process $J=(J_t)_{t\ge 0}$

$$\begin{aligned} J(t) = \frac{1}{c\,} \left( \begin{array}{lllll} \frac{\tau ^2}{1}\; t &{} \frac{\tau ^2}{2\,}\; t^2 &{}\ldots &{} \frac{\tau ^2}{p+1\,}\; t^{p+1} &{} 0 \\ \frac{\tau ^2}{2\,}\; t^2 &{} \frac{\tau ^2}{3\,}\; t^3 &{}\ldots &{} \frac{\tau ^2}{p+2\,}\; t^{p+2} &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \frac{\tau ^2}{p+1\,}\; t^{p+1} &{} \frac{\tau ^2}{p+2\,}\; t^{p+2} &{}\ldots &{} \frac{\tau ^2}{2p+1\,}\; t^{2p+1} &{} 0 \\ 0 &{}\ldots &{}\ldots &{} 0 &{} \frac{c}{2\,\tau }\; t \end{array}\right) ,\quad t\ge 0 \end{aligned}$$

at every $\theta \,{:}{=}\,(\vartheta _0,\ldots ,\vartheta _p,\tau )$. As a consequence of local asymptotic normality, there is a local asymptotic minimax theorem (Ibragimov and Khasminskii 1981; Davies 1985; Le Cam and Yang 2002; Kutoyants 2004; Höpfner 2014) which allows to identify optimal limit distributions for rescaled estimation errors in the statistical model (1); the theorem also specifies a particular expansion of rescaled estimation errors (in terms of the central sequence in local experiments at $\theta$) which characterizes asymptotic efficiency. We can construct asymptotically efficient estimators for the model (1), and these estimators have a simple and explicit form.

We turn to an application of the results obtained for model (1). Consider the problem of parameter estimation in a stochastic Hodgkin–Huxley model for the spiking behaviour of a single neuron belonging to an active network

$$\begin{aligned} \left\{ \begin{array}{l} dV_t = dY_t \;-\; F(V_t,n_t,m_t,h_t)\, dt \\ dn_t = \left\{ \alpha _n(V_t)(1-n_t) - \beta _n(V_t)(1-n_t) \right\} dt \\ dm_t= \left\{ \alpha _m(V_t)(1-m_t) - \beta _m(V_t)(1-m_t) \right\} dt \\ dh_t = \left\{ \alpha _h(V_t)(1-h_t) - \beta _h(V_t)(1-h_t) \right\} dt \end{array} \right. \end{aligned}$$

(2)

where input $dY_t$ received by the neuron is modelled by the increments of the stochastic process

$$\begin{aligned} Y_t = \vartheta \, t + X_t ,\quad dX_t = -\tau X_t\, dt + \sqrt{c\,} dW_t ,\quad (\vartheta ,\tau )\in (0,\infty )^2 \;. \end{aligned}$$

(3)

The functions F(., ., ., .) and $\alpha _j(.)$, $\beta _j(.)$, $j\in \{n,m,h\}$ are those of Izhikevich (2007) pp. 37–39. The stochastic model (2) extends the classical deterministic model with constant rate of input $a>0$

$$\begin{aligned} \left\{ \begin{array}{l} dV_t = a\, dt \;-\; F(V_t,n_t,m_t,h_t)\, dt \\ dn_t= \left\{ \alpha _n(V_t)(1-n_t) - \beta _n(V_t)(1-n_t) \right\} dt \\ dm_t= \left\{ \alpha _m(V_t)(1-m_t) - \beta _m(V_t)(1-m_t) \right\} dt \\ dh_t = \left\{ \alpha _h(V_t)(1-h_t) - \beta _h(V_t)(1-h_t) \right\} dt \end{array} \right. \end{aligned}$$

(4)

by taking into account ’noise’ in the dendritic tree where incoming excitatory or inhibitory spike trains emitted by a large number of other neurons in the network add up and decay. See Hodgkin and Huxley (1952), Izhikevich (2007), Ermentrout and Terman (2010) and the literature quoted there for the role of this model in neuroscience. Stochastic Hodgkin–Huxley models have been considered in Höpfner et al. (2016a, b), (2017) and Holbach (2020). For suitable data sets, membrane potential data hint to the existence of a quadratic variation which indicates the need for a stochastic modelization.

In systems (2) or (4), the variable $V=(V_t)_{t\ge 0}$ represents the membrane potential in the neuron; the variables $j=(j_t)_{t\ge 0}$, $j\in \{n,m,h\}$, are termed gating variables and represent—in the sense of averages over a large number of channels—opening and closing of ion channels of certain types. The membrane potential can be measured intracellularly in good time resolution whereas the gating variables in the Hodgkin–Huxley model are not accessible to direct measurement.

In a sense of equivalence of experiments as in Holbach (2019), the stochastic Hodgkin Huxley model (2)+(3) corresponds to a submodel of (1). This is of biological importance. Under the assumption that the stochastic model admits a fixed starting point which does not depend on $\theta \,{:}{=}\,(\vartheta ,\tau )$, we can estimate the components $\vartheta >0$ and $\tau >0$ of the unknown parameter $\theta =(\vartheta ,\tau )$ in equations (2)+(3) from the evolution of the membrane potential alone, and have at our disposal simple and explicit estimators $\breve{\theta }(n)=( \breve{\vartheta }(n) , \breve{\tau }(n) )$ with the following two properties (i) and (ii).

(i) With local parameter $h=(h_1,h_2)$ parametrizing shrinking neighbourhoods of $\theta =(\vartheta ,\tau )$, risks

$$\begin{aligned} \sup _{|h|\le C}\; E_{\left( {\vartheta +h_1/\sqrt{n^3\,}} \,,\, {\tau +h_2/\sqrt{n\,}} \right) }\left( \; L \left( \begin{array}{l} \sqrt{n^3\,} (\, \breve{\vartheta }(n) - (\vartheta +h_1/\sqrt{n^3\,}) \,) \\ \sqrt{n\,} (\, \breve{\tau }(n) - (\tau +h_2/\sqrt{n\,}) \,) \end{array}\right) \;\right) \end{aligned}$$

(5)

converge as $n\rightarrow \infty$ to

$$\begin{aligned} E\left( \; L \left( \begin{array}{l} \frac{3\sqrt{c\,}}{\tau }\, \int _0^1 s\; d\widetilde{W}^{(1)}_s \\ \sqrt{2\,\tau \,}\; \widetilde{W}^{(2)}_1 \end{array}\right) \;\right) \end{aligned}$$

(6)

where $\widetilde{W}=( \widetilde{W}^{(1)}, \widetilde{W}^{(2)} )$ is two-dimensional standard Brownian motion. Here C is an arbitrary constant, and $L:\mathbb {R}^2\rightarrow [0,\infty )$ any loss function which is continuous, subconvex and bounded.

(ii) We can compare the sequence of estimators $\breve{\theta }(n)=(\breve{\vartheta }(n),\breve{\tau }(n))$ for $\theta =(\vartheta ,\tau )$ in (5) to arbitrary estimator sequences $T(n)=( T^{(1)}(n) , T^{(2)}(n) )$ which can be defined from observation of the membrane potential up to time n, provided their rescaled estimation errors—using the same norming as in (5)—are tight. For all such estimator sequences,

$$\begin{aligned} \sup _{C\uparrow \infty }\; \liminf _{n\rightarrow \infty }\;\sup _{|h|\le C}\; E_{\left( {\vartheta +h_1/\sqrt{n^3\,}} \,,\, {\tau +h_2/\sqrt{n\,}} \right) }\left( \; L \left( \begin{array}{l} \sqrt{n^3\,} (\, T^{(1)}(n) - (\vartheta +h_1/\sqrt{n^3\,}) \,) \\ \sqrt{n\,} (\, T^{(2)}(n) - (\tau +h_2/\sqrt{n\,}) \,) \end{array}\right) \;\right) \end{aligned}$$

is always greater or equal than the limit in (6). This is the assertion of the local asymptotic minimax theorem. It makes sure that asymptotically as $n\rightarrow \infty$, it is impossible to outperform the simple and explicit estimator sequence $\breve{\theta }(n)=(\breve{\vartheta }(n),\breve{\tau }(n))$ which we have at hand.

The paper is organized as follows. Section 2 collects for later use convergence results for certain functionals of the Ornstein–Uhlenbeck process. Section 3 deals with local asymptotic normality (LAN) for the model (1): proposition 1 and theorem 1 in Sect. 3.1 prove LAN, the local asymptotic minimax theorem is corollary 1 in Sect. 3.1; we introduce and investigate estimators for $\theta =(\vartheta ,\tau )$ in Sects. 3.2 and 3.3; theorem 2 in Sect. 3.4 states their asymptotic efficiency. The application to parameter estimation in the stochastic Hodgkin–Huxley model (2)+(3) based on observation of the membrane potential is the topic of the final Sect. 4: see theorem 3 and corollary 2 there.

2 Functionals of the Ornstein Uhlenbeck process

We state for later use properties of some functionals of the Ornstein Uhlenbeck process

$$\begin{aligned} dX_t = -\tau \, X_t\, dt \,+\, \sigma \, dW_t ,\quad t\ge 0 \end{aligned}$$

(7)

with fixed starting point $x_0 \in \mathbb {R}$. $\tau >0$ and $\sigma >0$ are fixed, and $\,\nu \,{:}{=}\,\mathcal {N}(0,\frac{\sigma ^2}{2\tau })\,$ is the invariant measure of the process in (7); $\,X$ is defined on some $(\Omega ,\mathcal {A},P)$.

Lemma 1

For X defined by (7), for every $f\in L^1(\nu )$ and $\ell \in \mathbb {N}$, we have almost sure convergence as $r\rightarrow \infty$

$$\begin{aligned} \frac{\ell }{r^\ell } \int _0^r s^{\ell -1} f(X_s)\, ds \;\;\longrightarrow \;\; \nu (f) \;. \end{aligned}$$

Proof

(Höpfner and Kutoyants 2011, lemma 2.2; Holbach 2019, lemma 2.5, compare to Bingham et al. 1987 theorem 1.6.4 p. 33)

(1) We consider functions $f\in L^1(\nu )$ which satisfy $\nu (f)\ne 0$. The case $\ell =1$ is the well known ratio limit theorem for additive functionals of the ergodic diffusion X (Kutoyants 2004; Höpfner 2014 p. 214). Assuming that the assertion holds for $\ell =\ell _0\in \mathbb {N}$, define $\,A_r =\int _0^r s^{\ell _0-1} f(X_s)\, ds\,$. Stieltjes product formula for semimartingales with paths of locally bounded variation yields

$$\begin{aligned} \int _0^r s\, dA_s = r\, A_r \;-\; \int _0^r A_s\, ds ,\quad 0<r<\infty \;. \end{aligned}$$

Under our assumption, both terms on the right hand side are of stochastic order $O(r^{\ell _0+1})$: since $\,\frac{\ell _0}{s^{\ell _0}} A_s\,$ converges to $\,\nu (f)\ne 0\,$ almost surely as $s\rightarrow \infty$, the second term on the right hand side behaves as $\,\nu (f)\int _0^r \frac{s^{\ell _0}}{\ell _0} ds = \nu (f)\frac{r^{\ell _0+1}}{\ell _0(\ell _0+1)}\,$ as $r\rightarrow \infty$; the first term on the right hand side behaves as $\nu (f) \frac{r^{\ell _0+1}}{\ell _0}$. This proves the assertion for $\ell _0+1$.

(2) We consider functions $f\in L^1(\nu )$ such that $\nu (f)=0$, $f\ne 0$. Writing $f^+\ge 0$ for the positive part of f and $f^-\ge 0$ for the negative part, we have $f=f^+-f^-$ and $\alpha \,{:}{=}\,\nu (f^+)=\nu (f^-)>0$. For N arbitrarly large but fixed, step (1) applied to functions $\,h_N\,{:}{=}\, [f^+ - (1{-}\frac{1}{N}) f^-]\,$ and $\,g_N\,{:}{=}\, [(1{-}\frac{1}{N}) f^+ - f^- ]\,$ yields almost sure convergence

$$\begin{aligned} \lim _{r\rightarrow \infty }\; \frac{\ell }{r^\ell } \int _0^r s^{\ell -1}\, h_N(X_s)\, ds= & {} \int h_N d\nu = \frac{\alpha }{N} \\ \lim _{r\rightarrow \infty }\; \frac{\ell }{r^\ell } \int _0^r s^{\ell -1}\, g_N(X_s)\, ds= & {} \int g_N d\nu = -\frac{\alpha }{N} \end{aligned}$$

as $r\rightarrow \infty$. Thus, letting N tend to $\infty$, comparison of trajectories

$$\begin{aligned} \int _0^r s^{\ell -1}\, g_N(X_s)\, ds \;\le \; \int _0^r s^{\ell -1}\, f(X_s)\, ds \;\le \; \int _0^r s^{\ell -1}\, h_N(X_s)\, ds \end{aligned}$$

establishes the desired result for functions $f\in L^1(\nu )$ with $\nu (f)=0$. $\square$

Lemma 2

For X as above we have for every $\ell \in \mathbb {N}$

$$\begin{aligned} \frac{1}{r^\ell } \int _0^r s^\ell \, dX_s = X_r + \rho _\ell (r) ,\quad \lim _{r\rightarrow \infty }\rho _\ell (r)= 0 \quad \text{ almost } \text{ surely } \;. \end{aligned}$$

Proof

This is integration by parts

$$\begin{aligned} \int _0^r s^\ell \, dX_s = r^\ell \, X_r \;-\; \int _0^r X_s\; \ell s^{\ell -1}\, ds ,\quad r>0 \end{aligned}$$

(8)

and lemma 1 (with $f(x)=x$ and $\nu =\mathcal {N}(0,\frac{\sigma ^2}{2\tau })$) applied to the right hand side. $\square$

Lemma 3

For X defined by (7), for every $\ell \in \mathbb {N}_0$, we have convergence in law

$$\begin{aligned} \frac{1}{\sqrt{ n^{2\ell +1}} } \; \int _0^n s^{\ell }\, X_s\, ds \end{aligned}$$

as $n\rightarrow \infty$ to the limit

$$\begin{aligned} \frac{\sigma }{\tau } \int _0^1 s^{\ell }\, dB_s \end{aligned}$$

where B is standard Brownian motion.

Proof

Rearranging SDE (7) we write

$$\begin{aligned} \tau \, X_s\, ds = -dX_s + \sigma \, dW_s \end{aligned}$$

and have for every $\ell \in \mathbb {N}_0$

$$\begin{aligned} \tau \, \int _0^r s^\ell \, X_s\, ds = - \int _0^r s^\ell \, dX_s + \sigma \, \int _0^r s^\ell \, dW_s ,\quad r\ge 0 \;. \end{aligned}$$

(9)

In case $\ell =0$, the right hand side is $-(X_r-X_0)+\sigma W_r$, and the scaling property of Brownian motion combined with ergodicity of X yields weak convergence as asserted. In case $\ell \ge 1$, lemma 2 transforms the first term on the right hand side of (9), and we have

$$\begin{aligned} \tau \, \int _0^r s^\ell \, X_s\, ds = -r^\ell \left( \, X_r + \rho _\ell (r) \,\right) + \sigma \, \int _0^r s^\ell \, dW_s \;. \end{aligned}$$

(10)

The martingale convergence theorem (Jacod and Shiryaev 1987, VIII.3.24) shows that

$$\begin{aligned} \left( \, \frac{1}{\sqrt{ n^{2\ell +1}} } \int _0^{t n} s^\ell \, dW_s \,\right) _{t\ge 0} \end{aligned}$$

(11)

converges weakly in the Skorohod path space $D([0,\infty )\mathbb {R})$ to a continuous limit martingale with angle bracket $\,t \,\rightarrow \, \frac{1}{2\ell +1}t^{2\ell +1}\,$, i.e. to

$$\begin{aligned} \left( \, \int _0^t s^\ell \, dB_s \,\right) _{t\ge 0} \;. \end{aligned}$$

Scaled in the same way, the first term on the right hand side of (10)

$$\begin{aligned} - \frac{1}{\sqrt{n\,}}\, ( X_{tn} + \rho _\ell (tn) ) \; t^\ell \end{aligned}$$

is negligible in comparison to (11), uniformly on compact t-intervals, by ergodicity of X. $\square$

Lemma 4

(a) For every $\ell \in \mathbb {N}$ we have an expansion

$$\begin{aligned} \frac{1}{\sqrt{ n^{2\ell +1}} } \int _0^n s^\ell \, X_s\, ds = \frac{\sigma }{\tau } \frac{1}{\sqrt{ n^{2\ell +1}} } \int _0^{n} s^\ell \, dW_s \;-\; \frac{1}{\tau \sqrt{n\,}} ( X_n + \rho _\ell (n) ) \end{aligned}$$

(12)

where $\lim \limits _{n\rightarrow \infty } \rho _\ell (n) = 0\,$ almost surely. In case $\ell =0$ we have

$$\begin{aligned} \frac{1}{\sqrt{ n\,} } \int _0^n X_s\, ds = \frac{\sigma }{\tau } \frac{1}{\sqrt{ n\,} } W_n \;-\; \frac{1}{\tau \sqrt{n\,}} ( X_n - X_0 ) \;. \end{aligned}$$

(b) For every $\ell \in \mathbb {N}$, we have joint weak convergence as $n\rightarrow \infty$

$$\begin{aligned} \left( \, \frac{1}{\sqrt{n}} \int _0^n s^0\, X_s\, ds \,,\, \ldots \,,\, \frac{1}{\sqrt{ n^{2\ell +1}} } \; \int _0^n s^{\ell }\, X_s\, ds \,\right) \end{aligned}$$

(13)

with limit law

$$\begin{aligned} \frac{\sigma }{\tau } \left( \, \int _0^1 s^{0}\, dB_s \,,\, \ldots \,,\, \int _0^1 s^{\ell }\, dB_s \,\right) \;. \end{aligned}$$

Proof

Part (a) is (10) plus scaling as in the proof of lemma 3. For different $\ell \in \mathbb {N}_0$, the expansions (12) hold with respect to the same driving Brownian motion W from SDE (7): this gives (b). $\square$

3 The statistical model of interest

Consider now a more general problem of parameter estimation from continuous-time observation of

$$\begin{aligned} Y_t = R(t) \,+\, X_t ,\quad t\ge 0 \end{aligned}$$

(14)

where $R(\cdot )$ is a sufficiently smooth deterministic function which depends on some finite-dimensional parameter $\vartheta$, and where the Ornstein Uhlenbeck process $X=(X_t)_{t\ge 0}$, unique strong solution to

$$\begin{aligned} dX_t = -\tau \, X_t\, dt \,+\, \sqrt{c\,}\, dW_t \;, \end{aligned}$$

(15)

depends on a parameter $\tau >0$. The starting point $X_0\equiv x_0$ is deterministic. Then Y solves the SDE

$$\begin{aligned} dY_t = \left( \, S(t) - \tau \, Y_t \,\right) dt + \sqrt{c\, }dW_t ,\quad t\ge 0 \end{aligned}$$

(16)

where S depending on $\vartheta$ and $\tau$ is given by

$$\begin{aligned} S(t) = [\, R' \,+\, \tau \, R \,](t) \quad \text{ where }\quad R'\,{:}{=}\,\frac{d}{dt}R \;. \end{aligned}$$

(17)

Conversely, if a process Y is solution to an SDE of type (16), then solving $\,{R'} =-\tau R + S\,$ with suitable initial point $r_0$ we get a representation (14) for Y where

$$\begin{aligned} R(t) = r_0\, e^{-\tau t} \,+\, \int _0^t S(s)\, e^{-\tau (t-s)}\, ds \;. \end{aligned}$$

(18)

For examples of parametric models of this type, see e.g. Dehling et al. (2010), Franke and Kott (2013), Höpfner and Kutoyants (2009), Pchelintsev (2013), and example 2.3 in Höpfner and Kutoyants (2011). The constant $c>0$ in (15) is fixed and known: observing the trajectory of Y continuously in time, $\,\langle Y\rangle _t = c\, t\,$ equals the limit in probability $\lim \limits _{n\rightarrow \infty }\sum _{j=1}^{2^n} ( Y_{t j /2^n }-Y_{ t (j-1) / 2^n } )^2$ of squared increments, thus c is known almost surely and cannot be considered as a parameter.

We wish to estimate the unknown parameter $\theta \,{:}{=}\,(\vartheta ,\tau )$ based on time-continuous observation of Y in (14) over a long time interval, in the model

$$\begin{aligned} R_\vartheta (t) = \sum _{j=0}^p \vartheta _j\, t^j \end{aligned}$$

(19)

with real coefficients where we assume a leading coefficient $\,\vartheta _p>0\,$ such that trajectories of Y tend to $\infty$ almost surely as $t\rightarrow \infty$. Thus our parametrization is

$$\begin{aligned} \theta \, {:}{=}\, \left( \vartheta _0 , \vartheta _1, \ldots , \vartheta _{p-1}, \vartheta _p \,,\, \tau \right) ^\top \;\in \;\; \Theta \, {:}{=}\, { \mathbb {R}}^p{\times }(0,\infty ){\times }(0,\infty ) \end{aligned}$$

(20)

and in SDE (16) which governs the observation Y, $\,S$ depending on $\theta =(\vartheta ,\tau )$ has the form

$$\begin{aligned} S_{\theta }(t) = [R'_\vartheta + \tau R_\vartheta ](t) =\; \tau \,\vartheta _0 + \sum _{j=1}^p \,\vartheta _j\; t^{j-1} (\, j\,+\, \tau \, t \,) \;. \end{aligned}$$

(21)

3.1 Local asymptotic normality for the model (14)+(19)

Let $C\,{:}{=}\,C([0,\infty ),\mathbb {R})$ denote the canonical path space for continuous processes; with $\pi = (\pi _t)_{t\ge 0}$ the canonical process (i.e. $\pi _t(f)=f(t)$ for $f\in C$, $t\ge 0$) and $\mathcal {C}=\sigma (\pi _t:t\ge 0)$,

$$\begin{aligned} \mathbb {G} = (\mathcal {G}_t)_{t\ge 0} ,\quad \mathcal {G}_t\, {:}{=}\, \bigcap _{r>t} \sigma \left( \pi _s : s\le r \right) ,\quad t\ge 0 \end{aligned}$$

is the canonical filtration. Let $Q_\theta$ denote the law on $(C,\mathcal {C},\mathbb {G})$ of the process Y in (14) under $\theta \in \Theta$, cf. (20). By (14), (15), (16), (19) and (21), the canonical process $\pi =(\pi _t)_{t\ge 0}$ on $(C,\mathcal {C})$ under $Q_\theta$ solves

$$\begin{aligned} d\pi _t = \left( \, \left[ \, \tau \,\vartheta _0 + \sum _{j=1}^p \,\vartheta _j\; t^{j-1} (\, j\,+\, \tau \, t \,) \,\right] - \tau \, \pi _t \,\right) dt + \sqrt{c\, }dW_t \;. \end{aligned}$$

(22)

For pairs $\theta '\ne \theta$ in $\Theta$, probability measures $Q_{\theta '}$, $Q_\theta$ are locally equivalent relative to $\mathbb {G}$, and we write

$$\begin{aligned} \gamma '(s,y)= & {} \frac{ S_{\theta '}(s) - \tau ' y }{c} = \frac{ [R'_{\vartheta '} + \tau ' R_{\vartheta '}](s) -\tau ' y }{c}\\ \gamma (s,y)= & {} \frac{ S_\theta (s) - \tau y }{c} = \frac{ [R'_\vartheta + \tau R_\vartheta ](s) -\tau y }{c} \;. \end{aligned}$$

With $m^{\pi ,\theta }=\sqrt{c\,} dW_s$ the martingale part of $\pi$ under $\theta$, the likelihood ratio process of $Q_{\theta '}$ w.r.t. $Q_\theta$ relative to $\mathbb {G}$ (Lipster and Shiryaev 2001; Ibragimov and Khasminskii 1981; Jacod and Shiryaev 1987; Kutoyants 2004; Höpfner 2014 p. 162) is

$$\begin{aligned} L^{ \theta ' / \theta }_t = \exp \left( \, \int _0^t (\gamma '-\gamma )(s,\pi _s)\, \sqrt{c\, }dW_s - \frac{1}{2} \int _0^t (\gamma '-\gamma )^2(s,\pi _s) \, c\, ds \,\right) \;. \end{aligned}$$

(23)

In the integrand,

$$\begin{aligned}&c\, (\gamma '-\gamma )(s,\pi _s) = (R'_{\vartheta '} - R'_\vartheta )(s) \;-\; (\tau '-\tau )\pi _s + \tau 'R_{\vartheta '}(s) - \tau R_\vartheta (s) \\&\quad =(R'_{\vartheta '} - R'_\vartheta )(s) \;-\; (\tau '-\tau )( \pi _s - R_\vartheta (s) ) + \tau (R_{\vartheta '}-R_\vartheta )(s) + (\tau '-\tau )(R_{\vartheta '}-R_\vartheta )(s) \;, \end{aligned}$$

so we exploit (14) to write for short

$$\begin{aligned} c\, (\gamma '-\gamma )(s,\pi _s) = \left[ (R'_{\vartheta '} - R'_\vartheta ) + \tau (R_{\vartheta '}-R_\vartheta ) \right] (s) \;-\; (\tau '-\tau )X_s + (\tau '-\tau )(R_{\vartheta '}-R_\vartheta )(s) \end{aligned}$$

(24)

where X under $\theta =(\vartheta ,\tau )$ is the Ornstein Uhlenbeck process (15), and where

$$\begin{aligned} \left[ (R'_{\vartheta '} - R'_\vartheta ) + \tau (R_{\vartheta '}-R_\vartheta ) \right] (s) = \tau (\vartheta '_0-\vartheta _0) + \sum _{j=1}^p (\vartheta '_j-\vartheta _j)\, s^{j-1}\, [j + \tau s] \;. \end{aligned}$$

Localization at $\theta \in \Theta$ will be as follows: with notation

$$\begin{aligned}&{\vartheta _0'}(n,h)\, {:}{=}\, \vartheta _0 + \frac{1}{\sqrt{n\,}}\, h_0 ,\quad {\tau '}(n,h)\, {:}{=}\, \tau + \frac{1}{\sqrt{n\,}}\, h_{p+1} \quad , \\&\quad {\vartheta _j'}(n,h)\,{:}{=}\, \vartheta _j + \frac{1}{\sqrt{n^{2j+1}\,}}\, h_j ,\quad 1\le j\le p \end{aligned}$$

we insert

$$\begin{aligned} \theta '(n,h)=\left( \begin{array}{l} \vartheta _0'(n,h) \\ \vartheta _1'(n,h) \\ \ldots \\ \vartheta _p'(n,h) \\ \tau '(n,h) \end{array}\right) \quad \text{ where }\quad h=\left( \begin{array}{l} h_0 \\ h_1 \\ \ldots \\ h_p \\ h_{p+1} \end{array}\right) \quad \text{ is } \text{ such } \text{ that } \;\theta '(n,h)\in \Theta \end{aligned}$$

in place of $\theta '$ into (23); finally we rescale time. Define

$$\begin{aligned} \psi _n\, {:}{=}\, \left( \begin{array}{lllll} \frac{1}{\sqrt{n\,}} &{} 0 &{} \ldots &{} \ldots &{} 0 \\ 0 &{} \frac{1}{\sqrt{n^3\,}} &{} \ldots &{} \ldots &{} 0 \\ 0 &{} \ddots &{} \ddots &{}\ddots &{} 0 \\ 0 &{} \ldots &{} \ldots &{} \frac{1}{\sqrt{n^{2p+1}\,}} &{} 0 \\ 0 &{} \ldots &{} \ldots &{} 0 &{} \frac{1}{\sqrt{n\,}} \end{array} \right) \;. \end{aligned}$$

(25)

With local parameter h and local scale (25) at $\theta$, we obtain from (23)+(24)

$$\begin{aligned} L^{ (\theta + \psi _n h) \,/\, \theta }_{tn} = \exp \left( \, h^\top S_{n,\theta }(t) \;-\; \frac{1}{2}\; h^\top \!J_{n,\theta }(t)\; h + \rho _{n,\theta ,h}(t) \,\right) \end{aligned}$$

(26)

where $\rho _{n,\theta ,h}$ is some process of remainder terms, $\,S_{n,\theta }$ a martingale with respect to $Q_\theta$ and $(\mathcal {G}_{tn})_{t\ge 0}$

$$\begin{aligned} S_{n,\theta }(t)\, {:}{=}\, \frac{1}{\sqrt{c\,}} \left( \begin{array}{l} \frac{1}{\sqrt{n\,}} \int _0^{tn} \tau \; dW_s \\ \frac{1}{\sqrt{n^3\,}} \int _0^{tn} (1+\tau s)\; dW_s \\ \vdots \\ \frac{1}{\sqrt{n^{2j+1}\,}} \int _0^{tn} s^{j-1} (j+\tau s)\; dW_s\\ \vdots \\ \frac{1}{\sqrt{n^{2p+1}\,}} \int _0^{tn} s^{p-1} (p+\tau s)\; dW_s\\ - \frac{1}{\sqrt{n\,}} \int _0^{tn} X_s\; dW_s \end{array} \right) \end{aligned}$$

(27)

(again by (14), $X_s$ stands for $\pi _s-R_\theta (s)$ under $\theta$), and $\,J_{n,\vartheta }$ the angle bracket of $\,S_{n,\theta }$ under $\theta$.

Proposition 1

(a) For fixed $0<t<\infty$, components of $J_{n,\theta }(t)$ converge $Q_\theta$-almost surely as $n\rightarrow \infty$ to those of the deterministic process

$$\begin{aligned} J(t) = \frac{1}{c\,} \left( \begin{array}{lllll} \frac{\tau ^2}{1}\; t &{} \frac{\tau ^2}{2\,}\; t^2 &{}\ldots &{} \frac{\tau ^2}{p+1\,}\; t^{p+1} &{} 0 \\ \frac{\tau ^2}{2\,}\; t^2 &{} \frac{\tau ^2}{3\,}\; t^3 &{}\ldots &{} \frac{\tau ^2}{p+2\,}\; t^{p+2} &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ \frac{\tau ^2}{p+1\,}\; t^{p+1} &{} \frac{\tau ^2}{p+2\,}\; t^{p+2} &{}\ldots &{} \frac{\tau ^2}{2p+1\,}\; t^{2p+1} &{} 0 \\ 0 &{}\ldots &{}\ldots &{} 0 &{} \frac{c}{2\,\tau }\; t \end{array}\right) ,\quad t\ge 0 \;. \end{aligned}$$

(28)

For every $0<t<\infty$, the matrix J(t) is invertible.

(b) Let $\widetilde{W}$ denote a two-dimensional standard Brownian motion with components $\widetilde{W} ^{(1)}$ and $\widetilde{W} ^{(2)}$. In the cadlag path space $D=D([0,\infty ),\mathbb {R}^{p+2})$ (Jacod and Shiryaev 1987, chapters VI and VIII), martingales $S_{n,\theta }$ under $Q_\theta$ converge weakly as $n\rightarrow \infty$ to the limit martingale

$$\begin{aligned} S(t) = \left( \begin{array}{l} \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^0\, d \widetilde{W} ^{(1)}_s \\ \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^1 \, d \widetilde{W} ^{(1)}_s \\ \vdots \\ \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^p \, d \widetilde{W} ^{(1)}_s \\ \frac{1}{ \sqrt{2\,\tau \,} }\; \widetilde{W} ^{(2)}_t \end{array}\right) ,\quad t\ge 0 \;. \end{aligned}$$

(29)

Proof

The proof is in several steps. (1) We specify the angle bracket (or predictable quadratic covariation) process $J_{n,\vartheta }$ of $S_{n,\vartheta }$ under $Q_\theta$. Its state at time t

$$\begin{aligned} J_{n,\theta }(t)\, {:}{=}\, \left( \, J_{n,\theta }^{(i,j)}(t)\,\right) _{i,j=0,1,\ldots ,p{+}1} \end{aligned}$$

is a symmetric matrix of size $(p{+}2){\times }(p{+}2)$. Taking into account the norming factor in front of $S_{n,\theta }$ in (27) we consider throughout $cJ_{n,\theta }$. The entries are given as follows. We have

$$\begin{aligned} cJ_{n,\theta }^{(i,j)}(t) = \frac{1}{n^{i+j+1}}\int _0^{tn} s^{i+j-2}\, (i{+}\tau s)(j{+}\tau s)\, ds \quad {\mathop {\sim }\limits ^{n\rightarrow \infty }}\quad \tau ^2\, \frac{1}{i{+}j{+}1}\; t^{i+j+1} \end{aligned}$$

for all $1\le i,j \le p$. In the first line of $cJ_{n,\theta }(t)$ we have

$$\begin{aligned} cJ_{n,\theta }^{(0,0)}(t) = \tau ^2\, t ,\quad cJ_{n,\theta }^{(0,p+1)}(t) = - \frac{1}{n} \int _0^{tn} \tau \, X_s\, ds \end{aligned}$$

in first and last position, and in-between for $1\le j\le p$

$$\begin{aligned} cJ_{n,\theta }^{(0,j)}(t) = \frac{1}{n^{j+1}}\int _0^{tn} \tau \; s^{j-1} (j+\tau s)\, ds \quad {\mathop {\sim }\limits ^{n\rightarrow \infty }}\quad \tau ^2\, \frac{1}{j{+}1}\; t^{j+1}\;. \end{aligned}$$

For the last column of $cJ_{n,\theta }(t)$, the first entry $cJ_{n,\theta }^{(0,p+1)}(t)$ has been given above, the last entry is

$$\begin{aligned} cJ_{n,\theta }^{(p+1,p+1)}(t) = \frac{1}{n} \int _0^{tn} X^2_s\, ds \;, \end{aligned}$$

in-between we have for $1\le j\le p$

$$\begin{aligned} cJ_{n,\theta }^{(j,p+1)}(t) = -\frac{1}{n^{j+1}}\int _0^{tn} s^{j-1} (j+\tau s)\; X_s\; ds \;. \end{aligned}$$

It remains to consider the three integrals which are not deterministic: here lemma 1 establishes almost sure convergence

$$\begin{aligned} \frac{1}{n} \int _0^{tn} X^2_s\, ds \;\longrightarrow \; \frac{c}{2\tau }\, t , \quad \frac{1}{n} \int _0^{tn} \tau \, X_s\, ds \;\longrightarrow \; 0 , \quad \frac{1}{n^{j+1}} \int _0^{tn} s^{j-1} (j+\tau s) \, X_s\, ds \;\longrightarrow \; 0 \end{aligned}$$

as $n\rightarrow \infty$ under $Q_\theta$. This proves almost sure convergence of the components of $J_{n,\theta }(t)$ to the corresponding components of J(t) defined in (28).

(2) We prove that for every $0<t<\infty$, the matrix J(t) defined in (28) is invertible. For this it is sufficient to check invertibility of $(p{+}1){\times }(p{+}1)$ matrices

$$\begin{aligned} \widetilde{J}(t)\, {:}{=}\, \left( \; \frac{1}{i{+}j{+}1}\; t^{i+j+1} \;\right) _{i,j=0,\ldots ,p} \;. \end{aligned}$$

(30)

which up to the factor $\frac{\tau ^2}{c}$ represent the upper left block in J(t). We have to show that $\,\min \limits _{|u|=1} u^\top \widetilde{J}(t)\, u\,$ is strictly positive. In case $t=1$, the rows of $\widetilde{J}(1)$ are linearly independent vectors in $\mathbb {R}^{p+1}$, thus the assertion holds. For $t\ne 1$, associate $\,v(u) = \sqrt{t\,}\, (\,u_i\, t^i\,)_{0\le i\le p}\,$ to $u\in \mathbb {R}^{p+1}$. Then we have $\,u^\top \widetilde{J}(t)\, u = v(u)^\top \widetilde{J}(1)\, v(u)\,$, from which we deduce the assertion. Part a) of the proposition is proved.

(3) As an auxiliary step, we determine a martingale $\widetilde{S}$ which admits $\widetilde{J}$ defined in (30)

$$\begin{aligned} \widetilde{J} = (\widetilde{J}(t))_{t\ge 0} ,\quad \widetilde{J}(t) = \left( \widetilde{J}^{(i,j)}(t) \right) _{i,j=0,1,\ldots ,p} \end{aligned}$$

as its angle bracket. In integral representation we have

$$\begin{aligned} \widetilde{J}^{(i,j)}(t) = \int _0^t s^{i+j}\, ds = \int _0^t (\Psi _s \Psi _s)^{(i,j)}\, ds \end{aligned}$$

where $\Psi _s$ is a square root

$$\begin{aligned} \Psi _s\, {:}{=}\, \frac{1}{\sqrt{q(s)}\,} (s^{i+\ell })_{i,\ell =0,\ldots ,p} \quad \text{ with }\quad q(s)\,{:}{=}\, \sum _{\ell =0}^p s^{2\ell } \end{aligned}$$

for the matrix $(s^{i+j})_{i,j=0,\ldots ,p}$ (note that for fixed s, this matrix is not invertible). From this representation for the angle brackets $\widetilde{J}$ we obtain a representation of the martingale $\widetilde{S}$ (Ikeda and Watanabe 1989, theorem 7.1’ on p. 90):

$$\begin{aligned} \widetilde{S}= \left( \, \widetilde{S}^0 \,,\, \ldots \,,\, \widetilde{S}^p \,\right) ,\quad \widetilde{S}^i(t) = \sum _{j=0}^p \int _0^t \Psi _s^{(i,j)}\, d\widetilde{B}^j_s ,\quad 0\le i\le p \end{aligned}$$

with some $(p{+}1)$-dimensional standard Brownian motion

$$\begin{aligned} \widetilde{B}= \left( \, \widetilde{B}^0 \,,\, \ldots \,,\, \widetilde{B}^p \,\right) \;. \end{aligned}$$

Given the simple structure of the $\Psi _s$, we can define a new one-dimensional Brownian motion $\widetilde{W}^{(1)}$ by

$$\begin{aligned} \widetilde{W}^{(1)}_s\, {:}{=} \sum _{\ell =0}^p \int _0^t \frac{1}{\sqrt{q(s)\,}} s^\ell \, d\widetilde{B}^\ell _s \end{aligned}$$

and end up with

$$\begin{aligned} \widetilde{S}= \left( \, \widetilde{S}^0 \,,\, \ldots \,,\, \widetilde{S}^p \,\right) ,\quad \widetilde{S}^i(t)= \int _0^t s^i\, d\widetilde{W}^{(1)}_s \;,\; 0\le i\le p \;. \end{aligned}$$

(31)

(4) Now we can determine the martingale S which admits J defined in (28) as angle bracket. Since J(t) has a diagonal block structure where (up to multiplication with a constant in every block) the upper left block has been considered in step 3 whereas we have for the lower right block

$$\begin{aligned} \lim _{n\rightarrow \infty }\; \frac{1}{n} \int _0^{tn} X^2_s\, ds = \frac{c}{2\tau }\, t \end{aligned}$$

$Q_\theta$-almost surely by lemma 1, the desired representation is

$$\begin{aligned} S(t) = \left( \begin{array}{l} \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^0\, d \widetilde{W} ^{(1)}_s\\ \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^1 \, d \widetilde{W} ^{(1)}_s \\ \vdots \\ \frac{\tau }{ \sqrt{c\,} }\; \int _0^t s^p \, d \widetilde{W} ^{(1)}_s \\ \frac{1}{ \sqrt{2\,\tau \,} }\; \widetilde{W} ^{(2)}_t \end{array}\right) ,\quad t\ge 0 \end{aligned}$$

with $\widetilde{W}^{(1)}$ from (31), and with another one-dimensional Brownian motion $\widetilde{W}^{(2)}$ which is independent from $\widetilde{W}^{(1)}$. This is the form appearing in (29) of the proposition.

(5) On the basis of part (a) of the proposition, the martingale convergence theorem (Jacod and Shiryaev 1987, VIII.3.24) establishes weak convergence (in the path space $D([0,\infty ), \mathbb {R}^{p+2})$, under $Q_\theta$, as $n\rightarrow \infty$) of the martingales $S_{n,\theta }$ under $Q_\theta$ to the limit martingale S which has been determined in step (4). This finishes the proof of proposition 1. $\square$

As a consequence of proposition 1, we obtain local asymptotic normality (Le Cam 1969; Hajek 1970; Ibragimov and Khasminskii 1981; Davies 1985; Le Cam and Yang 2002; Pfanzagl 1994; Kutoyants 2004; Höpfner 2014, section 7.1).

Theorem 1

(a) At $\theta \in \Theta$, with local scale at $\theta$ given by $(\psi _n)_n$ from (25), quadratic expansions

$$\begin{aligned} \log L_n^{(\,\theta +\psi _n h_n) \,/\, \theta } = h_n^\top S_{n,\theta }(1) \;-\; \frac{1}{2}\, h_n^\top J_{n,\theta }(1)\, h_n + o_{(Q_\theta )}(1) ,\quad n\rightarrow \infty \end{aligned}$$

hold for arbitrary bounded sequences $(h_n)_n$ in $\mathbb {R}^{p+2}$; since $\Theta$ is open, $\,\theta +\psi _n h_n$ belongs to $\Theta$ for n large enough. Eventually as $n\rightarrow \infty$, $\,J_{n,\theta }(1)$ takes its values in the set of invertible $(p{+}2){\times }(p{+}2)$-matrices, $Q_\theta$-almost surely.

(b) For every $\theta \in \Theta$, we have weak convergence in $D([0,\infty ), \mathbb {R}^{(p+2)}{\times }\mathbb {R}^{{(p+2)}\times {(p+2)}})$ as $n\rightarrow \infty$

$$\begin{aligned} \mathcal {L}\left( \, \left( \, S_{n,\theta } \,,\, J_{n,\theta } \,\right) \mid Q_\theta \,\right) \;\longrightarrow \; \mathcal {L}\left( \, S \,,\, J \,\right) \end{aligned}$$

with S the martingale in (29) and J its angle bracket in (28).

(c) There is a Gaussian shift limit experiment $\mathcal {E}(S,J)$ with likelihood ratios

$$\begin{aligned} \exp \left( \, h^\top S(1) \;-\; \frac{1}{2}\; h^\top J(1)\; h \,\right) ,\quad h\in \mathbb {R}^{p+2} \;. \end{aligned}$$

Proof

(1) As a first step, weak convergence of $S_{n,\theta }$ to S under $Q_\theta$ in proposition 1 implies (Jacod and Shiryaev 1987, theorem VI.6.1) joint weak convergence of the martingale together with its angle bracket. This is part (b) of the theorem. For $0<t<\infty$ fixed, invertibility of $J_{n,\theta }(t)$, $Q_\theta$-almost surely for sufficiently large n, follows from invertibility of J(t) and componentwise almost surely convergence $J_{n,\theta }(t) \rightarrow J(t)$ by proposition 1.

(2) We can represent the limit experiment $\mathcal {E}(S,J)$ in (c) as $\{ \mathcal {N}( J(1)h , J(1) ) : h \in \mathbb {R}^{p+2} \}$.

(3) Fix a bounded sequence $(h_n)_n$ in $\mathbb {R}^{p+2}$, take n large enough so that $\theta +\psi _n h_n$ is in $\Theta$, and define

$$\begin{aligned} \rho _{n,\theta ,h_n}(t)\, {:}{=}\, \log L_{tn}^{(\,\theta +\psi _n h_n) \,/\, \theta } \;-\; \left\{ h_n^\top S_{n,\theta }(t) \;-\; \frac{1}{2}\, h_n^\top J_{n,\theta }(t)\, h_n \right\} ,\quad t\ge 0 \;. \end{aligned}$$

(32)

Using notation $\theta '(n,h)=\theta +\psi _n h$ as in (23)–(26), we split $\,\theta '(n,h_n){=}{:}(\vartheta '(n,h_n),\tau '(n,h_n))\,$ into a bloc $\,\vartheta '(n,h_n)=( \vartheta '_0(n,h_n) , \ldots , \vartheta '_p(n,h_n) )\,$ and the last component $\,\tau '(n,h_n)$. We write $h_{n,0}, h_{n,1}, \ldots , h_{n,p+1}$ for the components of the local parameter $h_n$. Comparing (26) to (23), we see that out of

$$\begin{aligned} c(\gamma '-\gamma )(s,\pi _s) = G(n,h_n)(s) + H(n,h_n)(s) \end{aligned}$$

to be considered in (23)+(24) we did consider

$$\begin{aligned}&H(n,h_n)(s)\, {:}{=}\, \left[ ( R'_{\vartheta '(n,h_n)}-R'_\vartheta ) + \tau ( R_{\vartheta '(n,h_n)}-R_\vartheta ) \right] (s) \;-\; ( \tau '(n,h_n) - \tau )X_s \\&\quad = h_{n,0}\, \frac{1}{\sqrt{n\,}}\; \tau \, + \sum _{i=1}^p \,h_{n,i}\, \frac{1}{\sqrt{ n^{2i+1}\,} } \, s^{i-1} ( i + \tau s ) \;-\; h_{n,p+1}\, \frac{1}{\sqrt{n\,}}X_s \end{aligned}$$

under the integral signs, whereas we did neglect contributions

$$\begin{aligned} G(n,h_n)(s) \,{:}{=}\, ( \tau '(n,h_n) - \tau ) ( R_{\vartheta '(n,h_n)} - R_\vartheta )(s) \end{aligned}$$

under the integral signs, both in the martingales and in the quadratic variations. With these notations, the remainder terms (32) have the form

$$\begin{aligned} \rho _{n,\theta ,h_n}(t) = \frac{1}{\sqrt{c\,}} \int _0^{tn} G(n,h_n)(s)\, dW_s \;-\; \frac{1}{2c}\int _0^{tn} \left[ 2 G(n,h_n) H(n,h_n) + G^2(n,h_n) \right] (s)\, ds \;. \end{aligned}$$

Recall that $(h_n)_n$ is a bounded sequence. By choice of the localization and by (19) we have

$$\begin{aligned} G(n,h_n)(s) = O\left( \frac{1}{\sqrt{n\,}}\right) \,\cdot \, \sum _{i=0}^p \,h_{n,i}\, \frac{1}{\sqrt{ n^{2i+1}\,} } \, s^i \;. \end{aligned}$$

Transforming the convergence arguments in the proof of proposition 1 into tightness arguments, the random objects

$$\begin{aligned} \int _0^{tn} H^2(n,h_n)(s)\, ds = O_{Q_\theta }(1) \end{aligned}$$

remain tight under $Q_\theta$ as $n\rightarrow \infty$, for every t fixed. The deterministic sequence

$$\begin{aligned} \int _0^{tn} G^2(n,h_n)(s)\, ds = O\left( \frac{1}{n} \right) \end{aligned}$$

vanishing as $n\rightarrow \infty$,

$$\begin{aligned} \int _0^{tn} [ G(n,h_n) H(n,h_n)] (s)\, ds = O_{Q_\theta }\left( \frac{1}{\sqrt{n\,}} \right) \end{aligned}$$

vanishes under $Q_\theta$ as $n\rightarrow \infty$ by Cauchy-Schwarz. The sequence of martingales

$$\begin{aligned} \left( \, \int _0^{tn} G(n,h_n)(s)\, dW_s \,\right) _{t\ge 0} \end{aligned}$$

has angle brackets which vanish as $n\rightarrow \infty$ for every t fixed, so the martingales itself vanish in $Q_\theta$-probability, uniformly over compact t-intervals as $n\rightarrow \infty$. With $0<t_0<\infty$ arbitrary, this proves

$$\begin{aligned} \sup \limits _{0\le t\le t_0}\left| \rho _{n,\theta ,h_n}(t) \right| \quad \text{ vanishes } \text{ in } Q_\theta \text{-probability } \text{ as } n\rightarrow \infty \end{aligned}$$

for the remainder terms (32). Since we did consider arbitrary bounded sequences $(h_n)_n$, we can reformulate the last assertion in the form

$$\begin{aligned} \sup \limits _{|h|\le C}\; \sup \limits _{0\le t\le t_0}\left| \rho _{n,\theta ,h}(t) \right| \quad \text{ vanishes } \text{ in } Q_\theta \text{-probability } \text{ as } n\rightarrow \infty \end{aligned}$$

for arbitrary $0<C<\infty$. We thus have proved part (a) of the theorem. The proof is finished. $\square$

The local asymptotic minimax theorem arises as a consequence of theorem 1, see Ibragimov and Khasminskii (1981), Davies (1985), Le Cam and Yang (2002), Kutoyants (2004), or Höpfner (2014) theorem 7.12. Note that it is interesting to consider quite arbitrary $\,\mathcal {G}_n$-measurable random variables $T_n$ taking values in $\mathbb {R}^{(p+2)}$ as possibly useful estimators for the unknown parameter $\theta \in \Theta$.

Corollary 1

For $\theta \in \Theta$, for arbitrary estimator sequences $(T_n)_n$ whose rescaled estimation errors

$$\begin{aligned} \mathcal {L}\left( \, \psi ^{-1}_n(T_n-\theta ) \mid \, Q_\theta \right) \end{aligned}$$

at $\theta$ are tight as $n\rightarrow \infty$, for arbitrary loss functions $L : \mathbb {R}^{(p+2)} \rightarrow [0,\infty )$ which are continuous, bounded and subconvex, the following local asymptotic minimax bound holds:

$$\begin{aligned} \sup _{C\uparrow \infty }\; \liminf _{n\rightarrow \infty }\; \sup _{|h|\le C}\; E_{\theta +\psi _n h} \left( \, L \left( \, \psi ^{-1}_n \left( T_n - (\theta +\psi _n h) \,\right) \,\right) \,\right) \,\ge \, E\left( \, L \left( \, J^{-1}(1)\, S(1) \,\right) \,\right) \;. \end{aligned}$$

Estimator sequences whose rescaled estimation errors at $\theta$ admit as $n\rightarrow \infty$ a representation

$$\begin{aligned} \psi ^{-1}_n (T_n-\theta ) = \left[ J_{n,\theta }(1)\right] ^{-1} S_{n,\theta }(1) + o_{Q_\theta }(1) = J^{-1}(1)\, S_{n,\theta }(1) + o_{Q_\theta }(1) \end{aligned}$$

(33)

have the property

$$\begin{aligned} \lim _{n\rightarrow \infty }\; \sup _{|h|\le C}\; E_{\theta +\psi _n h} \left( \, L \left( \, \psi ^{-1}_n \left( T_n - (\theta +\psi _n h) \,\right) \,\right) \,\right) = E\left( \, L \left( \, J^{-1}(1)\, S(1) \,\right) \,\right) \end{aligned}$$

for every $0<C<\infty$ fixed, and thus attain the local asymptotic minimax bound at $\theta$.

Remark 1

In theorem 1, the limit experiment $\mathcal {E}(S,J)$ at $\theta =(\vartheta ,\tau )\in \Theta$ depends on the component $\tau$ (the constant $c\,$ is not a parameter), by (28), but not on $\vartheta =(\vartheta _0,\vartheta _1,\ldots ,\vartheta _p)$. The $\tau$-component of $\mathcal {E}(S,J)$ is the well-known limit experiment when an ergodic Ornstein Uhlenbeck process (15) with backdriving force $\tau$ is observed over a long time interval (Kutoyants 2004; Höpfner 2014 section 8.1).

3.2 Estimating $(\vartheta _0,\ldots ,\vartheta _p)$ in the model (14)+(19)

By abuse of language, we write in this subsection $\,Y$ for $\pi$ on $(C,\mathcal {C})$ under $Q_\theta$, $\,X$ for $\pi -R_\theta$ under $Q_\theta$; as before $\sqrt{c\,} W$ denotes the martingale part of Y or X under $Q_\theta$ relative to $\mathbb {G}$. To estimate $\vartheta =(\vartheta _0,\ldots ,\vartheta _p) \in \mathbb {R}^p{\times }(0,\infty )$ in the model (14)+(19), consider

$$\begin{aligned} \widetilde{\vartheta }(t)\, {:}{=}\, \mathop {\mathrm{arginf}}_{\vartheta '=(\vartheta '_0,\ldots ,\vartheta '_p)}\; \int _0^t (Y(s)-R_{\vartheta '}(s))^2 \,ds \;. \end{aligned}$$

(34)

Least squares estimators (34) are uniquely determined—see (37) below—and have an explicit and easy-to-calculate form; we discuss their asymptotics under $\theta =(\vartheta ,\tau )$. Define martingales $\widetilde{S}_{n,\theta }$ with respect to $Q_\theta$ and $(\mathcal {G}_{tn})_{t\ge 0}$

$$\begin{aligned} \widetilde{S}_{n,\theta }(t)\, {:}{=}\, \frac{1}{\sqrt{c\,}} \left( \begin{array}{l} \frac{1}{\sqrt{n\,}} \int _0^{tn} \tau \; dW_s \\ \frac{1}{\sqrt{n^3\,}} \int _0^{tn} (1+\tau s)\; dW_s \\ \vdots \\ \frac{1}{\sqrt{n^{2p+1}\,}} \int _0^{tn} s^{p-1} (p+\tau s)\; dW_s \end{array} \right) ,\quad t\ge 0 \end{aligned}$$

(35)

which coincide with $S_{n,\theta }$ of (27) whose last component has been suppressed. Let $\widetilde{J}_{n,\theta }$ denote the angle bracket of $\widetilde{S}_{n,\theta }$ under $Q_\theta$. We consider also

$$\begin{aligned} \widetilde{\psi }_n\, {:}{=}\, \left( \begin{array}{llll} \frac{1}{\sqrt{n\,}} &{} 0 &{} \ldots &{} 0 \\ 0 &{} \frac{1}{\sqrt{n^3\,}} &{} \ldots &{} 0 \\ \vdots &{} &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} \frac{1}{\sqrt{n^{2p+1}\,}} \end{array}\right) \end{aligned}$$

(36)

which coincides with local scale $\psi _n$ of (25) whose last row and last column have been suppressed, and invertible deterministic $(p{+}1){\times }(p{+}1)$ matrices as defined in (30) in the proof of proposition 1:

$$\begin{aligned} \widetilde{J}(t)\, {:}{=}\, \left( \; \frac{1}{i{+}j{+}1}\; t^{i+j+1} \;\right) _{i,j=0,\ldots ,p} \;. \end{aligned}$$

Proposition 2

For every $\theta =(\vartheta ,\tau )\in \Theta$, rescaled estimation errors of the least squares estimator (34) admit a representation

$$\begin{aligned} \widetilde{\psi }_n^{-1}\! \left( \, \widetilde{\vartheta }(n) - \vartheta \,\right) = \left[ \widetilde{J}_{n,\theta } (1) \right] ^{-1} \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) = \left[ \frac{\tau ^2}{c} \widetilde{J} (1) \right] ^{-1} \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) \end{aligned}$$

as $n\rightarrow \infty$. $\square$

Proof

(1) Almost surely as $n\rightarrow \infty$, angle brackets $\widetilde{J}_{n,\theta }$ of $\widetilde{S}_{n,\theta }$ under $Q_\theta$ converge to

$$\begin{aligned} \frac{\tau ^2}{c} \left( \; \int _0^t s^{i+j}ds \;\right) _{i,j=0,\ldots ,p} \;=\quad \frac{\tau ^2}{c}\;\widetilde{J}(t) \end{aligned}$$

for fixed $0<t<\infty$. This has been proved in proposition 1.

(2) Least squares estimators $\widetilde{\vartheta }(t)$ in (34) are uniquely defined and have the explicit form

$$\begin{aligned} \left( \begin{array}{l} \int _0^t Y_s\, ds \\ \int _0^t s\, Y_s\, ds \\ \ldots \\ \int _0^t s^p\, Y_s\, ds \end{array}\right) = \widetilde{J}(t)\, \left( \begin{array}{l} \widetilde{\vartheta }_0(t) \\ \widetilde{\vartheta }_1(t) \\ \ldots \\ \widetilde{\vartheta }_p(t) \end{array}\right) = \widetilde{J}(t)\;\widetilde{\vartheta }(t) \;: \end{aligned}$$

(37)

to check this, take derivatives under the integral sign in (34), use (19) for $\,i = 0,1,\ldots ,p\,$

$$\begin{aligned} \frac{d}{d\vartheta '_i}\; (Y(s)-R_{\vartheta '}(s))^2 = -2\; (Y(s)-R_{\vartheta '}(s))\; \frac{d}{d\vartheta '_i} R_{\vartheta '}(s) = -2\; (Y(s)-R_{\vartheta '}(s))\, s^i \;, \end{aligned}$$

put integrals equal to zero and use the definition (30) of $\widetilde{J}(t)$. On the other hand, (19) shows

$$\begin{aligned} \left( \begin{array}{l} \int _0^t R_\vartheta (s)\, ds \\ \int _0^t s\, R_\vartheta (s)\, ds \\ \ldots \\ \int _0^t s^p\, R_\vartheta (s)\, ds \end{array}\right) = \widetilde{J}(t)\, \left( \begin{array}{l} \vartheta _0 \\ \vartheta _1 \\ \ldots \\ \vartheta _p \end{array}\right) \;. \end{aligned}$$

(38)

Thus (14) allows to write

$$\begin{aligned} \widetilde{J}(t) \left( \, \widetilde{\vartheta }(t) - \vartheta \,\right) = \left( \begin{array}{l} \int _0^t X_s\, ds \\ \int _0^t s\, X_s\, ds \\ \ldots \\ \int _0^t s^p\, X_s\, ds \end{array}\right) \;. \end{aligned}$$

(39)

The scaling property

$$\begin{aligned} \widetilde{\psi }_n \; \widetilde{J}(n)\; \widetilde{\psi }_n \;\; =\;\; \widetilde{J}(1) \end{aligned}$$

(40)

applied to (39) then yields the representation

$$\begin{aligned} \widetilde{\psi }_n^{-1} \left( \, \widetilde{\vartheta }(n) - \vartheta \,\right) = [\widetilde{J}(1)]^{-1} \left( \begin{array}{l} \frac{1}{\sqrt{n\,}} \int _0^n X_s\, ds \\ \frac{1}{\sqrt{n^3\,}} \int _0^n s\, X_s\, ds \\ \ldots \\ \frac{1}{\sqrt{n^{2p+1}\,}} \int _0^n s^p\, X_s\, ds \end{array}\right) \;. \end{aligned}$$

(41)

(3) Representations (12) in lemma 4 combined with the definition of $\widetilde{S}_{n,\theta }$ in (35) show that under $Q_\theta$ as $n\rightarrow \infty$, the vector on the right hand side of (41) can be written as

$$\begin{aligned} \frac{\sqrt{c\,}}{\tau } \left( \begin{array}{l} \frac{1}{\sqrt{n\,}} \int _0^n dW_s \\ \frac{1}{\sqrt{n^3\,}} \int _0^n s\, dW_s \\ \ldots \\ \frac{1}{\sqrt{n^{2p+1}\,}} \int _0^n s^p\, dW_s \end{array}\right) + o_{Q_\theta }(1) = \frac{\sqrt{c\,}}{\tau }\, \left[ \frac{\sqrt{c\,}}{\tau }\, \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) \right] + o_{Q_\theta }(1) \;. \end{aligned}$$

Taking into account step (1) this allows to write representation (41) of rescaled estimation errors as

$$\begin{aligned} \widetilde{\psi }_n^{-1} \left( \, \widetilde{\vartheta }(n) - \vartheta \,\right) = \left[ \, \frac{\tau ^2}{c} \, \widetilde{J}(1) \right] ^{-1} \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) = \left[ \widetilde{J}_{n,\theta }(1) \right] ^{-1} \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) \end{aligned}$$

which concludes the proof. $\square$

3.3 Estimating $\tau$ in the model (14)+(19)

Also in this subsection, $\,Y$ stands for $\pi$ on $(C,\mathcal {C})$ under $Q_\theta$, $\,X$ for $\pi -R_\theta$ under $Q_\theta$, and $\sqrt{c\,} W$ for the martingale part of Y or X under $Q_\theta$ relative to $\mathbb {G}$. To estimate $\tau >0$ in the model (14)+(19) based on observation of Y up to time n, define

$$\begin{aligned} \widetilde{\tau }(n) = \frac{ \sum _{i=0}^p \widetilde{\vartheta }_i(n) \int _0^n s^i dY_s \;-\; \int _0^n Y_s\, dY_s }{ \int _0^n Y^2_s ds \;-\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\, \widetilde{\vartheta }(n) } \end{aligned}$$

(42)

where $\widetilde{\vartheta }(n)$ is the least squares estimator (34), and $\widetilde{J}(n)$ is given by (30).

A motivation is as follows. With notations of Sect. 3.1 write the log-likelihood surface $\,\theta ' \,\rightarrow \, \log L_n^{ \theta ' / \theta }\,$ under $Q_\theta$ in the form

$$\begin{aligned} \log L^{ (\vartheta ',\tau ') / (\vartheta ,\tau ) }_t = \int _0^t (\gamma '-\gamma )(s,Y_s)\, dY_s \;-\; \frac{1}{2} \int _0^t ( [\gamma ']^2-\gamma ^2)(s,Y_s) \; c\, ds \;\;; \end{aligned}$$

neglect contributions which do not depend on $\theta '=(\vartheta ',\tau ')$; maximize in $\tau '>0$ on $\vartheta '$-sections $\,\Theta _{\vartheta '}{:}{=}\{ (\vartheta ',\tau '):\tau '>0\} \subset \Theta \,$ on which $\vartheta '$ remains fixed; finally, insert the estimate $\widetilde{\vartheta }(n)$ in place of $\,\vartheta '$. Making use of (37) the resulting estimator for the parameter $\tau >0$ is $\widetilde{\tau }(n)$ as specified in (42).

Proposition 3

As $n\rightarrow \infty$, rescaled estimation errors of the estimator (42) admit an expansion

$$\begin{aligned} \sqrt{n\,} \left( \, \widetilde{\tau }(n) - \tau \,\right) = -\; 2\,\tau \; \frac{1}{\sqrt{c\,n\,}}\int _0^n X_s \, dW_s + o_{Q_\theta }(1) = \frac{ - \frac{1}{\sqrt{c\,n\,}} \int _0^n X_s \, dW_s }{ \frac{1}{c\,n} \int _0^n X_s^2\, ds } + o_{Q_\theta }(1) \end{aligned}$$

under $\theta =(\vartheta ,\tau )\in \Theta$, with X solution to the Ornstein Uhlenbeck SDE (15) driven by W.

Proof

Combining (42) with (37) we have

$$\begin{aligned} \widetilde{\tau }(n) - \tau = \frac{ \sum _{i=0}^p \widetilde{\vartheta }_i(n) \int _0^n s^i (dY_s + \tau Y_s ds) \;-\; \int _0^n Y_s\, (dY_s + \tau Y_s ds) }{ \int _0^n Y^2_s ds \;-\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\, \widetilde{\vartheta }(n)} \;. \end{aligned}$$

(43)

(1) Consider the numerator

$$\begin{aligned} \sum _{i=0}^p \widetilde{\vartheta }_i(n) \int _0^n s^i (dY_s + \tau Y_s ds) \;-\; \int _0^n Y_s\, (dY_s + \tau Y_s ds) \end{aligned}$$

(44)

on the right hand side of (43). (37) and (38) allow to write

$$\begin{aligned} \int _0^n Y_s\; \tau R_\vartheta (s)\; ds= & {} \sum _{i=0}^p \;\vartheta _i \int _0^n s^i\; \tau Y_s\; ds = \tau \;\; \vartheta ^\top \widetilde{J}(n)\; \widetilde{\vartheta }(n) = \tau \;\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\; \vartheta \\= & {} \sum _{i=0}^p \; \widetilde{\vartheta }_i(n) \int _0^n s^i\; \tau R_\vartheta (s)\; ds \;. \end{aligned}$$

Adding and substracting this expression, (44) takes the form

$$\begin{aligned} \sum _{i=0}^p \widetilde{\vartheta }_i(n) \int _0^n s^i \left( \, dY_s + \tau Y_s ds - \tau R_\vartheta (s)ds \,\right) \;-\; \int _0^n Y_s\, \left( \, dY_s + \tau Y_s ds - \tau R_\vartheta (s)ds \,\right) \;. \end{aligned}$$

(45)

Exploiting first (19) and then (37) and (30) we can write

$$\begin{aligned} \int _0^n Y_s\; R'_\vartheta (s)\, ds= & {} \sum _{j=1}^p\; \vartheta _j\, \int _0^n j s^{j-1}\, Y_s\, ds = \sum _{j=1}^p\; \vartheta _j\, j\, \sum _{k=0}^p \frac{1}{(j{-}1)+k+1}\, n^{(j-1)+k+1}\; \widetilde{\vartheta }_k(n) \\= & {} \sum _{k=0}^p\; \widetilde{\vartheta }_k(n)\, \sum _{j=0}^{p-1} \frac{1}{k+j+1}\, n^{k+j+1}\; (j{+}1)\vartheta _{j+1} \\= & {} \sum _{k=0}^p\; \widetilde{\vartheta }_k(n)\, \int _0^n s^k\; \sum _{j=1}^p j\vartheta _j\, s^{j-1}\; ds = \widetilde{\vartheta }(n)^\top \left( \begin{array}{l} \int _0^n s^0\, R'_\vartheta (s)\, ds \\ \int _0^n s^1\, R'_\vartheta (s)\, ds \\ \vdots \\ \int _0^n s^p\, R'_\vartheta (s)\, ds \end{array}\right) \;. \end{aligned}$$

Adding and subtracting this expression to (45) we thus can write (44) as

$$\begin{aligned} \sum _{i=0}^p \widetilde{\vartheta }_i(n) \int _0^n s^i \left( \, dY_s + \tau Y_s ds - [ R'_\vartheta (s) {+} \tau R_\vartheta (s) ] ds \,\right) \;-\; \int _0^n Y_s\, \left( \, dY_s + \tau Y_s ds - [ R'_\vartheta (s) {+} \tau R_\vartheta (s) ] ds \,\right) \end{aligned}$$

which in virtue of (21) and (16) equals

$$\begin{aligned} \sum _{i=0}^p\; \widetilde{\vartheta }_i(n) \int _0^n s^i\, \sqrt{c\,} dW_s \;-\; \int _0^n Y_s\, \sqrt{c\,} dW_s \;. \end{aligned}$$

Using again (14), we have reduced the numerator (44) on the right hand side of (43) to

$$\begin{aligned} \sum _{i=0}^p\; (\widetilde{\vartheta }_i(n)-\vartheta _i) \int _0^n s^i\, \sqrt{c\,} dW_s \;-\; \int _0^n X_s\, \sqrt{c\,} dW_s \;. \end{aligned}$$

(46)

As in lemma 4, joint laws

$$\begin{aligned} \mathcal {L}\left( \; \left( \frac{1}{\sqrt{n\,}} \int _0^{t n} s^0\, dW_s \,,\, \ldots \,,\, \frac{1}{\sqrt{n^{2p+1}\,}} \int _0^{t n} s^p\, dW_s \right) _{t\ge 0} \;\right) \end{aligned}$$

do not depend on n, whereas by proposition 2 rescaled estimation errors

$$\begin{aligned} \left( \, \sqrt{n^{2i+1}\,} ( \widetilde{\vartheta }_i(n)-\vartheta _i) \,\right) _{i=0,1,\ldots ,p} \quad \text{ under } Q_\theta \end{aligned}$$

converge in law as $n\rightarrow \infty$, and thus are tight as $n\rightarrow \infty$. Terms $\int _0^n X_s\, dW_s$ in (46) are of stochastic order $O_{Q_\theta }(\sqrt{n\,})$ as $n\rightarrow \infty$, by proposition 1. As a consequence, our final representation (46) of the numerator (44) on the right hand side of (43) allows to write the rescaled estimation error as

$$\begin{aligned} \widetilde{\tau }(n) - \tau = \frac{ -\int _0^n X_s\, \sqrt{c\,} dW_s + O_{Q_\theta }(1)}{ \int _0^n Y^2_s ds \;-\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\, \widetilde{\vartheta }(n) } \;. \end{aligned}$$

(47)

(2) We consider the denominator

$$\begin{aligned} \int _0^n Y^2_s ds \;-\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\, \widetilde{\vartheta }(n) \end{aligned}$$

(48)

on the right hand side of (47)—i.e. on the right hand side of (43)—which we write as

$$\begin{aligned} \int _0^n Y^2_s ds \;-\; ( \widetilde{\vartheta }(n) - \vartheta )^\top \widetilde{J}(n)\, ( \widetilde{\vartheta }(n) - \vartheta ) \;-\; 2\, \vartheta ^\top \widetilde{J}(n)\, ( \widetilde{\vartheta }(n) - \vartheta ) \;-\; \vartheta ^\top \widetilde{J}(n)\, \vartheta \;. \end{aligned}$$

From (14)+(19) we have

$$\begin{aligned} \int _0^n Y_s^2\, ds = \int _0^n X_s^2\, ds + 2\sum _{i=0}^p\; \vartheta _i \int _0^n s^i X_s\, ds + \vartheta ^\top \widetilde{J}(n)\; \vartheta \end{aligned}$$

whereas (39) shows

$$\begin{aligned} \vartheta ^\top \widetilde{J}(n)\, ( \widetilde{\vartheta }(n) - \vartheta ) = \sum _{i=0}^p\; \vartheta _i \int _0^n s^i X_s\, ds \;. \end{aligned}$$

Thus we have reduced the denominator (48) to

$$\begin{aligned} \int _0^n X_s^2\, ds \;-\; ( \widetilde{\vartheta }(n) - \vartheta )^\top \widetilde{J}(n)\, ( \widetilde{\vartheta }(n) - \vartheta ) \;. \end{aligned}$$

The first summand in this expression is $O_{Q_\theta }(n)$, by lemma 1, whereas the second summand

$$\begin{aligned} ( \widetilde{\vartheta }(n) - \vartheta )^\top \widetilde{J}(n)\, ( \widetilde{\vartheta }(n) - \vartheta ) = \left( \, \widetilde{\psi }_n^{-1}(\widetilde{\vartheta }(n)-\vartheta ) \,\right) ^\top \widetilde{J}(1)\; \left( \, \widetilde{\psi }_n^{-1}(\widetilde{\vartheta }(n)-\vartheta ) \,\right) \end{aligned}$$

converges in law as $n\rightarrow \infty$ under $Q_\theta$, by (40) and proposition 2, and thus is tight as $n\rightarrow \infty$. Taking all this together, the denominator (48) on the right hand side of (43) under $Q_\theta$ satisfies

$$\begin{aligned} \int _0^n Y^2_s ds \;-\; \widetilde{\vartheta }(n)^\top \widetilde{J}(n)\, \widetilde{\vartheta }(n) = \int _0^n X_s^2\, ds + O_{Q_\theta }(1) ,\quad n\rightarrow \infty \;. \end{aligned}$$

(49)

(3) The proof is finished: taking together (43), (47) and (49), we have

$$\begin{aligned} \left( \, \widetilde{\tau }(n) - \tau \,\right) = \frac{ -\int _0^n X_s\, \sqrt{c\,} dW_s + O_{Q_\theta }(1) }{ \int _0^n X_s^2\, ds + O_{Q_\theta }(1) } \end{aligned}$$

and thus

$$\begin{aligned} \sqrt{n\,} \left( \, \widetilde{\tau }(n) - \tau \,\right) = \frac{ - \frac{1}{ \sqrt{c n\,} } \int _0^n X_s\, dW_s + O_{Q_\theta }(\frac{1}{\sqrt{n\,}}) }{ \frac{1}{c n} \int _0^n X_s^2\, ds + O_{Q_\theta }(\frac{1}{n}) } \;. \end{aligned}$$

By lemma 1, $\,\frac{1}{n} \int _0^n X_s^2\, ds$ converges $Q_\theta$-almost surely to $\frac{c}{2\tau }$: so proposition 3 is proved. $\square$

3.4 Efficiency in the model (14)+(19)

We can put together the results of subsections 3.2 and 3.3 to prove that for every $\theta \in \Theta$ as $n\rightarrow \infty$,

$$\begin{aligned} \widetilde{\theta }(n)\, {:}{=}\, (\widetilde{\vartheta }(n) , \widetilde{\tau }(n)) \end{aligned}$$

is an asymptotically efficient estimator sequence in the sense of the local asymptotic minimax theorem.

Theorem 2

Observing Y in (14)+(19) over the time interval [0, n] as $n\rightarrow \infty$, the sequence

$$\begin{aligned} \widetilde{\theta }(n)\, {:}{=}\, \left( \widetilde{\vartheta } (n) , \widetilde{\tau }(n) \right) \end{aligned}$$

defined by (34) and (42) is such that representation (33) of corollary 1 in Sect. 3.1 holds as $n\rightarrow \infty$:

$$\begin{aligned} \psi ^{-1}_n (\widetilde{\theta }(n)-\theta ) = \left[ J_{n,\theta }(1)\right] ^{-1} S_{n,\theta }(1) + o_{Q_\theta }(1) \;\; =\;\; J^{-1}(1)\, S_{n,\theta }(1) + o_{Q_\theta }(1) \;. \end{aligned}$$

The estimator sequence $(\widetilde{\theta }(n))_n$ is thus efficient at $\theta$ in the sense of the local asymptotic minimax theorem. This holds for all $\theta =(\vartheta ,\tau )\in \Theta$.

Proof

If we compare the set of definitions for $S_{n,\theta }$ in (27), J in (28), $\psi _n$ in (25) to the set of definitions for $\widetilde{S}_{n,\theta }$ in (35), $\widetilde{J}$ in (30), $\widetilde{\psi }_n$ in (36), we can merge the assertions of propositions 2 and 3

$$\begin{aligned} \widetilde{\psi }_n^{-1}\! \left( \, \widetilde{\vartheta }(n) - \vartheta \,\right)= & {} \left[ \frac{\tau ^2}{c} \widetilde{J} (1) \right] ^{-1} \widetilde{S}_{n,\theta }(1) + o_{Q_\theta }(1) \\ \sqrt{n\,} \left( \, \widetilde{\tau }(n) - \tau \,\right)= & {} -\; 2\,\tau \; \frac{1}{\sqrt{c\,n\,}}\int _0^n X_s \, dW_s + o_{Q_\theta }(1) \end{aligned}$$

under $Q_\theta$ as $n\rightarrow \infty$ into one assertion

$$\begin{aligned} \psi ^{-1}_n (\widetilde{\theta }(n)-\theta ) = J^{-1}(1)\, S_{n,\theta }(1) + o_{Q_\theta }(1) \;. \end{aligned}$$

Together with proposition 1 (a) in Sect. 3.1, this shows that condition (33) of corollary 1 in Sect. 3.1 is satisfied. But the last condition implies asymptotic efficiency of an estimator sequence for the unknown parameter in the model (14)+(19) at $\theta =(\vartheta ,\tau )\in \Theta$. $\square$

4 Application: inference in stochastic Hodgkin–Huxley models

Hodgkin–Huxley models play an important role in neuroscience and are considered as realistic models for the spiking behaviour of neurons (see Hodgkin and Huxley 1952; Izhikevich 2007; Ermentrout and Terman 2010). The classical deterministic model with constant rate of input is a 4-dimensional dynamical system with variables (V, n, m, h)

$$\begin{aligned} \left\{ \begin{array}{l} dV_t = a\, dt - F(V_t,n_t,m_t,h_t)\,dt \\ dn_t = [ \alpha _n(V_t) (1-n_t) - \beta _n(V_t) n_t ]\,dt \\ dm_t = [ \alpha _m(V_t) (1-m_t) - \beta _m(V_t) n_t ]\,dt \\ dh_t = [ \alpha _h(V_t) (1-h_t) - \beta _h(V_t) n_t ]\,dt \end{array} \right. \end{aligned}$$

(50)

where $a>0$ is a constant. The functions $(V,n,m,h)\rightarrow F(V,n,m,h)$ and $V\rightarrow \alpha _j(V)$, $V\rightarrow \beta _j(V)$, $j\in \{n,m,h\}$, are those of Izhikevich (2007) pp. 37–38 (i.e. the same as in Höpfner et al. (2016a), section 2.1). V takes values in $\mathbb {R}$ and models the membrane potential in the single neuron. The variables n, m, h are termed gating variables and take values in [0, 1]. Write $E_4\,{:}{=}\,\mathbb {R}\times [0,1]^3$ for the state space.

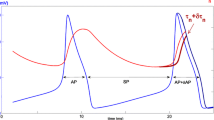
Depending on the value of the constant $a>0$, the following behaviour of the deterministic dynamical system is known, see Ermentrout and Terman (2010) pp. 63–66. On some interval $(0,a_1)$ there is a stable equilibrium point for the system. There is a bistability interval $\,\mathbb {I}_{\mathrm{bs}}=(a_1,a_2)\,$ on which a stable orbit coexists with a stable equilibrium point. There is an interval $(a_2,a_3)$ on which a stable orbit exists together with an unstable equilibrium point. At $a=a_3$ orbits collapse into equilibrium; for $a>a_3$ the equilibrium point is again stable. Here $0<a_1<a_2<a_3<\infty$ are suitably determined¹ endpoints for intervals. Equilibrium points and orbits depend on the value of a. Evolution of the system along an orbit yields a remarkable excursion of the membrane potential V which we interprete as a spike.

In simulations, the equilibrium point appears to be globally attractive on $(0,a_1)$, the orbit appears to be globally attractive on $(a_2,a_3)$; on the bistability interval $\mathbb {I}_{\mathrm{bs}}=(a_1,a_2)$, the behaviour of the system depends on the choice of the starting value: simulated trajectories with randomly chosen starting point either spiral into the stable equilibrium, or are attracted by the stable orbit.

We feed noise into the system. Prepare an Ornstein–Uhlenbeck process (15) with parameter $\tau >0$

$$\begin{aligned} dX_t = - \tau \, X_t\, dt + \sqrt{c\,}\, dW_t \end{aligned}$$

(51)

and replace input $\,a\,dt\,$ in the deterministic system (50) above by increments (16)

$$\begin{aligned} dY_t = \vartheta ( 1 + \tau t )\, dt \;-\; \tau \, dY_t + \sqrt{c\,}\, dW_t \end{aligned}$$

(52)

of the stochastic process Y in (14) which depends on the parameter $\vartheta >0$:

$$\begin{aligned} Y_t = \vartheta \, t + X_t ,\quad t\ge 0 \;. \end{aligned}$$

(53)

This yields a stochastic Hodgkin–Huxley model

$$\begin{aligned} \left\{ \begin{array}{l} dV_t = dY_t - F(V_t,n_t,m_t,h_t)\,dt \\ dn_t = [ \alpha _n(V_t) (1-n_t) - \beta _n(V_t) n_t ]\,dt \\ dm_t = [ \alpha _m(V_t) (1-m_t) - \beta _m(V_t) n_t ]\,dt \\ dh_t = [ \alpha _h(V_t) (1-h_t) - \beta _h(V_t) n_t ]\,dt \\ \end{array}\right. \end{aligned}$$

(54)

with parameters $\vartheta >0$ and $\tau >0$. By (54), the 5-dimensional stochastic system

$$\begin{aligned} \mathbb {X} = (\mathbb {X}_t)_{t\ge 0} ,\quad \mathbb {X}_t\, {:}{=}\, (V_t,n_t,m_t,h_t,Y_t) \end{aligned}$$

is strongly Markov with state space $E_5\,{:}{=}\,\mathbb {R}\times [0,1]^3\times \mathbb {R}$. Stochastic Hodgkin–Huxley models where stochastic input encodes a periodic signal have been considered in Höpfner et al. (2016a, b), (2017) and in Holbach (2019). A biological interpretation of the model (54) is as follows. The structure $\,dY_t=\vartheta dt + dX_t\,$ of input reflects superposition of some global level $\vartheta >0$ of excitation through the network with ’noise’ in the single neuron. Noise arises out of accumulation and decay of a large number of small postsynaptic charges, due to the spikes—excitatory of inhibitory, and registered at synapses along the dendritic tree— in spike trains which the neuron receives from a large number of other neurons in the network.

In simulations, the stochastic Hodgkin–Huxley model (54) which we consider in this section exhibits the following behaviour. For values of $\vartheta$ in neighbourhoods of the bistability interval $\mathbb {I}_{\mathrm{bs}}$ of (50), the system (54) alternates (possibly long) time periods of seemingly regular spiking with (possibly long) time periods of quiet behaviour. ’Quiet’ means that the system performs small random oscillations in neighbourhoods of some typical point. For smaller values of $\vartheta$, quiet behaviour prevails, for larger values of $\vartheta$ we see an almost regular spiking.

The aim of the present section is estimation of an unknown parameter

$$\begin{aligned} \theta \,=\, (\vartheta ,\tau ) \;\in \; \Theta ,\quad \Theta \, {:}{=}\, (0,\infty )^2 \end{aligned}$$

in the system (54) with stochastic input (52), based on observation of the membrane potential V over a long time interval. For this, our standing assumption will be:

$$\begin{aligned} \text{ a } \text{ starting } \text{ value } \mathbb {X}_0\equiv (V_0,n_0,m_0,h_0,Y_0)\in \mathrm{int}(E_5) \text{ is } \text{ deterministic, } \text{ fixed } \text{ and } \text{ known. } \end{aligned}$$

(55)

Assuming (55) we recover first, for the internal variables $j\in \{n,m,h\}$, the state $\,j_t\,$ at time t from the trajectory of V up to time t

$$\begin{aligned} \breve{j}_t\, {:}{=}\, j_0\, e^{ -\int _0^t (\alpha _j+\beta _j)(V_r)\, dr } + \int _0^t \alpha _j(V_s)\, e^{ -\int _s^t (\alpha _j+\beta _j)(V_r)\, dr }\, ds ,\quad t\ge 0 \;, \end{aligned}$$

(56)

and then, in virtue of the first equation in (54), the state $\,Y_t\,$ at time t of the process (53) of acccumulated dendritic input from the trajectory of V up to time t:

$$\begin{aligned} \breve{Y}_t = Y_0 + (V_t-V_0) + \int _0^t F(V_t,\breve{n}_t,\breve{m}_t,\breve{h}_t)\,dt ,\quad t\ge 0 \;; \end{aligned}$$

(57)

here and below we write ’’ to distinguish reconstructed variables. Thus $(V, \breve{n}, \breve{m}, \breve{h}, \breve{Y})$ reconstructs the trajectory of the 5-dimensional stochastic system $\mathbb {X}$ from observation of the membrane potential V and given starting point satisfying assumption (55). The motivation is from biology. For single neurons in active networks, the membrane potential can be measured intracellularly with very good time resolution, whereas the gating variables $j\in \{n,m,h\}$ in the stochastic system (54) represent averages over large numbers of certain ion channels and are not accessible to measurement.

Under assumption (55), the problem of estimating the unknown parameter $\theta =(\vartheta ,\tau )\in \Theta$ in the stochastic Hodgkin–Huxley system (54) based on observation of the membrane potential can be formulated as follows. Consider the canonical path space $(C,\mathcal {C})$, $C\,{:}{=}\,C([0,\infty ),\mathbb {R}^5)$, equipped with the canonical process $\pi =(\pi _t)_{t\ge 0}$ and the canonical filtration $\mathbb {G}=(\mathcal {G}_t)_{t\ge 0}$, and also the smaller filtration

$$\begin{aligned} \mathbb {G}^{(1)}=(\mathcal {G}_t^{(1)})_{t\ge 0} ,\quad \mathcal {G}_t^{(1)}\, {:}{=}\, \bigcap _{r>t} \sigma \left( \, \pi _0 \;,\; \pi _s^{(1)} : 0\le s\le r \,\right) \end{aligned}$$

generated by observation of the first component $\pi ^{(1)}$ of the canonical process $\pi$ knowing the starting point $\pi _0$ of $\pi$. For $\theta \in \Theta$, let $Q_\theta$ denote the law of the process $\mathbb {X}$ under $\theta =(\vartheta ,\tau )$ on $(C,\mathcal {C})$, with starting point (55) not depending on $\theta$. On $(C,\mathcal {C})$ we write for short

$$\begin{aligned} \zeta =(\zeta _t)_{t\ge 0} ,\quad \zeta \, {:}{=}\, \breve{\pi }^{(5)} \end{aligned}$$

(58)

for the reconstruction $\breve{\pi }^{(5)}$ of the fifth component $\pi ^{(5)}$ of $\pi$ (which under $Q_\theta$ represents accumulated dendritic input $Y_t=\vartheta t + X_t$, $t\ge 0$) from the first component $\pi ^{(1)}$ (which under $Q_\theta$ represents the membrane potential V) and the starting point $\pi _0$; on the lines of (57) we have

$$\begin{aligned} \zeta _t = \pi ^{(5)}_0 + (\pi ^{(1)}_t-\pi ^{(1)}_0) + \int _0^t F( \pi ^{(1)}_s , \breve{\pi }^{(2)}_s , \breve{\pi }^{(3)}_s , \breve{\pi }^{(4)}_s )\, ds ,\quad t\ge 0 \;. \end{aligned}$$

(59)

By definition of $\mathbb {G}^{(1)}$, the observed process $\,\pi ^{(1)}$ and the reconstructed processes $\,\zeta \,,\, \breve{\pi }^{(j)}$, $j\in \{2,3,4\}$, are $\mathbb {G}^{(1)}$-semimartingales. Write $\sqrt{c\,}\, W$ for the $\mathbb {G}^{(1)}$-martingale part of $\zeta$ or of $\pi ^{(1)}$ under $Q_\theta$. The likelihood ratio process of $Q_{\theta '}$ with respect to $Q_\theta$ relative to $\mathbb {G}^{(1)}$ is obtained in analogy to (23)+(24), special case $R_\vartheta (s)=\vartheta s$. Then the following is proposition 3.2 in Holbach (2020):

Proposition 4

(Holbach 2020) For pairs $\,\theta '=(\vartheta ',\tau ')$, $\theta =(\vartheta ,\tau )$ in $\Theta =(0,\infty )^2$, writing

$$\begin{aligned} M^{ \theta ' / \theta }_t\, {:}{=}\, \frac{1}{\sqrt{c\,}} \int _0^t \left\{ (\vartheta '-\vartheta )(1+\tau s) - (\tau '-\tau )(\zeta _s-\vartheta s) + (\tau '-\tau )(\vartheta '-\vartheta )s \right\} \, dW_s ,\quad t\ge 0 \;, \end{aligned}$$

likelihood ratios in the statistical model

$$\begin{aligned} \left( \, C \,,\, \mathcal {C}\,,\, \mathbb {G}^{(1)} \,,\, \{ Q_\theta :\theta \in \Theta \} \,\right) \end{aligned}$$

are given by

$$\begin{aligned} L^{ \theta ' / \theta }_t = \exp \left( \, M^{ \theta ' / \theta }_t - \frac{1}{2} \langle M^{ \theta ' / \theta }\rangle _t \right) ,\quad t\ge 0 \end{aligned}$$

(60)

where $\langle M^{ \theta ' / \theta }\rangle$ denotes the angle bracket of the martingale $M^{ \theta ' / \theta }$ under $Q_\theta$ relative to $\mathbb {G}^{(1)}$.

Note that under $Q_\theta$, the $\mathbb {G}^{(1)}$-adapted process $\,(\zeta _t-\vartheta t)_{t\ge 0}$ in the integrand of $M^{ \theta ' / \theta }$ represents the Ornstein Uhlenbeck process X of equation (51); the constant $\,c\,$ is known from quadratic variation of $\,\zeta \,$.

We know everything about the likelihoods (60): they are the likelihoods in the submodel where $\vartheta _0\equiv 0$ is fixed of the model considered in Sect. 3, case $p\,{:}{=}\, 1$. As a consequence, in the statistical model associated to the stochastic Hodgkin Huxley model, we have LAN at $\theta$, with local scale $\frac{1}{\sqrt{n^3\,}}$ for the $\vartheta$-component and $\frac{1}{\sqrt{n\,}}$ for the $\tau$-component, $\theta =(\vartheta ,\tau )\in \Theta$. We have a characterization of efficient estimators by the local asymptotic minimax theorem, and we did construct asymptotically efficient estimators. Since $\,\zeta \,$ is a $\mathbb {G}^{(1)}$-semimartingale, common $\mathbb {G}^{(1)}$-adapted determinations for $\theta \in \Theta$ of the stochastic integrals $\,\int s\, d\zeta _s\,$ and $\,\int \zeta _s\, d\zeta _s\,$ exist. According to (34), (37) and (42), we estimate the first component of the unknown parameter $\theta =(\vartheta ,\tau )$ in $\Theta =(0,\infty )^2$ in the system (54) by

$$\begin{aligned} \breve{\vartheta }(t)\, {:}{=}\, \mathop {\mathrm{arginf}}_{\vartheta '}\; \int _0^t (\zeta _s-\vartheta ' s)^2 \,ds = \frac{3}{t^3} \int _0^t s\, \zeta _s\, ds \end{aligned}$$

(61)

and then the second component by

$$\begin{aligned} \breve{\tau }(t) \,{:}{=}\, \frac{ \breve{\vartheta }(t) \int _0^t s\, d\zeta _s \;-\; \int _0^t \zeta _s\, d\zeta _s }{ \int _0^t \zeta _s^2\, ds \;-\; [\breve{\vartheta }(t)]^2\, t^3 / 3 } \;. \end{aligned}$$

(62)

The estimators $\breve{\vartheta }(t)$, $\breve{\tau }(t)$ are $\mathbb {G}^{(1)}_t$-measurable, $t\ge 0$. The structure of the likelihoods (60) is the structure of the likelihoods in Sect. 3 with $p\,{:}{=}\,1$, submodel $\vartheta _0\equiv 0$. The structure of the pair $(\breve{\vartheta }(t),\breve{\tau }(t))$ in (61)+(62) is the structure of the estimators $(\widetilde{\vartheta }(t),\widetilde{\tau }(t))$ in Sect. 3 with $p\,{:}{=}\,1$, submodel $\vartheta _0\equiv 0$. Under $Q_\theta$, we have from (27) and (28) and theorem 2 in Sect. 3.4 a representation

$$\begin{aligned} \left( \begin{array}{l} \sqrt{n^3\,} (\, \breve{\vartheta }(n) - \vartheta \,)\\ \sqrt{n\,} (\, \breve{\tau }(n) - \tau \,) \end{array}\right) = \left( \begin{array}{ll} \frac{\tau ^2}{3\, c} &{} 0 \\ 0 &{} \frac{1}{2\, \tau } \end{array}\right) ^{-1} \left( \begin{array}{l} \frac{1}{\sqrt{c\,n^3\,}} \int _0^n (1+\tau s)\, dW_s \\ \frac{-1}{\sqrt{c\,n\,}} \int _0^n (\zeta _s-\vartheta s)\, dW_s \end{array}\right) \;+\; o_{Q_\theta }(1) \end{aligned}$$

(63)

of rescaled estimation errors as $n\rightarrow \infty$, and proposition 1 in Sect. 3.1 shows convergence in law

$$\begin{aligned} \left( \begin{array}{l} \sqrt{n^3\,} (\, \breve{\vartheta }(n) - \vartheta \,) \\ \sqrt{n\,} (\, \breve{\tau }(n) - \tau \,) \end{array}\right) \quad \longrightarrow \quad \left( \begin{array}{l} \frac{3\sqrt{c\,}}{\tau }\, \int _0^1 s\; d\widetilde{W}^{(1)}_s \\ \sqrt{2\,\tau \,} \;\; \widetilde{W}^{(2)}_1 \end{array}\right) \end{aligned}$$

under $Q_\theta$ as $n\rightarrow \infty$, with some two-dimensional standard Brownian motion $\widetilde{W}$. Consider on $\,( C, \mathcal {C}, (\mathcal {G}^{(1)}_{tn})_{t\ge 0}, \{Q_\theta :\theta \in \Theta \})\,$ martingales

$$\begin{aligned} \breve{S}_{n,\theta }(t)\, {:}{=}\, \left( \begin{array}{l} \frac{1}{\sqrt{c\,n^3\,}} \int _0^{t n} (1+\tau s)\, dW_s \\ \frac{-1}{\sqrt{c\,n\,}} \int _0^{t n} (\zeta _s-\vartheta s)\, dW_s \end{array}\right) \end{aligned}$$

under $Q_\theta$, and let $\breve{J}_{n,\theta }$ denote their angle brackets under $Q_\theta$. Define local scale

$$\begin{aligned} \breve{\psi }_n\, {:}{=}\, \left( \begin{array}{ll} \frac{1}{\sqrt{n^3\,}} &{} 0 \\ 0 &{} \frac{1}{\sqrt{n\,}} \end{array}\right) \end{aligned}$$

and limit information

$$\begin{aligned} \breve{J}(t)\, {:}{=}\, \left( \begin{array}{ll} \frac{\tau ^2}{3\, c}\, t^3 &{} 0 \\ 0 &{} \frac{1}{2\, \tau }\, t \end{array}\right) \;. \end{aligned}$$

With these notations, theorem 1 in Sect. 3.1 and theorem 2 in Sect. 3.4 yield:

Theorem 3

In the sequence of statistical models

$$\begin{aligned} ( C, \mathcal {C}, (\mathcal {G}^{(1)}_{tn})_{t\ge 0}, \{Q_\theta :\theta \in \Theta \}) \end{aligned}$$

the following holds at every point $\theta =(\vartheta ,\tau )$ in $\Theta =(0,\infty )^2$:

(a) we have LAN at $\theta$ with local scale $(\breve{\psi }_n)_n$ and local parameter $h\in \mathbb {R}^2$:

$$\begin{aligned} \log L^{ \theta +\breve{\psi }_n h \,/\, \theta }_{tn} = h^\top \breve{S}_{n,\theta }(t) - \frac{1}{2} h^\top \!\breve{J}_{n,\theta }(t)\, h + o_{Q_\theta }(1) ,\quad n\rightarrow \infty \;; \end{aligned}$$

(b) by (63), rescaled estimation errors of $\,\breve{\theta }(n)\,{:}{=}\,(\breve{\vartheta }(n),\breve{\tau }(n))\,$ admit the expansion

$$\begin{aligned} \breve{\psi }_n^{-1} ( \breve{\theta }(n) - \theta ) = [\breve{J}(1)]^{-1} \breve{S}_{n,\theta }(1) + o_{Q_\theta }(1) = [\breve{J}_{n,\theta }(1)]^{-1} \breve{S}_{n,\theta }(1) + o_{Q_\theta }(1) ,\quad n\rightarrow \infty \;. \end{aligned}$$

When we observe—for some given starting point of the system—the membrane potential in a stochastic Hodgkin–Huxley model (54) up to time n, with accumulated stochastic input defined by (53) together with (51) which depends on an unknown parameter $\theta =(\vartheta ,\tau )$ in $\Theta =(0,\infty )^2$, the following resumes in somewhat loose language the assertion of the local asymptotic minimax theorem, corollary 1 in Sect. 3.1:

Corollary 2

For loss functions $L:\mathbb {R}^2\rightarrow [0,\infty )$ which are continuous, subconvex and bounded, for $0<C<\infty$ arbitrary, maximal risk over shrinking neighbourhoods of $\theta$

$$\begin{aligned} \lim _{n\rightarrow \infty }\;\sup _{|h|\le C}\; E_{\left( {\vartheta +h_1/\sqrt{n^3\,}} \,,\, {\tau +h_2/\sqrt{n\,}} \right) }\left( \; L \left( \begin{array}{l} \sqrt{n^3\,} (\, \breve{\vartheta }(n) - (\vartheta +h_1/\sqrt{n^3\,}) \,) \\ \sqrt{n\,} (\, \breve{\tau }(n) - (\tau +h_2/\sqrt{n\,}) \,) \end{array}\right) \;\right) \end{aligned}$$

converges as $n\rightarrow \infty$ to

$$\begin{aligned} E\left( \; L \left( \begin{array}{l} \frac{3\sqrt{c\,}}{\tau }\, \int _0^1 s\; d\widetilde{W}^{(1)}_s \\ \sqrt{2\,\tau \,} \;\; \widetilde{W}^{(2)}_1 \end{array}\right) \;\right) \;. \end{aligned}$$

Within the class of $(\mathcal {G}^{(1)}_n)_n$-adapted estimator sequences $(T_n)_n$ whose rescaled estimation errors at $\theta =(\vartheta ,\tau )$ are tight—at rate $\sqrt{n^3\,}$ for the $\vartheta$-component, and at rate $\sqrt{n\,}$ for the $\tau$-component—it is impossible to outperform the sequence $(\breve{\vartheta }(n),\breve{\tau }(n))$ defined by (61)+(62), asymptotically as $n\rightarrow \infty$.

Note that we are free to measure risk through any loss function which is continuous, subconvex and bounded.