Simulation of the quantum Bertrand–Edgeworth game

Abstract

In the Bertrand–Edgeworth duopoly game, two players compete in price to capture the market demand of a uniform product. The game is studied from a general perspective, so that players with different production costs and capacity constraints as well as the two more important rules dealing with unsatisfied demand (proportional and efficient) are taken into consideration. A quantization scheme is applied to the game with the aim of improving the results compared to the classic game. The quantum Bertrand–Edgeworth duopoly game is studied in this work via spatial numerical simulation, supporting the results analytically when it is possible. In this context, it is found that high entanglement induces a Pareto optimal solution ruled by the lower capacity of the players. The way in which the players’ entanglement acts in the game is examined through simulation, paying special attention to the critical value of entanglement from which the Pareto optimal solution emerges.

Appendix

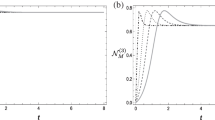
This Appendix aims to support the rationale behind the results emerging in the simulations of the symmetric game reported in Fig. 1.

1.1 Dynamics

Figure 13 shows the dynamics of the average over the lattice of prices, sales and payoffs in a simulation of the symmetric QBE ($a=10,c=1,k=5$) game with proportional rationing rule. In the $\gamma =0.0$ classic scenario of Fig. 13a, the average prices of both players heavily decrease from the initial $p=5.0$ in the first iterations and very smoothly afterwards, so that at $T=200$ both average prices look stabilized at values $\overline{p}_1=2.911$, $\overline{p}_2=3.346$. The average sales are also stable at $T=200$ with $\overline{d}_1=4.624$, $\overline{d}_2=2.334$. The average payoff of player 2 decreases from the first iterations down to its stabilization around $T=100$ in a fairly uniform way, being $\overline{u}_2=5.300$ at $T=200$. The average payoff of player-1 initially decreases but soon inverts this trend and commences to grow, so that from approximately $T=35$ it is $\overline{u}_1 > \overline{u}_2$, with stabilization of $\overline{u}_1$ also around $T=100$ and $\overline{u}_1(T=200)=8.824$. The standard deviations of the payoffs also appear stabilized from approximately $T=100$ down to low values lower than 0.5. The findings just reported in a particular example have general validity. Thus, the studied classic dynamical system can be considered as stationary at $T=200$ (as it is in the particular case of Fig. 13a), further iterations alter the average values reported at $T=200$ in a negligible extent. Remarkably, the simulation does not converge in the classic game to the $p_{1,2}=c=1.0$ NE but to higher and unequal prices.

Fig. 13

Dynamics of the average prices ($\overline{p}$), sales ($\overline{q}$) and payoffs ($\overline{u}$) in a simulation of the symmetric QBE ($a{=}10,c=1,k=5$) game. Proportional rationing rule. a $\gamma =0.0$. b $\gamma =5.0$

In the $\gamma =5.0$ simulation of Fig. 13b, the results regarding both players are virtually coincident, so that the red colour graphs apply not only for player-1 but also for player-2. Both average independent prices smoothly decrease from 5.0 down to very small values before $T=50$, and in parallel to this the average sales smoothly increase up to circa 2.25. The average entangled prices are so high in the initial time-steps that they are represented only from $T=35$. But from then on, the dramatic decreasing of the average entangled prices makes feasible their representation. In fact both entangled prices plummet down to $\overline{p^c}\simeq 5.5$ before $T=50$. The standard deviations of the prices slightly increase in the first iterations, but from approximately $T=15$ smoothly decrease, becoming zero soon before $T=40$. The standard deviations of the payoffs also become small at $T=50$, but show an unexpected parabolic aspect before this time-step.

The mean-field sales and payoffs ($q^\#$,$u^\#$) of both players coincide in Fig. 13b, so that only a somehow green+brown line labelled $u_1^\#\,u_2^\#$ may be appreciated with low T. The huge values of the mean-field entangled prices up to $T=35$, of course higher than $a=10$, induce zero mean-field payoff, but at $T=36$ the mean-field entangled prices decrease enough for the mean-field payoffs to take off and rocket from $p^\#(36)=0.116$ up to $p^\#(39)=10.021$. For higher time-steps the mean-field payoffs and the actual average payoffs virtually coincide.

The difficulties of the implemented simulation reported in Fig. 13a when dealing with a classic BE game with $k=5>2.25=(a-c)$ vanish in games with $k<(a-c)$. So, for example in the particular case of $k=2.0 <2.25$ considered in Fig. 14. The dynamics in Fig. 14a leads very quickly to reaching the expected values: $q_{1,2}=k=2$, $p_{1,2}=10-4=6$, $u_{1,2}=(6-1)2=10$. This $q_{1,2}=k$ solution cannot be improved, so that entangling the players has no positive effect. Thus, in Fig. 14b, both players still get $u^c_{1,2}=10$ from $q^c_{1,2}=2$, $p^c_{1,2}=6$, which arises from $p_{1,2}=6e^{-\gamma }$.

Fig. 14

Average prices ($\overline{p}$), sales ($\overline{q}$) and payoffs ($\overline{u}$) in a simulation of the symmetric QBE ($a{=}10,c=1,k=2$) game. Proportional rationing rule. a Dynamics up to $T=20$ with $\gamma =0.0$. b Average values at $T=100$ with variable $\gamma$

1.2 Response to a PO-player

Figure 15 describes the player-1 response in the simulation of a symmetric QBE game with proportional rationing rule when the price of all the cells of player-2 are fixed to $p_2(\gamma )=((a+c)/2)e^{-\gamma }$ . In Fig. 15a, only the red colour from player-1 looks appreciable in the p-plots, whereas the blue colour from player-2 is masked by the red colour, i.e. apparently the prices of both players are equal regardless of $\gamma$. But this is not so before $\gamma ^\blacktriangledown =3.453$, where $\overline{d^c}=\overline{p^c_2} -\overline{p^c_1} > \epsilon =0.001$, and consequently the player-1 wins the game and gets the maximum payoff attainable, whereas player-2 gets no demand and consequently zero payoff, as it is shown in Fig. 15b. Note that $\gamma ^\blacktriangledown =3.453$ is very close over $\gamma ^\blacktriangle =3.280$, the lower $\gamma$-landmark in Fig. 1 . The numerical values of the average prices, sales, payoffs and $\overline{d^c}$ for $\gamma =0.0, 1.0, 2.0, 3.0$ are shown in Table 2.

Fig. 15

The QBE ($a{=}10,c=1,k=5$) symmetric game in a simulation at T=200 . Player-1 updates the price, $p_2(\gamma )=((a+c)/2)e^{-\gamma }$. Variable entanglement $\gamma$ . Proportional rationing rule. a Average independent and entangled prices ($\overline{p},\overline{p^c}$), and sales ($\overline{q^c})$. b Average payoffs ($\overline{u^c}$)

From $\gamma ^\cdot =4.253$ onwards, it is $\overline{d^c} < \epsilon =0.001$ in Fig. 15, so that both players share the demand and reach the PO solution in Fig. 1 . Table 2 gives the exact numerical values of the average prices, sales and payoffs for $\gamma =5.0$ and $\gamma =6.0$, both greater than $\gamma ^\cdot$, where in fact the entangled prices of both players are equal up to the fifth decimal place. Incidentally, when approaching $\gamma =3.0$, the entangled prices decrease from the 5.5-plateau in Fig.15a; associated with this, the mean-field payoffs fairly coincide with the actual average payoffs in Fig. 1. At $\gamma =4.0\in [\gamma ^\blacktriangledown ,\gamma ^\cdot ]$ it is $\overline{q}_1=5.0=k>d^\cdot$ and $\overline{q}_2=1.0151$, with very close entangled prices providing the payoffs reported in Table 2, which indicate the drift to the PO solution with high $\gamma > 4.0$. In a simulation analogue to that in Fig. 15 but with the efficient rule, player-2 also gets positive average sale from circa $\gamma ^\blacktriangledown$.

Table 2 Numerical values of prices, sales and payoffs in the simulation of Fig.15

Values of $\epsilon$ smaller than 0.001 would delay the emergence of $\gamma ^\blacktriangledown$ and $\gamma ^\cdot$ in the scenario of Fig. 15, whereas both $\gamma$ landmarks will decrease with higher values of $\epsilon$. Thus, for example, in the $\epsilon =0.1$ simulation of Fig. 16, it is $\gamma ^\blacktriangledown = 1.099$ and $\gamma ^\cdot =1.941$. In Fig. 16a, it becomes apparent that before $\gamma ^\cdot$ the prices of player-1 (both independent and entangled) are below of those of player-2.

Fig. 16

The QBE ($a{=}10,c{=}1,k{=}5$) symmetric game in a simulation with $\epsilon {=}0.1$ at T=200 . Player-1 updates the price, $p_2(\gamma ){=}((a+c)/2)e^{-\gamma }$. Variable entanglement $\gamma$ . Proportional rationing rule. a Average independent and entangled prices ($\overline{p},\overline{p^c}$) and sales ($\overline{q^c})$. b Average payoffs ($\overline{u^c}$)

In Figs. 15, 16, the response to $p_2{=}p^\cdot (\gamma ){=}((a+c)/2)e^{-\gamma }$ virtually becomes $p_1{=}p_2-\epsilon e^\gamma$ ⁷, up to the $\gamma ^\cdot$ entanglement value from which the PO solution is reached. The value of $\gamma ^\cdot$ was given in Eq. (10) provided that $k>(a-c)/4$. Note that the $\gamma ^\cdot$ landmark decreases with the increase of $\epsilon$. and converges to $\frac{1}{2}\ln \big ( \frac{a-c}{\epsilon }-1\big )$ when k grows. Accordingly to this, with $a=10,c=1$ the $\gamma ^\cdot$ landmark converges with high k to $\gamma ^\cdot (\epsilon =0.001)=4.552$ and $\gamma ^\cdot (\epsilon =0.1)=2.244$. The $\gamma ^\blacktriangledown$ entanglement value from which the player-1 sells its maximum production capacity k is given in Eq. (17)⁸, provided that $k>(a-c)/2$ so that $c-(a-2k)>0$. Incidentally, $p_1{=}p_2-\epsilon e^\gamma$ is not negative up to $\gamma ^+=\frac{1}{2}\ln \big (\frac{a+c}{2\epsilon }\big )$. It is $\gamma ^+=4.306$ in Fig. 15 and $\gamma ^+=2.004$ in Fig. 16 close over the corresponding $\gamma ^\cdot$ values. Last but least, both $\gamma ^\blacktriangledown$ and $\gamma ^\cdot$ diverge as $\epsilon$ goes to zero.

$$\begin{aligned} \gamma ^\blacktriangledown =\frac{1}{2}\ln \left( \frac{c-(a-2k)}{\epsilon }-1\right) \end{aligned}$$

(17)

1.3 Payoff region

Figure 17 shows the non-negative payoffs region in the BE ($a=10,k_1=5,k_2=2,c_1=1$) game with proportional rationing rule. Both price values have been sampled in 100 points advancing from 0 up to 10 with a 10/100 increment, which explains the mottled (or discrete) aspect of the payoffs regions. The red-marked solutions denote the payoffs when $p_1=p_2$, whereas the blue-marked solutions denote the payoffs when $p_2=p_1/2$. The bullet-marked points indicate the location of the points with maximum payoff of the two-players, with that one in the border of the payoff region, i.e. a PO solution, box-framed.

In the $p_1=p_2$ scenario, the solution with maximum payoff of the player-2 is located in the border of the payoff region in the two scenarios of Fig. 17, so that they are PO solutions. These solutions are induced by entanglement in Fig.3 regarding Fig. 17a, i.e. $u_1{=}u_2{=}10.0$, and in Fig.6 regarding Fig. 17b, i.e. $u_1{=}10.0$, $u_2{=}8.0$; in both scenarios with $p_1{=}p_2{=}6.0$, $q_1{=}q_2{=}2.0$. In the two games of Fig. 17, the solutions corresponding to the player-1 in the $p_1=p_2$ scenario⁹ are not located in the border of the payoff region, thus there is room for the increase of the payoffs of both players, that is, they are not PO solutions.

In the $p_2{=}p_1/2$ scenario, the solution with maximum payoff of the player-1 is a proper PO solution in Fig. 17a¹⁰ and an almost-PO solution in Fig. 17b. These solutions are much more payoff-unbalanced than those reached with $p_1{=}p_2$.

Fig. 17

Non-negative payoffs region in the BE ($a=10,k_1=5,k_2=2,c_1=1$) game with proportional rationing rule. The red-marked solutions denote the payoffs when $p_1=p_2$. The blue-marked solutions denote the payoffs when $p_2=p_1/2$. a $c_2=1.0$. b $c_2=2.0$