Skip to main content
SpringerLink
Log in

Characterizing the Nash equilibria of a three-player Bayesian quantum game

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

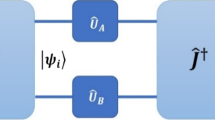
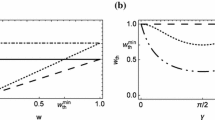
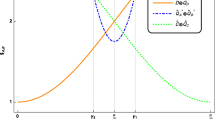
Quantum games with incomplete information can be studied within a Bayesian framework. We consider a version of prisoner’s dilemma (PD) in this framework with three players and characterize the Nash equilibria. A variation of the standard PD game is set up with two types of the second prisoner and the first prisoner plays with them with probability p and \(1-p\), respectively. The Bayesian nature of the game manifests in the uncertainty that the first prisoner faces about his opponent’s type which is encoded either in a classical probability or in the amplitudes of a wave function. Here, we consider scenarios with asymmetric payoffs between the first and second prisoner for different values of the probability, p, and the entanglement. Our results indicate a class of Nash equilibria (NE) with rich structures, characterized by a phase relationship on the strategies of the players. The rich structure can be exploited by the referee to set up rules of the game to push the players toward a specific class of NE. These results provide a deeper insight into the quantum advantages of Bayesian games over their classical counterpart.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. von Neumann, J., Morgenstern, O.: Theory of games and economic behavior. Princeton University Press, Princeton (1944)

  2. Nash, J.: Equilibrium points in n-person games. Proc. Natl. Acade. Sci. 36, 48 (1950)

  3. Nash, J.: Non-cooperative games. Ann. Math. 54, 286–295 (1951)

  4. Shubik, M.: Game theory models and methods in political economy. In: Arrow, K.J., Intriligator, M.D. (eds.) Handbook of Mathematical Economics, vol. 1, pp. 285–330. Elsevier (1981)

  5. Levy, G., Razin, R.: It takes two: an explanation for the democratic peace. J. Eur. Econ. Assoc. 2, 1–29 (2004)

  6. Axelrod, R.M., Dion, D.: The further evolution of cooperation. Science 242(4884), 1385 (1988)

    Article  ADS  Google Scholar 

  7. Shoham, Y.: Computer science and game theory. Commun. ACM Des. Games Purp. 51, 74 (2008)

    Article  Google Scholar 

  8. Meyer, D.: Quantum strategies. Phys. Rev. Lett. 82, 1052–1055 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  9. Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077–3080 (1999)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Eisert, J., Wilkens, M.: Quantum games. J. Mod. Opt. 47, 2543–2556 (2000)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  11. Bleiler S.A.: A formalism for quantum games and an application. arXiv:0808.1389 (2008)

  12. Khan, F.S., Humble, T.: No fixed point guarantee of Nash equilibrium in quantum games. arXiv:1609.08360 (2016)

  13. Kahn, F.S., Phoenix, S.J.D.: Gaming the quantum. Quantum Inf. Comput. 3(3–4), 231–244 (2013)

    MathSciNet  Google Scholar 

  14. Kahn, F.S., Phoenix, S.J.D.: Mini-maximizing two qubit quantum computations. Quantum Inf. Process. 12, 2807–3810 (2013)

    MathSciNet  Google Scholar 

  15. Kahn, F.S.: Dominant strategies in two-qubit quantum computations. Quantum Inf. Process. 14, 1799–1808 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Iqbal A., Chappell J.M., Li Q., Pearce C.E.M., Abbott D.: A probabilistic approach to quantum Bayesian games of incomplete information. Quantum Inf. Process. 13, 2783–2800 (2014)

  17. Benjamin, S.C., Hayden, P.M.: Multiplayer quantum games. Phys. Rev. A 64, 030301 (2001)

    Article  ADS  Google Scholar 

  18. Landsburg, E.S.: Nash equilibria in quantum games. Proc. Am. Math. Soc. 139, 4423. arXiv:1110.1351 (2011)

  19. Brunner, N., Linden, N.: Connection between Bell nonlocality and Bayesian game theory. Nat. Commun. 4, 2057 (2013)

    ADS  Google Scholar 

  20. Situ, H.: Two-player conflicting interest Bayesian games and Bell nonlocality. Quantum Inf. Process. 15, 137–145 (2016)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Iqbal, A., Chappell, J.M., Abbott, D.: Social optimality in quantum Bayesian games. Phys. A Stat. Mech. Appl. 436, 798–805 (2015)

    Article  MathSciNet  Google Scholar 

  22. Maitra, A., et al.: Proposal for quantum rational secret sharing. Phys. Rev. A 92, 022305 (2015)

    Article  ADS  Google Scholar 

  23. Li, Q., He, Y., Jiang, J.-P.: A novel clustering algorithm based on quantum games. J. Phys. A Math. Theor. 42, 445303 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Zableta, O.G., Barrangú, J.P., Arizmendi, C.M.: Quantum game application to spectrum scarcity problems. Phys. A 466, 455–461 (2017)

  25. Du, J., Li, H., Xu, X., Shi, M., Wu, J., Zhou, X., Han, R.: Experimental realization of quantum games on a quantum computer. Phys. Rev. Lett. 88, 137902 (2002)

    Article  ADS  Google Scholar 

  26. Prevedel, R., Andre, S., Walther, P., Zeilinger, A.: Experimental realization of a quantum game on a one-way quantum computer. New J. Phys. 9, 205 (2007)

    Article  ADS  Google Scholar 

  27. Buluta, I.M., Fujiwara, S., Hasegawa, S.: Quantum games in ion traps. Phys. Lett. A 358, 100 (2006)

    Article  ADS  MATH  Google Scholar 

  28. Harsanyi, J.C.: Games with incomplete information played by Bayesian players. Manag. Sci. 14, 159 (1967)

    Article  MathSciNet  MATH  Google Scholar 

  29. Parthasarathy, K.R.: An introduction to quantum stochastic calculus. Birkhauser, Basel (1992)

    Book  MATH  Google Scholar 

  30. Pitowsky, I.: Betting on the outcomes of measurements: a Bayesian theory of quantum probability. Stud. Hist. Philos. Mod. Phys. 34B, 395 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  31. Bolonek-Lason, K., Kosinski, P.: Note on maximally entangled Eisert–Lewenstein–Wilkens quantum games. Quantum Inf. Process. 14, 4413 (2015)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  32. Benjamin, S.C., Hayden, P.M.: Comment on “quantum games and quantum strategies”. Phys. Rev. Lett. 87, 069801 (2001)

    Article  ADS  Google Scholar 

  33. Du, J., Li, H., Xu, X., Zhou, X., Han, R.: Phase-transition-like behaviour of quantum games. J. Phys. A Math. Gen. 36, 6551–6562 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  34. Avishai, Y.: Some topics in quantum games. Masters Thesis, Ben Gurion University of the Negev, Beer Sheva, Israel (2012)

  35. Solmeyer, N., Balu, R.: Characterizing the Nash equilibria of three-player Bayesian quantum games, SPIE. arXiv:1703.03292 [quant-ph] (2017, forthcoming)

  36. Auman, R.: Subjectivity and correlation in randomized strategies. J. Math. Econ. 1, 67–96 (1974)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Sensors and Electron Devices Directorate, Army Research Laboratory, Adelphi, MD, 20783, USA

    Neal Solmeyer

  2. Mississippi Valley State University, 14000 Highway 82 West, Itta Bena, MS, 38941, USA

    Ricky Dixon

  3. Computer and Information Sciences Directorate, Army Research Laboratory, Adelphi, MD, 20783, USA

    Radhakrishnan Balu

Authors
  1. Neal Solmeyer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ricky Dixon
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Radhakrishnan Balu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Neal Solmeyer.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Solmeyer, N., Dixon, R. & Balu, R. Characterizing the Nash equilibria of a three-player Bayesian quantum game. Quantum Inf Process 16, 146 (2017). https://doi.org/10.1007/s11128-017-1593-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11128-017-1593-z

Keywords

Search

Navigation