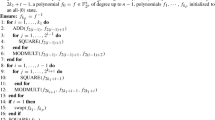Skip to main content
SpringerLink
Log in

Automatic synthesis of quantum circuits for point addition on ordinary binary elliptic curves

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

When designing quantum circuits for Shor’s algorithm to solve the discrete logarithm problem, implementing the group arithmetic is a cost-critical task. We introduce a software tool for the automatic generation of addition circuits for ordinary binary elliptic curves, a prominent platform group for digital signatures. The resulting circuits reduce the number of \(T\)-gates by a factor \(13/5\) compared to the best previous construction, without increasing the number of qubits or \(T\)-depth. The software also optimizes the (CNOT) depth for \({\mathbb F}_2\)-linear operations by means of suitable graph colorings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. As is common, we do not distinguish between \(T\)- and \(T^\dagger \)-gates in statements on the number of \(T\)-gates or the \(T\)-depth.

  2. As \((0,0)\not \in E_{a_2,a_6}(\mathbb {F}_{2^n})\), the neutral element \(\mathcal O\) can be represented as \((0,0)\).

References

  1. Al-Daoud, E., Mahmod, R., Rushdan, M., Kilicman, A.: A new addition formula for elliptic curves over GF\((2^n)\). IEEE Trans. Comput. 51(8), 972–975 (2002)

    Article  MathSciNet  Google Scholar 

  2. Amento, B., Rötteler, M., Steinwandt, R.: Efficient quantum circuits for binary elliptic curve arithmetic: reducing \(T\)-gate complexity. Quantum Inf. Comput. 13, 631–644 (2013)

    MathSciNet  Google Scholar 

  3. Amento, B., Rötteler, M., Steinwandt, R.: Quantum binary field inversion: improved circuit depth via choice of basis representation. Quantum Inf. Comput. 13, 116–134 (2013)

    MathSciNet  Google Scholar 

  4. Amy, M., Maslov, D., Mosca, M., Roetteler, M.: A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. IEEE Trans. Comput. Aided Design Integr. Circuits Syst. 32(6), 818–830 (2013). For a preprint version see [5]

  5. Amy, M., Maslov, D., Mosca, M., Roetteler, M.: A meet-in-the-middle algorithm for fast synthesis of depth-optimal quantum circuits. arXiv:1206.0758v3, January (2013)

  6. Beauregard, S., Brassard, G., Fernandez, J.M.: Quantum arithmetic on Galois fields. arXiv:quant-ph/0301163v1, January (2003)

  7. Bernstein, D.J., Lange, T.: Explicit-formulas database. http://www.hyperelliptic.org/EFD/index.html

  8. Bernstein, D.J., Lange, T., Farashahi, R.R.: Binary edwards curves. In: Oswald, E., Rohatgi, P. (eds.) Cryptographic Hardware and Embedded Systems—CHES 2008. Lecture Notes in Computer Science, vol. 5154, pp. 244–265. International Association for Cryptologic Research, Springer (2008)

  9. Cohen, H., Frey, G. (eds.): Handbook of Elliptic and Hyperelliptic Curve Cryptography: Discrete Mathematics and its Applications. Chapman & Hall/CRC, London (2006)

    Google Scholar 

  10. Cole, R., Ost, K., Schirra, S.: Edge-coloring bipartite multigraphs in \(O(E\log D)\) time. Combinatorica 21(1), 5–12 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  11. Institute for Quantum Computing. QCViewer. http://qcirc.iqc.uwaterloo.ca/index.php?n=Projects.QCViewer, 2013

  12. Python Software Foundation. Python Programming Language—Official Website. http://www.python.org (2013)

  13. Higuchi, A., Takagi, N.: A fast addition algorithm for elliptic curve arithmetic using projective coordinates. Inf. Process. Lett. 76, 101–103 (2000)

    Article  MathSciNet  Google Scholar 

  14. Kaye, P., Zalka, C.: Optimized quantum implementation of elliptic curve arithmetic over binary fields. arXiv:quant-ph/0407095v1, July (2004)

  15. López, J., Dahab, R.: Improved algorithms for elliptic curve arithmetic in \(GF(2^n)\). In: Tavares, S., Meijer, H. (eds.) Selected Areas in Cryptography—SAC’98, volume 1556 of Lecture Notes in Computer Science, pp. 201–212. Springer, Berlin (1999)

  16. Maslov, D., Mathew, J., Cheung, D., Pradhan, D.K.: An \(O(m^2)\)-depth quantum algorithm for the elliptic curve discrete logarithm problem over GF\((2^m)\). Quantum Inf. Comput. 9(7), 610–621 (2009). For a preprint version see [17]

    MATH  MathSciNet  Google Scholar 

  17. Maslov, D., Mathew, J., Cheung, D., Pradhan, D.K.: On the design and optimization of a quantum polynomial-time attack on elliptic curve cryptography. arXiv:0710.1093v2, February (2009)

  18. Menezes, A.J., van Oorschot, P.C., Vanstone, S.A.: Handbook of Applied Cryptography. CRC Press, Boca Raton (2001). Sample chapters available at http://cacr.uwaterloo.ca/hac/

  19. National Institute of Standards and Technology, Gaithersburg, MD 20899–8900. FIPS PUB 186–4. Federal Information Processing Standard Publication. Digital Signature Standard (DSS), July 2013. http://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4

  20. Alain Pointdexter. edge-coloring of a bipartite graph (Python recipe). http://code.activestate.com/recipes/498092-edge-coloring-of-a-bipartite-graph/, September 2013

  21. Rodríguez-Henríquez, F., Morales-Luna, G., López, J.: Low-complexity bit-parallel square root computation over \(GF(2^m)\) for all trinomials. IEEE Trans. Comput. 57(4), 472–480 (2008). For a preprint version see [22]

    Article  MathSciNet  Google Scholar 

  22. Rodríguez-Henríquez, F., Morales-Luna, G., López-Hernández, J.: Low complexity bit-parallel square root computation over \(GF(2^m)\) for all trinomials. Cryptology ePrint Archive: Report 2006/133, April 2006. http://eprint.iacr.org/2006/133

  23. Rötteler, M., Steinwandt, R.: A quantum circuit to find discrete logarithms on ordinary binary elliptic curves in depth O\((\log ^2 n)\). Quantum Inf. Comput. 14, 888–900 (2014)

  24. Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  25. Solinas, J.A.: An improved algorithm for arithmetic on a family of elliptic curves. In: Kaliski Jr., B.S. (ed.) Advances in Cryptology—CRYPTO ’97, Volume 1294 of Lecture Notes in Computer Science, pp. 357–371. Springer, Berlin (1997)

Download references

Acknowledgments

We thank Stephen Locke for helpful discussions on graph coloring and Brittanney Amento for kindly allowing us to use her Python code to generate quantum circuits for \({\mathbb F}_{2^n}\)-multiplication. We also would like to thank an anonymous referee for constructive comments. Most of this work was done while P.B. was with Florida Atlantic University. R.S. is supported by NATO’s Public Diplomacy Division in the framework of “Science for Peace”, Project MD.SFPP 984520.

Author information

Authors and Affiliations

  1. Salt Lake Community College, Salt Lake City, UT, 84123, USA

    Parshuram Budhathoki

  2. Florida Atlantic University, Boca Raton, FL, 33431, USA

    Rainer Steinwandt

Authors
  1. Parshuram Budhathoki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rainer Steinwandt
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Parshuram Budhathoki.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Budhathoki, P., Steinwandt, R. Automatic synthesis of quantum circuits for point addition on ordinary binary elliptic curves. Quantum Inf Process 14, 201–216 (2015). https://doi.org/10.1007/s11128-014-0851-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-014-0851-6

Keywords

Search

Navigation