1 Introduction

This paper investigates the behaviour of banks’ stock prices by matching classical macroeconomic equilibrium models dealing with households, banks, and non-financial firms. However, in contrast to that literature, the model strives to explain both market valuations and endogenous borrowing constraints in terms of risk. Such ‘financial friction’ is the cause of heterogeneous market dynamics ranging from a single equilibrium (i.e. representing stable growth) to (trade) cycles and chaos (i.e. mimicking turmoil). In fact, we prove that the only financially feasible equilibrium (where the lending rate paid to the banks is greater than the deposit rate rewarding the householders) is intrinsically unstable.

The idea that financial friction in macroeconomics may be held responsible for pricing bubbles and financial crises is put forth in Miao and Wang [1]. In that framework, Bella and Mattana [2] show that there is a Shilnikov chaotic attractor causing unpredictable outcomes, including a financial crisis. This has policy implications in terms of controls to be put in place to ensure that the system converges to a steady state.

The existence of market imperfections is widely known to cause observed prices to deviate from underlying value (see Grossman and Stiglitz [3]). As mentioned by Brown and Cliff [4], the notion of sentiments refers to the shared expectations of market participants in relation to a benchmark. When investors adopt a bullish stance they anticipate returns that surpass the average level, while bearish investors expect returns that fall below the average regardless of what that average may be.

In addition to the aforementioned peculiar modelling of “financial friction”, the novelty of the present paper lies in the mimicking of market sentiments as the proportion of bearish investors over the total. This is determined by key firms’ decisions depending on the liquidity constraint and related risk/reward profile. In fact, as in the real world, the combination of risk and market sentiment is the driving factor of market prices, being two sides of the same coin. The motivation of this work is to investigate the said linkage between risk/reward, liquidity constraint, and market sentiment. The proposed approach is deterministic as experimentally validated with real-world data in other research [5,6,7]. We prove that deposits and equity are management levers for chaos control/anticontrol and the only feasible equilibrium is unstable. Finally, through a test on real-world data, it is demonstrated that the proposed framework conforms to reality.

This paper is organised as follows. Section 2 summarises the relevant literature and provides some background on the topic. Section 3 describes the model and its three actors (households, banks, and non-financial institutions) subject to risk and reward constraints, the description of market sentiments as driving dynamics, and the derivation of competitive equilibria. Section 4 reports the numerical simulations, and a real-world application of the suggested model is made. Section 5 contains some concluding remarks.

2 Literature and background

2.1 On general equilibrium macroeconomic models, borrowing constraints, and market sentiments

As mentioned in introduction, general equilibrium macroeconomic models that adopt endogenous borrowing constraints for explaining financial friction in the banking sector can be found in many papers. Furthermore, self-fulfilling beliefs and market sentiments have been considered responsible for market bubbles.

Kehoe and Levine [8] derive endogenous debt limits from individual rationality constraints. Jermann and Quadrini [9] play with the properties of US firms’ financial flows by showing that while debt payout is countercyclical, equity payout is procyclical. Then, they find that a model with debt and equity financing helps to explain financial shocks; therefore, changes in credit conditions influence financial downturns. Alvarez and Jermann [10] study the implications of complete markets and endogenous solvency constraints for the efficiency and asset pricing of the equilibrium. They thereby show that “asset prices depend only on the valuation of agents with substantial idiosyncratic risk”. Albuquerque and Hopenhayn [11] present a general model of lending in the presence of endogenous constraints where borrowing is limited by liability so that debt repayment cannot always be enforced in its entirety. In such a framework “the value of outstanding debt restricts current access to short-term capital, but is itself determined by future access to credit”.

Using Bayesian methods, Miao et al. [12] estimate a dynamic stochastic general equilibrium model where stock market bubbles emerge “through a positive feedback loop mechanism supported by self-fulfilling beliefs”. Then, a so-called sentiment shock is suggested as a driving force of market bubbles. Its transmission to the real economy is through endogenous credit constraints, and it is found to be “the dominant force behind the internet bubbles and the Great Recession”.

Miao and Wang [1] suggest a model where the deposits of households are liabilities for the banks, where the latter are endogenously limited. There is no uncertainty about economic fundamentals. Banking bubbles are caused by a positive feedback loop mechanism and “changes in household confidence can cause the bubbles to burst, resulting in a financial crisis”.

Domeij and Ellingsen [13] demonstrate that, under rational expectations, dynamic general equilibrium models admit bubbles and Ponzi schemes. Those “rational bubbles” are consistent with USA debt, which is found to be “entirely a Ponzi scheme”. On the other hand “paying off public debt benefits only a small group of wealthy individuals”. Still, for rational bubbles, He [14] shows that “stock market prices of research and development (R &D) firms can include a bubble component when credit constraints are present”, so that bubbles have “the effect of expanding the borrowing and production capacities of R &D firms”. The effect is uneven because small firms benefit more than big firms, and likewise developing countries benefit more than developed ones. Guerrón-Quintana et al. [15] discuss a model switching between bubbly and bubbleless regimes and found evidence of recurrent bubbles in data for the USA. Furthermore, according to their simulations “the IT and housing bubbles together lifted U.S. GDP by almost 2 percentage points permanently”.

2.2 On chaotic dynamics in economy and financial markets

Regarding the vexed question of the presence of chaos in finance and economics, Faggini et al. [16], while conducting a comprehensive review of the subject, affirm that “no natural deterministic explanation can justify the observed financial fluctuations produced by external shocks or by inherent randomness”. On the other hand, theoretical and empirical studies bring to light numerous shreds of evidence about chaos and determinism in real-world data. Albulescu et al. [17], when investigating the price behaviour and efficiency of the Central and Eastern European (CEE) capital markets, “document the presence of nonlinearities and chaos which questions the efficient market hypothesis”. Similarly, Orlando et al. [6] found that for a wide range of empirical data (encompassing derivatives, bonds with short and long maturation periods, equities, emerging and developed markets, and corporate and government issuers), the “alternations between calm periods and financial turmoil, could be described by a low-dimensional deterministic model”. Moreover, they suggest a deterministic model which “performs at least as well as one of the best stochastic models” while offering “additional insight into the essential mechanisms that drive financial markets”. Thus, theoretically, extreme events can be modelled using deterministic models [18], and empirically, determinism can be observed in real data [19, 20].

Based on the assumption of fractality, Kristoufek [21] derives some implications according to the capital asset pricing model (CAPM) for the Dow Jones Industrial Average index. Orlando and Bufalo [7] considered “the Moody’s Seasoned Aaa Corporate Bond Yield Relative to Yield on 10-Year Treasury Constant Maturity as well as the ICE BofA US High Yield Index Option-Adjusted Spread” and found that a deterministic model is toe to toe in modelling time series’ features such as the moving average (MA), autoregression (AR), cointegration, and heteroscedastic volatility.

Orlando and Zimatore [22] also use a Kaldorian business cycle model to simulate real dynamics so that “nonlinear techniques such as recurrence quantification analysis, Poincaré Plot and related quantifiers can be applied”; this with the aim to “discover whether real and simulated business cycle dynamics have similar characteristics and validate the model as a suitable tool to simulate reality”, which led to the conclusion that “analysis of chaos brings evidence on fractal dimension and entropy measures for both real data and model’s simulations”. Finally, Barnett et al. [23] show that a New Keynesian (NK) model and an active monetary policy combined with a Ricardian fiscal policy (à la Leeper-Woodford) may induce the onset of a Shilnikov chaotic attractor. This effect can be interpreted in terms of a liquidity trap and may provide an alternative explanation to the controversial “loanable funds” theory of excessive saving.

2.3 On the Nash equilibrium, representative agents and chaos

As mentioned by Lampart et al. [24], the Nash equilibrium with time evolution has attracted a good deal of research [25,26,27]. In that study, the authors point out that the phenomenon is caused by intermittent chaos rather than the coexistence of attractors. This implies that even irregular economic systems can regulate themselves and reach a stable state without any external intervention. Thus, the classical Cournot heterogeneous model with optimal response can be used to derive the dynamical properties of the resulting system. This is achieved by considering ordinal utility instead of cardinal monetary amounts where the classical decision of quantity is disentangled from the decision on imitation for both representative agents of imitators and responders [24]. Bielawski et al. [28] studied the emergence of chaotic behaviour of Follow-the-Regularised Leader (FoReL) dynamics in games and found that an increase in the population size or the scale of costs in congestion games results in unstable chaotic behaviours. Furthermore, similarly to Lampart and Lampartová [29] and Lampart et al. [24], Bielawski et al. [28] demonstrate the coexistence of stable Nash equilibria and chaos where the creation of one chaotic attractor is simultaneous with the destruction of another. Elsadany and Awad [30] describe the behaviour of a duopolistic Bertrand competitive market with environmental taxes where representative agents are privatised or non-privatised public firms. In that context, the Nash equilibrium loses stability to such an extent that feedback control is needed to stabilise the market. Kang [31] provides a theoretical framework on international trade by trying to discover whether nations have incentives to pursue free trade. In his framework, representative agents maximise Cobb-Douglas utilities. Then, a Nash equilibrium with complete specialisation arises when productivity exceeds a given threshold.

Applications can be found in research and development (R &D) for reducing polluting emissions [32], firms’ incentives to invest in a circular economy [33], the software industry [34], spectrum/bandwidth sharing and pricing [35], etc.

2.4 On market sentiments, instability and speculative bubbles

According to Brown and Cliff [4], market imperfections are a well-known cause of prices deviating from their underlying value (see Grossman and Stiglitz [3]). One of the major market imperfections affecting large US stocks is the high cost of acquiring information related to their value. Due to the high costs of obtaining information on future stock returns, as well as the subjectivity of interpreting such information, stock prices are likely to trade within a range surrounding their true value in the absence of perfect information. The argument that market imperfections lead to deviations between observed prices and underlying value is supported by numerous empirical studies. For instance, insiders trading in their own stock earn superior returns, as demonstrated by Seyhun [36]. Donaldson and Kim [37] found that the Dow Jones Industrial Average (DJIA) is subject to “support” and “resistance” levels at multiples of 100. In a study on the October 1987 stock market crash, Siegel [38] concluded that considerable fluctuations in valuation could not be explained by changes in interest rates or future earnings. He, instead, attributed the changes in market returns around the time of the crash to shifts in investor sentiment.

For example, imitation can lead to speculative bubbles that destabilise markets and can result in much broader problems in the economy, as seen in the 2008 financial crisis. Market agents who focus on the long-term fundamental values of assets tend to stabilise the market by selling assets when prices exceed their fundamental values, and buying when prices fall below their fundamental values (Mackay [39], Baumol [40], Zeeman [41], Rosser [42]). However, agents who chase trends can destabilise markets by buying assets when prices are rising, causing them to rise even more, and vice versa. In times of rising price trends, trend chasers may achieve better returns than fundamentalists, and imitation of these successful trend chasers can cause other agents who would ordinarily have followed stabilising fundamentalist strategies to instead follow destabilising trend chasing strategies, which will tend to push the price further up. Additionally, when the price during a bubble finally peaks and starts to fall, trend chasers can then push the price down more rapidly if they imitate the panic selling of others (Rosser [43]).

Research conducted by Smith et al. [44] and further supported by subsequent studies has demonstrated that the inclination towards trend chasing speculation is an innate human trait. Even in simplified experimental markets with finite time horizons and clearly defined payment structures, bubbles have been observed to form due to people’s strong tendency to speculate and follow each other into destabilising speculation through imitation. While procedures that support procedural rationality in a world of bounded rationality can be effective, they can lead to bad outcomes if pursued too vigorously. The aforementioned bubbles can follow one of three patterns: a sharp decline after reaching a peak, a gradual and symmetrical decline after reaching a peak, or a gradual decline followed by a panic-driven crash. Aliber and Kindleberger [45] noted that, out of 47 historical speculative bubbles, five followed the first pattern of rising to a peak and then falling sharply, five followed the second pattern of rising to a peak and then declining gradually, and the vast majority of the remainder followed the final pattern of rising to a peak, declining gradually for a time, and ultimately collapsing in a panic-driven crash. According to Ahmed et al. [46], commodities are more likely to exhibit the first pattern of rising to a peak and then falling sharply. On the other hand, the housing bubble that peaked in mid-2006 followed the second pattern, with observable roughness around the peak that made it resemble the third pattern. However, this roughness at the national level was due to different cities’ housing market peaking at different times, with a final round of peaks as late as January 2007 before the decline. This pattern has historically been associated with real estate market bubbles, where the decline is more gradual and nearly symmetrical with the increase, reflecting the personal attachment that people have to their homes and the reluctance to accept their decline in value.

The final pattern is characterised by a period of financial distress and can be replicated in an agent-based model where agents shift strategies based on their relative successes, albeit not instantaneously [47, 48]. The delayed crash in the model is triggered by agents encountering financial constraints, similarly to how individuals may face margin calls in stock markets, highlighting the role of complexity in most speculative bubbles [42].

2.5 On autoregressive models for investors behaviour

Autoregressive (AR) and other similar models are widely used in finance. For example, Friedman and Roley [49] tested investors’ portfolio behaviour by comparing unitary, rational, and autoregressive interest rate expectations. In their study, they found that autoregressive expectations “consistently provide the best explanation of the data”. Spyrou [50] analyses the role of investors’ sentiments, as modelled via a vector autoregressive model (VAR), “in the determination of yield spreads during the financial crisis”. Hu et al. [51] adopt a Markov-Switching Vector Autoregressive (MS-VAR) model to study the relationship “between investor sentiment, stock market returns, and stock market volatility”. Rupande et al. [52] claim that volatility is linked to sentiment-driven noise trader activity, which is modelled by a Generalised Autoregressive Conditional Heteroscedasticity (GARCH) model. A GARCH model for volatilities of both stock returns and market sentiments has been proposed by Escobari and Jafarinejad [53]. Liu and Hamori [54] use a time-varying parameter vector autoregressive (TVP-VAR) to investigate “the connectedness of the returns and volatility of clean energy stock, technology stock, crude oil, natural gas, and investor sentiments”. Zhang et al. [55] adopt a vector autoregressive model “to study the influence of investor sentiment on the return rate of different types of P2P platforms”. Finally, Bonato et al. [56] examine “investor happiness in predicting the daily realised volatility” with a heterogeneous autoregressive (HAR) model.

2.6 On bounded rationality and consistent expectations

As discussed in Sögner and Mitlöhner [57], in models based on rational expectations, all agents have perfect knowledge of the equations that describe the economic system. This concept, first introduced by Muth [58], is highly demanding as it requires agents to have perfect information and high computational skills in order to solve their optimisation problems. These rational agents make decisions based on maximising their utility functions and learn in a statistically correct way. Through the interaction of these rational agents in corresponding markets, the rational expectations equilibrium (REE) is achieved. Thus, the REE is a natural outcome of the rational agent paradigm. Bounded rationality models have been proposed as an alternative to rational expectations. These models are based on behavioural foundations [59, 60] or discrete choice models [47, 48]. However, non-rational agent models allow for a wide range of possible approaches. For instance, the process of inference of new information can be modelled using linear or nonlinear techniques, genetic algorithms, and ad-hoc rules. Each forecasting technique can result in differing equilibrium behaviour, if equilibria already exist in the system. Although some models can explain certain stylised facts, some of the ad-hoc assumptions underlying bounded rationality models may not be justifiable from the rational expectations equilibrium perspective. Dwyer et al. [61] conducted an experiment to test the hypothesis of rational expectations in which they examined whether subjective forecasts are essentially the same as forecasts derived from the relevant economic theory, i.e. from the REE. The results of the experiment did not find statistically significant evidence of a systematic bias or incorrect use of available information. However, for approximately 40% of the forecasts the deviations from the actual events were predictable ex post, which challenges the assumption of perfectly rational agents. Linear forecasting, where the market clearing system matches agents’ demands to the equilibrium price (implied law of motion), and which fits the consistent expectations equilibrium (CEE) [62], is explored by Sögner and Mitlöhner [57].

According to Hommes and Sorger [63], a consistent expectations equilibrium (CEE) occurs when an agent’s expectations are self-fulfilling because the sample average and sample autocorrelations of the actual law of motion are equal to those of the perceived law of motion. This is focused on scenarios where beliefs are described by an AR(1) process, with three types of CEE examined for existence and stability: steady-state, two-cycle, and chaotic. The nonlinear cobweb model is utilised to demonstrate how these equilibria can emerge. Learning dynamics based on sample average and sample autocorrelations are also introduced, and the study investigates the stability of CEE under this learning process. The tent map is one such example of an autoregressive process of order one (AR(1)) process that mimics the learning process of agents over time as they adjust their control parameters based on their performance. Assuming that the learning optimisation follows said map, Hommes and Rosser [64] demonstrate that these parameters can converge on values that enable this simple heuristic to replicate the underlying chaotic dynamic, resulting in a consistent expectations equilibrium. With reference to that, Jungeilges [65] showed that the fixed point of the expectations-feedback system, identified as a chaotic CEE, is only a temporary phenomenon.

The tent map is also utilised by Stoop [66] to illustrate the issue of unstable or excessively noisy systems. To mitigate this problem, limiters in the form of barriers are introduced to prevent the system from moving into undesired areas of the phase space. The result is the emergence of stable cycles. However, the placement of the limiter around the maximal system response may not be optimal, whereas positioning the limiter near a period-one cycle tends to be more effective. A potential drawback of this approach is that it requires significant interventions, and, in democratic societies, transparent control policies are essential for its implementation.

3 The model

In this section, a model linking households, banks, non-financial firms, and market sentiments is proposed. In contrast to the literature, constraints and dynamics are based not only on budget constraints, but also on profitability and risk. Therefore, bank stock price b does not depend on past values and the market evaluation of its assets q. The latter depends on the perceived risk \(\rho \). In the market, risk is determined by investors that make their bets according to their bearish or bullish views. The proportion of bearish versus bullish bets is modelled by a discrete skew tent map. The bank stock price is then constructed using standard dynamical programming theory, more precisely, the Bellman equation. For this purpose, the influence of households, banks, and non-financial firms, together with competitive equilibrium, is taken into account. The derivation of this new model was partially motivated by Miao et al. [1] where, in contrast to the proposed framework, their model does not consider risk, liquidity, or profitability targets.

3.1 Households

The starting point is to consider banks and non-financial firms. Let us define the following variables: \(b_{\rho }\) banks asset price, \(\beta _t\) the outstanding shares for banks, \(s_t\) non-financial firm price, \(\alpha _t\) the outstanding shares for non-financial holdings, \(D_t\) deposits, where \(\rho \) is the risk depending on the time t. Then, the total assets are

$$\begin{aligned} \beta _t b_{\rho }+ \alpha _t s_t + D_t \, . \end{aligned}$$
(1)

Households receive compensation for their work \(w_t\) and their assets. The latter can be either in terms of profits \(\pi _t\) or in terms of the interest rate \(r^d_t\) on the deposits. In addition, households consume a quantity \(C_t\).

Therefore, the budget constraint is

$$\begin{aligned}{} & {} b_{\rho } {{\,\textrm{d}\,}}\beta _t + s_t {{\,\textrm{d}\,}}\alpha _t + {{\,\textrm{d}\,}}D_t = \beta _t \pi _t^b {{\,\textrm{d}\,}}t + \alpha _t \pi _t^s {{\,\textrm{d}\,}}t\nonumber \\{} & {} \quad + r_t^d D_t {{\,\textrm{d}\,}}t + w_t {{\,\textrm{d}\,}}t - C_t {{\,\textrm{d}\,}}t, \end{aligned}$$
(2)

where \(\pi _t^b\) and \( \pi _t^s\) represent the dividends paid by the banks and non-financial companies, respectively.

We define

$$\begin{aligned} r_t^b=\frac{\beta _t \pi _t^b}{b_{\rho }}, \quad r_t^s=\frac{\alpha _t \pi _t^s}{a_t} \end{aligned}$$
(3)

as the return from bank assets and the return from non-financial assets, respectively. In equilibrium, one should expect that the risk-adjusted returns from all investments are equal, i.e.

$$\begin{aligned} r_t^k=\frac{r_t^d}{\rho ^d_t} = \frac{r_t^b}{\rho _t} = \frac{r_t^s}{\rho ^s_t}, \end{aligned}$$
(4)

where \(r_t^k\) is the return on capital, while \(\rho ^d_t, \rho _t\), and \(\rho ^s_t\) represent the risk of deposits, investments in banks, and investments in non-financial firms, respectively.

3.2 Banks

\(N_t\) denotes the bank’s net worth (equity) before dividends and \(S_t\) the loans made to non-financial firms to finance capital expenditure \(K_t\). The balance sheet of the bank is therefore

$$\begin{aligned} V_t = N_t + D_t = S_t = K_t \,, \end{aligned}$$
(5)

where we assume that debt is equal to the bank’s liability and total assets \( V_t\) are made up of loans. Therefore, the only source of income for the bank is the return on loans \(r_t^l\), and the only cost is the return on deposits \(r_t^d\).

As lending carries a risk, the bank evaluates the expected risk-adjusted return from lending that should be above a certain target. In fact, the bank will not provide funds to a business below a given threshold in terms of risk/reward. In addition, banks monitor liquidity through the loan-to-deposit ratio (LDR). An LDR that is too high means that the bank may not have enough liquidity to cover any unexpected fund requirements. Conversely, with an LDR that is too low, the bank could underperform in terms of income. Thus, liquidity, uncertainty, and target profitability, as combined for example in the form of Risk-Adjusted Return On Capital (RAROC), limit a bank’s borrowing as follows:

$$\begin{aligned} D_t \le V_t ( \xi N_t), \end{aligned}$$
(6)

where \(\xi \in (0, 1] \) is a percentage of net assets and \(\xi N_t\) is the resulting capital (e.g. the CET1) according to the capital adequacy guidelines as outlined by the Basel Committee.

Thus, with \( \phi \) denoted as the bank capital requirement ratio, it holds that

$$\begin{aligned} N_t \ge \pi (D_t + N_t), \qquad \pi \in (0,1), \end{aligned}$$
(7)

or equivalently

$$\begin{aligned} D_t \le \frac{1-\phi }{\phi } N_t \,. \end{aligned}$$
(8)

Similarly, regarding banks’ per share dividends \(\pi _t^b \), they are supposed to be a fraction \(\theta \) of banks’ net worth \(N_t\)

$$\begin{aligned} \beta _t \pi _t^b\le \theta N_t, \qquad \theta \in (0,1), \end{aligned}$$
(9)

or equivalently

$$\begin{aligned} \pi _t^b\le \dfrac{\theta }{\beta _t} N_t, \qquad \theta \in (0,1), \end{aligned}$$
(10)

which is binding for a given \(\theta ^\star \)

$$\begin{aligned} \pi _t^b = \theta ^\star N_t. \end{aligned}$$
(11)

Essentially, there is a trade-off between the dividends that the company has to pay to reward the shareholders and the need to keep some assets \( N_t\) to run the business as indented.

Finally, it is assumed that both banks’ deposits and net worth are not negative

$$\begin{aligned} D_t \ge 0, \quad N_t > 0. \end{aligned}$$
(12)

Let \(b_{\rho }\) be the stock price of the bank, \(\delta _t\) be the per share debt, and \(b_{\rho }\) be a function of the per share equity \(n_t\). The dynamics of the budget constraint are

$$\begin{aligned} \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}n_t= r_{t}^l n_t + (r_{t}^l-r_{t}^d) \delta _t - \pi _t^b \,, \end{aligned}$$
(13)

where \(r_{t}^l\) is the lending rate.

3.3 Non-financial firms

Let us suppose that non-financial firms have a production function in the form of a constant return of scale.

$$\begin{aligned} Y_t = K_t^{\eta } L_t^{1-\eta }, \quad \eta \in (0,1), \end{aligned}$$
(14)

where \(Y_t, K_t\), and \(L_t\) are aggregate output, capital, and labour, respectively. Since profit maximisation implies that marginal output equals wages (\( w_t \))

$$\begin{aligned} (1-\eta ) K_t^{\eta } L_t^{-\eta } = w_t, \end{aligned}$$
(15)

the profit per unit of capital is

$$\begin{aligned} \frac{Y_t - w_t L_t}{K_t} = \eta K_t^{\eta -1} L_t^{1-\eta } . \end{aligned}$$
(16)

The profit is either distributed to shareholders or is used to pay interest on debt. Thus the equilibrium of the lending rate \(r_t^l\) should be equal to the capital return minus the depreciation rate \(\delta \) and the cost of capital represented by the remuneration to the shareholders \(r_t^s\);

$$\begin{aligned} r_t^l = \eta K_t^{\eta -1} L_t^{1-\eta } -\delta - r_t^s. \end{aligned}$$
(17)

3.4 Market sentiments as driving price dynamics

Assuming that investors are bearish or bullish, the proportion of the first over the total is described by the skew tent map

$$\begin{aligned} f_{\lambda }(v)= \lambda \min \{ v/a , (1-v)/(1-a) \} \end{aligned}$$
(18)

that can be recursively written as

$$\begin{aligned} v_{t+1}={\left\{ \begin{array}{ll} \lambda v_t/a &{}\textrm{for}~~ v_t \in [0,a] \\ \lambda (1-v_t)/(1-a) &{}\textrm{for}~~ v_t \in [a,1] \end{array}\right. }, \end{aligned}$$
(19)

where \(\lambda \in (0,1]\) is the maximality parameter depending on \(\theta \), and \(a \in (0,1)\) is a parameter determining the skewness (see Fig. 1).

Fig. 1
figure 1

Proportion of bearish investors for different a with \(\lambda =1\) representing how investors adjust to the business cycle

Full size image

First of all, notice that the functional relation \(\lambda =g(\theta ) \) is such that, ceteris paribus, the more available assets a company has, the higher the solvency (and therefore the lower the risk). Second, the sequence \(v_{n}\) modelled by Eq. (19) is comparable to a first-order autoregressive process with i.i.d. stochastic variables (Brock [67]). Moreover, a tent map is a B-process, i.e. it is isomorphic to a Bernoulli process (see Medio and Lines [68]). This is noteworthy because B-processes enjoy the “Very Weak Bernoulli (VWB)” property, which is an asymptotic form of independence (i.e. the expectation, conditioned on the past, converges in time to the unconditioned future). Said differently, for B-processes, the past becomes less and less relevant as time passes to predict the future. The tent map was also used by Hommes and Rosser [64] to mimic the learning process of agents over time. Their approach involved assuming that an AR(1) was adequate for capturing price dynamics, and agents proceeded to learn based on price data generated by a nonlinear map. As agents updated the parameters of their perceived linear law of motion, which also parameterised the actual nonlinear law of motion for the prices, the learning process eventually converged to a stable AR(1) process. Despite prices having been generated by a chaotic map, the agents had confidence in their perceived law of motion.

A classic Bernoulli process is the repeated toss of a fair coin, with 1/2 probability of heads and 1/2 tails. In the suggested model, the a parameter represents market sentiments under contingent conditions, thus determining the proportion of bearish investors. For example, Fig. 2 shows how pessimistic market sentiments affect the proportion of bearish investors, cycling between 45% and 90%, while Fig. 3 shows the convergence to the equilibrium. Tent maps are widely used in chaos theory as they display all the behaviours typical of deterministic chaotic dynamical systems and are semi-conjugated with the logistic map (Hirsch et al. [69], Tian et al. [70]).

Fig. 2
figure 2

Proportion of bearish investors looping in a limit 3 cycle between 0.45 and 0.9. Parameters: \(\lambda =1\), \(a=2/3\) and \(v_0=18/25\)

Full size image
Fig. 3
figure 3

Proportion of bearish investors converging to an unstable fixed point (i.e. a repeller Orlando and Taglialatela [71]). Parameters: \(\lambda =4/5\), \(a=1/7\) and \(v_0=2001/10{,}000\)

Full size image

If Z is a standard Gaussian variable, and \(\mu \) and \(\sigma >0\) are two real numbers, the distribution of the random variable risk is

$$\begin{aligned} \textrm{P}=e^{\mu +\sigma Z}; \end{aligned}$$
(20)

i.e. \(\textrm{P}\) is log-normally distributed with parameters \(\mu \) (expected value) and \(\sigma \) (standard deviation).

The higher the percentage of bearish investors, the greater the perceived risk \(\rho \). When bearish and bullish investors are equal in number, the perceived risk corresponds to the mode of the log-normal, i.e. \(\exp (\mu -\sigma )\).

The stock market value of the bank takes the following form:

$$\begin{aligned} b_{t} (n_t, q(\rho _t)) = V_t+ b_{t-1} =q (\rho _t) n_t(r) + b_{t-1}, \end{aligned}$$
(21)

where \(q_t\) is the price of a bank’s net assets based on the perceived risk, and \(b_{t-1}\) is an autoregressive (AR) moving average (MA) process with white noise \(\varepsilon _{t-1}\), and parameters c, \(\varphi _i\), \(\varpi _{j}\):

$$\begin{aligned} b_{t-1} = c + \sum _{i=1}^{t-2} \varphi _i b_{t-i}+ \sum _{j=1}^{t-2} \varpi _{j} \varepsilon _{t-j} \, . \end{aligned}$$
(22)

The ARMA model reflects the intertemporal linkage between past and current dynamics and is often denoted as ARMA(z, k), where z is the number of time lags of the AR, and k is the order of the MA. When cointegration is taken into account, the more general ARIMA(z, d, k) is adopted (with d denoting the degree of differencing). Concerning the interest rate and risk, the higher the discount rate r and the risk \(\rho \) are, the lower the price of the stock \(b_{\rho }\) is. Then, \(q_t\) could be described by one minus the cumulative inverse of the distribution function \(\Theta \) of the standardised Gaussian distribution (i.e. N(0,1)).

$$\begin{aligned} q(\rho _t) =1 - \Theta \left( \frac{\ln \rho _t - \mu }{\sigma }\right) . \end{aligned}$$
(23)

Equivalently

$$\begin{aligned} q(\rho _t)= & {} 1- \frac{1}{2} \left[ 1 + {{\,\textrm{erf}\,}}\left( \frac{\ln \rho _t - \mu }{\sigma \sqrt{2}}\right) \right] \nonumber \\= & {} \frac{1}{2} {{\,\textrm{erfc}\,}}\left( \frac{\ln \rho _t - \mu }{\sigma \sqrt{2}}\right) , \end{aligned}$$
(24)

where \({{\,\textrm{erf}\,}}\) is the error function and \({{\,\textrm{erfc}\,}}\) is its complementary. That means we are assuming that the risk \(\rho \in [0, \infty ]\), and that q tends to 1 when the risk goes to zero, and tends to zero when the risk goes to \(\infty \).

3.5 Competitive equilibrium

A competitive equilibrium consists of quantities \(\{C_t, \pi ^b_t, \pi ^s_t, K_t, N_t, D_t, L_t\}\) and prices \(\{V_t,r_t^l, w_t \}\) that households, bankers, and firms optimise such that

$$\begin{aligned} \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t} K_t = K_t^{\eta } L^{1-\eta }_t - \, \delta K_t \, - C_t \, . \end{aligned}$$
(25)

We write the bank’s stock value function as \(b_{\rho }(n_t)=b(n_t,q(\rho _t))\) and denote \(b_n\) and \(b_q\) the derivatives of b with respect to n and q, respectively. By standard dynamic programming theory, the bank’s value satisfies the Bellman equation:

$$\begin{aligned} r_t^d b (n_t,q(\rho _t))= & {} \max _{\pi _t^b,\delta _t} \pi _t^b + b_n (n_t,q(\rho _t))\frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t} n_t \nonumber \\{} & {} +\,b_q (n_t,q(\rho _t))\frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}(q(\rho _t)). \end{aligned}$$
(26)

Then substituting Eqs. (13) and (21) into Eq. (26) we get

$$\begin{aligned} r_t^d q(\rho _t) n_t= & {} \max _{\pi _t^b,d_t} \pi _t^b +q(\rho _t) ( r_t^l n_t +(r_t^l-r_t^d )d_t-\pi _t^b)\nonumber \\{} & {} +\,n_t \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}(q(\rho _t)). \end{aligned}$$
(27)

The current borrowing constraint (i.e. not depending on the past) derived from Eqs. (6) and (21) takes the form

$$\begin{aligned} d_t \le \xi q(\rho _t) n_t \, , \end{aligned}$$
(28)

where \(d_t\) is per share deposit. Equation (28) binds for a given \(\xi ^\star \in (0,1)\) so that

$$\begin{aligned} d_t=\xi ^\star q(\rho _t) n_t. \end{aligned}$$
(29)

Using equality Eq. (29) and replacing \(d_t\) in Eq. (27) and applying Eq. (11) we get

$$\begin{aligned}{} & {} \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}(q(\rho _t)) n_t=[r_t^d - r_t^l - (r_t^l-r_t^d)\xi ^\star q(\rho _t) + \theta ^\star ]\nonumber \\{} & {} \qquad \qquad q(\rho _t) n_t -\theta ^\star n_t. \end{aligned}$$
(30)

Finally, due to Eqs. (12), (30) can be reduced to obtain the investigated equation that depends only on \(q(\rho _t)\):

$$\begin{aligned} \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}(q(\rho _t))=[r_t^d - r_t^l - (r_t^l-r_t^d)\xi ^\star q(\rho _t) + \theta ^\star ] q(\rho _t) -\theta ^\star . \end{aligned}$$
(31)

Now, put \({{\,\textrm{d}\,}}/ {{\,\textrm{d}\,}}t \, q(\rho _t) = 0\), and by direct calculation the following theorems can be stated:

Lemma 1

Equation (31) has at most two equilibria. Moreover,

  1. 1.

    if \(r_t^l=r_t^d\) there is no equilibrium,

  2. 2.

    if \(r_t^l \ne r_t^d\) and \((r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star =0\) there is exactly one equilibrium,

    $$\begin{aligned} q^{0}_{\rho }=\dfrac{(r_t^l-r_t^d) - \theta ^\star }{2(r_t^d-r_t^l)\xi ^\star }, \end{aligned}$$
    (32)
  3. 3.

    if \(r_t^l \ne r_t^d\) and \((r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star >0\) then there are two equilibria

    $$\begin{aligned} q^{\pm }_{\rho }=\dfrac{(r_t^l-r_t^d) - \theta ^\star \pm \sqrt{(r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star }}{2(r_t^d-r_t^l)\xi ^\star }, \end{aligned}$$
    (33)
  4. 4.

    and if \(r_t^l \ne r_t^d\) and \((r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star <0\) then there is no equilibrium.

By a straightforward computation, using assumptions \(\theta ^\star \in (0,1)\) and \(\xi ^\star \in (0,1)\), stability of equilibria \(q^{0}_{\rho }\) and \(q^{\pm }_{\rho }\) can be detected:

Theorem 2

  1. 1.

    The equilibrium \(q^{0}_{\rho }\) is stable if \(r_t^d>r_t^l\), or \(r_t^d<r_t^l\) and \(r_t^l-r_t^d-\theta ^\star >0\) and

  2. 2.

    The equilibrium \(q^{0}_{\rho }\) is unstable if \(r_t^d<r_t^l\) and \(r_t^l-r_t^d-\theta ^\star <0\).

Remark 1

The unstable equilibrium \(q^{0}_{\rho }\), for \(r_t^d<r_t^l\) and \(r_t^l-r_t^d-\theta ^\star <0\), is the only economically sensible solution.

Theorem 3

  1. 1.

    If \(r_t^d>r_t^l\) the equilibrium \(q^{-}_{\rho }\) is unstable.

  2. 2.

    If \(r_t^d>r_t^l\) and \((r_t^l-r_t^d) - \theta ^\star +\) \(\sqrt{(r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star }>0\) the equilibrium \(q^{+}_{\rho }\) is unstable.

  3. 3.

    If \(r_t^d>r_t^l\) and \((r_t^l-r_t^d) - \theta ^\star + \sqrt{(r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star }<0\) the equilibrium \(q^{+}_{\rho }\) is stable.

  4. 4.

    If \(r_t^d<r_t^l\) and \((r_t^l-r_t^d) - \theta ^\star \pm \sqrt{(r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star }>0\) then \(q^{\pm }_{\rho }\) is stable.

  5. 5.

    If \(r_t^d<r_t^l\) and \((r_t^l-r_t^d) - \theta ^\star \pm \sqrt{(r_t^d-r_t^l+\theta ^\star )^2 + 4(r_t^l-r_t^d)\xi ^\star \theta ^\star }<0\) then \(q^{\pm }_{\rho }\) is unstable.

4 Numerical simulations

This section displays the numerical simulations obtained from Eq. (31) conveniently discretised to match the frequency of actual data. This is in line with the fact that Eq. (31) is continuous but not differentiable. Parameters and initial state variables are derived from real-world data as described in Sect. 4.1. A practical example created by fitting the suggested model over those data is given in Sect. 4.4.

All simulations were performed in MATLAB [72] with a graphical implementation of skew tent map Eq. (18).

4.1 Data and parameters

Citigroup Inc., one of the top three largest banking institutions in the USA, was considered a representative benchmark for our tests. The group is considered to be systemically important by the Financial Stability Board (FASB), having been deemed “too big to fail”. Retrieved data (billions of USD) for the fiscal year 2021 for Citibank are from [73] and [74] and are as follows, \(V=96,669, Q=42.195, N=2,291\), \(D=2,088\), \(\pi ^b = 4.247\). The share price was \(b=55.26\$\) (adj. close), total outstanding shares were \(\beta =2,082\) billion, and the calculated parameters are \(\xi ^\star = 2.160\%\), and \(\theta ^\star =0.185\%\). The lending rate and deposit rate (saving accounts) in the USA for the year 2021 were \(r^l=3.25\%\) [75] and \(r^d=0.06\%\) [76], respectively. The return from the bank’s assets, according to Eq. (3), is \(r^b=7.686\%\). Regarding the parameters of the cumulative distribution function \(\Theta \), we assume \(\mu =0\) and \(\sigma =0.5\). The time series of the Citigroup stock price (from 01/03/2009 to 01/05/2022) was retrieved from [77].

4.2 Global stock price risk-dependent dynamics

To understand the dynamics of the researched phenomena described by Eq. (31) it is necessary to explore the driving part of the model, that is the risk \(\rho \) defined in Eq. (24). Moreover, to depict the connection between the simulation and the real-world results interpretation, an orbit diagram and a bifurcation diagram are constructed.

In the first case, the orbit diagram is a projection plot of the initial, so-called transient, parts of the trajectories. In our case, for the orbit diagram, the first 500 iterations were projected. On the other hand, the bifurcation diagram, as an asymptotic behaviour tool constructed for a fixed initial condition, is a union of unique attractors generated for the concrete bifurcation value parameter. These attractors graphically represent periodic trajectories if isolated points are plotted; conversely, if a band (or a segment of lines) is marked, the quasi-periodic or chaotic regime appears. Both types of diagram have their economical interpretation as behaviour in a close or far-future corresponding to the orbit or bifurcation diagram, respectively.

In the case of asymptotic acting, dynamical analysis tools can be applied to distinguish between regular and irregular manners. For this purpose, the 0–1 test for chaos was applied. It is worth noticing that it was not possible to use the Lyapunov exponent characteristics since investigated model Eq. (31) is not differentiable. The outputs of the 0–1 test for chaos, denoted by K, returned a binary decision. More precisely, if K is close to 0, regularity appears (periodic, quasi-periodic), and if it reaches 1, an irregular pattern (chaos) is observable. Generally, K can be any number between -1 and 1 due to its definition. If the output of this test does not reach the previously mentioned detection values, the test is not relevant for numerous reasons: e.g. undersampling is needed [78], the trajectory is not in a steady state, or some type of intermittency appears. Note that this test was introduced by [79] (later on further developed [17, 80] and used on many different engineering type data [81, 82], as well as in continuous [83, 84] and discrete [24, 85] models).

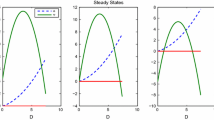
First of all, let us observe the dynamics of bank stock prices depending on the risk \(\rho _t\) for the fixed time t. Figure 4a depicts periodic evolutions for \(\lambda =1, a=2/3\), and the initial value \(v_0=18/25\). Conversely, Fig. 4b shows irregular progress for \(\lambda =1, a=0.9\), and \(v_0=0.61\). So, the risk \(\rho _t\) behaviour, from a dynamical point of view, is very rich.

Fig. 4
figure 4

Bank stock price dynamics with respect to the risk \(\rho _t\) for \(\lambda =1\) and a \(a=2/3\), \(v_0=18/25\)—regular case, b \(a=0.9\), \(v_0=0.61\)—irregular case

Full size image

In addition to the regular and irregular scheme, Fig. 5 shows transient evolution for \(\lambda =0.8, v_0=18/25\) and \(a=12/125\) (Fig. 5a), and \(a=112/125\) (Fig. 5b). Both of these evolutions correspond to homoclinic trajectories, with limiting values of 34 and 42.5 in Fig. 5a and b, respectively.

Fig. 5
figure 5

Transient trajectories of risk \(\rho _t\) for \(v_0=18/25\), \(t=5\), \(\lambda =0.8\), and a \(a=12/125\), b \(a=112/125\)

Full size image

Non-transient irregular (chaotic) evolvements are achieved in Fig. 6. Here, two qualitatively different progressions of \(\rho _t\) are given: in Fig. 6a, values of bank stock price are reached in two disjunct intervals, conversely to Fig. 6b, where values form just one band (Fig. 6a is constructed for system parameters \(v_0=18/25, \lambda =0.8, a=271/1000\) and Fig. 6b for \(v_0=18/25, \lambda =0.8, a=62/125\)).

Fig. 6
figure 6

Chaotic trajectories of risk \(\rho _t\) for \(v_0=18/25\), \(t=5\), \(\lambda =0.8\), and a \(a=271/1000\), b \(a=62/125\)

Full size image

On the contrary to the transience (that passes to regularity) shown in Fig. 5, gradual transient evolution in Fig. 8a and shock transient evolution in Fig. 8b are observed. In both cases, escaping from transience, irregular progress is achieved (in Fig. 8a, simulations were performed for the system parameters \(v_0=18/25, t=5, \lambda =0.6\), and \(a=461/1000\); in Fig. 8b for the parameters \(v_0=18/25, t=5, \lambda =0.6\), and \(a=501/1000\)). Corresponding to Fig. 8a and b, there are two bands in the bifurcation diagram in Fig. 9b. Consequently, we summarise:

Property 1

There are parameter settings of model Eq. (31) and initial conditions for which

  • transient or

  • non-transient

behaviours of the risk \(\rho _t\) progress appear.

Now, by varying one of the most important parameters a of the risk function \(\rho _t\), the orbit diagrams and bifurcation diagrams can be constructed. Recall that a corresponds to the skewness of the proportion of the bullish-bearish investors function representing market sentiments. Then, Figs. 2 and 3 show cycles or a tendency to a stable equilibrium, respectively.

In Fig. 7 results for \(\lambda =0.8\) are given, and in Fig. 9 for \(\lambda =0.6\). Call to mind that \(\lambda \) is the maximality parameter of \(\rho _t\) (in the underlined skew tent map, Eq. (18)), and its size effect is visible in the subinterval of a where chaos appears in (a), (b), and (c) of both Figs. 7 and 9.

Concretely, the intervals of diagram parameters corresponding to chaos are \(A_0=[0.2, 0.8]\) and \(A_1=[0.4, 0.6]\) in Figs. 7 and 9, respectively. It is clear that the length of \(A_0\) is greater than the length of \(A_1\), while \(\lambda \) is decreasing. This shrinking effect correlates to the core (e.g. the interval [f(f(1/2)), f(1/2)] of Eq. (18) for \(\lambda =1\) and \(a=1/2\)) of the skew tent map. In these intervals there are no transient evolvements. On the components, that is on \(C_0=[0,1]{\setminus } A_0=[0, 0.2]\cup [0.8, 1]\) and \(C_1=[0, 1]{\setminus } A_1=[0, 0.4]\cup [0.6, 1]\) for \(\lambda =0.8\) and \(\lambda =0.6\), respectively, transient behaviour is observable (see illustrative evolutions of the risk \(\rho _t\) in Figs. 5 and 8). As evident from Figs. 7c and 9c, \(\rho _t\) exhibits chaotic behaviour since K for \(a\in A_0\) or \(a\in A_1\), respectively, reach the value 1, while on the corresponding complements \(C_0\) and \(C_1\), where transience appears, a regular regime is asymptotically achieved since here K is close to 0. In these diagrams, the type of attractor (fixed point, connected band, or two portions of bands) is detectable (compare Figs. 7b with 6 and Figs. 9b with 8).

Hence, it can be concluded that:

Property 2

There are parameter settings of model Eq. (31) and initial conditions such that the bifurcation parameter a of risk \(\rho _t\) corresponds to

  1. 1.

    the regular evolution or

  2. 2.

    the irregular (chaos) progress.

Fig. 7
figure 7

Transient orbit diagram (a) and bifurcation diagram (b) of bank stock price varying a for \(v_0=18/25\), \(t=5\), and \(\lambda =0.8\). c Is the output of the 0–1 test for chaos related to (b)

Full size image
Fig. 8
figure 8

Trajectories of risk \(\rho _t\) for \(v_0=18/25\), \(t=5\), \(\lambda =0.6\), and a \(a=461/1000\)—transient to chaos, b \(a=501/1000\)—chaotic

Full size image
Fig. 9
figure 9

Transient orbit diagram (a) and bifurcation diagram (b) of bank stock price varying a for \(v_0=18/25\), \(t=5\), and \(\lambda =0.6\). c Is the output of the 0–1 test for chaos related to (b)

Full size image

4.3 Chaos control and anticontrol

As evident from the previous section, both transient and non-transient progress of the risk \(\rho _t\) can exhibit regular or chaotic patterns that can cause undesirable dynamics in a bank’s stock price.

By rewriting Eq. (29) we get

$$\begin{aligned} q(\rho _t) =\frac{d_t}{\xi ^\star n_t} \, , \end{aligned}$$
(34)

that is to say that the management team of a bank can influence investors’ perception of its risk, either by reducing debt or by increasing net assets.

For the model under consideration, the choice is between chaos suppression and chaos induction. For this purpose, let us consider the following difference equation:

$$\begin{aligned} x_{n+1}=F(x_n), \end{aligned}$$
(35)

and the related impulsive difference equation (introduced in [86]):

$$\begin{aligned} x_{n+1}={\left\{ \begin{array}{ll} F(x_n) &{}\textrm{if}~~ n \in \mathbb {N}\setminus T, \\ x_n+\psi &{}\textrm{if}~~ n \in T. \end{array}\right. } \end{aligned}$$
(36)

Typically, for chaos control/anticontrol, a constant injection quantity \(\psi \) is applied at every iteration \(n_i\) step with a periodic frequency \(T=\{n_i\}_{i\in \mathbb {N}}\) and \(n_i=i\Delta =\Delta , \, 2\Delta , \, 3\Delta , \, \dots \) (see, e.g. [29]).

Impulse control is only applied once in our case, in a consecutive finite number of iterations, reflecting the nature of the researched problem. That means \(T=\{t_k, t_{k+1}, t_{k+2}, \cdots , t_{k+l}\}\) where the time element injection index l determines when injections will be applied.

Chaos control is performed in Fig. 10. Here, the injection parameter \(\lambda \) is used (initially set as \(\lambda =1\)), and the injection value \(\Delta _{\lambda }\) varies from \(-\)0.4 to 0. In this regard, it should be noted that the primary component of Fig. 10a represents the range of \(\Delta _\lambda \) values between \(-\)0.3 and \(-\)0.4, where suppression is effective, resulting in the reduction of chaos to regular motion. Therefore, the crucial part is deliberately positioned at the beginning of the graph, preceding the chaotic cases that require a reversal of the axis order. Figure 10b displays the same ordering as Fig. 10a. The situation in Fig. 11 is similar to that of Fig. 10. The injection time index is set to \(T=[25, 50]\), and the reference parameter settings are \(v_0=0.61, a=0.9\), and \(t=5\). In Fig. 10a, for the reader’s convenience, two section planes (in red) are marked; they correspond to T where injections \(\Delta _{\lambda }\) are applied. As is visible, this procedure is successful for \(\Delta _{\lambda }\in [-0.4, -0.3]\); the case \(\Delta _{\lambda }=-0.3\) is highlighted in black. The transition from chaos to regularity (periodic in this case) is proved by the 0–1 test for chaos K; the transition border \(\Delta _{\lambda }=-0.3\) is highlighted in Fig. 10b. Here, the critical part of the 0–1 test for chaos K returns regularity for \(\Delta _{\lambda }\in [-0.4, -0.3]\). For \(\Delta _{\lambda } \in [-0.3, 0]\), the effect of suppression is negative or does not occur.

Conversely, if needed, chaos can be stimulated. In Fig. 11 (for the same parameter settings as in Fig. 10) chaos anticontrol (stimulation) is visible. Here, \(T=[15, 60]\) and \(\Delta _{\lambda } \in [-0.7, 0]\) where a successful stimulation effect on 100 iterations of the risk \(\rho _t\) is evident if \(\Delta _{\lambda } \in [-0.35, 0)\). The transition from cycles to chaos borders at \(\Delta _{\lambda }=-0.35\), as evidenced in Fig. 11b. Here, the critical part of the 0–1 test for chaos K returns chaos for \(\Delta _{\lambda }\in [-0.35, 0)\).

Property 3

There are system Eq. (31) parameters through which

  1. 1.

    the progress of the chaos of \(\rho _t\) can be controlled,

  2. 2.

    the regular evolution of \(\rho _t\) is stimulated to get chaos.

Fig. 10
figure 10

An illustration of how the application of a control can bring regularity into the dynamics: a a chaos control plot of the risk function \(\rho _t\) with a controlled \(\lambda \), b the output of the 0–1 test for chaos K related to (a). Notice that the \(\Delta _{\lambda }\) axis has been reversed, i.e. ordered from zero to negative values, to enhance the visibility of the results

Full size image
Fig. 11
figure 11

An illustration of how the application of an anticontrol can bring chaos into the dynamics: a a chaos anticontrol plot of the risk function \(\rho _t\) with a controlled \(\lambda \), b the output of the 0–1 test for chaos K related to (a). Notice that the \(\Delta _{\lambda }\) axis has been reversed, i.e. ordered from zero to negative values, to enhance the visibility of the results

Full size image
Table 1 ARIMA(1,1,1) model (Gaussian distribution)
Full size table
Fig. 12
figure 12

The ARIMA(1,1,1) model (blue dotted line) versus the actual Citigroup stock price time series (red continuous line)

Full size image
Fig. 13
figure 13

Equation (18) model (blue dotted line) versus actual data (red continuous line). Parameters \(\lambda = 0.3505\), \(a=0.2473\). Mean squared error (MSE) of the fitted model = 1.0131

Full size image

4.4 Real-world application and calibration of the model

To demonstrate how the suggested general framework might be implemented in the real world, we consider Eq. (21), firstly fitting the ARIMA model onto the stock price of Citigroup. Table (1) and Fig. 12 show the accuracy of the fitting, and the calibrated parameters.

Then, on the residuals of the ARIMA model, we calibrate Eq. (18) and obtain Fig. 13, thus confirming that the quality of the calibration is good.

5 Conclusion

In this article, through a classic macroeconomic equilibrium we have investigated how the price of bank’s stock varies according to market sentiments depending on investors’ perception of risk. However, unlike the classical approaches in the aforementioned equilibrium models, we assume that the market assessments and debt constraints are endogenous and dependent on risk. In our simulations, we have illustrated how the suggested specific methodology of so-called financial friction works. In particular, the suggested framework involves heterogeneous market dynamics ranging from equilibrium to limit cycles to chaotic dynamics. This is in agreement with empirical evidence showing that market variability can be either limited, or an extreme event that leads to financial disruption and turmoil.

In our analysis, we have proved that the equilibrium is intrinsically unstable [65] and that management and regulators have some levers in terms of chaos control policies they can put in place. Namely, these are indebtedness and net capital position. The ensuing risk/return profile affects market sentiment which, for us, is a decisive factor in determining market prices. Last but not least, we showed, by means of a real data-based test, that our framework conforms well to the historical dynamics taken into consideration.

Future research will compare a portfolio consisting of households, banks, and non-financial institutions with the proposed model. Additionally, Stoop [66] has explained that in cases of unstable or excessively noisy systems, limiters in the form of barriers are usually introduced to prevent the system from moving into undesired areas of the phase space. However, positioning the limiter around the maximal system response may not be optimal, whereas placing it near a period-one cycle tends to be more effective. As this approach requires a drastic intervention in the market, and arguably in the society as a whole, both investigating control over bounds and transparency of policymakers’ actions is worth considering.