1 Introduction

Chaotic scattering problems are important in nonlinear science since they appear in a wide variety of physical phenomena [1]. They often take place in open Hamiltonian systems [2], which are conservative systems characterized by a time-independent potential that exhibits different exits through which trajectories can escape towards infinity and never come back. Before escaping, trajectories can describe transient chaotic motions, so the characteristics of the escape (e.g., the escape times) have sensitive dependence on initial conditions. Furthermore, typical open Hamiltonian systems are nonhyperbolic [3], which means that chaotic saddles and KAM islands coexist in phase space. Since KAM islands are sets of initial conditions confined to invariant tori [4], trajectories belonging to a KAM island never escape. As the energy increases, the KAM islands are eventually destroyed once the system becomes hyperbolic. However, their path of destruction is quite complex and irregular, as shown in Refs. [5, 6].

In a previous manuscript [7], the authors have shown that the evolution of KAM islands exhibits four main metamorphoses insofar as the energy increases. These phenomena are characterized by a sudden fragmentation of the main KAM island, which in turn generates a decrease in its area. These metamorphoses have important consequences on the overall dynamical behavior of the system. In particular, the unpredictability increases as a consequence of a metamorphosis. In the context of chaotic scattering, we understand unpredictability as the difficulty in predicting the asymptotic behavior of a given initial condition. In the case of open Hamiltonian systems, the asymptotic behavior is the exit through which the trajectory escapes. Under this consideration, the basin entropy of the exit basins offers quantitative information about the unpredictability of a system (for further information see Ref. [7] and the references contained therein). The KAM islands appear embedded in the exit basins, forming compact regions of regular motion where a small perturbation in the initial condition cannot generate an escape. Therefore, KAM islands contribute to enhance the predictability of a system. A sudden reduction in the size of the KAM islands leads to an increase in the size of the basin, which constitutes the main obstruction to predictability. Therefore, a metamorphosis increases the unpredictability by reducing the size of the KAM islands. Since the metamorphoses affect the KAM islands, they do not appear within the hyperbolic regime, where the unpredictability of the system exhibits a monotonous decrease. Therefore, the different evolution of the unpredictability allows us to discern whether the regime is hyperbolic or nonhyperbolic.

In another vein, in a recent manuscript [8] the authors have demonstrated through computer-assisted proofs that typical Hamiltonian systems exhibit different types of bifurcations in their main families of periodic orbits. Since the KAM islands appear surrounding stable periodic orbits, we have conjectured that these bifurcations should be somehow related to the metamorphoses that appear within the nonhyperbolic regime of open Hamiltonian systems.

Confirming our conjecture, in this manuscript we show that the bifurcations of periodic orbits play an important role in these four metamorphoses. Although the metamorphoses are a consequence of the bifurcations, they do not occur for the same energy value. At each bifurcation, a chain of resonant islands and unstable periodic orbits is created around the main stable periodic orbit. Looking into an appropriate Poincaré section, we observe that the unstable fixed points corresponding to the unstable periodic orbits are connected through two smooth homoclinic orbits. In this situation, if the energy slightly increases, one of the homoclinic orbits becomes a homoclinic tangle, generating a metamorphosis where the KAM island fragments and its area is reduced. Depending on whether there is a single fixed point or several, the curve connecting them can be homoclinic or heteroclinic. Since the processes are identical in both situations, for the sake of grammatical simplicity, hereinafter we will refer the curve as homoclinic. Nonetheless, in cases where the nature of the curve is relevant, we will make a distinction between homoclinic and heteroclinic.

The organization of this paper is as follows. In Sect. 2, we describe the Hénon–Heiles system as a paradigmatic model in chaotic scattering. The explanations of the bifurcations and the metamorphoses that appear in the nonhyperbolic regime are shown in Sect. 3. Section 4 shows the different mechanism for which the metamorphoses take place. Besides, we generalize the previous results for a discrete system in Sect. 5. Finally, Sect. 6 summarizes the main results of this work and also provides some discussion of them.

2 Model description

In this work, we use as a paradigmatic model the Hénon–Heiles system [9] as in Refs. [7, 8]. This two-dimensional system is given by the following Hamiltonian:

$$\begin{aligned} {{\mathcal {H}}}=\frac{1}{2}(\dot{x}^2+{\dot{y}}^2)+\frac{1}{2}(x^2+y^2)+x^2y-\frac{1}{3}y^3. \end{aligned}$$
(1)

As a consequence, the equations of motion read:

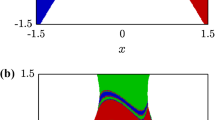
$$\begin{aligned}&\dot{x} = p_x, \nonumber \\&\dot{y} = p_y, \nonumber \\&\dot{p_x} = -x - 2xy , \nonumber \\&\dot{p_y} = -y - x^2 + y^2. \end{aligned}$$
(2)

Since there is no time dependence in the Hamiltonian function, the energy is a conserved quantity, \({{\mathcal {H}}}(x,y,p_x,p_y)=E\). Above the threshold \(E_e=1/6\), known as escape energy, the potential exhibits three symmetrical exits separated by an angle of \(2\pi /3\) radians, as can be seen in Fig. 1. For energies below \(E \approx 0.23\) the system is nonhyperbolic [7], so KAM islands appear in phase space. Therefore, this is the energy regime that interests us.

Fig. 1
figure 1

Isopotential curves of the Hénon–Heiles system for different values of the energy from \(E=0.01\) to \(E=0.5\). The color of the curves indicates the value of the energy, according to the color bar. For \(E<1/6\) the isopotential curves are closed, while for \(E>1/6\) the potential presents three symmetrical exits through which trajectories can escape towards infinity. (Color figure online)

Full size image

To visualize the four main metamorphoses in the Hénon–Heiles system, we show the evolution of the fraction \(f_k\) of initial conditions belonging to KAM islands as a function of the energy in Fig. 2. Metamorphoses are labeled with red dots. Although the nonhyperbolic regime remains until \(E\approx 0.23\), the last metamorphosis occurs at \(E=0.1947\), and the main KAM island loses its stability at \(E=0.2063\). Therefore, for \(E>0.2063\) only small scattered KAM tori can be found. Consequently, in Fig. 2 the maximum value of the studied energy is \(E=0.21\).

Fig. 2
figure 2

Fraction \(f_k\) of initial conditions belonging to a KAM island as a function of the energy of the Hénon–Heiles system. The red dots are located at four main metamorphoses where the size of the KAM islands decreases abruptly. (Color figure online)

Full size image

3 Bifurcations and metamorphoses

We have already mentioned that KAM islands undergo several metamorphoses that strongly affect the predictability of the system. Every KAM island surrounds a stable periodic orbit. However, it is known that in typical Hamiltonian systems these periodic orbits exhibit several bifurcations involving the creation of new stable and unstable periodic orbits [10]. According to the Poincaré-Birkhoff theorem [11, 12], the ratio of winding frequencies n/m of the new stable periodic orbits is a rational number (i.e., \(n,m \in {\mathbb {N}}\)). As a consequence, the stable orbits produce resonant islands around the main KAM island [13, 14]. In this section, we show that the bifurcations of periodic orbits play an important role in the metamorphoses of KAM islands and the subsequent effects on the dynamical behavior of the system.

Due to the triangular symmetry of the Hénon–Heiles system, its periodic orbits are also symmetric and can be obtained by following the systematic search for symmetric periodic orbits detailed in Ref. [15]. For completeness, we briefly explain the method here. Every symmetric periodic orbit must cross the y-axis perpendicularly. Any of the other symmetry axes could be also considered, but here for convenience we search for periodic orbits that are symmetric about the y-axis. Bearing this in mind, if a trajectory starts from \((0,y_0,\dot{x}_0,0)\) (we recall that \(\dot{x}_0=\sqrt{2E-y_0^2+2y_0^3/3}\) is fixed by the energy) and eventually it returns perpendicularly to the y-axis, then it is a symmetric periodic orbit. Periodic orbits appear in families of different multiplicity m, where m is the number of times the orbit crosses the y-axis before returning to it perpendicularly. Therefore, the period T of the symmetric periodic orbit is twice the time between perpendicular intersections.

Fig. 3
figure 3

Symmetric periodic orbits of the Hénon–Heiles system with \(E=0.2\). The multiplicity of the orbits is a \(m=1\) and b \(m=2\). The green (red) dots denote that the periodic orbit is stable (unstable) and are located at the perpendicular intersections of the periodic orbit with the y-axis. (Color figure online)

Full size image

To visualize the periodic orbits, we show in Fig. 3 two examples with multiplicities 1 and 2. The periodic orbit with \(m=1\) is unstable and belongs to a family of periodic orbits that loses its stability at \(E=0.1487<E_e\) (shown in Fig. 3a). The loss of stability occurs through a period-doubling bifurcation where two families of stable periodic orbits with \(m=2\) appear. These families are surrounded by the main KAM islands that appear within the open nonhyperbolic regime of the system, so hereinafter we will refer them as the main families. The periodic orbit of \(m=2\) (depicted in Fig. 3b) belongs to one of the main families.

The evolution of the KAM islands and the main family of periodic orbits as the energy increases can be conveniently represented in the (y, E) plane, as shown in Fig. 4. To generate this figure we consider \(\dot{y}=x=0\), so the initial conditions are launched perpendicularly to the y-axis. The main family of periodic orbits is represented in a different color depending on whether it is stable (green) or unstable (red). As we are above the escape energy, the KAM islands have been obtained from a grid of initial conditions where we have labeled the trapped trajectories in blue and the escaping trajectories in white. The horizontal dashed lines are located at the energy values where the metamorphoses occur. As we can see, the evolution of the KAM islands exhibits a fractal tree-like structure, where metamorphoses precede the appearance of self-similar branches. As we show in the next section, each branch corresponds to a resonant island that recedes into the chaotic sea, following its own path of destruction. For \(E=0.2063\), the main KAM island undergoes a period-doubling bifurcation where it becomes unstable, while two stable periodic orbits with \(m=4\) appear. For \(E=0.2105\), these two branches again undergo a period-doubling bifurcation where a total of 4 periodic orbits with \(m=8\) arise. This chain of period-doubling bifurcations continues until \(E=0.2111\), where all KAM islands associated with the main family are destroyed.

Fig. 4
figure 4

Evolution of the y coordinate of the main KAM island as a function of the energy of the Hénon–Heiles system. The solid line along the KAM island corresponds to the main family of periodic orbits. The color of the line indicates its stability, being green for stable and red for unstable. The horizontal dashed lines are located at the energy values where the metamorphoses occur. (Color figure online)

Full size image

In the following, we study individually the bifurcations of periodic orbits near the energy values where every metamorphosis occurs. The main branches of periodic orbits, overlapped with the KAM islands in the (y, E) plane, are depicted in Fig. 5. Each panel corresponds to a metamorphosis. The lower dark dashed line is located at the energy value where a bifurcation occurs, while the upper dark dashed line indicates the energy value of the metamorphosis.

Fig. 5
figure 5

Bifurcation diagrams showing the main bifurcations of the family of stable periodic orbits with \(m=2\), for energy values close to the a first, b second, c third, and d fourth metamorphosis. The color of the curves indicates the stability of the periodic orbits, being red for unstable and green for stable. The lower dashed line indicates the bifurcation that precedes the metamorphosis, which is indicated by the upper dark dashed line. For comparison purposes, the KAM islands are represented in blue color in the background of the image. The red dashed line appearing in panel (d) represents a bifurcation that is not directly associated with any of the metamorphoses. (Color figure online)

Full size image

The first metamorphosis (Fig. 5a) occurs for \(E=0.1721\) and is preceded by a period-doubling island chain bifurcation for \(E=0.1689\). This bifurcation is characterized by the creation of a chain of periodic orbits of double period around the main family, that does not change its stability (see [15] for a description of the main bifurcations of periodic orbits in Hamiltonian systems). In this case, 3 stable and 3 unstable periodic orbits of double period (\(m=4\)) appear. From these 6 periodic orbits, only two stable branches appear in the figure since the rest do not fall into our Poincaré section. Therefore, this representation allows us to detect the energy value where a bifurcation occurs, but for a deeper understanding and visualization of the bifurcations we must resort to Poincaré sections in the \((y,\dot{y})\) plane, as we show in the next section. On the other hand, the second metamorphosis (Fig. 5b) occurs for \(E=0.1771\) and is preceded by a period-quintupling island chain bifurcation for \(E=0.1754\). Therefore, one unstable and one stable periodic orbit emerge at the bifurcation point, each one with quintuple period (\(m=10\)).

The third metamorphosis (Fig. 5c) occurs for \(E=0.1846\) and is preceded by a saddle-node bifurcation for \(E=0.1844\), where a pair of stable and unstable periodic orbits with \(m=8\) are created. This bifurcation is not strictly a bifurcation of the main family, since the new periodic orbits are not created at the same location of the main stable periodic orbit. The third metamorphosis also differs from the others for another reason: it corresponds exactly to a bifurcation. For \(E=0.1846\) the main family undergoes a fourth-order touch-and-go bifurcation. When the energy is increased from \(E=0.1844\), the newly created unstable periodic orbits approach the main family and they “bounce,” after which they appear rotated an angle of \(\pi /2\) radians. This rotation generates that none of them fall in the \(x=0\) and \(\dot{y}=0\) Poincaré section, so they disappear from our diagram.

Fig. 6
figure 6

KAM islands in the \((y,\dot{y})\) Poincaré section for values of the energy near the first (a–c) and second (d–f) metamorphosis. Green (red) dots indicate the position of elliptic (hyperbolic) fixed points. Homoclinic (e, f) and heteroclinic (b, c) orbits are represented with dark dots and labeled as \(H_1\) and \(H_2\). In all panels, the main stable fixed point is separated from the chaotic sea by a last KAM curve, labeled as \(L_K\). Finally, the red dashed line indicates \(\dot{y}=0\), which is the line on which we have computed the periodic orbits. The value of the energy is a 0.1689, b 0.1715, c 0.1735, d 0.1753, e 0.1766, and f 0.1780. (Color figure online)

Full size image

Finally, the fourth metamorphosis (Fig. 5d) occurs for \(E=0.1947\) and is preceded by a saddle-node bifurcation for \(E=0.1945\). At the bifurcation point, three pairs of stable and unstable periodic orbits with \(m=2\) are created. Similar to the previous case, the newly created unstable periodic orbits approach to the main family. However, here the metamorphosis does not correspond to a bifurcation. After the metamorphosis has occurred, the unstable periodic orbits continue approaching to the main family. Once the energy reaches \(E=0.1967\), a third-order touch-and-go bifurcation occurs (see red dashed line in Fig. 5d). After the bifurcation, the unstable periodic orbits appear rotated an angle of \(\pi \) radians. At the bifurcation point the area of the main KAM islands is momentarily zero.

4 The mechanism explaining the metamorphoses

The results of the previous section served as numerical evidence for the complex set of bifurcations exhibited by the main family of periodic orbits. It is clear that the metamorphoses take place for energy values close to the bifurcations. However, the bifurcations are not directly responsible for the metamorphoses, but they provide the system with the chains of periodic orbits involved in the process. To shed light on the mechanisms explaining the metamorphoses, we study in this section the structure of KAM islands in both situations before and after the bifurcations and the metamorphoses.

The results are shown in Figs. 6 and 7, where the main KAM island is represented in the \((y,\dot{y})\) Poincaré section for different values of the energy. Each vertical series of panels corresponds to the KAM island before the bifurcation, after the bifurcation, and after the metamorphosis. Panels (a–c) and (d–f) in Fig. 6 correspond to the path to the first and second metamorphosis, respectively. On the other hand, panels (a–c) and (d–f) in Fig. 7 correspond to the path to the third and fourth metamorphosis, respectively. Red (green) dots denote unstable (stable) fixed points, that correspond to crosses of periodic orbits with the Poincaré section. The red dashed line is located at \(\dot{y}=0\), so it corresponds to the line on which we compute the periodic orbits. Only the fixed points that fall on the line \(\dot{y}=0\) are detected by the algorithm for computing periodic orbits. Therefore, only the fixed points with coordinate \(\dot{y}=0\) appeared in the bifurcation diagrams of Fig. 5.

Fig. 7
figure 7

KAM islands in the \((y,\dot{y})\) Poincaré section for values of the energy near the third (a–c) and fourth (d–f) metamorphosis. Green (red) dots indicate the position of elliptic (hyperbolic) fixed points. Homoclinic (b, c) and heteroclinic (e, f) orbits are represented with dark dots and labeled as \(H_1\) and \(H_2\). In all panels, the main stable fixed point is separated from the chaotic sea by a last KAM curve, labeled as \(L_K\). Finally, the red dashed line indicates \(\dot{y}=0\), which is the line on which we have computed the periodic orbits. The value of the energy is a 0.1842, b 0.1845, c 0.1850, d 0.1945, e 0.1947, and f 0.1950. (Color figure online)

Full size image

The mechanism that explains the metamorphosis is the same for all cases. Before the bifurcation, there is a single stable fixed point surrounded by KAM tori (see Figs. 6a, d and 7a, d). After the stable fixed point undergoes a bifurcation, a chain of stable (elliptic) and unstable (hyperbolic) fixed points surrounding the main stable fixed point appears (see Figs. 6b, e and 7b, e). Each elliptic point generates a resonant island. On the other hand, the stable and unstable manifolds of the hyperbolic points are smoothly connected, generating in each case two different homoclinic or heteroclinic orbits. In Figs. 6e and 7b there is only one hyperbolic point with quintuple and quadruple period, respectively, so the orbits are homoclinic. In Figs. 6b and 7e there are three hyperbolic points of double and same period of the main stable point, respectively. Therefore, in these cases the connection orbits are heteroclinic.

In all these situations, the homoclinic orbits are represented in the figures with dark dots. As we can see, one homoclinic orbit, labeled as \(H_1\), surrounds the resonant islands, while the other, labeled as \(H_2\), surrounds only the main elliptic point. Therefore, the resonant islands are completely surrounded by homoclinic orbits. Furthermore, they are inside the structure of the main KAM island, that is separated from the chaotic sea by a last KAM curve, labeled as \(L_K\). There is a complicated structure inside the last KAM curve. In addition to the KAM curves and the main resonant islands, the destruction of small islands has generated an inner chaotic domain. Being in this situation, if we slightly increase the energy, the stable and unstable manifolds of the hyperbolic fixed points intersect one another transversally at an infinite number of points. Therefore \(H_1\) becomes a homoclinic tangle and a metamorphosis occurs.

Without the “protection” provided by the smooth nature of \(H_1\), part of the structure of the KAM island is broken and the inner and outer chaotic domains merge. Now, the last KAM curve is defined by \(H_2\) and the resonant islands, once confined inside the last KAM curve, are located in the chaotic sea, as shown in Figs. 6c, f and 7c, f. As a matter of fact, a large number of initial conditions whose trajectories were confined inside the last KAM curve, now generate trajectories that move in the chaotic sea and eventually escape from the scattering region. This abrupt change in the structure of the KAM island is what generates the metamorphosis. Briefly, the mechanism explaining the metamorphoses is the transition of a homoclinic orbit, which changes from smooth to a homoclinic tangle. The consequence is a reduction of the fraction of initial conditions whose trajectories do not escape from the scattering region. The fragmentation of the structure of the KAM island converts extensive regions of regular behavior into chaotic regions. If we continue increasing the energy, the resonant islands move away from the main island, each of them exhibiting the same metamorphoses of the main island. For example, the resonant islands shown in Fig. 6c just experienced the second metamorphosis. This process is what generates the branches that can be observed in Fig. 5. Since the resonant islands exhibit the same metamorphoses as the main island, the tree-like structure is self-similar.

This process does not occur just four times, but infinite metamorphoses take place, involving a different number of resonant islands and hyperbolic fixed points. Nevertheless, most of these processes do not significantly affect the area of the KAM islands, so they are not responsible from abrupt changes on the overall dynamical behavior of the system. Note that the four main metamorphoses are related with the biggest chains of islands created at the lowest resonances (\(m=2\) creating 6 islands due to the symmetry of the system, \(m=3,4\), and 5.)

After the fourth metamorphosis (Fig. 7f), the three hyperbolic points approach the main elliptic point until a collision that generates a third-order touch-and-go bifurcation. After the bifurcation the island appears rotated an angle of \(\pi \) radians, as shown in Fig. 8. For higher energy values, the main KAM island continues its path of destruction characterized by a period-doubling cascade.

Fig. 8
figure 8

KAM islands in the \((y,\dot{y})\) Poincaré section for values of the energy a before (\(E=0.1966\)) and b after (\(E=0.1968\)) the third-order touch-and-go bifurcation. Green (red) dots indicate the position of elliptic (hyperbolic) fixed points. The heteroclinic orbit, which coincides with the last KAM curve, is represented with dark dots. The red dashed line indicates \(\dot{y}=0\), which is the line on which we have computed the periodic orbits. (Color figure online)

Full size image

5 Results for a discrete dynamical system

The above results have been obtained in the context of chaotic scattering in open Hamiltonian systems. However, KAM islands appear in a wide variety of conservative systems, so the metamorphoses could play an important role in different physical situations. In general, the presence of KAM islands has deep implications on the global properties of the system, such as transport [16] and decay correlations [17].

To reveal the generality of these results, and in particular to show that the four metamorphoses are ubiquitous in conservative systems, we have carried out an analysis of the evolution of the KAM islands in the standard map [18], which is a two-dimensional discrete dynamical system whose equations are given by:

$$\begin{aligned} \theta _{n+1}&= \theta _n + J_{n+1} \quad \text{ mod }\,2\pi ,\nonumber \\ J_{n+1}&= J_n + K\sin {\theta _n}, \end{aligned}$$
(3)

where \(K>0\) is a constant whose effect is to increase the intensity of the nonlinear perturbation. The modulo operation is necessary as the coordinate is cyclic.

For \(K<4\) the standard map has a main KAM island around a stable periodic orbit located at \((\theta ,J)=(\pi ,0)\). For \(K=4\) the main periodic orbit undergoes a period-doubling bifurcation where it loses its stability and two stable periodic orbits of double period appear. This bifurcation is equivalent to the one that occurs in the Hénon–Heiles system for \(E=0.1487\), so for comparative purposes here we focus our attention on one of these two new main KAM islands existing for \(K>4\). We represent the fraction \(f_k\) of the plane \((\theta ,J)\) that is occupied by KAM islands as a function of the parameter K in Fig. 9. This figure is qualitatively identical to Fig. 2 and exhibits four metamorphoses (red dots in the figure).

Fig. 9
figure 9

Fraction \(f_k\) of initial conditions belonging to a KAM island as a function of the parameter K of the standard map \(\theta _{n+1} = \theta _n + J_{n+1}\) (mod \( 2\pi \)); \(J_{n+1} = J_n + K\sin {\theta _n}\). The red dots are located at four metamorphoses where the size of the KAM islands decreases abruptly. (Color figure online)

Full size image
Fig. 10
figure 10

Main KAM island and resonant islands in the standard map \(\theta _{n+1} = \theta _n + J_{n+1}\) (mod \( 2\pi \)); \(J_{n+1} = J_n + K\sin {\theta _n}\) for values of the parameter K immediately after the a first (\(K=4.65\)), b second (\(K=4.83\)), c third (\(K=5.12\)), and d fourth (\(K=5.57\)) metamorphosis. Green (red) dots indicate the position of elliptic (hyperbolic) fixed points. Homoclinic (a, c) and heteroclinic (b, d) orbits define the last KAM curve and are represented with dark dots. (Color figure online)

Full size image

The metamorphoses that can be observed in Fig. 9 are preceded by the same type of bifurcations as the case of the Hénon–Heiles system. The mechanism explaining the metamorphoses is also identical. To show this, in Fig. 10 we represent the main KAM island for values of K immediately after the metamorphoses. As in the Hénon–Heiles system, the chains of resonant islands move away in the chaotic sea after the formation of the homoclinic tangle. Although Fig. 10 and panels (c, f) in Figs. 6 and 7 have been obtained in different systems, it is clear that they correspond to the same phenomenon. This fact suggests that, regardless of the system, the chains consisting of 3, 4, 5 and 6 resonant islands are always the main ones involved in metamorphoses. Chains with different number of resonant islands do not affect noticeably the size of the KAM islands.

6 Conclusions and discussion

In summary, in this work we have elucidated the mechanisms that explain the four main metamorphoses appearing within the nonhyperbolic regime of open Hamiltonian systems. Before each metamorphosis, a bifurcation takes place at or near the main family of stable periodic orbits. We have characterized these bifurcations, which correspond to period-doubling island chain, period-quintupling island chain and saddle-node types. After the bifurcation, a chain of resonant islands and unstable fixed points appear inside the structure of the main KAM island. As long as the homoclinic orbits connecting the unstable fixed points (periodic orbits) are smooth, the resonant islands and the inner chaotic domain coexist harmonically inside the main KAM region, which is delimited by a last KAM curve. The metamorphoses correspond to the formation of a homoclinic tangle that breaks the internal structure of the KAM island. As a consequence, the inner and outer chaotic domains join, and the resonant islands recede in the chaotic sea. This phenomenon generates an abrupt decrease in the area of the KAM islands, and therefore an increase in the area occupied by the chaotic regions. The main numerical evidence supporting our findings is based on bifurcation diagrams and on detailed representations of KAM islands, fixed points, and homoclinic orbits for energy values close to the metamorphoses.

We have shown our results in the Hénon–Heiles system, which is a paradigmatic example of two-dimensional time-independent Hamiltonian system. Likewise, we have generalized the results using the standard map, which is a general two-dimensional area-preserving map. Therefore, we expect that the mechanisms discussed here may appear in many different systems and physical situations. For example, the existence of KAM islands is a necessary condition for plasma confinement in tokamaks [19]. On the other hand, the stickiness phenomenon [20, 21] is relevant in chaotic transport of particles advected by fluid flows [22] and in conductance fluctuations in chaotic cavities [23], among other physical phenomena. Regardless of the possible applications, we hope that this work could contribute to the general understanding of the effects of KAM islands in Hamiltonian systems.