1 Introduction

With the second wave of Covid-19 turning grim in third world, lower-middle-income countries like India, where numbers of infected cases and deaths per day until 12 May 2021 are reaching record highs of 0.4 million and 4000, respectively [38]; it is the urgent requirement for an efficient mathematical tool to model and analyse epidemics and pandemics to predict their future course of outbreak and help develop rapid control strategies. To add to this is the spread of another growing epidemic of a rare fungal infection Mucormycosis or the ‘Black fungus’ typically infecting Covid-19 recovered patients as reflected by the exponential surge of 9000 cases reported in India by May 2021 [12, 16, 19]. Since interactions among the species in a pandemic have a greater complexity, it is difficult to solve their models that describe the disease analytically. Henceforth, formulating the model mathematically with a suitable tool that can imitate the disease more accurately helps in detecting its behavioural dynamics [58].

A chaotic propagation of a pandemic is characterised by extreme sensitivity to slight variation in initial conditions (ICs) of physical factors such as rise in the number of asymptomatic carriers, number of infected cases and small increase in the number of undetected cases.[82]. While studying a novel ongoing pandemic, chaos theory has been a powerful approach to define, model and analyse the exponentially propagating dynamics and extracting the underlying deterministic component by taking into account crucial factors as: variables relevant for the pandemic, equations that govern these variables, parameter values, constraints of the model and reformulation of the equations based on existing observations [53].

In order to determine whether the dissemination of a pandemic is chaotic, the following criteria may be taken into account [39]:

  1. 1.

    Aperiodicity, i.e. multiple solutions of the pandemic model exist, such that no two solutions repeat,

  2. 2.

    Sensitive, i.e. the epidemic is highly sensitive and give rise to divergent dynamics on a slight change of physical factors,

  3. 3.

    Long-term unpredictability, i.e. the propagation of the pandemic is unexpected and cannot be foreseen from one point to another,

  4. 4.

    Determinism, i.e. the outcome, amount and rate of spread, is determined by real changes in the physical conditions of the system.

Chaotic behaviour of pandemics have been extensively reported in low-mid-income countries such as, Plague epidemic in Bombay, India [51], chaotic epidemic crisis management in Mexico [72], Ebola Virus epidemic in Guinea, Liberia and Sierra Leone [52] and Dengue in Pakistan [4]; a brief review of this is given in the next section.

1.1 A brief review on impact of chaos on prominent epidemics

This section surveys some prominent epidemics that reveal chaotic dispersal.

  1. 1.

    Plague epidemic, India (1896–1911)

The Bombay epidemic, India, has been one of the earliest closely monitored diseases to have been recorded for investigating its causes, effect and control. The bubonic plague in 1896 did not stay confined to Bombay alone, it hit all over India [62]. The bacillus Yersinia Pestis, causing the bubonic plague, develops buboes in the infected, along with other symptoms such as fever, vomiting, bleeding and organ failure.

Impact of chaos (IOC): The earlier models of the bubonic plague [7] assume that a single species of rat and flea is responsible for the bubonic plague progression, and thus human infections are modelled as a by-product of rat infections. On the contrary, multiple epizootics of rats such as Mus decumanus and Mus rattus are reported to have caused the bubonic plague [61]. In 2015, a new model of plague, proposed in Mangiarotti [51] that took into account multiple epizootics of rats, led to the finding that the progression of the disease is chaotic in nature.

  • 2. Spanish flu (1918–1920)

The Spanish flu is one of the first global pandemic reported to have occurred in the era of modern medicine where the nature and course of the disease were studied as it unfolded [35]. The H1N1 strain of the influenza virus activates a cytokine storm which damages the immune system. With a mortality rate of 20%, this pandemic is said to have killed more than 100 million people, hampering the economy during the World War I.

IOC: Though chaotic dynamics of the Spanish Flu is not extensively reported, however Upadhyay et al. [79] reports that such influenza epidemics have bidirectional spread and are characterised by wave of chaos in a dominant mode.

  1. 3.

    HIV AIDS (1980–…)

The early eighties gave birth to a gradually growing pandemic of HIV/AIDS [35]. According to the recent WHO report, 76 million people have been infected with the HIV epidemic so far, 33 million have lost their lives and 38 million are presently infected by the end of 2019.

IOC: Bairagi et al. [8] reports that self-proliferation of host cells in non-delayed HIV models has chaotic immune response. Chaos is responsible for considerable fluctuations in host cells count in blood plasma of HIV patients.

  1. 4.

    Smallpox outbreak (1972)

The smallpox epidemic killed hundreds of millions of people up till the twentieth century with a mortality of 30%. Smallpox was eradicated in 1960s with mass vaccination on a global scale. However, the former Yugoslavia in 1972 saw a new wave of outbreak of smallpox. Though this outbreak was controlled within two months with mandatory revaccination, containment zones, quarantine measures, sealed borders and travel ban, yet it is significant for the research community to study the course of the outbreak as it marked the reappearance of an already eradicated epidemic.

IOC: Chaotic phenomenon has been reported to exist in smallpox epidemic models [29, 70]. Though smallpox is eradicated, however, its reappearance may be possible. As a result, Seward et al. [70] have devised an algorithm to supervise clinical and public health responses with respect to suspected smallpox cases.

  1. 5.

    Swine flu pandemic (April 2009–May 2010)

The Swine flu outbreak in Mexico in 2009, considered as a reprise of Spanish flu pandemic of 1918, rose steeply to pandemic proportions within weeks [77] infecting over 10% of the world population [26]. It was caused by H1N1 strain of the influenza virus.

IOC: The propagation of the epidemic in terms of chaotic waves is modelled in Upadhyay et al. [79], where conditions for Hopf and Turing bifurcations are evaluated. The reported models suggest that the Swine Flu epidemic has a complex dynamics of spatial spread through chaotic waves. Also the H1N1 flu strain can propagate both in forward and backward direction, i.e. the spread of influenza is bidirectional and that chaos phenomenon is an intrinsic property of dissemination of this epidemic.

  1. 6.

    Ebola virus epidemic (2013–2016)

The epidemic of the Ebola virus disease (EVD) appeared in Guinea, December 2013, from which it extended rapidly to Liberia and Sierra Leone and proved lethal until 2016. According to WHO database, the case fatalities rose till 90%. Ebola-Zaire, one of the five species of the Ebola virus, is responsible for infecting with a dangerous mortality rate of 70% [52].

IOC: The complex dynamical behaviour of the EVD epidemic, particularly in the middle stage of uncontrolled rapid propagation has been effectively defined by a chaotic model [52]. The chaotic model is derived from observational data released by WHO, and depicts that the diversified key parameters are difficult to be predicted and are dependent on the slightest change in ICs. This indicates that an uncontrolled case of chaos may result in an exponential rise in the number of infections and fatalities.

  1. 7.

    Cancer epidemic

As per WHO, cancer, one of the leading causes of death, is accounted for 9.6 million deaths in 2018 alone globally, with statistics of one in six deaths due to cancer. Cancer may be caused by chemical carcinogens such as drinking arsenic contaminated water and alcohol and smoking tobacco; physical carcinogens, such as being subjected to ultraviolet radiation; and biological carcinogens such as obesity, lack of physical activity or infections from viruses, bacteria etc. Recent literature reports studies on various forms of cancer epidemics, such as lung cancer epidemic [63], virus-related head and neck cancer epidemic [55] and liver cancer epidemic [23].

IOC: Itik and Banks [36] first reported the explicit existence of chaos in Cancer epidemic. Cancer models have been found to display deterministic chaos giving birth to complex oscillations indicative of long-term tumour relapse (Khajanchi et al., 2018) through period doubling route and Hopf bifurcations.

  1. 8.

    Dengue epidemic

WHO reports severe dengue epidemics re-emerged in 1950s in the South Asian countries of Philippines and Thailand with a comparatively recent outbreak in Singapore, 2005 [59]. Dengue is a mosquito-borne viral epidemic infecting 3.9 billion people in 128 countries, killing more than 20,000 people in 2012 [18].

IOC: Chaos results in high seasonality and complexity in the Dengue models [56]. This explains the irregular fluctuations in the empiric outbreak data of the Dengue epidemic [2]. Also, it is discovered that temporary cross-immunity expands the parameter range of chaotic dynamics leading to coexisting attractors [2] eventually causing multiple routes to chaos in Dengue epidemic models.

  1. 9.

    Cholera epidemic

The epidemic of Cholera first appeared in India in 1817 [24] and later spread to 52 countries infecting 4.3 million people worldwide. Cholera quickly spreads in densely populated areas with poor water sanitation. The prime symptoms of infection are severe watery diarrhoea, vomiting, body ache, fall in blood pressure, kidney failure, and if untreated may lead to death within 24 h [73].

IOC: Righetto et al. [68] have reported that the spread of cholera is chaotic with increasing values of the degree of seasonality. Parameter estimation and sensitivity analysis reveal the deterministic behaviour of the Cholera epidemic model [10].

  1. 10.

    Covid-19 pandemic

The most lethal of pandemics recently known with a deadly rate of exponential dissemination is the Coronavirus disease that broke out in 2019 (Covid-19). Jones and Strigul [39] considered global data set from 22 January to 30 May 2020, corresponding to 267 countries and have suggested that COVID-19 manifests the major qualitative characteristics of a chaotic system.

IOC: The vital factors for modelling Covid-19 pandemic such as number of confirmed cases per day, number of critical cases under intensive care per day and the cumulated number of fatalities per day have been found to interact chaotically [53]. The fractal dimension and the phase portrait analyses carried out in [31] reveal that Covid-19 is chaotic in nature. In fact, application of chaos theory to model Covid-19 is reported to be a promising tool in decision-making, thereby helping in tracking the effectiveness of control measures especially in countries where the number of cases are relatively low and rapid enforcement of control measures need to be adopted to prevent a catastrophic evolution of the pandemic [39].

1.2 Fractional-order (FO) dynamics of chaotic epidemic models

The literature survey carried out in previous section indicates that the modelling of epidemics is confined to IO models (IOMs) which often fail to encompass in-depth understanding of the dynamics of the epidemic such as contribution of asymptomatic transmission, range of unpredictability, critical cases with comorbidities and effect of past history of data. [41]. These limitations can be overcome by incorporating the extraordinary advantages of FO models (FOMs) in modelling real physical phenomena and improving control performance. The differences between FOM and IOM are as follows:

  1. 1.

    FO derivative being a non-ideal operator can incorporate non-ideal, i.e. non-integer values along with integer values, unlike models governed by IO derivatives which can incorporate only ideal, i.e. IO values.

  2. 2.

    FO derivative being a non-local operator has the capacity to store infinite memory of the past values calculated until the present time, unlike IO derivative which is a memory-less operator.

  3. 3.

    The FO parameter of FO derivatives is an additional parameter that grants the control engineers flexibility to incorporate more constraints for an efficient design.

  4. 4.

    The FO controllers have a larger stability region [25] and robustness [50] against plant uncertainties compared with IO controllers.

The solutions to the diffusion equation with fractional-order propagation are obtained at a quicker rate than the ordinary diffusion equation and may be asymmetric [30]. The FO chaotic epilepsy model proposed by Tene et al. [76] reported that the FOM induces faster synchronisation than IOM. Jan et al. [37], proposed the FOM of Dengue epidemic and found that the additional properties of heredity and memory effects of fractional calculus provide more realistic information about Dengue transmission through asymptomatic carriers. Recently, FOMs of Diabetes, HIV, Dengue, Migraine, Parkinson’s and Ebola Virus diseases proposed in Borah et al. [12, 16] revealed inherent unobserved dynamics as the FO varies. FOMs have lesser error compared to IOMs while delivering a closer fit to real data [65, 66]. As the propagation of COVID-19 is chaotic with long-range memory, it is essential to use a memory-enabled tool to model it. We blend the superior merits of fractional calculus with chaos theory [13, 14] to derive an adequate mathematical model, which behaves as close as possible to the practical epidemic.

1.3 Control of chaos in mathematical models of epidemics

This section presents a brief review on existing control strategies to stabilise and synchronise chaos in the mathematical models of epidemics as given in Table 1.

Table 1 Recent survey of control methods applied to epidemics modelled using chaos theory
Full size table

A state-dependent impulsive feedback controller is proposed [64] to regulate the spread of infectious epidemics like SARS, Dengue and Zika virus. Zhang et al. [86] have reported that an epidemic converges to a disease-free periodic solution if its threshold dynamics is controlled via reproduction number \({R}_{o}\). He and Banerjee [33] proposes a hard limiter controller to mitigate the dissemination of common influenza and H1N1 influenza epidemic. Seasonal outbreak of these types of infectious diseases is a natural phenomenon, so it is important to study epidemic models with seasonal fluctuation [85]. The hard limiter controller is applied to an epidemic model with seasonality and external noise, and it was found that variation in parameters such as temporary immunity rate, seasonality degree, noise degree and fractional order induce high sensitivity resulting in a chaotic model. For smaller values of the limiter, the system tends to a periodic system or a stable system, i.e. the disease tends to vanish. The dissipative control strategy [22] for a susceptible, infected and recovered (SIR)-type descriptor epidemic system like HBV (Hepatitis B virus) with nonlinear incidence rates bound by fuzzy characteristics is designed to control the change in the birth rate of population in the epidemic model to suppress chaos. A robust H∞ controller [21] is designed for discrete SI-type epidemic model with nonlinear incidence rates where the intrinsic birth rate is varied so that chaotic responses of the states of susceptible and infected in the epidemic disappear. A tracking controller [84] is designed such that the percentage of infective disease converges to zero to stabilise chaos in the epidemic model. Similarly, the tracking controller for stabilising hyperchaos in SEIR-type epidemic system with nonlinear transmission rate is designed in Yi et al. [83]. Active control method is proposed in Ansari et al. [6] such that the error states which are functions of susceptible, infected and information variables converge to zero [40] and thereby synchronisation is accomplished. Tan et al., [74] and Zhang et al. [85] propose a feedback control technique applied to SIR-type epidemic model with seasonal fluctuations for H1N1 and common influenza where Neimark-Sacker bifurcation period doubling route to chaos is discovered.

Some other control strategies such as optimal control based on two time-dependent control variables, viz insecticide use and vaccination [10] and predictive control strategy to determine the time and duration of social distancing policies [32], have been applied to Cholera epidemic, Dengue epidemic [4] and Covid-19 pandemic, respectively. However, they are all confined to IOMs only.

This paper aims to bridge the research gap between:

  1. 1.

    application of FO chaos theory to model pandemic propagation dynamics (chaotic and non-chaotic) that are not captured by IOMs,

  2. 2.

    application of FO strategies in controlling and synchronising these chaotic epidemic models to a disease-free equilibrium.

2 Fundamentals of FO calculus for modelling and control

The modelling of the epidemics and design of controllers to attain synchronisation is determined by FO stability theorems whose preliminaries are presented below.

The Caputo fractional derivative of order α of a continuous function \(f(t)\) is defined as in (1).

$$ D_{t}^{\alpha } f\left( t \right) = \frac{{{\text{d}}^{\alpha } f\left( t \right)}}{{{\text{d}}t^{\alpha } }} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{\Gamma \left( {w - \alpha } \right)}}\mathop \int \limits_{0}^{t} \frac{{f^{{\left( w \right)}} \left( \tau \right)}}{{\left( {t - \tau } \right)^{{\alpha - w + 1}} }}{\text{d}}\tau ,} \hfill & {w - 1 < \alpha < w,\,\,~w \in N} \hfill \\ {\frac{{{\text{d}}^{w} }}{{{\text{d}}t^{w} }}f\left( t \right),} \hfill & {\alpha = w~} \hfill \\ \end{array} } \right. $$
(1)

Let us define an FO nonlinear system (FONLS) as in (2),

$$ D_{t}^{\alpha } x\left( t \right) = f\left( {x\left( t \right),t} \right) $$
(2)

where the FOs lie in \(0 < \alpha < 1 \) and \(x\left( t \right) = \left[ {x_{1} , x_{2} , \ldots , x_{n} } \right]^{T} ,f\left( { x\left( t \right),t} \right) = \left[ {f_{1} \left( {x\left( t \right)} \right), f_{2} \left( {x\left( t \right)} \right), \ldots , f_{n} \left( {x\left( t \right)} \right)} \right]^{T} \left( {i = 1,2, ..., n} \right)\).

Theorem 1

([20]). The equilibrium points of a commensurate FONLS are asymptotically stable if for all the eigenvalues \(\lambda_{i} , \left( {i = 1, 2, . . ., n} \right)\) of the Jacobian matrix \(J = {\raise0.7ex\hbox{${\partial f}$} \!\mathord{\left/ {\vphantom {{\partial f} {\partial x}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\partial x}$}}\), where \(f = \left[ {f_{1} ,f_{2} , ...,f_{n} } \right]\)T, evaluated at the equilibrium point, satisfy the condition: \(\left| {{\text{arg}}\left( {{\text{eig}}\left( J \right)} \right)} \right| = |{\text{arg}}\left( {\lambda_{i} } \right)\left| \right\rangle \alpha \pi /2, i = 1,2, \ldots ,n\).

Lemma 1

([3, 15]). If \(x\left( t \right) \in {\mathbb{R}}\) is a continuous and derivable function, then, for any time instant \(\ge 0\),

$$ \frac{1}{2}D^{\alpha } x^{2} \left( t \right) \le x\left( t \right)D^{\alpha } x\left( t \right), \quad \forall \alpha \in \left( {0,1} \right] $$

where \(D^{\alpha } x\left( t \right)\) is the Caputo fractional derivative of \(x\left( t \right)\) of FO \(\alpha\).

2.1 Computation of the fractional-order differential equations (FODEs)

The Adams–Bashforth–Moulton method established on the predictor–corrector technique [27] is used to solve the FODEs. The FONLS (2) may be written in a Volterra integral equation as in (3),

$$ x_{i} \left( t \right) = x_{i} \left( 0 \right) + \frac{1}{\Gamma \alpha }\mathop \smallint \limits_{0}^{t} (t - \tau )^{\alpha - 1} f_{i} (x_{1} ,x_{2} , \ldots ,x_{n} ){\text{d}}\tau $$
(3)

where \({x}_{i}\left(0\right)\) are ICs of \({x}_{i}(t)\).

The corrector equation obtained by substituting \(h=\frac{T}{N}, {t}_{n}=nh\), for \((n={0,1},\dots ,N)\) for a unique solution in \([0,T]\) is as in (4).

$$ x_{ih} \left( {t_{n + 1} } \right) = x_{i} \left( 0 \right) + \frac{{h^{\alpha } }}{{{\Gamma }\left( {\alpha + 2} \right)}}f_{i} \left( {x_{1h}^{p} \left( {t_{n + 1} } \right), x_{2h}^{p} \left( {t_{n + 1} } \right), \ldots , x_{nh}^{p} \left( {t_{n + 1} } \right)} \right) + \frac{{h^{\alpha } }}{{{\Gamma }\left( {{\upalpha } + 2} \right)}}\sum a_{i,j,n + 1} f_{i} \left( {x_{1} \left( {t_{j} } \right), x_{2} \left( {t_{j} } \right), \ldots , x_{n} \left( {t_{j} } \right)} \right) $$
(4)

where \({a}_{i,j,n+1}=\left\{\begin{array}{l}{n}^{\alpha +1}-\left(n-\alpha \right){\left(n+1\right)}^{\alpha }, if\; j=0\\ {\left(n-j+2\right)}^{\alpha +1}+{\left(n-j\right)}^{\alpha +1}-2{(n-j+1)}^{\alpha +1}, if 1\le j\le n\\ 1, if\; j=n+1\end{array}\right.\)

The predicted value \(x_{ih}^{p} \left( {t_{n + 1} } \right)\) is determined by (5),

$$ x_{ih}^{p} \left( {t_{n + 1} } \right) = x_{i} \left( 0 \right) + \frac{1}{{{\Gamma }\left( \alpha \right)}}\mathop \sum \limits_{j = 0}^{n} b_{i,j,n + 1} f_{i} \left( {x_{ih} \left( {t_{j} } \right)} \right) $$
(5)

where \(b_{i,j,n + 1} = \frac{{h^{\alpha } }}{\alpha }\left( {\left( {n - j + 1} \right)^{\alpha } - \left( {n - j} \right)^{\alpha } } \right), 0 \le j \le n.\)

Errors are estimated by (6),

$$ e = \max \left\{ {\max \left| {x_{1} \left( {t_{j} } \right) - x_{1h} \left( {t_{j} } \right)} \right|,\max \left| {x_{2} \left( {t_{j} } \right) - x_{2h} \left( {t_{j} } \right)} \right|, \ldots ,\max \left| {x_{n} \left( {t_{j} } \right) - x_{nh} \left( {t_{j} } \right)} \right|} \right\} = O\left( {h^{\rho } } \right) $$
(6)

where \( j = \left( {0,1,2, \ldots ,N} \right),\rho = {\text{min}}\left\{ {2,1 + \alpha } \right\}\).

These theorems and definitions will be used in the proposed models and controllers designed in Sect. 5.

3 Proposed FO epidemic models (FOEMs) and design of FO controllers

This section presents FO chaotic models of three pandemics: Plague, Cancer and Covid-19, and design of FO control strategies to stabilise and synchronise chaos in the models.

3.1 FO Plague epidemic models (FOPEMs)

IOMs of chaotic plague epidemic models were proposed in Mangiarotti [51]. We present six FOPEMs, where \({x}_{1}, {x}_{2}\) and \({x}_{3}\) represent the numbers of human plague deaths, captured infected rats of the M. decumanus species and captured infected rats of the M. rattus species, respectively [12, 16].


(a) FOPEM \({{\varvec{M}}}_{0}\)

\({M}_{0}\) is a 10-term chaotic model given as in (7), where the tuning parameter \(\vartheta =0.598\).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3}-12.6237\vartheta {x}_{1} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(7)

(b) FOPEM \({{\varvec{M}}}_{1}\)

\({M}_{1}\) is a 11-term chaotic model given as in (8), where \(\vartheta =1\).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3}-12.6237\vartheta {x}_{1} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0213{x}_{3}^{2}+2.0814{x}_{2}-6.917{x}_{1}-0.0255{x}_{1}{x}_{3}+0.0078{x}_{1}{x}_{2}-0.0013{x}_{2}^{2}\end{array}\right.$$
(8)

(c) FOPEM \({{\varvec{M}}}_{2}\)

\({M}_{2}\) is also a 11-term chaotic model given as in (9), where \(\vartheta =0.9.\)

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.1434{x}_{3}^{2}+0.0674{x}_{2}{x}_{3}-12.7264\vartheta {x}_{1}-0.0025{x}_{2}^{2} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(9)

(d) FOPEM \({{\varvec{M}}}_{3}\)

\({M}_{3}\) is a 12-term chaotic model given as in (10), where \(\vartheta =0.945\).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0936{x}_{3}^{2}+0.0431{x}_{2}{x}_{3}-12.0677\vartheta {x}_{1} \\ {D}^{\alpha }{x}_{2}=0.0103{x}_{2}^{2}-0.0227{x}_{1}{x}_{2} (10) \\ {D}^{\alpha }{x}_{3}=0.0318{x}_{3}^{2}+1.7263{x}_{2}-6.6007{x}_{1}-0.0355{x}_{1}{x}_{3}+0.005967{x}_{1}{x}_{2}- \\ 0.004{x}_{1}^{2}-0.00007{x}_{2}^{2 }\end{array}\right.$$
(10)

(e) FOPEM \({{\varvec{M}}}_{4}\)

\({M}_{4}\) is a 10-term periodic model given as in (11), where \(\vartheta =1\).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3}-12.6237{\vartheta x}_{1} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(11)

(f) FOPEM \({{\varvec{M}}}_{5}\)

\({M}_{5}\) is a 11-term periodic model given as in (12), where \(\vartheta =1\)

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.1434{x}_{3}^{2}+0.0674{x}_{2}{x}_{3}-12.7264\vartheta {x}_{1}-0.0025{x}_{2}^{2} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(12)

Table 2 lists the dynamical analyses of FOPEMs to help predict critical transitions in biological systems [12, 16, 57].

Table 2 Investigation of dynamics of the FO Plague epidemic models
Full size table

Figure 1 depicts the attractors of the FOPEMs where \({M}_{0}, {M}_{1}, {M}_{2}, {M}_{3}\) are chaotic and \({M}_{4}, {M}_{5}\) are periodic. A representative bifurcation diagram is plotted for the FOPEM \({M}_{3}\) at \(\alpha =0.995\) against the tuning parameter \(\vartheta \) as the bifurcation parameter in Fig. 1g. The gradual evolution of chaos is distinctly visible through a period doubling pathway. The ranges of the tuning parameter for the corresponding attractor dynamics are\( \left[0, 0.265\right]\): (period 1), [0.265,0.576]: (period 2), [0.576, 0.874]: (period 4) and [0.875, 1]: (chaos). The value of \(\vartheta \) is chosen as 0.945 for \({M}_{3}\) for chaotic dispersal. Similarly, \(\vartheta \) for other FOPEMs are chosen.

Fig. 1
figure 1

Dynamical analysis of the FO Plague epidemic models

Full size image

3.1.1 FO controllers (FOCs) for stabilisation of chaos in FOPEMs

Three stabilisation controllers are designed in three subsections dedicated to FO fuzzy logic control (FOFLC), FO adaptive sliding mode control (FOASMC) and FO active backstepping control (FOABC). It is to be noted that these controllers are applied to stabilise chaos only in those FOPEMs which have chaotic dynamics, i.e. \({M}_{0}\), \({M}_{1}\),\({M}_{2}\) and \({M}_{3}\) as discussed in Table 2.

3.1.1.1 FOFLC:

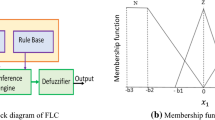
The design of an IO-based TS fuzzy logic control (TSFLC) is reported in Vaidyanathan [80]. The configuration of the system with a fuzzifier which converts the crisp inputs to linguistic variables using the membership functions stored in the database, the inference engine which simulates decisions by performing approximate reasoning, and the defuzzifier which converts the fuzzy output values into crisp values is represented in the block diagram of Fig. 2.

Fig. 2
figure 2

Fuzzy logic control system

Full size image

Let a chaotic, nonlinear system be defined as in (2) and controlled system as in (13).

$${D}^{\alpha }x\left(t\right)=f\left(x\left(t\right),t\right)+B.u$$
(13)

Here, \(u={({u}_{1},{u}_{2},\dots ,{u}_{n})}^{\mathrm{T}}\) is the control signal. The control input \(u\) in (13) is defined as in (14),

$${u}_{i}={u}_{eqi}+{u}_{Li}$$
(14)

where \(i={1,2},3,\dots ,n\), and \({u}_{\mathrm{eq}}=\) \(m({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n})\) is an \(n\)-dimensional vector field containing continuous, nonlinear functions. In FOFLC, \(u\) is calculated by weighted sum defuzzification method, and \(B\) is an \(n\times n\) identity matrix. Let \(X\) be the universe of discourse for the system defined in (13) and \({u}_{L}\) be based on fuzzy control rules.

The \({i}^{th}\) fuzzy control rule base for the FOFLC is defined as in (15),

$$ {\text{Rule: IF}}\,x_{1} \,{\text{is}}\,X_{i,1} \,{\text{AND}} \ldots {\text{AND}}\,x_{n} \,{\text{is}}\,X_{i,n} {\text{,THEN}}\,u_{L} = u_{i} \left( x \right),i = 1, \ldots ,r,\,r \in N $$
(15)

where \({X}_{i,1}, {X}_{i,2},\dots , {X}_{i,n}\) are fuzzy sets describing the linguistic terms (LTs) of input variables, \({u}_{L}={u}_{i}(x)\) is the control input of rule \(i\) and \(r\) is the total number of fuzzy rules.

Each fuzzy rule defined in (15) generates a weight defined as in (16).

$${\omega }_{i}\in \left[{0,1}\right], i=1,\dots ,r$$
(16)

From (16), it is assumed that for any \(x\in X\) in the input universe of discourse \(X\), there exists at least one weighted output among all rules that is nonzero. FO Lyapunov stability theorem applied to control the epidemic to a disease free equilibrium is as follows.

Theorem 2:

([47]). Let the origin be an equilibrium of the controlled epidemic (13), and there exists a Lyapunov function, \(V\left(x\right)={x}^{T}Tx\), where \(T\) is a positive definite matrix, on domain \(X\) containing the origin of \({R}^{n}\) such that\( {D}^{\alpha }V\left(x\right)\le 0\), for\( x\in X\). Let\(S=\{x\in X:{D}^{\alpha }V\left(x\right)=0\}\). If except the trivial solution\( x\left(t\right)\equiv 0\), there is no solution of (13) that exists identically in \(S\); then, the infection-free equilibrium at the origin is asymptotically stable in the domain\( X\).

On adding FOFLC to the FOPEM \({M}_{0}\) (7), we get (17).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3}-12.6237\vartheta {x}_{1}+ {u}_{1} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2}+{u}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}+{u}_{3}\end{array}\right.$$
(17)

On comparing (17) with (13), we have,

$$ f\left( {x_{1} ,x_{2} ,x_{3} } \right) = \left[ {\begin{array}{*{20}c} { - 0.0976x_{3}^{2} + 0.045x_{2} x_{3} - 7.5489726x_{1} } \\ {0.0107x_{2}^{2} - 0.0237x_{1} x_{2} } \\ {0.0108x_{3}^{2} + 1.4512x_{2} - 5.912x_{1} - 0.0147x_{1} x_{3} + 0.0041x_{1} x_{2} } \\ \end{array} } \right]\,{\text{and}}\,B.u = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} } \right].\left[ {\begin{array}{*{20}c} {u_{1} } \\ {u_{2} } \\ {u_{3} } \\ \end{array} } \right] $$
(18)

\({u}_{\mathrm{eq}1}, {u}_{\mathrm{eq}2}\; and\; {u}_{\mathrm{eq}3}\) of (14) are selected as in (19).

$$\left\{\begin{array}{l}{u}_{eq1}=0.0976{x}_{3}^{2}-0.045{x}_{2}{x}_{3} \\ {u}_{eq2}=-0.0107{x}_{2}^{2}+0.0237{x}_{1}{x}_{2} \\ {u}_{eq3}=-0.0108{x}_{3}^{2}+0.0147{x}_{1}{x}_{3}-0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(19)

Replacing (19) in (17) and (18), we get (20).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-7.5489726{x}_{1}+{u}_{L1} \\ {D}^{\alpha }{x}_{2}={u}_{L2} \\ {D}^{\alpha }{x}_{3}=1.4512{x}_{2}-5.912{x}_{1}+{u}_{L3}\end{array}\right.$$
(20)

The fuzzification module of FOFLC in Fig. 3 shows the triangular membership function of the LTs of the chosen linguistic variable \({x}_{1}\). Notations \(P,\; Z\; and\; N\) represent ‘positive’,’zero’ and ‘negative’, respectively, and the parameters chosen are \(b3=200, b2=190, b1=10, a1=10, a2=1590\; and \; a3=1600.\)

Fig. 3
figure 3

Membership function for FOFLC

Full size image

Table 3 describes the set of fuzzy control rules.

Table 3 Fuzzy rule base of FOFLCs for FOPEM \({M}_{0}\)
Full size table

The universe of discourse is, \(X = \left[ { - 200,1600} \right] \times \left[ {0,2500} \right] \times \left[ { - 200,400} \right]\).

The Lyapunov function is chosen as (21).

$$ V\left( x \right) = \frac{1}{2}\left( {x_{1}^{2} + x_{2}^{2} + x_{3}^{2} } \right) $$
(21)

Using Lemma 1,

$$ D^{\alpha } V\left( x \right) \le x_{1} u_{L1} - 7.5489726x_{1}^{2} + x_{2} u_{L2} + 1.4512x_{2} x_{3} - 5.912x_{1} x_{3} + x_{3} u_{L3} $$
(22)

Using Theorem 2, \({D}^{\alpha }V\left(x\right)=0\iff x={\left[{0,0},0\right]}^{T}\) which implies \(S=\{{0,0},0\}\). Since Theorem 2 is satisfied in the FO sense, the designed FOFLC converges the controlled epidemic \({M}_{0}\) to an infection-free asymptotically stable equilibrium. Similarly, the FOFLCs for the chaotic FOPEMs \({M}_{k}\),\(k=0,...,3\), and fuzzy rules \({R}_{i}\) \(i={1,2},3\) are designed as given in Table 4.

Table 4 Proposed FOFLCs to stabilise chaos in FOPEMs in antecedent \({x}_{1}\)
Full size table
3.1.1.2 FOASMC:

The function \(f(x\left(t\right),t)={[{f}_{1}\left(x\right),{f}_{2}\left(x\right),\dots ,{f}_{n}\left(x\right)]}^{\mathrm{T}}\) in FONLS (2) is an \(n\)-dimensional vector field which can be further broken into smooth functions as in (23),

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=a\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\varphi {x}_{1} \\ {D}^{\alpha }{x}_{2}={x}_{1}.b\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)+{x}_{3}.d\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\beta {x}_{2} \\ {D}^{\alpha }{x}_{3}={x}_{1}.c\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-{x}_{2}.d\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\gamma {x}_{3} \\ {D}^{\alpha }{x}_{n}={x}_{1}.e\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-{x}_{n-1}.g\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\dots -\tau {x}_{n}\end{array}\right.$$
(23)

where \(a\left(\bullet \right),\) \(b\left(\bullet \right),\) \(c\left(\bullet \right),\) \(d\left(\bullet \right),\) \(e\left(\bullet \right),\dots , g\left(\bullet \right)\) are smooth functions belonging to \({R}^{n}\to R\) space and \(\varphi , \beta , \gamma , \dots , \tau \) are positive constants [69].

An adaptive switching surface \(s\left( t \right)\) is considered such that the system satisfies the following condition in (24) to operate in sliding mode.

$$ s\left( t \right) = x_{1} \left( t \right) + \theta \left( t \right) = 0 $$
(24)

\(\theta \left( t \right)\) is an adaptive function whose fractional derivative is given in (25),

$$ D^{\alpha } \theta \left( t \right) = x_{2} .b\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) + x_{3} .c\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) + \ldots + x_{n} .e\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) + \varphi x_{1} + \rho x_{1} $$
(25)

where \(\rho\) is an arbitrary positive constant.

Using Caputo fractional derivative in (24), we obtain (26).

$$ D^{\alpha } x_{1} \left( t \right) = - x_{2} .b\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - x_{3} .c\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \ldots - x_{n} .e\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \varphi x_{1} - \rho x_{1} $$
(26)

Replacing the value of \({D}^{\alpha }{x}_{1}\left(t\right)\) from (26) into (23) yields (27).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-{x}_{2}.b\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-{x}_{3}.c\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\dots - {x}_{n}.e\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\varphi {x}_{1}-\rho {x}_{1}\\ {D}^{\alpha }{x}_{2}={x}_{1}.b\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)+{x}_{3}.d\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\beta {x}_{2} \\ {D}^{\alpha }{x}_{3}={x}_{1}.c\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-{x}_{2}.d\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\gamma {x}_{3} \\ {D}^{\alpha }{x}_{n}={x}_{1}.e\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-{x}_{n-1}.g\left({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n}\right)-\dots -\tau {x}_{n}\end{array}\right.$$
(27)

Using the Lyapunov function in (21) and Lemma 1, we have (28).

$$ D^{\alpha } V\left( x \right) \le - \left( {\varphi + \rho } \right)x_{1}^{2} - \beta x_{2}^{2} - \gamma x_{3}^{2} - \ldots - \tau x_{n}^{2} $$
(28)

According to fractional-order Lyapunov stability theorem [20], \(D^{\alpha } V\left( x \right) \le 0\) indicates the system is stable.

The ASMC law used in the sliding surface so that \(D^{\alpha } s\left( t \right) = 0\) is defined as in (29),

$$ u = u_{r} + u_{{{\text{eq}}}} $$
(29)

where \(u_{r} = \sigma {\text{sgn}} \left( s \right)\) is the reaching control law, \(\sigma\) is the reaching gain achieved by the adaptive law \(\dot{\sigma } = - \emptyset \left| s \right|\); \(\emptyset\) is a constant, and \(u_{{{\text{eq}}}}\) is the equivalent control law as in (30).

$$ u_{{{\text{eq}}}} = D^{\alpha } x_{1} \left( t \right) - a\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) + \varphi x_{1} $$
(30)

Replacing \(D^{\alpha } x_{1} \left( t \right)\) from (26) into (30), \(u_{{{\text{eq}}}}\) is obtained as (31).

$$ u_{eq} = - x_{2} .b\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - x_{3} .c\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \ldots - x_{n} .e\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \rho x_{1} - a\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) $$
(31)

Therefore, ASMC \(u\) of (29) is obtained as in (32),

$$ u = - x_{2} .b\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - x_{3} .c\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \ldots - x_{n} .e\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) - \rho x_{1} - a\left( {x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} } \right) + \sigma {\text{sgn}} \left( s \right) $$
(32)

where \(\rho ,\, \sigma \,{\text{and}}\,s\) are to be suitably chosen.

Now, the above ASMC strategy is applied to the FOPEM \(M_{0}\) (7).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3}-7.5489726{x}_{1}+{u}_{1} \\ {D}^{\alpha }{x}_{2}=0.0107{x}_{2}^{2}-0.0237{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=0.0108{x}_{3}^{2}+1.4512{x}_{2}-5.912{x}_{1}-0.0147{x}_{1}{x}_{3}+0.0041{x}_{1}{x}_{2}\end{array}\right.$$
(33)

Here, \(u={({u}_{1},{0,0})}^{\mathrm{T}},\) \({u}_{1}={u}_{r1}+{u}_{eq1}\) is the control signal.

Comparing system (33) with (23), we obtain (34).

$$\left\{\begin{array}{l}a\left({x}_{1},{x}_{2},{x}_{3}\right)=-0.0976{x}_{3}^{2}+0.045{x}_{2}{x}_{3} \\ \varphi =7.5489726 \\ b\left({x}_{1},{x}_{2},{x}_{3}\right)=-0.0237{x}_{2} \\ \beta =-0.0107{x}_{2} \\ c\left({x}_{1},{x}_{2},{x}_{3}\right)=-5.912-0.0147{x}_{3}+0.0041{x}_{2}\\ d\left({x}_{1},{x}_{2},{x}_{3}\right)=-1.4512 \\ \gamma =-0.0108{x}_{3}\end{array}\right.$$
(34)

From (31) and (32), the ASMC \(u_{1}\) is obtained as in (35).

$$ u_{1} = 0.0237x_{2}^{2} + 5.912x_{3} + 0.01123x_{3}^{2} - 0.0491x_{2} x_{3} - \rho x_{1} + \sigma sgn\left( s \right) $$
(35)

Suitable values of \(\rho , \sigma \) and \(s\) render the FOPEM, \({M}_{0}\) globally asymptotically stable. Similarly, the FOASMC for the chaotic FOPEMs, \({M}_{1}, {M}_{2}\) and \({M}_{3}\) are designed as given in Table 5.

Table 5 Proposed FOASMC and FOABC to stabilise chaos in FOPEMs
Full size table
3.1.1.3 FOABC:

The recursive active backstepping control is designed for the \(i{\text{th}}\) step, where the \(i{\text{th}}\)-order sub-system is stabilised with respect to a Lyapunov function \(V_{i}\) and virtual control \(\mu_{i}\) in the control input \(u_{i}\).

Let, \(w_{1} = x_{1}\),

$$ D^{\alpha } w_{1} = D^{\alpha } x_{1} = f_{1} \left( {x\left( t \right),t} \right) + u_{1} $$
(36)

such that \(x_{2} = \mu_{1} \left( {w_{1} } \right)\) is the virtual control input.

To stabilise sub-system \(w_{1}\), a Lyapunov function is chosen as in (37).

$$ V_{1} = \frac{{w_{1}^{2} }}{2} $$
(37)

Using FO Lemma 1, the Caputo fractional derivative of \(V_{1}\) is obtained as in (38).

$$ D^{\alpha } V_{1} \le w_{1} D^{\alpha } w_{1} = w_{1} \left[ {f_{1} \left( {x\left( t \right),t} \right) + u_{1} } \right] $$
(38)

Considering \(\mu_{1} = 0\), an appropriate expression of \(u_{1}\) is chosen such that \(D^{\alpha } V_{1} < 0\), and sub-system \(w_{1}\) is asymptotically stable. The error between \(x_{2}\) and \(\mu_{1}\) is given by (39).

$$ w_{2} = x_{2} - \mu_{1} $$
(39)

Therefore, the \((w_{1} ,w_{2} )\) sub-system is obtained, where \(x_{3} = \mu_{2} \left( {w_{1} ,w_{2} } \right)\) is the virtual controller. The stabilisation of \((w_{1} ,w_{2} )\) sub-system is done by choosing a Lyapunov function, \(V_{2}\) as in (40).

$$ V_{2} = V_{1} + \frac{{w_{2}^{2} }}{2} $$
(40)

Its Caputo derivative is as in (41).

$$ D^{\alpha } V_{2} \le D^{\alpha } V_{1} + w_{2} D^{\alpha } w_{2} = D^{\alpha } V_{1} + w_{2} \left[ {f_{2} \left( {x\left( t \right),t} \right) + u_{2} } \right] $$
(41)

Considering \(\mu_{2} = 0\), an appropriate expression of \(u_{2}\) is chosen such that \(D^{\alpha } V_{2} < 0\), making \((w_{1} ,w_{2} )\) sub-system asymptotically stable.

Similarly, virtual controllers are designed for subsequent sub-systems \((w_{1} ,w_{2} , \ldots ,w_{n} )\), which are stabilised by choosing Lyapunov functions as in (42) and appropriate controller expressions.

$$ V_{i} = V_{i - 1} + \frac{{w_{i}^{2} }}{2} $$
(42)

If \(D^{\alpha } V_{i} < 0\), for \(i = 1,2, \ldots ,n\)., the controlled system (13) is asymptotically stable.

Now, we apply FOABC to FOPEM \(M_{0} \left( 7 \right)\). From (36), we have,

$$ D^{\alpha } w_{1} = - 7.5489726w_{1} - 0.0976x_{3}^{2} + 0.045x_{2} x_{3} . $$
(43)

From (38), we have (44).

$$ D^{\alpha } V_{1} = - 7.5489726w_{1}^{2} + w_{1} \left( { - 0.0976x_{3}^{2} + 0.045\mu_{1} x_{3} w_{1} + u_{1} } \right) $$
(44)

\(D^{\alpha } V_{1} = - 7.5489726w_{1}^{2} - w_{1}^{2} < 0\), if \(\mu_{1} = 0\) and \(u_{1} = 0.0976x_{3}^{2} - w_{1}\), and sub-system \(w_{1}\) is asymptotically stable.

From (41), we get,

$$ D^{\alpha } V_{2} = - 7.5489726w_{1}^{2} - w_{1}^{2} + 0.045w_{1} w_{2} a_{2} + w_{2} \left( {0.0107w_{2}^{2} - 0.0237w_{1} w_{2} + u_{2} } \right) $$
(45)

\(D^{\alpha } V_{2} = - 7.5489726w_{1}^{2} - w_{1}^{2} - w_{2}^{2} < 0\), when \(\mu_{2} = 0\) and \(u_{2} = - 0.0107w_{2}^{2} + 0.0237w_{1} w_{2} - w_{2}\), and sub-system \((w_{1} ,w_{2} )\) is asymptotically stable.

Similarly, \(D^{\alpha } V_{3} = - 8.5489726w_{1}^{2} + 0.045w_{1} w_{2} w_{3} + w_{3} \left( {0.0108w_{3}^{2} + 1.4512w_{2} - 5.912w_{1} - 0.0147w_{1} w_{3} + 0.0041w_{1} w_{2} + u_{3} } \right) < 0\), and the sub-system \((w_{1} ,w_{2} ,w_{3} )\) is asymptotically stable.

Thus, chaos in FOPEM \(M_{0}\) is stabilised using FOABC. Similarly, the FOABC for remaining chaotic FOPEMs, \(M_{1} , M_{2} \) and \(M_{3}\) are designed as enlisted in Table 5.

3.1.2 FO Controllers for synchronisation of chaos in FOPEMs

The controllers in this section are applied to two pairs:

  1. a.

    Chaotic FOPEM \({M}_{0}\) acting as a slave synchronises with periodic FOPEM \({M}_{4}\) acting as a master

  2. b.

    Chaotic FOPEM \({M}_{2}\) acting as a slave synchronises with periodic FOPEM \({M}_{5}\) acting as a master

Let the FO master system be a periodic system defined in (46).

$$ D^{\alpha } y\left( t \right) = f\left( {y\left( t \right),t} \right) $$
(46)

where \(y\left( t \right) = \left[ {y_{1} , y_{2} , \ldots ,y_{n} } \right]^{{\text{T}}}\) is the state vector, \(y_{i} \left( 0 \right)\) represents the ICs and \(i = 1, 2, \ldots , n\). \(f\left( {y\left( t \right),t} \right)) = \left[ {f_{1} \left( y \right),f_{2} \left( y \right), \ldots ,f_{n} \left( y \right)} \right]^{{\text{T}}}\) is an \(n\)-dimensional vector field containing continuous functions of the master system.

Let the FO slave system be a chaotic system defined in (47).

$$ D^{\alpha } x\left( t \right) = f\left( {x\left( t \right),t} \right) + u $$
(47)

The errors between the master and slave are defined as in (48),

$$ e = x - y $$
(48)

where \(e = \left[ {e_{1} , e_{2} , \ldots ,e_{n} } \right]^{{\text{T}}}\) are the error states.

The FO error dynamics are obtained as in (49).

$$ D^{\alpha } e = D^{\alpha } x - D^{\alpha } y $$
(49)

Therefore, the goal is to design \(u\) such that the error states converge to zero as time approaches infinity, i.e. the trajectory of the slave system (47) asymptotically approaches and synchronise with the trajectory of the master system (46).

Two control strategies for synchronisation are proposed in the following subsections: FO fuzzy logic synchronisation control (FOFLSC) and FO active backstepping synchronisation control (FOABSC).

3.1.2.1 FOFLSC:

The ith fuzzy control rule for the FOFLSC is defined as in (50),

$$ {\text{Rule}}\,i:{\text{IF}}\,e_{1} \,{\text{is}}\,E_{i,1} \,{\text{AND}} \ldots {\text{AND}}\,e_{n} \,{\text{is}}\,E_{i,n} ,{\text{THEN}}\,\,u_{L} = u_{i} \left( e \right),i = 1, \ldots ,r,r \in N^{*} $$
(50)

where \(E_{i,1} , E_{i,2} , \ldots , E_{i,n}\) are fuzzy sets describing the LTs of input variables, \(u_{L} = u_{i} \left( e \right)\) is the control input of rule \(i\) and \(r\) is the total number of fuzzy rules following the same defuzzification process as in Sect. 5.1.1.1.

The Lyapunov function is defined as in (51).

$$ V\left( e \right) = \frac{1}{2}\left( {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + \ldots + e_{n}^{2} } \right) $$
(51)

From Theorem 2, it can be derived that if the origin is an equilibrium of the controlled system and \(V\left( e \right) = \frac{1}{2}\left( {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} + \ldots + e_{n}^{2} } \right)\) is a positive definite function on domain \(E\) containing the origin of \(R^{n}\) such that \(D^{\alpha } V\left( e \right) \le 0\), for \(i = 1,2, \ldots ,r\) and \(e \in E\), and \(S = \left\{ {e \in E:D^{\alpha } V\left( e \right) = 0} \right\}\), and suppose no solution of (49) can stay identically in \(S\) except the trivial solution \(e\left( t \right) \equiv 0\), then, the equilibrium at the origin is asymptotically stable in the domain \(E\).

We now apply FOFLSC to synchronise FOPEM \(M_{0}\) with \(M_{4}\). The periodic FOPEM, \( M_{4}\) is chosen as master and chaotic \(M_{0}\) as slave. The error dynamics are given by (52).

$$\left\{\begin{array}{l}{{D}^{\alpha }e}_{1}=-0.0976{(x}_{3}^{2}-{y}_{3}^{2})+0.045({x}_{2}{x}_{3}-{y}_{2}{y}_{3}) \\ -7.5489726{x}_{1}+12.6237{y}_{1}+{u}_{1} \\ {{D}^{\alpha }e}_{2}=0.0107{(x}_{2}^{2}-{y}_{2}^{2})-0.0237({x}_{1}{x}_{2}-{y}_{1}{y}_{2})+{u}_{2} \\ {{D}^{\alpha }e}_{3}=0.0108\left({x}_{3}^{2}-{y}_{3}^{2}\right)+1.4512{e}_{2}-5.912{e}_{1}-0.0147{(x}_{1}{x}_{3}-{y}_{1}{y}_{3}) \\ +0.0041({x}_{1}{x}_{2}-{y}_{1}{y}_{2})+{u}_{3}\end{array}\right.$$
(52)

\({u}_{\mathrm{eq}1}, {u}_{\mathrm{eq}2} \quad \mathrm{ and } \quad {u}_{\mathrm{eq}3}\) are selected as in (53).

$$\left\{\begin{array}{l}{u}_{eq1}=0.0976{(x}_{3}^{2}-{y}_{3}^{2})-0.045({x}_{2}{x}_{3}-{y}_{2}{y}_{3})+7.5489726{x}_{1}-12.6237{y}_{1} \\ {u}_{eq2}=-0.0107{(x}_{2}^{2}-{y}_{2}^{2})+0.0237({x}_{1}{x}_{2}-{y}_{1}{y}_{2}) \\ {u}_{eq3}=-0.0108\left({x}_{3}^{2}-{y}_{3}^{2}\right)+0.0147{(x}_{1}{x}_{3}-{y}_{1}{y}_{3})-0.0041({x}_{1}{x}_{2}-{y}_{1}{y}_{2})\end{array}\right.$$
(53)

From (49) and (50), we get

$$\left\{\begin{array}{l}{{D}^{\alpha }e}_{1}={u}_{L1} \\ {{D}^{\alpha }e}_{2}={u}_{L2} \\ {{D}^{\alpha }e}_{3}=1.4512{e}_{2}-5.912{e}_{1}+{u}_{L3}\end{array}\right.$$
(54)

and \(E=\left[-{1500,1500}\right]\times \left[-{2500,2000}\right]\times [-{800,600}]\).

From (51), the Lyapunov function is chosen as in (55).

$$ V\left( e \right) = \frac{1}{2}\left( {e_{1}^{2} + e_{2}^{2} + e_{3}^{2} } \right) $$
(55)

Using Caputo derivative, we have,

$$ D^{\alpha } V\left( e \right) = e_{1} u_{L1} + e_{2} u_{L2} + 1.4512e_{2} e_{3} - 5.912e_{1} e_{3} + e_{3} u_{L3} $$
(56)

Since, \(D^{\alpha } V\left( e \right) = 0 \Leftrightarrow e = \left[ {0,0,0} \right]^{T}\) which implies \(S = \left\{ {0,0,0} \right\}\). The fuzzy rules are derived as follows:

  1. i.

    For Rule 1, \(R_{1}\): for antecedent \(e_{1}\) as \(P\), we have the consequent as,

\(U_{L1} = \left[ {\begin{array}{*{20}c} {u_{L1} } \\ {u_{L2} } \\ {u_{L3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - e_{1} + 5.912e_{3} } \\ { - e_{2} - 1.4512e_{3} } \\ { - e_{3} } \\ \end{array} } \right]\), then \(D^{\alpha } V\left( e \right) = - e_{1}^{2} - e_{2}^{2} - e_{3}^{2} < 0.\)

  1. ii.

    For Rule 2, \(R_{2}\): for antecedent \(e_{1}\) as \(N\), we have the consequent as,

\(U_{L2} = \left[ {\begin{array}{*{20}c} {u_{L1} } \\ {u_{L2} } \\ {u_{L3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 6.5e_{1} + 5.912e_{3} } \\ { - 9.5e_{2} - 1.4512e_{3} } \\ { - e_{3} } \\ \end{array} } \right]\), then \(D^{\alpha } V\left( e \right) = - 6.5e_{1}^{2} - 9.5e_{2}^{2} - e_{3}^{2} < 0\).

  1. iii.

    For Rule 3, \(R_{3}\): for antecedent \(e_{1}\) as \(Z\), we have the consequent as

    $$ U_{L3} = \left[ {\begin{array}{*{20}c} {u_{L1} } \\ {u_{L2} } \\ {u_{L3} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - 6.5e_{1} + 5.912e_{3} } \\ { - 9.5e_{2} - 1.4512e_{3} } \\ { - 13e_{3} } \\ \end{array} } \right],\,{\text{then}}\, D^{\alpha } V\left( e \right) = - 6.5e_{1}^{2} - 9.5e_{2}^{2} - 13e_{3}^{2} < 0 $$

Thus, the errors, \(e={[{e}_{1},{e}_{2},{e}_{3}]}^{\mathrm{T}},\) converge to zero and the slave \({M}_{0}\) synchronises with the master \({M}_{4}.\) Similarly, the FOFLSC designed to synchronise FOPEMs, the chaotic \({M}_{2}\) with the periodic \({M}_{5}\) is as in Table 6.

Table 6 Proposed TSFLSC for synchronisation in FOPEMs, \({ M}_{0}\) (slave) with \({M}_{4}\) (master); and \({M}_{2}\) (slave) with \({M}_{5}\) (master) at antecedent \({e}_{1}\)
Full size table
3.1.2.2 FOABSC:

The periodic FOPEM,\({M}_{4}\) is chosen as master and chaotic \({M}_{0}\) as slave. According to the design procedure mentioned in subsection 3.1.1.3, \({e}_{3}={\mu }_{1}({w}_{1})\) is the virtual control input. The Lyapunov function is chosen as in (37) and its FO derivative is as in (57).

$${D}^{\alpha }{V}_{1}=-7.5489726{w}_{1}^{2}+{w}_{1}(-0.0976 ({y}_{3}+{x}_{3}){\mu }_{1}+0.045({x}_{2}{x}_{3}-{y}_{2}{y}_{3})+ 5.0747274{y}_{1}+{u}_{1})$$
(57)

\({D}^{\alpha }{V}_{1}=-7.5489726{w}_{1}^{2}-{w}_{1}^{2}<0\), i.e. sub-system \({w}_{1}\) is asymptotically stable when \({\mu }_{1}=0\) and \(u_{1} = 0.045\left( {x_{2} x_{3} - y_{2} y_{3} } \right) - 5.074727y_{1} - w_{1}\).

For the Lyapunov function, \(V_{2}\) in (58), we get its FO derivative in (59).

$$ V_{2} = V_{1} + \frac{{z_{3}^{2} }}{2} $$
(58)
$$ \begin{aligned} D^{\alpha } V_{2} & = - 8.5489726w_{1}^{2} - 0.0976 \left( {y_{3} + x_{3} } \right)w_{1} w_{3} \\ & \quad + w_{3} \left( {0.0108\left( {y_{3} + x_{3} } \right)w_{3} + 1.4512\mu_{2} - 5.912w_{1} - 0.0147(x_{1} x_{3} - y_{1} y_{3} } \right) \\ & \quad + 0.0041\left( {x_{1} x_{2} - y_{1} y_{2} } \right) + u_{3} ) \\ \end{aligned} $$
(59)

\(D^{\alpha } V_{2} = - 8.5489726w_{1}^{2} - w_{3}^{2} < 0\), when \(\mu_{2} = 0\) and \(u_{3} = 0.0976 \left( {y_{3} + x_{3} } \right)w_{1} - 0.0108\left( {y_{3} + x_{3} } \right)w_{3} + 5.912w_{1} + 0.0147(x_{1} x_{3} - y_{1} y_{3} ) - 0.0041\left( {x_{1} x_{2} - y_{1} y_{2} } \right) - w_{3}\), which makes sub-system \((w_{1} ,w_{3} )\) asymptotically stable.

Similarly, \(D^{\alpha } V_{3} = - 8.5489726w_{1}^{2} - w_{3}^{2} - w_{2}^{2} < 0\), which makes \((w_{1} ,w_{2} ,w_{3} )\) sub-system asymptotically stable.

Therefore, the synchronisation errors \(e = \left[ {e_{1} ,e_{2} ,e_{3} } \right]^{{\text{T}}}\) converge to zero and the controlled system, i.e. chaotic FOPEM \(M_{0} \) asymptotically approaches the trajectory of the periodic master system, FOPEM \( M_{4}\). Similarly, FOABSC is designed to synchronise chaotic FOPEM, \( M_{2}\) with periodic FOPEM, \( M_{5}\) as shown in Table 7.

Table 7 Proposed FOABSC for synchronisation in FOPEMs, \({M}_{0}\) (slave) with \({M}_{4}\) (master); and \({M}_{2}\) (slave) with \({M}_{5}\) (master)
Full size table

3.2 FO cancer epidemic model (FOCEM)

The proposed FOCEM is given as in (60), where \({x}_{1}\), \({x}_{2}\) and \({x}_{3}\) represent the tumour cell population, numbers of healthy cells and effector immune population, respectively. The IOM for the same was reported in Valle et al. [81].

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}={x}_{1}\left(1-{x}_{1}\right)-{{a}_{12}x}_{1}{x}_{2}-{a}_{13}{x}_{1}{x}_{3}\\ {D}^{\alpha }{x}_{2}={r}_{2}{x}_{2}\left(1-{x}_{2}\right)-{a}_{21}{x}_{1}{x}_{2} \\ {D}^{\alpha }{x}_{3}=\frac{{r}_{2}{x}_{1}{x}_{3}}{{x}_{1}+1}-{a}_{31}{x}_{1}{x}_{3}-{d}_{3}{x}_{3}\end{array}\right.$$
(60)

Here, \({a}_{12}\) denotes fractional tumour cells killed by healthy cells, \({a}_{13}\) is fractional tumour cells killed by effector cells, \({r}_{2}\) is healthy host cells growth rate, \({a}_{21}\) denotes fractional healthy cells killed by tumour cells, \({a}_{31}\) denotes fractional effector cells inactivated by tumour cells, \({d}_{3}\) denotes death rate of effector cells Valle et al. [81]. The phase solutions of the above system (60) with the parameter set {\({a}_{12}=1, {a}_{13}=2.5\), \({r}_{2}=4.5,\; {a}_{21}\)=1.5, \({a}_{31}=0.2, {d}_{3}=0.5\)} give rise to chaos [36]. The dynamical analysis of the FOCEM is given in Table 8.

Table 8 Investigation of dynamics of FOCEM
Full size table

The phase portraits of the FOCEM (60) in Fig. 4 confirm that they are chaotic in nature in their fractional dynamics.

Fig. 4
figure 4

Chaotic attractors of proposed FO Cancer epidemic model at \(\alpha =0.993\)

Full size image

3.2.1 FO Controllers for stabilisation of chaos in FOCEM

Using the design procedure discussed in Section 3.1.1.1, the FOFLCs for stabilising chaos in the FOCEM are given in Table 9.

Table 9 Proposed FOFLC to stabilise chaos in FOCEM in antecedent \({x}_{1}\)
Full size table

Similarly, using the design procedure discussed in Sects. 3.1.1.2 and 3.1.1.3, the FOASMC and FOABC for stabilising chaos in the FOCEM are given in Table 10.

Table 10 Proposed controllers FOASMC and FOABC to stabilise chaos in FOCEM
Full size table

Having designed the controllers for stabilisation and synchronisation in FOPEMs and FOCEM, we now proceed to their results, discussion and comparison.

4 Comparison of the FOCs in FOPEMs and FOCEM

Comparisons of stabilisation and synchronisation FOCs are presented in the following two subsections.

4.1 Comparison of the FOCs to stabilise chaos

The numerical simulation results of FOFLC, FOASMC and FOABC applied to the epidemics FOPEMs and FOCEM as designed in Sects. 3.1.1 and 3.2.1 to stabilise chaos are shown in Figs. 5, 6, 7, 8 and 9. A comparison is drawn in Table 11 where ‘state’ denotes the number of state variables controlled.

Fig. 5
figure 5

Chaos stabilisation in FO Plague epidemic model, \({M}_{0}\) at \(\alpha =0.98\)

Full size image
Fig. 6
figure 6

Chaos stabilisation in FO Plague epidemic model \({M}_{1}\) at \(\alpha =0.98\)

Full size image
Fig. 7
figure 7

Chaos stabilisation in FO Plague epidemic model \({M}_{2}\) at \(\alpha =0.995\)

Full size image
Fig. 8
figure 8

Chaos stabilisation in FO Plague epidemic model \({M}_{3}\) at \(\alpha =0.995\)

Full size image
Fig. 9
figure 9

Chaos stabilisation in FO Cancer epidemic model at \(\alpha =0.99\)

Full size image
Table 11 Comparison of the FOCs designed to stabilise chaos in FOPEMs and FOCEM
Full size table

From Table 11, it is noted that FOFLC is the fastest controller in terms of settling time, while FOASMC requires the least control effort to stabilise chaos. The designed controllers stabilise chaos in these models, and further illustrate that taking appropriate measures to reduce the number of infected rats will bring about a reduction in disease propagation. The proposed control strategies for chaos stabilisation may be accomplished by an efficient route of human action through medical intervention to methodically slow down the disease spread. The FOCEM stabilised using the proposed FOCs highlight the importance of maximum recruitment rate of effector cells being stronger than their inactivation rate by Cancer cells, on failure of which, necessary treatment is to be delivered to control tumour growth. In order to bring about zero tumour survival, the designed controllers aim at controlling the parameter assigned as fractional tumour cells killed by healthy cells.

4.2 Comparison of the FOCs to synchronise chaos

The numerical simulation results of applying the controllers FOFLSC and FOABSC for synchronisation as designed in Sect. 3.1.2 are shown in Figs. 10 and 11.

Fig. 10
figure 10

Synchronisation control for FOPEMs, \({M}_{4}\)(master) and \({M}_{0}\)(slave)

Full size image
Fig. 11
figure 11

Synchronisation control for FOPEMs, \({M}_{5}\)(master) and \({M}_{2}\)(slave)

Full size image

Chaotic models have a degree of unpredictability. The purpose of synchronisation is to synchronise the chaotic dynamical model with that of an unchaotic or periodic model so that the system is no longer chaotic, and the unpredictability in the epidemic spread is mitigated. As shown in Figs. 10 and 11, the error states \(E={[{e}_{1},{e}_{2},{e}_{3}]}^{\mathrm{T}}\) converge to zero and the controlled slave system asymptotically approaches the trajectory of the master system. The comparison drawn in Table 12 reveal that FOFLSC is faster than FOABSC. Since our models are chaotic and strongly sensitive to ICs, we analyse the robustness of the control of the proposed models by perturbing the models with different ICs. Then, the corresponding integral squared error ISE = \(\underset{0}{\overset{T}{\int\limits}}{e}^{2}\left(t\right){\mathrm{d}}t\) is computed after application of the same control action. The results obtained are listed in Tables 11 and 12 which prove that the control strategies applied to the proposed models are robust, since the controllers are successful in attaining the desired stabilisation dynamics even after perturbation in the ICs. Such robustness provides a good argument for the controllers to be effective in suppressing and synchronising chaos in the proposed models.

Table 12 Comparison of the FOCs designed to synchronise chaos in FOPEMs
Full size table

4.3 FO Covid-19 pandemic model (FOCovM)

The IOM of chaotic Covid-19 pandemic model is reported in Mangiarotti et al. [53]. The FOCovM is proposed in (61).

$$\left\{\begin{array}{l}{D}^{\alpha }{x}_{1}=-0.10530723{x}_{3}^{2}+2.343\times {10}^{-5}{x}_{1}^{2}-0.15204{x}_{2}({x}_{3}-0.01451520{x}_{1}) \\ {D}^{\alpha }{x}_{2}=-0.20517824{x}_{1}+0.44040714{x}_{2}+0.16060376{x}_{3}^{2} \\ {D}^{\alpha }{x}_{3}=-0.00011493{x}_{1}{x}_{3}-1.215\times {10}^{-5}{x}_{1}{x}_{2}+0.2844499{x}_{3}+2.38\times {10}^{-6}{x}_{1}{x}_{2}\end{array}\right.$$
(61)

where \({x}_{1}, {x}_{2}, {x}_{3}\) are the numbers of confirmed cases, critical cases under intensive care and cumulated number of fatalities per day, respectively.

The bifurcation diagram shown in Fig. 12 reveals the rich complex dynamics of Covid-19 pandemic as it progresses on increasing the FO parameter \(\alpha \) in (61), which otherwise remain concealed in the IO chaotic model. The FOCovM displays a period 1 attractor (P1), in the range \(\alpha \epsilon [0.95, 0.96]\), and bifurcates in two curves to give birth to a period 2 attractor (P2), in [0.96, 0.97]. On further splitting, P2 bifurcates into P4 (period 4) which eventually routes to chaos from \(\alpha =0.973\) onwards.

Fig. 12
figure 12

Bifurcation of Covid-19 pandemic model against the FO parameter \(\alpha \)

Full size image

The phase portraits of the FOCovM shown in Fig. 13 illustrate the gradual evolution of the chaotic attractor at \(\alpha =0.98\) from a P1 at \(\alpha =0.95\), complying with the bifurcation analysis of Fig. 12.

Fig. 13
figure 13

Phase portraits of FO Covid-19 pandemic model

Full size image

The design of controllers in the FOCovM for stabilisation of chaos to a disease-free equilibrium or synchronisation of the chaotic trajectory with a disease-free one is left open to interested researchers. The review carried out in this paper highlights the research gaps in epidemic modelling and control and leads to focus on some unexplored areas that may be a scope of research:

1. FO chaos theory in modelling pandemics: The spread of pandemics such as COVID-19 is deterministic chaos having long-range memory. The present existing IO chaotic models are memory-less models. Chaos theory along with the memory-enabled fractional calculus can be a promising tool in modelling these epidemic/pandemics by capturing real, physical and unmodelled dynamics compared to IOMs. Also the FOMs are capable of presenting more robust models compared to their IO counterparts [49, 50]

2. FO chaos theory in decision-making: The investigation of FO models and their analysis of propagation can be applied to other infected regions to help recognise the closest scenarios to predict the future behaviour of the course of the epidemic. These will serve as an efficient tool in decision making [53] to generate an early alert system and aid in adopting economic control strategies of vaccination,ICU facility, etc., especially in low-income countries with limited health infrastructure.

3. FO chaos theory in destination crisis management: Chaos theory provides a viable framework for the management of disaster in countries whose income is largely dependent on tourism [72] as was the case with the H1N1 influenza crisis in Mexico. FO chaos theory can be a new tool to define tourism crisis.

4. FO controllers for FO chaotic epidemics: In an epidemic governed by chaotic behaviour, a seemingly trivial event may initiate a set of events leading to a major crisis. FO controllers provide robust stability conditions for uncertain chaotic systems [17]. Compared with their IO counterparts, FOCs have more flexibility in choosing the suitable control parameters to control and stabilise the chaotic equilibrium to an infection-free equilibrium. This is another scope of research since such wide range of flexibility of FOCs will enhance adopting preventive control measure in a rapidly propagating epidemic. As an instance, the design of FOCs for stabilising and synchronising chaos in the ongoing chaotic Covid-19 model dynamics may be explored.

5 Conclusions

This brief survey reveals that chaotic waves are a dominant mode of epidemic/pandemic dispersal. Fractional calculus, possessing the features of flexibility, heredity and memory, can provide more accurate models of the chaotic pandemics by incorporating unmodelled dynamics as ultra-diffusive, undetected or asymptomatic transmission, critical cases with comorbidities, etc., that often fail to be encompassed by integer-order models. A conclusion drawn is that on applying fractional-order chaos to model Plague, Cancer and Covid-19 pandemics based on actual data, realistic transmission revealing in-depth insights to their propagation dynamics such as asymptotically periodic attractors that evolve into chaos is discovered. The stability of the disease-free equilibrium is achieved and synchronised using fractional-order control. The designed controllers in practical scenario may denote controlling the number of infected rats in Plague model, rate of recruitment of effector cells in Cancer model, injection of vaccine and prophylactic drug to susceptible individuals, social distancing, restriction of mobility, prior prediction of spread, etc., in Covid-19 model. Knowledge of propagation dynamics of pandemics as studied in this work facilitate judicious decision-making on timely and cost-effective control measures in low- and middle-income countries like India, which is struggling to battle the second wave of Covid-19 due to limited medical infrastructure: shortage of vaccines, oxygen supply, ICU beds, etc. Chaos and its unpredictability increase as FO operator increases; hence, it can be used as a parameter to analyse the progression of a pandemic and is an excellent tool to obtain a closer fit to the disease dynamics. It is to be noted that since chaos indicates hyped sensitivity to initial conditions, so a long-term prediction of the spread of the epidemic is never possible and substantial changes may occur unexpectedly. Nonetheless, this review will prove helpful to design quicker control measures to eliminate chaos, induce crisis management and decision-making in the pandemic using the more realistic approach of fractional-order chaos theory and thus curtail the unpredictability in the spread of the disease.