Comparison of different methodologies for the computation of damped nonlinear normal modes and resonance prediction of systems with non-conservative nonlinearities

Abstract

The nonlinear modes of a non-conservative nonlinear system are sometimes referred to as damped nonlinear normal modes (dNNMs). Because of the non-conservative characteristics, the dNNMs are no longer periodic. To compute non-periodic dNNMs using classic methods for periodic problems, two concepts have been developed in the last two decades: complex nonlinear mode (CNM) and extended periodic motion concept (EPMC). A critical assessment of these two concepts applied to different types of non-conservative nonlinearities and industrial full-scale structures has not been thoroughly investigated yet. Furthermore, there exist two emerging techniques which aim at predicting the resonant solutions of a nonlinear forced response using the dNNMs: extended energy balance method (E-EBM) and nonlinear modal synthesis (NMS). A detailed assessment between these two techniques has been rarely attempted in the literature. Therefore, in this work, a comprehensive comparison between CNM and EPMC is provided through two illustrative systems and one engineering application. The EPMC with an alternative damping assumption is also derived and compared with the original EPMC and CNM. The advantages and limitations of the CNM and EPMC are critically discussed. In addition, the resonant solutions are predicted based on the dNNMs using both E-EBM and NMS. The accuracies of the predicted resonances are also discussed in detail.

1 Introduction

To improve the structural design of a future engineering component, various nonlinear characteristics have to be taken into consideration in the dynamic analysis. The inclusion of nonlinearities makes the dynamic analysis of structural components exceptionally complicated, especially in the case of non-conservative nonlinearities. Non-conservative nonlinear forces are a class of nonlinear forces that either dissipate or provide energy to the structure, i.e. introduce nonlinear damping in the system. Frictional contact, for instance, can be considered as a nonlinear damping term with non-smooth characteristics. The existence of nonlinear damping terms makes the autonomous system non-conservative, therefore classic nonlinear modal analysis methods for conservative systems cannot be applied [13].

Nonlinear modal analysis has become a popular method to investigate the dynamic response of nonlinear systems in the literature. Unlike in a linear system, the superposition principle and orthogonality conditions are no longer valid in a nonlinear system. Nonlinear normal mode (NNM) has been developed to extend the concept of linear modes to nonlinear systems. There are two definitions for nonlinear modes: (1) the periodic motion definition and (2) the invariant manifold definition. The periodic motion definition can be traced back to the works by Rosenberg [23]. In [23], the NNM is defined as a vibration in unison, where all points in a structure reach their equilibrium position and extreme position simultaneously. However, the definition (1) does not apply to non-conservative systems, because the autonomous solutions are not typically in a periodic form. In definition (2), only one periodic orbit needs to be calculated for one computation. The whole NNM can be then computed as a family of periodic orbits by applying a continuation algorithm. Methods such as Harmonic balance method (HBM) [3], shooting method [10] and collocation method [2], to name a few, are common numerical tools to compute a family of periodic orbits. The second definition of the NNM was proposed by Shaw and Pierre [28]. In this definition, the NNM is defined as an invariant manifold tangent to a linear eigenspace of the system at the equilibrium position. In definition (2), the NNM is geometrically governed by a hypersurface in the phase space, which is tangent to the equilibrium point of the corresponding linear mode. Theoretically, the definition (2) can be extended to the non-conservative nonlinear systems as the assumption of a periodic orbit is no longer included. Both analytical and numerical methods can be used to compute the NNM based on the definition (2), where analytical methods are usually based on polynomial series expansions to parametrise the geometry of the manifold [28], whereas numerical methods rely on computing the solution of the partial differential equations that govern the manifold [22].

To extend the periodic motion definition of the NNM in a non-conservative nonlinear system, two main strategies have been proposed in the literature: (1) complex nonlinear mode (CNM) and (2) extended periodic motion concept (EPMC). The NNM in such a non-conservative nonlinear system is named as damped nonlinear normal mode (dNNM) [26]. Laxalde and Thouverez [18] used the concept of the CNM to describe the dNNM as a damped solution. According to CNM, the dNNM is formulated using a series of harmonic periodic functions with exponential decay. Thus, only the frequency domain methods (i.e. HBM) can be applied, see, e.g. [17, 37]. The second concept was proposed by Krack [11]. In EPMC, artificial viscous damping with an unknown damping ratio is introduced into the system to compensate the energy loss by the non-conservative nonlinearities leading to a periodic dNNM. Thanks to the artificial viscous damping, the dNNM can be treated as periodic solutions, and both HBM, as well as the shooting method, can be applied [11]. Jahn et al. [8] compares both concepts using two illustrative test cases. Furthermore, there is no justification why viscous damping is preferred in the EPMC. In this work, a variant of EPMC with artificial hysteretic damping is first attempted. From the author’s knowledge, it still is an open question in the literature which damping mechanism is preferred in EPMC. For the sake of clarity, in the following EPMC with artificial viscous damping as proposed by Krack [11] is called EPMC-V and the one with hysteretic damping is named as EPMC-H. In this work, the CNM and the two variants of EPMC (EPMC-V and EPMC-H) are compared in detail using four illustrative test cases and one engineering application.

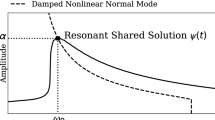
The use of the nonlinear modal analysis is usually limited by the disadvantage that the relation between the NNM and resonant solutions in forced response cannot be directly accessed. Thus, a direct relationship between the NNM and the resonant solutions in forced response has great practical importance in that the response amplitude at resonance is the information of most interest for engineers. The energy balance method (EBM) is a tool that relates the NNM solutions to the resonant solutions of the forced response in conservative nonlinear systems and can predict where the crossing between the forced response and the underlying NNM would occur. This crossing point is called “resonant shared solution” in [7]. Cenedese and Haller [4] provide a systematic mathematical analysis based on the Melnikov function, to identify the conditions under which conservative periodic orbits perturb into resonances of the forced response, thus defining the conditions of applicability of methods like the EBM. The EBM method in its original definition is applicable only to conservative nonlinear forces. In previous work from the authors [29], the EBM has been successfully extended to systems with non-conservative nonlinear characteristics by using their dNNMs. This extended EBM (E-EBM) was derived based on the EPMC [29]. E-EBM has been proven to be an efficient method to identify the direct relation between the dNNM and the resonant solutions in the nonlinear forced response for systems with frictional contact. In addition to the E-EBM, the nonlinear modal synthesis (NMS) is another method to establish a relation between the NNMs and the resonant solutions in forced response. The modal synthesis can be simply applied in a linear system, because of the superposition principle and orthogonality conditions between the linear normal modes. However, these relationships are invalid in a nonlinear system, so further assumptions are required. Krack et al. [14] described the NMS using CNM based on the single-nonlinear-mode theory [34]. In the present work, both E-EBM and NMS will be derived based on CNM and two variants of EPMC. Furthermore, E-EBM and NMS will be used to predict the resonant solutions for various systems with non-conservative nonlinearities.

In the present study, a comprehensive comparison is achieved for: (a) two concepts for dNNM computation including CNM and two variants of EPMC; (b) two numerical methods for resonant prediction including E-EBM and NMS. Two one Degree of Freedom (1-DoF) systems and an industrial application are tested: a 1-DoF system with frictional contact, a 1-DoF system with quadratic nonlinear damping and a full-scale blisk with friction ring damper. Then, the resonant solutions in forced responses are predicted using the dNNM and two numerical methods (E-EBM and NMS). This paper is organised as follows: the numerical formulations used to compute the dNNM are given in Sect. 2 followed by a detailed discussion of the advantages and limitations of CNM and two variants of EPMC; then, the E-EBM is introduced and explained in Sect. 3.2; after that, the formula used for the NMS is derived in Sect. 3.3; a detailed evaluation between E-EBM and NMS is also provided in Sect. 3. Section 4 shows the results from two illustrative 1-DoF systems. Then, a blisk with friction ring damper, as an industrial application, is described and results are given in Sect. 5 followed by the conclusions.

2 Damped nonlinear normal mode

In this section, two different concepts (CNM and EPMC) used to extend the periodic motion definition of the nonlinear modes in a non-conservative system will be described. Thanks to both concepts, the dNNMs in a system with non-conservative nonlinearities can be computed using the classic HBM in frequency domain [11, 12, 25]. In a nonlinear Equation of Motion (EoM), the nonlinear forces in the frequency domain are computed in an iterative scheme using the alternating frequency/time method (AFT) [3, 12, 25]. In addition, the well-known continuation technique is used to track the evolution of the dNNM with respect to the energy of the system.

In classic HBM, the EoM is solved in the frequency domain and solutions in the time domain are discretised by the Fourier series. The general EoM for the computation of the dNNM is given in the first, as Eq. (1). The dNNMs are usually considered as solutions of a system, where the linear damping and the external excitation force are not taken into account. $\underline{\underline{\mathbf{M }}}$ is the mass matrix; $\underline{\underline{\mathbf{K }}}$ is the stiffness matrix. $\underline{Q}(t)$ is the solution of the autonomous system. The double underline of the symbol represents matrices and the single underline of the symbol is used to represent vectors, and variable t does not appear explicitly in the following equations in this work. $\underline{F}_{\mathrm{nl}}$ is the non-conservative nonlinear force within the autonomous system. The basic assumptions and formulations are explained for different concepts, respectively.

$$\begin{aligned} \underline{\underline{\mathbf{M }}}\,\underline{\ddot{Q}}+\underline{\underline{\mathbf{K }}}\, \underline{Q}+\underline{F}_{\mathrm{nl}}(\underline{Q},\,\underline{\dot{Q}})= 0. \end{aligned}$$

(1)

2.1 Complex nonlinear mode

In a dynamic system with non-conservative nonlinear forces, solutions in Eq. (1) are not periodic any more. In CNM, the dNNMs are formulated by damped solutions, using multi-harmonic periodic function with an exponential decay, as shown in Eq. (2). n is the order of harmonics up to $N_{h}$ and j represents the imaginary parts. $\omega _{d}$ is the damped resonant frequency and $\beta$ is the loss factor, where $\omega _{d} = \omega _{0}\sqrt{1-\zeta ^{2}}$ and $\beta = \zeta \omega _{0}$. $\omega _{0}$ is the resonant frequency and $\zeta$ is the modal damping ratio. $\underline{\tilde{Q}}_{n}$ is the Fourier coefficients for nth order of harmonic.

$$\begin{aligned} \underline{Q}(t)= \mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{Q}}_{n}e^{(-n\beta +jn\omega _{d})t}}\right\} ;\,\,\, \underline{\tilde{Q}}_{n}= \underline{\tilde{Q}}^{c}_{n}-j\underline{\tilde{Q}}^{s}_{n}.\nonumber \\ \end{aligned}$$

(2)

Substitute Eq. (2) into Eq. (1), then the EoM can be rewritten as Eq. (3). $\underline{\tilde{F}}_{\mathrm{nl},\,n}$ is the nonlinear force in frequency domain for the nth order of harmonic. Then, Eq. (3) governs the dynamic equilibrium in frequency domain for the nth order of harmonic. $\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}$ is the complex dynamic stiffness for CNM and is assembled as represented in Eqs. (5, 7). The superscript $^{\mathrm{cnm}}$ represents the CNM. $\underline{\tilde{Q}}$ is a collection of Fourier coefficients representing the solutions: $\underline{\tilde{Q}}=[ \underline{\tilde{Q}}_{n=0}, \underline{\tilde{Q}}_{n=1},\ldots ,\underline{\tilde{Q}}_{n=N_{h}}]^{\text {T}}$. $\underline{\tilde{F}}_{\mathrm{nl}}$ is a collection of Fourier coefficients representing the nonlinear force: $\underline{\tilde{F}}_{\mathrm{nl}}=[ \underline{\tilde{F}}_{\mathrm{nl},\,n=0}, \underline{\tilde{F}}_{\mathrm{nl},\,n=1},\ldots ,\underline{\tilde{F}}_{\mathrm{nl},\,n=N_{h}}]^{\text {T}}$. $\underline{\mathcal {R}}$ is the residual of the EoM in frequency domain.

$$\begin{aligned}&\underline{\mathcal {R}}_{n} = (-n\beta +jn\omega _{d})^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}+\underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{n}+\underline{\tilde{F}}_{\mathrm{nl},\,n}(\underline{\tilde{Q}})\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned}&\underline{\mathcal {R}} = \underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}\,\underline{\tilde{Q}}+\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}}) \end{aligned}$$

(4)

$$\begin{aligned}&\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}=\begin{bmatrix}\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}_{n=0}&{}\underline{\underline{\mathbf{0 }}}&{}\ldots &{}\underline{\underline{\mathbf{0 }}}\\ [0.5ex]\underline{\underline{\mathbf{0 }}}&{}\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}_{n=1}&{}\ldots &{}\underline{\underline{\mathbf{0 }}}\\ [0.5ex]\vdots &{}\vdots &{}\ddots &{}\vdots \\ [0.5ex]\underline{\underline{\mathbf{0 }}}&{}\underline{\underline{\mathbf{0 }}}&{}\ldots &{}\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}_{n=N_{h}}\end{bmatrix} \end{aligned}$$

(5)

$$\begin{aligned}&\underline{\underline{\mathbf{Z }}}^{\mathrm{cnm}}_{ n}= \underline{\underline{\mathbf{K }}}\,-n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}\,-\underline{\underline{\bar{\mathbf{C }}}}_{n}^{\mathrm{cnm}} \end{aligned}$$

(6)

$$\begin{aligned}&\underline{\underline{\bar{\mathbf{C }}}}_{n}^{\mathrm{cnm}} =-2n^2\omega _{0}^2\zeta ^2 \underline{\underline{\mathbf{M }}}+2jn^2\omega _{0}^2\zeta \sqrt{1-\zeta ^{2}}\underline{\underline{\mathbf{M }}}. \end{aligned}$$

(7)

In CNM, both damped and undamped solutions can be reconstructed using the Fourier coefficients. To build an undamped solution, the resonant frequency $\omega _{0}$ and a zero loss factor $\beta$ are considered for Eq. (2), whereas the damped frequency $\omega _{d}$ and the actual loss factor $\zeta \omega _{0}$ govern the damped solution.

2.2 Extended periodic motion concept

In a system with non-conservative nonlinearities, the dNNMs are not periodic due to the energy exchanged by the non-conservative nonlinear force. In EPMC, an artificial damping term is introduced to balance the energy loss [11]. Thanks to this artificial damping, the energy loss is compensated and solutions of such a system become periodic. The damping ratio of the artificial damping is a free variable and will be determined in the computation of the dNNM. For example, in a system with friction damping, the energy dissipated because of the rubbing motion within the contact interface results in negative artificial damping. Then, energy dissipated by frictional contact is made up by this negative artificial damping effect. Finally, a periodically based dNNM can be obtained.

Two different types of artificial damping terms are explained: artificial viscous damping originally proposed by Krack [11] and artificial hysteretic damping firstly attempted by authors. In practice, there are two types of common damping mechanisms in both physical and mathematical concept: viscous damping and hysteretic (structural damping). Viscous damping mechanism usually denotes the fact that, in a microscopic view, the energy dissipation is caused by the resistive force while molecules of fluids are rubbing together. This resistive force opposes the velocity of molecules within fluids. Mathematically, viscous damping refers to a velocity proportional force as a product of a general damping matrix and a velocity vector, whereas hysteretic damping can be considered as the friction force between molecular layers within solids. Thus, the hysteretic damping force is proportional to the displacement from its equilibrium position. The hysteretic damping effect is mathematically achieved by using an imaginary stiffness, which guarantees a 90-degree phase shift relative to its original stiffness component. Compared to viscous damping, hysteretic damping is independent of the frequency. Both types of damping can be used in EPMC as an artificial damping term to balance the energy exchanged caused by the non-conservative nonlinear force. The EPMC with artificial viscous damping is named EPMC-V and the one with artificial hysteretic damping is named EPMC-H.

Thanks to the artificial damping term, a periodic solution can be assumed for Eq. (1) and similarly solved by classic HBM with CNM. Besides the HBM method, other methods can be used in EPMC to solve the EoM, i.e. shooting method, which is not applicable in CNM due to the aperiodicity. The periodic solutions expressed using multi-harmonics are shown in Eq. (8), where $\omega _{0}$ is the resonant frequency of the nonlinear autonomous system.

$$\begin{aligned} \underline{Q}(t)= \mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{Q}}_{n}e^{jn\omega _{0}t}}\right\} ;\,\,\, \underline{\tilde{Q}}_{n}= \underline{\tilde{Q}}^{c}_{n}-j\underline{\tilde{Q}}^{s}_{n}. \end{aligned}$$

(8)

2.2.1 Artificial viscous damping

A negative artificial viscous damping is introduced into Eq. (1) and the EoM becomes Eq. (9). $\zeta$ is the modal damping ratio. By substituting Eq. (8) into Eq. (9) for each harmonic order, the EoM in frequency domain is obtained as Eqs. (12, 13). $\underline{\underline{\mathbf{Z }}}^{ev}$ is the complex dynamic stiffness matrix and in the similar form with Eq. (5), and the superscript $^{ev}$ represents the EPMC-V.

$$\begin{aligned}&\underline{\underline{\mathbf{M }}}\,\underline{\ddot{Q}}-2\zeta \omega _{0}\underline{\underline{\mathbf{M }}}\,\underline{\dot{Q}}+\underline{\underline{\mathbf{K }}}\, \underline{Q}+\underline{F}_{\mathrm{nl}}(\underline{Q})= 0 \end{aligned}$$

(9)

$$\begin{aligned}&\underline{\mathcal {R}}_{n} =(jn\omega _{0})^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}-2jn\zeta \omega _{0}^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}+\underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{n}\nonumber \\&\quad +\,\underline{\tilde{F}}_{\mathrm{nl},\,n}(\underline{\tilde{Q}}) \end{aligned}$$

(10)

$$\begin{aligned}&\underline{\mathcal {R}} =\underline{\underline{\mathbf{Z }}}^{ev}\,\underline{\tilde{Q}}+\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}}) \end{aligned}$$

(11)

$$\begin{aligned}&\underline{\underline{\mathbf{Z }}}^{ev}_{ n}= \underline{\underline{\mathbf{K }}}-n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}\,-\underline{\underline{\bar{\mathbf{C }}}}_{n}^{ev} \end{aligned}$$

(12)

$$\begin{aligned}&\underline{\underline{\bar{\mathbf{C }}}}_{n}^{ev} =2jn\omega _{0}^2\zeta \underline{\underline{\mathbf{M }}}. \end{aligned}$$

(13)

2.2.2 Artificial hysteretic damping

A negative artificial hysteretic damping is introduced into the system to balance the energy dissipated by the non-conservative nonlinear force. The hysteretic damping is related to the linear stiffness and defined as $2j\zeta \,\underline{\underline{\mathbf{K }}}\,\underline{Q}$. The hysteretic can be only defined in the frequency domain, therefore, the EoM for EPMC-H is directly shown in the frequency domain as Eqs. (14, 15). The superscript $^{eh}$ represents the EPMC-H. $\underline{\underline{\mathbf{Z }}}^{eh}$ has a similar form with Eq. (5).

$$\begin{aligned} \underline{\mathcal {R}}_{n}= & {} (jn\omega _{0})^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}\,+(1-2j\zeta )\,\underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{n}\,\nonumber \\&+\,\underline{\tilde{F}}_{\mathrm{nl},\,n}(\underline{\tilde{Q}}) \end{aligned}$$

(14)

$$\begin{aligned}&\underline{\mathcal {R}}=\underline{\underline{\mathbf{Z }}}^{eh}\,\underline{\tilde{Q}}+\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}}) \end{aligned}$$

(15)

$$\begin{aligned}&\underline{\underline{\mathbf{Z }}}^{eh}_{ n}= \underline{\underline{\mathbf{K }}}-n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}-\underline{\underline{\bar{\mathbf{C }}}}_{n}^{eh} \end{aligned}$$

(16)

$$\begin{aligned}&\underline{\underline{\bar{\mathbf{C }}}}_{n}^{eh}=2j\zeta \underline{\underline{\mathbf{K }}}. \end{aligned}$$

(17)

2.3 Energy dependency and normalisation

Unlike linear normal modes, the nonlinear mode and its modal properties are highly modal energy-dependent. The dNNM $\underline{Q}$ and the resonant frequency $\omega _{0}$ vary with the level of energy within the nonlinear system. To capture this modal energy dependence, a new parameter, modal amplitude $\alpha$, is introduced into the system to quantify the modal energy. Then, modal displacement can be expressed as: $\underline{Q}= \alpha \cdot \underline{Q}_{m}$, where $\underline{Q}_{m}$ is the mass normalised modal displacement. The modal amplitude is the chasing parameter used in the continuation technique [1] to track the evolution of a specific dNNM with respect to the modal energy. The EoM for the computation of dNNM in the frequency domain is provided as Eq. (18). $\underline{\underline{\mathbf{Z }}}$ is the general dynamic stiffness matrix for both CNM and EPMC. The mass normalised modal displacement is achieved by applying Eq. (19) as a constraint. Besides, the absolute phase of the dNNM is arbitrary. Therefore, a phase normalisation is required and shown in Eq. (20).

$$\begin{aligned}&\alpha \cdot \underline{\underline{\mathbf{Z }}}\,\underline{\tilde{Q}}_{m}+\underline{\tilde{F}}_{\mathrm{nl}}(\alpha ,\, \underline{\tilde{Q}}_{m})= 0 \end{aligned}$$

(18)

$$\begin{aligned}&\underline{\tilde{Q}}_{m}^{\text {T}}\cdot (\underline{\underline{\mathbf{I }}}^{N_{h}}\otimes \underline{\underline{\mathbf{M }}})\cdot \underline{\tilde{Q}}_{m}= 1 \end{aligned}$$

(19)

$$\begin{aligned}&\text {imag}(\tilde{Q}_{m, n=1}^{1})=0. \end{aligned}$$

(20)

2.4 Alternating frequency/time method

The classic HBM is used to solve dynamic equations in frequency domain referring to Eqs. (4, 11, 15). The nonlinear force in frequency domain is represented by $\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}})$. It is complicated and expensive to directly compute the nonlinear force in the frequency domain, especially for frictional contact. Therefore, instead of a direct computation of the nonlinear force in frequency domain, the classic AFT method is used to calculate $\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}})$ [3, 12]. In the AFT method, $\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}})$ is calculated in an iterative scheme, alternating between the frequency and time domain, as demonstrated in Fig. 1. Different calculations are performed in different domains within the AFT scheme. AFT method can be only applied based on the fact that the solutions $\underline{Q}(t)$ and nonlinear force $\underline{F}_{\mathrm{nl}}(t)$ are all in a periodic form. The computation of the Jacobian matrices can be found in [24].

Fig. 1

Alternating frequency/time method

In EPMC, artificial damping is introduced to compensate for the energy exchanged leading to a periodic dNNM. Therefore, the AFT method can be directly applied to EPMC without any further assumption, whereas in CNM, the solutions of dNNM are assumed to be a sinusoidal solution with exponential decay leading to a damped solution instead of a periodic one. In the classic AFT process, the discrete Fourier transform is applied, whereas the exponential decay term cannot be specifically addressed. The non-conservative terms cannot be included in the nonlinear force by using the AFT method. Therefore, to adopt the classic AFT method into CNM, the terms that represent the exponential decay are simply eliminated leading to a periodic solution as described in [17]. In [8], a phase correction of the nonlinear force is applied to capture the decay term in CNM, whereas this phase correction can only be applied to a single DoF system analytically. In this work, the damped solutions from CNM are assumed to be periodic in the AFT procedure and terms representing the exponential decay are simply removed.

2.5 Continuation technique

For each value of the modal amplitude $\alpha$, the dNNM and its modal properties, i.e. the resonant frequency $\omega _{0}$ and the modal damping ratio $\zeta$ can be computed by solving Eqs. (18–20) using Newton’s method. In the nonlinear modal analysis, the evolution of the dNNM and its modal properties along the modal amplitude has great importance to understand the dynamics of such a nonlinear system. Therefore, the continuation technique [1] is used to track the evolution of dNNM and its modal properties along with the modal amplitude $\alpha$. This continuation technique is also used in the computation of the nonlinear forced response with respect to the excitation frequency.

In a classic continuation process, each step consists of two parts: a predictor and a corrector. In the predictor, the initial solutions are predicted based on a certain algorithm. Then, this predicted solution is iteratively converged to the actual solution following a correction constrain. In the present study, a secant predictor and an arclength corrector is used [1].

2.6 Discussion

To extend the periodic motion concept of the NNM for a nonlinear system with non-conservative nonlinearities, there are two concepts in the literature, namely CNM and EPMC. The former one used the concept of the complex mode and the dNNM is represented by a harmonic periodic solution with exponential decay. The latter one introduces an artificial damping term to balance the energy dissipated by the non-conservative nonlinear forces. Artificial viscous damping is used in the original EPMC (it is named EPMC-V) and artificial hysteretic damping is firstly attempted in the present work (referred EPMC-H). The numerical formulations for CNM and two variants of EPMC are derived in detail in this section. From the numerical perspective, several points are listed in Table 1.

Table 1 Comparison between complex nonlinear mode and two variants of extended periodic motion concept

The dynamic stiffness matrices in frequency domain for both concepts can be represented by: $\underline{\underline{\mathbf{K }}}-n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}-\underline{\underline{\bar{\mathbf{C }}}}_{n}$. The only difference is the $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ matrix, which has been derived in Eqs. (7, 13, 17) and is shown in Table 1. The $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ represents the dissipative term in the nonlinear EoM in frequency domain. The analytical Jacobian matrices of the $\delta \underline{\underline{\bar{\mathbf{C }}}}_{n}/\delta \omega _{0}$ and $\delta \underline{\underline{\bar{\mathbf{C }}}}_{n}/\delta \zeta$ are also provided in the table. One can always notice that EPMC-H has the simplest formulations for Jacobian matrices comparing with CNM and EPMC-V leading to a lower computational costs, this statement will be further discussed in Sect. 5.

In CNM, the solutions are assumed as the harmonic solution with exponential decay. To solve the EoM in the frequency domain, the AFT is a widely used method if the nonlinear forces cannot be explicitly defined in the frequency domain, whereas in the AFT procedure, it is complicated to treat the exponential decay terms. Most works of literature directly ignore the decay terms in AFT [18]. This treatment of the decay terms might raise the error if the system shows a large damping ratio.

As described in Sect. 2.2, there are two common damping models in physical and mathematical perspective: viscous damping and hysteretic damping. Both damping models can be used as an artificial damping term in the EPMC to study the dNNM for a system with a non-conservative nonlinear force. From the numerical formulations of the EPMC-V and EPMC-H [see Eqs. (12, 16)], the modal damping ratio from both EPMC-V and EPMC-H can be computed. There is a constant ratio between modal damping ratios computed from EPMC-V and EPMC-H if only the fundamental harmonic is present (or the solutions are dominated by the fundamental harmonic). In more detail, if the modal damping ratio from EPMC-H is $\zeta _{h}$ and $\zeta _{v}$ represents the modal damping ratio from EPMC-V. Then, the relation between $\zeta _{h}$ and $\zeta _{v}$ is governed by $\zeta _{h} = \zeta _{v}(\omega _{0}/\omega _{n})^2$, where $\omega _{0}$ is the resonant frequency of the dNNM and $\omega _{n}$ is the natural frequency of the linear mode. If a higher-order harmonic is responded, the artificial damping terms with different damping assumptions might affect the solutions. This statement will be further discussed in Sect. 4.2.2.

In EPMC, an artificial damping term is introduced to balance the energy dissipated by the non-conservative nonlinear force. Therefore, using the classic numerical methods to solve the EoM is achievable. If artificial viscous damping is introduced, both time domain methods (i.e. shooting method) and frequency domain methods (i.e. HBM) can be used, whereas for EPMC-H, the EoM can only be solved in the frequency domain. Furthermore, the application of the classic Floquet theorem to analyse the asymptotic stability of the periodic motions is possible for EPMC-V but not for EPMC-H, whereas Hill’s method can be used to investigate the stability of solutions in the frequency domain for EPMC-H [21].

The use of dNNM for experimental testing is also an important topic in the field of nonlinear dynamics. Although the experimental testing is clearly out of the scope of the present work, some comments about the application of CNM and EPMC in the experimental testing are briefly discussed. As for EPMC, in [35, 36], the complex stiffness was measured to determine the frequency and damping of the forced system. Therefore, using EPMC-H can provide a straightforward representation of the complex stiffness measured from the experiment, whereas the EPMC-V can be used for nonlinear modal testing by adding a velocity feedback [27].

3 Predicting resonant solution

In Sect. 2, the numerical methods used for the computation of dNNMs based on two concepts, CNM and EPMC, have been derived in detail. In this section, two numerical methods, E-EBM and NMS, for predicting the resonant solutions using dNNM are introduced and described. Then, a detailed evaluation is also provided in the last part of this section.

3.1 Computation of forced response

The general EoM in a forced system with non-conservative nonlinear forces is given in Eq. (21). $\underline{\underline{\mathbf{C }}}$ is the known symmetric damping matrix of the system. $\underline{Q}_{f}$ is the dynamic response of the forced system. $\underline{F}_{ e}$ is the external excitation force, $\underline{\hat{F}}_{ e}$ is a real unit vector of the excitation force and $\gamma$ is the excitation forcing level. $\Omega$ is the excitation frequency; $\varphi$ is the absolute phase of the excitation force. In this work, the external excitation force is considered as a simple harmonic excitation and the solution of the system is represented by multi-harmonics. After applying the HBM, the EoM can be transferred into the frequency domain and the residual of the EoM is given in Eq. (23). $\underline{\underline{\mathbf{Z }}}^{f}$ is the complex dynamic stiffness matrix and the superscript $^{f}$ represents the forced response. $\underline{\underline{\mathbf{Z }}}^{f}$ has a similar form with Eq. (5). The nonlinear forced response can be simply solved using the classic HBM, the AFT method and the continuation technique. In the continuation technique, the excitation frequency $\Omega$ is used as the chasing parameter in the computation of forced response.

$$\begin{aligned}&\underline{\underline{\mathbf{M }}}\,\underline{\ddot{Q}}_{f}+\underline{\underline{\mathbf{C }}}\,\underline{\dot{Q}}_{f}+\underline{\underline{\mathbf{K }}}\, \underline{Q}_{f}+\underline{F}_{\mathrm{nl}}(\underline{Q}_{f},\,\underline{\dot{Q}}_{f})\nonumber \\&\quad = \underline{F}_{ e}(\gamma , \Omega , \varphi ,t) \end{aligned}$$

(21)

$$\begin{aligned}&\underline{Q}_{f}(t) = \mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{Q}}_{f,\, n}e^{jn\Omega t}}\right\} ;\,\,\, \underline{F}_{ e}= \mathfrak {R}\{\gamma \underline{\hat{F}}_{ e}e^{j(\Omega t+\varphi )}\}\nonumber \\ \end{aligned}$$

(22)

$$\begin{aligned}&\underline{\mathcal {R}}_{n}^{f} = (jn\Omega )^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{f,\,n}\,+jn\Omega \,\underline{\underline{\mathbf{C }}}\,\underline{\tilde{Q}}_{f,\,n}\,+\underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{f,\,n}\,\nonumber \\&\qquad \qquad +\underline{\tilde{F}}_{\mathrm{nl},\,n}(\underline{\tilde{Q}}_{f})-\left\{ \begin{matrix} \gamma e^{j\varphi }\underline{\hat{F}}_{ e}&{}\quad \text {if}&{}\quad n=1\\ \underline{\mathbf{0 }}&{}\quad \text {if}&{}\quad n\ne 1 \end{matrix} \right. \end{aligned}$$

(23)

$$\begin{aligned}&\underline{\mathcal {R}}^{f} =\underline{\underline{\mathbf{Z }}}^{f}\,\underline{\tilde{Q}}_{f}+\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}}_{f})-[ \underline{\mathbf{0 }}, \gamma e^{j\varphi }\underline{\hat{F}}_{ e},\ldots ,\underline{\mathbf{0 }}]^{\text {T}} \end{aligned}$$

(24)

$$\begin{aligned}&\underline{\underline{\mathbf{Z }}}^{f}_{ n}=\underline{\underline{\mathbf{K }}}-n^2\Omega ^2\underline{\underline{\mathbf{M }}}+jn\Omega \,\underline{\underline{\mathbf{C }}}. \end{aligned}$$

(25)

3.2 Extended energy balance method

Resonant solutions of forced responses have great significance in many engineering problems. The E-EBM is a tool to predict the resonant solution in a forced system with non-conservative nonlinearities using its dNNM. E-EBM is based on the assumption that the resonant solution shows a high similarity with the dNNM. The numerical formulations of the E-EBM based on different concepts of the dNNM, including CNM and EPMC, are described in this section. The residual of the EoM in frequency domain for the computation of dNNMs is provided in Eq. (26), where $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ has been defined in Eqs. (7, 13, 17) and Table 1 for CNM and EPMC.

The E-EBM assumes that the resonant solution of nonlinear forced response and that of the dNNM are similar for small enough levels of damping and force. Therefore, these solutions can be assumed to be identical, and have been named as “resonant shared solutions”. The solution of an autonomous system bears resemblance to that of the nonlinear forced response at resonance. As shown in Eq. (27), when the excitation frequency $\Omega$ equals to the resonant frequency $\omega _{0}$. The dNNM and the resonant solutions are represented by the resonant shared solutions $\underline{\psi }$. Figure 2 shows an example of a resonant shared solution. Each solution points along the dNNM can be considered as a resonant shared solution with the nonlinear forced response with a certain excitation forcing level.

$$\begin{aligned}&\underline{\mathcal {R}}_{n}^{dnnm}= -n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}\,-\underline{\underline{\bar{\mathbf{C }}}}_{n} \underline{\tilde{Q}}_{n}\,\nonumber \\&\qquad \qquad \quad +\,\underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{n}\,+\underline{\tilde{F}}_{\mathrm{nl}\,n}(\underline{\tilde{Q}}) \end{aligned}$$

(26)

$$\begin{aligned}&\text {When}\,\Omega = \omega _{0} : \left\{ \begin{aligned}&\underline{\psi } = \underline{Q} \approx \underline{Q}_{f} \\[3ex]&\underline{\tilde{\psi }}=\alpha \cdot \underline{\tilde{Q}}_{ m}\approx \underline{\tilde{Q}}_{f}\end{aligned} \right. \end{aligned}$$

(27)

$$\begin{aligned}&\left. \begin{aligned}&\underline{\psi } = \mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{\psi }}_{n}e^{jn\omega _{0}t}}\right\} ;\\&\underline{Q} = \alpha \,\mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{Q}}_{m,\,n}e^{jn\omega _{0}t}}\right\} ;\\&\underline{Q}_{f} = \mathfrak {R}\left\{ \sum _{n=0}^{N_{h}} {\underline{\tilde{Q}}_{f,\,n}e^{jn\Omega t}}\right\} .\end{aligned} \right. \end{aligned}$$

(28)

Fig. 2

Demonstration of resonant shared solution between damped nonlinear normal mode and nonlinear forced response

For each level of the modal amplitude $\alpha$, the resonant shared solution $\underline{\psi }$, the resonant frequency $\omega _{0}$ and the modal damping ratio $\zeta$ are calculated using according to CNM or EPMC. The excitation forcing level $\gamma$ and the absolute phase of the excitation force $\varphi$ can be determined using the E-EBM if the damping matrix $\underline{\underline{\mathbf{C }}}$ and the vector of the excitation force $\underline{\hat{F}}_{ e}$ is given. Recalling Eqs. (24, 26) and assuming that the solution of the nonlinear forced response equals the resonant shared solution $\underline{\psi }$, the subtraction of Eqs. (26)–(24) must hold in its weak form. Then, the energy exchanged caused by the damping terms $E^{d}$ (or the forcing term $E^{f}(\gamma , \varphi )$) can be calculated by integrating the damping force (or the excitation force) times the velocity over one vibrational period $2\pi /\omega _{0}$. The calculation of $E^{f}(\gamma , \varphi )$ is given in Eq. (29) and it is same for both CNM and EPMC. Equations used for calculation of $E^{d}$ are described Eqs. (30–31). It is worth mentioning that $E^{d}$ includes two parts: the energy dissipated by the viscous damping $\underline{\underline{\mathbf{C }}}$ and dissipative term $\underline{\underline{\bar{\mathbf{C }}}}_{n}$. $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ has been defined in Eqs. (7, 13, 17) and Table 1 for CNM and EPMC.

$$\begin{aligned}&\left. \begin{aligned}E^{f}(\gamma , \varphi )&= E_{n=1}^{f}(\gamma , \varphi ) \\[2ex]&=\int _{0}^{\frac{2\pi }{\omega _{0}}}(j\omega _{0}\underline{\tilde{\psi }}_{1}e^{j\omega _{0} t})\cdot (\gamma e^{j\varphi }\underline{\hat{F}}_{ e,} e^{j\omega _{0} t})\,\,\,\delta t \\[2ex]&=\int _{0}^{\frac{2\pi }{\omega _{0}}}(j\omega _{0}\underline{\tilde{\psi }}_{1}e^{j\omega _{0} t})\cdot (\gamma e^{j\varphi }\underline{\hat{F}}_{ e,} e^{j\omega _{0} t})\,\,\,\delta t \\[2ex]&= \pi \mathfrak {R}\{\gamma \,e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\underline{\hat{F}}_{ e}\} \end{aligned} \right. \end{aligned}$$

(29)

$$\begin{aligned}&\left. \begin{aligned}E_{n}^{d}&=\int _{0}^{\frac{2\pi }{\omega _{0}}} \sum _{n=0}^{N_{h}} (jn\omega _{0}\underline{\tilde{\psi }}_{n}e^{jn\omega _{0} t})\cdot (jn\omega _{0}\,\underline{\underline{\mathbf{C }}}+\underline{\underline{\bar{\mathbf{C }}}}_{n})\\&\quad \cdot \,\underline{\tilde{\psi }}_{n}e^{jn\omega _{0} t}\,\,\,\delta t \\[2ex]&=\sum _{n=0}^{N_{h}}\pi \,\mathfrak {R}\{n^2\omega _{0}\,\underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{n}\,+n \underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\bar{\mathbf{C }}}}_{n} \underline{\tilde{\psi }}_{n}\} \end{aligned} \right. \end{aligned}$$

(30)

$$\begin{aligned}&\gamma = \frac{\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\underline{\hat{F}}_{ e} \}}{\sum _{n=0}^{N_{h}} \mathfrak {R}\{n^2 \omega _{0}\,\underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{n}\,+n\, \underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\bar{\mathbf{C }}}}_{n} \underline{\tilde{\psi }}_{n}\}}. \end{aligned}$$

(31)

In Sect. 2, the dNNM $\underline{Q}$, the resonant frequency $\omega _{0}$ and the modal damping ratio $\zeta$ are computed for a range of modal amplitude $\alpha$ using the formula in Sect. 2. For each particular value of $\alpha$, the dNNM can be seen as the resonant shared solution of a nonlinear forced response with a certain excitation forcing level $\gamma$. The energy exchanged by the damping terms $E^{d}$ and the forcing term $E^{f}(\gamma ,\varphi )$ are computed for each value of $\alpha$ using Eqs. (29–31). $E^{d}$ is a constant value for a given resonant shared solution, whereas $E^{f}$ depends on the value of forcing level $\gamma$ and forcing phase $\varphi$ [see Eq. (29)].

Fig. 3

The energy transferred by the damping term ($E_{d}$) for a fixed modal amplitude $\alpha$ and the energy transferred by the forcing terms ($E_{f}(\gamma , \varphi )$) for different excitation levels $\gamma$ with respect to the forcing phase $\varphi$

Figure 3 demonstrates the relation between the energy exchanged by the damping terms $E^{d}$ and the forcing term $E^{f}(\gamma ,\varphi )$. As shown in Fig. 3, the energy transfer caused by damping terms $E_{d}$ is constant for a certain level of modal amplitude $\alpha$, whereas the energy exchanged by the external excitation $E_{f}(\gamma , \varphi )$ varies with the forcing phase $\varphi$ and the excitation forcing level $\gamma$. To determine $\varphi$ and $\gamma$ is to find the single intersection between the curve of $E^{f}(\gamma , \varphi )$ and the constant value of $E^{d}$ that will occur at the maximum (if $E^{d}>0$) or the minimum (if $E^{d}<0$) of $E_{f}(\gamma , \varphi )$. Thus, a classic force amplitude curve can be built, if this operation is carried out for each value of modal amplitude $\alpha$. In a system with non-conservative nonlinear force, the modal damping ratio $\zeta$ can be either positive (like systems with nonlinear damping) or negative (systems with self-excited solutions). Based on the value of $E^{d}$ and $\zeta$, there are four situations in total. Readers are invited to refer to [29] for a detailed description. This work only focuses on the system with nonlinear damping, where $E^{d}>0$ and $\zeta >0$.

3.3 Nonlinear modal synthesis

The forced response of a linear system can be reconstructed from its linear normal modes. The synthesis of linear normal modes is very efficient thanks to the orthogonality condition and superposition principle [14], whereas in a nonlinear system, both orthogonality conditions and superposition principle are not valid anymore. Therefore, to achieve the NMS in a nonlinear system, a single-nonlinear-resonant-mode theory is applied [9]. According to this theory, the general dynamic response of a nonlinear system can be seen as a combination of a single nonlinear mode and a collection of linearised modes. The internal resonance is not considered under this assumption. The NMS can be used to construct the full nonlinear forced response using the nonlinear modes. This work aims to provide a detailed evaluation between NMS and E-EBM. Therefore, only the resonant solutions in the nonlinear forced responses are of interest. Readers are invited to refer to [14] for a detailed description of NMS. In [14], the NMS is applied on the dNNM computed using CNM with only the fundamental harmonic, whereas in the present work, the formula of NMS is derived from both CNM based dNNMs and EPMC based dNNMs with the consideration of multi-harmonics.

The EoM for nonlinear forced response in the frequency domain is provided as Eqs. (23, 24). The nonlinear force $\underline{\tilde{F}}_{\mathrm{nl}}(\underline{\tilde{Q}}_{f})$ is treated as a combination of an equivalent stiffness matrix $\underline{\underline{\mathbf{K }}}_{\mathrm{eq}}(\underline{\tilde{Q}}_{f})$ and an equivalent damping force $\underline{\tilde{D}}(\underline{\tilde{Q}}_{f})$. The equivalent stiffness matrix is used to represent the stiffening or softening effects caused by the nonlinear force, whereas the equivalent damping force indicates the dissipative effect from this non-conservative nonlinear force. Thus, the total nonlinear stiffness of the system is represented by $\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}(\underline{\tilde{Q}}_{f})$, which can be seen as a summation of the linear stiffness matrix $\underline{\underline{\mathbf{K }}}$ and the equivalent stiffness matrix $\underline{\underline{\mathbf{K }}}_{\mathrm{eq}}(\underline{\tilde{Q}}_{f})$, $\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}(\underline{\tilde{Q}}_{f}) = \underline{\underline{\mathbf{K }}}\, +\underline{\underline{\mathbf{K }}}_{\mathrm{eq}}(\underline{\tilde{Q}}_{f})$. For a better readability, the dependence of the $\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}$ and $\underline{\tilde{D}}$ on $\underline{\tilde{Q}}_{f}$ does not shown in the following equations. The equivalent damping force $\underline{\tilde{D}}$ can be either viscous damping ($\underline{\tilde{D}}_{n} = 2jnD\omega _{0}^2 \underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{f}$) or hysteretic damping ($\underline{\tilde{D}}_{n} = 2jD \underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{f}$), where D is the actual damping ratio raised from the nonlinear force. Thus, the EoM motion for computation of forced response can be represented by Eq. (32). The similar treatment is also applied to the residual of the dNNM as shown in Eq. (33), where $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ has been defined in Eqs. (7, 13, 17) and is shown in Table 1.

$$\begin{aligned}&\underline{\mathcal {R}}_{n} ^{f}= -n^2\Omega ^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{f,\,n}\,+jn\Omega \,\underline{\underline{\mathbf{C }}}\,\underline{\tilde{Q}}_{f,\,n}\,+\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}\,\underline{\tilde{Q}}_{f,\,n}\,\nonumber \\&\quad + \underline{\tilde{D}}_{n}-\left\{ \begin{matrix} \gamma e^{j\varphi }\underline{\hat{F}}_{ e}&{}\text {if}&{} n=1\\ \underline{\mathbf{0 }}&{}\text {if}&{} n\ne 1 \end{matrix} \right. \end{aligned}$$

(32)

$$\begin{aligned}&\underline{\mathcal {R}}_{n}^{dnnm}= -n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{n}\,-\underline{\underline{\bar{\mathbf{C }}}}_{n} \underline{\tilde{Q}}_{n}\,+\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}\,\underline{\tilde{Q}}_{n}\,+\underline{\tilde{D}}_{n}\nonumber \\ \end{aligned}$$

(33)

According to [14], the full forced response is synthesised by a single nonlinear mode and other linearised modes, whereas the present study focuses on the prediction of the resonant solution. At resonance, the resonant solution of the forced system is represented by a specific dNNM $\underline{\psi }$. Actually, under resonance, the contribution of other linearised modes has already been considered in this dNNM. For easy comparison between E-EBM, this specific dNNM is represented by the same symbol $\underline{\psi }$ with the “resonant shared solution” in E-EBM. $\underline{\psi }$ can be obtained using either CNM or EPMC. When the excitation frequency $\Omega$ equals the resonant frequency $\omega _0$ of dNNM $\underline{\psi }$, the resonant solution is dominated by this specific dNNM $\underline{\psi }$ as shown in Eq. (34). At this situation, the damping ratio D of the equivalent damping force $\underline{\tilde{D}}$ equals the modal damping ratio $\zeta$ of this specific dNNM $\underline{\psi }$. If the CNM and EPMC-V are used in the computation of the dNNM, the equivalent viscous damping ($2jnD\omega _{0}^2 \underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}$) is included [14], whereas in the case of EPMC-H, the equivalent hysteretic damping ($2jD \underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}$) is considered.

$$\begin{aligned} \left. \begin{aligned}\text {When } \Omega = \omega _{0}:&\underline{\tilde{\psi }} = \alpha \cdot \underline{\tilde{Q}}_{m} \approx \underline{\tilde{Q}}_{f};&D = \zeta . \end{aligned}\right. \nonumber \\ \end{aligned}$$

(34)

To determine the excitation forcing level $\gamma$ in NMS, Eq. (32) is formally projected onto each harmonic $\underline{\tilde{\psi }}_{n}e^{jn\omega _{0}t}$. It is important to emphasise that the $\underline{\tilde{\psi }}_{n}^{\text {H}} (-n^2\omega _0^2 \underline{\underline{\mathbf{M }}}\,+ \underline{\underline{\mathbf{K }}}_{\mathrm{nl}})\, \underline{\tilde{\psi }}_{n}= 0$, which is inherently fulfilled in accordance with the residual of dNNM given by Eq. (33).

For the 1st harmonic order with equivalent viscous damping:

$$\begin{aligned}&|-\omega _0^2 \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{\psi }}_{1}\,+j\omega _{0}\,\underline{\tilde{\psi }}_{n}^{\text {H}} \underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{1}\,+\underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{K }}}_{\mathrm{nl}}\,\underline{\tilde{\psi }}_{1}\,\nonumber \\&\quad +\,2j\omega _0^2\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{\psi }}_{1}|= \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\} \end{aligned}$$

(35)

$$\begin{aligned}&|j\omega _{0}\,\underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{1}\,+2j\omega _0^2\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{\psi }}_{1}|\nonumber \\&\quad = \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\} \end{aligned}$$

(36)

$$\begin{aligned}&\gamma _{n=1} = \frac{\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\}}{|j\omega _{0}\underline{\tilde{\psi }}_{1}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{1}\,+2j\omega _0^2\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{\psi }}_{1}|} \end{aligned}$$

(37)

For multi-harmonics:

$$\begin{aligned} \gamma = \frac{\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\}}{\sum _{n=0}^{N_{h}}|jn\omega _{0}\underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{n}\,+2jn\omega _0^2\zeta \underline{\tilde{\psi }}_{n}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{\psi }}_{n}|}\nonumber \\ \end{aligned}$$

(38)

For the 1st harmonic order with equivalent hysteretic damping:

$$\begin{aligned}&|-\omega _0^2 \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{M }}}\,\underline{\tilde{Q}}_{1}\,+j\omega _{0}\,\underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{C }}}\,\underline{\tilde{Q}}_{1}\,\nonumber \\&\quad +\,\underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{K }}}_{\mathrm{nl}}\,\underline{\tilde{Q}}_{1}\,+2j\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{K }}}\,\underline{\tilde{Q}}_{1}|= \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\}\nonumber \\ \end{aligned}$$

(39)

$$\begin{aligned}&|-\alpha ^2\omega _0^2+j\omega _{0}\,\underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{1}\,+\alpha ^2\omega _0^2+2j\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{K }}}\,\underline{\tilde{\psi }}_{1}|\nonumber \\&\quad = \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\} \end{aligned}$$

(40)

$$\begin{aligned}&\gamma _{n=1} = \frac{ \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\}}{|j\omega _{0}\underline{\tilde{\psi }}_{1}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{1}\,+2j\zeta \underline{\tilde{\psi }}_{1}^{\text {H}} \underline{\underline{\mathbf{K }}}\,\underline{\tilde{\psi }}_{1}|} \end{aligned}$$

(41)

For multi-harmonics:

$$\begin{aligned} \gamma = \frac{ \gamma \,\mathfrak {R}\{e^{j\varphi } \underline{\tilde{\psi }}_{1}^{\text {H}}\,\underline{\hat{F}}_{ e}\}}{\sum _{n=0}^{N_{h}}|jn\omega _{0}\underline{\tilde{\psi }}_{n}^{\text {H}}\underline{\underline{\mathbf{C }}}\,\underline{\tilde{\psi }}_{n}\,+2j\zeta \underline{\tilde{\psi }}_{n}^{\text {H}} \underline{\underline{\mathbf{K }}}\,\underline{\tilde{\psi }}_{n}|}. \end{aligned}$$

(42)

3.4 Discussion

E-EBM and NMS are only valid when the solution in forced response has a similar shape with a similar amplitude at a similar frequency to the solution with a specific amplitude of the studied dNNM. Therefore, the crossing solution between the forced response and the underlying dNNM can be effectively predicted. A situation with multiple crossing solutions might also happen in the emergence of the isola [4, 6], the existence of isola is not considered in this work. Predicting the isola is also achievable for E-EBM [29]. To achieve a comprehensive comparison between NMS and E-EBM, the formula used for computation of $\gamma$ for the 1st harmonic and multi-harmonics is provided in Table 2. Generally, NMS is based on projecting the EoM for the computation of the forced response formally onto each harmonic of the dNNM [14], whereas E-EBM is based on a fact that the net energy transfer between the dNNM and the resonant solution in forced response equals zero [29]. These two numerical methods start from different considerations and arrive at a similar formulation.

Table 2 Comparison between nonlinear modal synthesis and extended energy balance method

By looking at the formulation for the 1st harmonic (first two rows of Table 2), one can always notice that the formula for EPMC-H and EPMC-V is mathematically the same between the NMS and E-EBM, whereas for CNM, the denominator is different. In NMS, the conservative nonlinear force is treated as a joint effect from an equivalent nonlinear stiffness matrix $\underline{\underline{\mathbf{K }}}_{\mathrm{nl}}$ and an equivalent damping force $\underline{\tilde{D}}$. The determination of the damping models (viscous or hysteretic damping) for the equivalent damping force $\underline{\tilde{D}}$ has a great impact on the accuracy of the NMS. If the dNNM is computed using EPMC, the same damping model as the artificial damping can be used for this equivalent damping force $\underline{\tilde{D}}$, i.e. an equivalent viscous damping force can be used if the dNNM is computed using EPMC-V, whereas in CNM, the damping ratio is obtained from the decaying solutions. An additional assumption has to be made: the equivalent viscous damping force $\underline{\tilde{D}}$ is approximated using a viscous damping model or a hysteretic damping model with a damping ratio $\zeta$. In E-EBM, the total energy transferred is numerically calculated regardless of the damping assumption. Therefore, if only the 1st harmonic, is considered, the NMS and E-EBM have the same representation of the $\gamma$ if the dNNM is computed using EPMC.

If multi-harmonics are considered in the computation of dNNMs and used to predict the resonant solutions, the formula is provided in the last two rows of Table 2. The formula for EPMC in NMS and E-EBM handles the high order harmonics differently. The discrepancy between the NMS and the E-EBM will be discussed in Sect. 4.2.2 in together with the numerical results.

4 Illustrative test cases: 1-DoF systems

In this section, two illustrative 1-DoF systems are tested: a 1-DoF system with frictional contact and a 1-DoF system with quadratic nonlinear damping. The 1-DoF system with frictional contact with two different sets of parameters are investigated, the first one shows significant friction damping effects (named as Testcase I) and the second one has a low friction damping (named as Testcase II). Testcase III and Testcase IV refer to the 1-DoF system with quadratic nonlinear damping (Testcase IV has a greater damping ratio than Testcase III). In each test case, the dNNMs are computed using CNM and two variants of EPMC with the first 15th harmonics. In addition, the resonant solutions are predicted using E-EBM and NMS.

4.1 1-DoF system with frictional contact

The first illustrative 1-DoF system consists of a single point mass oscillator with a Jenkins element as shown in Fig. 4. The Jenkins element is used to model frictional contact between the mass oscillator and the ground. The maximum static friction is defined as $f_\mathrm{max}$ and $k_t$ is the tangential contact stiffness. There are two contact conditions in the present Jenkins element, which are sticking and sliding. The detailed formulations for the computation of the friction forcing $\underline{f}_{\mathrm{nl}}$ can be found in Eqs. (A.1–A.3). The EoMs used for the computation of the dNNM and the forced responses are shown in Eq. (43). The present 1-DoF system with frictional contact is tested for two different sets of parameters as shown in Table 3. $\gamma$ is the excitation forcing level and $\varphi$ is the absolute phase of the excitation. The value of $\gamma$ is expected to be predicted using dNNM coupled with E-EBM or NMS. The forced response will be computed to validate the resonant frequency and excitation forcing level predicted using the dNNM coupled with E-EBM or NMS.

$$\begin{aligned} \left. \begin{aligned}&\text {dNNM:}&m\,\underline{\ddot{q}}+k\, \underline{q}+ \underline{f}_{\mathrm{nl}}=0 \\&\text {Forced response:}&m\,\underline{\ddot{q}}+c\,\underline{\dot{q}}+k\, \underline{q}+\underline{f}_{\mathrm{nl}}= \gamma e^{j(\Omega t+\varphi )}. \end{aligned}\right. \nonumber \\ \end{aligned}$$

(43)

Fig. 4

1-DoF system with frictional contact

Table 3 Parameters for Testcase I and Testcase II

4.1.1 Testcase I

The parameters used for Testcase I are given in Table 3. The linear natural frequency $\omega _{n}$ of Testcase I is $1\,\mathrm{rad/s}$ and the linear sticking frequency is $2\,\mathrm{rad/s}$. The linear sticking frequency refers to the natural frequency when the Jenkins element is replaced by a linear spring with the same stiffness as the contact stiffness. The dNNMs for Testcase I are calculated using CNM and two variants of EPMC. The results are shown in the form of $\omega _{0}-q_{\mathrm{max}}$ curves and $\zeta -q_{\mathrm{max}}$ curves (see Fig. 5a, b). $\omega _{0}$ is the resonant frequency, $\zeta$ is the modal damping ratio, $q_{\mathrm{max}}$ is the vibration amplitude. Then, the resonances are predicted using the dNNMs and two numerical methods (E-EBM and NMS). From E-EBM and NMS, the $\gamma -q_{\mathrm{max}}$ curves can be built to demonstrate the relation between the excitation forcing level and the resonant amplitude (see Fig. 5c). The $\dot{q}-q$ envelopes, $\dot{q}-\ddot{q}$ envelopes and invariant manifolds are shown in Fig. 7. Then, four different cases with different values of $q_{\mathrm{max}}$ are highlighted in Fig. 5 (Case A $q_{\mathrm{max}} =1$, Case B $q_{\mathrm{max}} =2$, Case C $q_{\mathrm{max}} =4$, Case D $q_{\mathrm{max}} =6$,). These four cases are selected for a further detailed explanation. The resonant solutions, nonlinear forces and the hysteresis loops are shown in Fig. 6. In addition, the critical information for the four cases is listed in Table 4(a). To validate the resonant solutions predicted from the dNNM, the forced responses are computed using the $\gamma$ values predicted from the dNNM. The $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are shown in together with the full forced responses in Fig. 5d–f. The accuracy of the predicted $\omega _{0}$ and $\gamma$ can be directly observed in Fig. 5d–f.

Fig. 5

Testcase I: a–c Numerical results from the damped nonlinear normal mode within a range of modal amplitude; a $\omega _{0}-q_{\mathrm{max}}$ plot; b $\zeta -q_{\mathrm{max}}$ plot; c $\gamma -q_{\mathrm{max}}$ plot using extended energy balance method (circles) and nonlinear modal synthesis (diamonds); d–f Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves; d Complex nonlinear mode; e Extended periodic motion concept with artificial viscous damping; f Extended periodic motion concept with artificial hysteretic damping; Left: $\gamma -q_{\mathrm{max}}$ curves from nonlinear modal synthesis (Purple solid curves), $\gamma -q_{\mathrm{max}}$ curves from extended energy balance method (Grey dashed curves); Right: $\omega _{0}-q_{\mathrm{max}}$ (Black curves) and nonlinear forced response in different colours. (Color figure online)

Table 4 Resonances for Testcase I

By looking at Fig. 5a, the evolution of the $\omega _{0}$ with respect to the $q_{\mathrm{max}}$ is a typical phenomenon for systems with frictional contact [32]. At a low level of $q_{\mathrm{max}}$, the mass is stuck to the ground and the $\omega _{0}$ equals the linear sticking frequency. Increasing $q_{\mathrm{max}}$ leads to a sliding contact condition resulting in a softening effect. The $\omega _{0}$ starts to decrease and asymptotically reaches the natural frequency. By evaluating the $\omega _{0}$ obtained from CNM and two variants of EPMC, the $\omega _{0}$ computed using CNM is slightly different from the one obtained from EPMC (EPMC-V and EPMC-H show the same results). The accuracy of the $\omega _{0}$ is demonstrated in Fig. 5d–f and Table 4 using the four cases. The predicted $\omega _{0}$ is provided in the third column in Table 4(a) and the resonant frequency obtained from the forced responses is provided in Table 4(b). By comparing the values in Table 4, the $\omega _{0}$ obtained from CNM is less accurate than the one obtained from the EPMC. This inaccuracy can be directly observed in Fig. 5d–f, and it will be discussed in Sect. 4.1.2.

Fig. 6

Testcase I: Predicted resonant solutions using the damped nonlinear normal modes and resonant solutions from the forced response for four different cases (shown in Fig. 5); Case A $q_{\mathrm{max}}=1$, Case B $q_{\mathrm{max}}=2$, Case C $q_{\mathrm{max}}=4$, Case D $q_{\mathrm{max}}=6$; a–d $q(t)-t$ plots; e–h $f_{\mathrm{nl}}-t$ plots; i–l $f_{\mathrm{nl}}-q(t)$ plots; grey curves: obtained from the resonant solutions in forced response. (Color figure online)

Fig. 7

Testcase I: Invariant manifold; a–c $\dot{q}(t)-q(t)$ plot; d–f $\dot{q}(t)-\ddot{q}(t)$ plot; g–i Invariant manifolds

As for the evolution of the $\zeta$, the discrepancy between values from the CNM and two variants of EPMC cannot be ignored. As explained in Sect. 2.6, the hysteretic damping is independent on $\omega _{0}$, whereas viscous damping relates to $\omega _{0}$. If the solutions of the studied system are dominated by the fundamental harmonic, there is a constant ratio between the $\zeta$ computed from the EPMC-V and EPMC-H, $(\omega _{0}/\omega _{n})^2$. This can be simply proved by looking at any case in Table 4(a). Taking Case A as an example, the $\zeta$ from the EPMC-H is $0.43\%$ and $\zeta$ from the EPMC-V is $0.23\%$. If the $\zeta$ from EPMC-V is multiplied by a factor of $(\omega _{0}/\omega _{n})^2 = (1.37/1)^2$, then it equals the value obtained from the EPMC-H. From the author’s understanding, the damping ratio is an indicator to describe the damping effect and it highly depends on the damping assumption. Artificial damping is introduced in the EPMC to compensate for the energy loss in a period average. Therefore, all that truly matters is the periodic solutions and the actual energy loss. The periodic solutions, nonlinear hysteresis loops for four cases are shown in Fig. 6. From Fig. 6, the results from EPMC-V and EPMC-H show a great agreement with the resonant solutions from the forced response. Therefore, we can safely conclude that for Testcase I, both EPMC-V and EPMC-H can provide an equally good accuracy. By looking at the hysteresis loops, the energy dissipated (area under hysteresis loops) from CNM and EPMC is almost identical, even the predicted $\omega _{0}$ from CNM is less accurate.

The $\gamma$ values predicted from two concepts and two numerical methods show an excellent agreement, as shown in Fig. 5c. By looking at Figs. 5d–f and 6, the resonant solutions predicted from the dNNM corresponds to the resonant solutions from the forced response. For E-EBM, the $\gamma$ is determined by a balance of energy between the non-conservative nonlinear force and excitation force. From Fig. 6i–l, the energy dissipated computed from the CNM and two variants of EPMC is almost identical. Thus, the $\gamma$ calculated from the E-EBM for three strategies shows a negligible discrepancy. The accuracy of the NMS can be guaranteed because Testcase I is a simple 1-DoF system governed by the fundamental harmonic without the presence of modal interaction.

The invariant manifolds for CNM and two variants of EPMC are constructed using a finite number of periodic solutions, as shown in Fig. 7. It is difficult to identify the differences between the manifolds. Therefore, we can conclude that for Testcase I, both EPMC-V and EPMC-H can provide an accurate computation of the dNNM. For CNM, the resonant frequency slightly deviates from the actual value.

4.1.2 Testcase II

This 1-DoF system with another set of parameters is tested as Testcase II. The input parameters for the same model [Eq. (43) and Fig. 4] are provided in Table 3. The linear natural frequency $\omega _{n}$ of Testcase II is $188.4~\mathrm{rad/s}$ and linear sticking frequency is $213.3~\mathrm{rad/s}$. The similar $\omega _{0}-q_{\mathrm{max}}$ curves, $\zeta -q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are shown in Fig. 8a–c. The full forced response, $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are provided in Fig. 8d–f.

Fig. 8

Testcase II: a–c Numerical results from the damped nonlinear normal mode within a range of modal amplitude; a $\omega _{0}-q_{\mathrm{max}}$ plot; b $\zeta -q_{\mathrm{max}}$ plot; c $\gamma -q_{\mathrm{max}}$ plot using extended energy balance method (circles) and nonlinear modal synthesis (diamonds); d–f Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves; d Complex nonlinear mode; e Extended periodic motion concept with artificial viscous damping; f Extended periodic motion concept with artificial hysteretic damping; Left: $\gamma -q_{\mathrm{max}}$ curves from nonlinear modal synthesis (Purple solid curves), $\gamma -q_{\mathrm{max}}$ curves from extended energy balance method (Grey dashed curves); Right: $\omega _{0}-q_{\mathrm{max}}$ (Black curves) and nonlinear forced response in different colours. (Color figure online)

It is worth noticing that the maximum $\zeta$ achieved for Testcase II is $4.5\%$, which is much smaller than one from Testcase I (maximum $\zeta$ is around $45\%$). By considering $\omega _{0}-q_{\mathrm{max}}$ curves and Fig. 8d–f, the $\omega _{0}$ computed from the CNM shows higher accuracy than Testcase I. This can be explained by the fact that the accuracy of the CNM highly depends on the modal damping ratio. Because in CNM, the solutions are assumed as damped solutions in a periodic form with exponential decay, whereas in the AFT procedure, the decay terms are directly ignored and the damped solutions are treated as undamped periodic solutions. If a system with a large damping ratio (like Testcase I), the damped solutions are different from the undamped periodic solutions, especially the difference in the frequency. Thus, the periodic assumption in the AFT procedure can make non-negligible impacts on the accuracy of the CNM. On the other hand, for a system with lower damping ratio (like Testcase II), the damped frequency $\omega _{d}$ is very close to the resonant frequency $\omega _{0}$ ($\omega _{d} = \omega _{0}\sqrt{1-\zeta ^{2}}$). Therefore, treatment of the damped solutions in the AFT procedure does not have a significant influence on the accuracy of the CNM for systems with lower frictional damping.

4.2 1-DoF system with quadratic nonlinear damping

A 1-DoF system with quadratic nonlinear damping is investigated as the second illustrative system in this work. This system has been studied in [11]. The EoMs used for the computation of the dNNM and the forced responses are shown in Eq. (43). There is quadratic nonlinear $v\,\underline{q}^2 \,\underline{\dot{q}}$ in the EoMs. Two different values of v are considered: $v=0.02$ for Testcase III and $v=0.1$ for Testcase IV. $\gamma$ is the excitation forcing level and $\varphi$ is the absolute phase of the excitation. The value of $\gamma$ is expected to be predicted using dNNM coupled with E-EBM or NMS. The forced response will be computed to validate the resonant frequency and excitation forcing level predicted using the dNNM coupled with E-EBM or NMS.

$$\begin{aligned} \left. \begin{aligned}&\text {dNNM:}&\underline{\ddot{q}}+\underline{q}+ v\,\underline{q}^2 \,\underline{\dot{q}}=0 \\&\text {Forced response:}&\underline{\ddot{q}}+0.02\,\underline{\dot{q}}+\underline{q}+v\,\underline{q}^2 \,\underline{\dot{q}}= \gamma e^{j(\Omega t+\varphi )} \end{aligned}\right. \end{aligned}$$

(44)

4.2.1 Testcase III

The value of $v=0.02$ is used in Testcase III. The dNNMs for Testcase III are calculated using CNM and two variants of EPMC. The results are shown similarly with Testcase I. The evolution of the resonant frequency $\omega _{0}$ and the modal damping ratio $\zeta$ are plotted with respect to the vibration amplitude $q_{\mathrm{max}}$ curves, as shown in Fig. 9a, b. Then, the excitation forcing level $\gamma$ for the solutions of the dNNM are predicted using the dNNMs and two numerical methods (E-EBM and NMS). The $\gamma -q_{\mathrm{max}}$ curves are displayed in Fig. 9c. The $\dot{q}-q$ envelopes, $\dot{q}-\ddot{q}$ envelopes and invariant manifolds are shown in Fig. 7. To validate the resonant solutions predicted from the dNNM, the forced responses are computed using the $\gamma$ values predicted from the dNNM. The $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are shown in together with the full forced responses in Fig. 9d–f.

Fig. 9

Testcase III: a–c Numerical results from the damped nonlinear normal mode within a range of modal amplitude; a $\omega _{0}-q_{\mathrm{max}}$ plot; b $\zeta -q_{\mathrm{max}}$ plot; c $\gamma -q_{\mathrm{max}}$ plot using extended energy balance method (circles) and nonlinear modal synthesis (diamonds); d–f Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves; d Complex nonlinear mode; e Extended periodic motion concept with artificial viscous damping; f Extended periodic motion concept with artificial hysteretic damping; Left: $\gamma -q_{\mathrm{max}}$ curves from nonlinear modal synthesis (Purple solid curves), $\gamma -q_{\mathrm{max}}$ curves from extended energy balance method (Grey dashed curves); Right: $\omega _{0}-q_{\mathrm{max}}$ (Black curves) and nonlinear forced response in different colours. (Color figure online)

Fig. 10

Testcase III: Invariant manifold; a–c $\dot{q}(t)-q(t)$ plot; d–f $\dot{q}(t)-\ddot{q}(t)$ plot; g–i invariant manifolds

Fig. 11

Testcase IV: a–c Numerical results from the damped nonlinear normal mode within a range of modal amplitude; a $\omega _{0}-q_{\mathrm{max}}$ plot; b $\zeta -q_{\mathrm{max}}$ plot; c $\gamma -q_{\mathrm{max}}$ plot using extended energy balance method; d $\gamma -q_{\mathrm{max}}$ plot using nonlinear modal synthesis; e–g Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves from extended energy balance method; h–j Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves from nonlinear modal synthesis; e, h Complex nonlinear mode; f, i Extended periodic motion concept with artificial viscous damping; g, j Extended periodic motion concept with artificial hysteretic damping; Left: $\gamma -q_{\mathrm{max}}$ curves; Right: $\omega _{0}-q_{\mathrm{max}}$ (Black curves) and nonlinear forced response in different colours. (Color figure online)

By looking Fig. 9, the $\zeta -q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are almost identical, whereas for $\omega -q_{\mathrm{max}}$ curves, the one computed from the CNM shows a hardening effect and the other two show a softening effect. Similar findings can be also found in [8, 11]. The full forced responses of the present system are calculated using Eq. (44) and are shown in Fig. 9d–f. From Sect. 4.1, we have concluded that the accuracy of the CNM can be affected by the value of the nonlinear damping, i.e. a system with large nonlinear damping has lower accuracy. However, in Testcase III, the $\omega _{0}$ computed from CNM starts to increase at a low damping level when $q_{\mathrm{max}} = 0.57$ and $\zeta = 0.08\%$. From the author’s understanding, it is not rigorous to conclude that this evident inaccuracy comes from the periodic assumption in the AFT procedure. Further works are required to improve the accuracy of the CNM. To obtain a comprehensive comparison of dNNMs, the $\dot{q}-q$ envelopes, $\dot{q}-\ddot{q}$ envelopes and invariant manifolds of the studied mode are provided in Fig. 10. From the figure, it is difficult to identify any obvious differences between CNM and two variants of EPMC.

4.2.2 Testcase IV

The same 1-DoF system with quadratic nonlinear damping is tested with a different value of $v=0.1$ (named as Testcase IV). A similar nonlinear modal analysis is applied using the first 13 harmonics ($N_h =13$) and results are shown in this section. The $\zeta -q_{\mathrm{max}}$ curves, $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves are shown in Fig. 11a–c. From the figure, one can notice that there is a more observable discrepancy between the dNNM predicted from CNM and two variants of EPMC. First of all, from the CNM, Testcase IV exhibits a strong hardening effect, whereas the one from EPMC shows a softening effect. The initial findings of Testcase IV share a great similarity with Testcase III, but with remarkable features. It is worth noticing that the $\omega _{0}$ predicted using two variants of EPMC exhibits a slight discrepancy when the amplitude exceeds 6. This observation is different from the first three test cases. As mentioned in Sect. 2.6, if the dNNM of the studied system is dominated by the fundamental harmonic, the same dNNM can be obtained from EPMC-V and EPMC-H, whereas in Testcase IV, the discrepancy between the dNNM computed from EPMC-V and EPMC-H comes from the existence of higher-order harmonics. This statement will be further discussed in this section with the help of convincing results.

Fig. 12

Testcase IV: predicted resonant solutions using the damped nonlinear normal modes and resonant solutions from the forced response in the case of $\gamma =8$; a–e Complex nonlinear mode; f–j Extended periodic motion concept with artificial viscous damping; k–o Extended periodic motion concept with artificial hysteretic damping; a, f, k $q(t)-t$ plots; b, g, l $\dot{q}(t)-t$ plots; c, h, m $f_{\mathrm{nl}}-t$ plots; d, i, n $\dot{q}-q$ plots; e, j, o $f_{\mathrm{nl}}-q$ plots; grey curves: obtained from the crossing solutions in forced response; Blue dash-dot curves: prediction from extended energy balance method; Red dashed curves: prediction from nonlinear modal synthesis. (Color figure online)

By looking at the forced response in Fig. 11e–g, the crossing solutions can be still identified using the dNNM with E-EBM even the $\omega _{0}$ computed from CNM and EPMC is very different. However, the crossing solutions predicted using NMS show a great discrepancy with the actual crossing solutions between the forced response and the CNM based dNNM as shown in Fig. 11h. EPMC-H provides an almost equally well prediction of the crossing solution between the E-EBM and NMS. To further demonstrate the results, the predicted resonant frequency $\omega _{0}$ and the resonant amplitude $q_{\mathrm{max}}$ in the case of $\gamma = 8$ are listed in Table 5. The dNNM is computed using CNM and two variants of EPMC, and the resonant solutions are predicted using two numerical methods, namely E-EBM and NMS. Therefore, with a given value of $\gamma$, there are six predicted solutions as shown in Table 5. In addition, the values of $\omega _{0}$ and $q_{\mathrm{max}}$ for the crossing solutions are also provided in the second column of Table 5. The crossing solutions are taken at where the forced response ($\gamma = 8$) intersects with the underlying dNNM. From Table 5, one can notice that the error caused by E-EBM is always smaller than NMS. If the dNNM is computed according to CNM, the error in the prediction of $\omega _{0}$ and $q_{\mathrm{max}}$ is $4.7\%$ and $8.96\%$. From the table, one can always notice that EPMC-H provides a better prediction than CNM and EPMC-V either using NMS or E-EBM. These inaccuracies might from the combining effect between the dNNM computation and resonance prediction due to the presence of higher-order harmonics. Therefore, it is not rigorous to claim that EPMC-H can provide better results.

Fig. 13

Testcase IV: the contribution of the 1st harmonic, the 3rd harmonic and the 5th harmonic in the case of $\gamma =8$; a–c Complex nonlinear mode; d–f Extended periodic motion concept with artificial viscous damping; g–i Extended periodic motion concept with artificial hysteretic damping; a, d, g The 1st harmonic, $q_{n=1}(t)-t$ plots; b, e, h The 3rd harmonic, $q_{n=3}(t)-t$ plots; c, h, i The 5th harmonic, $q_{n=5}(t)-t$ plots; grey curves: obtained from the crossing solutions in forced response; Blue dash-dot curves: prediction from extended energy balance method; Red dashed curves: prediction from nonlinear modal synthesis. (Color figure online)

Fig. 14

Testcase IV: influence of the total order of harmonics using $N_h=1$, $N_h=3$ and $N_h=13$; a–c $\omega _{0}-q_{\mathrm{max}}$ plots for different values of $N_h$; d–f $\gamma -q_{\mathrm{max}}$ plots for $N_h=1$; g–i $\gamma -q_{\mathrm{max}}$ plots for $N_h=13$

To further investigate the influences caused by the higher-order harmonics, the $q(t)-t$ plots, $\dot{q}(t)-t$ plots, $f_{\mathrm{nl}}-t$ plots, $\dot{q}-q$ plots and $f_{\mathrm{nl}}-q$ plots in the case of $\gamma =8$ are shown in Fig. 12, where grey curves represent the crossing solutions in forced response; blue dash-dot curves for the prediction from E-EBM; red dashed curves for the prediction from NMS. The first row of Fig. 12 shows the results from CNM; the results from EPMC-V are provided in the second row; the third row for EPMC-H. By looking at the results in Fig. 12, the initial findings correspond to the observation from Table 5. For a close look at Fig. 12a, b, the differences between the results from E-EBM and NMS are mainly from higher-order harmonics. Therefore, we can safely confirm that the presence of higher-order harmonics makes a great impact on the accuracy of NMS and E-EBM. The contribution of the 1st harmonic, the 3rd harmonic and the 5th harmonic is also provided in Fig. 13. As mentioned above, the dNNMs are computed using the first 13 harmonics ($N_h =13$); the formula with multi-harmonics is applied in E-EBM and NMS. The $q_{n=1,3,5}$ is calculated using the formula: $q_n = \mathfrak {R}\{{\tilde{q}_{n}e^{jn\omega _{0}t}}\}$. From Fig. 13a, d, g, it is obvious to see that there are no significant differences for the 1st harmonic, whereas the NMS overestimated the contribution of the 3rd harmonic and the 5th harmonic. These findings correspond to the results in Table 5: NMS shows $+8.98\%$ error in the resonant amplitude if the dNNM is computed using CNM and $+3.34\%$ for EPMC-V.

Table 5 Resonances for Testcase IV in the case of $\gamma = 8$

The results shown above are computed using the first 13 harmonics ($N_h =13$). The total order of harmonics $N_h$ used in the HBM method can influence the accuracy of the results. In Fig. 14a–c, the $\omega _{0}-q_{\mathrm{max}}$ curves for different values of $N_h$ are shown. The green dash-dot curves represent for $N_h=1$; the purple dashed curves for $N_h=3$; the orange solid curves for $N_h=13$. For EPMC, if only the 1st harmonic is considered, the $\omega _{0}$ computed for the studied system is a constant value at 1. It is not accurate based on the observation in Fig. 11. In this 1-DoF system with quadratic nonlinear damping, the 3rd harmonic and the 5th harmonic are excited because of the nonlinear coupling effects. Therefore, the total order of harmonics $N_h$ has to be determined carefully to provide accurate results. For $\gamma -q_{\mathrm{max}}$ curves, if only the 1st harmonic is considered in the EPMC, the predicted values of $\gamma$ from the E-EBM and NMS are expected to be mathematically the same (refer Table 2). Because the E-EBM and NMS only handle the higher-order harmonics differently. For CNM, the results from the E-EBM and NMS are different (see Fig. 14d, g). This difference between the E-EBM and NMS can be seen as the consequence of the damping assumption used in the NMS, this statement has already been discussed in Sect. 3.4.

5 An industrial application: blisk with ring damper

Integrally bladed discs (or blisks) are important structural components within gas turbine engines. Blisks are highly loaded during the operation of gas turbine engines. Friction ring damper is an emerging damping technique for blisks to reduce vibration amplitude, which is located within the groove and underneath of the blisk. The dynamic response of ring dampers has been investigated by many researchers [15, 16, 19, 20]. Nonlinear modal analysis for friction ring damper has also been attempted in the literature, for lumped parameter model [33] and full-scale structure [17, 30, 31]. In this section, a full-scale blisk with friction ring damper is considered as an industrial test case to assess the dNNM computed from the CNM and two variants of EPMC.

5.1 Model description

A three-dimensional finite element (FE) model is used to represent the blisk with friction ring damper. This full-scale FE model is studied as an industrial application. The full annulus and a sector of the model are shown in Fig. 15. There are 30 sectors in total. A sector of the blisk and ring damper with cyclic symmetric boundary is used to model the full annulus. This FE model contains 1544 elements, where 1184 for the blisk sector and 360 for the ring sector. The model is made by homogenous titanium material. There is one contact interface between the underneath of the blisk and the upper surface of the ring damper. There are 143 contact nodes within the contact interface. The blisk is assumed as a perfectly tuned structure that exhibits a cyclic symmetry for the full annulus. The kinematic nonlinearity is ignored in the nonlinear vibration analysis.

Fig. 15

A three-dimensional blisk with ring damper: a a full annulus; b a sector

A linear modal analysis is applied to the blisk structure and a disc-dominated mode with nodal diameter 3 is selected and used for the following study. The mode shape of this selected mode is shown in Fig. 16. Then, a classical Campbell diagram is calculated through a rotor dynamic analysis. When the engine rotating speed is 2081 rpm and 27th engine order excitation is applied, the selected mode with a natural frequency of 2.195 frequency unit (FU) is excited. The value of the lowest natural frequency of the blisk is defined as 1 FU. Then, a nonlinear static analysis is used to obtain the contact pressure/gap distribution within contact interfaces. The pressure/gap is considered as the initial contact status in nonlinear modal analysis. A three-dimensional contact element is used to model the friction contact force [38]. Readers can refer [30] for detailed description.

Fig. 16

The mode shape of first disc-dominated mode with nodal diameter 3: a A full annulus; b a sector

5.2 Nonlinear modal analysis

The sector of blisk and ring damper is reduced using the classic Craig–Bampton method in the nonlinear modal analysis [5, 39]. The vibrational amplitude is taken from the displacement of the response node (see Fig. 15) in Z-axis. The numerical results from dNNM are shown in Fig. 17. The dNNMs are computed using the first three harmonics. The modal properties resonant frequency $\omega _{0}$, modal damping ratio $\zeta$ and excitation forcing level $\gamma$ are plotted against the vibrational amplitude of response DoF $q_{\mathrm{dmax}}$. It was verified that the results for the CNM and two variants of the EPMC show very high similarity, so that only the results from EPMC-H and E-EBM are shown in the following. The natural frequency of the studied mode for blisk is 2.195 FU. At low amplitude, the contact nodes within the contact interface are either separated or sticking depending on the initial contact condition from the nonlinear static analysis. The resonant frequency is around 2.201 FU at a low amplitude. When the structure is vibrating with a large amplitude, some contact nodes start to slide and energy is dissipated by those sliding nodes leading to a decreasing $\omega _{0}$. When the amplitude exceeds $0.1\,\mathrm{mm}$, those separated nodes are in contact and lead to a stiffer structure and an increasing $\omega _{0}$.

Fig. 17

Blisk with friction ring damper: a–c Numerical results from the damped nonlinear normal mode within a range of modal amplitude; a $\omega _{0}-q_{\mathrm{max}}$ plot; b $\zeta -q_{\mathrm{max}}$ plot; c $\gamma -q_{\mathrm{max}}$ plot using extended energy balance method (circles) and nonlinear modal synthesis (diamonds); d Using nonlinear forced response to validate $\omega _{0}-q_{\mathrm{max}}$ curves and $\gamma -q_{\mathrm{max}}$ curves; Left: $\gamma -q_{\mathrm{max}}$ curves from nonlinear modal synthesis (Purple solid curves), $\gamma -q_{\mathrm{max}}$ curves from extended energy balance method (Grey dashed curves); Right: $\omega _{0}-q_{\mathrm{max}}$ (Black curves) and nonlinear forced response in different colours. (Color figure online)

In Fig. 17b, a zero value of $\zeta$ can be observed at a low amplitude, when the contact nodes are either separated or sticking. When sliding contact condition occurs, $\zeta$ becomes positive representing the dissipative effect generated by frictional contact. The maximum value of $\zeta$ achieved is around $0.192\%$. From the design point of view, if the ring damper can be designed within the “valley” of $\zeta$, the efficiency and robustness of the damper can be guaranteed.

The $\gamma -q_{\mathrm{max}}$ curves computed from dNNM coupled with E-EBM and NMS are shown in Fig. 17c. The $\gamma$ predicted using E-EBM are represented by circles and diamonds for NMS. Generally, there is very difficult to identify the differences between $\gamma -q_{\mathrm{max}}$ curves from E-EBM and NMS. To validate that, the nonlinear forced response of the system is computed with several values of $\gamma$ ($10.13~\mathrm{N}$, $20.63~\mathrm{N}$, $41.85~\mathrm{N}$, $59.70~\mathrm{N}$ and $70.91~\mathrm{N}$, see Fig. 17d. The excitation force is applied on the same DoF where the vibrational response is taken as shown in Fig. 15. The nonlinear forced responses are calculated using classic HBM with the continuation technique. By assessing the resonant amplitude $q_{\mathrm{max}}$ in Fig. 17d, the results show a great agreement between the predicted resonances using E-EBM and NMS and resonant solutions in nonlinear forced response.

Table 6 Comparison of computational time for nonlinear modal analysis

Table 7 Comparison of computational time for nonlinear forced response

5.3 Computational efficiency

For an engineering design problem, the resonant amplitude is usually considered as one of the most important factors. Using dNNMs with E-EBM or NMS can instantly provide resonant information from dNNMs. The resonant information can be also obtained from another modelling strategy, by computing the nonlinear forced response. Therefore, in an industrial problem, computational efficiency remains important. The elapsed time used for the computation of dNNM by CNM and two variants of EPMC is given in Table 6 and the time used for computation of nonlinear forced response is given in Table 7.

The extra computational time for E-EBM or NMS is less than 3 s, which is much less than the time used for the computation of dNNM. The average time per step for CNM is 61.3 s, 59.2 s for EPMC-V and 57.0 s for EPMC-H. Both CNM and EPMC are solved using the same numerical methodology (HBM, AFT method and continuation technique) and same solver (scipy.optimize.fsolve in Python). Therefore, the differences in the computational time come from the computation of linear dynamic stiffness matrices $\underline{\underline{\mathbf{Z }}}$ and its analytical Jacobian matrices $\delta \underline{\underline{\mathbf{Z }}}/\delta \omega _{0}$, $\delta \underline{\underline{\mathbf{Z }}}/\delta \zeta$. As described in Sect. 2.6 and Table 1, the linear dynamic stiffness matrices are in a similar form between CNM and EPMC: $\underline{\underline{\mathbf{Z }}}_{n} = \underline{\underline{\mathbf{K }}}-n^2\omega _{0}^2\underline{\underline{\mathbf{M }}}-\underline{\underline{\bar{\mathbf{C }}}}_{n}$. The only difference is the $\underline{\underline{\bar{\mathbf{C }}}}_{n}$ matrices and its analytical Jacobian matrices of the $\delta \underline{\underline{\bar{\mathbf{C }}}}_{n}/\delta \omega _{0}$ and $\delta \underline{\underline{\bar{\mathbf{C }}}}_{n}/\delta \zeta$ are also provided in Table 1. The differences in the computational time for linear matrices can be simply explained by that EPMC-H has the simplest formula for $\delta \underline{\underline{\bar{\mathbf{C }}}}_{n}/\delta \omega _{0}$. In summary, CNM needs more computational time than EPMC. EPMC-H is the most time efficient method, which improves the modelling efficiency around $7\%$ than CNM.

In a forced response analysis, the computation of forced response has to be repeated for different values of excitation forcing level $\gamma$ to obtain an evolution of resonant solutions with respect to the resonant amplitude. Thus, using nonlinear forced response results in a heavy computational burden. Using the same configuration in the continuation technique and same solver (scipy.optimize.fsolve in Python), the time used for nonlinear forced response is given in Table 7. The minimum computational time is 5573 s for the case of $\gamma = 10.13\,\mathrm{N}$. The computational time increases with the value of $\gamma$. Since an increasing excitation forcing level can lead to a great relative displacement within the contact interface leading to more sliding contact nodes. Therefore, the more computational time is required for the computation of the nonlinear forced response with a larger value of $\gamma$. In summary, using dNNM with E-EBM and NMS has shown great accuracy with much lower computational cost to investigate the resonance, especially for large structures.

6 Conclusion

In this work, two different concepts, namely CNM and EPMC, used to compute dNNMs for dynamic systems with non-conservative nonlinearities have been compared. An alternative damping assumption in the EPMC is introduced using artificial hysteretic damping. The CNM and two variants of the EPMC are derived in the frequency domain. In addition, two numerical methods, namely E-EBM and NMS, for predicting the resonances in the forced response using damped nonlinear normal modes are also assessed. A thorough comparison: (a) two concepts for dNNM computation including CNM and two variants of EPMC; (b) two numerical methods for resonant prediction including E-EBM and NMS, is achieved using two illustrative 1-DoF systems and a full-scale blisk with friction ring damper.

By assessing the dNNMs from CNM and two variants of EPMC, several useful statements can be concluded. Firstly, the accuracy of the CNM can be significantly affected by the presence of large nonlinear damping and higher-order harmonics. Then, both hysteretic damping and viscous damping can be used as artificial damping in EPMC. The two variants of EPMC are mathematically equivalent if only the 1st harmonic is considered in the computation of dNNM and perform equally well. Furthermore, if higher-order nonlinear damping is present with a large damping ratio, the accuracy of EPMC can be slightly reduced. Finally, for a full-scale structure with friction dampers, similar results are obtained from CNM and two variants of EPMC. The EPMC with artificial hysteretic damping can improve the computational efficiency by $3\%$ than the original EPMC because of the simple formula of the analytical Jacobian matrices.

The resonant solutions are predicted using dNNMs coupled with E-EBM and NMS. E-EBM and NMS are based on a similar assumption that the solutions in forced response share a great similarity with the dNNM. E-EBM and NMS are mathematically equivalent in the formula with only the 1st harmonic, whereas the existence of higher-order harmonics has an impact on the accuracy of NMS. In addition, E-EBM is limited to predicting the resonant solutions, whereas NMS makes the synthesis of the full forced response possible.

Appendix A: Jenkins element

The Jenkins element is used to model the friction force. $k_{t}$ is the tangential contact stiffness; the maximum static friction force is $f_\mathrm{max}$. x(t) is periodic tangential displacement; w(t) is an internal variable that represents the relative displacement of contact point. The friction force $\underline{F}_{\mathrm{nl}}$ is calculated iteratively in time domain. For a current time step i, the displacement of contact point $w(t_{i})$ and the friction force $\underline{F}_{\mathrm{nl}}(t_{i})$ are calculated using equations below. The tangential friction forces are predicted in the first place using Eq. (A.1), then corrected in Eq. (A.2).

$$\begin{aligned}&f_\mathrm{pre} = k_{t}(x(t_{i})-w(t_{i-1})) \end{aligned}$$

(A.1)

$$\begin{aligned}&\underline{F}_{\mathrm{nl}}(t_{i})= \left\{ \begin{matrix}f_\mathrm{pre}&{}\quad \text {if}&{}\quad f_\mathrm{pre} <f_\mathrm{max} &{}\quad \text {Sticking}\\ f_\mathrm{max} \cdot f_\mathrm{pre} /\left| f_\mathrm{pre}\right| &{}\quad \text {if}&{}\quad f_\mathrm{pre} \ge f_\mathrm{max} &{}\quad \text {Sliding}\end{matrix}\right. \nonumber \\ \end{aligned}$$

(A.2)

$$\begin{aligned}&w(t_{i})= \left\{ \begin{matrix}w(t_{i-1}) &{}\quad \text {if}&{}\quad f_\mathrm{pre} <f_\mathrm{max} &{}\quad \text {Sticking}\\ x(t_{i})-\underline{F}_{\mathrm{nl}}(t_{i})/k_{t}&{}\quad \text {if}&{}\quad f_\mathrm{pre} \ge f_\mathrm{max} &{}\quad \text {Sliding}.\end{matrix}\right. \nonumber \\ \end{aligned}$$

(A.3)