1 Introduction

Depending on a dynamical system type and a kind of information that is useful for its investigations, different types of invariants characterizing system dynamics are applied. For instance, one may use Kolmogorov entropy [1, 2], correlation dimension [3, 4], Lyapunov energy function [5] to determine the stability of solutions and complexity of system dynamics [6]. However, in order to predict the influence of perturbations on solution of a system, Lyapunov exponents (LEs) are one of the most commonly applied tools. That is because these exponents determine the exponential convergence or divergence of trajectories that start close to each other. The existence of such numbers has been proved by Oseledec theorem [7], but the first numerical study of the system’s behavior using Lyapunov exponents had been done by Henon and Heiles [8], before the Oseledec theorem publication. The most important algorithms for calculating Lyapunov exponents for continuous systems have been developed by Benettin et al. [9] and Shimada and Nagashima [10], later improved by Benettin et al. [11] and Wolf [12]. In order to estimate Lyapunov exponents from a scalar time series, the Takens procedure [13] can be applied. This approach can be utilized also in the cases when discontinuities or time delays exist in the analyzed system. Numerical algorithms for such estimation have been developed by Wolf et al. [14], Sano and Sawada [15] and later improved by Eckmann et al. [16], Rosenstein et al. [17] and Parlitz [18]. Alternative method applicable to systems with discontinuities or time delays, based on synchronization phenomena, was elaborated by Stefanski [19,20,21,22].

Nowadays, Lyapunov exponents are employed in many different areas of scientific research such as: materials [23, 24], electric power systems [25], non-continuous systems [20, 22, 26,27,28,29], systems with time delay [21], aerodynamics [30], time series analysis [31,32,33,34], optimal control [35, 36], chaotic encryption and secure communication [37, 38], multi-objective optimization [39], parametric oscillations and fluctuating parameters [19, 40], neuronal models investigations [41].

Thus, there is still need to elaborate fast and simple methods of LE calculation. Recently, we have presented our simple and effective method of estimation of the largest Lyapunov exponent (LLE) from the perturbation vector and its derivative dot product. The method is based on a clear, geometrical reasoning. Its application involve only basic mathematical operations such as summing, multiplying, dividing. The method can be applied in different aspects of the nonlinear systems control. We investigated continuous systems [42], synchronization phenomena detection [43], time series in control systems [44,45,46].

The method presented previously was limited to calculation of the Largest Lyapunov exponent. In this paper, we have revealed that it is possible to apply it for estimation of the whole Lyapunov exponents spectrum too. Moreover, it has been shown that special features of the presented method enable to estimate the whole spectrum of n Lyapunov exponents by integration of \(\left( {n-1} \right) \) perturbations only. The algorithm has been tested for three examples: Lorenz system, Duffing oscillator and three Duffing oscillators coupled in the ring scheme. Selection of the exemplary systems can be justified by the fact that they exhibit different types of dynamical behavior depending on the analyzed parameters. Therefore, correctness of the method has been confirmed for periodic, quasiperiodic and chaotic trajectories [47]. Computation times and convergence rates have been compared with the classical method [47] that involves Gram–Schmidt orthonormalization and calculations of perturbations lengths logarithms. The method presented in [47] uses the same approach as algorithms described in [9, 11]. To authors’ best knowledge, no algorithms of LE spectrum estimation for continuous-time, smooth dynamical systems faster than [9,10,11, 47] have been published. In this paper, it has been revealed that application of our new algorithm increases the efficiency of the calculations compared to the classical method [47] when the order of the system is low: 2, 4 or 6. Such acceleration has been achieved not only due to integration of \(\left( {n-1} \right) \) perturbations instead of n, but also owing to the simplicity of the algorithm, which involves only the basic mathematical operations: addition, multiplication, division. Compared to the classical method, calculation of logarithms and normalization of perturbations after each iteration can be omitted. Therefore, authors claim that the method presented in this paper is the fastest one in the assumed range of applications if the order of the system is low enough.

Fig. 1
figure 1

Scheme of perturbation vectors and their derivatives

Full size image

2 The method

Assume that a dynamical system is described by the set of differential equations in the form:

$$\begin{aligned} \frac{\mathrm{d}{{\varvec{x}}}}{\mathrm{d}t}={{\varvec{f}}}\left( {{{\varvec{x}}}, t} \right) \end{aligned}$$
(1)

where \({{\varvec{x}}}\) is the state vector, t is the time and \({{\varvec{f}}}\) is a vector field that (in general) depends on \({{\varvec{x}}}\) and t. Evolution of any perturbation \({{\varvec{z}}}\) in such system can be found from the equation:

$$\begin{aligned} \frac{\mathrm{d}{{\varvec{z}}}}{\mathrm{d}t}={{\varvec{U}}}\left( {{{\varvec{x}}},t} \right) {{\varvec{z}}} \end{aligned}$$
(2)

where \({{\varvec{U}}}\left( {{{\varvec{x}}},t} \right) \) is the Jacobi matrix obtained by differentiation of \({{\varvec{f}}}\) with respect to \({{\varvec{x}}}\). As it has been shown in the previous paper [42], the value of LLE can be estimated from the following expression:

$$\begin{aligned} \lambda _1^{*} =\frac{\frac{\mathrm{d}{{\varvec{z}}}_\mathbf{1} }{\mathrm{d}t}\cdot {{\varvec{z}}}_\mathbf{1} }{\left| {{{\varvec{z}}}_\mathbf{1} } \right| ^{2}} \end{aligned}$$
(3)

where \({{\varvec{z}}}_\mathbf{1}\) is a perturbation vector, whose evolution can be obtained by numerical integration of Eq. (2). The approximate value of LLE (\(\lambda _1 )\) is obtained by averaging values of \(\lambda _1^*\) from subsequent computation steps. For time of integration long enough, the average value of \(\lambda _1^*\) converges to the LLE. Please note that formula (3) involves only the most basic mathematical operations—addition, multiplication and division. On the other hand, the classical method involves calculation of perturbation length and its logarithm after each iteration.

According to [47], each LE \(\lambda _i \) is the average rate of perturbation contraction or expansion in a particular subspace near a particular limit set. The LLE—\(\lambda _1 \)—is the average rate of perturbation length change in (almost) whole space in which system (1) is defined. Let this whole space be named \(W_1 \).

For a system of order n, there are n nested subspaces:

$$\begin{aligned} W_1 \supset W_2 \supset \ldots \supset W_n \end{aligned}$$
(4)

such that the dimension of subspace \(W_i \) is \(n+1-i\). In each subspace \(W_i \), a perturbation evolves, on the average, according to \(\lambda _i \). Therefore, i-th LE can be obtained from evolution of a perturbation in the subspace \(W_i \).

The classical method of LE spectrum estimation involves Gram–Schmidt orthonormalization and calculations of perturbations lengths logarithms [47]. In this approach, n perturbations \({{\varvec{z}}}_\mathbf{1} , {{\varvec{z}}}_\mathbf{2} , \ldots , {{\varvec{z}}}_{{\varvec{n}}}\) are integrated. Orthonormalization procedure assures that each perturbation \({{\varvec{z}}}_{{\varvec{i}}}\) evolves in the subspace \(W_i \). Values of LE are obtained by calculating natural logarithm of perturbations lengths after subsequent integration steps and averaging these values over time. The crucial fact is that in order to calculate whole spectrum of n LE, integration of n perturbations is necessary.

In the presented method, complexity of calculations is reduced. In order to estimate the whole spectrum of n LE, it is enough to integrate \(\left( {n-1} \right) \) perturbations. For clarity, in the next paragraph, the case of a second-order system is discussed. Authors demonstrate how integration of only one perturbation \({{\varvec{z}}}_\mathbf{1}\) enables to estimate both LE: \(\lambda _1 , \lambda _2 \). The subsequent paragraph covers the general case, i.e., estimation of a full LE spectrum of a \(n\mathrm{th}\)-order system using only \(\left( {n-1} \right) \) integrated perturbations.

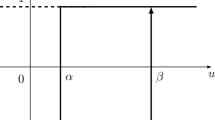
Let us assume that for a \(2\mathrm{nd}\)-order system, only one perturbation \({{\varvec{z}}}_\mathbf{1}\) is integrated. Obviously, using formula (3), LLE can be calculated. As \({{\varvec{z}}}_\mathbf{1}\) evolves according to (2), it tends to line up with the direction in which evolution of the perturbation is governed mainly by the value of \(\lambda _1 \), whereas the terms connected with \(\lambda _2 \) become negligible [47]. Therefore, throughout its evolution, \({{\varvec{z}}}_\mathbf{1}\) tends to a direction orthogonal to \(W_2 \). Let us also take any random vector \({{\varvec{z}}}_\mathbf{2}\), the length of which is nonzero and which is not parallel to \({{\varvec{z}}}_\mathbf{1}\) (Fig. 1).

Using the orthogonalization formula [47]:

$$\begin{aligned} {\tilde{{{\varvec{z}}}}}_\mathbf{2} ={{\varvec{z}}}_\mathbf{2} -{{\varvec{z}}}_\mathbf{1} *\frac{{{\varvec{z}}}_\mathbf{1} \cdot {{\varvec{z}}}_\mathbf{2} }{\left| {{{\varvec{z}}}_\mathbf{1} } \right| ^{2}} \end{aligned}$$
(5)

one obtains a vector \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) which is perpendicular to \({{\varvec{z}}}_\mathbf{1}\). Therefore, to a good approximation, \({\tilde{{{\varvec{z}}}}}_\mathbf{2} \in W_2 \). Notice that for a \(2\mathrm{nd}\)-order system, \(W_2\) is simply a line in \(W_1\) space. Thus, \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) must have the direction of a perturbation in \(W_2\) subspace, despite the fact that \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) has no connection with system (1) and the vector \({{\varvec{z}}}_\mathbf{2}\) was selected randomly. Moreover, it can be easily checked that the length of a perturbation does not affect the value obtained from formula (2). Summing up, one can use formula (2) to find the \(2\mathrm{nd}\) LE. It is only needed to use the vector \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) which lies in \(W_2\) instead of \({{\varvec{z}}}_\mathbf{1}\). The second LE can be found from the following expression:

$$\begin{aligned} \lambda _2^{*} =\frac{\frac{d{\tilde{{{\varvec{z}}}}}_\mathbf{2} }{dt}\cdot {\tilde{{{\varvec{z}}}}}_\mathbf{2} }{\left| {{\tilde{{{\varvec{z}}}}}_\mathbf{2}} \right| ^{2}} \end{aligned}$$
(6)

The approximate value of \(\lambda _2 \) is obtained by averaging values of \(\lambda _2^*\) from subsequent computation steps. For long enough time of integration, the average value of \(\lambda _2^*\) converges to the \(2\mathrm{nd}\) LE. Consequently, one does not need to integrate the \(2\mathrm{nd}\) perturbation; it is enough to find a correct direction of the vector \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\).

Let us now consider a system of order n. Suppose that \(\left( {n-1} \right) \) perturbations \({{\varvec{z}}}_\mathbf{1} , {{\varvec{z}}}_\mathbf{2} , \ldots , {{\varvec{z}}}_{{{\varvec{n}}}-\mathbf{1}} \) are integratedFootnote 1. Their time derivatives can be found from formula (2). As \({{\varvec{z}}}_\mathbf{1}\) evolves, it tends to line up with the direction in which evolution of the perturbation is governed mainly by the value of \(\lambda _1 \), whereas the terms connected with subsequent LE \(\lambda _2 , \lambda _3 , \ldots , \lambda _n \) become negligible [47]. Therefore, throughout its evolution, \({{\varvec{z}}}_\mathbf{1}\) tends to a direction orthogonal to \(W_2 \). The component \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) of the perturbation \({{\varvec{z}}}_\mathbf{2}\), which is perpendicular to \({{\varvec{z}}}_\mathbf{1}\), can be obtained by means of formula (5). To a good approximation \({\tilde{{{\varvec{z}}}}}_\mathbf{2} \in W_2 \). Moreover, \({\tilde{{{\varvec{z}}}}}_\mathbf{2}\) tends to a direction which is orthogonal to \(W_3 \). Consequently, vectors \(\tilde{\mathbf{z}}_{\mathbf{3}} , \tilde{\mathbf{z}}_\mathbf{4} , \ldots , \tilde{\mathbf{z}}_{{{\varvec{n}}}-\mathbf{1}}\) can be calculated using the following orthogonalization expression:

$$\begin{aligned} {\tilde{{{\varvec{z}}}}}_{{\varvec{k}}}= & {} {{\varvec{z}}}_{{\varvec{k}}} -{{\varvec{z}}}_\mathbf{1} *\frac{{{\varvec{z}}}_\mathbf{1} \cdot {{\varvec{z}}}_{{\varvec{k}}} }{\left| {\mathbf{z}_\mathbf{1} } \right| ^{2}}\nonumber \\&-\mathop \sum \limits _{i=2}^{k-1} {\tilde{{{\varvec{z}}}}}_{{\varvec{i}}} {*}\frac{{\tilde{{{\varvec{z}}}}}_{{\varvec{i}}} \cdot {{\varvec{z}}}_{{\varvec{k}}} }{\left| {{\tilde{{{\varvec{z}}}}}_{{\varvec{i}}} } \right| ^{2}},\quad \,k=3, 4,\ldots , \left( {n-1} \right) \end{aligned}$$
(7)

Formula (7) yields a vector \({\tilde{{{\varvec{z}}}}}_{{\varvec{k}}}\) which has no components in directions of \({{\varvec{z}}}_\mathbf{1} , {\tilde{{{\varvec{z}}}}}_\mathbf{2} , \ldots , {\tilde{{{\varvec{z}}}}}_{{{\varvec{k}}}-\mathbf{1}}\). Each of the vectors \({\tilde{{{\varvec{z}}}}}_{{\varvec{k}}}\), estimated by means of (7), approximately fulfills the condition \({\tilde{{{\varvec{z}}}}}_{{\varvec{k}}} \in W_k \) and tends to a direction orthogonal to \(W_{k+1} \). Therefore, the LE \(\lambda _2 , \lambda _3 , \ldots , \lambda _{n-1} \) can be estimated from the formula:

$$\begin{aligned} \lambda _k^{*} =\frac{\frac{d{\tilde{{{\varvec{z}}}}}_{{\varvec{k}}} }{dt}\cdot {\tilde{{{\varvec{z}}}}}_{{\varvec{k}}} }{\left| {{\tilde{{{\varvec{z}}}}}_{{\varvec{k}}}} \right| ^{2}},\quad \,k=2, 3,\ldots , \left( {n-1} \right) \end{aligned}$$
(8)

The approximate value of \(\lambda _k \) is obtained by averaging values of \(\lambda _k^*\) from subsequent computation steps. For long enough time of integration, the average value of \(\lambda _k^*\) converges to the \(k\mathrm{th}\) LE. Now, let us take any random vector \(z_n \) such that its length is nonzero and it is linearly independent from \({{\varvec{z}}}_\mathbf{1} , {\tilde{{{\varvec{z}}}}}_\mathbf{2} , \ldots , {\tilde{{{\varvec{z}}}}}_{{{\varvec{n}}}-\mathbf{1}} \). Using formula (7), one can orthogonalize the random vector \({{\varvec{z}}}_{{\varvec{n}}}\) with respect to \({{\varvec{z}}}_\mathbf{1} , {\tilde{{{\varvec{z}}}}}_\mathbf{2}, \ldots , {\tilde{{{\varvec{z}}}}}_{{{\varvec{n}}}-\mathbf{1}} \). In such a manner, \({\tilde{{{\varvec{z}}}}}_{{\varvec{n}}}\) is obtained. The length of \({\tilde{{{\varvec{z}}}}}_{{\varvec{n}}}\) is random, but owing to the orthogonalization process, it approximately fulfills the condition \({\tilde{{{\varvec{z}}}}}_{{\varvec{n}}} \in W_n \). Note that the order of the subspace \(W_n \) is equal to 1, so \(W_n \) is simply a line in the \(W_1 \) space. Therefore, \({\tilde{{{\varvec{z}}}}}_{{\varvec{n}}}\) must have the direction of a perturbation in the \(W_n \) space. Moreover, the value obtained from formula (8) is independent from the length of \({\tilde{{{\varvec{z}}}}}_{{\varvec{k}}}\). Concluding, one can apply formula (7) to orthogonalize a randomly selected random vector \({{\varvec{z}}}_{{\varvec{n}}}\) with respect to the integrated perturbations \({{\varvec{z}}}_\mathbf{1} , {\tilde{{{\varvec{z}}}}}_\mathbf{2} , \ldots , {\tilde{{{\varvec{z}}}}}_{{{\varvec{n}}}-\mathbf{1}}\) and then use the result \({\tilde{{{\varvec{z}}}}}_{{\varvec{n}}}\) to estimate the last LE by means of formula (8). In such a manner, it has been shown that it is enough to integrate \(\left( {n-1} \right) \) perturbations to estimate the full spectrum of LE of a \(n\mathrm{th}\)-order system.

3 Numerical simulations

Simulation programs were written in C++ using CodeBlocks 16.01. Graphs and diagrams were built with matplotlib library as a tool of Python programming language. In order to integrate the system of differential Eqs. (1)–(2), Runge-Kutta method of the fourth order was used. The integration step was chosen experimentally for each system.

In order to estimate the whole spectrum of Lyapunov exponents, the method requires to simulate \(\left( {n-1} \right) \) perturbations, where n is the order of the system. For example, for the second-order non-autonomous Duffing oscillator with external excitation [42], one perturbation was calculated. For the third-order autonomous system of Lorenz equations [48], two disturbances were observed. For three Duffing systems coupled in a ring scheme [50], which together constitute a system of the \(6\mathrm{th}\) order, five perturbations were integrated. After each integration step, subsequent perturbations were normalized and orthogonalized according to Eqs. (5), (7).

After every integration step, values \(\lambda _i^*\) are calculated for each perturbation. For the value of \(\lambda _1^*\), formula (3) is used; for \(\lambda _2^*, \lambda _3^*, \ldots , \lambda _n^*\), formula (8).

Fig. 2
figure 2

Bifurcation diagram of the Lorenz system (9)

Full size image

The simulation program remembered subsequent values of \(\lambda _i^*\) in n buffers of a fixed capacity. When buffers were full, the program calculated standard deviation of all the values in each of n buffers. If the standard deviation of values in any buffer was too high, buffers were cleared and computations were continued. Otherwise, if the value of standard deviation for each buffer was below a fixed threshold, the calculations were terminated. The final value of \(\lambda _i \) returned by the program was equal to the average of all values \(\lambda _i^*\) remembered in the i-th buffer.

4 Results of numerical simulations

In order to verify our method of the Lyapunov exponents spectrum estimation, three systems have been analyzed: Lorenz equations, Duffing oscillator with external periodic driving forcing and three Duffing systems coupled in a ring scheme. Firstly, the Lorenz system can be described with the following mathematical model [49]:

$$\begin{aligned} \begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {\dot{x} = \sigma \left( {y - x} \right) ,} \\ {\dot{y} = rx - y - xz,} \\ {\dot{z} = xy - \beta z;} \\ \end{array} } \right. } \\ \end{array} \end{aligned}$$
(9)

Jacobi matrix was used to simulate evolution of perturbations according to Eq. (2). For the Lorenz system (9), the Jacobi matrix is described by formula (10).

$$\begin{aligned} {{\varvec{U}}}\left( {{\varvec{x}}} \right) =\left( {{\begin{array}{ccc} {-\sigma }&{}\quad \sigma &{}\quad 0 \\ {r-z}&{} {-1}&{} {-x} \\ y&{} x&{} {-\beta } \\ \end{array} }} \right) \end{aligned}$$
(10)

System (9) is nonlinear and autonomous. The spectrum of Lyapunov exponents of the system was computed with two parameters fixed, \(\sigma =10, \beta =8/3\), while r was used as the control parameter in the range from 0 to 100. Initial conditions for \(r=0\) were set as a random three-element vector of magnitude 1. Initial perturbations were also chosen randomly and normalized to 1.

The bifurcation diagram of the state variable z in system (9) is shown in Fig. 2. The corresponding graph of LE spectrum calculated using the new method is depicted in Fig. 3, whereas the LE spectrum graph obtained by means of the classical method is shown in Fig. 4.

Fig. 3
figure 3

LE spectrum of the Lorenz system (9), calculated using the new method

Full size image
Fig. 4
figure 4

LE spectrum of the Lorenz system (9), calculated using the classical method

Full size image

The bifurcation diagram presented in Fig. 2, together with the LE diagram presented in Figs. 3, 4, demonstrates that the Lorenz system (9) is periodic for all the values of r smaller or equal to 24.7, whereas it is chaotic for most values of r larger or equal to 24.8. However, for some values of r above 24.8, periodic windows exist. Detailed information on different kinds of limit sets in dynamical systems can be found in [47]. It can be noticed that the graphs in Fig. 3 (the new method) and in Fig. 4 (the classical method) are in complete agreement. Moreover, both graphs are consistent with [48], which confirms the correctness of the algorithm presented in this paper.

The Duffing oscillator can be described by the following mathematical model [42]:

$$\begin{aligned} \ddot{x} + \beta \dot{x} + \alpha x^{3} = q\cos \left( {\eta t} \right) \end{aligned}$$
(11)

The linear stiffness in Eq. (11) was skipped as in [42], which enables to compare the results. Jacobi matrix was used to simulate evolution of perturbations according to Eq. (2). For the Duffing system (11), the Jacobi matrix is described by formula (12).

$$\begin{aligned} {\begin{array}{l} {{{\varvec{U}}}\left( {{\varvec{x}}} \right) =\left( {{\begin{array}{cc} 0&{}\quad 1 \\ {-3\alpha x^{2}}&{}\quad {-\beta } \\ \end{array} }} \right) } \\ \end{array} } \end{aligned}$$
(12)

The spectrum of Lyapunov exponents for the Duffing oscillator was computed with such fixed parameters as \(\beta =0.05, \alpha =1, \eta =0.5.\) Parameter q was used as the control parameter in the range from 0.5 to 1.8 [42]. In the simulation, a random vector of length 1 was used as initial condition. Initial perturbations were also random and normalized to 1.

The bifurcation diagram of the state variable x of the Duffing Eq. (11) is shown in Fig. 5. The corresponding graph of LE spectrum calculated using the new method is depicted in Fig. 6. The LE spectrum graph obtained by the classical method is presented in Fig. 7. In both cases, red line corresponds to the largest LE, while blue line corresponds to the second Lyapunov exponent of system (11).

Fig. 5
figure 5

Bifurcation diagram of the Duffing Eq. (11)

Full size image
Fig. 6
figure 6

LE spectrum of the Duffing Eq. (11), calculated using the new method

Full size image
Fig. 7
figure 7

LE spectrum of the Duffing Eq. (11), calculated with the classical method

Full size image
Fig. 8
figure 8

Bifurcation diagram of three Duffing systems in the ring scheme

Full size image
Fig. 9
figure 9

LE diagram of three coupled Duffing systems (13) obtained with the new method

Full size image

Figures 5, 6 and 7 show that the Duffing system is chaotic for most values of the parameter q in ranges from 0.693 to 0.738 and from 1.237 to 1.673. However, some periodic windows exist in these ranges too. For the values of r between 0.5 and 0.692, from 0.739 to 1.236 and from 1.674 to 1.8, the system is periodic. For the Duffing system, the generalized divergence of the flow is constant and equal to \(-\beta \) [49]. Sum of Lyapunov exponents has to be equal to the generalized divergence of the flow. Therefore, graphs of the first and second Lyapunov exponents should be symmetrical with respect to horizontal line \(\lambda =-\frac{\beta }{2}\). This fact was confirmed in Fig. 6 and in Fig. 7.

Next, we consider a ring of three Duffing systems [50]. The resulting system is given by:

$$\begin{aligned} \begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {\dot{x}_{i} = y_{i} } \\ {\dot{y}_{i} = - dy_{i} - ax_{i} - x_{i}^{3} + k\left( {x_{{p\left( i \right) }} - x_{i} } \right) } \\ \end{array} } \right. } \\ \end{array} \end{aligned}$$
(13)

where \(i=1, 2, 3\) and \(p\left( i \right) \) is the index of the previous oscillator in the ring, i.e., \(p\left( 3 \right) =2, p\left( 2 \right) =1, p\left( 1 \right) =3\). Jacobi matrix of system (13) is described by formula (14):

$$\begin{aligned} \mathbf{U}\left( \mathbf{x} \right) =\left( {{\begin{array}{cccccc} 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ { {u}_1 }&{}\quad {- {d}}&{}\quad 0&{}\quad 0&{}\quad {k}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0 \\ {k}&{}\quad 0&{}\quad { {u}_2 }&{}\quad {- {d}}&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \\ 0&{}\quad 0&{}\quad {k}&{}\quad 0&{}\quad { {u}_3 }&{}\quad {- {d}} \\ \end{array} }} \right) \end{aligned}$$
(14)

where \(u_i =-a-3x_i^2 -k\). System (13) is nonlinear and autonomous. The spectrum of Lyapunov exponents of the system was computed with two parameters fixed, \(d=0.3, a=0.1\), while the coupling coefficient k was used as the control parameter in the range from 0 to 4. Initial conditions for \(k=0\) were set as a random six-element vector of magnitude 1. Initial perturbations were also chosen randomly and normalized to 1. Please note that names of parameters are different in formulas (11) and (13). This is due to the fact that results of both simulations can be verified in two different sources. Results of calculations for system (11) can be checked in [42], whereas system (13) can be verified in [50].

The bifurcation diagram of the state variable \(x_3 \) in system (13) is depicted in Fig. 8. The corresponding graph of LE spectrum calculated using the new method is shown in Fig. 9. The LE spectrum graph obtained by the classical method is presented in Fig. 10.

Fig. 10
figure 10

LE diagram of three coupled Duffing systems (13) obtained with the classical method

Full size image

Figures 8, 9 and 10 demonstrate how dynamics of three Duffing systems (13) changes as the coupling strength increases [50]. For the values of k smaller than 0.24, one can notice that all the LEs are negative and the system tends to a stable fixed point. For the values of k between 0.24 and 0.38, one LE is equal to 0, which corresponds to a periodic solution. In the range of parameter k from 0.38 to 1.79, more than one LEs are zero and a quasiperiodic solution is obtained. Transition to chaos takes place for k equal to 1.79, followed by transition to hyperchaos as coupling coefficient reaches 1.9. Please note that the full spectrum of six LEs was obtained by integration of five perturbation vectors. However, if the task is to just detect chaos and hyperchaos, only one perturbation is necessary when our new method is applied, whereas integration of two perturbations is required if the classical method is used.

5 Computation time comparisons

In the previous sections, the novel method has been explained and results of its application have been demonstrated. It has been confirmed that the novel method requires integration of only \(\left( {n-1} \right) \) perturbations to estimate n Lyapunov exponents, which is expected to increase efficiency of calculations. Moreover, formulae (3) and (8), which are used for LE estimation in the new method, require only the most basic mathematical calculations—addition, multiplication and division. In such a manner, calculation of perturbation’s norm logarithm, which is necessary in the classical method, can be avoided. Therefore, there are two possible reasons for efficiency of the novel method. Firstly, size of the problem is reduced, because only \(\left( {n-1} \right) \) perturbations are integrated. However, computation speed gain due to this feature may vary with the order of the system. Secondly, application of formulae (3) and (8) instead of estimation of the logarithm of the perturbation norm can additionally shorten the computation time.

Firstly, influence of application of formulae (3) and (8) is analyzed without taking into account the number of perturbations to be integrated. When the classical method of LE estimation is applied, each computation step requires to calculate the norm of a perturbation. The norm can be treated as the square root of the dot product of the perturbation vector with itself. Then, the natural logarithm of the norm is calculated. On the other hand, formulae (3) and (8) of the new method require not only the perturbation vector, but also its time derivative. When both vectors are known, then according to (3) and (8), the dot product of the perturbation and its time derivative is divided by the dot product of the perturbation vector with itself.

Fig. 11
figure 11

Computation time of formula (3) divided by the average computation time of the classical method for the best case, when only one element of \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) in each row is nonzero

Full size image
Fig. 12
figure 12

Computation time of formula (3) divided by the average computation time of the classical method for the worst case, when all elements of \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) are nonzero

Full size image

Efficiency of both approaches has been tested by a C++ program. The program selects \(2*10^{7}\) vectors at random. Then, it checks how much time it takes to estimate natural logarithm of the norm of each of these vectors, just as it is done in the classical method of LE estimation [47]. Afterward, formula (3) is applied for each vector from the same set and time of these operations is also measured. In such a manner, efficiency of both methods of LE estimation can be compared. This test has been executed 100 times for different vector dimensions. The average, the minimum and the maximum computation time has been recorded for both methods.

However, an important issue arises: Efficiency of the novel method of LE estimation can be largely influenced by estimation of the perturbation’s derivative, which is required by the new method. If the Jacobi matrix \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) contains only few nonzero elements, then calculation of the perturbation’s derivative according to formula (2) is fast. When most elements of \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) are nonzero, then calculation of the perturbation’s derivative is slower. Therefore, two separate cases have been analyzed. In the best scenario, only one element in each row of \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) is nonzero. In the worst case, all elements of \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) are nonzero. Results for both cases with different vector dimensions are presented in Figs. 11 and 12. These figures represent the best case and the worst case, respectively. In each of these graphs, the computation time ratio is obtained by dividing computation time of formula (3) by the average time of calculations with the classical method, i.e., when the natural logarithm of the vector’s norm is estimated. Therefore, value 1 in the graph means that the computation time for both methods is equal. Values below 1 show that the new method is faster, and values above 1 indicate that the novel method is slower.

Figures 11 and 12 show that when order of the system is less or equal to 4, then evaluation of formula (3) or (8) is always faster than calculation of the natural logarithm of the perturbation’s norm. However, for higher order systems, evaluation of the perturbation’s norm logarithm can be faster if the Jacobi matrix \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) is dense enough. On the other hand, if \({{\varvec{U}}}\left( {{\varvec{x}}} \right) \) is sparse, then evaluation of formula (3) or (8) is faster than the classical formula for all vector dimensions under consideration.

Fig. 13
figure 13

LE spectrum estimation time for system (13) using the new method divided by the average computation time of the classical method

Full size image

Now, as the influence of using the simplified formulae (3) and (8) has been investigated, overall efficiency of the novel method can be checked on a practical example. To do so, the spectrum of Lyapunov exponents of Duffing systems coupled in ring scheme (13) has been estimated with both methods for different number of oscillators in the ring, from 1 to 5. Therefore, systems of orders \(2, 4, \ldots , 10\) have been investigated. The same coupling strength \(k=3.0\) has been used in all tests. For each number of oscillators, the Lyapunov exponents spectrum has been estimated 100 times using both methods. The orthonormalization process [47] has been performed after each iteration of both methods. The average, minimum and maximum computations times have been recorded. The results are presented in Fig. 13. The computation time ratio is obtained by dividing the calculations time of the novel method by the average time of calculations of the classical method. Therefore, just as in previous graphs, values below 1 indicate that the novel method is faster, whereas values above 1 show that the classical method performs better.

Figure 13 confirms that the novel method, presented in this paper, is faster than the classical method [47] in each test case, as long as order of system (13) is smaller or equal to 4. For the system with three oscillators and order 6, the novel method is faster in the average, but it is not faster in each trial. When more than three oscillators are coupled together, the classical method performs better.

6 Conclusions

The presented article shows that from dot products of perturbations vectors and their derivatives, one can easily extract the full spectrum of Lyapunov exponents. We have shown that full spectrum of LE for a system of order n can be obtained by integrating only \(\left( {n-1} \right) \) perturbations. Moreover, due to the fact that our method is based on very unsophisticated computations involving only basic mathematical operations such as summing, subtracting, multiplying, dividing, it is more efficient than the classical one when the order of the system is low enough. We have presented the theoretical description showing the mathematical simplicity of the method. The correctness and effectiveness of our method has been confirmed by simulations of autonomous and non-autonomous nonlinear dynamical systems of different orders. These results have been compared with the ones obtained using the classical algorithm. The efficiency of the new method has been compared to the method that involves the calculation of perturbations lengths logarithms and Gram–Schmidt orthonormalization. Firstly, it has been shown that application of the new, simple formulas for LE estimation is faster than calculation of the natural logarithm of perturbation’s norm for systems of dimension smaller or equal to 4, even if the Jacobi matrix of the system is dense. It has been revealed that if the Jacobi matrix is sparse, then the novel formulas can perform better even for systems of the dimension 10 or higher. Secondly, efficiency of the novel method has been verified for Duffing systems coupled in the ring scheme. It turned out that the novel method is in average faster if the dimension of the system is smaller or equal to 6. Obviously, efficiency of both methods may vary depending on properties of the system under consideration. Moreover, implementation of the method may influence the effectiveness. However, taking into account the obtained results, it can be stated that for low-dimensional, continuous-time, smooth systems, the presented method of LE spectrum estimation is the fastest one. The next step of the method’s development can be considered in estimation of LE in systems with discontinuities, with time delays and others.