Modal asymptotic analysis of sub-harmonic and quasi-periodic flexural vibrations of beams with cracks

Abstract

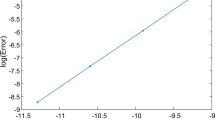
Nonlinear finite-DOF dynamical system is derived to describe the beam vibrations with transversal crack. The beam deflections are expanded by using the eigenmodes and contact parameter. The Galerkin method is applied to the partial differential equation, which describes the structure vibrations. Two- and three-DOF nonlinear dynamical systems with internal resonance are analyzed. The multiple scales method is used to investigate both the principle second resonance and the combination one. The resonance quasi-periodic and sub-harmonic motions are analyzed. The quasi-periodic motions are arisen due to the Neimark–Sacker bifurcation.

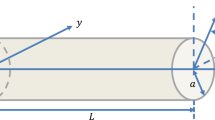
Appendix: Characteristics of the beam cross section

The crack function for the beam with rectangular cross section has the following form:

$$\begin{aligned} f\left( {x,z} \right) =\left[ {z-m\left( {z+\frac{a}{2}} \right) H\left( {d-a-z} \right) } \right] \exp \left[ {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right] ,\nonumber \\ \end{aligned}$$

(47)

where $H\left( {d-a-z} \right)$ is the Heaviside function. The parameter $\alpha$ characterizes the rate of the stress decay. This parameter is calculated in the paper [3]: $\alpha =1.276$. The parameter m is determined as [4]:

$$\begin{aligned} m=\left\{ {1+\frac{3}{4}\left( {\frac{a}{d}} \right) ^{2}-\frac{3}{2}\frac{a}{d}-\frac{1}{8}\left( {\frac{a}{d}} \right) ^{3}} \right\} ^{-1}.\left( {A1.2} \right) \nonumber \\ \end{aligned}$$

(48)

The displacement function $\varphi \left( {x,z} \right)$ takes the following form:

$$\begin{aligned} \varphi \left( {x,z} \right) =\left[ {z-\left( {z+\frac{a}{2}} \right) H\left( {d-a-z} \right) } \right] \exp \left[ {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right] .\nonumber \\ \end{aligned}$$

(49)

The parameter $\beta$ is calculated by Shen and Pierre [3]: $\beta =21.94$.

The parameters of the system (4) are presented in the form of the double integrals:

$$\begin{aligned}&I=\mathop \int \limits _A z^{2}{} { dA};~ L_1 =\mathop \int \limits _A f\varphi { dA};\quad K=\mathop \int \limits _A zfdA;\nonumber \\&K_1 =\mathop \int \limits _A z\varphi dA;\quad L_3 =\mathop \int \limits _A f^{I}\varphi { dA};\nonumber \\&L_2 =\mathop \int \limits _A f\varphi ^{I}dA;\quad L=\mathop \int \limits _A f^{2}dA;\quad K_2 =\mathop \int \limits _A z\varphi ^{I}dA;\nonumber \\&L_4 =\mathop \int \limits _A f^{II}\varphi dA;\quad L_5 =\mathop \int \limits _A f^{I}\varphi ^{I}dA;\nonumber \\&Q_1 =\frac{I+\gamma \left( {L_1 -K-K_1 } \right) }{I+\gamma \left( {L-2K} \right) }, \end{aligned}$$

(50)

where $f^{I}=\frac{\hbox {d}f}{\hbox {d}x}$. The functions (A.1, A.2, A.3) are substituted into the equations (A.4). As a result, it is obtained:

$$\begin{aligned}&I=\frac{4}{3}bd^{3};\\&L_1 =I\left( {1-\frac{1}{m}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) exp\left( {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&K=0;\\&K_1 =I\left( {1-\frac{1}{m}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&L_3 =-\frac{\alpha }{d}I\left( {1-\frac{1}{m}} \right) exp\left( {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&L_2 =-\frac{2\beta }{d}I\left( {1-\frac{1}{m}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) exp\left( {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&L=\left( {m-1} \right) Iexp\left( {-2\alpha \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&K_2 =K_1^I ;\\&L_4 =\frac{\alpha ^{2}}{d^{2}}I\left( {1-\frac{1}{m}} \right) exp\left( {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) ;\\&L_5 =\frac{2\beta \alpha }{d^{2}}I\left( {1-\frac{1}{m}} \right) exp\left( {-2\beta \frac{\left| {x-x_c } \right| }{d}} \right) exp\left( {-\alpha \frac{\left| {x-x_c } \right| }{d}} \right) . \end{aligned}$$