Skip to main content
SpringerLink
Log in

Geometric singular perturbation method to the existence and asymptotic behavior of traveling waves for a generalized Burgers–KdV equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

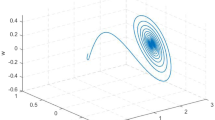
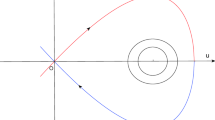
In this paper, we discuss the existence and asymptotic behavior of traveling waves for a generalized Burgers–KdV equation. We show the heteroclinic orbits of the associated ordinary differential equations for the generalized Burgers–KdV equation with a special convolution kernel and then establish the existence result of traveling wave solutions for the Burgers–KdV equation by employing geometric singular perturbation theory and the linear chain trick. And the asymptotic behavior of traveling waves is obtained by using the standard asymptotic theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular channel, and on a new type of long stationary waves. Phil. Mag. 39, 422–443 (1895)

    Article  MATH  Google Scholar 

  2. Feudel, F., Steudel, H.: Nonexistence of prolongation structure for the Korteweg-de Vrie-Burgers equation. Phys. Lett. A 107, 5–8 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  3. Burgers, J.M.: Mathematical examples illustrating relations occurring in the theory of turbulent fluid motion. Trans. R. Neth. Acad. Sci. Amst. 17, 1–53 (1939)

    MathSciNet  Google Scholar 

  4. Feng, Z., Knobel, R.: Traveling waves to a Burgers–Korteweg–de Vries-type equation with higher-order nonlinearities. J. Math. Anal. Appl. 328, 1435–1450 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  5. David, C., Fernando, R., Feng, Z.: On solitary wave solutions of the compound Burgers–Korteweg–de Vries equation. Phys. Lett. A 375, 44–50 (2007)

    MathSciNet  Google Scholar 

  6. Shen, J.: Shock wave solutions of the compound Burgers–Korteweg–de Vries equation. Appl. Math. Comput. 196, 842–849 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  7. Li, J.: Singular Nonlinear Travelling Wave Equations: Bifurcations and Exact Solutions. Science Press, Beijing (2013)

    Google Scholar 

  8. Li, X., Wang, M.: A sub-ODE method for finding exact solutions of a generalized KdV–mKdV equation with high-order nonlinear terms. Phys. Lett. A 361, 115–118 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  9. Triki, H., Taha, T.R., Wazwaz, A.M.: Solitary wave solutions for a generalized KdV–mKdV equation with variable coefficients. Math. Comput. Simul. 80, 1867–1873 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Li, Z.: Constructing of new exact solutions to the GKdV–mKdV equation with any-order nonlinear terms by \((G^{\prime }/G)\)-expansion method. Appl. Math. Comput. 217, 1398–1403 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  11. Ceballos, J.C., Sepu’lveda, M., Villagra’n, O.P.V.: The Korteweg–de Vries–Kawahara equation in a bounded domain and some numerical results. Appl. Math. Comput. 190, 912–936 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  12. Wahlquist, H.D., Estabrook, F.B.: B\(\ddot{a}\)klund transformations for solitons of the Korteweg-de Vries equation. Phys. Rev. Lett. 31, 1386–1390 (1973)

    Article  MathSciNet  Google Scholar 

  13. Huang, Y.: Exact multi-wave solutions for the KdV equation. Nonlinear Dyn. 77, 437–444 (2014)

    Article  Google Scholar 

  14. Li, W., Sun, Y., Wang, Z.: Entire solutions in the Fisher-KPP equation with nonlocal dispersal. Nonlinear Anal. Real World Appl. 11(4), 2302–2313 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  15. Ashwin, P., Bartuccelli, M.V., Gourley, S.A.: Traveling fronts for the KPP equation with spatio-temporal delay. Z. Angew. Math. Phys. 53, 103–122 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  16. Kenig, C.E., Ponce, G., Vega, L.: Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle. Commun. Pure Appl. Math. 46, 527–620 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  17. Escauriaza, L., Kenig, C.E., Ponce, G., et al.: On uniqueness properties of solutions of the k-generalized KdV equations. J. Funct. Anal. 244, 504–535 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  18. Hek, G.: Geometric singular perturbation theory in biological practice. J. Math. Biol. 60, 347–386 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  19. Fenichel, N.: Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31, 53–98 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  20. Jones, C.K.R.T.: Geometrical singular perturbation theory. In: Johnson, R. (ed.) Dynamical Systems, Lecture Notes in Mathematics, vol. 1609. Springer, New York (1995)

    Google Scholar 

  21. Ogawa, T.: Travelling wave solutions to a perturbed Korteweg-de Vries equation. Hiroshima J. Math. 24, 401–422 (1994)

    MATH  Google Scholar 

  22. Zhao, Z.: Solitary waves of the generalized KdV equation with distributed delays. J. Math. Anal. Appl. 344, 32–41 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  23. Zhao, Z., Xu, Y.: Solitary waves for Korteweg-de Vries equation with small delay. J. Math. Anal. Appl. 368, 43–53 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  24. Xu, Y., Du, Z.: Existence of traveling wave fronts for a generalized KdV–mKdV equation. Math. Model. Anal. 19(4), 509–523 (2014)

    Article  MathSciNet  Google Scholar 

  25. Fu, Y., Liu, Z.: Persistence of travelling fronts of KdV–Burgers–Kuramoto equation. Appl. Math. Comput. 216, 2199–2206 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  26. Mansour, M.B.A.: A geometric construction of traveling waves in a generalized nonlinear dispersive–dissipative equation. J. Geom. Phys. 69, 116–122 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  27. Mansour, M.B.A.: Traveling wave solutions for a singularly perturbed Burgers-KdV equation. Pramana J. Phys. 73, 799–806 (2009)

    Article  Google Scholar 

  28. Mansour, M.B.A.: Traveling waves for a dissipative modified KdV equation. J. Egypt. Math. Soc. 20, 134–138 (2012)

    Article  MATH  Google Scholar 

  29. Liang, F., Gao, H.: Existence of traveling wave solutions for a reaction–diffusion equation with nonlocal delay (in Chinese). Acta Math. Sci. 31A(5), 1273–1281 (2011)

    MathSciNet  Google Scholar 

  30. Ou, C., Wu, J.: Persistence of wavefronts in delayed nonlocal reaction–diffusion equations. J. Differ. Equ. 238, 219–261 (2007)

    Article  MathSciNet  Google Scholar 

  31. Berglunda, N., Gentz, B.: Geometric singular perturbation theory for stochastic differential equations. J. Differ. Equ. 191, 1–54 (2003)

    Article  Google Scholar 

  32. Verhulst, F.: Singular perturbation methods for slow–fast dynamics. Nonlinear Dyn. 50, 747–753 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  33. Liu, W.: One-dimensional steady-state PoissonCNernstCPlanck systems for ion channels with multiple ion species. J. Differ. Equ. 246, 428–451 (2009)

    Article  MATH  Google Scholar 

  34. Lu, N., Zeng, C.: Normally elliptic singular perturbations and persistence of homoclinic orbits. J. Differ. Equ. 250, 4124–4176 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  35. Maesschalck, P.De, Dumortier, F.: Slow–fast Bogdanov–Takens bifurcations. J. Differ. Equ. 250, 1000–1025 (2011)

    Article  MATH  Google Scholar 

  36. Dumortier, F., Roussarie, R.: Multiple canard cycles in generalized Liénard equations. J. Differ. Equ. 174, 1–29 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  37. Dumortier, F.: Compactification and desingularization of spaces of polynomial Liénard equations. J. Differ. Equ. 224, 296–313 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  38. Caubergh, M., Dumortier, F.: Hilbert’s 16th problem for classical Liénard equations of even degree. J. Differ. Equ. 244, 1359–1394 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  39. Lv, G., Wang, M.: Existence, uniqueness and asymptotic behavior of traveling wave fronts for a vector disease model. Nonlinear Anal. 11, 2035–2043 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  40. Gourley, S.A., Ruan, S.G.: Convergence and traveling wave fronts in functional differential equations with nonlocal terms: a competition model. SIAM. J. Math. Anal. 35, 806–822 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  41. Ruan, S., Xiao, D.: Stability of steady states and existence of traveling wave in a vector disease model. Proc. R. Soc. Edinb. 134 A, 991–1011 (2004)

    Article  MathSciNet  Google Scholar 

  42. Lin, G., Li, W.: Bistable wavefronts in a diffusive and competitive Lotka–Volterra type system with delays. J. Differ. Equ. 244, 487–513 (2008)

    Article  MATH  Google Scholar 

  43. Li, C., Zhu, H.: Canard cycles for predator–prey systems with Holling types of functional response. J. Differ. Equ. 254, 879–910 (2013)

    Article  MATH  Google Scholar 

Download references

Acknowledgments

This work is supported by the Natural Science Foundation of China (Grant No. 11471146), PAPD of Jiangsu Higher Education Institutions and postgraduate training project of Jiangsu Province and Jiangsu Normal University. The authors express their sincere thanks to the anonymous reviewers for their valuable comments and suggestions for improving the quality of the paper.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, 221116, China

    Ying Xu, Zengji Du & Lei Wei

Authors
  1. Ying Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zengji Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lei Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zengji Du.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Du, Z. & Wei, L. Geometric singular perturbation method to the existence and asymptotic behavior of traveling waves for a generalized Burgers–KdV equation. Nonlinear Dyn 83, 65–73 (2016). https://doi.org/10.1007/s11071-015-2309-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2309-5

Keywords

Mathematics Subject Classification

Search

Navigation