Skip to main content
SpringerLink
Log in

Complex nonlinearities of rogue waves in generalized inhomogeneous higher-order nonlinear Schrödinger equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

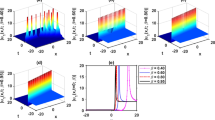
In this paper, the Nth-order rogue waves are investigated for an inhomogeneous higher-order nonlinear Schrödinger equation. Based on the Heisenberg ferromagnetic spin system, the higher-order nonlinear Schrödinger equation is generated. The generalized Darboux transformation is constructed by the Darboux matrix. The solutions of the Nth-order rogue waves are given in terms of a recursive formula. There are complex nonlinear phenomena in the rogue waves, add the first-order to the fourth-order rogue waves are discussed in some figures obtained by analytical solutions. It is shown that the general Nth-order rogue waves contain \(2n-1\) free parameters. The free parameters play a crucial role to affect the dynamic distributions of the rogue waves. The results obtained in this paper will be useful to understand the generation mechanism of the rogue wave.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Müller, P., Garrett, C., Osborne, A.: Rogue waves. Oceanography 18, 66–75 (2005)

    Article  Google Scholar 

  2. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A 373, 675–678 (2009)

    Article  MATH  Google Scholar 

  3. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1058 (2007)

    Article  Google Scholar 

  4. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Matter rogue waves. Phys. Rev. A 80, 033610 (2009)

    Article  Google Scholar 

  5. Ganshin, A.N., Efimov, V.B., Kolmakov, G.V., Mezhov-Deglin, L.P., McClintock, P.V.E.: Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 101, 065303 (2008)

    Article  Google Scholar 

  6. Kharif, C., Pelinovsky, E.: Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B/Fluids 22, 603–634 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  7. Janssen, P.A.: Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33, 863–884 (2003)

    Article  MathSciNet  Google Scholar 

  8. Onorato, M., Osborne, A.R., Serio, M., et al.: Freak waves in random oceanic sea states. Phys. Rev. Lett. 86, 5831–5834 (2001)

    Article  Google Scholar 

  9. Peregrine, D.H.: Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Ser. B 25, 16–43 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  10. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E 80, 026601 (2009)

    Article  Google Scholar 

  11. Zhu, H.P.: Nonlinear tunneling for controllable rogue waves in two dimensional graded-index waveguides. Nonlinear Dyn. 72, 873–882 (2013)

    Article  Google Scholar 

  12. Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62–69 (1971)

    MathSciNet  Google Scholar 

  13. Matveev, V.B., Salle, M.A.: Darboux Transformation and Solitons. Springer, Berlin (1991)

    Book  Google Scholar 

  14. Zhaqilao, : On Nth-order rogue wave solution to the generalized nonlinear Schrödinger equation. Phys. Lett. A 377, 855–859 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. Dai, C.Q., Zhu, H.P.: Superposed Akhmediev breather of the (3+1)-dimensional generalized nonlinear Schrödinger equation with external potentials. Ann. Phys. 341, 142–152 (2014)

    Article  MathSciNet  Google Scholar 

  16. Yang, B., Zhang, W.G., Zhang, H.Q., Pei, S.B.: Generalized Darboux transformation and rogue wave solutions for the higher-order dispersive nonlinear Schrödinger equation. Phys. Scripta 88, 065004 (2013)

    Article  Google Scholar 

  17. Jiang, H.J., Xiang, J.J., Dai, C.Q., Wang, Y.Y.: Nonautonomous bright soliton solutions on continuous wave and cnoidal wave backgrounds in blood vessels. Nonlinear Dyn. 75, 201–207 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Ling, L.M., Guo, B.L., Zhao, L.C.: High-order rogue waves in vector nonlinear Schrödinger equations. Phys. Rev. E 89, 041201 (2014)

    Article  Google Scholar 

  19. Lü, X., Peng, M.S.: Painlevé-integrability and explicit solutions of the general two-coupled nonlinear Schrödinger system in the optical fiber communications. Nonlinear Dyn. 73, 405–410 (2013)

    Article  MATH  Google Scholar 

  20. Wang, Y.Y., Dai, C.Q., Wang, X.G.: Stable localized spatial solitons in PT-symmetric potentials with power-law nonlinearity. Nonlinear Dyn. 77, 1323–1330 (2014)

    Article  MathSciNet  Google Scholar 

  21. Dai, C.Q., Wang, X.G., Zhou, G.Q.: Stable light-bullet solutions in the harmonic and parity-time-symmetric potentials. Phys. Rev. A 89, 013834 (2014)

    Article  Google Scholar 

  22. Radha, R., Kumar, V.R.: Explode-decay solitons in the generalized inhomogeneous higher-order nonlinear Schrödinger equations. Zeitschrift fur Naturforschung A 62, 381–386 (2007)

    MATH  Google Scholar 

  23. Calogero, F., Degasperis, A.: Conservation laws for classes of nonlinear evolution equations solvable by the spectral transform. Commun. Math. Phys. 63, 155–176 (1978)

    Article  MathSciNet  MATH  Google Scholar 

  24. Lakshmanan, M., Bullough, R.K.: Geometry of generalised nonlinear Schrödinger and Heisenberg ferromagnetic spin equations with linearly x-dependent coefficients. Phys. Lett. A 80, P287–292 (1980)

    Article  MathSciNet  Google Scholar 

  25. Abdulleav, F.: Theory of Soliton in Inhomogeneous Media. New York (1984)

  26. Chen, H.H., Liu, C.S.: Nonlinear wave and soliton propagation in media with arbitrary inhomogeneities. Phys. Fluids 21, 377–380 (1978)

    Article  MATH  Google Scholar 

  27. Zhong, W.Z., Bai, Y.Q., Wu, K.: Generalized inhomogeneous Heisenberg ferromagnet model and generalized nonlinear Schrödinger equation. Phys. Lett. A 352, 64–68 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  28. Guo, B.L., Ling, L.M., Liu, Q.P.: Nonlinear Schrodinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E 85, 026607 (2012)

    Article  Google Scholar 

  29. Dubard, P., Gaillard, P., Klein, C., Matveev, V.B.: On multi-rogue wave solutions of the NLS equation and position solutions of the KdV equation. Eur. Phys. J. Special Top. 185, 247–258 (2010)

    Article  Google Scholar 

  30. Dubard, P., Matveev, V.B.: Multi-rogue waves solutions of the focusing NLS equation and the KP-I equation. Nat. Hazards Earth Syst. Sci. 11, 667–672 (2011)

    Article  Google Scholar 

Download references

Acknowledgments

The authors gratefully acknowledge the support of the National Natural Science Foundation of China (NNSFC) through Grant Nos. 11290152, 11072008 and 10732020, the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB).

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Beijing University of Technology, Beijing, 100022, People’s Republic of China

    N. Song, W. Zhang & M. H. Yao

  2. Department of Mathematics, North University of China, Taiyuan, 030051, Shanxi, People’s Republic of China

    N. Song

Authors
  1. N. Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. H. Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to W. Zhang.

Appendix

Appendix

Analytical expressions of the coefficients in Eq. (21) are given as

$$\begin{aligned} \varphi _1^{[2]}= & {} \left( \frac{1}{\sqrt{a}}\left( \frac{i}{96}\left( 27648a^{9}t^{3}{\varepsilon }^{2}+2304a^{7}t^{3}{\varepsilon }\right. \right. \right. \nonumber \\&-\,96a^{3}xt^{2}-192a^{3}x^{2}t+64a^{5}t^{3}-240ta\nonumber \\&-\,12t^{3}a^{3}1152ia^{6}t^{3}{\varepsilon }+27648ia^{8}xt^{2}{\varepsilon }^{2}\nonumber \\&+\,4608ia^{6}xt^{2}{\varepsilon }-1152a^{5}xt^{2}{\varepsilon }-2304a^{5}x^{2}t{\varepsilon }\nonumber \\&\times \,110592a^{11}t^{3}{\varepsilon }^{3}+192ia^{4}xt^{2}+6912ia^{8}t^{3}{\varepsilon }^{2}\nonumber \\&-\,48ia^{2}x^{2}t-12ia^{2}xt^{2}-5952t{\varepsilon }a^{3}-192aa_1\nonumber \\&-\,48 i x-12it-144a^{5}t^{3}{\varepsilon }-192iab_1 \nonumber \\&\left. -\,64ia^{2}x^{3}-ia^{2}t^{3}+48ia^{4}t^{3}\right) \nonumber \\&-\,\frac{1}{32}\sqrt{a}\left( {-4x+48it{\varepsilon }a^{3}-t+4ita} \right) ^{2}\nonumber \\&+\,1/16a^{-3/2}+\frac{1}{768}\sqrt{a}\big ( -4x+48it{\varepsilon }a^{3}\nonumber \\&-\,t+4ita \big )\big (-1152a^{6}t^{3}{\varepsilon }-192a^{4}xt^{2}\nonumber \\&+\,192x+48t-48a^{4}t^{3}-4608a^{6}xt^{2}{\varepsilon }\nonumber \\&-\,1152ia^{5}xt^{2}{\varepsilon }-2304ia^{5}x^{2}t{\varepsilon }\nonumber \\&-\,27648a^{8}xt^{2}{\varepsilon }^{2}+64a^{2}x^{3}+a^{2}t^{3}-6912a^{8}t^{3}{\varepsilon }^{2}\nonumber \\&+\,48a^{2}x^{2}t+12a^{2}xt^{2}-960ita-12ia^{3}t^{3}\nonumber \\&\times \,64ia^{5}t^{3}-768iaa_1 +768ab_1 -23808it{\varepsilon }a^{3}\nonumber \\&-\,144ia^{5}t^{3}{\varepsilon }-96ia^{3}xt^{2}+27648ia^{9}t^{3}{\varepsilon }^{2}\nonumber \\&\times \,2304ia^{7}t^{3}{\varepsilon }-192ia^{3}x^{2}t\nonumber \\&\left. \left. +\,110592ia^{11}t^{3}{\varepsilon }^{3}\big )\right) \right) e^{\frac{i}{2}\theta },\nonumber \\ \end{aligned}$$
$$\begin{aligned} \varphi _1^{[2]}= & {} \left( {-\frac{1}{\sqrt{a}}\left( \frac{i}{96}\right. \left( 110592a^{11}t^{3}{\varepsilon }^{3}+27648a^{9}t^{3}\right. {\varepsilon }^{2}} \right. \nonumber \\&+\,2304a^{7}t^{3}{\varepsilon }-96a^{3}xt^{2}+192a^{3}x^{2}t\nonumber \\&+\,27648ia^{8}xt^{2}{\varepsilon }^{2}-48ia^{2}x^{2}t+64a^{5}t^{3}\nonumber \\&-240ta-12t^{3}a^{3}+1152ia^{6}t^{3}{\varepsilon } 12ia^{2}xt^{2}\nonumber \\&+\,6912ia^{8}t^{3}{\varepsilon }^{2}+192ia^{4}xt^{2}-48ix-12it\nonumber \\&-\,ia^{2}t^{3}-192iab_1+48ia^{4}t^{3}-64ia^{2}x^{3}\nonumber \\&-\,1152a^{5}xt^{2}{\varepsilon }-2304a^{5}x^{2}t{\varepsilon }-192aa_1 \nonumber \\&\left. \left. -\,5952t{\varepsilon }a^{3}-144a^{5}t^{3}{\varepsilon }4608ia^{6}xt^{2}{\varepsilon } \right) \right) \nonumber \\&-\frac{1}{32}\sqrt{a}\Big ( {-4x+48it{\varepsilon }a^{3}-t+4ita} \Big )^{2}\nonumber \\&+\,1/16a^{-3/2}+ \frac{1}{768}\sqrt{a}\Big ( -4x+48it{\varepsilon }a^{3}\nonumber \\&-\,t+4ita\Big )\Big (-96ia^{3}xt^{2}-192ia^{3}x^{2}t\nonumber \\&+\,192x+48t+64ia^{5}t^{3}+110592ia^{11}t^{3}{\varepsilon }^{3}\nonumber \\&+\,27648ia^{9}t^{3}{\varepsilon }^{2}-768iaa_1-12ia^{3}t^{3}\nonumber \\&-\,960ita+12a^{2}xt^{2}+48a^{2}x^{2}t-192a^{4}xt^{2}\nonumber \\&+\,768ab_1 -144ia^{5}t^{3}{\varepsilon }+2304ia^{7}t^{3}{\varepsilon }\nonumber \\&-23808it{\varepsilon }a^{3}-4608a^{6}xt^{2}{\varepsilon }-27648a^{8}xt^{2}{\varepsilon }^{2}\nonumber \\&-48a^{4}t^{3}+a^{2}t^{3}+64a^{2}x^{3}-6912a^{8}t^{3}{\varepsilon }^{2}\nonumber \\&-1152t^{3}a^{6}{\varepsilon } \quad -1152ia^{5}xt^{2}{\varepsilon }\nonumber \\&\left. -\,2304ia^{5}x^{2}t{\varepsilon } \Big ) \right) e^{-\frac{i}{2}\theta }. \end{aligned}$$
(38)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, N., Zhang, W. & Yao, M.H. Complex nonlinearities of rogue waves in generalized inhomogeneous higher-order nonlinear Schrödinger equation. Nonlinear Dyn 82, 489–500 (2015). https://doi.org/10.1007/s11071-015-2170-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2170-6

Keywords

Search

Navigation