Skip to main content
SpringerLink
Log in

The integral bifurcation method combined with factoring technique for investigating exact solutions and their dynamical properties of a generalized Gardner equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

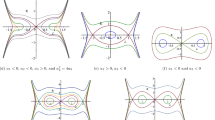
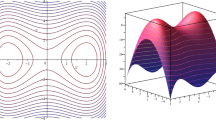
It is well known that it is difficult to obtain exact solutions of some partial differential equations with highly nonlinear terms or high order terms because these kinds of equations are not integrable in usual conditions. In this paper, by using the integral bifurcation method and factoring technique, we studied a generalized Gardner equation which contains both highly nonlinear terms and high order terms, some exact traveling wave solutions such as non-smooth peakon solutions, smooth periodic solutions and hyperbolic function solutions to the considered equation are obtained. Moreover, we demonstrate the profiles of these exact traveling wave solutions and discuss their dynamic properties through numerical simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Fokas, A.S.: On a class of physically important integrable equations. Physica D 87, 145–150 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  2. Tzirtzilakis, E., Marinakis, V., Apokis, C., Bountis, T.: Soliton-like solutions of higher order wave equations of the Korteweg-de-Vries type. J. Math. Phys. 43(12), 6151–6161 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  3. Tzirtzilakis, E., Xenos, M., Marinakis, V., Bountis, T.: Interactions and stability of solitary waves in shallow water. Chaos Solitons Fract. 14, 87–95 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  4. Li, J., Wu, J., Zhu, H.: Traveling waves for an integrable higher order KdV type wave equations. Int. J. Bifurcation Chaos 16(8), 2235–2260 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  5. Li, J.: Dynamical understanding of loop soliton solution for several nonlinear wave equations. Sci. China Ser. A: Math. 50(6), 773–785 (2007)

    Article  MATH  Google Scholar 

  6. Li, J., Rui, W., Long, Y., He, B.: Travelling wave solutions for a higher order wave equation of KdV type (III). Math. Biosci. Eng. 3(1), 125–135 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  7. Rui, W., Long, Y., He, B.: Some new travelling wave solutions with singular or nonsingular character for the higher order wave equation of KdV type (III). Nonlinear Analysis 70, 3816–3828 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  8. Wu, X., Rui, W., Hong, X.: A generalized KdV equation of neglecting the highest order infinitesimal term and its exact traveling wave solutions. Abstr. Appl. Analysis, 2013, Art. ID 656297, 33 pp (2013)

    Google Scholar 

  9. Marinakis, V.: Integrable third order equations of the KdV type. J. Math. Sci. Adv. Appl. 5(2), 317–332 (2010)

    Google Scholar 

  10. Marinakis, V.: Higher-order equations of the KdV type are integrable. Adv. Math. Phys. 2010, Art. ID 329586, 5 pp (2010)

  11. Li, J., Zhang, J.: Bifurcations of travelling wave solutions for the generalization form of the modified KdV equation. Chaos Solitons Fract. 21, 899–913 (2004)

    Article  MATH  Google Scholar 

  12. Bi, Q.: Peaked singular wave solutions associated with singular curves. Chaos Solitons Fract. 31, 417–423 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  13. Wang, Y., Tian, B., Wang, P., Li, M., Jiang, Y.: Bell-polynomial approach and soliton solutions for the Zhiber–Shabat equation and (2+1)-dimensional Gardner equation with symbolic computation. Nonlinear Dyn. 69(4), 2031–2040 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  14. Lü, X., Tian, B., Zhang, H., Xu, T., Li, H.: Generalized (2+1)-dimensional Gardner model: bilinear equations, Bäcklund transformation, Lax representation and interaction mechanisms. Nonlinear Dyn. 67(3), 2279–2290 (2012)

    Article  MATH  Google Scholar 

  15. Rui, W., He, B., Long, Y., Chen, C.: The integral bifurcation method and its application for solving a family of third-order dispersive PDEs. Nonlinear Analysis 69(4), 1256–1267 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  16. Rui, W., Long, Y., He, B., Li, Z.: Integral bifurcation method combined with computer for solving a higher order wave equation of KdV type. Int. J. Comput. Math. 87, 119–128 (2008)

    MathSciNet  Google Scholar 

  17. Rui, W., Long, Y.: Integral bifurcation method together with a translation–dilation transformation for solving an integrable 2-component Camassa–Holm shallow water system. J. Appl. Math. 2012, Art. ID 736765, 21 pp (2012)

    Google Scholar 

  18. Ma, W.X., Wu, H., He, J.: Partial differential equations possessing Frobenius integrable decompositions. Phys. Lett. A 364, 29–32 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  19. Ma, W.X., Lee, J.H.: A transformed rational function method and exact solutions to the \(3+1\) dimensional JimboCMiwa equation. Chaos Solitons Fract. 42, 1356–1363 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  20. Ma, W.X., Fuchssteiner, B.: Explicit and exact solutions to a Kolmogorov–Petrovskii–Piskunov equation. Int. J. Non-linear Mech. 31(3), 329–338 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  21. Ma, W.X., Huang, T., Zhang, Y.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82, art. ID 065003, 8 pages (2010)

    Google Scholar 

  22. Ma, W.X., Zhu, Z.N.: Solving the \((3+1)\)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl. Math. Comput. 218, 11871–11879 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  23. Ma, W.X.: Complexiton solutions to the Korteweg-de-Vries equation. Phys. Lett. A 301, 35–44 (2002)

    Google Scholar 

  24. Ma, W.X.: Bilinear equations, Bell polynomials and linear superposition principle. J. Phys. Conf. Ser. 411, Art. ID 012021 (2013). doi:10.1088/17426596/411/1/012021

  25. Ma, W.X.: Generalized bilinear differential equations. Stud. Nonlinear Sci. 2(4), 140–144 (2011)

    Google Scholar 

Download references

Acknowledgments

This study was supported the Natural Science Foundation of China under Grant No. 11361023, the Natural Science Foundation of Chongqing Normal University under Grant No. 13XLR20 and the Program Foundation of Chongqing Innovation Team Project in University under Grant No. KJTD201308.

Author information

Authors and Affiliations

  1. Department of Mathematics, Chongqing Normal University, Chongqing , 401331, People’s Republic of China

    Weiguo Rui

Authors
  1. Weiguo Rui
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Weiguo Rui.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rui, W. The integral bifurcation method combined with factoring technique for investigating exact solutions and their dynamical properties of a generalized Gardner equation. Nonlinear Dyn 76, 1529–1542 (2014). https://doi.org/10.1007/s11071-013-1226-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-1226-8

Keywords

Search

Navigation