The numerical influence of additional parameters of inertia representations for quaternion-based rigid body dynamics

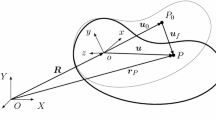
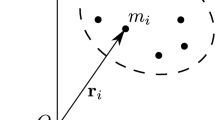
Abstract

Different inertia representations can lead to different formulations of the differential-algebraic equations for the quaternion-based rigid body dynamics. In this paper, the inertia representations are classified into $\alpha$-type and $\gamma$-type, according to the additional parameters in the kinetic energy. These two types of representations and the corresponding parameters $\alpha$ and $\gamma$ are theoretically equivalent if the constraint $\boldsymbol{q}^{T}\boldsymbol{q} = 1$ is satisfied exactly. Nevertheless, the error estimation demonstrates that they can present entirely different numerical features in simulation and suggests that the parameter $\gamma$ can be used to optimize the numerical performance of the integrations in simulation. To further verify the numerical difference between the inertia representations of $\alpha$-type and $\gamma$-type, the corresponding modified Hamilton’s equations are discretized by the IMS (implicit midpoint scheme), EMS (energy–momentum preserving scheme) and Gauss–Lobatto SPARK methods. Numerical performance for the examples of the spinning symmetrical top is shown to result from the comprehensive effect of the discretization schemes including the distribution of discretized points and the convergence order, the inertia representations and their combinations. Numerical results further suggest that the integrations of $\gamma$-type are superior to those of $\alpha$-type and the optimized values of $\gamma$ can be used to achieve better numerical accuracy, convergence speed and stability.

Appendices

Appendix A: The Gauss SPARK methods in unified form

1.1 A.1 A unified formulation of SPARK methods

In Sect. 4.2.1, we present two types of Gauss SPARK methods based on the discontinuous collocation type methods. It is more efficient in computation to derive a unified formulation of SPARK methods in which the discretization schemes are formulated with Butcher style tableaux of SPARK coefficients.

One step of an ($s$, $p$)-SPARK method applied to the Hamiltonian system of (12) with consistent initial values ($\boldsymbol{q}_{k}$, $\boldsymbol{p}_{k}$) at $t_{k}$ and step-size $\Delta t$ is given as follows [24, 28]:

$$\begin{gathered} \begin{aligned} &\boldsymbol{k}_{i} = H_{\boldsymbol{p}}( \boldsymbol{Q}_{i}, \boldsymbol{P}_{i}),\quad i = 1,\ldots,s, \\ &\hat{\boldsymbol{k}}_{i} = - H_{\boldsymbol{q}}( \boldsymbol{Q}_{i}, \boldsymbol{P}_{i}),\quad i = 1,\ldots,s, \\ &\tilde{\boldsymbol{k}}_{i} = - g_{\boldsymbol{q}}( \tilde{\boldsymbol{Q}}_{i})\varLambda _{i},\quad i = 0,\ldots,p, \end{aligned} \end{gathered}$$

(A.1)

$$\begin{gathered} g(\tilde{\boldsymbol{Q}}_{i}) = 0,\quad i = 0, 1,\ldots,p, \end{gathered}$$

(A.2)

$$\begin{gathered} \boldsymbol{q}_{k + 1} = \boldsymbol{q}_{k} + \Delta t\sum _{j = 1} ^{s} \boldsymbol{k}_{j}b_{j}, \end{gathered}$$

(A.3)

$$\begin{gathered} g(\boldsymbol{q}_{k + 1}) = 0, \end{gathered}$$

(A.4)

$$\begin{gathered} \boldsymbol{p}_{k + 1} = \boldsymbol{p}_{k} + \Delta t\sum _{j = 1} ^{s} b_{j}\hat{\boldsymbol{k}}_{j} + \Delta t\sum _{j = 0}^{p} \tilde{b}_{j}\tilde{\boldsymbol{k}}_{j}, \end{gathered}$$

(A.5)

$$\begin{gathered} g_{\boldsymbol{q}}(\boldsymbol{q}_{k + 1})H_{\boldsymbol{p}}( \boldsymbol{q}_{k + 1},\boldsymbol{p}_{k + 1}) = 0, \end{gathered}$$

(A.6)

where $\varLambda _{i}$ for $i = 0, 1,\ldots,p$ is the Lagrange multiplier. $\boldsymbol{Q}_{i}$, $\tilde{\boldsymbol{Q}}_{i}$ and $\boldsymbol{P} _{i}$ denote quantities discretized as the inner points, defined by

$$ \begin{aligned} \boldsymbol{Q}_{i} &= \boldsymbol{q}_{k} + \Delta t\sum _{j = 1}^{s} \boldsymbol{k}_{j}a_{ij},\quad i = 1,\ldots,s, \\ \tilde{\boldsymbol{Q}}_{i} &= \boldsymbol{q}_{k} + \Delta t\sum _{j = 1} ^{s} \boldsymbol{k}_{j}\bar{a}_{ij},\quad i = 0,\ldots,p, \\ \boldsymbol{P}_{i}& = \boldsymbol{p}_{k} + \Delta t\sum _{j = 1}^{s} \hat{\boldsymbol{k}}_{j}\hat{a}_{ij} + \Delta t\sum _{j = 0}^{p} \tilde{\boldsymbol{k}}_{j}\tilde{a}_{ij},\quad i = 1,\ldots,s. \end{aligned} $$

(A.7)

The coefficients $(b_{j},c_{j})_{j = 1}^{s}$ and $(\tilde{b}_{j}, \tilde{c}_{j})_{j = 0}^{p}$ are generally two distinct quadrature formulas and the SPARK coefficients can be expressed in the form of Butcher style tableaux:

$$\begin{aligned} \textstyle\begin{array}{l|l} c_{i} & a_{ij} \\\hline A & b_{j} \end{array}\displaystyle \qquad \textstyle\begin{array}{l|l} & \hat{a}_{ij} \\\hline \hat{A} & \hat{b}_{j} \end{array}\displaystyle \qquad \textstyle\begin{array}{l|l} & \tilde{a}_{ij} \\\hline \tilde{A} & \tilde{b}_{j} \end{array}\displaystyle \qquad \textstyle\begin{array}{l|l} \tilde{c}_{i} & \bar{a}_{ij} \\\hline \bar{A} & \end{array}\displaystyle \end{aligned}$$

To ensure the existence and uniqueness of the SPARK solution [24, 28], we should assume $\bar{a}_{0j} = 0$ and $\bar{a}_{pj} = b_{j}$ for $j = 1,\ldots,s$, which imply that $\tilde{\boldsymbol{Q}}_{0} = \boldsymbol{q}_{k}$ and $\tilde{\boldsymbol{Q}}_{p} = \boldsymbol{q} _{k + 1}$. Hence Eqs. (A.2), (A.4) and (A.6) give $p+1$ independent constraints to solve $p + 1$ Lagrange’s multipliers (i.e., $\varLambda _{i}$, $i = 0,\ldots,p$).

We are especially interested in the SPARK methods whose coefficients are the weights and nodes of Gauss quadrature, to have an optimal order of convergence. The Gauss SPARK coefficients satisfy the following conditions [24, 28]:

$$\begin{aligned} &\!\begin{aligned} &B(s){:}\quad \sum _{i = 1}^{s} b_{i}c_{i}^{k - 1} = \frac{1}{k},\quad k = 1,\ldots,2s, \\ &C(s){:}\quad \sum _{j = 1}^{s} a_{ij}c_{j}^{k - 1} = \frac{c_{i}^{k}}{k},\quad k = 1,\ldots,s,\ i = 1,\ldots,s, \end{aligned} \end{aligned}$$

(A.8)

$$\begin{aligned} &\hat{C}(s){:}\quad \sum _{j = 1}^{s} \hat{a}_{ij}\hat{c}_{j}^{k - 1} = \frac{ \hat{c}_{i}^{k}}{k},\quad k = 1,\ldots,s,\ i = 1,\ldots,s, \end{aligned}$$

(A.9)

$$\begin{aligned} &\tilde{B}(p){:}\quad \sum _{i = 0}^{p} \tilde{b}_{i}\tilde{c}_{i}^{k - 1} = \frac{1}{k},\quad k = 1,\ldots,2p, \end{aligned}$$

(A.10)

$$\begin{aligned} &\tilde{C}(p){:}\quad \sum _{j = 0}^{p} \tilde{a}_{ij}\tilde{c}_{j}^{k - 1} = \frac{c _{i}^{k}}{k},\quad k = 1,\ldots,p + 1, i = 1,\ldots,s, \end{aligned}$$

(A.11)

and

$$ \bar{C}(s){:}\quad \sum _{j = 1}^{s} \bar{a}_{ij}c_{j}^{k - 1} = \frac{ \tilde{c}_{i}^{k}}{k},\quad k = 1,\ldots,s,\ i = 0,\ldots,p. $$

(A.12)

The two types of Gauss SPARK methods concerned in this paper can be obtained by the following conditions.

s-stage Lobatto IIIA-B method

Let$p = s - 1$, $\bar{a}_{(i - 1)j} = a_{ij}$, $\tilde{a} _{i(j - 1)} = \hat{a}_{ij}$, $b_{j} = \hat{b}_{j} = \tilde{b}_{j - 1}$, $\tilde{c}_{i - 1} = c_{i}$, for$i = 1,\ldots,s$, $j = 1,\ldots,s$, and$c_{1},\ldots ,c_{s}$, be the s nodes of the Lobatto quadrature. The Lobatto IIIA-B SPARK method is defined with the coefficients$a_{ij}$, $b_{j}$and$\hat{a}_{ij}$determined by

$$ \hat{a}_{i1} = \hat{b}_{1},\qquad \hat{a}_{is} = 0\quad \text{for}\ i = 1,\ldots,s $$

(A.13)

and

$$ B(s),\quad C(s)\quad\text{and}\quad \hat{C}(s - 2) $$

(A.14)

with the conditions$B(s)$, $C(s)$and$\hat{C}(s)$defined by (A.8) and (A.9).

s-stage Gauss Lobatto method

Let$p = s$, $\hat{a}_{ij} = a_{ij}$, $b_{j} = \hat{b}_{j}$, for$i = 1,\ldots,s$, and$c_{1},\ldots ,c_{s}$be the s nodes of the Gauss quadrature and$\tilde{c}_{1}, \ldots ,\tilde{c}_{s}$be the$s+1$nodes of the Lobatto quadrature. The Gauss–Lobatto SPARK method is defined with the coefficients$a_{ij}$, $b_{j}$, $\tilde{a}_{ij}$, $\tilde{b}_{i}$and$\bar{a}_{ij}$, determined by

$$ \tilde{a}_{i0} = \tilde{b}_{0},\qquad \tilde{a}_{is} = 0\quad\text{for}\ i = 1,\ldots,s $$

(A.15)

and

$$ B(s),\quad C(s),\quad \tilde{B}(s),\quad \tilde{C}(s - 2)\quad \text{and}\quad\bar{C}(s) $$

(A.16)

with the conditions$B(s)$, $C(s)$, $\tilde{B}(p)$, $\tilde{C}(p)$and$\bar{C}(s)$defined by (A.8)–(A.12).

1.2 A.2 Butcher style tableaux of Gauss SPARK coefficients

SPARK coefficients can be calculated by substituting nodes of quadrature and the solution conditions presented by Lobatto IIIA-B or Gauss–Lobatto SPARK methods into (A.8)–(A.12). The Lobatto nodes of quadrature $c_{1},c_{2},\ldots ,c_{s}$ are the zeros of

$$ \frac{d^{s - 2}}{dx^{s - 2}} \bigl( x^{s - 1}(x - 1)^{s - 1} \bigr). $$

(A.17)

The Gauss nodes of quadrature $c_{1},c_{2},\ldots ,c_{s}$ are the zeros of the $s$th shifted Legendre polynomial

$$ \frac{d^{s}}{dx^{s}} \bigl( x^{s}(x - 1)^{s} \bigr). $$

(A.18)

1.2.1 A.2.1 SPARK coefficients for s-stage -Lobatto IIIA-B SPARK methods

The 2-stage and 3-stage Lobatto IIIA-B SPARK methods correspond to the following Butcher style tableaux of SPARK coefficients:

$$\begin{aligned} \textstyle\begin{array}{c|c@{\quad}c} 0 & 0 & 0 \\ 1 & 1/2 & 1/2 \\ \hline A & 1/2 & 1/2 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} & 1/2 & 0 \\ & 1/2 & 0 \\ \hline \hat{A} & 1/2 & 1/2 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} & 1/2 & 0 \\ & 1/2 & 0 \\ \hline \tilde{A} & 1/2 & 1/2 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} 0 & 0 & 0 \\ 1 & 1/2 & 1/2 \\ \hline \bar{A} & & \end{array}\displaystyle \end{aligned}$$

and

$$\begin{aligned} &\textstyle\begin{array}{c|c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0\\ 1/2 & 5/24 & 1/3 & -1/24\\ 1 & 1/6 & 2/3 & 1/6 \\\hline A & 1/6 & 2/3 & 1/6 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c@{\quad}c} & 1/6 & -1/6 & 0 \\ & 1/6 & 1/3 & 0 \\ & 1/6 & 5/6 & 0 \\\hline \hat{A} & 1/6 & 2/3 & 1/6 \end{array}\displaystyle \\ &\textstyle\begin{array}{c|c@{\quad}c@{\quad}c} & 1/6 & -1/6 & 0\\ & 1/6 & 1/3 & 0\\ & 1/6 & 5/6 & 0\\\hline \tilde{A} & 1/6 & 2/3 & 1/6 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c@{\quad}c} 0 & 0 & 0 & 0 \\ 1/2 & 5/24 & 1/3 & -1/24 \\ 1 & 1/6 & 2/3 & 1/6 \\\hline \bar{A} & & & \end{array}\displaystyle \end{aligned}$$

1.2.2 A.2.2 SPARK coefficients for s-stage Gauss–Lobatto SPARK methods

The 1-stage and 2-stage Gauss–Lobatto SPARK methods correspond to the following Butcher style tableaux of SPARK coefficients:

$$\begin{aligned} \textstyle\begin{array}{c|c} 1/2 & 1/2 \\\hline A & 1 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c} & 1/2 \\\hline \hat{A} & 1 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} & 1/2 & 0 \\\hline \tilde{A} & 1/2 & 1/2 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c} 0 & 0 \\ 1 & 1 \\\hline \bar{A} & \end{array}\displaystyle \end{aligned}$$

and

$$\begin{aligned} &\textstyle\begin{array}{c|c@{\quad}c} 1/2 - {\sqrt{3}} / {6} & 1/4 & 1/4 - {\sqrt{3}} / {6} \\ 1/2 + {\sqrt{3}} / {6} & 1/4 + {\sqrt{3}} / {6} & 1/4 \\ \hline A & 1/2 & 1/2 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} & 1/4 & 1/4 - {\sqrt{3}} / {6} \\ & 1/4 + {\sqrt{3}} / {6} & 1/4 \\ \hline \hat{A} & 1/2 & 1/2 \end{array}\displaystyle \\ & \textstyle\begin{array}{c|c@{\quad}c@{\quad}c} & 1/6 & 1/3 - {\sqrt{3}} / {6} & 0 \\ & 1/6 & 1/3 + {\sqrt{3}} / {6} & 0 \\\hline \tilde{A} & 1/6 & 2/3 & 1/6 \end{array}\displaystyle \qquad \textstyle\begin{array}{c|c@{\quad}c} 0 & 0 & 0 \\ 1/2 & 1/4 + {\sqrt{3}} / {8} & 1/4 - {\sqrt{3}} / {8} \\ 1 & 1/2 & 1/2 \\ \hline \bar{A} & & \\ \end{array}\displaystyle \end{aligned}$$

Appendix B: Algorithms in pseudocode formats

2.1 B.3 Implicit midpoint scheme and energy–momentum conserving scheme

The implicit midpoint scheme and the energy–momentum conserving scheme presented by (53) and (61) can be summarized in pseudocode format in Table 15.

Table 15 State-space integration algorithm of order 2

2.2 B.4 Gauss SPARK methods

Consider the SPARK method presented by (A.1)–(A.6). We can define the residual vectors in the following form:

$$ \textstyle\begin{array}{l@{\qquad}l@{\qquad}l} \boldsymbol{r} = \left [ \textstyle\begin{array}{c} \boldsymbol{r}_{\boldsymbol{q}} \\ \boldsymbol{r}_{\boldsymbol{p}} \\ \boldsymbol{r}_{c} \end{array}\displaystyle \right ] & \textstyle\begin{array}{l} \boldsymbol{r}_{\boldsymbol{q}} = [\boldsymbol{r}_{\boldsymbol{q},1} ^{T},\ldots,\boldsymbol{r}_{\boldsymbol{q},s}^{T}]^{T} \\ \boldsymbol{r}_{\boldsymbol{q}} = [\boldsymbol{r}_{\boldsymbol{q},1} ^{T},\ldots,\boldsymbol{r}_{\boldsymbol{q},s}^{T}]^{T} \\ \boldsymbol{r}_{c} = [r_{c,1}^{T},\ldots,r_{c,p}^{T}]^{T} \end{array}\displaystyle & \textstyle\begin{array}{l} \boldsymbol{r}_{\boldsymbol{q},i} = \boldsymbol{k}_{i} - H_{ \boldsymbol{p}}( \boldsymbol{Q}_{i}, \boldsymbol{P}_{i}),\quad i = 1,\ldots,s , \\ \boldsymbol{r}_{\boldsymbol{p},i} = \hat{\boldsymbol{k}}_{i} + H_{ \boldsymbol{q}}( \boldsymbol{Q}_{i}, \boldsymbol{P}_{i}),\quad i = 1,\ldots,s , \\ r_{c,i} = g(\tilde{\boldsymbol{Q}}_{i}),\quad i = 1,\ldots,p , \end{array}\displaystyle \end{array} $$

(B.1)

where $\boldsymbol{Q}_{i}$, $\boldsymbol{P}_{i}$ and $\tilde{\boldsymbol{Q}}_{i}$ are defined by (A.7) and $\tilde{\boldsymbol{k}}_{i} = - g_{\boldsymbol{q}}( \tilde{\boldsymbol{Q}}_{i})\varLambda _{i}$. Define the unknowns as

$$ \boldsymbol{x} = \left[ \textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \boldsymbol{k}_{1}^{T} & \boldsymbol{k}_{2}^{T} & \cdots & \boldsymbol{k}_{s}^{T} & \hat{\boldsymbol{k}}_{1}^{T} & \hat{\boldsymbol{k}}_{2}^{T} & \cdots & \hat{\boldsymbol{k}}_{s}^{T} & \varLambda _{0} & \varLambda _{1} & \cdots & \varLambda _{p - 1} \end{array}\displaystyle \right]^{T}. $$

(B.2)

Then the Gauss SPARK methods can be summarized uniformly in pseudocode format as in Table 16.

Table 16 Algorithm for Gauss SPARK methods