Skip to main content
SpringerLink
Log in

An efficient image encryption algorithm based on multi chaotic system and random DAN coding

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

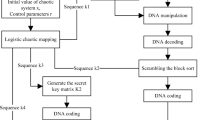
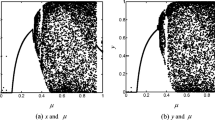
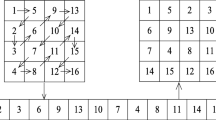
This paper presents a digital image encryption scheme based on multi chaotic system and random DNA coding. Firstly, the initial values and parameter values of 2D Logistic-adjusted-Sine mapping (2D-LASM) and Logistic-Sine system (LSS) are obtained from SHA256 hash values of the original image. In the scrambling stage, the chaotic sequences generated by 2D-LASM are used to get two column scrambling matrices and row scrambling matrix, respectively. The elements of the second column scrambling matrix and row scrambling matrix are used as row and column coordinates in the scrambling process. Then apply it to scrambling the DNA encoded image, which can complete the row and column scrambling at the same time. In the diffusion stage, we proposed a new diffusion method. Through the chaotic sequence generated by the LSS, a DNA coding sequence is obtained. DNA XOR operation is carried out on the central point and horizontal line of the image, and then spread from the central line to the upper and lower directions of the matrix to achieve the purpose of multi-directional diffusion and improve the encryption efficiency. Experimental results and security analysis show that the algorithm executes fast and has strong security. It can resist many attacks, such as statistical attacks, brute attacks, plaintext / select plaintext attacks, etc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

The images used to support the findings of this study are included within the article.

References

  1. Alvrez G, Li S (2006) Some basic cryptographic requirements for chaos-based cryptosystems[J]. Int J Bifur Chaos 16(8):2129–2151

    Article  MathSciNet  Google Scholar 

  2. Behnia S, Akhshani A, Mahmodi H, Akhavan A (2008) A novel algorithm for image encryption based on mixture of chaotic maps[J]. Chaos, Solitons Fractals 35(2):408–419

    Article  MathSciNet  Google Scholar 

  3. Cao C, Sun K, Liu W (2018) A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map[J]. Signal Process 143:122–133

    Article  Google Scholar 

  4. Dagadu JC, Li J-P, Addo PC (2019) An image cryptosystem based on pseudorandomly enhanced chaotic DNA and random permutation[J]. Multimed Tools Appl 78(17):24979–25000

    Article  Google Scholar 

  5. Deng X, Liao C, Zhu C, Chen Z (2014) Image encryption algorithms based on chaos through dual scrambling of pixel position and bit [J]. Journal on Communications 35(3):216–223 (Chinese)

    Google Scholar 

  6. Gao TG, Chen Z (2008) A new image encryption algorithm based on hyper-chaos[J]. Phys Lett A 372(4):394–400

    Article  Google Scholar 

  7. Hua Z, Zhou Y (2016) Image encryption using 2D Logistic-adjusted-Sine map[J]. Inf Sci 339:237–253

    Article  Google Scholar 

  8. Huang CK, Nien HH (2009) Multi chaotic systems based pixel shuffle for image encryption[J]. Opt Commun 282(11):2123–2127

    Article  Google Scholar 

  9. Liu H, Wang X, Kadir A (2012) Image encryption using DNA complementary rule and chaotic maps[J]. Appl Soft Comput 1212(5):1457–1466

    Article  Google Scholar 

  10. Matthews R (1989) On the derivation of a chaotic encryption algorithm[J]. Cryptologia 8(1):29–42

    Article  MathSciNet  Google Scholar 

  11. Nestor T, Dieu NJD, Jacques K et al (2019) A multidimensional Hyperjerk oscillator: dynamics analysis, analogue and embedded systems implementation, and its application as a cryptosystem [J]. Sensors 20(1):83

    Article  Google Scholar 

  12. Pak C, An K, Jang P et al (2018) A novel bit-level color image encryption using improved 1D chaotic map[J]. Multimed Tools Appl 78(9):12027–12042

    Article  Google Scholar 

  13. Ran T, Yi X, Yue W (2007) Double image encryption based on random phase encoding in the fractional Fourier domain[J]. Opt Express 15(24):16067–16079

    Article  Google Scholar 

  14. Shen J, Jin X, Zhou C (2005) A color image encryption algorithm based on magic cube transformation and modular arithmetic operation[C]. In: Conference on advances in multimedia information processing-pcm. Springer-Verlag

  15. Souyah A, Faraoun KM (2016) A review on different image encryption approach[C]. In: 4th international symposium on modelling and implementation of complex systems (MISC). Lecture notes in networks and systems, pp 3–18

  16. TSafack N, Kengne J, Abd-El-Atty B et al (2020) Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption[J]. Inf Sci 515:191–217

    Article  Google Scholar 

  17. Wang Y, Wong K-W, Liao X, Chen G (2011) A new chaos-based fast encryption algorithm[J]. Appl Soft Comput 11(1):514–522

    Article  Google Scholar 

  18. Wang X-Y, Zhang Y-Q, Bao X-M (2015) A novel chaotic image encryption scheme using DNA sequence operations[J]. Opt Lasers Eng 73:53–61

    Article  Google Scholar 

  19. Wang X, Yu W, Zhu X, Unar S (2019) Image encryption scheme based on chaos and DNA plain operations[J]. Multimed Tools Appl 78(18):26111–26128

    Article  Google Scholar 

  20. Watson JD, Crick FHC (2003) Molecular structure of nucleic acids[J]. Am J Psychiatr 160(4):623–624

    Article  Google Scholar 

  21. Wu Y, Yang G, Jin H, Noonan JP (2012) Image encryption using two-dimensional logistic chaotic map[J]. Journal of Electronic Imaging 21(1):013014

    Article  Google Scholar 

  22. Yang J, Hao W (2018) Color image encryption algorithm based on chaotic system and dynamic DNA coding and operation[J]. Comput Eng 44(2):151–157 (Chinese)

    Article  Google Scholar 

  23. Yang FF, Mou J, Cao YH, Chu R (2020) An image encryption algorithm based on BP neural network and hyperchaotic system[J]. China Communications 17(5):21–28

    Article  Google Scholar 

  24. Zhou N, Zhang A, Zheng F, Gong L (2014) Novel image compression-encryption hybrid algorithm based on key-controlled measurement matrix in compressive sensing[J]. Opt Laser Technol 62:152–160

    Article  Google Scholar 

  25. Zhou Y, Bao L, Chen CLC (2014) A new 1D chaotic system for image encryption[J]. Signal Process 97:172–182

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 61876201).

Author information

Authors and Affiliations

  1. College of Computer Science and Technology, Chongqing University of Posts and Telecommunications, Chongqing, People’s Republic of China

    Jiming Zheng, Zheng Luo & Qingxia Zeng

  2. Key Lab of Intelligent Analysis and Decision Complex Systems, Chongqing University of Posts and Telecommunications, Chongqing, 400065, China

    Jiming Zheng

Authors
  1. Jiming Zheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zheng Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qingxia Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiming Zheng.

Ethics declarations

Conflicts and interest

The authors declare that there are no conflicts and interest regarding the publication of this paper.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zheng, J., Luo, Z. & Zeng, Q. An efficient image encryption algorithm based on multi chaotic system and random DAN coding. Multimed Tools Appl 79, 29901–29921 (2020). https://doi.org/10.1007/s11042-020-09454-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-020-09454-9

Keywords

Search

Navigation