On the vibration of laminated nonhomogeneous orthotropic shells

Abstract

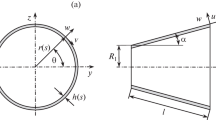
In this paper, an analytical procedure is given to study the free vibration of the laminated homogeneous and non-homogeneous orthotropic conical shells with freely supported edges. The basic relations, the modified Donnell type motion and compatibility equations have been derived for laminated orthotropic truncated conical shells with variable Young’s moduli and densities in the thickness direction of the layers. By applying the Galerkin method, to the basic equations, the expressions for the dimensionless frequency parameter of the laminated homogeneous and non-homogeneous orthotropic truncated conical shells are obtained. The appropriate formulas for the single-layer and laminated complete conical and cylindrical shells made of homogeneous and non-homogeneous, orthotropic and isotropic materials are found as a special case. Finally, the influences of the non-homogeneity, the number and ordering of layers and the variations of the conical shell characteristics on the dimensionless frequency parameter are investigated. The results obtained for homogeneous cases are compared with their counterparts in the literature.

Appendices

Appendix A

L _ij (i,j=1,2) are differential operators and defined by follows:

(A.1)

where the expressions $\delta_{\bar{k}},\Delta_{\bar{k}}$ $(\bar{k} = 1,2,\ldots,16)$ are defined as follows:

(A.2)

in which

(A.3)

in which

(A.4)

Appendix B

The expressions Q _i (i=1,2,…,5) are defined as follows:

(B.1)

in which

(B.2)