1 Introduction

Given a random variable \(\zeta\) with values in \((0,\infty )\) the inverse first-passage time problem for reflected Brownian motion consists of finding a lower semi-continuous function \(b:[0,\infty ] \rightarrow [0,\infty ]\) such that the first-passage time

$$\begin{aligned} \tau _b :=\inf \{t> 0 : |{B_t}| \ge b(t)\} \end{aligned}$$

of b by a Brownian motion \((B_t)_{t\ge 0}\) has distribution according to \(\zeta\). A first application was proposed by Hull and White (2001) and Avellaneda and Zhu (2001) in the context of credit risk, in order to use the solutions to model the default time of a company as first-passage time, when data about the distribution of the default time is given. Since then, several methods have been found in order to simulate the unknown solutions of the inverse first-passage time problem, e.g. see Zucca and Sacerdote (2009), Song and Zipkin (2011). Regarding this, another computational objective is often to sample from the conditional distribution

$$\begin{aligned} \mathbb {P}({B_t \in \cdot \vert \;}{\tau _b > t}), \quad t \ge 0. \end{aligned}$$
(1)

If the boundary b was known, a possible approach would be acceptance-rejection-sampling or a particle system similar to the model in Burdzy et al. (2000). But in the inverse first-passage time problem the boundary b is unknown, and it is natural to ask, whether given \(\zeta\) one can construct an interacting particle system only depending on the distribution of \(\zeta\), which yields, as macroscopic limit, the unique solution to the inverse first-passage time problem or the corresponding conditioned distribution Eq. (1). In the special case that \(\zeta\) is exponential, the distribution Eq. (1) was found in De Masi et al. (2019a) as the hydrodynamic limit of the so-called N-branching Brownian motion (N-BBM) in terms of the solution of a free boundary problem. In the N-BBM finitely many particles evolve as independent Brownian motions but branch individually with rate 1. At each branching time the rightmost particle is removed from the system, in such a way that the population size is kept constant. A natural way to obtain a particle system corresponding to more general distributions of \(\zeta\) would be to adjust the branching rate of the system in De Masi et al. (2019a) into the hazard rate of \(\zeta\), if it exists. But from a computational point of view a more efficient way would be to dismiss the branching and to only keep the selection mechanism at certain removal times.

In our approach we aim to choose these removal times in such a way, that the particle system macroscopically behaves in the desired way Eq. (1). In order to motivate this let us present one of the two main situations for which our main result Theorem 1 is designed. Let \(\zeta\) be a random variable with values in \((0,\infty )\). For \(N\in \mathbb {N}\) let

$$\begin{aligned} T_1 \le \ldots \le T_N \end{aligned}$$

be the order statistics corresponding to N independent samples from \(\zeta\). Let

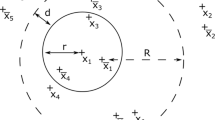
$$\begin{aligned} (X_t^i )_{i\in A(t) , t\ge 0} \end{aligned}$$

be the process, which results from the following scheme. We start with N independent Brownian motions on \(\mathbb {R}\). At every timepoint \(T_{i}\) we remove the particle with the largest absolute value from the system. Between the timepoints \(T_i\) the particles perform independent Brownian motion. We define the index set A(t) of surviving particles up to a time t, as the particles which have not been removed up to this time. See for instance Fig. 1 for a realization of the process initialized with 4 particles. A more formal definition will be given in Section 2. The consequence of our main result Theorem 1 is the following.

Fig. 1
figure 1

Illustration of the non-branching system, \(N=4\)

Full size image

Let b be the solution to the inverse first-passage time problem corresponding to \(\zeta\). For every \(t>0\) with \(\mathbb {P}\left( \zeta> t \right) >0\) holds

$$\begin{aligned} \frac{1}{N} \sum\limits_{i\in A(t)} \delta _{X_t^i} ([-a,a]) \overset{N\rightarrow \infty }{\longrightarrow } \mathbb {P}\left( B_t \in [-a,a], \tau _b > t \right) \end{aligned}$$
(2)

almost surely for every \(a\ge 0\). This means that, roughly speaking, drawing the removal times from the distribution of \(\zeta\) results in removing the particles which pass the boundary b. Correspondingly, this matches with the property that the distribution of the first-passage time \(\tau _b\) is equal to \(\zeta\).

The particle system from Eq. (2) can be seen as a very simple case of a more general class of particle systems with topological interactions. Prototypes of this generic class are the basic model presented in Carinci et al. (2016) and the N-BBM model of De Masi et al. (2019a) discussed above, in which removed particles are re-injected into the system. The latter model has been further modified in De Masi et al. (2019b) and generalized in Groisman and Soprano-Loto (2021), where the generalization consists of a branching rate dependent on the position of the particles. On top of that, the work of Atar (2020) presents two very general systems, namely the so-called RAB model (removal at boundary) and RAQ model (removal at quantile). In the RAB model, the injection of new particles is governed by a given function and a so-called injection measure, and the removal of particles is also governed by a given function, but restricted to the right-most particle. Under suitable conditions existence of the hydrodynamic limit is proven, where it is identified as a solution to a partial differential equation with an additional so-called order-respecting absorption condition. In the RAB model it is possible to set the injections to zero and to choose specific removal times such that the RAB model becomes a special case of the particle system in our main result Theorem 1. For details see Remark 3.

The inverse first-passage time problem is a well studied problem in probability. The existence of solutions was established in Anulova (1980) and general uniqueness results were shown in Ekström and Janson (2016) and Klump and Kolb (2022). Likewise, qualitative properties of solutions were studied, such as the behavior at zero in Cheng et al. (2006), continuity in Chen et al. (2011), Ekström and Janson (2016), Potiron (2021), higher regularity in Chen et al. (2022) or the shape in Klump and Kolb (2022). For further references see Klump (2022). For an overview of the methods for simulating the boundary see Section 4.

This paper is organized as follows. In Section 2 we introduce the formal definition of the particle system and present our main result. The proof of the main result Theorem 1 is to be found in Section 3. In Section 4 we present a method for the simulation of the unknown solutions of the inverse first-passage time problem, which is related to the particle system of Theorem 1.

2 Notation and Main Result

We call a function \(g: [0,\infty ] \rightarrow [0,1]\) survival distribution, if \(g(t) = \mathbb {P}\left( \zeta > t \right)\) for a random variable \(\zeta\) with values in \((0, \infty )\). We denote

$$\begin{aligned} t^g :=\sup \{t>0 : g(t) >0 \}. \end{aligned}$$

Let \(\mathcal {P}\) denote the space of probability measures on \(\mathbb {R}\). Given \(\mu \in \mathcal {P}\) and a standard Brownian motion \((W_t)_{t\ge 0}\) independent from \(X_0\), denote by \(\mathbb{P}_\mu\) a measure under which

$$\begin{aligned} B_t :=W_t + X_0 \end{aligned}$$

is a Brownian motion with initial state \(X_0 \sim \mu\). For \(\mu \in \mathcal {P}\) and a survival distribution g we denote the set of solutions of the inverse first-passage time problem by

$$\begin{aligned} ifpt(g , \mu ) := \{b \text { lower semicontinuous} : \mathbb {P}_{\mu } \left( \tau _b > t \right) = g(t)\; \forall t\ge 0\} \end{aligned}$$

and abbreviate by abuse of notation \(ifpt( g , 0 ) :=ifpt(g, \delta _0)\), where \(\delta _0\) is the Dirac measure. Anulova showed existence of solutions in (1980). Uniqueness of the solution was established in Ekström and Janson (2016) and Klump and Kolb (2022), in the sense that all solutions coincide on \((0,t^g)\).

Let us prepare the formal definitions of the particle system. For a particle number N and random vector of starting points \((X_0^1, \ldots , X_0^N)\) with values in \(\mathbb {R}^N\), let \((B^1 , \ldots , B^N)\) be a N-dimensional Brownian motion with initial configuration \((X_0^1, \ldots , X_0^N)\). Furthermore, from now on let

$$\begin{aligned} 0 =:t_0^{N}< t_1^{N} \le \ldots \le t_N^{N} \end{aligned}$$
(3)

be \(N+1\) fixed timepoints. Let the number of timepoints up to a time t be denoted by

$$\begin{aligned} k^{N}(t) :=\sup \left\{ k \in \{0, 1, \ldots , N\} : t_k^{N} \le t \right\} . \end{aligned}$$
(4)

Set \(A_0 :=\{1, \ldots , N\}\) and define inductively for \(\ell \in \{1, \ldots , N\}\)

$$A_\ell:=A_{\ell-1}\setminus\left\{\underset{i\in A_{\ell-1}}{\text{arg max}}\vert B_{t_\ell^N}^i\vert\right\}.$$

The continuous time particle system we want to consider is then the system with empirical measure

$$\begin{aligned} \chi ^N_t :=\frac{1}{\vert A_{k^{N}(t)} \vert } \sum _{i\in A_{k^{N}(t)}} \delta _{B^i_t}. \end{aligned}$$

In words, we do no more than remove the particle with largest absolute value from the system at the removal times Eq. (3). Recall that, given a survival distribution g, our goal is to choose the removal times in such a way that the empirical measure behaves as in Eq. (2). Observe that then, for \(b\in ifpt(g , \mu )\), it is necessary that

$$\begin{aligned} \frac{\vert A_{k^{N}(t)} \vert }{N} \overset{N\rightarrow \infty }{\longrightarrow } \mathbb {P}_{\mu } \left( \tau _b > t \right) = g(t) \end{aligned}$$
(5)

almost surely. Regarding this, note that we have \(\vert A_{k^{N}(t)} \vert = N- k^N (t)\). Our following main result shows that the necessary behavior Eq. (5) actually gives rise to a sufficient condition, where it is worth mentioning that we do not impose conditions on g.

Theorem 1

Let g be a survival distribution. Assume that, for every \(t\in (0,t^g)\), the sequence of Eq. (3) fulfills

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) . \end{aligned}$$
(6)

Let \(\mu \in \mathcal {P}\) be symmetric with finite first absolute moment. Let \(b\in ifpt(g , \mu )\) and define

$$\begin{aligned} \mu _t :=\mathbb {P}_\mu ({B_t \in \cdot \vert \, }{\tau _b > t}) \end{aligned}$$

for \(t\in (0,t^g)\). Let \((X_0^1, \ldots , X_0^N) \sim \mu ^{\otimes N}\). Then

$$\begin{aligned} \chi ^N_{t}([-a,a]) \overset{N\rightarrow \infty }{\longrightarrow } \mu _{t} ([-a,a]) \end{aligned}$$

almost surely for every \(a\ge 0\).

Remark 1

The condition that \(\mu\) shall be symmetric with finite first absolute moment is needed for the application of the convergence result of Theorem 2.2 of Klump and Kolb (2022) and is expected to be a technical condition.

Remark 2

The assumption Eq. (6) is to be understood as an assumption on the sequence of ordered timepoints

$$\begin{aligned} t_1^{N} \le \ldots \le t_N^{N} \end{aligned}$$

from Eq. (3). The two main situations, which we want to cover up with this assumption are the following.

  • As in the situation of Eq. (2), let \(T_{k}\) denote the kth order statistic of N independent samples \(\zeta _1 , \ldots , \zeta _N\) of the distribution given by g. Then if we choose \(t_k^N :=T_{k}\) for fixed \(t\in (0,t^g)\) we have

    $$\begin{aligned} \frac{k^N (t)}{N} = \frac{1}{N} \sum\limits _{k=1}^N {\mathbbm{1}}_{\{\zeta _k \le t\}} \overset{N\rightarrow \infty }{\longrightarrow } \mathbb{P}({\zeta _1 \le t}) = 1 -g(t) \end{aligned}$$

    almost surely by the law of the large numbers.

  • A deterministic choice of removal times is given by

    $$\begin{aligned} t^{N}_k :=g^{-1} \left( \frac{N-k}{N} \right) , \quad k\in \{1, \ldots , N \}, \end{aligned}$$

    where \(g^{-1}\) denotes the generalized inverse as defined in Eq. (21). The property \(\lim _{N\rightarrow \infty } N^{-1} k^N (t) = 1- g(t)\) is established in Lemma 14 in the appendix.

Before we begin with the preparation for the proof of Theorem 1 we give an overview of the relation between this particle system and the two particle systems in Atar (2020).

Remark 3

In the RAB model of Atar (2020), the injection of new particles is governed by a given function \(I:[0,\infty ) \rightarrow [0,\infty )\) and a so-called injection measure, and the removal of particles is also governed by a function \(J:[0,\infty ) \rightarrow [0,\infty )\), but restricted to the right-most particle. Under suitable conditions the hydrodynamic limit is identified as a solution to a partial differential equation with an additional so-called order-respecting absorption condition.

Let g be a given survival distribution. Then, if we choose in the RAB model of Atar (2020) the injections to be zero, i.e. \(I\equiv 0\), and the removal function to be \(J(t) :=1- g(t)\), we end up with the one-sided version of the system from Theorem 1 with the specific removal times

$$\begin{aligned} t^N_k = \inf \{ t \ge 0 : \lfloor {N (1-g(t))}\rfloor \ge k \}, \end{aligned}$$

which corresponds to the second point of Remark 2 and meet the condition of Theorem 1 by Lemma 14. The conditions of the result of Atar (2020) regarding the hydrodynamic limit of the RAB model are fulfilled if g is absolutely continuous and Hölder continuous with exponent strictly larger than 1/2.

In the RAQ model of Atar (2020) there are also no injections, but the removal is restricted to empirical quantiles among the particles, where the target quantile does not depend on the number of particles. Hence, the system cannot be adjusted to remove the right-most particle.

Thus, the common statement of the work of Atar (2020) and this article is the result that for survival distributions, which are absolutely continuous and Hölder continuous with exponent larger than 1/2, the hydrodynamic limit of the system with the quantile timepoints of the second point of Remark 2 exists. However, in Atar (2020) the hydrodynamic limit is described by means of a partial differential equation, whereas we interpret it probabilistically in terms of the inverse first-passage time problem.

3 Proof of The Main Theorem 1

3.1 Construction of Stochastic Barriers

For \(m\in \mathbb {N}\) let \((t_k^{(m)})_{k\in \{1,\ldots , n_m\}}\) be a fixed sequence such that

$$\begin{aligned} 0 =:t_0^{(m)} < t_1^{(m)} \le t_2^{(m)}\le \ldots \le t_{n_m}^{(m)} \le t^g \end{aligned}$$
(7)

with \(n_m \in \mathbb {N}\cup \{\infty \}\).

We denote the index of the timepoint at the left of time \(t\in (0,t^g)\) by

$$\begin{aligned} k^{(m)} (t) :=\sup \{ k\in \mathbb {N}_0 : t_k^{(m)} \le t\} \end{aligned}$$

and the corresponding timepoint by \((t)_m :=t^{(m)}_{k^{(m)}(t)}\).

Parametrized with \(m\in \mathbb {N}\) we will construct two processes whose empirical measures serve as almost sure lower and upper bounds of \(\chi _t^N\) in the two-sided stochastic order for every \(N \ge m\). The following technique of notation and construction for the particle system is inspired by De Masi et al. (2019a).

Define \(A_0^+ :=\{1, \ldots , N\}\) and inductively for \(k\in \{1, \ldots , n_m\}\)

$$\begin{aligned} A_k^+ :=A_k^{+,m} :=\{ i\in A_{k-1}^+ : \vert B_{t_k^{(m)}}^i \vert \le q_k^{+,N} \} \end{aligned}$$

where

$$\begin{aligned} q_{k}^{+,N} :=q_{k}^{+,N,m} :=\inf \left\{ a \ge 0 : \sum\limits_{i\in A_{k-1}^+} {\mathbbm{1}}_{\{{\vert B_{t_k^{(m)}}^i \vert \le a}\}} \ge N - k^{N}(t_k^{(m)}) \right\} . \end{aligned}$$

In words, for the construction of \(A_k^+\), from timepoint \(t_{k-1}^{(m)}\) to \(t_k^{(m)}\) we count the number of particles, which would have been removed in between these timepoints in the non-branching process and remove this number at time \(t_k^{(m)}\) at once from the system by cutting off the particles with largest absolute value at time \(t_k^{(m)}\). For an illustration see Fig. 2.

Fig. 2
figure 2

Illustration of the \(A^+\)-process for the non-branching system, \(N=4\)

Full size image

Further let \(A_1^-\) be a uniformly chosen random subset of \(\{1 , \ldots , N \}\) with \(N - k^{N}(t_1^{(m)})\) elements and for \(k\in \{2 , \ldots , m\}\) define inductively

$$\begin{aligned} A_k^- :=A_k^{-,N} :=\{ i\in A_{k-1}^- : \vert B_{t_{k-1}^{(m)}}^i \vert \le q_{k}^{-,N} \} \end{aligned}$$

where

$$\begin{aligned} q_{k}^{-,N}:=q_{k}^{-,N,m} :=\inf \left\{ a \ge 0 : \sum _{i\in A_{k-1}^-} \mathbbm{1}_{\{{\vert B_{t_{k-1}^{(m)}}^i \vert \le a}\}} \ge N - k^{N}(t_k^{(m)}) \right\} . \end{aligned}$$
(8)

In words, for the construction of \(A_k^-\), we again count the number of particles which would be removed from the non-branching process between \(t_k^{(m)}\) and \(t_{k-1}^{(m)}\), but in contrary to \(A_k^+\) we remove this number of particles from the system by cutting off the particles with largest absolute value at time \(t_{k-1}^{(m)}\). For an illustration see Fig. 3.

Fig. 3
figure 3

Illustration of the \(A^-\)-process for the non-branching system, \(N=4\)

Full size image

Define the empirical measures

$$\begin{aligned} \xi _{k}^{\pm ,N} :=\frac{1}{\vert A_{k}^{\pm } \vert } \sum\limits_{i\in A_{k}^\pm } \delta _{B_{t_k^{(m)}}^i} \end{aligned}$$

and

$$\begin{aligned} \chi ^{\pm ,N}_t :=\frac{1}{\vert A^\pm _{k^{(m)}(t)} \vert } \sum\limits_{i\in A^\pm _{k^{(m)}(t)}} \delta _{B^i_t} \end{aligned}$$
(9)

We want to compare the empirical measures of the processes at the timepoints \((t_k^{(m)})_{k\in \{1, \ldots , n_m\}}\) by a suitable coupling, which in our case demands that the particle numbers of both processes are equal. Note that by the definitions it follows immediately that

$$\vert A_\ell \vert= N -\ell , \quad \ell \in \{1, \ldots ,N\}$$

and

$$\vert A^{\pm }_k \vert= N - k^{N}(t_k^{(m)}),\quad k\in \{ 1, \ldots , n_m\}.$$

 

Therefore, we have at time \(t_k^{(m)}\) that

$$\begin{aligned} \vert A^\pm _{k^{(m)}(t_k^{(m)})} \vert = N- k^{N}(t_k^{(m)}) = \vert A_{k^{N}(t_k^{(m)})} \vert . \end{aligned}$$

It is more convenient to couple rather the discrete time step processes instead of just the continuous time process, even if it is the case that for a \(k\in \{1, \ldots ,n_m-1\}\) holds \(t_k^{(m)} = t_{k+1}^{(m)}\), which then implies that in the discrete time process from k to \(k+1\) does not happen anything. We define

$$\xi _k^{m,N}:=\frac{1}{\vert A_{k^{N}(t_k^{(m)})} \vert } \sum\limits_{i \in A_{k^{N}(t_k^{(m)})}} \delta _{B^i_{t_k^{(m)}}}$$

and

$$\chi ^{m,N}_t:=\frac{1}{\vert A_{k^{N}((t)_m)} \vert } \sum\limits_{i\in A_{k^{N}((t)_m)}} \delta _{B_t^i}.$$

3.2 Coupling of Stochastic Barriers

Lemma 2

For probability measures \(\mu,\nu\) we write \(\mu \preceq \nu\) , if \(\mu ([-a,a]) \geq \nu([-a,a])\) for every \(a\geq0\) . In the following we call this ordering the two-sided stochastic order. There exists a coupling  \((\tilde{\xi }^{+,N} , {\xi }^{m,N}, \tilde{\xi }^{-,N} )\) of the tripel of random measures \(({\xi }^{+,N} , {\xi }^{m,N}, {\xi }^{-,N})\) such that, for every k,

$$\begin{aligned} \tilde{\xi }_{k}^{+,N} \preceq {\xi }^{m,N}_{k} \preceq \tilde{\xi }_{k}^{-,N} \end{aligned}$$

almost surely. Thus, for \(t\in (0,t^g)\) there exists also a coupling \((\tilde{\chi }_{t}^{+,N} , {\chi }^{m,N}_{t} , \tilde{\chi }_{t}^{-,N})\) with

$$\begin{aligned} \tilde{\chi }_{t}^{+,N} \preceq {\chi }^{m,N}_{t} \preceq \tilde{\chi }_{t}^{-,N}. \end{aligned}$$

Before proving Lemma 2 we give some preliminaries. Our strategy for the first part of the lemma will be an induction over k. In each single step, the only thing we have to ensure about our constructed coupling is then, that the ordering property is preserved by the dynamics of the involved processes. In order to achieve this in a rigorous way, we will first introduce notation which enables us to crystallize out the dynamics of the involved processes in one step. Then we state some auxiliary statements about set orderings, which will help us to construct the desired couplings.

Let \(M\in \mathbb {N}\) and \(y,x, z \in \mathbb {R}^M\). Let \(B^y , B^x\), \(B^z\) denote M-dimensional Brownian motions with \(B^{y,i}_0 = y_i\), \(B^{x,i}_0 = x_i\) and \(B^{z,i}_0 = z_i\). Fix \(t\ge 0\) and timepoints \(s_0 :=0 \le s_1 \le \ldots \le s_j \le t\) with \(j\le M\). Define

$$A_t^{+,y} (\kern0.1500emj) :=\left\{ i\in \{ 1, \ldots , M \} : \vert B_t^{y,i} \vert \le q_t^{+,y} \right\}$$

where

$$\begin{aligned} q_t^{+,y} :=\inf \left\{ a\in \mathbb {R}: \sum\limits_{i=1}^M \mathbb {1}_{\{\vert B_t^{y,i} \vert \le a\}} \ge M-j \right\} . \end{aligned}$$

Let \(A^x (s_1) :=\{1, \ldots , M\}\) and for \(\ell \in \{2, \ldots , j\}\)

$$A^x(s_1,\dots,s_\ell):=A^x(s_1,\dots,s_{\ell-1})\setminus\left\{\underset{{}_{i\in A^x(s_1,\dots,s_{\ell-1})}}{\mathrm{arg\;max}}\vert B_{s_\ell}^{x,i}\vert\right\}.$$

Further define

$$\begin{aligned} A^{-,z} (\kern0.1500emj) :=\left\{ i \in \{ 1, \ldots , M \} : \vert z_i \vert \le q_t^{-,z}\right\} \end{aligned}$$

where

$$\begin{aligned} q_t^{-,z} :=\inf \left\{ a \ge 0 : \sum _{i=1}^M \mathbb {1}_{\{{\vert z_i \vert \le a}\}} \ge M-j \right\} . \end{aligned}$$

For \(x\in \mathbb {R}^n\) and a subset \(A\subseteq \mathbb {R}\) let us introduce the notation

$$\begin{aligned} \vert x \cap A \vert :=\sum\limits_{i=1}^n \mathbb {1}_{A} (x_i) = \left| \left\{ i \in \{1, \ldots ,n\} : x_i \in A \right\} \right| . \end{aligned}$$

Definition 1

For \(x = (x_1, \ldots , x_n) \in \mathbb {R}^n\) and \(y = (y_1 , \ldots , y_m) \in \mathbb {R}^m\) define the partial order

$$\begin{aligned} x \preceq y \; :\Leftrightarrow \; \left| x \cap [-a,a] \right| \ge \left| y\cap [-a,a] \right| \quad \forall a \ge 0. \end{aligned}$$
(10)

In this case, call x dominated by y.

Note that, if \(x\preceq y\), it directly follows that \(n \ge m\).

Lemma 3

Let \(x\in \mathbb {R}^n\) and \(y\in \mathbb {R}^m\) with \(n\ge m\), such that \(\vert x_i \vert \le \vert y_i \vert\) for all \(i\in \{1, \ldots , m\}\). Then \(x\preceq y\).

Proof

Let \(a\in \mathbb {R}\). We have

$$\begin{aligned} I :=\{ i \in \{1, \ldots , m\} : \vert y_i \vert \le a \} \subseteq J :=\{j\in \{1, \ldots , m\} : \vert x_j \vert \le a\}. \end{aligned}$$

Thus

$$\begin{aligned} \vert x \cap [-a,a] \vert = \vert \{ i \in \{1, \ldots , n\} : \vert x_i \vert \le a \} \vert \ge \vert J \vert \ge \vert I \vert = \vert y \cap [-a,a] \vert , \end{aligned}$$

which shows the statement.

Lemma 4

Let \(x\in \mathbb {R}^n\) and \(y\in \mathbb {R}^m\). Then the following conditions are equivalent:

  1. (i)

    \(x\preceq y\)

  2. (ii)

    \(n\ge m\) and there exists an injective function \(\pi : \{1, \ldots , m\} \rightarrow \{1, \ldots , n\}\) such that \(\vert x_{\pi (\kern0.1500emj)} \vert \le \vert y_{j} \vert\) for every \(j\in \{1, \ldots , m\}\).

If \(\vert y_{i} \vert\) and \(\vert x_i \vert\) are non-decreasing as functions of i then \(\pi\) can be chosen as the identity.

Proof

Without loss of generality we can assume that \(\vert y_{i} \vert\) and \(\vert x_i \vert\) are non-decreasing in i. Then the implication from (ii) to (i) follows from Lemma 3 above. For the remaining direction note that (i) directly implies \(n \ge m\). By our initial assumption it is left to show that \(\vert x_j \vert \le \vert y_j \vert\) for every \(j \in \{1,\ldots ,m\}\). For this we will carry out an induction over m. For \(m=1\) the statement is clear. Let now \(m \ge 2\), \(x\preceq y\), and assume the implication from (i) to (ii) holds for all n-tuples \(\tilde{x}\) and \((m-1)\)-tuples \(\tilde{y}\). We will first show that \(\vert x_1 \vert \le \vert y_1 \vert\). In order to see this consider

$$\begin{aligned} 1 \le \vert y\cap [-\vert y_1 \vert ,\vert y_1 \vert ] \vert \le \vert x\cap [-\vert y_1 \vert ,\vert y_1 \vert ] \vert . \end{aligned}$$

Since \(\vert x_i \vert\) is non-decreasing in i this implies \(\vert x_1 \vert \le \vert y_1 \vert\). Now define

$$\begin{aligned} \tilde{x} = (x_2 , \ldots , x_n) \qquad \text { and } \qquad \tilde{y} = (y_2 , \ldots , y_m). \end{aligned}$$

Let \(a\ge 0\). If \(a\ge \vert y_1 \vert\) we have

$$\begin{aligned}\ \begin{aligned} \vert (y_2 ,\ldots ,y_k)\cap [-a,a] \vert&= \vert y\cap [-a,a] \vert -1 \\&\le \vert x\cap [-a,a] \vert -1 = \vert (x_2 , \ldots , x_n)\cap [-a,a] \vert , \end{aligned} \end{aligned}$$

where the last equality holds since \(\vert x_1 \vert \le \vert y_1 \vert \le a\). This means \(\tilde{x} = \{x_2 , \ldots , x_n\} \preceq \tilde{y} = \{y_2 ,\ldots ,y_m\}\). But by the assumption of the induction for \((m-1)\)-tuples this means that for \(j\in \{2, \ldots , m \}\) we have \(\vert x_{j} \vert \le \vert y_j \vert\). All in all we have shown that \(\vert x_{j} \vert \le \vert y_j \vert\) for all \(j\in \{1, \ldots , m\}\).

Definition 2

For a m-tuple \(z= (z_1 , \ldots , z_m) \in \mathbb {R}^m\) define \(\varrho _k\) with \(k\le m\) as the function, which assigns to z the k-tuple consisting of the first k entries of z, which has the smallest absolute value. This means that \(\varrho _k (z)\) is defined by

  • \(\varrho _k (z) = (z_{\iota (1)} , \ldots , z_{\iota (k)})\), for an increasing, injective map \(\iota : \{1, \ldots , k\} \rightarrow \{1, \ldots ,m\}\),

  • for \(i\in \{1,\ldots , k \}\) and \(j\in \{1, \ldots , m\}\), if \(\vert x_{\iota (i)} \vert = \vert x_j \vert\) for \(\iota (i) \ge j\), then \(j \in \iota (\{1,\ldots ,k\})\),

  • \(\vert x_{i} \vert \le \vert x_j \vert\) for all \(i\in \iota (\{1, \ldots , k\})\), \(j \notin \iota (\{1, \ldots , k\})\).

Lemma 5

Let \(x\in \mathbb {R}^n\) and \(y\in \mathbb {R}^m\) with \(n\ge m\) and \(x\preceq y\). Then, for every \(m \le k \le n\), holds \(\varrho _k (x) \preceq y\).

Proof

By Lemma 4 we can assume without loss of generality that \(\vert x_i \vert\) and \(\vert y_i \vert\) are non-decreasing in i. Note that then \(\varrho _k (x) = (x_1 , \ldots , x_k)\). For every \(j\in \{1,\ldots , m\}\) we have by the lemma above that \(\vert x_j \vert \le \vert y_j \vert\). By Lemma 3 above the statement follows.

In the following situation the set ordering can be expressed by the two-sided stochastic order. The proof is immediate.

Lemma 6

Let \(x\in \mathbb {R}^n\) and \(y\in \mathbb {R}^m\) and \(n=m\). Then \(x\preceq y\) if and only if \(\frac{1}{n}\sum _{i=1}^n \delta _{x_i} \preceq \frac{1}{m}\sum _{j=1}^m \delta _{y_j}\).

Now we begin with the preparation of the coupling, where the key idea is to imitate the dynamics of the particle process with coupled Brownian paths. The existence of the required couplings of Brownian paths in the following statements can be seen from the explicit construction in the proof of Lemma 3.2 in Klump and Kolb (2022). For the formulation of the following lemmas we use the partial order defined in Eq. (10).

Recall that \(B^y , B^x, B^z\) denote M-dimensional Brownian motions with \(B^{y,i}_0 = y_i\), \(B^{x,i}_0 = x_i\) and \(B^{z,i}_0 = z_i\).

Lemma 7

Let \(x,y \in \mathbb {R}^M\). Assume that \(B^y\) and \(B^x\) are coupled in such a way that \(\vert B_t^{y,i} \vert \le \vert B_t^{x,i} \vert\) for all \(t\ge 0\). Then

$$\begin{aligned} (B^{y,i}_t)_{i\in A^{+,y}_t (j) } \preceq (B^{x,i}_t)_{i\in A^x (s_1 , \ldots , s_j)}. \end{aligned}$$

Proof

Since

$$\begin{aligned} (B^{y,i}_t)_{i\in \{1, \ldots , M\}} \preceq (B^{x,i}_t)_{i\in \{1, \ldots , M\}} \preceq (B^{x,i}_t)_{i\in A^x (s_1 , \ldots , s_j)} \end{aligned}$$

and \(\vert A^x (s_1 , \ldots , s_j) \vert = M-j\) by Lemma 5 we can deduce that

$$\begin{aligned} (B^{y,i}_t)_{i\in A^{+,y}_t (j) } = \varrho _{M-j} ( (B^{y,i}_t)_{i\in \{1, \ldots , M\}} ) \preceq (B^{x,i}_t)_{i\in A^x (s_1 , \ldots , s_j)} \end{aligned}$$

which proves the statement.

Lemma 8

Let \(x,z\in \mathbb {R}^M\). Let \(B^x\) be given as in Lemma 7 and assume that \(x \preceq z\). Then there exists a Brownian motion \(B^z\) such that

$$\begin{aligned} (B^{x,i}_t)_{i\in A^x (s_1 , \ldots , s_j)} \preceq (B^{z,i}_t)_{i\in A^{-,z} (j) }. \end{aligned}$$

Proof

Define \(s_{j+1} :=t\). Assume that for \(\ell \in \{0,1, \ldots , j\}\) up to time \(s_{\ell }\) we have found \(B^z\) and the ordering is already fulfilled. This means that we assume

$$\begin{aligned} \tilde{x} :=(B^{x,i}_{s_{\ell }})_{i\in A^x (s_1 , \ldots , s_{\ell })} \preceq (B^{z,i}_{s_{\ell }})_{i\in A^{-,z} (j)} =:\tilde{z}. \end{aligned}$$

By Lemma 4 there exists an injective map \(\pi _0 : A^{-,z}_t (\kern0.1500emj) \rightarrow A^x (s_1 , \ldots , s_\ell )\) such that \(\vert \tilde{z}_i \vert \ge \vert \tilde{x}_{\pi _0 (i)} \vert\) for all \(i\in A^{-,z} (\kern0.1500emj)\). Let \(W^{\tilde{z}}\) be a \(\vert \tilde{z} \vert\)-dimensional Brownian motion with \(W^{\tilde{z}}_0 = \tilde{z}\) such that \(\vert W^{\tilde{z}, i}_u \vert \ge \vert B^{x,\pi _0(i)}_{u + s_\ell } \vert\) for all \(u\ge 0\) and \(i\in A^{-,z} (\kern0.1500emj)\). Set

$$\begin{aligned} B^{z,i}_s :=W^{\tilde{z}, i}_{s - s_\ell }, \quad s\in (s_{\ell } , s_{\ell +1} ],\quad i\in A^{-,z} (\kern0.1500emj). \end{aligned}$$

We have then, by Lemma 4, that \((B^{x,i}_{s_{\ell +1}})_{i\in A^x (s_1 , \ldots , s_{\ell })} \preceq (B^{z,i}_{s_{\ell +1}})_{i\in A^{-,z} (j)}\) since

$$\begin{aligned} \vert B^{z,i}_{s_{\ell +1}} \vert = \vert W^{\tilde{z},i}_{s_{\ell +1} - s_\ell } \vert \ge \vert B^{x, \pi _0 (i)}_{s_{\ell +1}} \vert \end{aligned}$$

for all \(i\in A^{-,z}\). By Lemma 5 follows that

$$\begin{aligned} (B^{x,i}_{s_{\ell +1}})_{i\in A^x (s_1 , \ldots , s_{\ell +1})} = \varrho _{A^x (s_1 ,\ldots , s_\ell ) -1} (B^{x,i}_{s_{\ell +1}})_{i\in A^x (s_1 , \ldots , s_{\ell })}) \preceq (B^{z,i}_{s_{\ell +1}})_{i\in A^{-,z} (\kern0.1500emj)}, \end{aligned}$$

where \(\varrho _k\) is defined in Definition 2. By induction the statement follows.

With these coupling lemmas we are now ready to prove Lemma 2.

Proof of Lemma 2

Assume the statement for \(k\in \{ 0, \ldots , n_m-1\}\). Let \(M :=N - k^{N}(t_k^{(m)}) = \vert A_{k^{(N)}(t_k^{(m)})} \vert\) and \(x,y,z \in \mathbb {R}^M\) such that

$$\begin{aligned} \frac{1}{M}\sum\limits_{i=1}^M \delta _{y_i} = \tilde{\xi }^{+,N}_{t^{(m)}_k},\quad \frac{1}{M}\sum\limits_{i=1}^M \delta _{x_i} = \tilde{\xi }^{m,N}_{t^{(m)}_k}, \quad \frac{1}{M}\sum\limits_{i=1}^M \delta _{z_i} = \tilde{\xi }^{-,N}_{t^{(m)}_k}. \end{aligned}$$

By the assumption of the induction we have \(y\preceq x \preceq z\). The underlying process from \({\xi }_{k}^{m,N}\) to \({\xi }_{k+1}^{N}\) has its particles removed at the timepoints

$$\begin{aligned} s_1 :=t^{N}_{k^{N}(t_{k}^{(m)})+1} - t^{(m)}_k , \ldots , s_j :=t^{N}_{k^{N}(t_{k+1}^{(m)})} - t^{(m)}_k \end{aligned}$$

with altogether

$$\begin{aligned} j :=k^{N}(t_{k+1}^{(m)}) - k^{N}(t_{k}^{(m)}) \end{aligned}$$

particles removed. (As mentioned before \(j=0\) is possible.) To achieve a coupling between \({\xi }_{k+1}^{m,N}\) and \({\xi }_{k+1}^{-,N}\) we can take an arbitrary Brownian motion \(B^x\) and corresponding to that, \(B^z\) as produced in Lemma 8 with starting points x and z. For the coupling between \({\xi }_{k+1}^{m,N}\) and \({\xi }_{k+1}^{+,N}\) we take a Brownian motion \(B^y\) with starting point y coupled to \(B^x\) in the way required by Lemma 7. We obtain a coupling of \({\xi }_{k+1}^{+,N} , {\xi }_{k+1}^{m,N}, {\xi }_{k+1}^{-,N}\) by defining

$$\begin{aligned} \tilde{\xi }_{k+1}^{+,N}&:=\frac{1}{\big \vert A^{+,y}_{t_{k+1}^{(m)} -t_k^{(m)}} (\kern0.1500emj) \big \vert } \sum _{i \in A^{+,y}_{t_{k+1}^{(m)} -t_k^{(m)}} (\kern0.1500emj)} \delta _{B^{y,i}_{t_{k+1}^{(m)} -t_k^{(m)}}},\\ {\xi }_{k+1}^{m,N}&:=\frac{1}{\big \vert A^x ( s_1 , \ldots , s_j) \big \vert } \sum\limits_{i\in A^x ( s_1 , \ldots , s_j)} \delta _{B^{x,i}_{t_{k+1}^{(m)} -t_k^{(m)}}},\\ \tilde{\xi }_{k+1}^{-,N}&:=\frac{1}{\big \vert A^{-,z} (\kern0.2000emj) \big \vert } \sum\limits_{i \in A^{-,z}(\kern0.1500emj )} \delta _{B^{z,i}_{t_{k+1}^{(m)} -t_k^{(m)}}}, \end{aligned}$$

where we use the notation of Lemma 8 and Lemma 7. Since

$$\begin{aligned} \begin{aligned} N - k^{(N)}(t_{k+1}^{(m)})&= \big \vert A^{+,y}_{t_{k+1}^{(m)} -t_k^{(m)}} (\kern0.1500emj) \big \vert \\&= \vert A^x (s_1 ,\ldots , s_j) \vert = \vert A^{-,z}(\kern0.1500emj) \vert \end{aligned} \end{aligned}$$

we have by Lemmas 7 and 8 combined with Lemma 6 that this coupling fulfills the desired ordering property, namely that

$$\begin{aligned} \begin{aligned} \tilde{\xi }_{k+1}^{+,N} \preceq {\xi }_{k+1}^{m,N} \preceq \tilde{\xi }_{k+1}^{-,N}. \end{aligned} \end{aligned}$$

The statement for the discrete time processes follows therefore by induction.

Now observe that, if for \(t\ge 0\) we have \(t > t^{(m)}_{k^{(m)}(t)}\) we can start with the coupled configurations of \(\tilde{\xi }^{+,N}_{k^{(m)}(t)} , {\xi }^{m,N}_{k^{(m)}(t)}, \tilde{\xi }^{-,N}_{k^{(m)}(t)}\) and choose the increments of \(B^y\) and \(B^z\) in such a way that the particle systems stay ordered up to time t. See for example the proof of Lemma 3.2 in Klump and Kolb (2022) for such a coupling.

3.3 Hydrodynamic Limit of Stochastic Barriers

As next step we will establish a hydrodynamic limit for the lower and upper stochastic barriers \(\chi _t^{\pm ,N}\).

We define \(P_t\) as the operator of convolution of measures with the Gaussian probability kernel, this is

$$\begin{aligned} P_t (\mu ) (\mathop {}\!\textrm{d}x) :=\mathbb {P}_{\mu } \left( B_t \in \mathop {}\!\textrm{d}x\; \right) = \int _{\mathbb {R}} \frac{1}{\sqrt{2\pi t}} e^{-\frac{(x-y)^2}{2t}} \mathop {}\!\textrm{d}\mu (y) \mathop {}\!\textrm{d}x \end{aligned}$$

for \(t\ge 0\) and \(\mu \in \mathcal {P}\) with the convention \(P_0(\mu ) = \mu\). Furthermore, we define the quantile-truncation \(T_\alpha\) of measures by

$$\begin{aligned} T_\alpha (\mu ) :=\mu ( \cdot \vert [-q_\alpha , q_\alpha ] ), \end{aligned}$$

for \(\alpha \in (0,1]\) and \(\mu \in \mathcal {P}\), where

$$\begin{aligned} q_\alpha :=q_\alpha (\mu ) :=\inf \{c \ge 0 : \mu ([-c,c]) \ge \alpha \}. \end{aligned}$$

We define \(\alpha _k^{(m)} :=g(t_k^{(m)} ) / g(t_{k-1}^{(m)})\) for \(k\in \{1,\ldots , n_m\}\) such that \(t_k^{(m)} < t^g\). Let \(S^{-,m}_1 :=P_{t_1^{(m)}} (\mu )\) and

$$\begin{array}{l} S_k^{+,m} (\mu ):=T_{\alpha _k^{(m)}} \circ{} P_{t_k^{(m)}- t_{k-1}^{(m)}} \circ \ldots{} \circ T_{\alpha _1^{(m)}} \circ aP_{t_1^{(m)}} (\mu ),\\ S_k^{-,m} (\mu ):= P_{t_{k}^{(m)} - t_{k-1}^{(m)}} \circ T_{\alpha _k^{(m)}} \circ \ldots{} \circ P_{t_2^{(m)} - t_1^{(m)}}\circ T_{\alpha _2^{(m)}} \circ P_{t_1^{(m)}} (\mu ) \end{array}$$
(11)

and

$$\begin{aligned} \begin{aligned} q^{+}_{k} :=q^{+,m}_{k}&:=\sup {\text {supp}}(S_k^{+,m} (\mu )), \quad k\in \{ 1, \ldots , n_m \},\\ q^{-}_{k} :=q^{-,m}_{k}&:=\sup {\text {supp}}( T_{\alpha _k^{(m)}} \circ S_{k-1}^{-,m} (\mu )), \quad k\in \{ 2, \ldots , n_m \}, \end{aligned} \end{aligned}$$
(12)

for k such that \(t_k^{(m)} < t^g\). Set \(q^+_k :=0\) if \(t_k^{(m)} = t^g\).

Theorem 9

Assume that, for every \(t\in (0,t^g)\), it holds

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) . \end{aligned}$$

Let \(\varphi : \mathbb {R}\rightarrow \mathbb {R}\) be a measurable and bounded function and \(t\in (0,t^g)\). Then

$$\begin{aligned} \chi ^{\pm , N}_t (\varphi ) \rightarrow P_{t - (t)_m} \circ S_{k^{(m)}(t)}^{\pm ,m}(\mu ) (\varphi ) \end{aligned}$$

almost surely as \(N\rightarrow \infty\).

Proof

In order to bring the empirical process together with the deterministic quantiles, in the following we use ideas from the proof of Proposition 3 in De Masi et al. (2019a). Define \(F^{\pm ,N}_0 (i) :=F^\pm _0 (i) :=1\) and

$$\begin{aligned} F^{+,N}_k(i)&:=\mathbb{1}_{\{\vert B^i_{t_1^{(m)}} \vert \le q^{+,N}_{1} , \ldots , \vert B^i_{t_k^{(m)}} \vert \le q^{+,N}_{k}\}},\\ F^+_k (i)&:=\mathbb{1}_{\{\vert B^i_{t_1^{(m)}} | \le q^{+}_{1} , \ldots , \vert B^i_{t_k^{(m)}} \vert \le q^{+}_{k}\}},\\ F^{-,N}_k(i)&:=F_1^{-,N} (i) \mathbb{1}_{\{\vert B^i_{t_1^{(m)}} \vert \le q^{-,N}_{2} , \ldots , \vert B^i_{t_{k-1}^{(m)}} \vert \le q^{-,N}_{k}\}}, \\ F^-_k (i)&:=F_1^- (i) \mathbb{1}_{\{\vert B^i_{t_1^{(m)}} \vert \le q^{-}_{2} , \ldots , \vert B^i_{t_{k-1}^{(m)}} \vert \le q^{-}_{k}\}},\\ F^{-,N}_1 (i)&:=F^-_1 (i) :=\mathbb{1}_{\{i\in A^-_1\}}.\end{aligned}$$

We claim that, for every \(k \in \{0, \ldots , k^{(m)}(t)\}\), we have that

$$\begin{aligned} \frac{1}{N}\sum\limits_{i=1}^N \left| F^{\pm , N}_k (i) - F^{\pm }_k (i) \right| \rightarrow 0 \end{aligned}$$
(13)

almost surely as \(N\rightarrow \infty\). With this at hand the statement would follow since we have for any \(s\ge t_k^{(m)}\) that

$$\begin{aligned}&\left| \frac{\vert A^{\pm }_k \vert }{N}\cdot \frac{1}{\vert A^{\pm }_k \vert } \sum\limits_{i\in A^{\pm }_k} \varphi (B^i_s) - g(t_k^{(m)}) P_{s - t_k^{(m)}} \circ S_k^{\pm ,m}(\mu ) (\varphi ) \right| \\ {}&\le \left| \frac{1}{N}\sum _{i\in A^{\pm }_k} \varphi (B^i_{s}) - \frac{1}{N} \sum\limits_{i=1}^N \varphi (B^i_{s}) F^{\pm }_k (i) \right| \\ {}& + \left| \frac{1}{N} \sum _{i=1}^N \varphi (B^i_{s}) F^{\pm }_k (i) - g(t_k^{(m)}) P_{s - t_k^{(m)}} \circ S_k^{\pm ,m}(\mu ) (\varphi ) \right| . \end{aligned}$$

This sum tends to zero as \(N\rightarrow \infty\) by observing that

$$\begin{aligned}&\left| \frac{1}{N}\sum\limits_{i\in A^{\pm }_k} \varphi (B^i_{s}) - \frac{1}{N} \sum\limits_{i=1}^N \varphi (B^i_{s}) F^{\pm }_k (i) \right| \\&= \left| \frac{1}{N}\sum\limits_{i = 1}^N \varphi (B^i_{s}) F^{\pm , N}_k (i) - \frac{1}{N} \sum _{i=1}^N \varphi (B^i_{s}) F^{\pm }_k (i) \right| \\&\le \Vert \varphi \Vert _\infty \frac{1}{N}\sum\limits_{i = 1}^N \big \vert F^{\pm , N}_k (i) - F^{\pm }_k (i) \big \vert \rightarrow 0 \end{aligned}$$

and noting that, by the law of large numbers,

$$\begin{aligned} \begin{aligned}&\left| \frac{1}{N} \sum _{i=1}^N \varphi (B^i_{s}) F^{+}_k (i) - g(t_k^{(m)}) P_{s - t_k^{(m)}} \circ S_k^{+,m}(\mu ) (\varphi ) \right| \\&= \left| \frac{1}{N} \sum _{i=1}^N \varphi (B^i_{s}) F^{+}_k (i) - \mathbb {E}_{\mu }\left[ \varphi (B^1_{s}) F^{+}_k (1) \right] \right| \rightarrow 0 \end{aligned} \end{aligned}$$
(14)

almost surely as \(N\rightarrow \infty\) in the \(F^+\)-case. For the \(F^-\)-case first note that

$$\begin{aligned} \frac{1}{N} \sum\limits_{i=1}^N F_1^- (i) = \frac{N - k^{N}(t_1^{(m)})}{N} \rightarrow g(t_1^{(m)}) \end{aligned}$$

by definition and thus, by Lemma 13 and the law of large numbers, it follows that

$$\begin{aligned}&\frac{1}{N} \sum\limits_{i=1}^N \varphi (B^i_{s}) F^{-}_k (i) = \frac{1}{N} \sum\limits_{i=1}^N \varphi (B^i_{s}) F_1^- (i) \mathbb{1}_{\{\vert B^i_{t_1^{(m)}} \vert \le q^{-}_{2} , \ldots , \vert B^i_{t_{k-1}^{(m)}} \vert \le q^{-}_{k}\}}\\&\overset{N\rightarrow \infty }{\longrightarrow } g(t_1^{(m)}) \mathbb{E}_{\mu }\left[ \varphi (B^i_{s}) ; \; \vert B^i_{t_1^{(m)}} \vert \le q_2^- , \ldots , \vert B^i_{t_{k-1}^{(m)}} \vert \le q_k^- \right] \\&= g(t_k^{(m)}) P_{s - t_k^{(m)}} \circ S_k^{-,m} (\mu ) ( \varphi ) \end{aligned}$$
(15)

almost surely. Now assume that Eq. (13) holds true for fixed \(k \in \{0, \ldots , k^{(m)}(t)-1\}\). We have

$$\begin{aligned} \begin{aligned}&\frac{1}{N}\sum\limits_{i=1}^N \left| F^{+, N}_{k+1} (i) - F^{+}_{k+1} (i) \right| \\&= \frac{1}{N}\sum\limits_{i=1}^N \left| F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - F^{+}_k (i)\mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&\le \frac{1}{N}\sum\limits_{i=1}^N \left| F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&+ \frac{1}{N}\sum _{i=1}^N \left| F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} - F^{+}_k (i)\mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&\le \frac{1}{N}\sum\limits_{i=1}^N F^{+, N}_k (i) \left| \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&+{\le } + \frac{1}{N}\sum\limits_{i=1}^N \left| F^{+, N}_k (i)- F^{+}_k (i) \right| . \end{aligned} \end{aligned}$$

The last term is tending to zero by assumption while the remaining term can be written as follows.

$$\begin{aligned}&\frac{1}{N}\sum\limits_{i=1}^N F^{+, N}_k (i) \left| \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&= \frac{1}{N}\sum\limits_{i=1}^N {\text {sgn}}(q^{+,N}_{k+1} - q^{+}_{k+1}) F^{+, N}_k (i) \left( \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}}\right) \\&= \left| \frac{1}{N}\sum\limits_{i=1}^N F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} - F^{+, N}_k (i) \mathbb {1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&\le \left| \frac{1}{N}\sum\limits_{i=1}^N F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+,N}_{k+1}\}} -F^{+}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\& + \left| \frac{1}{N}\sum _{i=1}^N F^{+}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} - F^{+, N}_k (i) \mathbb{1}_{\{\vert B^i_{t_{k+1}^{(m)}} \vert \le q^{+}_{k+1}\}} \right| \\&\le \left| \frac{1}{N}\sum\limits_{i=1}^N F^{+}_{k+1} (i) - \frac{1}{N}\sum _{i=1}^N F^{+, N}_{k+1} (i) \right| + \frac{1}{N}\sum\limits_{i=1}^N \left| F^{+, N}_k (i) -F^{+}_k (i) \right| . \end{aligned}$$

Again by assumption the last term tends to zero. An analogous reasoning can be made for the upper barrier. Thus the statement left to show is

$$\begin{aligned} \left| \frac{1}{N}\sum\limits_{i=1}^N F^{\pm }_{k+1} (i) - \frac{1}{N}\sum\limits_{i=1}^N F^{\pm , N}_{k+1} (i) \right| \rightarrow 0 \end{aligned}$$

as \(N \rightarrow \infty\). But on the one hand we have almost surely

$$\begin{aligned} \frac{1}{N}\sum\limits_{i=1}^N F^{\pm ,N}_{k+1} (i) = \frac{\big \vert A_{k+1}^\pm \big \vert }{N} = \frac{N - k^N (t_{k+1}^{(m)})}{N} \rightarrow g (t_{k+1}^{(m)}). \end{aligned}$$

On the other hand it holds almost surely

$$\begin{aligned} \frac{1}{N}\sum\limits_{i=1}^N F^{\pm }_{k+1} (i) \rightarrow g (t_{k+1}^{(m)}), \end{aligned}$$

which can be seen from the arguments in Eqs. (14) and (15) for \(\varphi \equiv 1\).

Lemma 10

Let \(t\in (0,t^g)\). Assume that

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) \end{aligned}$$

and \(\lim _{m\rightarrow \infty } g((t)_m) = g(t)\). Then, for measurable, bounded \(\varphi : \mathbb {R}\rightarrow \mathbb {R}\) holds

$$\begin{aligned} \lim _{m\rightarrow \infty }\limsup _{N\rightarrow \infty } \big \vert \chi _t^N \varphi - \chi _{t}^{m,N} \varphi \big \vert = 0 \end{aligned}$$

almost surely.

Proof

We have that

$$\begin{aligned} \begin{aligned}&\big \vert \chi _{t}^N \varphi - \chi _{t}^{m,N} \varphi \big \vert \\&= \left| \frac{ 1}{\vert A_{k^{N} (t)} \vert }\sum\limits_{i\in A_{k^{N} (t)}} \varphi (B_{t}^i) - \frac{1}{\vert A_{k^{N}((t)_m)} \vert } \sum\limits_{i\in A_{k^{N}((t)_m)}} \varphi ( B^i_{t} ) \right| \\&\le \frac{1}{\vert A_{k^{N}(t)} \vert } \sum\limits_{i\in A_{k^{N}((t)_m)}} \big \vert \varphi ( B^i_{t} ) - \frac{\vert A_{k^{N}(t)} \vert }{\vert A_{k^{N}((t)_m)} \vert } \varphi ( B^i_{t} ) \big \vert \\& + \frac{1}{\vert A_{k^{N}(t)} \vert } \sum _{i\in A_{k^{N}((t)_m)} \setminus A_{k^{N}(t)}}\big \vert \varphi ( B^i_{t} ) \big \vert \\&\le 2\Vert \varphi \Vert _\infty \frac{1}{\vert A_{k^{N}(t)} \vert } \left( \vert A_{k^{N}((t)_m)} \vert - \vert A_{k^{N}(t)} \vert \right) \\&= 2\Vert \varphi \Vert _\infty \frac{1}{N - k^{N}(t)} \left( k^{N}(t) - k^{N}((t)_m) \right) \\&\overset{N\rightarrow \infty }{\longrightarrow } 2\Vert \varphi \Vert _\infty \frac{1}{g(t)} \left( g((t)_m)- g(t) \right) \end{aligned} \end{aligned}$$

which converges to 0 as \(m\rightarrow \infty\) by assumption.

3.4 Proof of Theorem 1

Now we will put the results together to yield Theorem 1.

Proof of Theorem 1

Let \(t\in (0,t^g)\). Without loss of generality we assume that \(g(t)<1\). Using the coupling of Lemma 2 we get that for a number \(a\ge 0\) we have

$$\begin{aligned} \tilde{\chi }_{t}^{+,N} ([-a,a]) \ge {\chi }_{t}^{m,N} ([-a,a]) \ge \tilde{\chi }_{t}^{-,N} ([-a,a]) \end{aligned}$$

yielding by Theorem 9 that

$$\begin{aligned} \begin{aligned}&P_{t - (t)_m} \circ S^{+,m}_{k^{(m)}(t) } (\mu ) ([-a,a]) \ge \limsup _{N\rightarrow \infty } {\chi }_{t}^{m,N} ([-a,a])\\&\ge \liminf _{N\rightarrow \infty } {\chi }_{t}^{m,N} ([-a,a]) \ge P_{t - (t)_m} \circ S^{-,m}_{k^{(m)}(t)} (\mu ) ([-a,a]). \end{aligned} \end{aligned}$$
(16)

Now we take the specific choice \(t_k^{(m)} :=k2^{-n}t\). Note that then \((t)_m =t\) and \(S^{\pm ,m}_k (\mu )\) coincide, respectively, with \(\mu ^{+,m}_k\) and \(\tilde{\mu }_k^{-,m}\) from Theorem 2.2 in Klump and Kolb (2022). By the convergence of Theorem 2.2 in Klump and Kolb (2022) we have then, since \(\mu _{t}\) is non-atomic, that

$$\begin{aligned} \begin{aligned}&\lim _{m\rightarrow \infty } S^{+,m}_{k^{(m)} (t)} (\mu ) ([-a,a]) \\&= \lim _{m\rightarrow \infty } S^{-,m}_{k^{(m)} (t)} (\mu ) ([-a,a]) = \mu _{t} ([-a,a]). \end{aligned} \end{aligned}$$

As a consequence of Eq. (16) and Lemma 10 we obtain that

$$\begin{aligned} \lim _{N\rightarrow \infty }\chi ^N_{t}([-a,a]) = \mu _{t} ([-a,a]) \end{aligned}$$

almost surely.

4 Application: Simulation of Inverse First-passage Time Solutions

This section is devoted to present simulations of solutions of the inverse first-passage time problem. This is done by a Monte-Carlo method, which is extracted from the proof of Theorem 1.

We give a short overview of the existing methods to simulate the solutions of the inverse first-passage time problem. In the context of credit risk modeling Hull and White (2001) and Avellaneda and Zhu (2001) proposed approximation approaches in the case of very regular survival distributions g. In Avellaneda and Zhu (2001) the idea is based on a free boundary problem related to the problem in Cheng et al. (2006). The idea from Hull and White (2001) is based on a numerical approximation of a discrete scheme of quantiles, which is related to the our sequence of quantiles from Eq. (12). The work of Zucca and Sacerdote (2009) presents two methods for the one-sided inverse first-passage time problem. The so-called PLMC method is based on a continuous, piecewise linear approximation, which is estimated by a Monte-Carlo method. The so-called VIE method numerically approximates the solution of a Volterra integral equation, the so-called Master equation (cf. Section 14, Peskir and Shiryaev (2006)). The author of Abundo (2006) transfers the latter method to the case of reflected Brownian motion. The authors of Gür and Pötzelberger (2021) propose a modified VIE method by estimating the integral equation by using the empirical distribution of g. In Civallero and Zucca (2019) an approach related to the VIE method is used to obtain numerical solutions if the underlying process is a component of a two dimensional Ornstein-Uhlenbeck process instead of Brownian motion. A further approach can be found in Song and Zipkin (2011), which is related to the tangent-method for the first-passage time problem. Regarding the literature on numerical solutions to the first-passage time problem see for example Herrmann and Tanré (2016), Herrmann and Zucca (2019), Herrmann and Zucca (2020).

In the context of the inverse problem, bounds for the discretization error of the methods of Zucca and Sacerdote (2009) were given therein, but all in all a rigorous study and comparison of the existing methods for the solutions of the inverse first-passage time problem has yet to be provided.

Here, for a given survival distribution g and \(m\in \mathbb {N}\), we consider the sequence of lower semicontinuous functions

$$\begin{aligned} \begin{aligned} b_m (s) :={\left\{ \begin{array}{ll} q^{+,m}_{k} &{}: s= t_k^{(m)}, k\in \{1, \ldots , n_m\},\\ \infty &{}: \text {else}, \end{array}\right. } \qquad s\in [0,t^g], \end{aligned} \end{aligned}$$
(17)

where \(q^{+,m}_k\) is the quantile from Eq. (12) and \(t_k^{(m)}\), \(k\in \{1, \ldots , n_m\}\), are the timepoints from Eq. (7). Note that the quantiles \(q^{+,m}_k\), \(k\in \{1, \ldots , n_m\}\), are given by the following inductive scheme: As long as \(g(t_k^{(m)}) >0\), if \(q^{+,m}_1 , \ldots , q^{+,m}_{k-1}\) are already given, \(q^{+,m}_k\) is the unique element from \([0,\infty ]\) such that

$$\begin{aligned} \mathbb {P}_{\mu } \left( \vert B_{t_k^{(m)}} \vert \le q^{+,m}_k , \vert B_{t_{k-1}^{(m)}} \vert \le q^{+,m}_{k-1} , \ldots , \vert B_{t_1^{(m)}} \vert \le q^{+,m}_1 \right) = g(t_k^{(m)}). \end{aligned}$$

Note that, in terms of Eq. (17), this means that

$$\begin{aligned} \mathbb {P}_{\mu } \left( \tau _{b_m} > t_k^{(m)} \right) = g(t_k^{(m)}). \end{aligned}$$

This discretization scheme was already used in the existence result by Anulova (1980) and the uniqueness results of Ekström and Janson (2016), Klump and Kolb (2022), see Remark 4 for details on the convergence. In our setting, heuristically, a Monte-Carlo approximation is given by the random functions

$$\begin{aligned} \begin{aligned} b_m^N (s) :={\left\{ \begin{array}{ll} q^{+,N,m}_{k} &{}: s= t_k^{(m)}, k\in \{1, \ldots , n_m\},\\ \infty &{}: \text {else}, \end{array}\right. }\quad s\in [0,t^g], \end{aligned} \end{aligned}$$
(18)

where \(q^{+,N,m}_k\) is the empirical quantile from Eq. (8) and was given by the following inductive scheme: For \(N\in \mathbb {N}\), timepoints as in Eq. (3) were given. For \(q^{+,N,m}_1 , \ldots , q^{+,N,m}_{k-1}\) already known, we defined

$$\begin{aligned} q_{k}^{+,N,m} :=\inf \Bigg \{ a \ge 0 : \sum _{i\in A_{k-1}^+} \mathbb{1}_{\{\vert B_{t_k^{(m)}}^i \vert \le a\}} \ge N - k^{N}(t_k^{(m)}) \Bigg \}, \end{aligned}$$

where \(k^N\) is the function defined in Eq. (4) and

$$\begin{aligned} A_{k-1}^+ :=\left\{ i\in \{1,\ldots , N\} : \vert B_{t_{k-1}^{(m)}}^i \vert \le q_{k-1}^{+,N}, \ldots , \vert B_{t_{1}^{(m)}}^i \vert \le q_{1}^{+,N} \right\} . \end{aligned}$$

We begin with the following statement.

Lemma 11

Let g be a survival distribution. Assume that the timepoints from Eq. (3) fulfill that, for every \(t\in (0,t^g)\), we have

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) . \end{aligned}$$

Then, for every \(k\in \{1, \ldots , n_m\}\), it holds that

$$\begin{aligned} \lim _{N\rightarrow \infty } b_m^N (t_k^{(m)}) = b_m (t_k^{(m)}) \end{aligned}$$

almost surely.

Proof

Without loss of generality we can assume that \(k = k^{(m)}(t_k^{(m)})\). By assumption we have that, for every \(t\in (0,t^g)\), holds

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) . \end{aligned}$$

Assume that \(\liminf _{N\rightarrow \infty } q_k^{+,N,m}< R < q_k^{+,m}\). We obtain, by Theorem 9, that

$$\begin{aligned} 0&= \limsup _{N\rightarrow \infty } \frac{1}{N} ({\vert \{ i\in A_k^{+,N} : \vert B_{t_k^{(m)}}^i \vert \le q_k^+ \} \vert - \vert \{ i\in A_k^{+,N} : \vert B_{t_k^{(m)}}^i \vert \le q_k^{+,N} \} \vert })\\&\ge \liminf _{N\rightarrow \infty } \frac{1}{N} ({\vert \{ i\in A_k^{+,N} : \vert B_{t_k^{(m)}}^i \vert \le q_k^+ \} \vert - \vert \{ i\in A_k^{+,N} : \vert B_{t_k^{(m)}}^i \vert \le R \} \vert })\\&= \lim _{N\rightarrow \infty } \frac{1}{N} \sum\limits_{i\in A_k^{+,N}}\mathbb{1}_{(R , q_k^+)}(\vert B_{t_k^{(m)}}^i \vert )= \mathbb {P}_{\mu } \left( \vert X_{t_k^{(m)}} \vert \in (R, q_k^+) , \tau _{b_m}>t_k^{(m)} \right) > 0. \end{aligned}$$

If we assume that \(\limsup _{N\rightarrow \infty } q_k^{+,N,m}> R > q_k^{+,m}\), we analogously obtain a contradiction. These contradictions show that

$$\begin{aligned} \lim _{N\rightarrow \infty } b_m^N (t_k^{(m)}) = \lim _{N\rightarrow \infty } q_k^{+,N,m} = q_k^{+,m} = b_m (t_k^{(m)}) \end{aligned}$$

almost surely.

Remark 4

Note that the discrete scheme of Eq. (17) is a deterministic approximation of the inverse first-passage time solution. For this type of approximation the author of Anulova (1980) uses a notion of convergence, which is equivalent to the \(\Gamma\)-convergence of lower semicontinuous functions as it was used in Klump and Kolb (2022) and Klump (2022). Let b be unique solution to the inverse first-passage time problem which vanishes off \((0,t^g)\). If \(t_k^{(m)}\), \(k\in \{1, \ldots , n_m\}\), are suitably chosen, the statement of Lemma 2.3.35 in Klump (2022) yields that

$$\begin{aligned} b_m\mathbb {1}_{{(0,t^g)}} \overset{\Gamma }{\rightarrow } b, \end{aligned}$$

where \(\overset{\Gamma }{\rightarrow }\) denotes the \(\Gamma\)-convergence. This includes the choices in Eq. (19) and Fig. 6 below.

For an implementation, we have to make specific choices of the sequence of timepoints \((t_k^{(m)})_{k\in \{1,\ldots , n_m\}, m \in \mathbb {N}}\). In the following we will work with two choices.

4.1 Timesteps as Quantiles of the Survival Distribution

In this subsection we make the specific choice of quantiles

$$\begin{aligned} t^{(m)}_k = g^{-1} \left( \frac{m-k}{m} \right) , \quad k\in \{1, \ldots , m \}, \end{aligned}$$
(19)

of the survival distribution g, where \(g^{-1}\) denotes the generalized inverse from Eq. (21). This choice is motivated by Remark 5.

Fig. 4
figure 4

Left: The exact boundary \(b_{\text {L}}(t) = \mathbb {1}_{(0,1)}(t) \sqrt{-t \log (t)}\) from Example 1. Right: The approximated boundary \(b_m^N\) with timesteps \(t^{(m)}_k = g^{-1} \left( \frac{m-k}{m} \right)\) using the first-passage time distribution of \(b_{\text {L}}\) for \(m = 10^5\) and \(N= 10^7\), where the generalized inverse of g is obtained numerically from the density of \(\tau _{b_{\text {L}}}\) from Example 1

Full size image

Remark 5

If we take as removal times

$$\begin{aligned} t^N_k :=t_k^{(N)} = g^{-1}\left( \frac{N-k}{k} \right) , \quad k\in \{1, \ldots , N\}, \end{aligned}$$

then, by Lemma 14, we have that, for every \(t\in (0,t^g)\), it holds

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) . \end{aligned}$$

The specific choice of \(t^{(m)}_k = g^{-1} \left( \frac{m-k}{m} \right)\) simplifies the representation of \(b_m^N (t_k^{(m)})\) for those \(N \ge m\) such that \(m \vert N\). Namely, if

$$\begin{aligned} N = m \ell , \end{aligned}$$

for some \(\ell \in \mathbb {N}\), using the definition Eq. (8) we have

$$\begin{aligned} b_m^N (t_k^{(m)}) = q_k^{+,m}&= \inf \left\{ a \ge 0 : \sum _{i \in A^+_{k-1}} \mathbb{1}_{\{ \vert B^i_{t_k^{(m)}} \vert \le a\}} \ge N - k^N (t_k^{(m)}) \right\} \\&= \inf \left\{ a \ge 0 : \sum _{i \in A^+_{k-1}} \mathbb {1}_{\{\vert B^i_{t_k^{(m)}} \vert \le a\}} \ge m \ell - k\ell \right\} . \end{aligned}$$

Hence, in the procedure at every time step the constant number of \(\ell\) particles is removed. Note that for the implementation, the choice of \(t^N_k\) becomes irrelevant.

As first example we use a known solution of the two-sided first-passage time problem.

Example 1

(Lerche (1986)) We will call \(b_{\text {L}}(t) = \mathbb {1}_{{(0,1)}}(t) \sqrt{-t \log (t)}\) Lerche’s boundary. If the Brownian motion has initial distribution \(\delta _0\) the corresponding survival distribution of the first-passage time of \(b_{\text {L}}\) is given by

$$\begin{aligned} \begin{aligned} \mathbb {P}_{0} \left( \tau _{b_{\text {L}}} >t \right)&= 1 - 2 \Phi ( - b_{\text {L}}(t) / \sqrt{t} ) - \frac{2}{\pi } b_{\text {L}}(t)\\&= 1 - 2 \Phi (- \sqrt{-\log (t)}) - \frac{2}{\pi } \sqrt{-t\log (t)}, \end{aligned} \end{aligned}$$

where \(\Phi (x) = \int _{-\infty }^x (2\pi )^{-\frac{1}{2}} e^{-\frac{z^2}{2}} \mathop {}\!\textrm{d}z\). In Fig. 4 we compare the approximation by our Monte-Carlo method with the exact boundary \(b_{\text {L}}\).

For examples for unknown boundaries see Fig. 5.

Fig. 5
figure 5

The approximated boundaries \(b_m^N\) with timesteps \(t^{(m)}_k = g^{-1} \left( \frac{m-k}{m} \right)\) for the Weibull distribution \(g_{\text {Weibull}(1,2)}(t) = e^{-t^2}\) and the Gamma distribution \(g_{\Gamma (2,1)}(t) = 1 - \gamma (2, t)\), where \(\gamma\) is the lower incomplete gamma function, for \(m=10^5\), \(N=10^7\)

Full size image

The timesteps given by the quantiles of the survival distribution will avoid the regions with comparatively sparse probability mass. This can result in an inappropriate simulation of the unknown boundary as it would be the case for the log-logistic distribution from Fig. 6.

4.2 Timesteps as Equidistant Points

As alternative to the quantiles of the survival distribution we could also use any other form of timesteps. Note that in general we have

$$\begin{aligned} b_m^N (t_k^{(m)}) = q_k^{+,N,m}&= \inf \left\{ a \ge 0 : \sum\limits_{i\in A_{k-1}^+} \mathbb{1}_{\{\vert B_{t_k^{(m)}}^i \vert \le a\}} \ge N - k^{N}(t_k^{(m)}) \right\} \\&= \inf \left\{ a \ge 0 : \frac{1}{\vert A_{k-1}^+ \vert }\sum \limits_{i\in A_{k-1}^+} \mathbb{1}_{\{\vert B_{t_k^{(m)}}^i \vert \le a\}} \ge \frac{N - k^{N}(t_k^{(m)}) }{\vert A_{k-1}^+ \vert }\right\} \\&= \inf \left\{ a \ge 0 : \frac{1}{\vert A_{k-1}^+ \vert }\sum _{i\in A_{k-1}^+} \mathbb{1}_{\{\vert B_{t_k^{(m)}}^i \vert \le a\}} \ge \frac{N - k^{N}(t_k^{(m)}) }{N - k^{N}(t_{k-1}^{(m)}) }\right\} . \end{aligned}$$

If, for every \(t\in (0,t^g)\), it holds

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{k^N (t)}{N} = 1- g(t) \end{aligned}$$

then we have

$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{N - k^{N}(t_k^{(m)}) }{N - k^{N}(t_{k-1}^{(m)}) } = \frac{g(t_k^{(m)}) }{g(t_{k-1}^{(m)}) }. \end{aligned}$$

Therefore, it is reasonable to substitute \(b_m^N (t_k^{(m)})\) by the simpler empirical quantile

$$\begin{aligned} \tilde{b}_m^N (t_k^{(m)}) :=\tilde{q}_k^{+,N,m} :=\inf \left\{ a \ge 0 : \frac{1}{\vert \tilde{A}_{k-1}^+ \vert }\sum\limits _{i\in \tilde{A}_{k-1}^+} \mathbb{1}_{\{\vert B_{t_k^{(m)}}^i \vert \le a\}} \ge \frac{g(t_k^{(m)}) }{g(t_{k-1}^{(m)}) }\right\} , \end{aligned}$$

where inductively

$$\begin{aligned} \tilde{A}_k^+ :=\tilde{A}_k^{+,m} :=\{ i\in \tilde{A}_{k-1}^+ : \vert B_{t_k^{(m)}}^i \vert \le \tilde{q}_k^{+,N} \} \end{aligned}$$
(20)

for \(k\in \{1, \ldots , n_m\}\), which is heuristically another form of Monte-Carlo approximation. From the inductive scheme it follows that

$$\begin{aligned} \vert \tilde{A}_k^+ \vert = \left\lceil \vert \tilde{A}_{k-1}^+ \vert \cdot \frac{g(t_k^{(m)}) }{g(t_{k-1}^{(m)}) } \right\rceil \end{aligned}$$

for \(k\in \{1, \ldots , n_m\}\), which implies by induction and \(\vert \tilde{A}_0^+ \vert = N\) that

$$\begin{aligned} \lim _{N\rightarrow \infty }\frac{\vert \tilde{A}_k^+ \vert }{N} = g(t_k^{(m)}). \end{aligned}$$
Fig. 6
figure 6

The approximated boundaries \(\tilde{b}_m^N\) with timesteps \(t^{(m)}_k = \frac{k}{m}\) for the log-logistic distribution \(g_{\text {LL}(1,8)}(t) = (1+t^8)^{-1}\) and the Fréchet distribution \(g_{\text {Frechet}(1)}(t) = 1 -\exp (- \frac{1}{t})\) for \(m=10^5\) and \(N=10^7\)

Full size image

The following statement is proved analogously as Lemma 11 by using Theorem 15.

Lemma 12

For every \(k\in \{1, \ldots , n_m\}\) it holds that

$$\begin{aligned} \lim _{N\rightarrow \infty } \tilde{b}_m^N (t_k^{(m)}) = b_m (t_k^{(m)}) \end{aligned}$$

almost surely.

For examples with the use of equidistant timesteps \(t^{(m)}_k = \frac{k}{m}\) see Fig. 6.