Exact Conditioning of Gaussian Fields on Wavelet Coefficients

Abstract

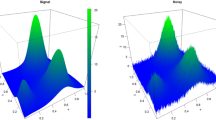
A new approach is presented to ensure exact conditioning of Gaussian fields on wavelet decomposition coefficients and hard data. The approach uses a matrix formulation of discrete wavelet decomposition enabling to compute all the required covariances and cross-covariances between hard data, points to simulate and the imposed wavelet coefficients at all scales. Two small examples show that the approach reproduces exactly the information provided, even when the wavelet information is unrelated to the true underlying image. For larger images, the approach of post-conditioning by cokriging is used to palliate the strong memory requirements of the matrix approach. The modified method remains exact and is shown to be computationally realistic for large problems. This marks a significant improvement over previously published methods where conditioning to wavelet coefficients was only approximate. After soft data calibration to wavelet coefficients at a given scale, the approach enables to simulate realizations fully consistent with the known wavelet coefficients and available hard data.

Appendix: Proof of Exact Conditioning on HD and Wavelet Coefficients

The sampling matrix $\mathbf {H}$, of size $m \times n_t$ (with $n_t=n_1+n_2$) recovers all the image pixels (HD or to simulate) in vector $\mathbf {y}$. Each row of this matrix has a single 1 in the column corresponding to a pixel, and 0 elsewhere. One has

$$\begin{aligned} \mathbf {z}_{\mathbf {sim}}=\mathbf {Hy}_{\mathbf {sim}}, \end{aligned}$$

(13)

where $\mathbf {z}_{\mathbf {sim}}$ is the vector of length $m$ extracted from the simulated vector $\mathbf {y}_{\mathbf {sim}}=\left[ \begin{array}{c} \mathbf {y}_{\mathbf {1 \cdot 2}} \\ \mathbf {y}_{\mathbf {2}} \end{array} \right]$, and where $\mathbf {y}_{\mathbf {1 \cdot 2}}$ is obtained from Eq. 11.

Defining the $m \times n_t$ matrix ${\tilde{\mathbf {F}}}$ as simply $\mathbf {F}$ with lines reordered following the partition in $\mathbf {y}$, matrix ${\tilde{\mathbf {F}}}$ can also be partitioned as

$$\begin{aligned} {\tilde{\mathbf {F}}} = \left[ \begin{array}{c} \tilde{\mathbf {F}}_{\mathbf {1}}\\ \tilde{\mathbf {F}}_{\mathbf {2}}\\ \end{array} \right] .\ \end{aligned}$$

(14)

With these definitions, one has

$$\begin{aligned} \mathbf {K}_{\mathbf {11}}=\tilde{\mathbf {F}}_{\mathbf {1}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {1}}^{\mathbf {T}}, \,\,\mathbf {K}_{\mathbf {12}}=\tilde{\mathbf {F}}_{\mathbf {1}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^\mathbf {T}, \quad \text {and}\quad \mathbf {K}_{\mathbf {22}}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_\mathbf {2}^{\mathbf {T}}. \end{aligned}$$

(15)

Using Eqs. 10, 11, and 15 and posing $\mathbf {r=Lx}$, and noting that ${\mathbf {y}}_{\mathbf {2}}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}$

$$\begin{aligned} \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}_{\mathbf {sim}}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {Hy}_{\mathbf {sim}} = \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H} \left[ \begin{array}{c} \tilde{\mathbf {F}}_{\mathbf {1}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^\mathbf {T}(\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}})^{\mathbf {-1}}\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}+\mathbf {r} \\ \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z} \end{array} \right] . \end{aligned}$$

(16)

The latter can be rewritten as

$$\begin{aligned} \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}_{\mathbf {sim}}=\tilde{\mathbf {F}}_\mathbf {2}\mathbf {H}\tilde{\mathbf {F}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_\mathbf {2}^\mathbf {T}(\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}})^{\mathbf {-1}}\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}+\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H} \left[ \begin{array}{c} \mathbf {r}\\ \mathbf {0} \end{array} \right] . \end{aligned}$$

(17)

Because $\mathbf {H}\tilde{\mathbf {F}}=\mathbf {I}_{\mathbf {m}}$, one gets

$$\begin{aligned} \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}_{\mathbf {sim}}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}+\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H} \left[ \begin{array}{c} \mathbf {r}\\ \mathbf {0} \end{array} \right] . \end{aligned}$$

(18)

Using Eqs. 10 and 15, the vector $\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H}\left[ \begin{array}{c} \mathbf {r}\\ \mathbf {0} \end{array} \right]$ has variance-covariance matrix

$$\begin{aligned} \mathbf {K}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H} \left[ \begin{array}{cc} \tilde{\mathbf {F}}_{\mathbf {1}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {1}}^{\mathbf {T}} - \tilde{\mathbf {F}}_{\mathbf {1}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^\mathbf {T}(\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}})^{\mathbf {-1}}\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {1}}^{\mathbf {T}} &{} \mathbf {0}\\ \mathbf {0} &{} \mathbf {0} \end{array} \right] . \mathbf {H}^{\mathbf {T}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}} \end{aligned}$$

(19)

The right member can be rewritten, as

$$\begin{aligned} \mathbf {K}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {H}\tilde{\mathbf {F}} \left( \mathbf {K}_{\mathbf {zz}} - \mathbf {K}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}}(\tilde{\mathbf {F}}_{\mathbf {2}}{\mathbf {K}}_{\mathbf {zz}}\tilde{\mathbf {F}}_{\mathbf {2}}^{\mathbf {T}})^{\mathbf {-1}}\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {K}_{\mathbf {zz}} \right) \tilde{\mathbf {F}}^{\mathbf {T}} \mathbf {H}^{\mathbf {T}} \tilde{\mathbf {F}}_\mathbf {2}^{\mathbf {T}} \end{aligned}$$

(20)

using again the equality $\mathbf {H}\tilde{\mathbf {F}}=\mathbf {I}_{\mathbf {m}}$, and simplifying, one gets $\mathbf {K}=\mathbf {0}$, which implies that $\tilde{\mathbf {F}}_{2}\mathbf {H}\left[ \begin{array}{c} \mathbf {r}\\ \mathbf {0} \end{array} \right] = \mathbf {0}$ as $E[\mathbf {r}]=\mathbf {0}$. Hence, substituting in Eq. 18,

$$\begin{aligned} \tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}_{\mathbf {sim}}=\tilde{\mathbf {F}}_{\mathbf {2}}\mathbf {z}, \end{aligned}$$

(21)

which proves that all the HD data and wavelet coefficients are exactly reproduced.