Discovering a taste for the unusual: exceptional models for preference mining

Abstract

Exceptional preferences mining (EPM) is a crossover between two subfields of data mining: local pattern mining and preference learning. EPM can be seen as a local pattern mining task that finds subsets of observations where some preference relations between labels significantly deviate from the norm. It is a variant of subgroup discovery, with rankings of labels as the target concept. We employ several quality measures that highlight subgroups featuring exceptional preferences, where the focus of what constitutes ‘exceptional’ varies with the quality measure: two measures look for exceptional overall ranking behavior, one measure indicates whether a particular label stands out from the rest, and a fourth measure highlights subgroups with unusual pairwise label ranking behavior. We explore a few datasets and compare with existing techniques. The results confirm that the new task EPM can deliver interesting knowledge.

1 Introduction

Consider a survey where detailed preferences of sushi types have been collected, along with information about the respondents. For each example in the dataset, we have personal details (age, gender, income, etc.) as well as a set of sushi types, ordered by preference (Kamishima 2003). By mapping the demographic attributes and unusual preferences, marketeers would be able to target key demographics where specific sushi types have greater potential.

The study of preference data has been approached from a number of perspectives, grouped under the name Preference Learning (PL) (e.g., as Label Ranking; de Sá et al. 2016; Cheng et al. 2013; Vembu and Gärtner 2010) Typically, the aim is to build a global predictive model, supported by preference mining methods (Fürnkranz and Hüllermeier 2010), such that the preferences can be predicted for new cases. However, in several areas, such as marketing, there is also great value in identifying subpopulations whose preferences deviate from the norm. If the preference of some sushi type by a certain age group or in a certain region is markedly different from the average population, then the vendor can develop specific strategies for those groups. Finding coherent groups of customers to focus on is an invaluable part of promotion strategies.

In this work, the term preference is not strictly interpreted as a literal preference, but instead as an order relation $object_1 \succ object_2$. An order relation can represent several phenomena: a person likes $sushi_1$ more than $sushi_2$ (Kamishima 2003); $\lambda _1$ is more likely to occur than $\lambda _2$ (Hüllermeier et al. 2008); $algorithm_1$ is better than algorithm $algorithm_2$ (Brazdil et al. 2003). In this context, unusualness is the extent to which some groups show different preferences from average behavior.

Arguably the most generic setting for discovering local, supervised deviations is that of subgroup discovery (SD) (Lavrac et al. 2004). The aim of SD is to discover subgroups in the data for which the target shows an unusual distribution, as compared to the overall population (Klösgen and Zytkow 2002). SD is a generic task in the sense that the actual nature of the target variable can be quite diverse. For example, SD approaches have been developed for binary, nominal (Abudawood et al. 2009) and numeric target variables (Jorge et al. 2006; Jin et al. 2014), as well as multiple targets (Duivesteijn et al. 2012; Umek and Zupan 2011).

We extend the work on exceptional preferences mining (EPM) (de Sá et al. 2016), which focuses on the discovery of meaningful subgroups with exceptional preference patterns. When applying SD to a new context, the main task is to determine what constitutes an interesting subgroup. In EPM, different quality measures determine the interestingness based on how the preferences in the subgroup, differ from the preferences in the whole data. A set of EPM quality measures reflect different facets of interestingness one might have about the unusualness of a set of preferences.

In this work, we include a more comprehensive experimental setup and propose a new quality measure. We employ EPM on several real-world datasets, using four distinct quality measures. These measures define the type of exception that is identified to either encompass the entire label space or focus on more local peculiarities. In particular, two of them look for overall exceptional preferences; a third measure assesses if one particular label behaves exceptionally; the remaining measure quantifies the exceptional behavior of a single pair of labels.

Finally, to consolidate the previous work on EPM, we compare EPM with a subgroup discovery approach known as Distribution Rules (DR) (Jorge et al. 2006).

We start by introducing Label Ranking in Sect. 2 and subgroup discovery in Sect. 3. Then, in Sect. 4 we introduce exceptional preferences mining and analyze the results obtained in Sect. 5. Finally, we conclude this paper in Sect. 6.

2 Label ranking

In Label Ranking, given an instance x from the instance space $\mathbb {X}$, the goal is to predict the ranking of the labels $\mathcal {L} = \{\lambda _1,\ldots ,\lambda _k\}$ associated with x (Hüllermeier et al. 2008). A ranking can be represented as a strict total order over $\mathcal {L}$, defined on the permutation space $\varOmega$.

The Label Ranking task is similar to the classification task, where instead of a class we want to predict a ranking of the labels. As in classification, we do not assume the existence of a deterministic $\mathbb {X} \rightarrow \varOmega$ mapping. Instead, every instance is associated with a probability distribution over $\varOmega$ (Cheng et al. 2009). This means that, for each $x \in \mathbb {X}$, there exists a probability distribution $\mathcal {P}( \cdot | x)$ such that, for every $\pi \in \varOmega$, $\mathcal {P}(\pi | x)$ is the probability that $\pi$ is the ranking associated with x. The goal in Label Ranking is to learn the mapping $\mathbb {X} \rightarrow \varOmega$. The training data is defined as D, which is a bag of $n$ records of the form $x=(a_1,\ldots ,a_m,\pi )$, where {$a_1,\ldots ,a_m\}$ is set of values from $m$ independent variables $\mathcal {A}_1,\ldots ,\mathcal {A}_m$ describing instance x and $\pi$ is the corresponding target ranking.

Rankings can be represented with total or partial orders and vice-versa.

Total orders A strict total order over $\mathcal {L}$ is defined as a binary relation, $\succ$, on a set $\mathcal {L}$ (Chankong and Haimes 2008), which is:

• 1. Irreflexive: $\lambda _a\nsucc \lambda _a$

• 2. Transitive: $\lambda _a\succ \lambda _b$ and $\lambda _b\succ \lambda _c$ implies $\lambda _a\succ \lambda _c$

• 3. Asymmetric: if $\lambda _a \succ \lambda _b$ then $\lambda _b\nsucc \lambda _a$¹

• 4. Connected: For any $\lambda _a,\lambda _b$ in $\mathcal {L}$, either $\lambda _a\succ \lambda _b$ or $\lambda _b\succ \lambda _a$

A strict ranking (Vembu and Gärtner 2010), a complete ranking (Dembczynski et al. 2010), or simply a ranking can be represented by a strict total order over $\mathcal {L}$. A strict total order can also be represented as a permutation $\pi$ of the set $\{1, \ldots , k\}$, such that $\pi (a)$ is the position, or rank, of $\lambda _a$ in $\pi$. For example, the strict total order $\lambda _3 \succ \lambda _1 \succ \lambda _2 \succ \lambda _4$ can be represented as $\pi =\left( 2,3,1,4\right)$.

However, in real-world ranking data, we do not always have clear and unambiguous preferences, i.e. strict total orders (Brandenburg et al. 2013). Hence, sometimes we have to deal with indifference (Brinker and Hüllermeier 2007) and incomparability (Cheng et al. 2010). For illustration purposes, let us consider a survey where a set of $n$ consumers rate $k$ sushi types. If a consumer feels that two sushi types have identical taste, then these can be expressed as indifferent so they are assigned the same rank (i.e. a tie).

To represent ties, we need a more relaxed setting, called non-strict total orders, or simply total orders, over $\mathcal {L}$, by replacing the binary strict order relation, $\succ$, with the binary partial order relation, $\succeq$ where the following properties hold (Chankong and Haimes 2008):

• 1. Reflexive: $\lambda _a\succeq \lambda _a$

• 2. Transitive: $\lambda _a\succeq \lambda _b$ and $\lambda _b\succeq \lambda _c$ implies $\lambda _a\succeq \lambda _c$

• 3. Antisymmetric: $\lambda _a \succeq \lambda _a$ and $\lambda _b\succeq \lambda _a$ implies $\lambda _a=\lambda _b$

• 4. Connected: For any $\lambda _a,\lambda _b$ in $\mathcal {L}$, either $\lambda _a\succeq \lambda _b$, $\lambda _b\succeq \lambda _a$ or $\lambda _b=\lambda _a$

These non-strict total orders can represent partial rankings (rankings with ties) (Vembu and Gärtner 2010). For example, the non-strict total order $\lambda _1 \succ \lambda _2 = \lambda _3 \succ \lambda _4$ can be represented as $\pi =\left( 1,2,2,3\right)$.

Additionally, real-world data may lack preference data regarding two or more labels, which can be defined as incomparability (Chiclana et al. 2009). Continuing with the sushi survey, if a consumer never tried one or two sushi types, $\lambda _a$ and $\lambda _b$, it leads to incomparability, $\lambda _a \perp \lambda _b$. In other words, the consumer cannot decide whether the sushi types are equivalent or select one as the preferred, because he never tasted at least one of them. In this cases, we can use partial orders.

Partial orders Similar to total orders, there are strict and non-strict partial orders. Let us consider the non-strict partial orders (which can also be referred to as partial orders) where the binary relation, $\succeq$, over $\mathcal {L}$ is (Chankong and Haimes 2008):

• 1. Reflexive: $\lambda _a\succeq \lambda _a$

• 2. Transitive: $\lambda _a\succeq \lambda _b$ and $\lambda _b\succeq \lambda _c$ implies $\lambda _a\succeq \lambda _c$

• 3. Antisymmetric: $\lambda _a \succeq \lambda _a$ and $\lambda _b\succeq \lambda _a$ implies $\lambda _a=\lambda _b$

We can represent partial orders with subrankings (Henzgen and Hüllermeier 2014) or incomplete rankings (Cheng et al. 2010). For example, the partial order $\lambda _1 \succ \lambda _2 \succ \lambda _4$ can be represented as $\pi =\left( 1,2,0,3\right)$, where 0 represents $\lambda _1, \lambda _2, \lambda _4 \perp \lambda _3$.

Several learning algorithms proposed for modeling Label Ranking data can be grouped as decomposition-based or direct (de Sá et al. 2018). Decomposition methods divide the problem into several simpler problems (e.g., multiple binary problems). An example is ranking Ranking by Pairwise Comparisons (RPC) (Fürnkranz and Hüllermeier 2003), which decomposes the LR problem into a set of binary classification problems. A learning method is trained with all examples for which either a pairwise comparison (or pairwise preference) $\lambda _i \succ \lambda _j$ or $\lambda _j \succ \lambda _i$ is known (Fürnkranz and Hüllermeier 2003). The resulting predictions are then combined to predict a total or partial ranking (Cheng et al. 2013). Direct methods, on the other hand, treat the rankings as target objects without any decomposition. Examples of that include decision trees (Todorovski et al. 2002; Cheng et al. 2009), k-Nearest Neighbors (Brazdil et al. 2003; Cheng et al. 2009) and the linear utility transformation (Har-Peled et al. 2002; Dekel et al. 2003).

Consensus ranking When dealing with sets of rankings, as permutations or total/partial orders, it is often useful to define a consensus ranking. A consensus ranking can be seen as an overall ranking that has the highest agreement with a given set of rankings (Cook et al. 2007). Different methods to derive the consensus ranking can be found in the literature (Sculley 2007; Svendová and Schimek 2017). For example, in Cook et al. (1996) a consensus ranking for players is proposed as the ranking which deviates the least from the outcomes in the tournament.

In the context of Label Ranking it is common to use the average ranking as the consensus ranking (Brazdil et al. 2000). The average ranking is obtained by computing the average of the ranks, where the label with the lowest values is ranked in first place, and so on.

3 Subgroup discovery and exceptional model mining

Subgroup discovery (SD) (Klösgen and Zytkow 2002) is a data mining framework that seeks subsets of the dataset (satisfying certain user-specified constraints) where something exceptional is going on. In SD, we assume a flat-table dataset D, which is a bag of $n$ records of the form $x=(a_1,\ldots ,a_m,t_1,\ldots ,t_\ell )$. We call $\{a_1,\ldots ,a_m\}$ the descriptors and $\{t_1,\ldots ,t_\ell \}$ the targets, and we denote the collective domain of the descriptors by $\mathcal {A}$. We are interested in finding interesting subsets, called subgroups, that can be formulated in a description language $\mathcal {D}$. In order to formally define subgroups, we first need to define the following auxiliary concepts.

Definition 1

(Pattern and coverage) Given a description language $\mathcal {D}$, a pattern $p\in \mathcal {D}$ is a function $p:\mathcal {A}\rightarrow \{0,1\}$. A pattern p covers a record x iff $p(a_1,\ldots ,a_m)=1$.

Patterns induce subgroups, and subgroups are associated with patterns, in the following manner.

Definition 2

(Subgroup) A subgroup corresponding to a pattern p is the bag of records $S_p\subseteq D$ that p covers:

$$\begin{aligned} S_p=\left\{ x\in D\;\mid \;p\left( a_1,\ldots ,a_m\right) =1\right\} \end{aligned}$$

The exact choice of the description language is left to the domain expert or analyst. A typical choice is the use of conjunctions of conditions on attributes. Restricting the findings of SD from all subsets to only subgroups that can be defined in such a way, yields results of the following form:

$$\begin{aligned} \text {Age}\ge 30\;\wedge \;\text {Likes}=\text {Salmon Roe}\quad \text {is unusual} \end{aligned}$$

instead of the form:

$$\begin{aligned} S\subseteq D\quad \Rightarrow \quad \text {interesting}. \end{aligned}$$

SD delivers subgroups in a form with which the dataset domain experts are familiar. In other words, the focus of SD lies on delivering interpretable results.

Formally, the interestingness of a subgroup can be measured using any characteristics available from its associated pattern. In practice, it depends on the task we are trying to solve. Therefore, we should define one or more quality measures to assess the interestingness we want to explore.

Definition 3

(Quality Measure) A quality measure is a function $\varphi :\mathcal {D}\rightarrow \mathbb {R}$.

In the most common form of pattern mining, frequent itemset mining (Agrawal et al. 1996), interestingness is measured by the frequency of the pattern. Subgroup discovery (Klösgen and Zytkow 2002), on the other hand, measures interestingness in a supervised form. One designated target variable $t_1$ is identified in the dataset, and subgroup interestingness is measured by an unusual distribution of that target. Hence, considering that a survey revealed that the majority of Japanese people like Fatty tuna sushi, an interesting subgroup could refer to a group of people for which the majority prefers Tuna roll:

$$\begin{aligned} \text {Age}\ge 30\;\wedge \;\text {Lives in region}=\text {Hokkaido}\quad \Rightarrow \quad \text {Likes}=\text {Tuna roll} \end{aligned}$$

If instead of a single target, multiple targets $t_1,\ldots ,t_\ell$ are available, and if we are not interested in finding unusual target distributions, but unusual target interactions, we can employ Exceptional Model Mining (EMM) (Duivesteijn 2013; Duivesteijn et al. 2016) instead of SD. EMM is instantiated by selecting two things: a model class and a quality measure. Typically, a model class is defined to represent the unusual interaction between multiple targets we are interested in. A specific quality measure that employs concepts from that model class must be defined to express exactly when an interaction is unusual and, therefore, interesting. For example, suppose that there are two target attributes: a person’s height ($t_1$), and the average height of his/her grandparents ($t_2$). We may be interested in the correlation coefficient between $t_1$ and $t_2$. In this case, we would use EMM with the correlation model class (Leman et al. 2008). Given a subgroup $S\subseteq D$, we can estimate the correlation between the targets within this subset by the sample correlation coefficient.

For very small subgroups, one easily finds an unusual distribution of the target. Hence, to favor larger subgroups, one defines the quality measure such that it balances the exceptionality of the target distribution with the size of the subgroup.

3.1 Search strategy

In the EMM process, we explore a large search space, guided by a user-defined quality measure that expresses the type of exceptionality we seek. Typically, subgroups are found by a level-wise search through attribute space (Duivesteijn 2013). However, we consider the exact search strategy to be a parameter of the algorithm.

EMM strives to find descriptions that satisfy certain user-specified constraints. Usually these constraints include lower bounds on the quality of the description and size of the induced subgroup. More constraints may be imposed as the question at hand requires; domain experts may for instance request an upper bound on the complexity of the description.

Most SD algorithms traverse the search space of candidate descriptions in a general-to-specific way: they treat the space as a lattice whose structure is defined by a refinement operator $\eta :\mathcal {D}\rightarrow 2^\mathcal {D}$. This operator determines how descriptions can be extended into more complex descriptions by atomic additions. Most applications (including ours) assume $\eta$ to be a specialization operator: every description $q\in \mathcal {D}$ that is an element of the set $\eta (p)$, is more specialized than the description p itself. The algorithm results in a ranked list of descriptions (or the corresponding subgroups) that satisfy the user-defined constraints.

In this EMM setting, a greedy best-first search strategy is chosen. At each level, the descriptions according to our quality measure $\varphi$ are sorted, and refined to create the candidate descriptions for the next level. We define constraints on single attributes and define the corresponding subgroups as those records satisfying each one of those constraints. The search is constrained by an upper bound on the complexity of the description (also known as the search depth, $d$) and a lower bound on the support of the corresponding subgroup. Due to its greediness, this search strategy provides no guarantee of optimality (Heusner et al. 2017).

3.1.1 Best-first search algorithm in EMM

In Algorithm 1, we outline the pseudo-code of the Best-first search algorithm for EMM. In this code, we assume that there is a subroutine called satisfiesAll that tests whether a candidate description satisfies all conditions in a given set (to allow, for instance, the domain expert to express constraints on the resulting descriptions, such as a bounded complexity). The PriorityQueue() is a queue, with unbounded length, where the elements are stored and sorted with the corresponding quality; One elementary operation, insert_with_priority, is for adding an element to the PriorityQueue.

The resultSet is a PriorityQueue maintaining the descriptions ordered by the quality measure. Nothing is ever explicitly removed from the resultSet. Hence, the resultSet maintains the final result that we seek. When all candidates have been explored or the maximum time is exceeded, the execution ends.

3.2 Distribution rules

Distribution Rules (DR) is a SD method that analyzes a single target variable. However, rather than a representative value (e.g., the mean), DR identify unusual distributions of the target (Jorge et al. 2006; Lucas et al. 2007). The approach finds subgroups, expressed as association rules with a statistical distribution on the consequent. A DR may be formally defined as:

$$\begin{aligned} S \rightarrow t = Dist_t|A \end{aligned}$$

where S is a set of conditions corresponding to the antecedent part of a DR (a subgroup), t is a property of interest (or target) and $Dist_t|S$ is an empirical distribution of t when S is observed. $Dist_t|S$ is represented by a set of pairs $\left\langle t_i,freq\left( t_i\right) \right\rangle$, where $t_i$ is one particular value of t found when S is observed and $freq\left( t_i\right)$ is the frequency of $t_i$ when the items from S are observed.

4 Exceptional preferences mining

Exactly what constitutes an interesting deviation in preferences is governed by the employed quality measure, and the target concept (binary, numeric, preferences, ...). Thus, different measures are required to evaluate different types of targets. SD approaches have been developed for binary, nominal (Abudawood et al. 2009) and numeric target variables (Jin et al. 2014; Jorge et al. 2006), for targets encompassing multiple attributes (Umek and Zupan 2011) and also distributions (Jorge et al. 2006) (Sect. 3.2). However, none of these approaches is able to capture all the sets of preferences that can be derived from rankings within a SD framework. For that we use, exceptional preferences mining (EPM) (de Sá et al. 2016), which is the search for subgroups with deviating preferences.

In EPM, the target concept at hand consists of a single target t, which would make sense in SD. However, that target object is a ranking of labels, $\pi \in \varOmega$ (as defined in Sect. 2) which can be represented as a set of pairwise comparisons. Hence it represents interactions between multiple individual labels, which is more consistent with the EMM scenario.

Some other approaches to mine preferences and ranks can be found in the literature (Henzgen and Hüllermeier 2014; Van et al. 2014). However, these approaches tackle different problems from the one we address in this paper. In Henzgen and Hüllermeier (2014), the authors suggest an approach to mine the rankings with association rules that search for subranking patterns Our approach goes beyond this as it relates the ranking patterns with descriptors (otherwise referred to as independent variables). From a different perspective, Van et al. (2014) suggests a ranked tiling approach to search for rank patterns, whereas we are interested in the preference relations derived from the ranks.

In the Label Ranking context (Sect. 2), when the number of labels is large, the search for preference patterns can be hard to analyze and visualize. A real-world example is the Sushi dataset (Kamishima 2003), which represents the preferences of 5000 persons over 10 types of sushi. Even this relatively modest number of sushi types can be ranked in a large number of combinations. This may have a significant effect on the data, as it is shown in this dataset, where more than 98% of the 5000 rankings present in this dataset are unique. This illustrates why it can be more difficult to directly learn a ranker that associates a reliable complete ranking for any subset in the instance space, $\mathbb {X}$, when the number of labels is non-trivial.

4.1 Preference matrix

Before we discuss the approach in detail, we introduce an alternative representation of rankings that can be useful to look for different categories of exceptionality. Let us define a function, $\omega$, assigning a numeric value to the pairwise comparison of the labels $\lambda _i$ and $\lambda _j$:

$$\begin{aligned} \omega \left( \lambda _i,\lambda _j\right) = \left\{ \begin{array}{ll} 1 &{} \text{ if } \lambda _i \succ \lambda _j (\lambda _i \text{ preferred } \text{ to } \lambda _j) \\ -1 &{} \text{ if } \lambda _i \prec \lambda _j (\lambda _j \text{ preferred } \text{ to } \lambda _i) \\ 0 &{} \text{ if } \lambda _i \sim \lambda _j (\lambda _i \text{ indifferent } \text{ to } \lambda _j) \\ n/a &{} \text{ if } \lambda _i \perp \lambda _j (\lambda _i \text{ incomparable } \text{ to } \lambda _j) \end{array} \right. \end{aligned}$$

Note that, by definition, $\omega \left( \lambda _i,\lambda _j\right) = - \omega \left( \lambda _j,\lambda _i\right)$.

4.1.1 Preference matrix of one ranking

We can use $\omega$ to represent a ranking $\pi$ as a Preference Matrix (PM), $M_\pi$:

$$\begin{aligned} M_{\pi }\left( i,j\right) = \omega _{\pi }\left( \lambda _i,\lambda _j\right) \end{aligned}$$

$M_\pi$ is, by definition, an antisymmetric matrix with trace equal to zero, $tr\left( M_\pi \right) =0$. PMs can represent partial or incomplete orders but can also be aggregated to represent sets of rankings from an entire dataset D or subgroup S.

If needed, one can also derive a ranking from a PM. How to do so is a non-trivial question, which has received some attention in research fields with similar types of matrices (Hüllermeier et al. 2008). The straightforward way is to sum the rows of the PM and then assign a score to each corresponding label. Higher values correspond to a relatively more preferred label.

In terms of the complexity of the generation of PMs, it is basically a pairwise decomposition problem. Therefore, the complexity is $\mathcal {O}\left( k^2 \right)$ per matrix, where $k$ is the number of labels in the ranking. Even though any number of labels is theoretically permitted in label ranking, in practice the number of labels is usually smaller than 20. Hence, the computational cost of generating PMs should not be a problem.

4.1.2 Preference matrix of a set of rankings

To represent sets of rankings with a PM, for example a dataset D or subgroup S, the entries of $M_{\pi }$ need to be aggregated. In this work we only consider aggregations with the mean or the mode. In the presence of incomplete rankings, some $M_\pi$ will have entries with one or more n / a. In that case, the entries are ignored. For example, let us consider a set of $n$ rankings in a dataset D and the mean as the aggregation metric. We define the aggregated $M_{D}$ as:

$$\begin{aligned} M_{D}\left( i,j\right) = \frac{1}{n_{val}} \displaystyle \sum \limits _{\pi \in D} M_{\pi }\left( i,j\right) \end{aligned}$$

where $M_{\pi }$ is the PM of ranking $\pi$ and $1\le n_{val}\le n$ is the number of entries which are not n / a. In the extreme case where all the entries are n / a, $M_{D}\left( i,j\right) = n/a$.

Alternatively, one can also aggregate $M_{D}$ or $M_{S}$ using the mode.² That is, several modes are used to represent the preferences of a population D or a subgroup S. In this case, $M_{S}$ represents the most frequent occurring values contained in the entries of the set of $M_{\pi }, \pi \in S$. In cases where two or more modes per entry are obtained, the median is used.

For illustration, let us consider the PM of the example dataset $\hat{D}$ (cf. Table 1):

$$\begin{aligned} M_{\hat{D}}= \begin{bmatrix} 0&0&0&0.5 \\ 0&0&-1&0 \\ 0&1&0&1 \\ -0.5&0&-1&0 \\ \end{bmatrix} \end{aligned}$$

This representation enables easy detection of partial order relations in a set. If entry $M_{\hat{D}}\left( i,j\right) =1$ or $M_{\hat{D}}\left( i,j\right) =-1$, then we can conclude that all rankings in $\hat{D}$ agree that $\lambda _i\succ \lambda _j$ or $\lambda _i\prec \lambda _j$, respectively. If row i has all the values very close to 1, then $\lambda _i$ is systematically preferred to the remaining labels in the corresponding dataset.

Table 1 Example dataset $\hat{D}$

The records in the illustrative dataset $\hat{D}$ contain distinct total orders (Table 1). But its PM clearly shows that $\lambda _3$ is always preferred to $\lambda _2$ ($M_{\hat{D}}\left( 3,2\right) =1$). This information can be easily obtained from the PM, but is hard to read directly from Table 1. Even though, if we analyze carefully, $\lambda _3$ is always preferred to $\lambda _2$, this pattern is based on different ranks, namely, $3 > 1$, $2 > 1$, $4 > 2$ and $3>2$. Thus, unless one is looking specifically for this pattern, it would be quite hard to find. In real datasets, with more examples and labels, the task would be even harder. Conversely, $\lambda _4$ is never preferred to $\lambda _3$, which is represented by $M_{\hat{D}}\left( 4,3\right) =-1$. In some cases, the overall trend is not as clear (e.g., $\lambda _1$ is preferred to $\lambda _4$ but not always) and in other cases, there is no trend at all (e.g., $\lambda _1$ and $\lambda _2$).

Representing a set of rankings as a PM has another advantage over the traditional permutation representation. On a PM, we can naturally derive a varied set of metrics to search for preference patterns in a set of rankings by characterizing parts of the matrix. For example, it enables simple labelwise (by rows/columns of the PM) and pairwise (by single entries of the PM) analysis of preferences (see Sect. 4.3).

On the other hand, PMs can also have limitations in comparison to the traditional representations, like permutations. In particular, the choice of the aggregation metrics can hide relevant information in the PMs. For example, when using the mean, if half of the rankings have the opposite order of the other half (e.g., $\lambda _1\succ \lambda _2\succ \lambda _3\succ \lambda _4$ and $\lambda _4\succ \lambda _3\succ \lambda _2\succ \lambda _1$) this results in a PM with all entries equal to zero. Because the same happens when all rankings are complete ties, there is no way for the method to detect this difference in the preferences. Therefore, in an attempt to mitigate this, subgroups with a PM containing only zeros are ignored. That is, only subgroups for which we can infer at least one pairwise preference can be considered interesting in this exceptional preferences mining approach.

Finally, to aid in the interpretation of ranking trends within subgroups we use a visual representation of the PMs that is a set of colored tiles (Fig. 1). Each tile represents an entry of the PM. The entries of a PM can vary from $-1$ to 1. The negative entries of the matrix are represented with red tiles, the positive with green tiles, and 0 is represented in white. The colored tiles fade out as they get closer to 0.

Fig. 1

PM representation of the set of rankings in $\hat{D}$ (cf. Table 1). Dark green tiles represent 1 and dark red tiles represent − 1 (Color figure online)

4.2 Characterizing ranking exceptionality

In EPM, we want to search for exceptional preference (or ranking) behavior. Because preferences are represented with rankings, we can distinguish three categories of exceptionality concerning rankings: rankingwise, labelwise and pairwise.

Measures that fall into the first category, rankingwise, will use all the entries of the PM, and therefore, benefit subgroups with exceptional complete rankings. This is, if the average ranking of the population is $\lambda _1\succ \lambda _2\succ \lambda _3\succ \lambda _4$, subgroups with an average ranking of $\lambda _4\succ \lambda _3\succ \lambda _2\succ \lambda _1$ will be deemed the most interesting. However, finding a reasonable set of rankingwise exceptional preferences can be challenging in some cases. Considering the example of the Sushi dataset mentioned before, with more than 98% of unique rankings, it will be difficult to observe unusual complete rankings that occur very frequently, due to the low number of ranking repetitions.

Labelwise measures, are less restrictive and focus on rows/columns of the PMs. Therefore, they look for subgroups where at least one label is unusually ranked higher (or lower) in comparison to the whole population. The preferences of these subgroups can be represented as incomplete rankings. Considering a population where we observe that $\lambda _1,\lambda _2,\lambda _3\succ \lambda _4$, therefore, subgroups where $\lambda _4\succ \lambda _1,\lambda _2,\lambda _3$ will be interesting. Note that, the following list of complete rankings agree with $\lambda _4\succ \lambda _1,\lambda _2,\lambda _3$ : $\lambda _4\succ \lambda _3\succ \lambda _2\succ \lambda _1$, $\lambda _4\succ \lambda _2\succ \lambda _3\succ \lambda _1$, $\lambda _4\succ \lambda _3\succ \lambda _1\succ \lambda _2$, $\lambda _4\succ \lambda _1\succ \lambda _2\succ \lambda _3$ and $\lambda _4\succ \lambda _1\succ \lambda _3\succ \lambda _2$. As an example, if a subgroup ranks $tekka-maki$ consistently in the top 3 while the majority in the dataset ranks it in the last 3, this type of measures will find it to be very interesting.

Finally, pairwise measures pick single entries of the PM, which makes them look for unusual pairwise preferences. Considering a population where the majority agrees that $\lambda _1\succ \lambda _4$, any subgroup where most of the subjects agree that $\lambda _4\succ \lambda _1$ will be considered very interesting. This means that, if a population displays this preference $tamago \succ kappa-maki$, a subgroup where most people prefer $kappa-maki \succ tamago$ will be deemed interesting by these type of measures. Our assumption is that, even though over 98% of the total rankings in the Sushi dataset are unique, there is plenty of information present in these rankings: the partial orders and pairwise comparisons can reveal interesting subgroups.

4.3 Characterizing exceptional subgroups

In this section we formally define the quality measures for EPM, which evaluate how exceptional the preferences are in the subgroups. A subgroup can be considered interesting both by the amount of deviation (distance) and by its size (number of records covered by the subgroup, as discussed in Sect. 3) (Dzyuba and van Leeuwen 2013). Since, reasonable quality measures should take both these factors into account, we divide the quality measures into two parts: the distance component and the size component.

$$\begin{aligned} QM_S = size_S \cdot distance_S \end{aligned}$$

In order to allow direct comparisons between different quality measures, both components are normalized to the interval $\left[ 0,1\right]$. A common measure for the size in subgroup discovery is $\sqrt{s}$ (Klösgen 1996), where $s$ is the size of the subgroup. To normalize, we use the square root of the fraction of the dataset covered by S: $size_S=\sqrt{s/n}$.

Before introducing the distance components, let us first define a distance (or difference) matrix $L_S$, as the distance matrix between two PMs, $M_S$ and $M_D$:

$$\begin{aligned} L_S = \frac{1}{2}\left( M_D-M_S\right) \end{aligned}$$

where $S\subseteq D$ (the division by 2 limits the distance to the interval $\left[ -1,1\right]$). We can measure different properties of $L_S$ and represent them with a numeric value. This way we get an indicator of the quality of the distance of preferences for a subgroup. Consider the subgroup $\hat{S_1}: A_1 \ge 0.3$, which covers the last two cases from our example dataset $\hat{D}$. Its PM is:

$$\begin{aligned} M_{\hat{S_1}}= \begin{bmatrix} 0&1&1&1 \\ -1&0&-1&0 \\ -1&1&0&1 \\ -1&0&-1&0 \\ \end{bmatrix} \end{aligned}$$

The first row clearly reveals that $\lambda _1$ is always preferred to all other labels in this subgroup. If we compute the distance matrix $L_{\hat{S_1}}$ we get:

$$\begin{aligned} L_{\hat{S_1}}= \begin{bmatrix} 0&-0.5&-0.5&-0.25 \\ 0.5&0&0&0 \\ 0.5&0&0&0 \\ 0.25&0&0&0 \\ \end{bmatrix} \end{aligned}$$

Thus, the distance matrix $L_{\hat{S_1}}$ confirms that the behavior of $\lambda _1$ is exceptional in $\hat{S_1}$ while for the other labels, the behavior is the same as in the original dataset.

4.4 Quality measures

In this section we introduce the quality measures used in this work. We propose 4 quality measures: 2 rankingwise, 1 labelwise and 1 pairwise (Sect. 4.2). We describe 3 previously proposed measures (de Sá et al. 2016) and introduce a new one.

As we are interested in subgroups with exceptional preferences, we should be able to measure a preference distance. For that we can use the distance matrix $L_S$. The distance measures we employ, typically consider a particular subset of the entries of the distance matrix $L_S$. Because rankings have inter-label relations that can be explored (Henzgen and Hüllermeier 2014), there are many ways to tackle this, for example, to use less restrictive measures to look for unusual behaviors of partial rankings.

To the best of our knowledge, as in most EMM approaches (Leeuwen and Knobbe 2012), none of the following quality measures are guaranteed of having anti-monotonicity properties.

4.4.1 Rankingwise measures

Rankingwise quality measures should prefer subgroups whose average rankings are very different to the average ranking of the complete dataset, i.e. maximizing the distance between complete rankings.

Rankingwise norm If one is searching for subgroups whose average ranking is as close as possible to the inverse ranking of the population, one should use the Rankingwise Norm quality measure, RWNorm. Given a set of subgroups with same size, this measure gives the highest score to subgroups whose rankings are the inverse of the population.

In other words, this is done by maximizing all the entries of the distance matrix $L_S$. Maximizing the distance of preferences is also maximizing the magnitude of $L_S$. The most fundamental mathematical way to measure the magnitude of a vector or matrix is the norm. Hence we can use the Frobenius norm of $L_S$ as a distance measure.

$$\begin{aligned} \text {RWNorm}(S) = \sqrt{s/n} \cdot ||L_S||_F = \sqrt{s/n} \cdot \sqrt{\displaystyle \sum \nolimits _{i=1}^{k}\displaystyle \sum \nolimits _{j=1}^{k} L_S\left( i,j\right) ^2 } \end{aligned}$$

As mentioned in Sect. 4.1.2, the PMs can be aggregated with mean or the mode. That is, the entries of the PMs of the dataset, $M_D$, and the subgroup, $M_S$, are aggregated with the mode. Therefore, a different distance matrix $L_S$ is measured. To make clear when we use the mode, we refer to $RWNorm-Mode$.

Rankingwise covariance Covariance is used in statistics to measure the extent to which two variables change in comparison with each other. In simple terms, a positive value indicates that when one increases, the other also increases. If they behave in opposite directions, the covariance is negative.

As in RWNorm, we are interested in subgroups with complete rankings that contradict the preferences in the general population. Hence, we can use covariance to measure the deviations of preferences. The entries of a row in the PM $M_S$ represent how a label relates to the remaining labels in the subgroup S. By abuse of notation, the rows of $M_S$ and $M_D$ can be seen as independent variables, which allows us to measure the covariance between labels. That is, we can compare the PM values of a label in a subgroup S with the corresponding values of the same label in D using their covariance.

Since our aim is to find opposite preferences in comparison to the population, we are interested in a negative covariance:

$$\begin{aligned} RWCov\left( S \right) = - \sqrt{s/n} \cdot cov\left( vec\left( M_D\right) , vec\left( M_S\right) \right) \end{aligned}$$

Where, $vec\left( M_D\right)$ and $vec\left( M_S\right)$ stands for the vectorization of matrices $M_D$ and $M_S$ respectively. As mentioned in Sect. 4.1, the PMs are antisymmetric, which implies that the average of the entries is always zero. Hence it does not matter if one includes the diagonal or not in this particular case.

In comparison to RWNorm, we expect this measure to be more conservative because it requires that most of the entries behave in opposite directions. On the other hand, this measure is better at distinguishing one subgroup whose overall deviation is due to one label deviating strongly and the others not so much, from one where all labels have small deviations.

4.4.2 Labelwise measures

The fact that only one label behaves differently, disregarding the interaction between the other labels, can also be interesting (Cheng et al. 2013). Therefore, it is useful to define labelwise measures that look for subgroups where a label shows unusual behavior. Depending on the application at hand, a subgroup can be considered interesting when at least one label is under- or over-appreciated in comparison to the population. For example, a data analyst might be interested in finding subgroups where the preference for a particular type of sushi is substantially different, when compared to the population.

Labelwise norm We can measure the preference distance of each label, in a subgroup S, by computing the norm of the rows from $L_S$. This measure considers only the maximum value of the set of rows, hence high values of the measure indicate that, at least, one label behaves differently:

$$\begin{aligned} \text {LWNorm}(S) = \sqrt{s/n} \cdot \max \limits _{i=1,\ldots , k}\sqrt{\displaystyle \sum \nolimits _{j=1}^{k} L_S\left( i,j\right) ^2} \end{aligned}$$

Other examples of labelwise measures could be, for example, a variant of this one, but based on the second highest score by label. In that case, it would find subgroups where at least 2 labels are behaving in an unusual way.

4.4.3 Pairwise measures

In PL, Pairwise Preferences (Hüllermeier et al. 2008) are often the focus of the analysis, decomposing the preferences into pairs label-vs-label. In EPM, if we are interested in subgroups with at least one pair of labels with distinctive preference behavior we can use pairwise measures.

Pairwise max We can employ the following pairwise quality measure:

$$\begin{aligned} \text {PWMax}(S) = \sqrt{s/n} \cdot \max \limits _{i,j=1,\ldots , k} |L_S\left( i,j\right) | \end{aligned}$$

This quality measure is the least restrictive of this set: a subgroup is interesting if one pair of labels interacts unusually, disregarding all other label interactions.

One alternative pairwise measure could be the pairwise minimum, which would provide the lower bound of PWMax for each subgroup.

4.5 Tackling false discoveries

In SD, one aims to find subsets of the dataset that are interesting in some sense. As such, the space of candidates to be considered for what essentially amounts to a statistical test is vast. Hence, SD suffers from the multiple comparisons problem (Hochberg and Tamhane 1987): when testing a large number of a null hypotheses, by definition, some will incorrectly be rejected. Namely, with a significance level of $\alpha$, $\alpha$ out of each 100 null hypotheses tested are expected to be incorrectly rejected.

For supervised local pattern mining, to which SD belongs, a swap-randomization-based statistical test procedure has been developed (Duivesteijn and Knobbe 2011). First, a number of copies of the original dataset is generated, and in each of the copies the target attributes are swap randomized. All other attributes are kept intact. This means that the search space of the mining algorithm and the distribution of the targets remains intact, but the connections between the search space and the target space are broken. The procedure then involves running the algorithm to be tested on each copy of the dataset, and reporting the best subgroup found, according to the selected quality measure. Any subgroup that is found on such a copy of the dataset is interesting only because of random effects. Hence, these are artificially generated false discoveries. The procedure then builds a global model over the artificial false discoveries, the so-called Distribution of False Discoveries (DFD). Then, the subgroups found on the original dataset can be assigned a p value, corresponding to the null hypothesis that a subgroup with this quality is generated by the same process that generated the DFD. Refuting the null hypothesis essentially refutes the hypothesis that the subgroup found is a false discovery.

The DFD validation procedure has only one parameter: the number of dataset copies. This number must be large enough to satisfy certain conditions arising in the global modeling involved in creating the DFD. As noted in Duivesteijn and Knobbe (2011), typically, 100 copies are enough.

5 Experiments

In this section we start with a description of the experimental setup (Sect. 5.1), then we present some statistics of the datasets used (Sect. 5.2). Then we present the results obtained (Sect. 5.3) and finally we compare our findings with the results of an alternative approach (Sect. 5.4).

5.1 Implementation and experimental setup

We incorporate exceptional preferences mining in the Cortana³ software package (Meeng and Knobbe 2011). This package delivers a generic framework for SD, implements several SD instances, and offers many generic features allowing for different SD approaches. The description language consists of logical conjunctions of conditions on single attributes.

Our experiments use a greedy best-first search approach (Algorithm 1). The numeric strategy used for this experiments is an on the fly discretization approach of 8 equal-width bins. For every extreme of the bin we use a set of numeric operators such as $\ge$ and $\le$.

All the findings we present in this paper have gone through the DFD validation procedure (Sect. 4.5) with 100 copies, and all have been found significant at a significance level of $\alpha =1$%.

All the subgroups presented in this manuscript were found in less than 3 minutes of execution time, on an Intel Core i7 5500U CPU @ 2.40GHz with 16GB of RAM. The DFD validation procedure, for depths bigger than 4 can take more than 30 minutes, depending on the dataset.

5.2 Datasets

To illustrate domain-specific interpretation of the results, we experiment with some real-world datasets (Table 2). The Algae dataset⁴ is based on the COIL 1999 Competition Data from UCI (Lichman 2013). This dataset concerns the frequencies of algae populations in different environments. This dataset consists of 340 examples, each representing measurements of a sample of water from different European rivers in different periods. The measurements include concentrations of chemical substances such as nitrogen (in the form of nitrates, nitrites and ammonia), oxygen and chlorine. Also the pH, season, river size and flow velocity are registered. For each sample, we have the preference relations of 7 types of algae which represent the concentrations ordered from larger to smaller concentrations. Those with 0 frequency are placed in last position and equal frequencies are represented with ties. Missing values are set to 0.

The Sushi preference dataset (Kamishima 2003), is composed of demographic data about 5000 people and their sushi preferences. Each person sorted a set of 10 different sushi types by preference. The 10 types of sushi, are (a) shrimp, (b) sea eel, (c) tuna, (d) squid, (e) sea urchin, (f) salmon roe, (g) egg (h) fatty tuna, (i) tuna roll and (j) cucumber roll.

The Top7movies dataset is a subset of the MovieLens 1M Dataset (Harper and Konstan 2016).⁵ The original dataset has 1 million ratings from 6000 users on 4000 movies. For each user, we have its demographic data, such as gender, age, occupation and zipcode. Using the zipcode R package (Breen 2012), we obtained the city, state, latitude and longitude related to the given zipcodes of the users. We selected the subset of users which have rated all the 7 most rated movies. This means that, in the end we obtained demographic data and a ranking of 7 movies per user. The labels in this dataset represent the following movies:

• a) American Beauty (1999)

• b) Star Wars: Episode IV—A New Hope (1977)

• c) Star Wars: Episode V—The Empire Strikes Back (1980)

• d) Star Wars: Episode VI—Return of the Jedi (1983)

• e) Jurassic Park (1993)

• f) Saving Private Ryan (1998)

• g) Terminator 2: Judgment Day (1991)

Examples which contained rankings with complete ties were removed.

We also study data with socio-economic information from regions of Germany and its electoral results, the datasets GermanElections2005 and GermanElections2009. The 413 records correspond to the administrative districts of Germany, which are described by 39 attributes. Both datasets are parts of data which was extracted from a publicly available database of the German Federal Office of Statistic (Boley et al. 2013). A similar study has been presented in Grosskreutz et al. (2010), but restricted to the city of Cologne.

In terms of independent attributes we have: age and education of the population, economic indicators (e.g., GDP growth, percentage of unemployment), indicators of the labor workforce in different sectors such as production, public service, etc. In terms of the target, we transformed the election results of the five major political parties for the federal elections in 2005 and 2009 into rankings. In this dataset the labels represent:

• a) CDU (conservative)

• b) SPD (center-left)

• c) FDP (liberal)

• d) Green (center-left)

• e) Left (left-wing)

We also choose to experiment with a Label Ranking dataset from the Data Repository of Paderborn University,⁶ since this set of data is well-known in the preference learning community (Cheng et al. 2009). In particular, we use the Cpu-small dataset which was transformed from a regression dataset (Cheng et al. 2009). The target ranking, with 5 labels, was derived for each example from the order of the values of 5 numerical variables (which are then no longer used as independent variables). In the process, the features were normalized, and its names replaced by $A1, A2, \ldots , A_6$. Therefore, in this case, the reported subgroups cannot be interpreted as in the original dataset domain.

Table 2 Dataset details

The percentage of unique rankings $U_\pi$ (Table 2) measures the proportion of distinct rankings in the dataset:

$$\begin{aligned} U_\pi = \frac{\#\text {distinct rankings}}{n} \end{aligned}$$

where $n$ is the size of the data. We also show the expected number of different rankings given $n$ examples, $E\left( U_\pi \right)$. This is, if we randomly pick $n$ rankings of a fixed size $k$, we should expect $E\left( U_\pi \right)$ rankings. By comparison with $U_\pi$ we can have an idea if there are any biases in the behaviors of the rankings.

Considering the case of the Sushi dataset (Table 2), with an $U_\pi = 98$%, if we randomly pick 100 instances (i.e. 100 users and its rankings), we will probably have 98 distinct rankings. This means that, it will be extremely unlikely to find more than 3 users with the very same preferences. On the other hand, because the $U_\pi =98$% is close to the $E\left( U_\pi \right) =99$%, we should also not expect very strong biases in the ranking behaviors. For these reasons, we expect that it will be harder to find complete ranking patterns in this dataset.

Looking into the $E\left( U_\pi \right)$ of the two german elections datasets, their $U_\pi$ is considerably less than its expected value. This seems to indicate that, not all rankings have equal probability in this election scenario. However, because we know that in elections it is very unusual that all parties have equal chances of being in all positions, across different regions, it makes sense.

5.3 Results

In this section we show some of the most interesting results obtained with the different quality measures.

5.3.1 Study on the behavior and biases of the quality measures

With each of the introduced quality measures, one can find subgroups featuring exceptional ranking behavior. The exceptionality is measured in (sometimes subtly) different ways for the different quality measures; which quality measure one uses depends on what type of exceptional ranking one is looking for. The quality measures we have outlined in Sect. 4.4 all live at a different level of granularity: a subgroup is flagged up as interesting by the one measure if only a single pair of labels has an exceptional relative ranking, by the other measure if a single label has an exceptional ranking relative to all others, and by the last measure if overall label behavior is exceptional. This difference in scope implies that the measures are correlated, but not perfectly so. In this section, we explore the resulting differences in focus between the quality measures, to allow the user to make an informed choice.

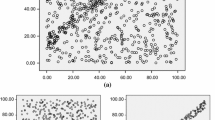
The result of this exploration is displayed in Fig. 2. We generate 10,000 random subgroups, whose scores are evaluated by all quality measures. The generation is performed by randomly combining descriptions until the maximum depth is reached. The search depth is fixed to 3, to allow some diversity of combinations. For each pair of quality measures, Fig. 2 contains a scatterplot displaying the relation of the scores.

Fig. 2

Comparison of the scores of the quality measures on random subgroups obtained on the Cpu-Small dataset

The first row shows the subgroups of RWNorm and the vertical axis represents its score. The horizontal axis represents the scores of each quality measure, in the following order: RWNorm, RWNorm-Mode, RWCov, LWNorm and PWMax. The second row shows the subgroups of RWNorm-Mode, and so on.

As expected, some quality measures have a different but congruent bias. We can observe that 3 measures have a very similar bias, RWNorm, LWNorm and PWMax. This is somewhat expected, since they basically have the same measure, but applied in different parts of the distance matrix $L_S$.

The RWNorm-Mode shows a distinct behavior from the latter group. This measure is based on a different distance matrix $L_S$, obtained from the difference between the modes of the population $M_D$ and the modes of the subgroups $M_S$. Its behavior can be explained with a simple example. Consider only one entry of $L_S$, and let us assume that 51% of the subjects of a population agree that $\lambda _a\succ \lambda _b$. Then, a reasonably-sized subgroup where 51% agree that $\lambda _b\succ \lambda _a$ and the remaining 49% agree that $\lambda _a\succ \lambda _b$, will have a very high score with this measure. In fact, in this subgroup, only 2% fewer of the subjects prefer $\lambda _a\succ \lambda _b$, compared to the overall population. For the measures RWNorm, LWNorm and PWMax, subgroups of this type will not be very interesting, unless that difference is bigger. This explains the behavior of the line on the top-left, observed on the second row of Fig. 2, where RWNorm-Mode compares to RWNorm, LWNorm and PWMax. The rest of the behavior seems to be in line with the other measures.

Table 3 Total number of significant subgroups found per dataset, with depth 1, using the different quality measures

Finally, RWCov, seems to have the most different bias. That is because it is not based on the distance matrix $L_S$; instead, it directly measures the negative correlation between the population $M_D$ and the subgroups $M_S$. Therefore, with this quality measure, we will find subgroups that do not necessarily maximize preference distance, but instead feature unusual preference behavior in a abstract sense.

Now, let us focus on the number of subgroups obtained per measure, in terms of the given datasets in Table 3. Using a best-first search to find subgroups, we compare the number of subgroups obtained, per quality measure per dataset. For simplicity, we use a search depth of 1. RWCov is, by far, the measure that identifies the least number of subgroups throughout measures and datasets. This seems to indicate that this measure is very restrictive, as expected (Sect. 4.4).

5.3.2 German elections

With the GermanElections2005 dataset, using the PWMax with a search depth of 1, we found 62 significant subgroups. The best subgroup, $\text {Region} = \text {East}$, indicates that the party with label e in comparison to the party with label c has a very different behavior from the majority. In fact, while on 75% of the districts in Germany the FDP party (label c) was more voted than the Left party (label e), on the 2005 elections, all the 87 districts from East Germany voted more on the Left party than on the FDP party. This shows a great example of an extreme inversion of preferences.

The second best subgroup obtained, compares the center-left Green party (label d) with the left-wing Left party (label e). The Green party had more votes than the Left party on 72% of the districts in Germany. On the other hand, on 88% of the districts where the average income is less or equal than 16,979, the Left party was more voted than the Green party.

To compare with the German elections of 2009, we used the GermanElections2009 dataset with the same settings and found 57 significant subgroups. As in the 2005 elections, the best subgroup shows that 100% of the districts in east Germany gave more votes to the Left party than on the Green party, in comparison to only 27% in the whole Germany. The second best subgroup, as in the 2005 case, compares the center-left Green party (label d) with the left-wing Left party (label e). However, in this case, 94% of the districts, where the average income is less or equal than 16,979, the Left party was in advantage in comparison to the Green party. Comparing to the 88% of 2005, we realize that, in 2009, 6 p.p. more districts, where the average income was $\le$16,979, increased the votes in the Left party, in comparison to the Green party.

Continuing with the GermanElections2009 and using the LWNorm with a search depth of 2, we found 2965 significant subgroups. The most relevant is expressed with a simple condition $\text {Region} = \text {East}$. This subgroup is interesting because it shows that, in most regions of East Germany, the Left party is often one of the top voted parties. In Fig. 3 we can clearly see the distribution of the ranks. We observed that, the Left party was either first or second in the elections of 2009 in 97% of the districts in East Germany. Moreover, it was 3rd place in 3% of them. Other subgroups encountered show a very similar behavior in terms of the label that represents the Left party, like:

• $\text {Children Population} \le 14.8\% \wedge \text {Income} \le 16,634$

• $\text {Children Population} \le 14.8\% \wedge \text {Unemployment} \ge 8.4$%

Fig. 3

Histograms representing the relative position of the Left party obtained in the 2009 elections of districts in Germany. In red, the subgroup $\text {Region} = \text {East}$ and in blue the distribution for all districts (Color figure online)

Fig. 4

Histograms representing the relative position of the Left party obtained in the 2009 elections of districts in Germany. In red, the subgroup $\text {Income}~\ge ~18{,}442$ and in blue the distribution for all districts (Color figure online)

On the other hand, we also found subgroups were the Left party is often the least voted party. Some examples are:

• $\text {Income} \ge 18{,}442$

• $\text {Income} \ge 17{,}791 \wedge \text {Youth unemployment} \le 8.5$%

In Fig. 4 we can visualize the distribution of $\text {Income} \ge 18442$.

Finally, in Fig. 5 we can visualize the PM of subgroups which are described by the name of the state. This visualization clearly shows some nuances in the voting behavior on the different states of Germany.

Fig. 5

PM representation of some subgroups described by the feature State in comparison to the base matrix (All districts). The subgroups are sorted by relevance (first row, first column: most relevant; second row, second column: least relevant)

From a different perspective, if we look at the average rankings of each PM from Fig. 5 we obtain:

• $CDU \succ \mathbf {Left} \succ SPD \succ FDP \succ Green$ (Thuringia)

• $\mathbf {Left} \succ \mathbf {SPD} \succ CDU \succ FDP \succ Green$ (Brandenburg)

• $\mathbf {Left} \succ CDU \succ SPD \succ FDP \succ Green$ (Saxony-Anhalt)

• $CDU \succ \mathbf {Left} \succ SPD \succ FDP \succ Green$ (Saxony)

• $CDU \succ SPD \succ FDP \succ \mathbf {Green} \succ Left$ (Bavaria)

• $CDU \succ SPD \succ FDP \succ Left \succ Green$ (All states)

We highlight (in bold) the parties which got a better relative position in the corresponding state, in comparison to the overall average ranking. As one can conclude from most of the rankings in this list, at least one party (one label), seems to have its position changed relatively to the others. This clearly shows that the method is working as expected.

This analysis, also shows the potential of EPM as a tool to study election data. By looking at different levels of granularity of the preferences, EPM does not necessarily focus on the winners, but rather on major preference shifts. Also, considering the elections application, different ranking aggregation metrics can be used to comply with the Condorcet method (de Condorcet 1785).

5.3.3 Top7Movies

With the LWNorm quality measure, we found 2 significant subgroups for a search depth of 2. The members of the first subgroup, people older than 34 years old living bellow a latitude of 32.9, seem to dislike the most voted movie American Beauty, more than usual (Fig. 6). This subgroup, includes people from different states, such as Arizona, California, Florida, Georgia, Louisiana, New Mexico, Texas and even Hawaii. An interesting conclusion we can draw, is that, this group voted in Star Wars: Episode IV—A New Hope and Saving Private Ryan with high scores.

Fig. 6

PM representation of the dataset Top7Movies (base matrix), the subgroup $Age~\ge ~35 \wedge Latitude \le 32.9$ (subgroup matrix) and the difference (difference matrix)

On the other hand they seem to dislike American Beauty and Jurassic Park. In fact, the average ranking of this subgroup is $b\succ \mathbf {f} \succ c \succ d \succ g \succ \mathbf {a} \succ e$ and the average ranking of the whole population is $b\succ c \succ \mathbf {a} \succ \mathbf {f} \succ d \succ g \succ e$.

5.3.4 Algae

With the Algae dataset, we obtain results about the concentrations of algae with the RWNorm measure. Results seem to indicate that during Spring, the species of algae a, b and c are much more common in rivers than the others species. This can be easily concluded by studying the PM representation of the subgroup (Fig. 7). On the other hand, we also see an interesting behavior during the Autumn season.

Fig. 7

PM representation of the subgroups $Season = Spring$ (left subgroup matrix) and $Season = Autumn$ (right subgroup matrix) from the Algae dataset

With the LWNorm measure, we find a bit more than 400 subgroups with maximum depth 2, the best of which is presented in Fig. 8. In the subgroup, the label a is strongly preferred over all others, while the image is much more nuanced over the whole dataset. If we ignore the label a, the PMs for both the overall dataset and the subgroup are rather bland, and their difference is not very pronounced. But for this one particular label a, the behavior on the subgroup is extremely clear-cut, and the LWNorm quality measure picks up on that effect.

Fig. 8

PM representation of the dataset Algae (base matrix) and the subgroup $V10 \le 59 \wedge V6 \le 11.87$ (subgroup matrix), with difference matrix on the right

Using a depth of 3 with the same measure, we found around 5400 subgroups. We show the best one in Fig. 9. One interesting aspect of this subgroup is that it shows an opposite behavior, in comparison to the one in Fig. 8, in terms of the label a (as it is clear from the difference matrix).

Fig. 9

PM representation of the dataset Algae (base matrix) and the subgroup $V10 \ge 137.78 \wedge V6 \ge 14.32 \wedge V9 \ge 60.83$ (subgroup matrix), with difference matrix on the right

The visual representations of the PM clearly reveal the effect of the LWNorm quality measure in this dataset. We can also observe from the description of the subgroups obtained, that the variables V10 and V6 are highly correlated with the presence of the algae a.

5.3.5 Sushi

Considering the high percentage of unique rankings in the sushi dataset (Table 2) we do not expect to find strong patterns in the whole PM, therefore, we focus on labelwise ranking patterns.

With the LWNorm measure, we find 149 subgroups on the Sushi dataset. We present the best subgroup using this measure in Fig. 10. The subgroup (Males over 30 years) shows a preference for Sea Urchin, since the majority of men rank this sushi type in the top 4. By contrast, in the whole population, more than half rate it between 5th to 10th, and every fifth person rate it in the last place.

Fig. 10

Percentage of ranks for Sea Urchin (Sushi dataset) for all individuals in comparison to the subgroup (males older than 30 years)

5.3.6 Cpu-small

On the Cpu-small dataset, we used the RWCov quality measure. Experiments with a maximum depth of 4, found 275 significant subgroups. In Fig. 11 we can visualize the PM of the most relevant subgroup found. The PM of this subgroup, of size 62, shows deviations in all the entries of the matrix, which is a good indicator that this measure is working as expected.

Fig. 11

PM representation of the dataset Cpu-small (base matrix), the subgroup $A5 \ge 0.710 \wedge A6 \ge 2.143 \wedge A3\le 0.755$ (subgroup Matrix) and the difference (difference matrix)

In terms of the rankings, the average ranking of the whole dataset is $\left( 2,4,3,1,5\right)$, and the average ranking in this subgroup is $\left( 3,1,5,4,2\right)$. The Kendall $\tau$ correlation of these two rankings is $-0.4$, which confirms the unusualness of the subgroup.

We could also observe that, despite having obtained 275 significant subgroups, there were many subgroups whose PM was very similar and showing the same unusual behavior. This could also be observed in terms of the ranking derived from their PM.

5.3.7 Comparison of different aggregation metrics

As mentioned in Sect. 4.1, different metrics can be used in the aggregation of PM. To test how this choice can affect the model, we analyzed some results were PMs are aggregated with the mode (instead of the the mean), however, for the sake of space, we only present one dataset and one quality measure, RWNorm-Mode.

Using the mode as the aggregation, RWNorm-Mode quality measure, we found 131 significant subgroups of depth 2 on the Cpu-small dataset. As a point of comparison, we obtained 155 significant subgroups, with the same settings, using the RWNorm quality measure (aggregation with the mean). Despite the similar number of subgroups found, the two groups of subgroups are quite distinct. This is somehow expected from the previous analysis of the quality measures in Sect. 5.3.1.

A striking difference is that the rankings of the subgroups from RWNorm-Mode are consistently different from the ones obtained with RWNorm. However, despite being different, the average rankings of the subgroups have a similar correlation (in terms of the Kendall $\tau$) to the average ranking of the population.⁷ In other words, the subgroups are at a similar “preference distance” from the population. This seems to indicate that RWNorm-Mode can be a complementary measure with RWNorm.

The behavior described above, is also observed on the remaining datasets presented in Table 2. For the sake of space, let us consider the best subgroup, according to RWNorm-Mode, depicted in Fig. 12. This subgroup is described by: $A4 \ge -\,0.22354$. In Fig. 12 we can observe that the difference matrix of the best subgroup has very faint colored tiles, which means that the PM is not very different from the PM of the whole dataset. On the other hand, these small differences are quite spread along the difference matrix, which, when summed up, makes it interesting too.

Fig. 12

Representation of the PMs, aggregated with the mode, of the dataset Cpu-small (base matrix), the subgroup $A4 \ge -0.22354$ (subgroup matrix) and the difference (difference matrix)

Fig. 13

Distributions of the correlation between the average ranking and each ranking belonging to the best subgroup found with RWNorm-Mode (green) and RWNorm (brown) (Color figure online)

From a different perspective, in Fig. 13 we compare the distributions of the correlation between the average ranking of the dataset and each one of the rankings that are part of the best subgroup. We measure this correlation in terms of the Kendall $\tau$ correlation coefficient. As seen in Fig. 13, the distributions are similar. This behavior was also observed in other subgroups and other datasets. Therefore, this confirms what we observed above, that RWNorm-Mode and RWNorm find different subgroups but with similar ’preference distances’.

Aggregating a PM with the mode can yield either 1, 0 or $-1$ in contrast to the mean where any value in the interval $[-1,1]$ is possible. Therefore, the mean can measure exceptionality on subgroups with the same mode as the dataset (e.g., label a in Fig. 8). On the other hand, the mode can detect subgroups where the majority of the pairs behave differently. Therefore, depending on the task, the best choice of the aggregation metric for the quality measures can change. However, we believe that the best way is to complement the use of RWNorm-Mode with RWNorm and vice versa.

5.4 Comparison with distribution rules

In this section, we compare subgroups found with our algorithm (using Cortana) with subgroups from a different approach, Distribution Rules (DR) (using CAREN Azevedo and Jorge 2010 software⁸). As mentioned before (Sect. 3.2), Distribution Rules are a SD method that looks for unusual target distributions (Jorge et al. 2006; Lucas et al. 2007). Cortana and CAREN can be used for mining other structures of data. For simplicity, in this work we refer to Cortana and CAREN as the tools with our preference learning approaches.

DR use a numeric target to construct the distributions. Since we have rankings as targets, we propose a simple way to represent individual rankings as numeric values. For each example we compute the similarity score between its ranking and the average ranking (consensus ranking Brazdil et al. 2003) of the dataset. Given that, the similarity measure that we use is the Kendall $\tau$, the new target can have values in the range $\left[ -1,1\right]$.

We show in Table 4 how the example dataset $\hat{D}$ would look like under this transformation. Considering that the average ranking of the rankings in $\hat{D}$ is: $\left( 2,3,1,4\right)$, for the second example in $\hat{D}$, we do: $\tau \left( \left( 2,3,1,4\right) , \left( 3,2,1,4\right) \right) = 0.66$.

Table 4 Example dataset $\hat{D}$ with the proposed alternative representation in the rightmost column of the table

For a fair comparison between the two methods, we discretized the numeric attributes beforehand with an equal width discretization of 8 bins. We handle the discretized numerical attributes as a nominal, not ordinal, scale. In terms of the property of interest (target), this numerical variable does not have to be previously discretized, because the method works with raw distributions (Lucas et al. 2007).

In terms of the experimental setup, we will use the same maximum search depth for both methods. In Cortana, we take the RWNorm quality measure. For each subgroup, we perform a Kolmogorov–Smirnov statistical test to compare the target distribution of the subgroup with the target distribution of the whole population. Subgroups which are deemed interesting, are the ones whose distributions differ significantly from the distribution of the whole population.

We will use the term subgroup and distribution rules interchangeably to refer to distribution rules. However, when there is the need to differentiate from subgroups found with Cortana and CAREN, we will use the terms subgroups and distribution rules, respectively.

5.4.1 German elections

With the GermanElections2009 dataset, we found 1597 significant distribution rules using CAREN and 1073 subgroups with Cortana for a search depth of 2. The most interesting distribution rules are not only in line with the subgroups found, in this experiment, but also with the ones previously discussed in Sect. 5.3.2. For the sake of simplicity, we only show the top five subgroups obtained by both approaches in Table 5. It is clear from Table 5 that the subgroups found by CAREN are very similar from the subgroups of Cortana, despite their very distinct approaches.

Table 5 Comparison of subgroups found by CAREN and Cortana

The distribution of the most interesting subgroup, $\text {Region} = \text {East}$, is represented in Fig. 14. We can observe that, the majority of the rankings in the whole dataset have a similarity of 0.8 with the average ranking. On the other hand, the rankings of this subgroup, have at most a similarity of 0.7.

Fig. 14

Graphical representation of the distributions of the target of the subgroup $\text {Region} = \text {East}$ (in bold) in comparison to the whole target distribution in GermanElections2009

5.4.2 Top7Movies

In this section, we analyze a set of DR found with the Top7Movies dataset and compare to the subgroups obtained with Cortana. We found 7 significant DR with CAREN and a search depth of 2. In Fig. 15 we can see the description and the distributions of the DR found on the Top7Movies dataset.

Fig. 15

Graphical representation of the distributions rules found in Top7Movies dataset

With Cortana, we found 7 significant subgroups with a search depth of 2. From this set, 3 subgroups are the same (but in a different order), as we can see from Table 6.

Table 6 Comparison of subgroups found by CAREN and Cortana

We note that, in the Label Ranking context, despite the similarities between the subgroups found both by CAREN and Cortana, the interpretation of the rankings is richer with a PM than with a distribution. PM are better for spotting slight nuances in the preference patterns, for example, when a particular label is under- or over-appreciated. Moreover, if we want to search for partial ranking patterns such as labels or simply label-vs-label, it is simpler to visualize and handle it with a PM. This mean that, EPM, due to its representation of rankings, has a bigger margin for the creation of new quality measures.

6 Conclusions

In this work, we empirically show how exceptional preferences mining (EPM) can be used in problems where the target concept can be represented as a preference of a set of labels, such as rankings or pairwise comparisons. The results are a set of subgroups, that can be described in terms of a conjunction of few conditions on some attributes, where the label preferences are exceptional in some sense. The presented subgroups form clear coherent parts of the search space, which means that EPM finds deviating preferences that are actionable for domain experts, since their description in terms of attributes should be familiar to them.

All subgroups whose PM deviates significantly from the Preference Matrix (PM) for the whole dataset are considered to be interesting. We used four quality measures for EPM that instantiate this concept of ‘interesting’ to different levels, Rankingwise, Labelwise and Pairwise. The RWNorm, RWNorm-Mode and RWCov quality measures consider a subgroup interesting if the full set of preference relations is substantially displaced. The LWNorm quality measure highlights subgroups where any one label interacts exceptionally with the other labels, agnostic of how those other labels interact with each other. The PWMax quality measure finds a subgroup interesting if any one pair of labels display exceptional preference relations. Hence, by choosing the appropriate quality measure, EPM delivers subgroups featuring preference relations that are exceptional at your preferred scope.

To show the potential of the approach, we provided experiments on several datasets. The experiments with the RWNorm quality measure on the Algae dataset revealed several interesting conditions that can affect the populations of the different species of algae from rivers. The experiments with the LWNorm quality measure on the Sushi dataset illustrate the relative merit of this quality measure: it focuses on subgroups where one particular label is exceptionally under- or over-appreciated. The subgroup presented has a penchant for Sea Urchin (cf. Fig. 10). The PWMax measure shows its potential on the German2005elections dataset by identifying several subgroup with strong exceptional preferences with respect to the different parties. The experiments with the RWCov quality measure on the Cpu-small dataset (e.g., Fig. 11) reveal a subgroup with quite unusual preference behavior. Finally, the RWNorm-Mode was compared to the RWNorm measure, in different experiments, and we could observe that it revealed some interesting subgroups too. Moreover, we concluded that RWNorm-Mode and RWNorm can be complementary measures to study exceptional preference patterns.

As we argued in Sect. 3, one of the main benefits of a local pattern mining method such as EPM is that it delivers interpretable results. That means that the resulting subgroups are ideally suited to instigate real-world policies and actions. For this reason, we studied several real-world datasets.

We also compared the results found with EPM with an alternative approach, the Distribution Rules (DR). Despite their very different setting, the subgroups found by this method were very similar to the ones found with Cortana. In our opinion, this simple comparison empirically shows that our suggested quality measures for EPM are finding relevant patterns. In terms of interpretation, PM are better than distribution rules to detect slight nuances in the preference patterns, for example, when a particular label is under- or over-appreciated. In some cases, information which is not easy to obtain with the usual representations of rankings, is clearly revealed through the PM visualization (see Sect. 5.3.2).

From this study, we also understand some limitations of our approach. We observed that, in some cases, despite having obtained many significant subgroups, most of them are specializations of simpler subgroups with very similar average rankings, if not equal. This means that, many different subgroups are finding the same ranking behaviors.

EPM also has the disadvantage to be time consuming. A large number of labels combined with a still reasonably high search depth makes the statistical tests very time consuming.

As future work we would like to study alternative ways to represent and look for patterns in rankings, for example for rankings with a large number of labels as well as for partial orders. Finally, we would also like to study how pruning techniques such as minimum improvement can be used to filter out subgroups, that are specializations of simpler subgroups, but have very similar PMs.