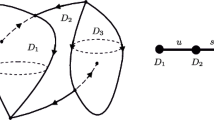
We study gradient-like flows with no heteroclinic intersections on an n-dimensional (n ≥ 3) sphere from the point of view of topological conjugacy. We prove that the topological conjugacy class of such a flow is completely determined by the bicolor tree corresponding to the frame of separatrices of codimension 1. We show that for such flows the notions of topological equivalence and topological conjugacy coincide (which is not the case if there are limit cycles and connections.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. Smale, “On gradient dynamical systems,” Ann. Math. (2) 74, 199–206 (1961).
Ya. B. Pesin and A. A. Yurchenko, “Some physical models described by the reaction–diffusion equation, and coupled map lattices,” Russ. Math. Surv. 59, No. 3, 481–513 (2004).
V. Grines, T. Medvedev, O. Pochinka, and E. Zhuzhoma, “On heteroclinic separators of magnetic fields in electrically conducting fluids,” Physica D 294, 1–5 (2015).
A. M. Leontovich and A. G. Maier, “On trajectories defining the qualitative structure of partition of a sphere into trajectories” [in Russian], Dokl. AN SSSR 14, No 5, 251–257 (1937).
A. M. Leontovich and A. G. Maier, “On a scheme defining the topological structure of partition into trajectories” [in Russian] Dokl. AN SSSR 103, No 4, 557–560 (1955).
M. M. Peixoto, “On the classification of flows on 2-manifolds,” Dynamical Syst., Proc. Sympos. Univ. Bahia, Salvador 1971, 389–419 (1973).
A. A. Oshemkov and V. V. Sharko, “Classification of Morse–Smale flows on two-dimensional manifolds,” Sb. Math. 189, No 8, 1205–1250 (1998).
S. V. Piljugin, “Phase diagrams determining Morse–Smale systems without periodic trajectories on spheres,” Differ. Equations 14, 170–177 (1978).
A. O. Prishlyak, “Morse–Smale vector fields without closed trajectories on three-dimensional manifolds,” Math. Notes 71, No. 2, 230–235 (2002).
V. Kruglov, “Topological conjugacy of gradient-like flows on surfaces,” Din. Sist., Simferopol’ 8, No 1, 15–21 (2018).
S. Smale, “Differentiable dynamical systems,” Bull. Am. Math. Soc. 73, No. 6, 747–817 (1967).
V. Z. Grines, T. V. Medvedev, and O. V. Pochinka, Dynamical Systems on 2- and 3-Manifolds, Springer, Cham (2016).
M. Brown, “Locally flat imbeddings of topological manifolds,” Ann. Math. (2) 75, 331–341 (1962).
V. Z. Grines, E. Ya. Gurevich, and O. V. Pochinka, “Combinatorial invariant of Morse–Smale diffeomorphisms without heteroclinic intersections on the sphere Sn, n ≥ 4,” Math. Notes 105, No. 1, 132–136 (2019).
J. jun. Palis and W. de Melo, Geometric Theory of Dynamical Systems. An Introduction Springer, New York etc. (1982).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Problemy Matematicheskogo Analiza 104, 2020, pp. 21-27.
Rights and permissions
About this article
Cite this article
Kruglov, V.E., Pochinka, O.V. Criterion for the Topological Conjugacy of Multi-Dimensional Gradient-Like Flows with No Heteroclinic Intersections on a Sphere. J Math Sci 250, 22–30 (2020). https://doi.org/10.1007/s10958-020-04993-w
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-020-04993-w