An integrated model for the transshipment yard scheduling problem

Abstract

A hub-and-spoke railway system is an efficient way of handling freight transport by land. A modern rail–rail train yard consists of huge gantry cranes that move the containers between the trains. In this context, we consider a rail–rail transshipment yard scheduling problem (TYSP) where the containers arrive to the hub and need to be placed on a train that will deliver them to their destination. In the literature, the problem is decomposed hierarchically into five subproblems, which are solved separately. First, the trains have to be grouped into bundles in which they visit the yard. Next, the trains have to be assigned to tracks within these bundles, namely parking positions. Then the final positions for the containers on trains have to be determined. Next, the container moves that need to be performed are assigned to the cranes. Finally, these moves have to be sequenced for each crane for processing. In this paper, an integrated MILP model is proposed, which aims to solve the TYSP as a single optimization problem. The proposed formulation also enables us to define more robust and complex objective functions that include key characteristics from each of the above-mentioned subproblems. The strength of our proposed formulation is demonstrated via computational experiments using the data from the literature. Indeed, the results show that the TYSP can be solved without the use of decomposition techniques and more insight can be obtained from the same input data used to solve particular single decomposed subproblems.

1 Introduction

According to a recent study by the Organisation for Economic Co-operation and Development (OECD), an intergovernmental organization with 54 member countries, global trade-related freight and emissions are increasing and are set to quadruple by 2050.¹ Among all modes of transport, rail continues to be very attractive as it has one of the smallest $\hbox {CO}_2$ emissions and enables transportation of larger quantities of goods between the major destinations. Also, if compared with air transshipment, rail is much cheaper and when compared to other land transport possibilities, rails are much less obstructed by the traffic congestion and more popular than inland waterway transportation.

Fig. 1

Schematic representation of shunting yard as presented in Boysen et al. (2012a)

Fig. 2

Schematic representation of rail–rail terminal as presented in Boysen et al. (2012a)

Modern railway systems have rail–rail transshipment yards where containers are not specifically received or dispatched, but simply transferred on their way to their destination between the rails. This transfer is achieved by using gantry cranes that operate above the trains. The cranes allow for a fast and reliable container handling and are therefore considered as a very important part of the hub-and-spoke railway system. Although broad studies have been conducted in the area of railway optimization (Cordeau et al. 1988) and intermodal transportation (Crainic and Kim 2007) in general, the literature on rail–rail transshipment yards is scarce, mainly focusing on traditional shunting yards. In these conventional yards, as one can see in Fig. 1, the position of a container is changed by rearranging railcars via shunting hills (humps) and a system of track switches (Dahlhaus et al. 2000; Hansmann and Zimmermann 2008; Gatto et al. 2009; Jacob et al. 2011; Boysen et al. 2012b) (classification tracks). However, the surveys by Bontekoning et al. (2004) and Macharis and Bontekoning (2004) show that the modern rail–rail transshipment yard in which containers are positioned with the help of gantry cranes, is an emerging technology and gives a chance for a more efficient transshipment.

Figure 2 illustrates a schematic representation of a modern rail–rail transshipment yard (Boysen et al. 2012a). As one can see, the containers can be transshipped among trains without the need to exchange railcars. This is done with the help of huge gantry cranes operating above the tracks and the containers can be moved directly between the trains. However, if the receiving train of a given container is not present in the terminal then it will be moved to the storage area that usually consists of a sorter with buffer and a transport system that moves the container to a suitable position where it is stored temporarily using the so-called shuttle cars. That container can be later retrieved from the storage and placed on the desired train. This operation is called a split move, as opposed to a direct move, because it requires two crane operations. An example of this kind of rail–rail system, also known as Mega Hub, is Hanover–Lehrte in Germany (Rotter 2004) or Port Bou on the border between France and Spain (Martinez et al. 2004).

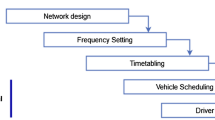
In the recent studies, the rail–rail transshipment yard scheduling problem has been decomposed hierarchically into following subproblems:

• (1) Schedule time slots to service the trains.

• (2) Assign a railway track to each train.

• (3) Decide on the outbound positions of the containers on trains.

• (4) Assign container moves to gantry cranes.

• (5) Create a schedule for cranes to move all containers to their target outbound positions.

Subproblem 1 is often called a bundling of trains. Train yards have a limited number of tracks available to process the incoming trains simultaneously and thus we have to group the trains into bundles (time slots) in which they are operated. Due to safety issues, the gantry cranes cannot move while the trains are moving, thus the trains are processed in a given bundle and no train can leave the station before containers from all the trains are moved to their outbound positions. Once all the trains have been assigned to a bundle, it is essential to assign tracks to individual trains within a bundle. This influences the distance the cranes have to cover when moving from one train to another, which is called a vertical move, and is solved within subproblem 2. However, the container could be placed to the front of the train, in the middle or in the back, which would also have an impact on the crane movement. If a crane has to move on longer distance, it could create conflicts with other cranes and cause collisions that need to be avoided. The final position of the container on its receiving train is set by solving subproblem 3, which causes horizontal moves along the train. Next, we have to assign the container moves to gantry cranes by solving subproblem 4. Quite often we have to consider limitations on the horizontal area each crane is moving in order to avoid collisions. There are train yards with cranes operating on different heights allowing them to move one over another, but only when the over-passing crane carries no container, see Dorndorf and Schneider (2010). This and many more safety constraints require us to pick only those moves for a given crane that can be handled by it, while keeping a balanced workload for all of them. Finally, we have to sequence the assigned moves on the cranes defined as problem 5. Even though we kept safety measures while solving the previous problem, we have to consider the possibility of cranes colliding with each other. In practice, when solving the last problem, we also have to consider how the containers are transferred to and picked from the storage, as those operations will affect the container availability and usually have an impact on the crane schedule.

Even though decomposing a complex problem into a series of subproblems and solving them sequentially is a useful way of finding good feasible solutions, it is well known that such methods can lead to sub-optimal solutions. Therefore, in this paper we present a single model that will allow us to solve three of the five presented problems simultaneously: one bundling, two train to track assignment and three decide on the outbound positions. This way we are using more input data and our model is able to provide better crane schedules as input for subproblems 4 and 5. To the best of authors’ knowledge, an integrated approach to this important problem has not been covered in the existing literature and is the focus of our paper.

The remainder of the paper is structured as follows. In sect. 2, the literature review of the work related to the rail–rail transshipment yard problem is presented. Section 3 contains a problem description and mathematical model. Results of computational experiments are presented in Sect. 4. Finally, Sect. 5 summarizes the paper.

2 Literature review

In the literature, the subproblems defined in Sect. 1 are solved separately. The assignment of trains to bundles, subproblem 1, is investigated in Boysen et al. (2011) and extended in Boysen et al. (2012c). A basic transshipment yard scheduling problem is presented that minimizes a weighted objective function that considers split moves and the number of revisits by the trains. The problem is shown to be NP-hard in the strong sense and the authors present different heuristics and exact solution procedures. Kellner et al. (2012) present a solution procedure that can be used to solve a decision variant of problem 2, i.e. the parking problem of trains. The assignment of a given bundle of trains to tracks aims to minimize the makespan of train processing. A genetic algorithm is presented and tested in a simulation study. The same problem is also solved in Alicke and Arnold (1998) using a simpler approach. The authors consider only the tracks assignment of trains without including horizontal parking positions, sorter operations or multiple cranes. Instead, they develop a simple priority weighting value for container moves based on their total horizontal distance, which is used to approximate the workload between two trains. These weights are then applied to solve a quadratic assignment problem to determine the track assignment of trains. Bostel and Dejax (1998) propose a solution for problem 3. The authors aim to determine the initial and the final positions of a container in such a way that they are as close together as possible, so the travel distances of cranes and the resulting costs of train processing are minimized. It is assumed that each container can be stored on any railcar and weight restrictions are not considered. A similar approach is also discussed in Corry and Kozan (2008). Static and disjoint crane areas for problem 4 are investigated in Boysen and Fliedner (2010) for a bundle of trains with given parking positions to minimize the makespan of train processing. The sorting system is assumed to be activated whenever the initial and the final positions of a container move are in different crane areas.

A paper that jointly treats problems 4 and 5 is given by Alicke (2002). A given set of crane moves is assigned to cranes with overlapping areas of operation, which are blocked whenever a crane enters an area. If one of the positions of a container move falls in that overlapping area, the procedure decides which of two neighbouring cranes process that move. This model takes the speed and the availability of shuttle cars from the sorter system into account. The problem is modelled as a constraint satisfaction problem and tested on datasets supposed to reflect the situation of the Mega Hub in Hannover–Lehrte in Germany. The authors propose and compare different heuristic rules for fixing variables of the constraints. Related problems also occur within container terminals and have been covered by Zhu and Lim (2006), Moccia et al. (2006), Lim et al. (2007) and Sammarra et al. (2007).

3 Problem description

In this section, we present a mixed integer linear programming model that integrates the bundling, track assignment and outbound positioning subproblems. Obviously, it is not possible to bundle the trains in such a way that every container will go directly to the train with correct destination. Frequently, the cranes have to make two moves on the same container—first a drop off in the storage area and later a pick up from there to position the container on the receiving train. This operation is called a split move. A split move can occur in two situations—either the receiving train will arrive in a later bundle and the container can only be taken then, or it was supposed to go on a train that was already processed in an earlier bundle, which means that the train will have to revisit the station. In order to minimize double-handling of the containers, it is desirable that both split moves and revisits are avoided. In what follows, we provide further details about the problem.

We have been given a maximum number of the tracks, G, on the train yard, the total number of trains, N, that needs to be scheduled with L containers on every train. Observe that a smaller number of containers can easily be modelled that way by assuming that there are containers that will not be moved. The total number of containers, C, is, therefore, equal to $N \times L$. We know for every container on which train car it is (i.e. its inbound position on the train) and we also know the receiving train. The task is to find the outbound position for each container that will minimize the total processing time of the cranes, which is calculated as the total number of vertical and horizontal moves performed by the cranes.

Vertical moves are dependent on the train assignment to the tracks, horizontal moves depend on the car positioning for each container. If a container requires a split move, a penalty is introduced. The penalty for using storage is equal to the maximum distance the crane will have to move in worst case and is equal to $2 \times ( G + L )$. We assume in this paper that the capacity of the storage area is unlimited. If the storage space was limited not all problem instances from the literature could be solved. We could introduce a penalty for overflowing the storage area, but this is left as a future work.

The following decision variables are defined:

$x_{n, j, k}$ :

Train n is assigned to bundle j and track k; $x_{n, j, k} \in \{0; 1\}$

$o_{i, p}$ :

Container i leaves the train yard on car p of its receiving train; $o_{i, p} \in \{0; 1\}$

$d_{i}$ :

Container i is moved directly to its receiving train; $d_{i} \in \{0; 1\}$

$s_{i}$ :

Container i requires a split move for transferring to its receiving train; $s_{i} \in \{0; 1\}$

$r_{n}$ :

Train n needs to revisit the train yard to pick all its remaining containers; $r_{n} \in \{0; 1\}$

$h_{i}$ :

Number of places container i is moved horizontally; $h_{i} \in \mathbb {Z}^+$

$v_{i}$ :

Number of places container i is moved vertically; $v_{i} \in \mathbb {Z}^+$

$b_{n_1, n_2}$ :

Trains $n_1$ and $n_2$ are in the same bundle; $b_{n_1, n_2} \in \{0; 1\}$; $n_1 < n_2$

$p_{n_1, n_2}$ :

Train $n_1$ is in an earlier bundle than train $n_2$; $p_{n_1, n_2} \in \{0; 1\}$;

From the problem description above, we have the following input data:

N :

Number of trains

G :

Number of tracks

L :

Length of station (measured in the number of containers)

C :

Total number of containers, $C = N \times L$

J :

Number of bundles, $J = \left\lceil \frac{N}{G}\right\rceil$

$c_{i, p}$ :

Container i arrives on railcar p; $c_{i, p} \in \{0; 1\}$

$\mathrm{arr}_{i}$ :

The train id on which container i should arrive in the train yard; $1\le \mathrm{arr}_i\le N$

$\mathrm{dep}_{i}$ :

The train id on which container i should depart from the train yard; $1\le \mathrm{dep}_i\le N$

C(n):

Set of containers that should be moved to train n

$C(n_1, n_2)$ :

Set of containers that should be moved from train $n_1$ to train $n_2$

In the following equations, we will use indexes:

• $i = 1\ldots C$

• $j = 1\ldots J$

• $n, n_1, n_2 = 1\ldots N$

• $k, k_1, k_2 = 1\ldots G$

• $p, p_1, p_2 = 1\ldots L$

With all the above information provided we want to assign as many containers to the proper trains as possible while trying to reduce the potential processing times by keeping the inbound and outbound positions of the containers close to each other. In other words, we would like to minimize the following objective function:

$$\begin{aligned} \min \sum _{i = 1}^{C} \left( h_{i} + v_{i} + M \times s_{i}\right) + \sum _{n = 1}^{N} M_2 \times r_{n}, \end{aligned}$$

(1)

where M and $M_2$ are constants that are defined in the following section.

The first part of the objective function minimizes the total number of vertical moves made between the tracks and horizontal moves made along the trains. We assume that a split move (i.e. storing a container in a storage and not moving it directly from train to train) will generate maximum possible vertical and horizontal moves (either because the receiving train will arrive in later bundle or was already handled and has to revisit the station). The penalty for a split move is equal to $( G + L )$, so it is always undesirable when compared to a direct move. This function only minimizes the distances between a container’s inbound and outbound positions and does not take into account the moves that cranes have to perform in-between without carrying any containers. We neither decide on which moves should be performed by which crane and how the cranes operate—this is a future task that can be handled once the outbound positions of the containers are known, nor do we consider the order in which the containers are moved. Thus we assume that all outbound positions are empty—the containers that arrived on the trains will be moved either to the receiving train or to the storage area, making the train fully available to receive new containers, but we do not check “when” this would happen. As stated above, the penalty for a split move M is equal to $( G + L )$, whereas the penalty for a train revisit is equal to 24 split moves, which is equal to $24 \times ( G + L )$. The reasoning behind these values is as follows: a split move takes around 2, 5 mins to process and the average time of a revisit is 60 mins. Thus, the ratio between $M_2$ and M is equal to $\frac{60}{2.5} = 24$.

For a schedule to be feasible, following constraints have to be satisfied:

$$\begin{aligned}&d_{i} + s_{i} = 1; \forall _{i} \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{p = 1}^{L} o_{i, p} = 1; \forall _{i}\end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i \in C(n)} o_{i, p} \le \left\lceil \frac{|C(n)|}{L} \right\rceil ; \forall _{p} \forall _{n}\end{aligned}$$

(4)

$$\begin{aligned}&\sum _{j = 1}^{J} \sum _{k = 1}^{G} x_{n, j, k} = 1; \forall _{n}\end{aligned}$$

(5)

$$\begin{aligned}&\sum _{n = 1}^{N} x_{n, j, k} \le 1; \forall _{j} \forall _{k}\end{aligned}$$

(6)

$$\begin{aligned}&\sum _{k = 1}^{G} x_{n_1, j, k} + \sum _{k = 1}^{G} x_{n_2, j, k} - 1 \le b_{n_1, n_2}; \forall _{j} \forall _{n_1} \forall _{n_2}\end{aligned}$$

(7)

$$\begin{aligned}&\sum _{k = 1}^{G} x_{n_1, j, k} + b_{n_1, n_2} - 1 \le \sum _{k = 1}^{G} x_{n_2, j, k}; \forall _{j} \forall _{n_1} \forall _{n_2}\end{aligned}$$

(8)

$$\begin{aligned}&b_{n_1, n_2} + \sum _{k = 1}^{G} x_{n_2, j, k} - 1 \le \sum _{k = 1}^{G} x_{n_1, j, k}; \forall _{j} \forall _{n_1} \forall _{n_2}\end{aligned}$$

(9)

$$\begin{aligned}&\sum _{i \in C(n_1, n_2) \cup C(n_2, n_1)} s_{i} = |C(n_1, n_2) \cup C(n_2, n_1)| \nonumber \\&\times ( 1 - b_{n_1, n_2} ); \forall _{n_1} \forall _{n_2}\end{aligned}$$

(10)

$$\begin{aligned}&\sum _{n_1 = 1}^{n_2 - 1} b_{n_1, n_2} + \sum _{n_3 = n_2 + 1}^{N} b_{n_2, n_3} \le G - 1; \forall _{n_2}\end{aligned}$$

(11)

$$\begin{aligned}&b_{n_1, n_2} + b_{n_2, n_3} - 1 \le b_{n_1, n_3}; \forall _{n_1 \le n_2 \le n_3}\end{aligned}$$

(12)

$$\begin{aligned}&| k_1 - k_2 | \times \left( \sum _{j = 1}^{J} x_{{arr}_{i}, j, k_1} + \sum _{j = 1}^{J} x_{{dep}_{i}, j, k_2} - 1 \right) \nonumber \\&\le v_i; \forall _{i} \forall _{k_1} \forall _{k_2}\end{aligned}$$

(13)

$$\begin{aligned}&|p_1 - p_2 | \times ( c_{i, p_1} + o_{i, p_2} - 1 ) \le h_i; \forall _{i} \forall _{p_1} \forall _{p_2}\end{aligned}$$

(14)

$$\begin{aligned}&\sum _{j_2 = 1}^{j} \sum _{k = 1}^{G} ( x_{n_1, j_2, k} - x_{n_2, j_2, k} ) \le p_{n_1, n_2}; \forall _{j} \forall _{n_1} \forall _{n_2}\end{aligned}$$

(15)

$$\begin{aligned}&\text {if } |C(n_2, n_1)| > 0 \text { then } r_{n_1} \ge p_{n_1, n_2}; \forall _{n_1} \forall _{n_2}\end{aligned}$$

(16)

$$\begin{aligned}&b_{n_1, n_2} + p_{n_1, n_2} + p_{n_2, n_1} = 1; \forall _{n_1} \forall _{n_2} \end{aligned}$$

(17)

Equations 2 ensure that each container is either to be moved directly between trains or through a split move. Each container must have an outbound position assigned, which is defined in Eq. 3. Next, in constraints 4 each position on a given train is taken at most $\left\lceil \frac{|C(n)|}{L}\right\rceil$ times. Equation 5 ensure that each train is assigned to exactly one bundle and one track. Since each bundle has at most G trains and the trains do not occupy the same track in a given bundle, each track in a given bundle is taken at most one time. This is defined in constraints 6. The model can be improved if it is known that the number of trains is divisible by the number of tracks, which would mean that each bundle has exactly G trains in it and the inequality could be changed to equality in this constraint. Constraints 7 ensure that when trains $n_1$ and $n_2$ are assigned to the same bundle then variable $b_{n_1,n_2}$ becomes 1. However, it is also essential to ensure that $b_{n_1,n_2}$ becomes 0 in the case when trains $n_1$ and $n_2$ are assigned to different bundles. This is achieved by constraints 8 and 9. Equation 10 say that if trains $n_1$ and $n_2$ do not belong to the same bundle, containers between them cannot be exchanged without causing split moves. As there are in any bundle at most G tracks available, constraints 11 guarantee that there are at most $G - 1$ other trains in a bundle with any other train $n_2$. Then a transitive relation for variable $b_{n_1, n_2}$ is expressed in constraints 12.

Fig. 3

Two undistinguishable solutions according to Boysen et al. (2011), which have different objective values in integrated model

If a container i arrives at track $k_1$ on car $p_1$ of train $arr_i$ and departs from track $k_2$ on car $p_2$ of its receiving train $dep_i$, the cranes will have to make $|k_1-k_2|$ and $|p_1-p_2|$ vertical and horizontal moves, respectively. These are more formally defined by constraints 13 and 14. It is worth noting that penalties of vertical and horizontal moves are independent of which bundles trains $\mathrm{arr}_i$ and $\mathrm{dep}_i$ of a container i are assigned as we only measure here the direct movements of containers. Next in constraints 15, we set the value of $p_{n_1, n_2}$ to 1 if train $n_1$ is in an earlier bundle than train $n_2$. If a train $n_1$ arrives before train $n_2$ and there are containers that need to be transported from $n_2$ to $n_1$, then the train $n_1$ has to revisit the station. This is implied by constraints 16. Finally, Eq. 17 is used to improve the lower bound by restricting that only one of these situations can occur: trains $n_1$ and $n_2$ are in the same bundle; train $n_1$ is in an earlier bundle than train $n_2$ or train $n_2$ is in an earlier bundle than train $n_1$.

We extend this model to include additional constraints for arrival and departure times of the trains. The time constraints can be expressed as availability of the train within a given bundle. If a train n is not available in a bundle j, because it has not arrived yet to the station, then we set $\sum _k x_{n, j, k}$ to zero. For each train n and all tracks k, we set the variable $x_{n, j, k}$ to 0 if the $j < \mathrm{Arrival}_n$ and $j > \mathrm{Departure}_n$, where $\mathrm{Arrival}_n$ and $\mathrm{Departure}_n$ are bundle numbers or in other words time slots of availability, in which the train n can enter the train yard.

To compare the results from our integrated model with the literature, we need to change the objective function. The model in Boysen et al. (2011) minimizes the number of split moves and revisits, ignoring the positioning of containers. Therefore, in order to compare the performance of our model with Boysen et al. (2011), we use the same set of variables and constraints as defined earlier but formulate the objective function as follows:

$$\begin{aligned} \min \sum _{i = 1}^{C} M \times s_{i} + \sum _{n = 1}^{N} M_2 \times r_{n} \end{aligned}$$

(18)

To fully understand the differences between our model and the one from Boysen et al. (2011), we present two solutions for the problem at hand. The toy-example instance has four trains, four containers per train and two tracks. Therefore, we provide two bundles to perform the container movements. According to the objective function from the referenced paper, both solutions presented in Fig. 3 have two split moves which require two revisits, so they are considered equally good. Also, both solutions are optimal in terms of the problem 1: bundling—there is no better train to track assignment that could reduce the number of split moves or revisits. However, if we consider the crane movements, it is easy to notice that in the second solution the containers that are to be swapped are much closer to each other. In fact, they do not require any horizontal movements, which was the case in Solution 1. This will reduce the processing time of each bundle and will make only Solution 2 an optimal solution. The larger instances with more trains and containers have much more complex, but similar situations in which bundle assignment could lead to multiple equally good solutions. These solutions can be differentiated by taking into consideration the crane movements and distances between the container positions and that is what the proposed model is doing.

4 Computational experiments

Extensive computational experiments were performed using the datasets from Boysen et al. (2011) with arrival and departure restrictions. In the datasets from Boysen et al. (2011), the information about initial positioning of the containers was missing, so we added this information to the datasets by sequentially placing the containers for a particular receiving train one after the other. For example, if train A had 5 and 16 containers for trains B and C, respectively, then in train A positions from $1\ldots 5$ are occupied by containers for train B and positions from $6\ldots 21$ are occupied by containers for train C. We implemented the model using Gurobi software and the tests were conducted using an Intel i5 1, 7 GHz machine with 4 GB of RAM memory, setting the time limit to 20 mins and the threads limit of the solver to two due to the Hyper Threading technology available on the machine. Finally, we compared the results with Boysen et al. (2011) regarding the number of revisits and the number of split moves. Obviously, our model provides a solution with additional information on the outbound positions of the containers, but as this information was not present in Boysen et al. (2011), we could not compare those results.

Table 1 Number of split moves over 2240 instances solved

Table 2 Number of revisits over 2240 instances solved

Table 3 Average difference in number of split moves in comparison to Boysen et al. (2011)

Table 4 Average difference in number of revisits in comparison to Boysen et al. (2011)

Tables 1 and 2 show the total number of split moves and revisits over all the instances that were solved. We can notice that the more containers there are per train, the more revisits and split moves are required within the instances. It is also worth noting that for instances with two, four and six tracks, there were 12 trains considered and therefore for the same number of trains and containers the total number of split moves and revisits decreases as additional tracks provide higher flexibility. However, for eight tracks, we had 16 trains; thus this has higher total values in the tables as compared to the solution with six tracks. In most instances, the revisits are forced due to the impossible assignment of two trains in the same bundle with respect to the arrival and departure restrictions.

Tables 3 and 4 show the average difference in number concerning split moves and revisits over all solved instances. The difference is calculated by subtracting from our result the value obtained by Boysen et al. (2011). Thus, if the difference is lower than 0 then it means that we have more split moves or revisits compared to Boysen et al. (2011). However, if the difference is higher than 0 then we managed to obtain a lower number of split moves or revisits. These values were calculated and we took the average over all solved instances. The aggregated results are presented in the tables.

First we notice that on average the difference in most cases is <1. It means that the results obtained by our model are not very different to the ones in Boysen et al. (2011). Indeed, most of the instances are solved exactly the same way with respect to split moves and revisits. However, some solutions differ by different allocations of split moves and revisits. The ratio between these two operations was $\frac{1}{24}$ and in most cases solutions differ in a way that there is one more revisit but twenty-four split moves less (and multiples of that) in the original solution when compared to our result and vice versa. If we consider the eight track instances, we can notice that for a larger number of containers per train we obtained higher differences. This is caused by the time limit we used in our computational study and those instances were just not solved to optimality by the solver, which is especially noticeable for the instances with 54 containers per train. Over all 2240 instances, only 111 had a different result to Boysen et al. (2011), and among them 72 were instances with eight tracks, which were the hardest to solve and did not complete within the time limit.

To perform a fair comparison between our model and Boysen et al. (2011), we removed the horizontal and vertical movements from the objective function as stated in 18. This creates a model that minimizes the total number of split moves and revisits. As a result, we obtained exactly the same objective functions scores as in Boysen et al. (2011). The average solving time for Gurobi was 3, 13 s, but one should keep in mind that the solver performs a pre-solve routine to remove redundant constraints (in this case the constraints about the positioning of the containers). The maximum solving time was 46, 81 s for the biggest instances available.

Our results show that the decomposition from Sect. 1 works very well for the rail–rail transshipment yard scheduling problem. However, having a more integrated model that solves three out of five subproblems using the same amount of information has benefits. Our approach considers a wider spectrum of information and provides a global optimum for the set of problems instead of the local optimum for a given subproblem. Even though in most cases the solutions are exactly the same, there are instances which have different trains to bundle assignments caused by the optimization of container positioning to minimize the total crane movements. This would not have been possible if the decomposed problems were solved one after another.

5 Conclusions

In this paper, we propose a more general approach to solve the transshipment yard scheduling problem. A mathematical model has been formulated, implemented and tested in an extensive computational study. The obtained results are very interesting in comparison to previous works in this field. It appears that the more general approach has provided very similar, if not exactly the same, solutions for the instances analysed in the literature. Thus the decomposition scheme seems to work well for this problem. However, the important difference between the existing approaches and the one proposed in this paper is the information that we receive as output of the model. The mathematical model presented above allows us to answer three out of five questions raised by the decomposition scheme, while the previous approaches answered only one specific question. The benefit of the proposed approach is that it uses the same amount of input information to provide a solution, which is much richer in information when compared to an existing approach. Not surprisingly, it is at the cost of computational time that is required to generate the answers, but might be a more feasible solution in scenarios where the outbound positioning of the containers is also very important. The obtained result is a global optimum for the three subproblems considered in this paper, while previous approaches provided an optimal solution for a single subproblem which most likely is only locally optimal if the other subproblems derived from the decomposition are included. Finally, the proposed model is solved to optimality (if time allows). But there is huge potential for new heuristics to be created based on the research and understanding of the model.