Free-Stream Preservation for Curved Geometrically Non-conforming Discontinuous Galerkin Spectral Elements

Abstract

The under integration of the volume terms in the discontinuous Galerkin spectral element approximation introduces errors at non-conforming element faces that do not cancel and lead to free-stream preservation errors. We derive volume and face conditions on the geometry under which a constant state is preserved. From those, we catalog eight constraints on the geometry that preserve a constant state. Numerical examples are presented to illustrate the results.

Appendix

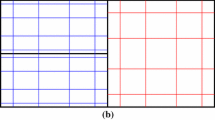
For ensuring the watertight condition, we require the geometry interpolants of the large face and the child faces, shown in Fig. 8, to match. The interpolation of the interpolant from the large face to the child faces is exact. The interpolation of the product of two interpolants is not. For completeness, we present a proof here, though only for edges in a two dimensional mesh. The proof for two dimensional faces in a three dimensional mesh will follow the same approach due to the tensor product approximation.

Fig. 8

Subdivision of interpolants. The polynomials $U^{L}$ and $U^{R}$ will be constructed to match U on their respective intervals

Define the polynomial of degree N over the interval $[-1,1]$ to be

$$\begin{aligned} U\left( s \right) = \sum \limits _{j = 0}^N {{U_j}{\ell _j}\left( s \right) }. \quad s \in [-1,1] \end{aligned}$$

(49)

Next subdivide the interval into two pieces $\xi \in [-1,1]$ and $\eta \in [-1,1]$ and two mappings

$$\begin{aligned} s = \left\{ \begin{aligned} \frac{\xi -1 }{2}\quad \xi \in [-1,1] \\ \frac{\eta +1}{2}\quad \eta \in [-1,1]. \\ \end{aligned} \right. \end{aligned}$$

(50)

Define the two polynomials that take on the values of U at the interpolation points on the left and right intervals, i.e

$$\begin{aligned} {U_{L}}\left( \xi \right) = \sum \limits _{n = 0}^N {U\left( {\frac{{{\xi _n-1}}}{2}} \right) {\ell _n}\left( \xi \right) } , \quad {U_{R}}\left( \eta \right) = \sum \limits _{n = 0}^N {U\left( {\frac{{{\eta _n+1}}}{2}} \right) {\ell _n}\left( \eta \right) }. \end{aligned}$$

(51)

Now we assume that we have two polynomials that match on the short and the long intervals. That is,

$$\begin{aligned} U\left( s \right) = \sum \limits _{j = 0}^N {{U_j}{\ell _j}\left( s \right) } \quad U \ne 0, \quad V\left( s \right) = \sum \limits _{j = 0}^N {{V_j}{\ell _j}\left( s \right) } \quad V \ne 0. \end{aligned}$$

(52)

We then project the product of the two onto the polynomial space

$$\begin{aligned} W(s) = {{\mathbb {I}}^N}\left( {UV} \right) = \sum \limits _{j = 0}^N {{U_j}{V_j}{\ell _j}\left( s \right) }, \end{aligned}$$

(53)

and break the interval into two, as in (51), and define interpolants on each half

$$\begin{aligned} {W_L}\left( \xi \right)= & {} {\mathbb {I}}_L^N\left( {UV} \right) = \sum \limits _{j = 0}^N {U\left( {\frac{{{\xi _j} - 1}}{2}} \right) V\left( {\frac{{{\xi _j} - 1}}{2}} \right) {\ell _j}\left( \xi \right) } \nonumber \\ {W_R}\left( \xi \right)= & {} {\mathbb {I}}_R^N\left( {UV} \right) = \sum \limits _{j = 0}^N {U\left( {\frac{{{\eta _j} + 1}}{2}} \right) V\left( {\frac{{{h_j} + 1}}{2}} \right) {\ell _j}\left( \eta \right) } . \end{aligned}$$

(54)

Then we prove that

$$\begin{aligned} W\left( {\frac{{\xi - 1}}{2}} \right) \ne {W_L}\left( \xi \right) ,\quad W\left( {\frac{{\eta + 1}}{2}} \right) \ne {W_R}\left( \eta \right) , \end{aligned}$$

(55)

that is, the interpolation of the product onto the polynomials of degree N on each half does not equal the interpolant of the product over the whole interval.

To prove this, we examine the error of the interpolants. We know from basic numerical analysis that

$$\begin{aligned} E(s) = UV - W(s) = \frac{1}{{\left( {N + 1} \right) !}}\frac{{{\partial ^{N + 1}}\left( {UV} \right) }}{{\partial {s^{N + 1}}}}\prod \limits _{i = 0}^N {\left( {s - {s_i}} \right) } \end{aligned}$$

(56)

and that $E(s)=0$ at precisely the $N+1$ interpolation points, $s_{i},\; i=0,1,\ldots ,N$. Similarly for the interpolant on the left,

$$\begin{aligned} {E_L}(\xi ) = U\left( {\frac{{\xi - 1}}{2}} \right) V\left( {\frac{{\xi - 1}}{2}} \right) - {W_L}(\xi ) = \frac{1}{{\left( {N + 1} \right) !}}\frac{{{\partial ^{N + 1}}\left( {UV} \right) }}{{\partial {\xi ^{N + 1}}}}\prod \limits _{i = 0}^N {\left( {\xi - {\xi _i}} \right) }.\qquad \end{aligned}$$

(57)

That interpolant vanishes at precisely $N+1$ points $\xi _{i}$ and nowhere else unless the derivative of the product vanishes.

The Gauss and Gauss–Lobatto points are symmetric and distinct about the middle of the interval and so there are twice as many (distinct) points $\xi _{i}$ on the interval $s\in [-1,0]$ as there are nodes $s_{i}$. Therefore, there exist nodes $\xi _{i}$ that are not equal to any node $s_{i}$. Let us choose, then, one such $\xi _{i}$ such that $s=(\xi _{i}-1)/2$ is not a node of the interpolation on s. Then $E_{L}\left( \xi _{i}\right) =0$, i.e., $U\left( (\xi _{i}-1)/2\right) V\left( (\xi _{i}-1)/2\right) =W_{L}\left( \xi _{i}\right)$, but $E\left( (\xi _{i}-1)/2\right) \ne 0$ so that $U\left( (\xi _{i}-1)/2\right) V\left( (\xi _{i}-1)/2\right) \ne W\left( (\xi _{i}-1)/2\right)$ and the result follows.