Accurate Asymptotic Preserving Boundary Conditions for Kinetic Equations on Cartesian Grids

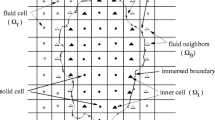
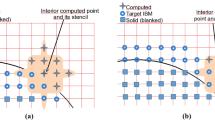
Abstract

A simple second-order scheme on Cartesian grids for kinetic equations is presented, with emphasis on the accurate enforcement of wall boundary conditions on immersed bodies. This approach preserves at the discrete level the asymptotic limit towards Euler equations up to the wall, thus ensuring a smooth transition towards the hydrodynamic regime. We investigate exact, numerical and experimental test cases for the BGK model in order to assess the accuracy of the method.

Appendix

We present the Newton–Raphson algorithm to compute the discrete Maxwellian distribution function. The first three moments of the distribution functions are known and we define the collision invariant $\mathbf{m }(\varvec{\xi })=(1,\varvec{\xi },\frac{1}{2}|\varvec{\xi }|^{2})^{T}$. The Maxwellian distribution function $M_{f}$ is computed such that, with the given quadrature rule:

$$\begin{aligned} \langle M_{f},\mathbf{m }(\varvec{\xi }) \rangle =\left( \begin{array}{c} \rho \\ \rho \mathbf{U }\\ E \end{array}\right) \end{aligned}$$

where $(\rho ,\rho \mathbf{U },E)=\langle f,\mathbf{m }(f)\rangle$, that is the moments are computed from $f$ approximately, using the given quadrature rule.

We are looking for $M_{f}$ under the form: $M_{f}=\text{ exp }(\varvec{\alpha }\cdot \mathbf{m }(\varvec{\xi }))$. Let us define the function:

$$\begin{aligned} \mathbf{F }(\varvec{\alpha })=\langle \text{ exp }(\varvec{\alpha }\cdot \mathbf{m }(\varvec{\xi })),\mathbf{m }(\varvec{\xi })\rangle -\underline{\varvec{\rho }} \end{aligned}$$

with $\underline{\varvec{\rho }}=(\rho ,\mathbf{U },E)^{T}$, the macroscopic variables computed from the moments of $f$. The discrete Maxwellian verifies $\mathbf{F }(\varvec{\alpha })=0$. Thus, the problem of computing the discrete Maxwellian reduces to find $\varvec{\alpha }$ such that $\mathbf{F }(\varvec{\alpha })=0$. This is done with a Newton–Raphson algorithm. The initial value of $\varvec{\alpha }$ corresponds to the continuous Maxwellian:

$$\begin{aligned} \varvec{\alpha }_{c}=\Big (\text{ ln }\left( {\displaystyle {\rho \over (2\pi T)^{N/2}}}\right) -{\displaystyle {|\mathbf{U }|^{2} \over 2T}},{\displaystyle {\mathbf{U } \over T}},-{\displaystyle {1 \over T}}\Big ) \end{aligned}$$

The algorithm is summarized as follows:

In the case of the reduced models, the algorithm is identical but the function $\mathbf{F }$ is defined as:

$$\begin{aligned} \mathbf{F }(\varvec{\alpha })&= \langle \widetilde{M_{\phi }},\mathbf{m }_{1}(\varvec{\xi })\rangle + \langle \widetilde{M_{\psi }}, \mathbf{e }_{3}\rangle - \langle f, \mathbf{m }_{1}(\varvec{\xi })\rangle \quad \text{ in } \text{1D }\\ \mathbf{F }(\varvec{\alpha })&= \langle \widetilde{M_{\phi }},\mathbf{m }_{2}(\varvec{\xi })\rangle + \langle \widetilde{M_{\psi }}, \mathbf{e }_{4}\rangle - \langle f, \mathbf{m }_{2}(\varvec{\xi })\rangle \quad \text{ in } \text{2D } \end{aligned}$$

where $\mathbf{e }_{3}=(0,0,1)^{T},\,\mathbf{e }_{4}=(0,0,0,1)^{T},\,\mathbf{m }_{1}(\varvec{\xi })=(1,\xi _{u},\frac{1}{2}|\xi _{u}|^{2})^{T},\,\mathbf{m }_{2}(\varvec{\xi })=(1,\xi _{u},\xi _{v},\frac{1}{2}(\xi _{u}^{2}+\xi _{v}^{2}))^{T}$. And:

$$\begin{aligned} \varvec{\alpha }_{c}&= \Big (\text{ ln }({\displaystyle {\rho \over \sqrt{2\pi T}}})-{\displaystyle {u^{2} \over 2T}},{\displaystyle {u \over T}},-{\displaystyle {1 \over T}}\Big )^{T}\quad \text{ in } \text{1D }\\ \varvec{\alpha }_{c}&= \Big (\text{ ln }({\displaystyle {\rho \over 2\pi T}})-{\displaystyle {u^{2}+v^{2} \over 2T}},{\displaystyle {u \over T}},{\displaystyle {v \over T}},-{\displaystyle {1 \over T}}\Big )^{T}\quad \text{ in } \text{2D } \end{aligned}$$

The Newton–Raphson algorithm give the expression of $\widetilde{M_{\phi }}$. $\widetilde{M_{\psi }}$ is then easily computed with the formula:

$$\begin{aligned} \widetilde{M_{\psi }}={\displaystyle {(N-d)T \over 2}}\widetilde{M_{\phi }} \end{aligned}$$