Skip to main content
SpringerLink
Log in

Computing the k-resilience of a synchronized multi-robot system

  • Published:
Journal of Combinatorial Optimization Aims and scope Submit manuscript

Abstract

We study an optimization problem that arises in the design of covering strategies for multi-robot systems. Consider a team of n cooperating robots traveling along predetermined closed and disjoint trajectories. Each robot needs to periodically communicate information to nearby robots. At places where two trajectories are within range of each other, a communication link is established, allowing two robots to exchange information, provided they are “synchronized”, i.e., they visit the link at the same time. In this setting a communication graph is defined and a system of robots is called synchronized if every pair of neighbors is synchronized. If one or more robots leave the system, then some trajectories are left unattended. To handle such cases in a synchronized system, when a live robot arrives to a communication link and detects the absence of the neighbor, it shifts to the neighboring trajectory to assume the unattended task. If enough robots leave, it may occur that a live robot enters a state of starvation, failing to permanently meet other robots during flight. To measure the tolerance of the system under this phenomenon we define the k-resilience as the minimum number of robots whose removal may cause k surviving robots to enter a state of starvation. We show that the problem of computing the k-resilience is NP-hard if k is part of the input, even if the communication graph is a tree. We propose algorithms to compute the k-resilience for constant values of k in general communication graphs and show more efficient algorithms for systems whose communication graph is a tree.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. In practice, the trajectories need not be congruent provided they are not too different in length and a suitable range of speeds is available to the robots.

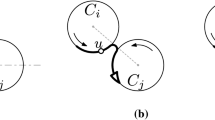
  2. Note that a path between two robots may have two arcs in the same trajectory, see Fig. 5c for an example. Therefore, distinct indexes i and j may exist such that \(C_i=C_j\). This does not affect the proof of the claim because it is not required that the arcs belong to different trajectories.

  3. Subset of nodes in a graph that does not contain two adjacent nodes.

  4. A caterpillar tree is a tree in which all the vertices are within distance 1 of a central path.

  5. \(T_{gcd}(n)=O(\log n(\log \log n)^2\log \log \log n)\) according to Stehlé and Zimmermann (2004).

  6. \(\tilde{O}\) notation hides polylogarithmic factors.

References

  • Acevedo JJ, Arrue BC, Díaz-Báñez JM, Ventura I, Maza I, Ollero A (2014) One-to-one coordination algorithm for decentralized area partition in surveillance missions with a team of aerial robots. J Intell Robot Syst 74(1–2):269–285

    Article  Google Scholar 

  • Alejo D, Díaz-Báñez JM, Cobano JA, Pérez-Lantero P, Ollero A (2013) The velocity assignment problem for conflict resolution with multiple aerial vehicles sharing airspace. J Intell Robot Syst 69(1–4):331–346

    Article  Google Scholar 

  • Bereg S, Caraballo LE, Díaz-Báñez JM, López MA (2017) Computing the k-resilience of a synchronized multi-robot system. In: 33rd European workshop on computational geometry (EuroCG17), pp 65–68

  • Bernard M, Kondak K, Maza I, Ollero A (2011) Autonomous transportation and deployment with aerial robots for search and rescue missions. J Field Robot 28(6):914–931

    Article  Google Scholar 

  • Brunner AP (2015) Isolation in synchronized drone formations. Master thesis, University of Denver

  • Casado LG, García I, Szabó PG, Csendes T (2001) Packing equal circles in a square II. — new results for up to 100 circles using the TAMSASS-PECS algorithm, pp 207–224. Springer US, Boston

  • Chevaleyre Y (2004) Theoretical analysis of the multi-agent patrolling problem. In: Proceedings IEEE/WIC/ACM international conference on intelligent agent technology, 2004 (IAT 2004), pp 302–308

  • Codenotti B, Gerace I, Vigna S (1998) Hardness results and spectral techniques for combinatorial problems on circulant graphs. Linear Algebra Appl 285(1):123–142

    Article  MathSciNet  MATH  Google Scholar 

  • Cusick TW (1973) View-obstruction problems. Aequ Math 9(2–3):165–170

    Article  MathSciNet  MATH  Google Scholar 

  • Czyzowicz J, Gąsieniec L, Kosowski A, Kranakis E (2011) Boundary patrolling by mobile agents with distinct maximal speeds. In: Demetrescu C, Halldórsson MM (eds), Algorithms—ESA 2011. Lecture notes in computer science, vol 6942. Springer, Berlin, pp 701–712

  • Díaz-Báñez JM, Caraballo LE, Lopez MA, Bereg S, Maza I, Ollero A (2015) The synchronization problem for information exchange between aerial robots under communication constraints. In: 2015 International conference on robotics and automation (ICRA), IEEE

  • Díaz-Báñez JM, Caraballo LE, Lopez M, Bereg S, Maza I, Ollero A (2017) A general framework for synchronizing a team of robots under communication constraints. IEEE Trans Robot PP(99):1–8

    Google Scholar 

  • Dumitrescu A, Ghosh A, Tóth CD (2014) On fence patrolling by mobile agents. Electron J Comb 21(3):P3–4

    MathSciNet  MATH  Google Scholar 

  • Kawamura A, Kobayashi Y (2015) Fence patrolling by mobile agents with distinct speeds. Distrib Comput 28(2):147–154

    Article  MathSciNet  MATH  Google Scholar 

  • Kawamura A, Soejima M (2015) Simple strategies versus optimal schedules in multi-agent patrolling. In: Paschos VT, Widmayer P (eds), Algorithms and complexity. Lecture notes in computer science, vol 9079. Springer, pp 261–273

  • Maranas Costas D, Floudas Christodoulos A, Pardalos Panos M (1995) New results in the packing of equal circles in a square. Discrete Math 142(1):287–293

    Article  MathSciNet  MATH  Google Scholar 

  • Pasqualetti F, Franchi A, Bullo F (2012) On cooperative patrolling: optimal trajectories, complexity analysis, and approximation algorithms. IEEE Trans Robot 28(3):592–606

    Article  Google Scholar 

  • Stehlé D, Zimmermann P (2004) A binary recursive gcd algorithm. In: Algorithmic number theory. Lecture notes in computer science, vol 3076. Springer, Berlin, pp 411–425

  • Szabó PG, Csendes T, Casado LG, García I (2001) Packing equal circles in a square I.—problem setting and bounds for optimal solutions. Springer US, Boston, pp 191–206

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, University of Texas at Dallas, 800 West Campbell Road, Richardson, TX, 75080, USA

    Sergey Bereg

  2. Higher Technical School of Engineering, University of Seville, Camino de los Descubrimientos, 41092, Seville, Spain

    Luis-Evaristo Caraballo & José-Miguel Díaz-Báñez

  3. Department of Computer Science, University of Denver, 2360 South Gaylord Street, Denver, CO, 80208, USA

    Mario A. Lopez

Authors
  1. Sergey Bereg
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luis-Evaristo Caraballo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. José-Miguel Díaz-Báñez
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mario A. Lopez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergey Bereg.

Additional information

A 4-page abstract of this paper appeared in the informal and non-selective workshop EuroCG17 (Bereg et al. 2017). This research has received funding from the projects GALGO (Spanish Ministry of Economy and Competitiveness, MTM2016-76272-R AEI/FEDER,UE) and CONNECT (EU-H2020/MSCA under Grant Agreement 2016-734922). Sergey Bereg was supported in part by NSF award CCF-1718994.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bereg, S., Caraballo, LE., Díaz-Báñez, JM. et al. Computing the k-resilience of a synchronized multi-robot system. J Comb Optim 36, 365–391 (2018). https://doi.org/10.1007/s10878-018-0297-3

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10878-018-0297-3

Keywords

Search

Navigation