Robust optimization of supply chain network design in fuzzy decision system

Abstract

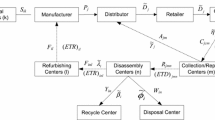
This paper presents a new robust optimization method for supply chain network design problem by employing variable possibility distributions. Due to the variability of market conditions and demands, there exist some impreciseness and ambiguousness in developing procurement and distribution plans. The proposed optimization method incorporates the uncertainties encountered in the manufacturing industry. The main motivation for building this optimization model is to make tools available for producers to develop robust supply chain network design. The modeling approach selected is a fuzzy value-at-risk (VaR) optimization model, in which the uncertain demands and transportation costs are characterized by variable possibility distributions. The variable possibility distributions are obtained by using the method of possibility critical value reduction to the secondary possibility distributions of uncertain demands and costs. We also discuss the equivalent parametric representation of credibility constraints and VaR objective function. Furthermore, we take the advantage of structural characteristics of the equivalent optimization model to design a parameter-based domain decomposition method. Using the proposed method, the original optimization problem is decomposed to two equivalent mixed-integer parametric programming sub-models so that we can solve the original optimization problem indirectly by solving its sub-models. Finally, we present an application example about a food processing company with four suppliers, five plants, five distribution centers and five customer zones. We formulate our application example as parametric optimization models and conduct our numerical experiments in the cases when the input data (demands and costs) are deterministic, have fixed possibility distributions and have variable possibility distributions. Experimental results show that our parametric optimization method can provide an effective and flexible way for decision makers to design a supply chain network.

Appendix

In this appendix, we deal with the method of PCV reduction, parametric possibility distributions of the reduced fuzzy variables and their properties.

Let $(\Gamma , \mathcal {A}, \tilde{\mathrm{P}}\mathrm{os})$ be a fuzzy possibility space (Liu and Liu 2010), where $\Gamma$ is an abstract space of generic elements $\gamma$ and $\mathcal {A}$ is a class of subsets of $\Gamma$ that is closed under arbitrary unions, intersections and complement in $\Gamma$. Assume that $\tilde{\xi }$ is a type-2 fuzzy variable with secondary possibility distribution $\tilde{\mu }_{\tilde{\xi }}(x)$. To reduce the uncertainty in $\tilde{\mu }_{\tilde{\xi }}(x)$, we employ the lower and upper possibility critical values (PCVs) of $\tilde{\mu }_{\tilde{\xi }}(x)$ as the representing values of the regular fuzzy variable (RFV) $\tilde{\mu }_{\tilde{\xi }}(x)$. According to Bai and Liu (2014), the lower PCV of $\tilde{\mu }_{\tilde{\xi }}(x)$ with respect to possibility, denoted by $\mathrm{VaR}^L_\alpha (\tilde{\mu }_{\tilde{\xi }}(x))$, is defined as

$$\begin{aligned} \mathrm{VaR}^L_\alpha (\tilde{\mu }_{\tilde{\xi }}(x))=\inf \{\,t\mid \mathrm{Pos}\{\tilde{\mu }_{\tilde{\xi }}(x)\le t\}\ge \alpha \}, \end{aligned}$$

while the upper PCV of $\tilde{\mu }_{\tilde{\xi }}(x)$ with respect to possibility, denoted by $\mathrm{VaR}^U_\alpha (\tilde{\mu }_{\tilde{\xi }}(x))$, is defined as

$$\begin{aligned} \mathrm{VaR}^U_\alpha (\tilde{\mu }_{\tilde{\xi }}(x))=\sup \{\,t\mid \mathrm{Pos}\{\tilde{\mu }_{\tilde{\xi }}(x)\ge t\}\ge \alpha \}. \end{aligned}$$

The method is referred to as the PCV reduction. The variables obtained by the methods of lower and upper PCV reduction are called the lower and upper reduced fuzzy variables, and denoted by $\xi ^L$ and $\xi ^U$, respectively.

We call $\tilde{\xi }$ a type-2 triangular fuzzy variable if its secondary possibility distribution $\tilde{\mu }_{\tilde{\xi }}(x)$ is the following RFV

$$\begin{aligned}&\!\!\!\left( \frac{x-r_1}{r_2-r_1}-\theta _l\min \left\{ \frac{x-r_1}{r_2-r_1}, \frac{r_2-x}{r_2-r_1}\right\} ,\frac{x-r_1}{r_2-r_1},\frac{x-r_1}{r_2-r_1}\right. \\&\quad \left. +\,\theta _r\min \left\{ \frac{x-r_1}{r_2-r_1},\frac{r_2-x}{r_2-r_1}\right\} \right) \end{aligned}$$

for any $x\in [r_1,r_2]$, and the next RFV

$$\begin{aligned}&\!\!\!\left( \frac{r_3-x}{r_3-r_2}-\theta _l\min \left\{ \frac{r_3-x}{r_3-r_2}, \frac{x-r_2}{r_3-r_2}\right\} ,\frac{r_3-x}{r_3-r_2},\frac{r_3-x}{r_3-r_2}\right. \\&\left. \quad +\,\theta _r\min \left\{ \frac{r_3-x}{r_3-r_2},\frac{x-r_2}{r_3-r_2}\right\} \right) \end{aligned}$$

for any $x\in [r_2,r_3]$, where $\theta _l,\theta _r\in [0,1]$ are two parameters characterizing the degree of uncertainty that $\tilde{\xi }$ takes the value $x$. For convenience, we denote a type-2 triangular fuzzy variable $\tilde{\xi }$ with the above secondary possibility distribution by $(\tilde{r}_1,\tilde{r}_2,\tilde{r}_3;\theta _l,\theta _r)$.

Theorem 1

Let $\tilde{\xi }=(\tilde{r}_1,\tilde{r}_2,\tilde{r}_3;\theta _l,\theta _r)$ be a type-2 triangular fuzzy variable. If we denote $\theta =(\theta _l,\theta _r)$, then the reduced fuzzy variables $\xi ^L$ and $\xi ^U$ have the following parametric possibility distributions

$$\begin{aligned}&\!\!\!\mu _{\xi ^L}(x;\theta ,\alpha )\nonumber \\&\quad =\left\{ \begin{array}{ll} (1-\theta _l+\alpha \theta _l)\frac{x-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [r_1,\frac{r_1+r_2}{2}]\\ \frac{(1+\theta _l-\alpha \theta _l)x-(1-\alpha )\theta _lr_2-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [\frac{r_1+r_2}{2},r_2]\\ \frac{-(1+\theta _l-\alpha \theta _l)x+(1-\alpha )\theta _lr_2+r_3}{r_3-r_2}, &{} \mathrm{if}~~x\in [r_2,\frac{r_2+r_3}{2}]\\ (1-\theta _l+\alpha \theta _l)\frac{r_3-x}{r_3-r_2}, &{}\mathrm{if}~~x\in [\frac{r_2+r_3}{2},r_3], \end{array}\right. \end{aligned}$$

(12)

$$\begin{aligned}&\!\!\!\mu _{\xi ^U}(x;\theta ,\alpha )\nonumber \\&\quad =\left\{ \begin{array}{ll} (1+\theta _r-\alpha \theta _r)\frac{x-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [r_1,\frac{r_1+r_2}{2}]\\ \frac{(1-\theta _r+\alpha \theta _r)x+(1-\alpha )\theta _rr_2-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [\frac{r_1+r_2}{2},r_2]\\ \frac{-(1-\theta _r+\alpha \theta _r)x-(1-\alpha )\theta _rr_2+r_3}{r_3-r_2}, &{} \mathrm{if}~~x\in [r_2,\frac{r_2+r_3}{2}]\\ (1+\theta _r-\alpha \theta _r)\frac{r_3-x}{r_3-r_2}, &{}\mathrm{if}~~x\in [\frac{r_2+r_3}{2},r_3]. \end{array}\right. \end{aligned}$$

(13)

Proof

We only prove Eq. (12), and Eq. (13) can be proved similarly.

Note that the secondary possibility distribution $\tilde{\mu }_{\tilde{\xi }}(x)$ of $\tilde{\xi }$ is the following triangular RFV

$$\begin{aligned}&\!\!\!\left( \frac{x-r_1}{r_2-r_1}-\theta _l\min \left\{ \frac{x-r_1}{r_2-r_1}, \frac{r_2-x}{r_2-r_1}\right\} ,\frac{x-r_1}{r_2-r_1},\frac{x-r_1}{r_2-r_1}\right. \\&\quad \left. +\,\theta _r\min \left\{ \frac{x-r_1}{r_2-r_1},\frac{r_2-x}{r_2-r_1}\right\} \right) \end{aligned}$$

for any $x\in [r_1,r_2]$, and

$$\begin{aligned}&\!\!\!\left( \frac{r_3-x}{r_3-r_2}-\theta _l\min \left\{ \frac{r_3-x}{r_3-r_2}, \frac{x-r_2}{r_3-r_2}\right\} ,\frac{r_3-x}{r_3-r_2},\frac{r_3-x}{r_3-r_2}\right. \\&\quad \left. +\,\theta _r\min \left\{ \frac{r_3-x}{r_3-r_2},\frac{x-r_2}{r_3-r_2}\right\} \right) \end{aligned}$$

for any $x\in [r_2,r_3]$. Since $\xi ^L$ is the lower PCV reduction of $\tilde{\xi }$, we have

$$\begin{aligned}&\mu _{\xi ^L}(x;\theta ,\alpha )\\&\quad =\mathrm{Pos}\{\xi ^L=x\}\\&\quad =\left\{ \begin{array}{ll} \frac{x-r_1}{r_2-r_1}-(1-\alpha )\theta _l\min \left\{ \frac{x-r_1}{r_2-r_1}, \frac{r_2-x}{r_2-r_1}\right\} , &{} \mathrm{if}~~x\in [r_1,r_2]\\ \frac{r_3-x}{r_3-r_2}-(1-\alpha )\theta _l\min \left\{ \frac{r_3-x}{r_3-r_2}, \frac{x-r_2}{r_3-r_2}\right\} , &{} \mathrm{if}~~x\in [r_2,r_3] \end{array}\right. \\&\quad =\left\{ \begin{array}{ll} (1-\theta _l+\alpha \theta _l)\frac{x-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [r_1,\frac{r_1+r_2}{2}]\\ \frac{(1+\theta _l-\alpha \theta _l)x-(1-\alpha )\theta _lr_2-r_1}{r_2-r_1}, &{} \mathrm{if}~~x\in [\frac{r_1+r_2}{2},r_2]\\ \frac{-(1+\theta _l-\alpha \theta _l)x+(1-\alpha )\theta _lr_2+r_3}{r_3-r_2}, &{} \mathrm{if}~~x\in [r_2,\frac{r_2+r_3}{2}]\\ (1-\theta _l+\alpha \theta _l)\frac{r_3-x}{r_3-r_2}, &{}\mathrm{if}~~x\in [\frac{r_2+r_3}{2},r_3], \end{array} \right. \end{aligned}$$

which completes the proof of Eq. (12). $\square$

Theorem 2

Let $\tilde{\xi }=(\tilde{r}_1,\tilde{r}_2,\tilde{r}_3;\theta _l,\theta _r)$ be a type-2 triangular fuzzy variable, and $\xi ^L$ its lower PCV reduced fuzzy variable.

• (i) If  $\beta \in (0,(1-(1-\alpha )\theta _l)/4]$, then $\mathrm{Cr}\{\xi ^L\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \frac{(1-2\beta -(1-\alpha )\theta _l)r_1+2\beta r_2}{1-\theta _l+\alpha \theta _l}\le r. \end{aligned}$$

• (ii) If  $\beta \in ((1-(1-\alpha )\theta _l)/4,0.5]$, then $\mathrm{Cr}\{\xi ^L\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \frac{(1-2\beta )r_1+(2\beta +(1-\alpha )\theta _l)r_2}{1+\theta _l-\alpha \theta _l}\le r. \end{aligned}$$

• (iii) If  $\beta \in (0.5,(3+(1-\alpha )\theta _l)/4]$, then $\mathrm{Cr}\{\xi ^L\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \frac{(2-2\beta +(1-\alpha )\theta _l)r_2+(2\beta -1)r_3}{1+\theta _l-\alpha \theta _l}\le r. \end{aligned}$$

• (iv) If  $\beta \in ((3+(1-\alpha )\theta _l)/4,1]$, then $\mathrm{Cr}\{\xi ^L\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \frac{(2-2\beta )r_2+(2\beta -1-(1-\alpha )\theta _l)r_3}{1-\theta _l+\alpha \theta _l}\le r. \end{aligned}$$

Proof

We only prove assertions $(i)$-$(ii)$, and assertions $(iii)$-$(iv)$ can be proved similarly.

Since $\xi ^L$ is the lower reduced fuzzy variable of $\tilde{\xi }$, its parametric possibility distribution $\mu _{\xi ^L}(x)$ is given by Eq. (12).

If $\beta \le 0.5$, then by the definition of credibility measure (Liu and Liu 2002), we have

$$\begin{aligned} \mathrm{Cr}\{\xi ^L\le r\}&= \frac{1}{2}\left( 1+\sup _{x\le r}\mu _{\xi ^L} (x;\theta ,\alpha )-\sup _{x>r}\mu _{\xi ^L}(x;\theta ,\alpha )\right) \\&= \frac{1}{2}\sup _{x\le r}\mu _{\xi ^L}(x;\theta ,\alpha ). \end{aligned}$$

Thus $\mathrm{Cr}\{\xi ^L\le r\}\ge \beta$ is equivalent to $\sup _{x\le r}\mu _{\xi ^L}(x;\theta ,\alpha )\ge 2\beta$. If we denote

$$\begin{aligned} \xi ^L_{\inf ,\mathrm{Pos}}(\beta )=\inf \left\{ r\mid \sup _{x\le r} \mu _{\xi ^L}(x;\theta ,\alpha )\ge \beta \right\} \end{aligned}$$

for $\beta \in (0,1]$, then we have $\xi ^L_{\inf ,\mathrm{Pos}}(2\beta )\le r$.

Note that $\mu _{\xi ^L}((r_1+r_2)/2)=(1-(1-\alpha )\theta _l)/2$. If $0<2\beta \le (1-(1-\alpha )\theta _l)/2$, i.e., $\beta \in (0,(1-(1-\alpha )\theta _l)/4]$, then $\xi ^L_{\inf ,\mathrm{Pos}}(2\beta )$ is the solution of the following equation

$$\begin{aligned} (1-\theta _l+\alpha \theta _l)\frac{x-r_1}{r_2-r_1}-2\beta =0. \end{aligned}$$

Solving the above equation, we have

$$\begin{aligned} \xi ^L_{\inf ,\mathrm{Pos}}(2\beta )=\frac{(1-2\beta -(1-\alpha )\theta _l)r_1+2\beta r_2}{1-\theta _l+\alpha \theta _l}. \end{aligned}$$

On the other hand, if $1\ge 2\beta >(1-(1-\alpha )\theta _l)/2$, i.e., $\beta \in ((1-(1-\alpha )\theta _l)/4,0.5]$, then $\xi ^L_{\inf ,\mathrm{Pos}}(2\beta )$ is the solution of the following equation

$$\begin{aligned} \frac{(1+\theta _l-\alpha \theta _l)x-(1-\alpha )\theta _lr_2-r_1}{r_2-r_1}-2\beta =0. \end{aligned}$$

Solving the above equation, we have

$$\begin{aligned} \xi ^L_{\inf ,\mathrm{Pos}}(2\beta )=\frac{(1-2\beta )r_1+(2\beta +(1-\alpha ) \theta _l)r_2}{1+\theta _l-\alpha \theta _l}. \end{aligned}$$

The proof of theorem is complete. $\square$

Theorem 3

Let $\tilde{\xi }_i=(\tilde{r}_1^i,\tilde{r}_2^i,\tilde{r}_3^i;\theta _{l,i},\theta _{r,i})$ be a type-2 triangular fuzzy variable, and $\xi _i^U$ its upper PCV reduced fuzzy variable for $i=1,2,\ldots ,n$. Suppose $\tilde{\xi }_1,\tilde{\xi }_2,\ldots ,\tilde{\xi }_n$ are mutually independent, $(1-\alpha _1)\theta _{r,1}\le (1-\alpha _2)\theta _{r,2}\le \cdots \le (1-\alpha _n)\theta _{r,n}$ and $k_i\ge 0$ for $i=1,2,\ldots ,n$.

• (i) If  $\beta \in (0,(1+(1-\alpha _1)\theta _{r,1})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^nk_i\frac{(1-2\beta +(1-\alpha _i)\theta _{r,i})r^i_1+2\beta r^i_2}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

• (ii) If there exists an $i_0$, $1\le i_0<n$ such that  $\beta \in ((1+(1-\alpha _{i_0})\theta _{r,i_0})/4,(1+(1-\alpha _{i_0+1})\theta _{r,i_0+1})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned}&\sum _{i=1}^{i_0}k_i\frac{(1-2\beta )r^i_1+(2\beta -(1-\alpha _i) \theta _{r,i})r^i_2}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\\&\quad + \sum _{i=i_0+1}^nk_i\frac{(1-2\beta +(1-\alpha _i)\theta _{r,i})r^i_1+2\beta r^i_2}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

• (iii) If  $\beta \in ((1+(1-\alpha _n)\theta _{r,n})/4,0.5]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^nk_i\frac{(1-2\beta )r^i_1+(2\beta -(1-\alpha _i) \theta _{r,i})r^i_2}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

• (iv) If  $\beta \in (0.5,(3-(1-\alpha _n)\theta _{r,n})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^nk_i\frac{(2-2\beta -(1-\alpha _i)\theta _{r,i})r^i_2 +(2\beta -1)r^i_3}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

• (v) If there exists an $i_0$, $1\le i_0<n$ such that  $\beta \in ((3-(1-\alpha _{i_0+1})\theta _{r,i_0+1})/4,(3-(1-\alpha _{i_0})\theta _{r,i_0})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned}&\sum _{i=1}^{i_0}k_i\frac{(2-2\beta -(1-\alpha _i)\theta _{r,i})r^i_2 +(2\beta -1)r^i_3}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\\&\qquad + \sum _{i=i_0+1}^nk_i\frac{2(1-\beta )r^i_2+(2\beta -1+(1-\alpha _i)\theta _{r,i}) r^i_3}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\\&\quad \le r. \end{aligned}$$

• (vi) If $\beta \in ((3-(1-\alpha _1)\theta _{r,1})/4,1]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

  $$\begin{aligned} \sum _{i=1}^nk_i\frac{2(1-\beta )r^i_2+(2\beta -1+(1-\alpha _i)\theta _{r,i}) r^i_3}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

Proof

We only prove assertions $(i)$-$(iii)$, and assertions $(iv)$-$(vi)$ can be proved similarly.

Since $\xi ^U_i$ is the upper reduced fuzzy variable of $\tilde{\xi }_i$, its parametric possibility distribution is as follows

$$\begin{aligned}&\!\!\!\mu _{\xi _i^U}(x;\theta ,\alpha )\\&\quad =\left\{ \begin{array}{ll} (1+\theta _{r,i}-\alpha _i\theta _{r,i})\frac{x-r^i_1}{r^i_2-r^i_1}, &{} \mathrm{if}~~x\in [r^i_1,\frac{r^i_1+r^i_2}{2}]\\ \frac{(1-\theta _{r,i}+\alpha _i\theta _{r,i})x+(1-\alpha _i)\theta _{r,i}r^i_2-r^i_1}{r^i_2-r^i_1}, &{} \mathrm{if}~~x\in [\frac{r^i_1+r^i_2}{2},r^i_2]\\ \frac{-(1-\theta _{r,i}+\alpha _i\theta _{r,i})x-(1-\alpha _i)\theta _{r,i}r^i_2+r^i_3}{r^i_3-r^i_2}, &{} \mathrm{if}~~x\in [r^i_2,\frac{r^i_2+r^i_3}{2}]\\ (1+\theta _{r,i}-\alpha _i\theta _{r,i})\frac{r^i_3-x}{r^i_3-r^i_2}, &{}\mathrm{if}~~x\in [\frac{r^i_2+r^i_3}{2},r^i_3]. \end{array} \right. \end{aligned}$$

Denote $\xi =\sum _{i=1}^nk_i\xi ^U_i$. If $\beta \le 0.5$, then we have

$$\begin{aligned} \mathrm{Cr}\{\xi \le r\}&= \frac{1}{2}\left( 1+\sup _{x\le r}\mu _{\xi } (x;\theta ,\alpha )-\sup _{x>r}\mu _{\xi }(x;\theta ,\alpha )\right) \\&= \frac{1}{2}\sup _{x\le r}\mu _{\xi }(x;\theta ,\alpha ). \end{aligned}$$

Thus $\mathrm{Cr}\{\xi \le r\}\ge \beta$ is equivalent to $\sup _{x\le r}\mu _{\xi }(x;\theta ,\alpha )\ge 2\beta$. If we denote

$$\begin{aligned} \xi _{\inf ,\mathrm{Pos}}(\beta )=\inf \left\{ r\mid \sup _{x\le r} \mu _{\xi }(x;\theta ,\alpha )\ge \beta \right\} \end{aligned}$$

for $\beta \in (0,1]$, then we have $\xi _{\inf ,\mathrm{Pos}}(2\beta )\le r$.

Since $\xi ^U_1,\xi ^U_2,\ldots ,\xi ^U_n$ are mutually independent fuzzy variables, by Liu and Gao (2007), we have

$$\begin{aligned} \xi _{\inf ,\mathrm{Pos}}(2\beta )&= \left( \sum _{i=1}^nk_i\xi ^U_i\right) _{\inf ,\mathrm{Pos}}(2\beta )\\&= \sum _{i=1}^nk_i\xi ^U_{i,\inf ,\mathrm{Pos}}(2\beta )\le r. \end{aligned}$$

Note that $\mu _{\xi _i^U}((r^i_1+r^i_2)/2)=(1+(1-\alpha _i)\theta _{r,i})/2$. If $0<2\beta \le (1+(1-\alpha _i)\theta _{r,i})/2$, i.e., $\beta \in (0,(1+(1-\alpha _i)\theta _{r,i})/4]$, then for each $i$, $\xi ^U_{i,\inf ,\mathrm{Pos}}(2\beta )$ is the solution of the following equation

$$\begin{aligned} (1+\theta _{r,i}-\alpha _i\theta _{r,i})\frac{x-r^i_1}{r^i_2-r^i_1}-2\beta =0. \end{aligned}$$

Solving the above equation, we have

$$\begin{aligned} \xi ^U_{i,\inf ,\mathrm{Pos}}(2\beta )=\frac{(1-2\beta +(1-\alpha _i)\theta _{r,i})r^i_1+2\beta r^i_2}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}. \end{aligned}$$

On the other hand, if $1\ge 2\beta >(1+(1-\alpha _i)\theta _{r,i})/2$, i.e., $\beta \in ((1+(1-\alpha _i)\theta _{r,i})/4,0.5]$, then for each $i$, $\xi ^U_{i,\inf ,\mathrm{Pos}}(2\beta )$ is the solution of the following equation

$$\begin{aligned} \frac{(1-\theta _{r,i}+\alpha _i\theta _{r,i})x+(1-\alpha _i) \theta _{r,i}r^i_2-r^i_1}{r^i_2-r^i_1}-2\beta =0. \end{aligned}$$

Solving the above equation, we have

$$\begin{aligned} \xi ^U_{i,\inf ,\mathrm{Pos}}(2\beta )=\frac{(1-2\beta )r^i_1+(2\beta -(1-\alpha _i) \theta _{r,i})r^i_2}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}. \end{aligned}$$

According to the inequalities $(1-\alpha _1)\theta _{r,1}\le (1-\alpha _2)\theta _{r,2}\le \cdots \le (1-\alpha _n)\theta _{r,n}$, we have the following results.

If $0<2\beta \le (1+(1-\alpha _1)\theta _{r,1})/2$, then $\beta \le (1+(1-\alpha _i)\theta _{r,i})/4$ for $i=1,2,\ldots ,n$. Therefore, if  $\beta \in (0,(1+(1-\alpha _1)\theta _{r,1})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

$$\begin{aligned} \sum _{i=1}^nk_i\frac{(1-2\beta +(1-\alpha _i)\theta _{r,i})r^i_1+2\beta r^i_2}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

If there exists an $i_0$, $1\le i_0<n$ such that $(1+(1-\alpha _{i_0})\theta _{r,i_0})/2<2\beta \le (1+(1-\alpha _{i_0+1})\theta _{r,i_0+1})/2$, i.e., $\beta \in ((1+(1-\alpha _{i_0})\theta _{r,i_0})/4,(1+(1-\alpha _{i_0+1})\theta _{r,i_0+1})/4]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

$$\begin{aligned}&\sum _{i=1}^{i_0}k_i\frac{(1-2\beta )r^i_1+(2\beta -(1-\alpha _i) \theta _{r,i})r^i_2}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\\&\quad + \sum _{i=i_0+1}^nk_i\frac{(1-2\beta +(1-\alpha _i)\theta _{r,i})r^i_1+2\beta r^i_2}{1+\theta _{r,i}-\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

If $1\ge 2\beta >(1+(1-\alpha _n)\theta _{r,n})/2$, then $\beta \ge (1+(1-\alpha _i)\theta _{r,i})/4$ for $i=1,2,\ldots ,n$. Therefore, if  $\beta \in ((1+(1-\alpha _n)\theta _{r,n})/4,0.5]$, then $\mathrm{Cr}\{\sum _{i=1}^nk_i\xi ^U_i\le r\}\ge \beta$ is equivalent to

$$\begin{aligned} \sum _{i=1}^nk_i\frac{(1-2\beta )r^i_1+(2\beta -(1-\alpha _i) \theta _{r,i})r^i_2}{1-\theta _{r,i}+\alpha _i\theta _{r,i}}\le r. \end{aligned}$$

The proof of theorem is complete. $\square$