Dynamics of ramping bursts in a respiratory neuron model

Abstract

Intensive computational and theoretical work has led to the development of multiple mathematical models for bursting in respiratory neurons in the pre-Bötzinger Complex (pre-BötC) of the mammalian brainstem. Nonetheless, these previous models have not captured the pre-inspiratory ramping aspects of these neurons’ activity patterns, in which relatively slow tonic spiking gradually progresses to faster spiking and a full-blown burst, with a corresponding gradual development of an underlying plateau potential. In this work, we show that the incorporation of the dynamics of the extracellular potassium ion concentration into an existing model for pre-BötC neuron bursting, along with some parameter adjustments, suffices to induce this ramping behavior. Using fast-slow decomposition, we show that this activity can be considered as a form of parabolic bursting, but with burst termination at a homoclinic bifurcation rather than as a SNIC bifurcation. We also investigate the parameter-dependence of these solutions and show that the proposed model yields a greater dynamic range of burst frequencies, durations, and duty cycles than those produced by other models in the literature.

Appendices

Appendix 1

1.1 Constants and parameters

The complete list of parameters used for this model is shown below. Certain parameters were fixed for all simulations, while others were varied for different tests. These instances will be noted.

Universal & Experimental Constants:

• Elementary Charge: $q=1.602 \times 10^{-19}$ C.

• Avogadro Constant: $N_{A} = 6.022 \times 10^{23}$ $\frac{1}{mol}$.

• Unit Time Constant: $\tau = 1000$ $\frac{ms}{s}$.

• Ratio of Volumes: $\beta = 14.555$ (modified from Barreto and Cressman (2011), $\beta = 7$).

• Membrane Capacitance: $C = 36$ pF (taken from Rybak et al. (2007)).

Derived Constants:

• Current Conversion Constant: $\gamma = 7.214 \times 10^{-3}$ $\frac{mM}{s \cdot pA}$ (derived in Appendix 2).

Maximal Conductances:

• $\bar{g}_{Na} = 150$ nS (taken from Jasinski et al. (2013)).

• $\bar{g}_{NaP} = 5$ nS (taken from Bacak et al. (2016b)). Varied as parameter in Sect. 4.

• $\bar{g}_{K} = 160$ nS (taken from Jasinski et al. (2013)).

• $\bar{g}_{L} = 2.5$ nS (taken from Jasinski et al. (2013), $\bar{g}_{L} \in [ 2,3 ]$). Varied as parameter in Sect. 4.

• $\bar{g}_{Syn} = 0.365$ nS. (Introduced in this paper to represent constant synaptic drive, in contrast to model in Bacak et al. (2016b) where $\bar{g}_{Syn} = 0$). Varied as parameter in Sect. 4.

Ion Concentrations & Reversal Potentials:

• $[Na^{+}]_{out}=120$ mM (taken from Jasinski et al. (2013)).

• $[Na^{+}]_{in}=15$ mM (taken from Izhikevich (2007), $[Na^{+}]_{in} \in [5, 15]$ mM).

• $E_{Na} = 26.7 \cdot \log {\frac{[Na^{+}]_{out}}{[Na^{+}]_{in}}} = 55.5$ mV. (Consistent with Rybak et al. (2007), $E_{Na} = 55$ mV).

• $[K^{+}]_{in} = 160$ mM (modified from Izhikevich (2007); Jasinski et al. (2013), $[K^{+}]_{in} = 140$ mM).

• $E_{L} = -68$ mV (taken from Jasinski et al. (2013)).

• $E_{Syn} = -10$ mV (taken from Jasinski et al. (2013)).

Parameters for Fast Sodium $(I_{Na})$ and Persistent Sodium ($I_{NaP}$):

• $V_{m_{Na}} = -43.8$ mV, $k_{m_{Na}} = 6$ mV, $V_{\tau _{m_{Na}}} = -43.8$ mV, $k_{\tau _{m_{Na}}} = 14$ mV.

• $V_{h_{Na}} = -67.5$ mV, $k_{h_{Na}} = -11.8 mV$, $V_{\tau _{h_{Na}}} = -67.5$ mV, $k_{\tau _{h_{Na}}} = -12.8$ mV.

• $V_{m_{NaP}} = -47.1$ mV, $k_{m_{NaP}} = 3.1$ mV, $V_{\tau _{m_{NaP}}} = -47.1$ mV, $k_{\tau _{m_{NaP}}} = 6.2$ mV.

• $V_{h_{NaP}} = -60$ mV, $k_{h_{NaP}} = -9$ mV, $V_{\tau _{h_{NaP}}} = -60$ mV, $k_{\tau _{h_{NaP}}} = 9$ mV.

• $\bar{\tau }_{m_{Na}} =0.25$ mS, $\bar{\tau }_{h_{Na}} = 8.46$ mS, $\bar{\tau }_{m_{NaP}} =1$ mS, $\bar{\tau }_{h_{NaP}} = 5000$ mS.

• All of these parameters were taken directly from Bacak et al. (2016a), with the exception of $k_{h_{Na}}$, which was altered from a value of $-10.8$ mV to the listed value of $-11.8$ mV.

Parameters for Delayed Rectifier Potassium Current $(I_{K})$:

• $n_{A} = 0.01$ $\frac{1}{mV}$, $n_{A_{V}} = 44$ mV, $n_{A_{k}} = 5$ mV, $n_{B} = 0.17$, $n_{B_{V}} = 49$ mV, $n_{B_{k}} = 40$ mV.

• All values taken from Bacak et al. (2016b).

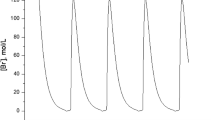
Parameters for Diffusion of Extracellular Potassium $([K^{+}]_{out})$:

• $k_{bath}=4$ mM (taken from Barreto and Cressman (2011)).

• $\tau _{diff} = 750$ mS (numerically equivalent to the formulation in Barreto and Cressman (2011), which uses $\frac{1}{\tau _{diff}} \equiv \frac{\epsilon }{\tau }$, where $\epsilon =1.333$ Hz and $\tau =1000 \frac{\mathrm{mS}}{\mathrm{s}}$).

Parameters for Glia:

• $\bar{G} = 10 \frac{mM}{s}$, $\bar{K} = 5 mM$, ${z_{K}} = 6 \frac{1}{mM}$.

• These parameter values were altered from those in Barreto and Cressman (2011). In Barreto and Cressman (2011), the concentration of $[K^{+}]_{out}$ remains far below the mid-point value of the sigmoidal function in Eq. (10). The parameters were adjusted such that the range of dynamic $[K^{+}]_{out}$ was distributed over the midpoint of Eq. (10), ensuring that the nonlinear behavior of glial cells was represented.

Appendix 2

1.1 Derivation of $\gamma$ 

Our initial assumption is that the neuron is roughly spherical, or rather that the majority of the cell’s volume is contained in a sphere. From Barreto and Cressman (2011), the radius of the neuron is taken to be approximately $r=7.0$ $\mu \mathrm{m}$. Hence, the internal volume of the neuron can be approximated as $V_{in} = \frac{4}{3} \pi r^3 = 1.44 \times 10^{-9}$ mL.

The internal concentration $c_{in}$ can be determined from the total number of ions N, the internal volume $V_{in}$, and Avogadro’s Constant $N_{A}$:

$$\begin{aligned} c_{in} = N \cdot \frac{1}{N_A} \cdot \frac{1}{V_{in}}. \end{aligned}$$

Note that the ions we are measuring concentrations of are $Na^{+}$ and $K^{+}$, both of which have a $+1$ charge. Letting $q=1.60 \times 10^{-19}$ C, we can express the concentration in terms of total charge, Q:

$$\begin{aligned} c_{in} = \frac{N}{V_{in} N_{A}} \cdot \frac{q}{q} = \frac{Q}{q V_{in} N_{A}}. \end{aligned}$$

Differentiating, we get:

$$\begin{aligned} \frac{dc_{in}}{dt} = \frac{d}{dt} \left( \frac{Q}{q V_{in} N_{A}} \right) = \frac{dQ}{dt} \cdot \frac{1}{q V_{in} N_{A}} = I \cdot \frac{1}{q V_{in} N_{A}}. \end{aligned}$$

By taking the ratio of this expression to the current, we can determine:

$$\begin{aligned} \gamma \equiv \frac{1}{q V_{in} N_{A}} = 7.2 \times 10^{3} \frac{\mathrm{mol}}{\mathrm{C} \cdot \mathrm{mL}}. \end{aligned}$$

By the following dimensional analysis manipulation, we obtain:

$$\begin{aligned} \frac{\mathrm{mol}}{\mathrm{C} \cdot \mathrm{mL}} &\cdot \left( 10^{3} \frac{\mathrm{mmol}}{\mathrm{mol}} \cdot 10^{3} \frac{\mathrm{mL}}{\mathrm{L}} \cdot \frac{\mathrm{mM} \cdot \mathrm{L}}{\mathrm{mmol}} \cdot \frac{\mathrm{C}}{\mathrm{A} \cdot \mathrm{s}} \right.\\& \left.\cdot 10^{-12}\frac{\mathrm{A}}{\mathrm{pA}} \cdot 10^{-3} \frac{\mathrm{s}}{\mathrm{ms}} \right) = 10^{-9} \frac{\mathrm{mM}}{\mathrm{ms} \cdot \mathrm{pA}}. \end{aligned}$$

Thus, we conclude:

$$\begin{aligned} \gamma = 7.214 \times 10^{-6} \text { }\frac{\mathrm{mM}}{\mathrm{ms}} \cdot \frac{1}{\mathrm{pA}}. \end{aligned}$$

(12)

Appendix 3

1.1 A closer look at transitions in behavior as $E_{K}$ is varied

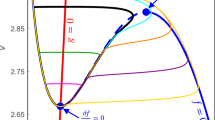
As illustrated in Fig. 1, if the $K^{+}$ concentration is held fixed, then shifting the $E_{K}$ value has a clear effect on the long-term periodic behavior of the model neuron. Each periodic behavior, whether tonic spiking or bursting, can be depicted as a stable limit cycle projected to the ($h_{NaP},V$) phase space. As shown in Fig. 3, with increases in $E_K$, the stable oscillation switches from tonic spiking to bursting, and then, with additional increases, from bursting back to spiking. Which behavior arises depends on whether the periodic orbit family of the fast subsystem terminates in a SNIC bifurcation or a homoclinic bifurcation and on where this termination lies relative to the $h_{NaP}$ nullcline.

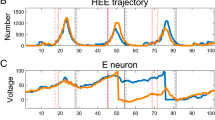
Here we construct a bifurcation diagram to present in more detail the changes in stable periodic behavior that occur with $E_{K}$ as a bifurcation parameter. More specifically, when the neuronal system exhibits bursting, each burst is composed of a finite number of action potentials, each associated with an approximately constant $V, h_{NaP}$. Therefore, for each fixed $h_{NaP}$, we identify the corresponding periodic spiking or bursting attractor and record the $h_{NaP}$ value at which each spike occurs within this attractor (Fig. 8).

Fig. 8

Bifurcation diagram of attracting dynamics of the neuronal model with $[K ^{+}]_{out}$ (and hence $E_{K}$) used as the bifurcation parameter, varied in steps of 0.001 mV. (A) Bifurcation diagram over the entire bursting interval. Each blue dot represents an $h_{NaP}$ value on a single spike within the attractor for the corresponding $E_K$. Insets show voltage and $h_{NaP}$ time courses at the fixed values of $E_K$ marked by the numbered vertical dashed lines on the diagram. (B-C) Zoomed views of different parts of the diagram in (A)

In this bifurcation diagram, each dot denotes the value of $h_{NaP}$ at which an action potential occurs during 80 seconds of simulated bursting behavior, for a corresponding fixed value of $E_K$. For each $E_K$, the spikes from the first 55 seconds of neuron simulation are not shown, such that the diagram omits the transient state and only reflects the attractors of the system. For sufficiently low $E_K$, the stable dynamics consists of periodic tonic spiking, characterized by a single $h_{NaP}$ value for each $E_K$ in the diagram. As $E_K$ increases, the transition from a tonic spiking state to a bursting state appears to arise through a chaotic period doubling mechanism (Fig. 8A,B), estimated numerically to occur just above $E_K = -91.2$ mV.

The transition from bursting back to tonic spiking, depicted in Fig. 8A,C, is less clear cut. The spike branch at highest $h_{NaP}$ values seems to disappear instantly as $E_K$ increases. We expect that this change is related to the phenomena shown in Figs. 1C, 3D. In the solution displayed in Fig. 1C, it appears that bursting is about to begin, but instead a plateau of depolarization block occurs. From Fig. 3D, we can appreciate that the AH point has moved to smaller $h_{NaP}$ than that of the fold point, such that the trajectory’s initial jump to the active phase does not yield a full spike. Only after $h_{NaP}$ drifts to lower values, below the AH point, can spiking ensue. With an additional increase in $E_K$ to just below $-83.1$ mV, most of the remaining spike branches disappear together, leaving only a cluster of values near $h_{NaP}=0.155$. We also notice pockets of variability in $h_{NaP}$ as $E_K$ varies between $-83.4$ and $-83.1$ mV. Interestingly, inspection of the voltage trace suggests that periodic spiking begins at about $E_K = -82.6$ mV, above the value at which most of the collection of $h_{NaP}$ branches disappears.

Elucidating the details of this bifurcation is beyond the scope of our consideration of ramping bursts in the full model and remains for future inquiry, which would require more detailed simulations and analysis.

Appendix 4

1.1 1-fast-2-slow Analysis

The dynamics of ramping bursts can be understood through a fast-slow decomposition analysis. The first step was the fast-slow decomposition analysis discussed in Sect. 3.2. As shown in Fig. 3, this analysis involved fixing $[K^{+}]_{out}$ and determining the geometry that governs the model trajectory in the $\left( V, h_{NaP} \right)$-phase space. This analysis can naturally be extended into a three-dimensional fast-slow decomposition by including $[K^{+}]_{out}$, or equivalently $E_K$, as a second slow variable. The various important geometric objects identified with fixed $[K^{+}]_{out}$ values, namely critical manifolds, fast subsystem saddle-node and Andronov-Hopf (AH) bifurcation points, and corresponding fast subsystem periodic orbits become higher dimensional surfaces and curves when projected to the $\left( V, h_{NaP}, E_K \right)$-phase space. For instance, the individual AH points become an AH curve, and the periodic orbits initiated there form a smooth manifold originating from this curve. A visualization of this three-dimensional structure is illustrated in Fig. 9, along with the superimposed trajectory of a neuron with dynamic $[K^{+}]_{out}$ exhibiting ramping bursts.

Fig. 9

The periodic trajectory of the ramping burst solution in $(V, h_{NaP}, E_{K})$-space is color coded temporally, progressing in time from blue to yellow. Additionally, the two black arrows indicate the direction that the trajectory travels. The upper and lower blue surfaces represent stable components of the critical manifold; white/blue surfaces between these are unstable components, which meet in a saddle-node curve at negative $h_{NaP}$ (not shown). Also shown are the AH curve (red) and the surfaces of maximal and minimal V along the family of periodic orbits originating at the AH curve (green)

The period during which spiking occurs or active phase of the burst occurs where the trajectory oscillates between the prongs of the green periodic orbit manifold in Fig. 9. As discussed in Sect. 3.3, this oscillation drives build-up of $[K^{+}]_{out}$, moving the trajectory in the direction of increasing $E_{K}$. This potassium ion build-up causes an increase in spiking frequency within the burst, facilitating further external potassium accumulation through a positive feedback loop. This process continues until the trajectory reaches a point along the homoclinic curve where the periodic orbit family terminates and returns to the hyperpolarized stable component of the critical manifold. This corresponds to the quiescent phase of the burst, where the trajectory remains until it reaches the saddle-node curve where it returns to the active phase. Additional insight arises from visualizing the local minima and maxima that occur throughout the active phase of the burst. In Fig. 10 these local extrema are connected into two curves. Clearly, the trajectory of the neuron travels along the family of periodic orbits during the burst, moving away from and back towards the homoclinic curve as time advances and $E_K$ increases. Furthermore, the neuron experiences a decline in spike amplitude when it pulls away from the edge of the periodic orbit family where it starts and terminates.

Fig. 10

Once again, the red curve indicates fast subsystem AH points and the green manifold consists of extremal voltages of periodic orbits emanating from the AH curve. Superimposed on this manifold are traces of minimum (lower, orange) and maximum (upper, red-orange) values of voltage attained for each spike within the burst, connected into smooth curves