Membrane potential resonance in non-oscillatory neurons interacts with synaptic connectivity to produce network oscillations

Abstract

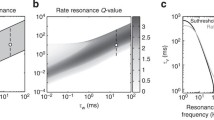
Several neuron types have been shown to exhibit (subthreshold) membrane potential resonance (MPR), defined as the occurrence of a peak in their voltage amplitude response to oscillatory input currents at a preferred (resonant) frequency. MPR has been investigated both experimentally and theoretically. However, whether MPR is simply an epiphenomenon or it plays a functional role for the generation of neuronal network oscillations and how the latent time scales present in individual, non-oscillatory cells affect the properties of the oscillatory networks in which they are embedded are open questions. We address these issues by investigating a minimal network model consisting of (i) a non-oscillatory linear resonator (band-pass filter) with 2D dynamics, (ii) a passive cell (low-pass filter) with 1D linear dynamics, and (iii) nonlinear graded synaptic connections (excitatory or inhibitory) with instantaneous dynamics. We demonstrate that (i) the network oscillations crucially depend on the presence of MPR in the resonator, (ii) they are amplified by the network connectivity, (iii) they develop relaxation oscillations for high enough levels of mutual inhibition/excitation, and (iv) the network frequency monotonically depends on the resonators resonant frequency. We explain these phenomena using a reduced adapted version of the classical phase-plane analysis that helps uncovering the type of effective network nonlinearities that contribute to the generation of network oscillations. We extend our results to networks having cells with 2D dynamics. Our results have direct implications for network models of firing rate type and other biological oscillatory networks (e.g, biochemical, genetic).

Appendices

Appendix A: Two-cell networks of passive cells do not produce limit cycle oscillations

Here we consider system (1) with g_k = 0 (k = 1, 2) and I_syn,k given by (3) and (4).

1.1 A.1 Linearization and eigenvalues

The linearization of system (1) with g_k = 0 (k = 1, 2) and I_syn,k given by Eqs. (3) and (4) reads

$$ \frac{dv_1}{dt} = F_{v_1} (v_1 - \bar{v}_1) + F_{v_2} (v_2-\bar{v}_2), $$

(16)

$$ \frac{dv_2}{dt} = G_{v_1} (v_1 - \bar{v}_1) + G_{v_2} (v_2-\bar{v}_2), $$

(17)

where

$$ C_1 F_{v_1} = -g_{L,1} - G_{syn,2,1} S_{\infty}(\bar{v}_2), \ \ \ \ \ \ \ $$

(18)

$$ C_1 F_{v_2} = -G_{syn,2,1} S_{\infty}^{\prime}(\bar{v_2}) (\bar{v}_1-E_{syn,1}), $$

(19)

$$ C_2 G_{v_1} = -G_{syn,1,2} S_{\infty}^{\prime}(\bar{v_1}) (\bar{v}_2-E_{syn,2}), $$

(20)

$$ C_2 G_{v_2} = -g_{L,2} - G_{syn,1,2} S_{\infty}(\bar{v}_1), \ \ \ \ \ \ \ \ \ $$

(21)

The eigenvalues (r₁ and r₂) are given by

$$ 2 r_{1,2} = F_{v_1}+G_{v_2} \pm \sqrt{(F_{v_1}-G_{v_2})^2 + 4 F_{v_2} G_{v_1}}. $$

(22)

The first two terms in Eq. (22) are always negative (provided g_L,1 > 0 and g_L,2 > 0). The second term in the radicand is positive if $F_{v_{2}}$ and $G_{v_{1}}$ have the same sign and negative if $F_{v_{2}}$ and $G_{v_{1}}$ have different signs. Therefore, the fixed-point for networks with the same type of connections (both excitatory or both inhibitory) can be either stable nodes or saddles, while the fixed-points for excitatory-inhibitory networks can be either stable nodes or stable foci (e.g., Fig. 16).

Fig. 16

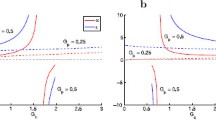
Two-cell networks of passive cells: phase-plane diagrams for representative parameter values. (a) Mutually inhibitory networks of passive cells. The v₁- and v₂-nullclines are given by Eqs. (5) and (6), respectively. Black dots indicate stable fixed-points (nodes) and gray dots indicate unstable fixed-points (saddles). Cells and connectivity are identical. The parameter G_in represents G_in,1,2 = G_in,2,1. As G_in increases (from a1 to a3), the v₁- and v₂-nullclines transition from quasi-linear to nonlinear and the system undergoes a pitchfork bifurcation as a stable fixed-point (a1) looses stability and two additional stable fixed-points are created (a3). Heterogeneous networks have non-symmetric phase-plane diagrams and show a qualitatively similar behavior, but bistability results from saddle-node bifurcations. We used the following parameter values: g_L,1 = g_L,2 = 0.25, E_in,1 = E_in,2 = − 20, v_hlf = 0, v_slp = 1. Excitatory-inhibitory networks of passive cells. The v₁- and v₂-nullclines are given by Eqs. (5) and (6), respectively. Black dots indicate stable nodes and gray dots indicate stable foci. The parameter G_ex,1,2 = 0.01 is fixed. As G_in,2,1 increases (from b1 to b3), the fixed-point transitions from stable nodes to stable foci and back to stable nodes. We used the following parameter values: g_L,1 = g_L,2 = 0.25, E_in,1 = − 20, E_ex,2 = 60, v_hlf = 0, v_slp = 1

1.2 A.2 Absence of limit cycles

We compute

$$ \begin{array}{@{}rcl@{}} U &=& \frac{\partial}{\partial v_1}\left( \frac{dv_1}{dt}\right) + \frac{\partial}{\partial v_2}\left( \frac{dv_2}{dt}\right) \\ &=& - \left( \frac{1}{C_1} [ g_{L,1} + G_{syn,2,1} S_{\infty}(v_2) ] \right.\\ &&\qquad\left.+ \frac{1}{C_2} [ g_{L,2} + G_{syn,1,2} S_{\infty}(v_1) ] \right). \end{array} $$

(23)

Since U < 0 for all v₁ and v₂ (provided g_L,1 > 0 and g_L,2 > 0), then by the Bendixson-Dulac theorem (Guckenheimer and Holmes 1983), there are no limit cycles in the (v₁,v₂)-plane. This argument breaks down when either g_L,1 < 0 or g_L,2 < 0 and small enough, indicating a strong positive feedback effect generated by an ionic process.

Appendix B: Dynamics of autonomous and forced 2D cells

We consider the following system

$$ C \frac{dv}{dt} = -g_{L} v - g w + A_{in} \sin{(2 \pi f t / 1000)}, $$

(24)

$$ \tau \frac{dw}{dt} = v- w, \hspace{4.8cm} $$

(25)

where the parameters g_L, g, C and τ are as in system (1)-(2) by omitting the subindex (k), A_in is the input amplitude, and f is the input frequency. We assume here that all intrinsic parameters (g_L, g, C and τ) are positive. The constraint g > 0 indicates that the ionic current that the term gw linearizes is a resonant process (negative feedback) (Richardson et al. 2003; Rotstein and Nadim 2014b). The linearized parameter g_L captures the effects of the biophysical leak current and possibly another ionic amplifying process (positive feedback) provided by an additional current. Strong enough amplifying processes may cause g_L to be negative.

1.1 B.1 Autonomous 2D cells

The eigenvalues for system (24)-(25) are given by

$$ r_{1,2} = \frac{1}{2 \tau C} \left[ -(g_L \tau + C) \pm \sqrt{(g_L \tau - C)^2 - 4 g \tau C} \right]. $$

(26)

System (1)-(2) (A_in = 0) has a uniquefixed-point (v̄,w̄) = (0, 0). This fixed-point is stable provided g_Lτ + C > 0. It is a stable node if the radicand in Eq. (26) is non-negative and a stable focus otherwise. We refer the reader for details on the dependence of the fixed-point type (node or focus) with the model parameters to Rotstein and Nadim (2014b).

1.2 B.2 Forced 2D cells: impedance profiles and resonant frequencies

The impedance profile for system (24)-(25) is given by Richardson et al. (2003) and Rotstein and Nadim (2014b)

$$ Z(\omega) = \sqrt{\frac{1+\tau^2 \omega^2}{(g_L + g - \tau C \omega^2)^2 + (g_L \tau + C)^2 \omega^2}}, $$

(27)

where ω = 2πf/1000. The resonant frequency is given by

$$ \omega_{res} = \frac{1}{\tau} \sqrt{-1 + \tau \sqrt{g^2 + 2 g_L g + 2 \frac{g}{\tau}}}, $$

(28)

where for simplicity C = 1. The impedance peak Z_max is given by

$$ \begin{array}{@{}rcl@{}} Z_{max}^2 \!&=&\! Z^2(\omega_{res}) \\ \!&=&\! \left( g_L^2 - \frac{1}{\tau^2} \!- \!2 \frac{g}{\tau} + \frac{2}{\tau} \sqrt{\frac{g (2 + g \tau + 2 g_L \tau)}{\tau}},\right)^{-1}. \\ \end{array} $$

(29)

The resonant properties of 2D linear systems, including their relationship between the intrinsic properties of the unforced cells (e.g, eigenvalues, intrinsic oscillatory frequencies) and the dynamic mechanism of generation of resonance have been investigated extensively by us and other authors (Richardson et al. 2003; Rotstein 2014a, b).

An important aspect to note, relevant for this paper, is that resonance can occur in the absence of damped oscillations; i.e., when the fixed-point is a stable node. In this paper we focus on resonators that do not show damped oscillations.

1.3 B.3 Quasi-displacement of impedance profiles: fixed peak values and changing resonant frequencies

From Eq. (29) we can compute the value of g as a function of Z_max and the other model parameters

$$ g = \frac{(Z^2_{max} + \tau^2 - Z^2_{max} g_L^2 \tau^2)^2}{4 Z^2_{max} \tau (-\tau^2 + Z^2_{max} (1 + g_L \tau)^2)}. $$

(30)

Equation (30) relates the model parameters of a forced 2D linear system of the form (24)-(25) for which the impedance peak Z_max is constant. In order to calculate the balanced values of g and τ, if they exist, for given values of Z_max and g_L (fixed) we proceed as follows. First we take values of τ within certain range and compute the corresponding values of g using Eq. (30). For these values of g_L, g and τ we compute ω_res using (28) and C = 1. In this way we have g = g(τ) and ω_res = ω_res(τ) for a given value of Z_max.

Appendix C: Self-inhibited 2D cells do not produce sustained (limit cycle) oscillations

We consider system (1)-(2) with v_k = v_j, E_syn,k = E_in and G_syn,jk = G_in in I_syn,k (3). For simplicity we omit the subindex.

Our discussion below is based on the values for the synaptic parameters we use in this paper (E_in = − 20, v_hlf = 0 and v_slp = 1) for which S_∞(v = E_in) ∼ 0. The results we present are valid for a larger range of parameter values provided S_∞(v = E_in) is small enough (the sigmoid function S_∞ changes fast enough around v_hlf and is negligible at v = E_in).

From our discussion above (Section B), the uncoupled system (G_in = 0) has a stable fixed-point. We expect this to persist for small enough values of G_in.

1.1 C.1 Fixed point

The fixed-points of the self-inhibited 2D system are the zeros of

$$ H(v) = -(g_L+g) v - G_{in} S_{\infty}(v) (v - E_{in}) $$

(31)

whose derivative is given by

$$ H^{\prime}(v) = -(g_L+g) - G_{in} S_{\infty}(v) - G_{in} S^{\prime}_{\infty}(v) (v-E_{in}). $$

(32)

The first two terms in Eq. (32) are negative, while the third one is negative provided v > E_in. However, for v < E_in this third term is negligible. Therefore, H(v) is a decreasing function for all v. Because H(v) < 0 for large enough values of v, a fixed-point exists if H(v) > 0 for some v. The first term in Eq. (31) is positive for negative values of v and so is the second term provided v < E_in. Therefore, the self-inhibited cell has a unique fixed-point (v̄^∗,v̄^∗). Since H(0) = G_inS_∞(0)E_in < 0 and H(E_in) = −(g_L + g)E_in > 0, then E_in < v̄^∗ < 0.

The stability properties of the fixed-point (v̄^∗,v̄^∗) are determined by looking at the equation for the eigenvalues (26) with g_L substituted by gL∗ = g_L + G_inS∞′(v̄^∗)(v̄^∗− E_in) + G_inS_∞(v̄^∗) > g_L. Therefore, the stability of the fixed-point is preserved. If (v̄,v̄) is a stable node, then (v̄^∗,v̄^∗) is a node for all values of G_in (Fig. 17a). In contrast, if (v̄,v̄) is a stable focus, then (v̄^∗,v̄^∗) remains a stable focus for small enough values of G_in, but it transitions to a stable node for large enough values of G_in (Fig. 17b).

Fig. 17

Self-inhibited resonator: phase-plane diagrams for representative parameter values. The v- and w-nullclines are given by (8) and (9), respectively. Black dots indicate stable nodes and gray dots indicate stable foci. ag_L = 0.25. The fixed-point for the uncoupled system is a stable node. bg_L = 0.01. The fixed-point for the uncoupled system is a stable focus. We used the following parameter values: g = 0.25, τ = 100, E_in = − 20, v_hlf = 0, v_slp = 1

1.2 C.2 Absence of limit cycles

Because the self-inhibited 2D systems is relatively simple we do not expect the existence of limit cycles. We address this in the region R = {(v,w) ∈ R² : v > E_in}. We compute

$$ \begin{array}{@{}rcl@{}} U \!&=&\! \frac{\partial}{\partial v}\left( \frac{dv}{dt}\right) + \frac{\partial}{\partial w}\left( \frac{dw}{dt}\right) \\ \!&=&\! -\frac{g_{L}}{C} - \frac{G_{in}}{C} S_{\infty}(v)- \frac{G_{in}}{C} S^{\prime}_{\infty}(v)(v - E_{in}) - \frac{1}{\tau}. \end{array} $$

(33)

By substituting $S_{\infty }^{\prime }(v)=S_{\infty }(v)(1-S_{\infty }(v)) > 0$ where S_∞, given by Eq. (4), we obtain

$$ \begin{array}{@{}rcl@{}} U &=& \frac{\partial}{\partial v}\left( \frac{dv}{dt}\right) + \frac{\partial}{\partial w}\left( \frac{dw}{dt}\right) \\ &=& -\frac{1}{C} \left( g_L+\frac{1}{\tau}+G_{in} S_{\infty}(v) \right.\\ &&\qquad\quad\left. + \frac{G_{in}}{v_{slp}} S_{\infty}(v) (1-S_{\infty}(v)) \right). \end{array} $$

(34)

If v > E_in (assuming g_L > 0), then U < 0. Thus, by the Bendixson-Dulac theorem (Guckenheimer and Holmes 1983), there are no limit cycles lying entirely in the region R.