1 Introduction

The Jaynes–Cummings model describes a simplified model of an atom coupled to an electromagnetic field in the rotating wave approximation [1,2,3,4]. We can analytically treat the electromagnetic field as a harmonic oscillator while modelling the atom as a two-level system, representing the two states of an atom. A standard analysis of this model involves applying the Jaynes–Cummings Hamiltonian to an initial coherent state—a minimum uncertainty state that is Gaussian in phase space [5]. One crucial feature of this model is the system takes the field mode prepared in a coherent state and evolves into a Schrödinger cat state, that is, to good approximation, a separable state. This makes the setup appealing for continuous mode quantum information processing applications [6, 7].

If one introduces more atoms coupled to the field mode then the behaviour can get even more interesting, this is known as the Tavis–Cummings model [8]. In the interaction picture, the Tavis–Cummings model is described by the Hamiltonian

$$\begin{aligned} {\hat{H}}_{\mathrm {TC}} = \sum _i^{N}\left( \hat{a}^{\dag } \hat{\sigma }_{-} ^{(i)} + \hat{a} \hat{\sigma }_{+} ^{(i)} \right) , \end{aligned}$$
(1)

where \({\hat{\sigma }}_{\pm }^{(i)}\) is the operator \({\hat{\sigma }}_{\pm } = ({\hat{\sigma }}_x \pm \mathrm {i}{\hat{\sigma }}_y)/2\) that acts on the \(i^{\text {th}}\) atom. Note that when \(N=1\), this is simply the interaction picture of the Jaynes–Cummings model, also note that we have set \(\hbar = 1\) throughout.

The two levels of each atom are described by the states \(\left| \uparrow \right\rangle _a\) and \(\left| \downarrow \right\rangle _a\). The subscript a indicates that these are the atomic states; later, we will use a subscript f for the field mode. Applying the operator \({\hat{\sigma }}_{\pm }\) to these states results in \({\hat{\sigma }}_{+}\left| \uparrow \right\rangle _a = \left| \downarrow \right\rangle _a\) and \({\hat{\sigma }}_{-}\left| \downarrow \right\rangle _a = \left| \uparrow \right\rangle _a\). Similarly \(\hat{a}\) and \(\hat{a}^{\dag }\) are the standard annihilation and creation operators for the field mode. They are so named as they annihilate and create a photon in the electromagnetic field mode.

Starting with the multi-qubit system in an atomic Schrödinger cat state and the field mode in a coherent state, one finds that the Schrödinger cat state will swap between the atoms and the field mode. That is, an initial Schrödinger cat state in the atom will transfer, causing the Schrödinger cat state to appear in the field mode, leaving an approximate coherent state in the atom. Further application of the Tavis–Cummings model results in the Schrödinger cat state returning from the field mode into the atomic state. Once more, this has potential for continuous mode quantum information processing applications.

When using coherent states and Schrödinger cat states in optical quantum information processing, the further away in phase space the two coherent states are, the less overlap they have; note that as the states are Gaussian, there is always a nonzero overlap. Similarly in the Tavis–Cummings model, the further away the initial coherent state is from the origin, the more robust the resulting Schrödinger cat state is [9]. Typically we can label each coherent state as \(\left| \alpha _i \right\rangle _f\), where \(\alpha _i\) is a complex number that describes the position of the coherent state in phase space, and relates to the average number of photons in a given coherent state, where \({\bar{n}} = \sqrt{|\alpha |}\).

When coupling this initial coherent states to a single atom using the Jaynes–Cummings model, one can also specify the atom field coupling strength of g; this coupling strength is typically present as a coefficient in Eq. (1); however, we have simply set it equal to one in this analysis. From this coupling strength g and the average number of photons, there are three timescales that are traditionally important. The first is the Rabi time \(t_R=\pi /\left( g\sqrt{{\bar{n}}}\right)\); the next sets the envelope of the atomic inversion \(t_c= \sqrt{2}/g\), which is a Gaussian envelope and in this way distinguishable from damping effects; the last and most important is the first revival time \(t_r=2 \pi \sqrt{{\bar{n}}}/g\). As we increase the number, N, some of these time scales change [1, 10]. The most important is that the first revival time is \(t_{r_1}=t_r/N\).

This scaling led to the idea that introducing more atoms to a system could in fact be a mechanism for overcoming decoherence for some continuous mode quantum information processing applications providing the dominating damping terms were in the field mode [9]. This study made use of a Wigner function of a general angular momentum state as well as the usual Wigner function for the field mode to visualize the various effects of decoherence on the system’s dynamics [11]. Importantly the Wigner function of the atomic system could be used to demonstrate that, as the number of qubits increased, the effect decoherence on the cat-swap process is reduced. We note here this result also indicates that by measuring negative values this could lead to an efficient verification and validation procedure.

The issue with mapping this system’s state onto an angular momentum state is that it is not necessarily bijective, where it only allows the representation of states that are symmetric under permutation of atoms. They only map atomic states by a Dicke mapping of a single given value of angular momentum [12]. For the study of a cat-swap process, this was not an issue as both the Tavis–Cummings Hamiltonian as field decoherence conserved angular momentum. This is not generally true for more realistic system Hamiltonians or environments.

What we describe in this paper is the complete representation in phase space for systems such as those described by the Tavis–Cummings model. We illustrate how signatures of certain important quantum correlation, or their absence, manifest. One of the key observations is that, for pure states, signatures of entanglement can be clearly seen if certain visualization methods are used, such as those used in this paper. This is because Wigner functions of separable states are themselves separable, i.e.  not written as a products of functions of different degrees of freedom. Thus, if we plot the Wigner function in such a way that any correlation between the phase space of one subsystem can be seen to be correlated with another we may not only see the entanglement correlations but also get deeper insight into the nature of these correlations over the phase space.

This will allow for general study beyond the Tavis–Cummings model and should also provide a framework for verification and validation of important quantum states for information processing and sensing applications.

2 Composite systems in phase space

We can calculate the Wigner function [13,14,15] of a system of arbitrary components by taking the expectation value of a suitable displaced parity operator over all its possible configurations—the phase space [16,17,18,19]. The total displaced parity operator for the composite system simply comprises the tensor product of the displaced parity operators for each element of the system.

In the Tavis–Cummings model the displaced parity operator for the field mode is the usual textbook displaced spatial parity \({\hat{\varPi }}_f(q,p)\) [20, 21]. Each atom will be represented by the generalized displaced spin parity \({\hat{\varPi }}_i(\theta _i,\phi _i)\). This leads to a total system parity—and the kernel needed to generate the system’s informationally complete representation in phase space—as

$$\begin{aligned} {\hat{\varPi }}\left( q,p,\varvec{\theta },\varvec{\phi }\right) = {\hat{\varPi }}_f(q,p) \otimes \left[ \bigotimes _{i=1}^N {\hat{\varPi }}_i(\theta _i,\phi _i) \right] . \end{aligned}$$
(2)

Specifically, the Wigner function will be

$$\begin{aligned} W\left( q,p,\varvec{\theta },\varvec{\phi } \right) = {{\,\mathrm{Tr}\,}}\left[ {{\hat{\rho }}}\, {\hat{\varPi }}\left( q,p,\varvec{\theta },\varvec{\phi }\right) \right] . \end{aligned}$$
(3)

where \(\varvec{\theta } = (\theta _1, \ldots \theta _N)\) and \(\varvec{\phi } = (\phi _1, \ldots \phi _N)\). To calculate the Wigner functions, all we need now is the method to determine each displaced parity.

For the field mode, the displaced parity operator \({\hat{\varPi }}_f(q,p)\) is constructed from the spatial parity

$$\begin{aligned} {\hat{\varPi }}_f = \mathrm {e}^{\mathrm {i}\pi \,\hat{a}^{\dag } \hat{a}}, \end{aligned}$$
(4)

which is the operator that takes a coherent state \(\left| \alpha \right\rangle _f\) to \(\left| -\alpha \right\rangle _f\). We then displace this parity operator with the field displacement operator

$$\begin{aligned} {\hat{D}}(q,p) = \exp \left( \alpha \hat{a}^{\dag }- \alpha ^*\hat{a} \right) =\exp \left( \mathrm {i}[p \hat{{q}} - {q} \hat{{p}} \right] ), \end{aligned}$$
(5)

where the displacement operator displaces a state in phase space. \(\hat{q}\) and \(\hat{p}\) are the position and momentum operators that are related to the creation and annihilation operators by \(\hat{q} = (\hat{a} + \hat{a}^{\dag })/\sqrt{2}\) and \(\hat{p} = \mathrm {i}(\hat{a}^{\dag }- \hat{a})/\sqrt{2}\), further \(\alpha = (q + \mathrm {i}p)/\sqrt{2}\).

The simplest coherent state is the vacuum state that describes the state of a field mode with no photons; we denote the vacuum state by \(\left| 0 \right\rangle _a\). In phase space, the vacuum state is represented as a Gaussian distribution with minimum uncertainty that is centred at the origin—the point with zero position and zero momentum. A coherent state \(\left| \alpha \right\rangle\) can be generated from this vacuum state by displacing it through phase space, where

$$\begin{aligned} \left| \alpha \right\rangle _f = \hat{D} \left( \sqrt{2}\mathrm {Re}(\alpha ),\sqrt{2}\mathrm {Im}(\alpha )\right) \left| 0 \right\rangle _f. \end{aligned}$$
(6)

The displaced parity operator for the Wigner function of the field mode is then defined in terms of these operators, where

$$\begin{aligned} {\hat{\varPi }}_f(q,p)= {{\hat{D}}}(q,p) {\hat{\varPi }}_f {{\hat{D}}}^\dag (q,p) \end{aligned}$$
(7)

Examples of the Wigner function for different field mode states are given in Fig. 1a–d. Figure 1a, b shows two coherent states, displaced in opposite directions from the origin, where \(\alpha = 3\). Figure 1c then shows the superposition of these two coherent states, resulting in the Schrödinger cat state in the field mode. We then show a statistical mixture of these two states in Fig. 1d. Comparing the pure, superposition state in Fig. 1c with the statistical mixture in Fig. 1d, we can see how the quantum correlations present as interference fringes between the two coherent states.

Fig. 1
figure 1

Examples of the Wigner functions for coherent states in a field mode and multi-qubit states. Here, a–d show examples of coherent states in a field mode. Directly below are the two-qubit examples in e–h, where \(\left| \pm \right\rangle _a = (\left| \uparrow \right\rangle _a \pm \left| \downarrow \right\rangle _a)/\sqrt{2}\). In the last row, i–l, examples of the corresponding five-qubit states are shown. In the first two columns, we consider simple coherent states for the respective systems. We then consider the superposition of these coherent states in the third column (c, g, k). This is followed by the statistical mixture of the coherent states in d, h and l. The colour bar goes from \(-\eta\) to \(\eta\), where the maximal values differ for the different systems. For a–d, \(\eta = 2\), for e–h, \(\eta = 1+\sqrt{3}/2\), and for i–l, \(\eta = ((1+\sqrt{3})/2)^5\). This figure is taken with permission from Ref. [22] (Color figure online)

Full size image

The discrete analog of a coherent state, the spin coherent state, is defined similarly to a displaced vacuum state. Except now this displacement is a rotation over a spherical phase space. Such a rotation is defined by the Euler angles

$$\begin{aligned} {\hat{U}}(\theta ,\phi ,\varPhi )=\exp {(\mathrm {i}{\hat{\sigma }}_z\phi )}\exp {(\mathrm {i}{\hat{\sigma }}_y\theta )}\exp {(\mathrm {i}{\hat{\sigma }}_z\varPhi )}. \end{aligned}$$
(8)

A spin coherent state can then be generated by displacing \(\left| \uparrow \right\rangle _a\), where \(\left| \theta ,\phi \right\rangle _a = {\hat{U}}(\theta ,\phi ,\varPhi )\left| \uparrow \right\rangle _a\) and \({\hat{\sigma }}_z\left| \uparrow \right\rangle _a = \left| \uparrow \right\rangle _a\). For multi-qubit states, the spin coherent state is the symmetric rotation of an initial tensor product state \(\left| \uparrow \right\rangle ^{\otimes N}\). For a symmetric rotation, we then need to take the N-fold tensor product of \({\hat{U}}(\theta ,\phi ,\varPhi )\), where the Euler angles are equal in each space. This results in the N-qubit spin coherent state \(\left| \theta ,\phi \right\rangle _a^N = {\hat{U}}(\theta ,\phi ,\varPhi )^{\otimes N} \left| \uparrow \right\rangle _a^{\otimes N}\), where the \(\varPhi\) degrees of freedom only contribute a global phase to the state.

To generate the displaced parity operator for the Wigner function, we then need to introduce the generalized parity operator for a single qubit

$$\begin{aligned} {\hat{\pi }}=\frac{1}{2}\left(\mathbbm {1} +\sqrt{3}\hat{\sigma }_{z}\right), \end{aligned}$$
(9)

so that

$$\begin{aligned} {\hat{\varPi }}_i(\theta _i,\phi _i) = {\hat{U}}_i(\theta _i,\phi _i,\varPhi _i) {\hat{\pi }} {\hat{U}}_i^\dag (\theta _i,\phi _i,\varPhi _i), \end{aligned}$$
(10)

for Euler angles \(\theta _i\) and \(\phi _i\), where the index i denotes that this is for the ith qubit. Note that the \(\varPhi _i\) degree of freedom cancels out as it commutes over the parity operator.

For a two-qubit state, we can then generate the kernel

$$\begin{aligned}&{\hat{\varPi }}(\theta _1,\phi _1,\theta _2,\phi _2) \nonumber \\&\quad = {\hat{U}}_1(\theta _1,\phi _1,\varPhi _1) {\hat{\pi }} {\hat{U}}_1^\dag (\theta _1,\phi _1,\varPhi _1) \nonumber \\&\qquad \otimes \, {\hat{U}}_2(\theta _2,\phi _2,\varPhi _2) {\hat{\pi }} {\hat{U}}_2^\dag (\theta _2,\phi _2,\varPhi _2); \end{aligned}$$
(11)

this alone gives a function with four degrees of freedom. It is then necessary to reduce this in order to generate a visualization of the phase space. As we are considering symmetric states, we can then take the symmetric approach with the displaced parity operator, where, in analogy to the spin coherent state construction, we take what is known as the equal-angle slice, i.e. \(\theta _1=\theta _2 = \theta\) and \(\phi _1=\phi _2=\phi\).

Examples of the two-qubit Wigner function plotted with the equal-angle slice are shown in Fig. 1e–h. We have also shown similar states for five qubits in Fig. 1i–l. Each distribution has been plotted on a sphere as well as projected onto a unit disc with the Lambert azimuthal area-preserving map [23]. We have included both as the spherical presentation follows intuition much better, the benefit of the area-preserving map is that it allows us to see the full surface of the sphere while fully preserving the area—an important metric when considering probability distributions. As such, this representation will be preferred later on when considering the definition of an informationally complete Wigner function to visualize correlations in coupled atom–field systems.

Figure 1e, f shows two spin coherent states, both on orthogonal sides of the sphere. We can see the Gaussian-like behaviour of these states on the spheres. The behaviour becomes clearer as we consider more qubits, where in Fig. 1i, j there are clear Gaussians, one on each side of the sphere.

Figure 1g, k then shows the superpositions of these two spin coherent states for two and five qubits, respectively, resulting in two- and five-qubit Greenberger–Horne–Zeilinger (GHZ) states [24]. Like in the case for the field mode in Fig. 1c, this superposition results in oscillations in the Wigner function between the two coherent states. These oscillations fluctuate between positive and negative values, where the number of oscillations corresponds to the number of qubits in the GHZ state. Also like the field mode in Fig. 1d, when we take the statistical mixture of the two coherent states, the oscillations disappear, and we are left with two coherent states, one on each side of the sphere.

For these states, we can see that the equal-angle slice of the Wigner function presents enough information to get a good visualization of the quantum correlations that manifest in multi-qubit states. However, this equal-angle approach is not possible when considering atoms coupled to a field mode. A method to visualize such states has been considered in Refs. [18, 25]. This method was used to visualize atomic orbitals in Ref. [25] and for considering the Jaynes–Cummings model in Ref. [18].

In order to visualize states with heterogeneous degrees of freedom, we begin with the phase space distribution of the field mode. We then discretize this phase space into a grid. At each point, we then plot the full Wigner function for those set values of q and p. Since we are dealing with two- and five-qubit states, the equal-angle slice is taken for the remaining degrees of freedom.

At every set value of q and p, we then plot the remaining degrees of freedom. We then set the value of the opacity at that point in phase space proportional to the maximum absolute value over \(\theta\) and \(\phi\) at that point in position and momentum space.

As an example, see Fig. 2, where we show this method of visualizing the coherent state from Fig. 1a coupled to the GHZ state from Fig. 1g. These are shown as reduced Wigner functions in Fig. 2a, b, respectively. The full Wigner function is shown in Fig. 2c. Since there is no entanglement between the field mode and the two-qubit state, the Wigner function is then simply a replication of the reduced atomic state at every discrete point in position and momentum phase space. The opacity is then set by the coherent state in the field mode, which acts like an envelope over atomic states. When there are correlations between the degrees of freedom, this is no longer the case. Examples of these non-local correlations will be considered when we look at the Wigner function during the Tavis–Cummings evolution, which we will now discuss.

Note that much of the text and results that follow are taken, edited and adapted from Chapter 5 of RR’s PhD thesis [22]. It has been extracted and reordered here as we believe that doing so provides an excerpt that is valuable as a stand-alone piece.

Fig. 2
figure 2

Example of the full Wigner function for two atoms coupled to a field mode, showing the state \(\left| \alpha \right\rangle (\left| \uparrow \downarrow \right\rangle +\left| \downarrow \uparrow \right\rangle )/\sqrt{2}\). This is also the initial state for the two-qubit Tavis–Cummings model. The reduced Wigner functions for the field mode and the atom are shown in a and b, respectively. Our visualization of the full Wigner function is shown in c. In order to maximize the available visual information at each point in phase space, the opacity is set by the largest value of the Wigner function at this point in (q, p). We then plot the angular dependence as a small disc with the Lambert equal area azimuthal plot at that position. In all future plots, we will simply refer to this kind of plot as the visualization of the full Wigner function in order to avoid repetition. The value of \(\eta\) in the colour bar is \(\eta = 2\) in a, \(\eta = (1+\sqrt{3}/2)\) in b, and \(\eta = (2+\sqrt{3})\) in c. This figure is taken with permission from Ref. [22] (Color figure online)

Full size image

3 Two-atom Tavis–Cummings interaction

We will now consider a two-qubit example of the Hamiltonian in Eq. (1); starting with the initial state

$$\begin{aligned} \frac{1}{\sqrt{2}}\left| \alpha \right\rangle _f\left( \left| \uparrow \downarrow \right\rangle _a + \left| \downarrow \uparrow \right\rangle _a\right) = \frac{1}{\sqrt{2}}\left| \alpha \right\rangle _f\left( \left| ++ \right\rangle _a - \left| -- \right\rangle _a\right) , \end{aligned}$$
(12)

where \(\alpha =3\) from Eq. (6), the Wigner function for this state is already presented in Fig. 2.

Fig. 3
figure 3

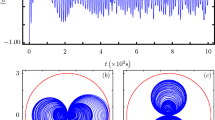
Wigner functions for three points in the evolution of the Tavis–Cummings model with initial state \(\left| \alpha \right\rangle _f(\left| \uparrow \downarrow \right\rangle _a+\left| \downarrow \uparrow \right\rangle _a)/\sqrt{2}\). The graph in a shows the von Neumann entropy of the two qubits in cyan, starting at 0, and the qubit inversion (\(\langle \hat{\sigma }_{z} ^{(1)}\rangle\)) in red, starting with a value of \(-1\), throughout the entire evolution. The three points are marked out on this graph by vertical coloured lines. The Wigner functions for the first point are shown in b–d, showing an entanglement between the field mode and the qubits. The second point is shown in e–g, where the atom and field mode have decoupled, where the atomic Schrödinger cat state has been swapped into the field mode, showing a spin coherent state in the atomic state and a Schrödinger cat state in the field mode. The last point is a at the point of the revival of the Rabi oscillations at \(t = t_r\), where the Wigner functions are shown in h–j. The values of \(\eta\) for the colour bar are \(\eta = 2\) for the reduced Wigner functions for the field mode in b, e and h; \(\eta = (1+\sqrt{3}/2)\) for the reduced atomic Wigner functions in c, f and i; \(\eta = (2+\sqrt{3})\) for the visualization of the full Wigner function in d, g and j. This figure is taken with permission from Ref. [22] (Color figure online)

Full size image

Further points in the evolution of the two-qubit Tavis–Cummings model are shown in Fig. 3. Here we show snapshots at three points of interest during the evolution. In Fig. 3a, we show the von Neumann entropy over time, where

$$\begin{aligned} S(\rho )=-{{\,\mathrm{Tr}\,}}\left[ \rho _a \ln \rho _a \right] , \end{aligned}$$
(13)

where \(\rho _a = \mathrm {Tr}_f\left[ \rho \right]\), is the reduced density matrix of the two-qubit state, tracing out the field mode. The von Neumann entropy is shown in cyan, starting with a value of \(S(\rho )=0\). Note that we consider the entropy of the atom pair rather than the atoms individually, this is in order to calculate the coupling between the atoms as a pair with the field mode. Also in Fig. 3a, we show the atomic inversion, \(\langle \hat{\sigma }_{z} ^{(1)}\rangle\), of the state through time. The atomic inversion starts with a value of -1 and is shown in red. The atomic inversion begins with a brief oscillation to then stabilize out to a constant value of zero for some time. Towards the end of the evolution shown, the oscillations then revive again. This behaviour is known as the collapse and revival of the Rabi oscillations [26].

The first point of interest is the first local maximum of entropy, indicated in Fig. 3a by the first vertical line, shown in blue. The Wigner functions for the state at this point in the evolution are shown in the first box below Fig. 3b–d, also in blue. This shows the emergence of a Schrödinger cat state in the field mode. The reduced two-qubit state is quite clearly heavily mixed, which is to be expected as this is a point of high entropy.

Turning our attention to the Wigner function, we again get the overall shape of a Schrödinger cat state in the field mode, where the atomic states in each of the two cats are pointing in almost orthogonal directions. The top of the Schrödinger cat state has spin coherent state pointing towards to left and the bottom cat is made of spin coherent states orientated to the right.

The quantum correlations between the atoms and the field mode become apparent when considering the area between the two cats. The quantum correlations manifest here with high Wigner function values, where in the reduced state this area has much lower values. In fact, the characteristic feature of entanglement here is that the atomic states here are traceless—the overall positive value is equal to the overall negative value. A feature of quantum correlation in informationally complete Wigner functions was noted in Ref. [18].

The second point of interest is shown in Fig. 3a by the next vertical line, in pink. The corresponding Wigner functions are shown in the pink box Fig. 3e–g. At this point in the evolution, the field and the atoms are decoupling from the entanglement generated in the previous state. This can be seen in the entropy as it reaches a local minimum, close to the initial value of 0. This is where the information from the qubit has transferred to the field mode, swapping the atomic Schrödinger cat state to a Schrödinger cat state in the field mode. The two-atom state is in an almost pure spin coherent state at every point in phase space, where the Wigner function for the field mode shows the definite signature of a Schrödinger cat state. The fact that the Wigner function is almost a direct product of the two reduced Wigner functions is demonstrative of the extent that the two systems have decoupled.

The third point is during the revival phase, given by the vertical yellow line in Fig. 3a. At this point, the cat has swapped back to the qubit, resulting in the atomic Schrödinger cat state being returned, as can be seen in the Wigner functions for this state in Fig. 3e–g. The field mode, in Fig. 3h, however, is not the initial coherent state. There is an identifiable concentration of quasi-probabilities on the left-hand side, forming a somewhat squeezed coherent state. The correlations in the middle of the field mode resemble a sort of noisy number state. Similar patterns emerge in the Wigner function in Fig. 3j, where there are atomic cat states in the main coherent lump on the left-hand side, with some residual entanglement in the part that resembles a number state.

4 Five-atom Tavis–Cummings interaction

Demonstrations of how quantum information can be shared between a discrete-variable and continuous-variable system have so far been given for a two-qubit model. It was shown how a Schrödinger cat state can be transferred to the field mode from a two-atom state. For the two-qubit Tavis–Cummings model, this was achieved by having the field mode initially in a coherent state \(\left| \alpha \right\rangle _f\), at \(\alpha = 3\). This was done in order for the cat to faithfully swap from the two-atom state into the field mode.

Fig. 4
figure 4

Points in the five-qubit Tavis–Cummings evolution with an initial state of \(\left| \alpha \right\rangle _f\left( \left| + \right\rangle _a^{\otimes 5} - \left| - \right\rangle _a^{\otimes 5} \right) /\sqrt{2}\). The top rows, a, d and g, show the reduced Wigner functions for the field mode, with the reduced atomic Wigner functions inset in b, e and h. The visualization of the full Wigner function for these states are shown in the bottom row, in c, f and i, respectively. Note that for all the atomic Wigner functions, the equal-angle slice has been taken. This figure shows the evolution from the initial state in a–c to where the quantum information transfers to the field mode in the form of a Schrödinger cat state in d–f and then returns to the atomic state in g–i, albeit with some noise from an imperfect transfer of quantum information. Note here how there is a difference in the colour bar from earlier figures, this was done in order to highlight the oscillations in the atomic Schrödinger cat states. The values of \(\eta\) are \(\eta = 2\) for the Wigner function for the field mode, \(\eta = ((1+\sqrt{3})/2)^5\) for the five-qubit Wigner function, and \(\eta = 2((1+\sqrt{3})/2)^5\) for the visualization of the full Wigner function. This figure is taken with permission from Ref. [22] (Color figure online)

Full size image
Fig. 5
figure 5

Wigner function for two points in the five-qubit Tavis–Cumming model. The points chosen here are between the points in the evolution shown in Fig. 4, where a–c are between the first two points of Fig. 4, and d–f are between the second and third points in Fig. 4. Figure 4 shows the points at which the information had been transferred between the systems. Here are points where the information is halfway through being transferred, creating entangled hybrid Schrödinger cat states. The colour bar values are \(\eta = 2\) for the reduced Wigner functions for the field mode in a and d, \(\eta = ((1+\sqrt{3})/2)^5\) for the reduced atomic Wigner functions in b and e, and between \(\eta = 2((1+\sqrt{3})/2)^5\) for the visualization of the full Wigner function in c and f (Color figure online)

Full size image

Now, we will consider what happens in the five-qubit Tavis–Cummings model. Here we choose to investigate how quantum information can be shared from an initial atomic Schrödinger cat state to a field mode in the vacuum state, to see how this compares to the two-qubit model considered earlier. The initial state is then

$$\begin{aligned} \frac{1}{\sqrt{2}}\left| 0 \right\rangle _f\left( \left| + \right\rangle _a^{\otimes N} - \left| + \right\rangle _a^{\otimes N} \right) . \end{aligned}$$
(14)

Like the Jaynes–Cummings model with a vacuum initial state—see Ref. [18] to see a demonstration of this in phase space—information is transferred back and forth between the atom and the field modes with each cycle of the Rabi oscillations. However, like the coherent state case, these Rabi oscillations collapse and revive over time, meaning that there is not a perfect transfer of quantum information from the initial atomic Schrödinger cat state the field mode. This will give an opportunity to consider the full Wigner function as a tool for understanding this loss in the system, allowing an understanding of the increased entropy.

Figure 4 shows the evolution of the initial state in Eq. (14) with the five-atom Tavis–Cummings model Hamiltonian. Here, two periods of the Rabi cycle are shown, starting with the initial state. The next point is then after one cycle of the Rabi oscillations where the Schrödinger cat state has first been transferred to the field mode. We then show the state after the second cycle of the Rabi oscillations, where the Schrödinger cat state has returned to the atoms, regenerating a five-qubit atomic Schrödinger cat state.

The initial state is shown in Fig. 4a–c, where, as expected, there is a vacuum state in the field mode and a five-atom Schrödinger cat state. This produces the full Wigner function of an envelope of a coherent state where there is a GHZ state at every point in phase space. Note here that the colour bar has been slightly adapted from earlier figures, this is in order to highlight the oscillations in the GHZ state. The range of position and momentum has also been decreased, in order to more clearly see the finer detail in the atomic states.

Figure 4d–f shows the point at which the Schrödinger cat state has been swapped to the field mode. In Fig. 4d, the reduced Wigner function for the field mode shows the Schrödinger cat state, while Fig. 4e shows the reduced Wigner function for the atoms, in the equal-angle slice. Since the quantum information has left, the atomic state now resembles an atomic coherent state. Since the transfer in this model is not a perfect state transfer, like in the Jaynes–Cummings model example, the atomic coherent state appears somewhat squeezed. Inspection of the visualization of the full Wigner function in Fig. 4f reveals why this is the case. At some points in phase space, the coherent state has more faithfully transferred to the atomic state; however, at most points residual entanglement can be seen in the full state.

Next Fig. 4g–i shows the point where the Schrödinger cat state returns to the atom. Like in Fig. 4d–f, this is not a perfect transfer of quantum information as impurities can be seen in both the reduced Wigner functions in Fig. 4g, h for the field mode and the atoms, respectively. The main difference can be seen in the atomic Wigner function in Fig. 4h where the oscillations in the GHZ state are lower in amplitude. Only when looking at the visualization of the full Wigner function in Fig. 4i, it is clear why there is this decrease in amplitude. Here, it can be seen at the origin of the field mode, a strongly formed GHZ state is present, and as you get further away from the centre, imperfections appear in the full quantum state.

Instead of considering these points in the evolution where the Schrödinger cat is strongly in one of the systems, we can take the points between the transfers. At these points, there are highly entangled states generated between the atom and the field mode. These highly entangled midpoints are shown in Fig. 5, where Fig. 5a–c shows a point between the first two points in Figs. 4 and Fig. 5d–f shows a point between the second and third points in Fig. 4. At both points, it can be seen in the reduced Wigner functions that there is a drop in quantum correlations for what would be expected for a Schrödinger cat state in either system. Further the reduced Wigner function for the atomic states in Fig. 5b, e shows the two atomic coherent states moving closer together in phase space.

In the visualization of the full Wigner functions in Fig. 5c, f, the two atomic coherent states can been seen in each of the field mode Schrödinger cats, where they are pointing in different directions in each of the cats, at the top and the bottom of the figures, in the field mode. Between the two cats, in the centre of Fig. 5c, f, the emergence of quantum correlations from the entanglement between the different systems can be seen from the manifestation of traceless states.

It can further be seen that the first entangled state in Fig. 5c is much cleaner than the state in Fig. 5f later on in the evolution. The atomic states in Fig. 5c are quite pure with little noise when far away from the correlations in the centre. However, the atomic states in Fig. 5f are far more noisy, where the purest atomic coherent state exhibits some level of quantum interference, shown by the increased manifestation of negative quasi-probabilities.

5 Conclusions

By taking a holistic approach to phase space methods, rather than just analysing the reduced Wigner functions, it is now possible to understand local and non-local correlations in quantum states. In this work, we have demonstrated how our approach allows an intuitive visualization of the process of swapping quantum information between two different systems. The understanding of this kind of process is useful, especially with the development of technologies such as quantum memory. Understanding how efficiently information can be swapped between one system to another will provide a way into understanding how efficient such technologies are, as the efficacy of quantum memory can only be as good as the information received from the state.

Our method does more than provide a reliable route to visualize, verify and validate hybrid and composite quantum systems. We have observed it also provides a mechanism for certifying quantum state preparation where, for example, making a joint measurement of the phase space of an ancillary system (in the model here—the field mode) certifies the state of the rest of the system (here the set of spins). We are confident that many more applications in sensing and validation of quantum states will arise as we further explore more and more complex systems in their entire phase space.