Abstract
Search-based satisfiability procedures try to build a model of the input formula by simultaneously proposing candidate models and deriving new formulae implied by the input. Conflict-driven procedures perform non-trivial inferences only when resolving conflicts between formulæ and assignments representing the candidate model. CDSAT (Conflict-Driven SATisfiability) is a method for conflict-driven reasoning in unions of theories. It combines inference systems for individual theories as theory modules within a solver for the union of the theories. This article augments CDSAT with a more general lemma learning capability and with proof generation. Furthermore, theory modules for several theories of practical interest are shown to fulfill the requirements for completeness and termination of CDSAT. Proof generation is accomplished by a proof-carrying version of the CDSAT transition system that produces proof objects in memory accommodating multiple proof formats. Alternatively, one can apply to CDSAT the LCF approach to proofs from interactive theorem proving, by defining a kernel of reasoning primitives that guarantees the correctness by construction of CDSAT proofs.
Similar content being viewed by others
1 Introduction
The satisfiability problem is one of checking if a given formula has a model. In the propositional case (SAT) the input is usually a formula in conjunctive normal form (a set of clauses), and a model is an assignment of truth values to propositional variables that satisfies all the clauses. Many SAT solvers employ a conflict-driven search strategy, known as Conflict-Driven Clause Learning (CDCL), in which the solver extends a partial assignment until it satisfies all clauses, or a conflict arises as the assignment falsifies a clause. Non-trivial inference steps are performed in response to a conflict to roll back the partial assignment and direct the search elsewhere [44, 45]. This conflict-driven style inspired the design of several solvers for quantifier-free fragments of arithmetic (e.g., [8, 16, 17, 21, 36, 37, 40, 46] for more references). These conflict-driven theory solvers decide the satisfiability of sets of literals in the theory.
The problem of deciding the satisfiability of a quantifier-free formula in a theory is known as Satisfiability Modulo a Theory (SMT). MCSAT, for Model Constructing SATisfiability, integrates a CDCL-based SAT solver and a conflict-driven model-constructing theory solver [6, 24, 31, 34, 35, 56]. CDSAT, for Conflict-Driven SATisfiability, generalizes MCSAT to a generic union of disjoint theories whose solvers may or may not be model-constructing [11].
In CDSAT, both Boolean and first-order terms are given assignments in a trail representing the candidate model as a partial assignment. First-order terms are assigned constant symbols representing individuals of the corresponding sort in a model’s domain (e.g., integer terms are assigned integer constants). Since CDSAT accepts such first-order assignments also as part of the input, CDSAT is an engine to determine the satisfiability of a quantifier-free formula modulo a union of theories (SMT) and possibly modulo an initial assignment of values to terms appearing in the input formula. We call this generalization of SMT satisfiability modulo assignment (SMA).
CDSAT is presented as a transition system that combines multiple theory solvers, all or some of which are conflict-driven, into a conflict-driven solver for the union of the theories. More precisely, CDSAT combines theory inference systems, called theory modules, and performs the conflict-driven search for all theories. A theory module is an abstraction of a theory solver. Propositional logic is regarded as one of the theories. Every theory module can expand the trail in two ways: either by deciding the value of a term or by performing an inference. Theory inferences are applied to propagate consequences of the assignments on the trail, to detect conflicts, and to explain such conflicts, all in the respective theory. A conflict in CDSAT is a set of assignments from the trail that is unsatisfiable. The inferences can be used to transform the conflict into a Boolean one, susceptible of conflict analysis. The analysis solves the conflict, producing a lemma and undoing some assignments on the trail.
In conflict-driven reasoning, it is essential that the system learns a lemma from a solved conflict, because the lemma immediately thwarts any attempt to repeat a failed search path. In CDSAT [11], lemma learning is limited to the case of backjumping that simply flips the truth assignment of a Boolean term that was involved in the conflict. The first contribution of the present article is a CDSAT transition system with a more general and more flexible lemma learning capability. The new lemma learning mechanism subsumes the old one, allows both learn-and-backjump and learn-and-restart, and it enables CDSAT to form and learn new clauses. With this addition, CDSAT reduces to CDCL, if propositional logic is the only theory, and to MCSAT, if propositional logic and another theory with a conflict-driven solver are the only theories.
The theory modules need to satisfy a completeness property that is strong enough to ensure that CDSAT determines whether the input problem has a model in the union of the theories. For such a model to exist, the theories need to agree on what they have in common. As disjoint theories only share equality and sorts, the theories need to agree on which shared terms are equal and on the cardinalities of shared sorts. The standard approach to this problem in the literature is the equality-sharing (Nelson-Oppen) scheme (e.g., [9, 23, 42, 48, 49] for a survey covering also several extensions). In order to reach an agreement on which shared terms are equal, each theory solver propagates the (disjunctions of) equalities between shared variables that are entailed by its part of the problem. For cardinalities, the equality-sharing method requires the theories to be stably infinite (every satisfiable formula has a model with countably infinite domain), so that the shared sorts can be interpreted as countably infinite domains.
For model-constructing theory solvers the equality-sharing scheme can be implemented by model-based theory combination (MBTC) [23]. In MBTC a theory solver may decide an equality, between terms occurring in the problem, that is true in its candidate model, even if it is not entailed by its part of the problem. If it turns out later that such an equality is not entailed, it will cause a conflict, so that the responsible solver will retract it and amend its model. MBTC was born out of the observation that, especially when the input is found satisfiable, it is generally less expensive for a theory solver to enumerate the equalities satisfied in a candidate theory model than those entailed.
In the equality-sharing method, including MBTC, solvers are combined as black-boxes. If a conflict-driven model-constructing theory solver is included, as in MBTC, its model-constructing and conflict-driven operations remain hidden inside the black-box. When combination of theories by equality sharing or MBTC is integrated with the CDCL procedure in the DPLL(\({\mathcal {T}}\)) or CDCL(\({\mathcal {T}}\)) paradigm (e.g., [13, 23, 42, 50]), the candidate model on the trail and the public conflict-driven reasoning is propositional. The CDCL procedure plays a central role, while the theory solvers are satellites that signal theory conflicts or submits theory lemmas to CDCL.
In CDSAT all theory modules, including a CDCL module for propositional logic, cooperate as peers to build a model for the union of the theories on the shared trail, and the conflict-driven reasoning happens in the union of the theories. Each theory module has a view of the shared trail, comprising its theory assignments as well as equalities or disequalities implied by assignments of other theories. The idea of MBTC is subsumed, since in CDSAT any theory module can decide an equality that is true in its view of the shared trail. Furthermore, CDSAT does not require stable infiniteness, provided there is a leading theory, its module is complete, and the other modules are leading-theory-complete. The leading theory knows all the sorts in the union of theories, and it aggregates any constraints that the theories may impose on the cardinality of shared sorts. The aggregated constraints are enforced as axioms or theorems of the leading theory and as inference rules of its module. A theory module is complete if it can expand any assignment that is not satisfied by a model of its theory. Leading-theory-completeness also requires that the module can expand an assignment, if its theory model does not agree on cardinalities of shared sorts and equality of shared terms with a model of the leading theory.
In previous work [11] we showed that if the theory modules are sound and leading-theory-complete, CDSAT is sound and complete. Furthermore, we exemplified the notion of theory module by listing theory modules for propositional logic, also known as the Boolean theory (\(\textsf {Bool} \)), the theory of equality with uninterpreted function symbols (\(\textsf {EUF} \)), the theory of arrays (\(\textsf {Arr} \)), and linear rational arithmetic (\(\textsf {LRA} \)). A non-conflict-driven solver can be abstracted into a black-box theory module, whose only inference rule invokes the solver to detect a theory conflict on the trail. However, it was not shown that these modules are leading-theory-complete. The second contribution of the present article is a collection of completeness theorems showing that the above theory modules are leading-theory-complete for all suitable leading theories. Moreover, we prove that if all modules are black-boxes, CDSAT emulates the equality-sharing method (covering also MBTC), and we demonstrate the role of the leading theory by considering the case where at-most cardinality constraints need to be enforced.
A key difference between conflict-driven theory reasoning and conflict-driven propositional reasoning is that theory inference rules may explain conflicts by inferences that generate new (i.e., non-input) terms. If the transition system allows this kind of expansion, termination requires that all new terms come from a finite basis (e.g., [24]). For conflict-driven reasoning in a union of theories, this issue must be approached locally, because no inference system should be authorized to generate infinitely many terms, and globally, because the interaction of multiple inference systems should preserve finiteness. In previous work [11] we showed that if every theory module is equipped with a finite local basis for its theory, and a finite global basis for the union of the theories does exist, CDSAT is guaranteed to halt. However, finite local bases for the above modules were not exhibited. The third contribution of the present article is a collection of finite local bases for those modules, with a technique for the generic construction of a finite global basis from given finite local bases.
Proofs are important in SMT/SMA, because many applications require the solver to generate either a satisfying assignment or a proof of unsatisfiability. CDCL-based SAT solvers generate proofs by resolution [57]. Since such proofs are huge, more sophisticated and compact proof formats have been investigated (e.g., [22, 29, 32, 33]). The DPLL(\({\mathcal {T}}\)) or CDCL(\({\mathcal {T}}\)) paradigm naturally supports the generation of proofs by resolution, where the theory lemmas are plugged in as leaves with black-box subproofs [3, 12, 27, 38]. This style has been implemented in solvers such as Z3 [3], veriT [2, 27], and CVC4 [38] and extended in several ways (e.g., [2, 38]). In CDSAT, the CDCL-based SAT solver loses its centrality as the only conflict-driven component, and all theory modules contribute directly to the proof, including new terms. Even if propositional resolution with theory subproofs is chosen as the final proof format, CDSAT proofs cannot be reconstructed in the same way as CDCL(\({\mathcal {T}}\)) proofs, because the structure and the operations of CDSAT differ from those of CDCL(\({\mathcal {T}}\)). The fourth contribution of the present article comprises two approaches to generate CDSAT proofs.
The first approach is a proof-carrying CDSAT transition system, where proof terms record the information needed to generate proofs. We describe different ways to turn proof terms into proofs, including producing resolution proofs with theory lemmas. These proof objects can then be checked directly by a verified checker [53] or exported to a proof format verifiable by proof checkers. Thus, proof-carrying CDSAT can slot into pipelines from proof-search to proof-checking [1, 5, 7], where a minimal amount of proof information (e.g., an unsatisfiable core) may be sufficient for a theorem prover to regenerate a proof in its own format. The second approach works by specifying a small kernel of primitives in LCF style [30, 47], so that building proof objects in memory can be avoided. If CDSAT is implemented on top of this kernel, the LCF-type abstraction ensures that an  answer is correct by construction, and CDSAT can be used as a trusted external oracle for interactive proof tools.
answer is correct by construction, and CDSAT can be used as a trusted external oracle for interactive proof tools.
In summary, the original contributions of the present article include:
-
1.
An extension of the CDSAT transition system with a more general and more flexible lemma learning capability;
-
2.
Definitions of finite local bases and proofs of leading-theory-completeness of the modules for \(\textsf {Bool} \), \(\textsf {EUF} \), \(\textsf {Arr} \), and \(\textsf {LRA} \), as well as for a generic black-box module, and a generic module for at-most cardinality constraints;
-
3.
A general technique to construct a finite global basis for a union of theories from finite local bases of the theories; and
-
4.
Approaches to endow CDSAT with proof generation either by producing proof objects in memory or in LCF style.
This article is organized as follows. Section 2 contains basic definitions for CDSAT. Section 3 is subdivided in three parts: Sect. 3.1 describes the CDSAT transition system with enhanced lemma learning; Sect. 3.2 illustrates via examples the novel lemma learning capabilities; and Sect. 3.3 presents other definitions, including that of leading-theory-completeness, discussing how the soundness, completeness, and termination results for CDSAT [11] extend to the transition system in Sect. 3.1. Section 4 presents theory modules, local finite bases, and leading-theory-completeness theorems for \(\textsf {Bool} \), \(\textsf {LRA} \), \(\textsf {EUF} \), \(\textsf {Arr} \), a generic stably infinite theory, and a generic theory with at-most cardinality constraints. Section 5 portrays the technique to get a global basis from local ones. Sections 6 and 7 cover the two approaches to proof generation in CDSAT.
Lemma learning and proof generation for CDSAT appeared in a conference version [10] of the present article.
2 Basic Definitions
Let \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\) be disjoint theories, each defined by its signature \(\varSigma _{k} {=} (S_k,F_k)\) and axiomatization \({\mathcal {A}}_k\), where \(S_k\) is the set of sorts and \(F_k\) is the set of symbols, for all k, \(1\le k\le n\). Every theory has the sort \(\textsf {prop} \) of the Boolean values and sorted equality symbols: \({\,\simeq _{S}\,} = \{{\,\simeq _{s}\,}{{:}}s{\times }s{\rightarrow }\textsf {prop} \mid s\in S_k\}\subseteq F_k\). The sorts of equalities may be omitted. Disjointness means that the theories do not share symbols except equality on shared sorts. Often one of the theories is the Boolean theory \(\textsf {Bool} \), with the logical connectives \(\lnot \), \(\wedge \), and \(\vee \) as symbols. Formulæ are terms of sort \(\textsf {prop} \). The union of \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\) is denoted \({\mathcal {T}}_{\infty }\), with signature \(\varSigma _{\infty }{=} (S_\infty ,F_\infty )\), where \(S_\infty {=} \bigcup _{k=1}^n S_k\) and \(F_\infty {=} \bigcup _{k=1}^n F_k\), and axiomatization \(\bigcup _{k=1}^n {\mathcal {A}}_k\).
Let \({\mathcal {T}}_{}\), \(\varSigma _{}\), and S stand for \({\mathcal {T}}_{k}\), \(\varSigma _{k}\), and \(S_k\) (\(1\,{\le }\,k\,{\le }\,n\)), or for \({\mathcal {T}}_{\infty }\), \(\varSigma _{\infty }\), and \(S_\infty \). We assume a collection \({\mathcal {V}}^{}= ({\mathcal {V}}^{s})_{s\in S}\) of disjoint sets of variables, where \({\mathcal {V}}^{s}\) is the set of variables of sort s. We use x, y, and z for variables, t and u for terms of any sort, l and p for formulæ, and \(\unlhd \) for the subterm ordering. If \(\varSigma = (S,F)\) is a signature with \(F\subseteq F_\infty \), the \(\varSigma \)-foreign subterms of a term t are those subterms whose root symbol is not in F, including variables. Non-variable \(\varSigma \)-foreign subterms can be regarded as variables, without replacing them explicitly with new variables. This is accomplished by defining the free \(\varSigma \)-variables of t as its \(\varSigma \)-foreign subterms with a \(\unlhd \)-maximal occurrence. For a term t, the set of its free \(\varSigma \)-variables is denoted  , and the set of its free \(\varSigma \)-variables of sort s is denoted
, and the set of its free \(\varSigma \)-variables of sort s is denoted  . For a set X of terms,
. For a set X of terms,  and
and  .
.
A \({{\mathcal {T}}}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\) interprets each \(s\in S\) as a non-empty domain \(s^{\mathcal {M}}\) with \(\textsf {prop} ^{\mathcal {M}}= \{\textsf {true},\textsf {false}\}\), each \(v\in {\mathcal {V}}^{s}\) as an element \(v^{\mathcal {M}}\) in \(s^{\mathcal {M}}\), each \(f\in F\) with \(f:(s_1{\times }\cdots {\times }s_m){\rightarrow }s\) as a function \(f^{\mathcal {M}}\) from \(s_1^{\mathcal {M}}{\times }\cdots {\times }s_m^{\mathcal {M}}\) to \(s^{\mathcal {M}}\), and each \(\simeq _{s}\) as the function \(\simeq _{s}^{\mathcal {M}}\) from \(s^{\mathcal {M}}{\times }s^{\mathcal {M}}\) to \(\{\textsf {true},\textsf {false}\}\) that returns \(\textsf {true}\) if and only if its arguments are the same element. The interpretation of terms and formulæ is defined as usual, with the interpretation of term t denoted \({\mathcal {M}}(t)\). We write \({{\mathcal {T}}}\)-model when the variables do not matter.
CDSAT works with assignments that assign to terms values of the appropriate sort. For example, assuming theories \(\textsf {Bool} \), \(\textsf {Arr} \), and a fragment of arithmetic, \(((x > 1) \vee (y < 0)) {\leftarrow }_{{}}\textsf {true}\), \(y {\leftarrow }_{{}}{-1}\), \(z {\leftarrow }_{{}}\sqrt{2}\), \((\mathrm{store}(a,i,v) {\,\simeq _{}\,}b) {\leftarrow }_{{}}\textsf {true}\), \(\mathrm{select}(a,j) {\leftarrow }_{{}}3\), and \((\mathrm{select}(a,j) {\,\simeq _{}\,}v) {\leftarrow }_{{}}\textsf {true}\) are assignments. The standard approach to define what the values are is to extend the signature with sorted constant symbols to name all individuals in the domains used to interpret the sorts (e.g., the appropriate set of numerals for a fragment of arithmetic).
For each \({\mathcal {T}}_{k}\), \(1\,{\le }\,k\,{\le }\,n\), a conservative theory extension \({\mathcal {T}}_{k}^+\) is a theory with signature \(\varSigma _{k}^+ = (S_k,F_k^+)\), where \(F_k^+\) adds to \(F_k\) a possibly empty set of new constant symbols, called \({\mathcal {T}}_{k}\)-values, accompanied by new axioms as needed (e.g., \(\sqrt{2}\) with \(\sqrt{2}\cdot \sqrt{2}{\,\simeq _{}\,}2\)). For numerals, as for \(\textsf {true}\) and \(\textsf {false}\), a \({\mathcal {T}}_{k}\)-value is both the domain element and the constant symbol that names it. \(F_k^+\) may be infinite, but it is countable (e.g., using the algebraic reals as real numbers). The trivial extension only adds \(\{\textsf {true}, \textsf {false}\}\) as \({\mathcal {T}}_{k}\)-values. We assume that the extended theories are still disjoint except for \(\textsf {true}\) and \(\textsf {false}\).
The union of \({\mathcal {T}}_{1}^+,\ldots ,{\mathcal {T}}_{n}^+\) is a conservative extension \({\mathcal {T}}_{\infty }^+\) of \({\mathcal {T}}_{\infty }\), with signature \(\varSigma _{\infty }^{+}= (S_\infty ,F_\infty ^+)\) for \(F_\infty ^+=\bigcup _{k=1}^n F^{+}_k\). Conservativity means that \({\mathcal {T}}_{}^+\)-unsatisfiability implies \({\mathcal {T}}_{}\)-unsatisfiability for \(\varSigma _{}\)-formulæ: if CDSAT detects \({\mathcal {T}}_{\infty }^+\)-unsatisfiability, the problem is \({\mathcal {T}}_{\infty }\)-unsatisfiable; if the problem is \({\mathcal {T}}_{\infty }\)-satisfiable, there is a \({\mathcal {T}}_{\infty }^+\)-model that CDSAT can discover. The symbols \({\mathfrak {c}}\) and \({\mathfrak {q}}\), possibly with subscripts, are used for values, reserving \({\mathfrak {b}}\) for \(\textsf {true}\) or \(\textsf {false}\).
Recalling that \({\mathcal {T}}\) stands for either a \({\mathcal {T}}_{k}\) (\(1\,{\le }\,k\,{\le }\,n\)) or \({\mathcal {T}}_{\infty }\), a \({\mathcal {T}}\)-assignment is an assignment of \({\mathcal {T}}\)-values to \({\mathcal {T}}_{\infty }\)-terms. Formally, a \({\mathcal {T}}\)-assignment is a set \(J = \{ u_1 {\leftarrow }_{{}}{\mathfrak {c}}_1, \ldots , u_m {\leftarrow }_{{}}{\mathfrak {c}}_m \}\), where, for all i, \(1\le i\le m\), \(u_i\) is a \({\mathcal {T}}_{\infty }\)-term and \({\mathfrak {c}}_i\) a \({\mathcal {T}}\)-value of the same sort. The set of terms that occur in J is \(G(J) = \{t\mid t\unlhd u_i, 1\le i\le m\}\), and \(G_s(J)\) is the subset of the terms of sort s in G(J). The set of free variables of J is  . We use J for generic \({\mathcal {T}}\)-assignments, A for generic singleton assignments, L or K for Boolean singleton assignments, H and E for \({\mathcal {T}}_{\infty }\)-assignments.
. We use J for generic \({\mathcal {T}}\)-assignments, A for generic singleton assignments, L or K for Boolean singleton assignments, H and E for \({\mathcal {T}}_{\infty }\)-assignments.
The flip \(\overline{L}\) of L assigns to the same formula the opposite Boolean value. Since \(\lnot \) is a function symbol in the signature of \(\textsf {Bool} \), one can write \(l{\leftarrow }_{{}}\textsf {true}\) and \(l{\leftarrow }_{{}}\textsf {false}\), that are one the flip of the other, and also \(\lnot l{\leftarrow }_{{}}\textsf {true}\) and \(\lnot l{\leftarrow }_{{}}\textsf {false}\), that are also one the flip of the other. Clearly, \(l{\leftarrow }_{{}}\textsf {true}\) and \(\lnot l{\leftarrow }_{{}}\textsf {false}\) are equivalent and so are \(l{\leftarrow }_{{}}\textsf {false}\) and \(\lnot l{\leftarrow }_{{}}\textsf {true}\). The simplest form is preferred when writing assignments: for example, if l is \(\lnot a\), where a is a propositional variable, it is preferable to use \(a{\leftarrow }_{{}}\textsf {true}\) and \(a{\leftarrow }_{{}}\textsf {false}\). Furthermore, \(l{\leftarrow }_{{}}\textsf {true}\) is abbreviated as l, \(l{\leftarrow }_{{}}\textsf {false}\) as \({\overline{l}}\), and \((t{\,\simeq _{}\,}u){\leftarrow }_{{}}\textsf {false}\) as \(t{\,\not \simeq _{}\,}u\).
An assignment is plausible if for no L it contains both L and \(\overline{L}\). A Boolean assignment only assigns Boolean values, while a first-order assignment only assigns non-Boolean values. An SMT problem is presented as a plausible Boolean assignment \(\{l_1{\leftarrow }_{{}}\textsf {true},\ldots ,l_m{\leftarrow }_{{}}\textsf {true}\}\), abbreviated \(\{l_1,\ldots ,l_m\}\), while an SMA problem also includes first-order assignments.
The theory view, or \({\mathcal {T}}_{}\)-view, \(H_{{\mathcal {T}}_{}}\) of a \({\mathcal {T}}_{\infty }\)-assignment H comprises the \({\mathcal {T}}_{}\)-assignments in H and all equalities or disequalities between terms of a sort in S that are entailed by first-order assignments in H. If \(\{x{\leftarrow }_{{}}3, y{\leftarrow }_{{}}3, z{\leftarrow }_{{}}4\}\subseteq H\), the \({\mathcal {T}}_{}\)-view \(H_{{\mathcal {T}}_{}}\) also includes \(x{\,\simeq _{}\,}y\), \(x \not \simeq z\), and \(y \not \simeq z\), for every \({\mathcal {T}}_{}\) having the sort of x, y, and z. If H is Boolean, \(H_{{\mathcal {T}}_{}} = H\). As a \({\mathcal {T}}_{i}\)-assignment (\(1\le i\le n\)) is a special case of \({\mathcal {T}}_{\infty }\)-assignment, the \({\mathcal {T}}_{}\)-view of a \({\mathcal {T}}_{i}\)-assignment is also defined.
A \({\mathcal {T}}_{}^+\)-model \({{\mathcal {M}}}\) endorses a \({\mathcal {T}}_{}\)-assignment J, written \({{\mathcal {M}}}\models J\), if \({{\mathcal {M}}}\) satisfies \(u{\,\simeq _{}\,}{\mathfrak {c}}\) for all pairs \((u{\leftarrow }_{{}}{\mathfrak {c}})\in J\). It follows that if \(\{u{\leftarrow }_{{}}{\mathfrak {c}}, t{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq J\), then \({{\mathcal {M}}}\) also satisfies \(u{\,\simeq _{}\,}t\). If \({{\mathcal {M}}}\models J_{{\mathcal {T}}_{}}\), that is, \({{\mathcal {M}}}\) endorses the \({\mathcal {T}}_{}\)-view of J, then \({{\mathcal {M}}}\) also satisfies \(u \not \simeq t\), for all pairs \(u{\leftarrow }_{{}}{\mathfrak {c}}_1\) and \(t{\leftarrow }_{{}}{\mathfrak {c}}_2\) in J with \({\mathfrak {c}}_1\ne {\mathfrak {c}}_2\). Thus, \({{\mathcal {M}}}\models J_{{\mathcal {T}}_{}}\) is generally stronger than \({{\mathcal {M}}}\models J\). A \({\mathcal {T}}_{}\)-assignment J is satisfiable, if there is a \({\mathcal {T}}_{}^+\)-model \({{\mathcal {M}}}\) such that \({{\mathcal {M}}}\models J_{{\mathcal {T}}_{}}\), and it is unsatisfiable otherwise, written \(J\models \bot \). We write \(J\models L\) if \({{\mathcal {M}}}\models L\) for all \({\mathcal {T}}_{}^+\)-models \({{\mathcal {M}}}\) such that \({{\mathcal {M}}}\models J_{{\mathcal {T}}_{}}\). All this applies to a \({\mathcal {T}}_{\infty }\)-assignment H, for which we say that \({{\mathcal {M}}}\) globally endorses H if \({{\mathcal {M}}}\models H_{{\mathcal {T}}_{\infty }}\), also written \({{\mathcal {M}}}\models ^G H\) to emphasize “globally.”
A theory module \({\mathcal {I}}_{k}\) for theory \({\mathcal {T}}_{k}\) (\(1\,{\le }\,k\,{\le }\,n\)) is an inference system with inferences of the form \(J\vdash _{{\mathcal {I}}_{k}} L\), or \(J\vdash _{k} L\) for short, where J is a \({\mathcal {T}}_{k}\)-assignment and L is a Boolean assignment. Theory modules are required to be sound: if \(J\vdash _{k} L\) then \(J\models L\). In the sequel, assignment stands for \({\mathcal {T}}_{\infty }\)-assignment.
3 CDSAT with Lemma Learning
In this section we present the CDSAT transition system with lemma learning. Section 3.1 presents the CDSAT transition system as in [11], except that the \(\textsf {Backjump}\) rule of [11] is replaced by a new \(\textsf {LearnBackjump}\) rule that introduces a more general and more flexible lemma learning mechanism. Section 3.2 analyzes in detail the working of \(\textsf {LearnBackjump}\): it is more general because it enables CDSAT to learn new clauses, whereas \(\textsf {Backjump}\) only flips a Boolean term; it is more flexible because it enables a CDSAT search plan to choose the destination level upon backjumping; and it can simulate the \(\textsf {Backjump}\) rule. Section 3.3 includes the definitions of basis and leading-theory-completeness (from [11]), and discusses how the arguments of the proofs of soundness, termination, and completeness of CDSAT in [11] are modified to have \(\textsf {LearnBackjump}\) in place of \(\textsf {Backjump}\).
3.1 The CDSAT Transition System with Lemma Learning
CDSAT works with a trail \(\varGamma \), defined as a sequence of distinct singleton assignments that are either decisions or justified assignments. A decision is written  to convey guessing, and it can be either a Boolean or a first-order assignment. A justified assignment is written
to convey guessing, and it can be either a Boolean or a first-order assignment. A justified assignment is written  , where H, the justification of A, is a set of singleton assignments that appear before A in \(\varGamma \). The elements of the input assignment \(H_0\) are listed in \(\varGamma \) as justified assignments with empty justification. The only justified assignments that are first-order assignments are the input first-order assignments of an SMA problem; all non-input justified assignments are Boolean. A non-input justified assignment
, where H, the justification of A, is a set of singleton assignments that appear before A in \(\varGamma \). The elements of the input assignment \(H_0\) are listed in \(\varGamma \) as justified assignments with empty justification. The only justified assignments that are first-order assignments are the input first-order assignments of an SMA problem; all non-input justified assignments are Boolean. A non-input justified assignment  is due to either an inference \(J\vdash _{k} L\) for some theory \({\mathcal {T}}_{k}\), \(1\,{\le }\,k\,{\le }\,n\), or a conflict-solving transition. A justified assignment
is due to either an inference \(J\vdash _{k} L\) for some theory \({\mathcal {T}}_{k}\), \(1\,{\le }\,k\,{\le }\,n\), or a conflict-solving transition. A justified assignment  is sound if for all \({\mathcal {T}}_{\infty }^+\)-models \({\mathcal {M}}\), if \({\mathcal {M}}\models ^G {H_0{\cup } H}\) then \({\mathcal {M}}\models A\). A trail can be seen as an assignment by ignoring order and justifications.
is sound if for all \({\mathcal {T}}_{\infty }^+\)-models \({\mathcal {M}}\), if \({\mathcal {M}}\models ^G {H_0{\cup } H}\) then \({\mathcal {M}}\models A\). A trail can be seen as an assignment by ignoring order and justifications.
Given a trail \(\varGamma \) with assignments \(A_0,\ldots ,A_m\), the level of a singleton assignment \(A_i\), \(0\le i\le m\), is given by \(\textsf {level}_{\varGamma }(A_i) = 1 + \max \{\textsf {level}_{\varGamma }(A_j) \mid j < i \}\), if \(A_i\) is a decision, and \(\textsf {level}_{\varGamma }(A_i) = \textsf {level}_{\varGamma }(H)\), if \(A_i\) is a justified assignment  . The level of a set of singleton assignments \(H\subseteq \varGamma \) is given by \(\textsf {level}_{\varGamma }(H) = 0\), if \(H = \emptyset \), and \(\textsf {level}_{\varGamma }(H) = \max \{\textsf {level}_{\varGamma }(A) \mid A\in H\}\), otherwise. As the level of
. The level of a set of singleton assignments \(H\subseteq \varGamma \) is given by \(\textsf {level}_{\varGamma }(H) = 0\), if \(H = \emptyset \), and \(\textsf {level}_{\varGamma }(H) = \max \{\textsf {level}_{\varGamma }(A) \mid A\in H\}\), otherwise. As the level of  depends on its justification, not on its position on the trail, the trail is not organized as a stack, and
depends on its justification, not on its position on the trail, the trail is not organized as a stack, and  can be added to the trail after assignments of greater level. This behavior and assignment A are called late propagation. \({\varGamma }^{\le {m}}\) denotes the restriction of \(\varGamma \) to its elements of level at most m.
can be added to the trail after assignments of greater level. This behavior and assignment A are called late propagation. \({\varGamma }^{\le {m}}\) denotes the restriction of \(\varGamma \) to its elements of level at most m.
The state of a CDSAT-derivation is either a trail \(\varGamma \) or a conflict state  , where \(\varGamma \) is a trail, and E is a conflict, that is, an assignment such that \(E\subseteq \varGamma \) and \(H_0\cup E \models \bot \). The CDSAT transition system features trail rules, denoted \(\longrightarrow \), and conflict-state rules, denoted \(\Longrightarrow \), with transitive closure \(\Longrightarrow ^*\) and \(\uplus \) for disjoint union (see Fig. 1). As CDSAT may place on the trail assignments for new (i.e., non-input) terms, for termination all terms must come from a finite set \({{\mathcal {B}}}\), called global basis, which is determined based on the input and does not change during the derivation. While terms come from \({{\mathcal {B}}}\), values come from \(F_\infty ^+\), which may be infinite: a derivation will use a finite subset of \(F_\infty ^+\) that is not fixed beforehand. An assignment H is in \({{\mathcal {B}}}\) if \(t\in {{\mathcal {B}}}\) for all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in H\).
, where \(\varGamma \) is a trail, and E is a conflict, that is, an assignment such that \(E\subseteq \varGamma \) and \(H_0\cup E \models \bot \). The CDSAT transition system features trail rules, denoted \(\longrightarrow \), and conflict-state rules, denoted \(\Longrightarrow \), with transitive closure \(\Longrightarrow ^*\) and \(\uplus \) for disjoint union (see Fig. 1). As CDSAT may place on the trail assignments for new (i.e., non-input) terms, for termination all terms must come from a finite set \({{\mathcal {B}}}\), called global basis, which is determined based on the input and does not change during the derivation. While terms come from \({{\mathcal {B}}}\), values come from \(F_\infty ^+\), which may be infinite: a derivation will use a finite subset of \(F_\infty ^+\) that is not fixed beforehand. An assignment H is in \({{\mathcal {B}}}\) if \(t\in {{\mathcal {B}}}\) for all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in H\).
Rule \(\textsf {Decide}\) adds a decision \(u{\leftarrow }_{{}}{\mathfrak {c}}\) if it is acceptable for a theory module \({\mathcal {I}}_k\) in its view \(\varGamma _{{\mathcal {T}}_{k}}\) of trail \(\varGamma \). Acceptability comprises three requirements: (1) \(\varGamma \) does not assign a \({\mathcal {T}}_k\)-value to u; (2) if \(u{\leftarrow }_{{}}{\mathfrak {c}}\) is first-order, there is no inference \(J\cup \{u{\leftarrow }_{{}}{\mathfrak {c}}\}\vdash _{{\mathcal {I}}_k} L\) such that \(\overline{L} \in \varGamma _{{\mathcal {T}}_{k}}\) for \(J\subseteq \varGamma _{{\mathcal {T}}_{k}}\); and (3) u is relevant to \({\mathcal {T}}_k\) in \(\varGamma _{{\mathcal {T}}_{k}}\). The latter means that either (i) \(u\in G(\varGamma _{{\mathcal {T}}_{k}})\), \({\mathcal {T}}_k\) has its sort and values for it, so that \({\mathcal {I}}_k\) can decide an assignment to u; or (ii) u is an equality \(u_1{\,\simeq _{}\,}u_2\) such that \(u_1,u_2\in G(\varGamma _{{\mathcal {T}}_{k}})\), \({\mathcal {T}}_k\) has their sort, but does not have values for their sort, so that \({\mathcal {I}}_k\) can decide the truth value of \(u_1{\,\simeq _{}\,}u_2\).
By Condition (1), if \(L\!\!\!\!\in \!\!\!\!\varGamma \), both L and \(\overline{L}\) are unacceptable for all theories. By Condition (2), if \(\{x{\leftarrow }_{{}}1,\ \overline{x < y}\}\subseteq \varGamma \), then \(y{\leftarrow }_{{}}2\) is unacceptable for \(\textsf {LRA} \), as \(\{x{\leftarrow }_{{}}1,\ y{\leftarrow }_{{}}2\}\vdash _{{\mathcal {I}}_\textsf {LRA} } x < y\) by an \(\textsf {LRA} \)-evaluation inference (cf. Sect. 4.4). By Condition (3), if \(\{f(u_1){\leftarrow }_{{}}\textsf {red},\ u_2{\leftarrow }_{{}}\textsf {yellow}\}\subseteq \varGamma \), where f is a function from colors to colors, \(u_1{\leftarrow }_{{}}\textsf {yellow}\) is relevant to a theory of colors by (i), while \(u_1{\,\simeq _{}\,}u_2\) is relevant to \(\textsf {EUF} \) by (ii), provided \(\textsf {EUF} \) has the sort of colors. A decision \(u{\leftarrow }_{{}}{\mathfrak {c}}\) is forced when \({\mathfrak {c}}\) is the only acceptable value for u, such as if \(\{u{\,\simeq _{}\,}t,\ t{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq \varGamma \) for \(\textsf {EUF} \), or \(\{u\le t,\ t\le u,\ t{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq \varGamma \) for \(\textsf {LRA} \).
Rule \(\textsf {Deduce}\) expands \(\varGamma \) with a Boolean singleton assignment justified by a theory inference \(J\vdash _{k} L\) from assignments J already in \(\varGamma \). Sound theory inferences yield sound justified assignments. The system proceeds with decisions and deductions until a conflict arises: if \(J\vdash _{k} L\) and \(\overline{L}\in \varGamma \), the assignment \(J\cup \{\overline{L}\}\) is a conflict. \(\textsf {Deduce}\) encompasses propagation, by deducing an assignment entailed in the theory by assignments in \(\varGamma \), and conflict explanation, by performing theory inferences that allow a theory conflict to surface in \(\varGamma \) as a Boolean conflict. For example, given a series of decisions \(u_2{\leftarrow }_{{}}\textsf {yellow},\ f(u_1){\leftarrow }_{{}}\textsf {red},\ u_1{\leftarrow }_{{}}\textsf {yellow},\ f(u_2){\leftarrow }_{{}}\textsf {blue}\), a module for the theory of colors can deduce (propagate) \(f(u_1){\,\not \simeq _{}\,}f(u_2)\) and \(u_1{\,\simeq _{}\,}u_2\) by equality inferences (cf. Fig. 3 in Sect. 3.3), and a module for \(\textsf {EUF} \) can detect the conflict by deducing \(\{u_1{\,\simeq _{}\,}u_2,\ f(u_1){\,\not \simeq _{}\,}f(u_2)\}\vdash _{\textsf {EUF} } \bot \) (cf. Sect. 4.2). If the conflict is at level 0, rule \(\textsf {Fail}\) returns unsat. Otherwise, rule \(\textsf {ConflictSolve}\) returns the trail \(\varGamma ^\prime \) produced by the conflict-state rules, so that the search can resume.
The conflict-state rules handle both first-order and Boolean assignments and their interplay. Conflict-solving as in CDCL involves flipping a Boolean assignment L into \(\overline{L}\), recording that L was tried and failed. A first-order assignment \(u{\leftarrow }_{{}}{\mathfrak {c}}\) cannot be flipped: its complement would be the set of all other values for u, which is not a singleton and not even a finite set in general. Thus, \(u{\leftarrow }_{{}}{\mathfrak {c}}\) is undone, not flipped. Since \(u{\leftarrow }_{{}}{\mathfrak {c}}\) may appear in justifications, undoing it requires the removal of all its consequences (i.e., justified assignments with \(u{\leftarrow }_{{}}{\mathfrak {c}}\) in the justification). A Boolean decision \(\overline{L}\) is then forced (for a consequence L of \(u{\leftarrow }_{{}}{\mathfrak {c}}\) in the conflict) to prevent repeating the same first-order decision \(u{\leftarrow }_{{}}{\mathfrak {c}}\) that caused a conflict. Another remark is that since each assignment has a level, conflict solving can proceed by considering an assignment that stands out, because its level is the greatest level in the conflict. Clearly, such an assignment is not unique in general.
The main workhorse of conflict solving is the \(\textsf {Resolve}\) rule. \(\textsf {Resolve}\) explains a conflict \(E\uplus \{A\}\) by replacing a justified assignment A with its justification H (see Fig. 1). Since \(H_0\cup E\uplus \{A\}\models \bot \), and  is sound, \(H_0\cup E\cup H\models \bot \) follows, and \(E\cup H\) is still a conflict. If A is first-order, it is an input assignment (\(H = \emptyset \)), and \(\textsf {Resolve}\) removes A from the conflict, not from the trail. For example, \(\textsf {Resolve}\) turns a conflict \(\{u_1{\,\simeq _{}\,}u_2,\ f(u_1){\,\not \simeq _{}\,}f(u_2)\}\) into \(\{u_1{\,\simeq _{}\,}u_2,\ f(u_1){\leftarrow }_{{}}\textsf {red},\ f(u_2){\leftarrow }_{{}}\textsf {blue}\}\), if
is sound, \(H_0\cup E\cup H\models \bot \) follows, and \(E\cup H\) is still a conflict. If A is first-order, it is an input assignment (\(H = \emptyset \)), and \(\textsf {Resolve}\) removes A from the conflict, not from the trail. For example, \(\textsf {Resolve}\) turns a conflict \(\{u_1{\,\simeq _{}\,}u_2,\ f(u_1){\,\not \simeq _{}\,}f(u_2)\}\) into \(\{u_1{\,\simeq _{}\,}u_2,\ f(u_1){\leftarrow }_{{}}\textsf {red},\ f(u_2){\leftarrow }_{{}}\textsf {blue}\}\), if  is on the trail. Intuitively, one can think of \(\textsf {Resolve}\) continuing to unfold the conflict, until it contains an assignment A that stands out in the above sense. This outstanding assignment A is either a first-order or a Boolean assignment.
is on the trail. Intuitively, one can think of \(\textsf {Resolve}\) continuing to unfold the conflict, until it contains an assignment A that stands out in the above sense. This outstanding assignment A is either a first-order or a Boolean assignment.
If A is a first-order assignment with \(\textsf {level}_{\varGamma }(A) = m\), rule \(\textsf {UndoClear}\) applies by going back to \({\varGamma }^{\le {m-1}}\) (see Fig. 1), which means that it undoes A and clears the trail of all its consequences. Note that \(m{-}1 \ge 0\) implies \(m>0\), that is, A is a decision. \(\textsf {UndoClear}\) solves the above conflict produced by \(\textsf {Resolve}\) by removing \(f(u_2){\leftarrow }_{{}}\textsf {blue}\), whose level is \(m=4\), and  . Going back to \(\,\,{\varGamma }^{\le {\,m-1}}\) does not represent a loop, because \({\varGamma }^{\le {m-1}}\) is new, as it must contain some late propagation. Indeed, A was acceptable when it was decided, which means it did not cause a conflict. If A became later part of a conflict, it must be that some late propagation L with \(\textsf {level}_{\varGamma }(L) < m\) was added to the trail after A, so that L is in \({\varGamma }^{\le {m-1}}\). In the example, the late propagation is \(u_1{\,\simeq _{}\,}u_2\) on level 3. A \(\textsf {Deduce}\) step based on \(u_1{\,\simeq _{}\,}u_2\vdash _{\textsf {EUF} } f(u_1){\,\simeq _{}\,}f(u_2)\) adds \(f(u_1){\,\simeq _{}\,}f(u_2)\) to the trail, making \(f(u_2){\leftarrow }_{{}}\textsf {red}\) a forced decision.
. Going back to \(\,\,{\varGamma }^{\le {\,m-1}}\) does not represent a loop, because \({\varGamma }^{\le {m-1}}\) is new, as it must contain some late propagation. Indeed, A was acceptable when it was decided, which means it did not cause a conflict. If A became later part of a conflict, it must be that some late propagation L with \(\textsf {level}_{\varGamma }(L) < m\) was added to the trail after A, so that L is in \({\varGamma }^{\le {m-1}}\). In the example, the late propagation is \(u_1{\,\simeq _{}\,}u_2\) on level 3. A \(\textsf {Deduce}\) step based on \(u_1{\,\simeq _{}\,}u_2\vdash _{\textsf {EUF} } f(u_1){\,\simeq _{}\,}f(u_2)\) adds \(f(u_1){\,\simeq _{}\,}f(u_2)\) to the trail, making \(f(u_2){\leftarrow }_{{}}\textsf {red}\) a forced decision.
If A is a Boolean assignment L in a conflict \(E\uplus \{L\}\) such that \(\textsf {level}_{\varGamma }(E) = m\) and \(\textsf {level}_{\varGamma }(L) > m\), CDSAT [11] applies the \(\textsf {Backjump}\) rule, which solves the conflict by producing the trail  . In other words, it jumps back to level m and adds to the trail the justified assignment
. In other words, it jumps back to level m and adds to the trail the justified assignment  , which is sound because \(H_0\cup (E\uplus \{L\}) \models \bot \) yields \(H_0\cup E\models \overline{L}\). Here the \(\textsf {Backjump}\) rule is replaced with the more general \(\textsf {LearnBackjump}\), which behaves like \(\textsf {Backjump}\) when H and L in its definition in Fig. 1 are \(\{L\}\) and \(\overline{L}\), respectively. \(\textsf {LearnBackjump}\) and the notion of clausal form mentioned in Fig. 1 will be illustrated in Sect. 3.2.
, which is sound because \(H_0\cup (E\uplus \{L\}) \models \bot \) yields \(H_0\cup E\models \overline{L}\). Here the \(\textsf {Backjump}\) rule is replaced with the more general \(\textsf {LearnBackjump}\), which behaves like \(\textsf {Backjump}\) when H and L in its definition in Fig. 1 are \(\{L\}\) and \(\overline{L}\), respectively. \(\textsf {LearnBackjump}\) and the notion of clausal form mentioned in Fig. 1 will be illustrated in Sect. 3.2.
Last, \(\textsf {UndoDecide}\) covers a situation where \(\textsf {Resolve}\) cannot apply. Reconsider \(\textsf {Resolve}\) explaining a conflict \(E\uplus \{A\}\) by replacing a Boolean justified assignment A with its justification H. The condition of \(\textsf {Resolve}\) in Fig. 1 requires that H does not contain a first-order decision \(A^\prime \) such that \(\textsf {level}_{\varGamma }(A^\prime ) = m = \textsf {level}_{\varGamma }(E\uplus \{A\})\). Indeed, suppose that A is  and \(\textsf {level}_{\varGamma }(E) < m\): if \(\textsf {Resolve}\) unfolds \(E\uplus \{A\}\) into \(E\uplus \{A^\prime \}\), \(\textsf {UndoClear}\) becomes applicable. If \(\textsf {UndoClear}\) undoes \(A^\prime \), and then \(\textsf {Decide}\) retries \(A^\prime \), and \(\textsf {Deduce}\) reiterates
and \(\textsf {level}_{\varGamma }(E) < m\): if \(\textsf {Resolve}\) unfolds \(E\uplus \{A\}\) into \(E\uplus \{A^\prime \}\), \(\textsf {UndoClear}\) becomes applicable. If \(\textsf {UndoClear}\) undoes \(A^\prime \), and then \(\textsf {Decide}\) retries \(A^\prime \), and \(\textsf {Deduce}\) reiterates  , the system loops. Thus, \(\textsf {Resolve}\) is forbidden, and either \(\textsf {UndoDecide}\) or \(\textsf {LearnBackjump}\) applies. If an assignment other than L in the conflict has level m (see the condition of \(\textsf {UndoDecide}\) in Fig. 1), \(\textsf {UndoDecide}\) undoes \(A^\prime \) and its consequences by going back to \({\varGamma }^{\le {m-1}}\) and decides \(\overline{L}\). If L is the only assignment of level m in the conflict, \(\textsf {LearnBackjump}\) applies like \(\textsf {Backjump}\).
, the system loops. Thus, \(\textsf {Resolve}\) is forbidden, and either \(\textsf {UndoDecide}\) or \(\textsf {LearnBackjump}\) applies. If an assignment other than L in the conflict has level m (see the condition of \(\textsf {UndoDecide}\) in Fig. 1), \(\textsf {UndoDecide}\) undoes \(A^\prime \) and its consequences by going back to \({\varGamma }^{\le {m-1}}\) and decides \(\overline{L}\). If L is the only assignment of level m in the conflict, \(\textsf {LearnBackjump}\) applies like \(\textsf {Backjump}\).
The CDSAT transition system is non-deterministic, as it leaves room for heuristic choices. Thus, multiple CDSAT-derivations from a given input exist. The addition of a search plan that controls the application of the transition rules yields a CDSAT procedure, whose derivation from a given input is unique.
3.2 Lemma Learning in CDSAT
The CDCL procedure can learn a propositional resolvent that was generated to explain a conflict. For example, consider a CDSAT trail containing

where  and
and  belong to the input assignment \(H_0\) and have level 0;
belong to the input assignment \(H_0\) and have level 0;  has level 1,
has level 1,  has level 2, and
has level 2, and  is a late propagation and has level 1. Clause \(a \vee b\) is a conflict clause for CDCL, and \(\{a \vee b,\ \overline{a},\ \overline{b}\}\) is a conflict for CDSAT. The CDCL procedure can learn \(b\vee d\), resolvent of \(a \vee b\) and the CDCL justification \(\lnot a\vee d\) of \(\overline{a}\).
is a late propagation and has level 1. Clause \(a \vee b\) is a conflict clause for CDCL, and \(\{a \vee b,\ \overline{a},\ \overline{b}\}\) is a conflict for CDSAT. The CDCL procedure can learn \(b\vee d\), resolvent of \(a \vee b\) and the CDCL justification \(\lnot a\vee d\) of \(\overline{a}\).
CDSAT [11] can apply the \(\textsf {Backjump}\) rule, which fires when CDSAT reaches a conflict state  , where \(\textsf {level}_{\varGamma }(E) = m\) and \(\textsf {level}_{\varGamma }(L) > m\), producing the trail
, where \(\textsf {level}_{\varGamma }(E) = m\) and \(\textsf {level}_{\varGamma }(L) > m\), producing the trail  . In the example, \(E = \{a \vee b,\ \overline{a}\}\), \(L = \overline{b}\), \(\textsf {level}_{\varGamma }(E) = 1\), \(\textsf {level}_{\varGamma }(L) = 2 > 1\), and \(\textsf {Backjump}\) produces the trail
. In the example, \(E = \{a \vee b,\ \overline{a}\}\), \(L = \overline{b}\), \(\textsf {level}_{\varGamma }(E) = 1\), \(\textsf {level}_{\varGamma }(L) = 2 > 1\), and \(\textsf {Backjump}\) produces the trail

Alternatively, CDSAT [11] can \(\textsf {Resolve}\) the conflict into \(\{a \vee b,\ \overline{d},\ \lnot a\vee d,\ \overline{b}\}\) and then apply \(\textsf {Backjump}\) to yield the trail

Either way, CDSAT [11] learns b, not \(b\vee d\). The new rule \(\textsf {LearnBackjump}\) of Fig. 1 enables CDSAT to learn the justified assignment  from the conflict \(\{a \vee b,\ \overline{d},\ \lnot a\vee d,\ \overline{b}\}\), forming clause \(b\vee d\) from the subset \(\{\overline{d},\ \overline{b}\}\) of the conflict.
from the conflict \(\{a \vee b,\ \overline{d},\ \lnot a\vee d,\ \overline{b}\}\), forming clause \(b\vee d\) from the subset \(\{\overline{d},\ \overline{b}\}\) of the conflict.
In general, \(\textsf {LearnBackjump}\) empowers CDSAT to turn any Boolean subset of a conflict into a disjunction of Boolean terms, that the system can learn, and that we call clause, slightly abusing the terminology because Boolean terms are formulæ. This requires \(\vee \in F_\infty \), which is the case whenever \({\mathcal {T}}_{\infty }\) includes propositional logic. If \(\vee \not \in F_\infty \), only unit clauses will be learned. Suppose that \(E\uplus H\) is a conflict, where H contains only Boolean assignments. This means that \(H_0\cup (E\uplus H) \models \bot \), where \(H_0\) is the input assignment. If H is a singleton L, we have \(H_0\cup (E\uplus \{L\})\models \bot \), hence \(H_0\cup E\models \overline{L}\), and  can be learned. If H is not a singleton, it can be rewritten as the singleton
can be learned. If H is not a singleton, it can be rewritten as the singleton
whose flip is \(((\bigwedge _{(l{\leftarrow }_{{}}\textsf {true})\in H} l) \wedge (\bigwedge _{(l{\leftarrow }_{{}}\textsf {false})\in H} \lnot l)) {\leftarrow }_{{}}\textsf {false}\). In order to get a clause, the latter assignment can be rewritten in the equivalent form
leading to the next definition.
Definition 1
(Clausal form of an assignment in a conflict) Given a conflict \(E\uplus H\), where H is a Boolean assignment, the clausal form of H is the singleton Boolean assignment \(((\bigvee _{(l{\leftarrow }_{{}}\textsf {true})\in H}\lnot l)\vee (\bigvee _{(l{\leftarrow }_{{}}\textsf {false})\in H} l)) {\leftarrow }_{{}}\textsf {true}\), or, equivalently, \(((\bigwedge _{(l{\leftarrow }_{{}}\textsf {true})\in H} l)\wedge (\bigwedge _{(l{\leftarrow }_{{}}\textsf {false})\in H} \lnot l)) {\leftarrow }_{{}}\textsf {false}\).
The new rule \(\textsf {LearnBackjump}\) allows CDSAT to perform learning and backjumping, or learning and restart, and it subsumes the \(\textsf {Backjump}\) rule [11], adding the capability of learning clauses. We examine these features in this order. Learning and backjumping is the generic behavior of \(\textsf {LearnBackjump}\). This rule singles out a Boolean subset H of the conflict \(E\uplus H\), such that \(\textsf {level}_{\varGamma }(H) > \textsf {level}_{\varGamma }(E)\). Then, it solves the conflict by jumping back to a level m, such that \(\textsf {level}_{\varGamma }(E)\le m < \textsf {level}_{\varGamma }(H)\), and learning a clausal form L of H. The system learns L by adding to the trail the justified assignment  , which is sound, because \(H_0\cup (E\uplus H)\models \bot \) implies \(H_0\cup E\models L\), as L is a clausal form of H. As L may be a new Boolean term, it must belong to \({{\mathcal {B}}}\). Note that H does not necessarily contain all Boolean assignments in the conflict: it is the search plan that chooses a Boolean subset H and a destination level m.
, which is sound, because \(H_0\cup (E\uplus H)\models \bot \) implies \(H_0\cup E\models L\), as L is a clausal form of H. As L may be a new Boolean term, it must belong to \({{\mathcal {B}}}\). Note that H does not necessarily contain all Boolean assignments in the conflict: it is the search plan that chooses a Boolean subset H and a destination level m.
Example 1
Consider the conflict on the last line of Fig. 2. If \(\textsf {LearnBackjump}\) is applied with \(H = \{l_2,l_4\}\), and \(E = \{(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5),(\lnot l_4{\vee }l_5)\}\), \(((\lnot l_2{\vee }\lnot l_4)\leftarrow \textsf {true})\) is a clausal form of H, \(\textsf {level}_{\varGamma }(H) = 4\), and \(\textsf {level}_{\varGamma }(E) = 0\), so that any destination level m such that \(0\le m < 4\) can be picked. A standard choice for m would be the second highest level in the conflict, namely \(m=2\), in which case the \(\textsf {LearnBackjump}\) step jumps over decision \(A_3\) and yields

The derivation continues from level 2 with \(\lnot l_2{\vee }\lnot l_4\) added to level 0.
We consider next learning and restart. It is common to restart after learning a clause, and search plans with aggressive restart proved successful in SAT solving. \(\textsf {LearnBackjump}\) makes this kind of search plan possible in CDSAT. Assume that the destination level m is chosen to be the smallest, that is, \(m = \textsf {level}_{\varGamma }(E)\). If \(\textsf {level}_{\varGamma }(E)\) is 0, \(\textsf {LearnBackjump}\) produces a trail of the form  , performing a restart and adding
, performing a restart and adding  to level 0.
to level 0.
Example 2
The \(\textsf {LearnBackjump}\) step of Example 1 with destination level \(m = 0\) generates

We analyze next how \(\textsf {LearnBackjump}\) subsumes the \(\textsf {Backjump}\) rule [11] recalled in Sect. 3.1 and at the beginning of this section. \(\textsf {LearnBackjump}\) behaves in the same way as \(\textsf {Backjump}\), if it picks as H a singleton L, as \(\overline{L}\) is a clausal form of a singleton Boolean assignment L in a conflict. However, while \(\textsf {Backjump}\) goes back to level \(m = \textsf {level}_{\varGamma }(E)\), \(\textsf {LearnBackjump}\) allows to choose any destination level m such that \(\textsf {level}_{\varGamma }(E)\le m < \textsf {level}_{\varGamma }(L)\).
Example 3
In the conflict on the last line of Fig. 2, the level of \(l_4\) is greater than that of the rest of the conflict \(E = \{(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5),l_2,(\lnot l_4{\vee }l_5)\}\), as \(\textsf {level}_{\varGamma }(l_4) = 4 > \textsf {level}_{\varGamma }(E) = 2\). Thus, \(\textsf {Backjump}\) could apply; \(\textsf {LearnBackjump}\) mimics it with \(H = \{l_4\}\) and \(m = 2\) to yield

Alternatively, if \(m = 3\), \(\textsf {LearnBackjump}\) produces

The side-conditions \(\overline{L}\notin \varGamma \) and \(L\not \in \varGamma \) prevent \(\textsf {LearnBackjump}\) from breaking plausibility or adding to the trail a clause that is already there.
Example 4
Consider the first conflict in Fig. 2:  . For a \(\textsf {LearnBackjump}\) step with \(E = \{\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\}\) and \(H = \{l_2, l_4, l_5\}\), we have \(\textsf {level}_{\varGamma }(H) = 4\) and \(\textsf {level}_{\varGamma }(E) = 0\). Regardless of the choice of destination level m, \(0\le m < 4\), a clausal form of H is redundant since clause \(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\) is already on the trail and \(\textsf {LearnBackjump}\) does not add it.
. For a \(\textsf {LearnBackjump}\) step with \(E = \{\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\}\) and \(H = \{l_2, l_4, l_5\}\), we have \(\textsf {level}_{\varGamma }(H) = 4\) and \(\textsf {level}_{\varGamma }(E) = 0\). Regardless of the choice of destination level m, \(0\le m < 4\), a clausal form of H is redundant since clause \(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\) is already on the trail and \(\textsf {LearnBackjump}\) does not add it.
Unlike \(\textsf {Backjump}\), \(\textsf {LearnBackjump}\) does not require that the conflict contains a singleton assignment L of level greater than the rest of the conflict.
Example 5
In the first conflict in Fig. 2 both \(l_4\) and \(l_5\) have level 4. If we apply \(\textsf {LearnBackjump}\) with \(H = \{l_4,l_5\}\), \(E = \{(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5),l_2\}\), \(\textsf {level}_{\varGamma }(H) = 4\), \(\textsf {level}_{\varGamma }(E) = 2\), and destination level \(m = 2\), the resulting trail is

where \((\lnot l_4 \vee \lnot l_5)\leftarrow \textsf {true}\) on level 2 is a clausal form of H.
We inspect last the learning of clauses. In CDCL, the last conflict clause generated prior to backjumping is called backjump clause: the procedure learns this clause and jumps back to a prior level, undoing at least one decision and satisfying the learned clause by placing one of its literals on the trail. An assertion clause is a conflict clause such that only one of its literals, termed assertion literal, is falsified on the current, or greatest, level of the trail. The First Unique Implication Point (1UIP) heuristic [45] picks as backjump clause the first generated assertion clause, as destination level the smallest where the assertion literal is undefined and all other literals of the assertion clause are false, and places the assertion literal on the trail.
The \(\textsf {Backjump}\) rule of CDSAT [11] generalizes this behavior, taking into account that, unlike in CDCL, a CDSAT trail is not a stack. \(\textsf {Backjump}\) applies to a conflict \(E\uplus \{L\}\) such that \(\textsf {level}_{\varGamma }(L) {>} \textsf {level}_{\varGamma }(E)\), but \(\textsf {level}_{\varGamma }(L)\) is not necessarily the current one, and \(\textsf {Backjump}\) puts  on the trail without learning an assertion clause. However, if a CDSAT conflict has the form \(E\uplus \{L\}\) with \(\textsf {level}_{\varGamma }(L) {>} \textsf {level}_{\varGamma }(E)\), it is possible to extract from the conflict an assertion clause, and \(\textsf {LearnBackjump}\) does it.
on the trail without learning an assertion clause. However, if a CDSAT conflict has the form \(E\uplus \{L\}\) with \(\textsf {level}_{\varGamma }(L) {>} \textsf {level}_{\varGamma }(E)\), it is possible to extract from the conflict an assertion clause, and \(\textsf {LearnBackjump}\) does it.
Let \(\kappa = l_1{\vee }{\cdots }{\vee } l_q\) be an assertion clause and \(l_q\) its literal such that \(L=(l_q{\leftarrow }_{{}}\textsf {false})\) is on the current level. Assume that \(\kappa \in {{\mathcal {B}}}\). In order to learn \(\kappa \), it suffices to take the Boolean subset \(H = H^\prime \uplus \{L\}\) of the conflict that makes \(\kappa \) false: for all i, \(1{\le } i{\le } q\), \((l_i{\leftarrow }_{{}}\textsf {false})\in H\) if and only if \(l_i\in \kappa \) and \((l_i{\leftarrow }_{{}}\textsf {true})\in H\) if and only if \(\lnot l_i\in \kappa \). By Definition 1, the assignment \(K = (\kappa {\leftarrow }_{{}}\textsf {true})\) is a clausal form of H. Let E be the rest of the conflict. Then the system applies \(\textsf {LearnBackjump}\) with destination level \(m = \textsf {level}_{\varGamma }(E\uplus H^\prime )\), which means that \(m \ge \textsf {level}_{\varGamma }(H^\prime )\). This choice satisfies the condition \(\textsf {level}_{\varGamma }(E) \le m < \textsf {level}_{\varGamma }(H)\), because \(\textsf {level}_{\varGamma }(E) \le \textsf {level}_{\varGamma }(E\uplus H^\prime ) < \textsf {level}_{\varGamma }(H) = \textsf {level}_{\varGamma }(L)\). This \(\textsf {LearnBackjump}\) step yields the trail

and \(\kappa \) is learned. The theory module for \(\textsf {Bool} \) features inference rules for unit propagation (see Sect. 4.1) that allow the inference:
Indeed, K is \((l_1\vee \ldots \vee l_{q-1} \vee l_q)\leftarrow \textsf {true}\), and \(H^\prime \) makes \(l_1,\ldots ,l_{q-1}\) false, so that unit propagation infers \(l_q\). Since L makes \(l_q\) false, \(\overline{L}\) makes \(l_q\) true. Because the destination level m of the \(\textsf {LearnBackjump}\) step was chosen in such a way that \(m \ge \textsf {level}_{\varGamma }(H^\prime )\), the premises \(K,H^\prime \) of inference (1) are all on the trail  . Furthermore, literal \(l_q\) is in \({\mathcal {B}}\), since L was on the trail. Thus, all conditions for a \(\textsf {Deduce}\) step with inference (1) are met. The resulting trail is
. Furthermore, literal \(l_q\) is in \({\mathcal {B}}\), since L was on the trail. Thus, all conditions for a \(\textsf {Deduce}\) step with inference (1) are met. The resulting trail is

which is similar to the  produced by \(\textsf {Backjump}\), except for the learned clause K. The advantage is that K can be reused in future branches of the search. The smaller the level of
produced by \(\textsf {Backjump}\), except for the learned clause K. The advantage is that K can be reused in future branches of the search. The smaller the level of  , which is \(\textsf {level}_{\varGamma }(E)\), the longer K may remain on the trail and be used for inferences.
, which is \(\textsf {level}_{\varGamma }(E)\), the longer K may remain on the trail and be used for inferences.
Example 6
Continuing Example 1 from

rule \(\textsf {Deduce}\) with inference (1) generates

A comparison between Examples 3 and 6 shows the difference between \(\textsf {LearnBackjump}\) imitating \(\textsf {Backjump}\), and a \(\textsf {LearnBackjump}\) \(\textsf {Deduce}\) sequence that backjumps, learns the assertion clause, and asserts the assertion literal by \(\textsf {Deduce}\). A CDSAT search plan may restrict the application of \(\textsf {LearnBackjump}\) to 1UIP assertion clauses and couple it with \(\textsf {Deduce}\) systematically.
3.3 Soundness, Completeness, and Termination with Lemma Learning
In this section we present definitions about theory modules that appeared in [11], but must be reproduced because they are indispensable for what follows in Sects. 4 and 5, and we discuss how replacing \(\textsf {Backjump}\) with \(\textsf {LearnBackjump}\) is harmless for the soundness, termination, and completeness of CDSAT.
Every theory module includes the equality inference rules of Fig. 3. The first two rules allow any module to infer an assignment to an equality from assignments to its sides. Indeed, in the presence of first-order assignments, there are two ways to make an equality \(t_1{\,\simeq _{s}\,} t_2\) true: either assign the same value to \(t_1\) and \(t_2\) or assign \(\textsf {true}\) to \(t_1{\,\simeq _{s}\,} t_2\). Dually, there are two ways to make \(t_1{\,\simeq _{s}\,} t_2\) false: either assign distinct values to \(t_1\) and \(t_2\) or assign \(\textsf {false}\) to \(t_1{\,\simeq _{s}\,} t_2\). The first two equality rules provide a bridge between these two ways (cf. the two ways for a term to be relevant to a theory in Sect. 3.1). The remaining equality rules are standard rules for reflexivity, symmetry, and transitivity.
In order to explain theory conflicts, theory inferences may introduce new (i.e., non-input) terms. For termination, all new terms must come from a finite local basis associated with the module and dependent on the input problem. We say that a set X of terms is closed if (i) it is closed with respect to the subterm ordering, or \(\unlhd \)-closed for short: for all \(u \in X\), \(t \unlhd u\) implies \(t \in X\), and (ii) it is closed with respect to equality: for all \(t, u \in X\) of sort s, \(s\ne \textsf {prop} \), \((t {\,\simeq _{s}\,} u)\in X\). The second condition excludes \(\textsf {prop} \), because otherwise a non-empty closed set is necessarily infinite, as it would contain, for all terms t of sort s, the infinite series \(l_1 = (t {\,\simeq _{s}\,} t)\), \(l_2 = (l_1 {\,\simeq _{\textsf {prop} }\,} l_1)\), \(l_3 = (l_2 {\,\simeq _{\textsf {prop} }\,} l_2)\), etc. The closure \(\Downarrow X\) of a set X of terms is the smallest closed set containing X. The closure operation is idempotent, as \(\Downarrow (\Downarrow X) =\ \Downarrow X\), and monotone: if \(X\subseteq Y\) then \(\Downarrow X \subseteq \ \Downarrow Y\).
Definition 2
(Basis) A basis for theory \({\mathcal {T}}\) with signature \(\varSigma \) is a function \(\textsf {basis} _{}\) from sets of terms to sets of terms, such that for all sets X of terms:
-
\(X \subseteq \textsf {basis} _{}(X)\) (extensiveness),
-
If X is finite then \(\textsf {basis} _{}(X)\) is finite (finiteness),
-
\(\textsf {basis} _{}(X) = \textsf {basis} _{}(\Downarrow X) =\ \Downarrow \textsf {basis} _{}(X)\) (closedness),
-
For all sets Y of terms, if \(X \subseteq Y\) then \(\textsf {basis} _{}(X) \subseteq \textsf {basis} _{}(Y)\) (monotonicity),
-
\(\textsf {basis} _{}(\textsf {basis} _{}(X)) = \textsf {basis} _{}(X)\) (idempotence), and
-
 (no introduction of foreign terms).
(no introduction of foreign terms).
For each theory \({\mathcal {T}}_{k}\) in the union, \(1\,{\le }\,k\,{\le }\,n\), the theory module \({\mathcal {I}}_{k}\) has a basis, called local basis and denoted \(\textsf {basis} _{{\mathcal {I}}_k}\) or \(\textsf {basis} _{k}\), such that for all sets X of terms (e.g., \(X = G(H_0)\) for input assignment \(H_0\) in a CDSAT-derivation), \(\textsf {basis} _{k}(X)\) contains all terms that \({\mathcal {I}}_{k}\) can generate starting from those in X. Given a \({\mathcal {T}}\)-assignment J, we abbreviate \(\textsf {basis} _{}(G(J))\) as \(\textsf {basis} _{}(J)\). The global basis \({\mathcal {B}}\) is stable if for all k, \(1\,{\le }\,k\,{\le }\,n\), \(\textsf {basis} _{k}({\mathcal {B}})\subseteq {\mathcal {B}}\).
Definition 3
(Assignment expansion) A \({\mathcal {T}}\)-module \({\mathcal {I}}_{}\) with local basis \(\textsf {basis} _{}\) expands a \({\mathcal {T}}\)-assignment J by adding either (1) a \({\mathcal {T}}\)-assignment A that is acceptable for \({\mathcal {I}}_{}\) in J, or (2) a Boolean assignment \(l{\leftarrow }_{{}}{\mathfrak {b}}\) derived by an \({\mathcal {I}}_{}\)-inference \(J^\prime \vdash _{{\mathcal {I}}_{}} (l{\leftarrow }_{{}}{\mathfrak {b}})\) such that \(J^\prime \subseteq J\), \((l{\leftarrow }_{{}}{\mathfrak {b}})\notin J\), and \(l\in \textsf {basis} _{}(J)\).
Case (1) covers \(\textsf {Decide}\) and Case (2) covers \(\textsf {Deduce}\), \(\textsf {Fail}\), and \(\textsf {ConflictSolve}\).
Definition 4
(One-theory-completeness) Given theory \({\mathcal {T}}\), a \({\mathcal {T}}_{}\)-module \({\mathcal {I}}_{}\) is complete for \({\mathcal {T}}_{}\), if, for all plausible \({\mathcal {T}}\)-assignments J, either \({\mathcal {I}}_{}\) can expand J or there exists a  -model \({\mathcal {M}}\) such that \({\mathcal {M}}\models {J}\).
-model \({\mathcal {M}}\) such that \({\mathcal {M}}\models {J}\).
For completeness in a union \({\mathcal {T}}_{\infty }\) of theories, the theories need to agree on cardinalities of shared sorts and equalities between shared terms. CDSAT achieves this by requiring that every theory agrees on both counts with a leading theory, say \({{\mathcal {T}}}_1\), which has all the sorts, that is, such that \(S_1 = S_\infty \).
Definition 5
(Leading-theory-compatibility) Let \({{\mathcal {T}}}_1\) be the leading theory, \({\mathcal {T}}\), \(\varSigma \), and S stand for \({\mathcal {T}}_{k}\), \(\varSigma _k\), and \(S_k\), \(2\,{\le }\,k\,{\le }\,n\), and N be a set of terms. A \({\mathcal {T}}\)-assignment J is leading-theory-compatible with \({\mathcal {T}}\) sharing N, if for all \({{{\mathcal {T}}}_1^+}[{\mathcal {V}}^{}_1]\)-model \({\mathcal {M}}_1\) such that \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\) with  , there exists a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\) with
, there exists a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\) with  , such that (i) \({\mathcal {M}}\models J\), (ii) for all sorts \(s\in S\), \(\vert {s^{\mathcal {M}}} \vert = \vert {s^{{\mathcal {M}}_1}} \vert \), and (iii) for all \(s\in S\) and terms \(u, u^\prime \in N\) of sort s, \({\mathcal {M}}(u) = {\mathcal {M}}(u^\prime )\) if and only if \({\mathcal {M}}_1(u) = {\mathcal {M}}_1(u^\prime )\).
, such that (i) \({\mathcal {M}}\models J\), (ii) for all sorts \(s\in S\), \(\vert {s^{\mathcal {M}}} \vert = \vert {s^{{\mathcal {M}}_1}} \vert \), and (iii) for all \(s\in S\) and terms \(u, u^\prime \in N\) of sort s, \({\mathcal {M}}(u) = {\mathcal {M}}(u^\prime )\) if and only if \({\mathcal {M}}_1(u) = {\mathcal {M}}_1(u^\prime )\).
Since in a worst-case scenario all terms are shared, the next definition picks as set of shared terms the set of all terms occurring in the assignment.
Definition 6
(Leading-theory-completeness) For a non-leading theory \({\mathcal {T}}\), a \({\mathcal {T}}\)-module \({\mathcal {I}}_{}\) is leading-theory-complete, if for all plausible \({\mathcal {T}}\)-assignments J, either \({\mathcal {I}}_{}\) can expand J or J is leading-theory-compatible with \({\mathcal {T}}\) sharing G(J).
Note that if \({\mathcal {I}}_{}\) cannot expand J, all applicable equality inference steps (see Fig. 3) have been applied, and therefore \(J = J_{{\mathcal {T}}}\).
The next theorem summarizes the requirements for soundness, termination, and completeness of CDSAT: Sects. 4 and 5 will show how to fulfill those for completeness and termination, respectively.
Theorem 1
CDSAT with lemma learning and global basis \({{\mathcal {B}}}\) is
-
Sound: if the theory modules are sound, whenever a CDSAT-derivation reaches state
 , the input problem is unsatisfiable;
, the input problem is unsatisfiable; -
Terminating: if \({{\mathcal {B}}}\) is finite and closed, every CDSAT-derivation from an input problem in \({{\mathcal {B}}}\) is guaranteed to terminate; and
-
Complete: if there is a leading theory \({{\mathcal {T}}}_1\), module \({\mathcal {I}}_{1}\) is complete for \({{\mathcal {T}}}_1\), modules \({\mathcal {I}}_{k}\)’s, \(2\,{\le }\,k\,{\le }\,n\), are leading-theory-complete, and \({{\mathcal {B}}}\) is stable, whenever a CDSAT-derivation from an input problem in \({{\mathcal {B}}}\) reaches a state other than
 such that no transition rule applies, there exists a \({\mathcal {T}}_{\infty }^+\)-model that globally endorses the assignment on the trail, hence the input problem.
such that no transition rule applies, there exists a \({\mathcal {T}}_{\infty }^+\)-model that globally endorses the assignment on the trail, hence the input problem.
We conclude this section with a discussion of how the soundness, termination, and completeness arguments for CDSAT [11] carry over to CDSAT with \(\textsf {LearnBackjump}\). The proof of soundness rests on soundness of the theory modules and on showing that CDSAT transitions transform sound states into sound states, meaning that justified assignments are sound and conflicts are indeed conflicts: \(\textsf {LearnBackjump}\) does not change this, because it adds sound justified assignments.
The proof of termination begins by using acceptability of decisions to show that a CDSAT trail does not contain distinct assignments to the same term, unless they are input assignments. For Boolean assignments, this means that CDSAT rules preserve plausibility, and so does \(\textsf {LearnBackjump}\), since in essence it flips a Boolean assignment. Next, the closedness of \({{\mathcal {B}}}\) and the relevance of decided termsFootnote 1 are employed to show that if the input assignment \(H_0\) is in \({{\mathcal {B}}}\), so are all derived trails: this holds also with \(\textsf {LearnBackjump}\), because the learned clause is required to be in \({{\mathcal {B}}}\). Then, one uses the finiteness of \({{\mathcal {B}}}\) to get an upper bound on trail length, hence a trail measure, and shows that CDSAT transitions reduce the trail measure with respect to a well-founded ordering: \(\textsf {LearnBackjump}\) does it like \(\textsf {Backjump}\).
For completeness, one preliminarily observes that if \({\mathcal {B}}\) is stable, then it is closed (by extensiveness and closedness of all \(\textsf {basis} _{k}\)’s, see Definition 2). Then, one uses the closedness of \({\mathcal {B}}\) and the completeness of the theory modules to show that, whenever a CDSAT-derivation reaches a state other than  such that no transition rule applies, its trail \(\varGamma \) is model-describing. Replacing \(\textsf {Backjump}\) with \(\textsf {LearnBackjump}\) preserves this result, because if \(\textsf {LearnBackjump}\) does not apply, \(\textsf {Backjump}\) does not apply either, as \(\textsf {LearnBackjump}\) subsumes \(\textsf {Backjump}\). \(\varGamma \) is model-describing if \(\varGamma _{{\mathcal {T}}_{1}}\) is endorsed by a \({\mathcal {T}}_{1}^+\)-model, and for all k, \(2\,{\le }\,k\,{\le }\,n\), \(\varGamma _{{\mathcal {T}}_{k}}\) is leading-theory-compatible with \({\mathcal {T}}_{k}\) sharing the set of shared terms of the problem. The generic assignment J of the definitions of leading-theory-compatibility and leading-theory-completeness (see Definitions 5 and 6) is instantiated to \(\varGamma _{{\mathcal {T}}_{k}}\), and a theory module \({\mathcal {I}}_k\), \(2\,{\le }\,k\,{\le }\,n\), is leading-theory-complete sharing \(G(\varGamma _{{\mathcal {T}}_{k}})\), hence sharing the set of shared terms of the problem, since the latter is a subset of \(G(\varGamma _{{\mathcal {T}}_{k}})\) for all problems. The proof of completeness is achieved by showing that a model-describing trail is globally endorsed by a \({\mathcal {T}}_{\infty }^+\)-model, which is independent of transition rules.
such that no transition rule applies, its trail \(\varGamma \) is model-describing. Replacing \(\textsf {Backjump}\) with \(\textsf {LearnBackjump}\) preserves this result, because if \(\textsf {LearnBackjump}\) does not apply, \(\textsf {Backjump}\) does not apply either, as \(\textsf {LearnBackjump}\) subsumes \(\textsf {Backjump}\). \(\varGamma \) is model-describing if \(\varGamma _{{\mathcal {T}}_{1}}\) is endorsed by a \({\mathcal {T}}_{1}^+\)-model, and for all k, \(2\,{\le }\,k\,{\le }\,n\), \(\varGamma _{{\mathcal {T}}_{k}}\) is leading-theory-compatible with \({\mathcal {T}}_{k}\) sharing the set of shared terms of the problem. The generic assignment J of the definitions of leading-theory-compatibility and leading-theory-completeness (see Definitions 5 and 6) is instantiated to \(\varGamma _{{\mathcal {T}}_{k}}\), and a theory module \({\mathcal {I}}_k\), \(2\,{\le }\,k\,{\le }\,n\), is leading-theory-complete sharing \(G(\varGamma _{{\mathcal {T}}_{k}})\), hence sharing the set of shared terms of the problem, since the latter is a subset of \(G(\varGamma _{{\mathcal {T}}_{k}})\) for all problems. The proof of completeness is achieved by showing that a model-describing trail is globally endorsed by a \({\mathcal {T}}_{\infty }^+\)-model, which is independent of transition rules.
4 Completeness of Theory Modules
In previous work we defined theory modules for Bool, EUF, Arr, LRA, and generic Nelson-Oppen theories [11]. In this section we add a theory module for a generic non-stably infinite theory, we specify local bases for all these theory modules, and we prove that all these theory modules are leading-theory-complete for all suitable leading theories, fulfilling a key requirement for the completeness of CDSAT (see Theorem 1).
A theory module is an inference system, that is, a set of inference rules, and it represents an abstraction with respect to a theory satisfiability procedure. A theory satisfiability procedure implements the inference rules of the module, a search plan, and other algorithmic components, such as those of a full-fledged CDCL procedure for Bool, a congruence-closure algorithm for EUF, or an LRA-procedure that keeps polynomials in normal form as sums of monomials and maintains lower and upper bounds for each rational variable.
We begin with a lemma that will be used several times in the sequel. Given a \({\mathcal {T}}\)-assignment J, let \({\simeq _{s}^{J}}\) be the binary relation over \(G_s(J)\) defined by \({t_1} {\simeq _{s}^{J}} {t_2}\) if and only if \((t_1{\,\simeq _{s}\,}t_2)\in J\). The lemma shows that if module \({\mathcal {I}}\) for theory \({\mathcal {T}}\) cannot expand J, the relation \({\simeq _{s}^{J}}\) is an equivalence, and J provides \({\mathcal {T}}\)-values for all terms that are relevant to \({\mathcal {T}}\). For terms of sort s other than \(\textsf {prop} \), this result relies on two hypotheses: first, J does not exhaust the supply of s-sorted \({\mathcal {T}}\)-values, so that a decision is doable; second, the only \({\mathcal {I}}\)-rules with first-order assignments as premises are equality inferences (see Fig. 3), so that the analysis of acceptability of decisions is module-independent. If \({{\mathcal {T}}}^+\) offers infinitely many s-sorted \({\mathcal {T}}\)-values, the first hypothesis is satisfied a priori.
Lemma 1
If \({\mathcal {T}}\)-module \({\mathcal {I}}_{}\) cannot expand a plausible \({\mathcal {T}}\)-assignment J, then:
-
1.
For all sorts \(s\in S\backslash \{\textsf {prop} \}\), the relation \({\simeq _{s}^{J}}\) is an equivalence, and if \(\{ t_1{\leftarrow }_{{}}{\mathfrak {c}}_1,\ t_2{\leftarrow }_{{}}{\mathfrak {c}}_2\}\subseteq J\), then \({\mathfrak {c}}_1\) and \({\mathfrak {c}}_2\) are identical if and only if \(t_1{\simeq _{s}^{J}}t_2\);
-
2.
Assignment J gives a value to every formula that is relevant to \({\mathcal {T}}\) in J;
-
3.
Assignment J gives a value to every term t of sort \(s\in S\backslash \{\textsf {prop} \}\) that is relevant to \({\mathcal {T}}\) in J, provided that (i) there exists a \({\mathcal {T}}\)-value of sort s that J does not use, and (ii) the only \({\mathcal {I}}_{}\)-inferences involving first-order assignments of sort s are equality inferences.
Proof
All claims are proved by way of contradiction.
-
1.
Assume that \({\simeq _{s}^{J}}\) is not reflexive. This means there exists a term \(t\in G_s(J)\) such that \((t{\,\simeq _{s}\,}t)\not \in J\). The Boolean assignment \(t{\,\simeq _{s}\,}t\) can be derived by reflexivity (see Fig. 3), and \((t{\,\simeq _{s}\,}t)\in \textsf {basis} _{{\mathcal {I}}_{}}(J)\) since \(\textsf {basis} _{{\mathcal {I}}_{}}(J)\) is closed and therefore contains all equalities between terms in \(G_s(J)\) for \(s\ne \textsf {prop} \). Thus, \({\mathcal {I}}_{}\) can expand J, which is a contradiction. The cases for symmetry and transitivity are analogous. Similarly, assume that \(\{t_1{\leftarrow }_{{}}{\mathfrak {c}}_1,\ t_2{\leftarrow }_{{}}{\mathfrak {c}}_2\}\subseteq J\), \({\mathfrak {c}}_1\) and \({\mathfrak {c}}_2\) are identical, but \((t_1{\,\simeq _{s}\,}t_2)\not \in J\): then \({\mathcal {I}}_{}\) can expand J by an equality inference deriving \(t_1{\,\simeq _{s}\,}t_2\). Conversely, assume \({(t_1{\,\simeq _{s}\,}t_2)}\in J\), and \({\mathfrak {c}}_1\) and \({\mathfrak {c}}_2\) are distinct: by plausibility \((t_1{\,\not \simeq _{s}\,}t_2)\not \in J\), and \({\mathcal {I}}_{}\) can expand J by an equality inference deriving \({t_1{\,\not \simeq _{s}\,}t_2}\).
-
2.
Assume l is a relevant formula without assigned value. Then \(l{\leftarrow }_{{}}{\mathfrak {b}}\) (for either truth value) is acceptable for \({\mathcal {I}}_{}\) in J, and therefore \({\mathcal {I}}_{}\) can expand J.
-
3.
Assume that J does not assign a value to such a relevant term t. We find an acceptable assignment for t, so that \({\mathcal {I}}_{}\) can expand J. It suffices to find a value that does not cause a conflict (see Sect. 3.1 for acceptability). Consider the \({\simeq _{s}^{J}}\)-equivalence class e of t (the relation \({\simeq _{s}^{J}}\) is an equivalence by Part (1)). If none of the terms in e are assigned a value in J, then \(t{\leftarrow }_{{}}{\mathfrak {c}}\), where \({\mathfrak {c}}\) is the \({\mathcal {T}}\)-value of sort s that J does not use, is acceptable, because otherwise there would be an assignment \((t_2{\leftarrow }_{{}}{\mathfrak {c}}_2)\in J\) and an equality inference \(t{\leftarrow }_{{}}{\mathfrak {c}}, t_2{\leftarrow }_{{}}{\mathfrak {c}}_2\vdash _{} t{\,\not \simeq _{}\,}t_2\) such that \((t{\,\simeq _{}\,}t_2)\in J\), meaning \(t_2\in e\) is assigned a value. If for a term \(t_1\in e\), J contains \(t_1{\leftarrow }_{{}}{\mathfrak {c}}_1\), then \(t{\leftarrow }_{{}}{\mathfrak {c}}_1\) is acceptable, because otherwise there would be an assignment \((t_2{\leftarrow }_{{}}{\mathfrak {c}}_2)\in J\) and an equality inference \(t{\leftarrow }_{{}}{\mathfrak {c}}_1, t_2{\leftarrow }_{{}}{\mathfrak {c}}_2\vdash _{} (t{\,\simeq _{}\,}t_2){\leftarrow }_{{}}{\mathfrak {b}}\) such that \((t{\,\simeq _{}\,}t_2){\leftarrow }_{{}}\overline{{\mathfrak {b}}}\in J\): if \({\mathfrak {b}}\) is \(\textsf {true}\), then \({\mathfrak {c}}_1\) is \({\mathfrak {c}}_2\), \(t_1{\simeq _{s}^{J}} t_2\) (by Part (1)), hence \(t{\simeq _{s}^{J}} t_2\) by transitivity (since \(t_1\in e\)), so that \(\{t{\,\simeq _{}\,}t_2,\ t{\,\not \simeq _{}\,}t_2\}\subseteq J\), violating plausibility; if \({\mathfrak {b}}\) is \(\textsf {false}\), then \({\mathfrak {c}}_1\) and \({\mathfrak {c}}_2\) are distinct, \((t{\,\simeq _{}\,}t_2)\in J\), hence \(t{\simeq _{s}^{J}} t_2\), and, by transitivity (since \(t_1\in e\)), \(t_1{\simeq _{s}^{J}} t_2\), so that \({\mathfrak {c}}_1\) and \({\mathfrak {c}}_2\) should be identical by Part (1). \(\square \)
The definition of leading-theory-compatibility with theory \({\mathcal {T}}\) (see Definition 5) refers to a generic set N of shared terms and considers models whose sets of variables include the set of free variables of \(J\cup N\), for J a \({\mathcal {T}}\)-assignment. The definition of leading-theory-completeness (see Definition 6) instantiates N to be G(J) in order to cover all possible sets of shared terms. Thus, when proving leading-theory-completeness we are interested in showing the existence of a \({\mathcal {T}}\)-model whose set of variables includes  , with \(\varSigma \) the signature of theory \({\mathcal {T}}\). Clearly,
, with \(\varSigma \) the signature of theory \({\mathcal {T}}\). Clearly,  . On the other hand, in general,
. On the other hand, in general,  , because there can be two \(\varSigma \)-foreign terms \(u, t\in G(J)\) such that \(u\lhd t\), so that
, because there can be two \(\varSigma \)-foreign terms \(u, t\in G(J)\) such that \(u\lhd t\), so that  , but
, but  . The following remark is stated as a corollary of Lemma 1, because Lemma 1 will be applied to show that a \({\mathcal {T}}\)-assignment J assigns values to all terms in G(J), or to all equalities between terms in G(J), and then the following corollary will be applied to conclude that in such cases
. The following remark is stated as a corollary of Lemma 1, because Lemma 1 will be applied to show that a \({\mathcal {T}}\)-assignment J assigns values to all terms in G(J), or to all equalities between terms in G(J), and then the following corollary will be applied to conclude that in such cases  , so that it suffices to build a \({\mathcal {T}}\)-model whose set of variables includes
, so that it suffices to build a \({\mathcal {T}}\)-model whose set of variables includes  .
.
Corollary 1
For all signatures \(\varSigma =(S,F)\) and assignments J, if either (1) for all terms \(t\in G(J)\) there is an assignment \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\), or (2) for all distinct terms \(t,u\in G_s(J)\) of sort \(s\in S\setminus \{\textsf {prop} \}\) there is an assignment \(((t\simeq u){\leftarrow }_{{}}{\mathfrak {b}})\in J\), then  .
.
Proof
The direction  is trivially true, as \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\) implies \(t\in G(J)\). The direction
is trivially true, as \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\) implies \(t\in G(J)\). The direction  follows from either hypothesis. \(\square \)
follows from either hypothesis. \(\square \)
The corollary is true regardless of signature \(\varSigma \); however, it will be applied to a \({\mathcal {T}}\)-assignment J and the signature \(\varSigma \) of theory \({\mathcal {T}}\).
The following lemma is useful to prove leading-theory-completeness for a theory module \({\mathcal {I}}_1\) and then extend the result to a module \({\mathcal {I}}_2\) with additional inference rules, that is, such that \({\mathcal {I}}_1\subseteq {\mathcal {I}}_2\) (modules are sets of inference rules).
Lemma 2
Let \({\mathcal {I}}_1\) and \({\mathcal {I}}_2\) such that \({\mathcal {I}}_1\subseteq {\mathcal {I}}_2\) be modules for a theory \({\mathcal {T}}\). If all inference rules in \({\mathcal {I}}_2 \backslash {\mathcal {I}}_1\) take only Boolean assignments as premises, then if \({\mathcal {I}}_1\) is leading-theory-complete, \({\mathcal {I}}_2\) also is leading-theory-complete.
Proof
We need to show that \({\mathcal {I}}_2\) can expand a plausible \({\mathcal {T}}\)-assignment J whenever \({\mathcal {I}}_1\) can (see Definition 6). If \({\mathcal {I}}_1\) expands J by an inference (Case (2) of Definition 3), then \({\mathcal {I}}_2\) can do it too, since \({\mathcal {I}}_1\subseteq {\mathcal {I}}_2\). If \({\mathcal {I}}_1\) expands J by a decision (Case (1) of Definition 3), we need to show that the decision is acceptable also for \({\mathcal {I}}_2\). By way of contradiction, suppose that the decision is acceptable for \({\mathcal {I}}_1\) but not for \({\mathcal {I}}_2\). By definition of acceptability (see Sect. 3), this means that the decision is a first-order assignment \(u{\leftarrow }_{{}}{\mathfrak {c}}\) and there is an inference \(J^\prime \cup \{u{\leftarrow }_{{}}{\mathfrak {c}}\}\vdash _{{\mathcal {I}}_2} L\) with \(\overline{L} \in J\) and \(J^\prime \subseteq J\). Furthermore, this \({\mathcal {I}}_2\)-inference applies a rule in \({\mathcal {I}}_2 \backslash {\mathcal {I}}_1\), because \(u{\leftarrow }_{{}}{\mathfrak {c}}\) is acceptable for \({\mathcal {I}}_1\). It follows that this rule in \({\mathcal {I}}_2 \backslash {\mathcal {I}}_1\) takes a first-order assignment as premise, contradicting the hypothesis that all rules in \({\mathcal {I}}_2 \backslash {\mathcal {I}}_1\) take only Boolean assignments as premises. \(\square \)
Let x be an arbitrary variable of sort \(\textsf {prop} \), \(\top \) stand for \((x{\,\simeq _{\textsf {prop} }\,}x){\leftarrow }_{{}}\textsf {true}\), and \(\bot \) for \(x{\,\not \simeq _{\textsf {prop} }\,}x\): no model endorses \(\bot \) and \(\vdash _{} \top \) is an equality inference.
4.1 Propositional Logic
For propositional logic the signature \(\varSigma _{\textsf {Bool} }\) has only the sort \(\textsf {prop} \) and symbols \({\,\simeq _{\textsf {prop} }\,}\) for equality, \(\lnot {{:}}\textsf {prop} \rightarrow \textsf {prop} \) for negation, \(\vee {{:}}(\textsf {prop} {\times }\textsf {prop} )\rightarrow \textsf {prop} \) for disjunction, and \(\wedge {{:}}(\textsf {prop} {\times }\textsf {prop} )\rightarrow \textsf {prop} \) for conjunction. Let \(\textsf {Bool} ^{+}\) be the trivial extension, and \({\mathcal {I}}_{\textsf {Bool} }^\textsf {eval}\) the module that only adds to the equality inference rules of Fig. 3 an inference rule for evaluation of formulæ:
where l is in the closure of formulæ \(l_1,\ldots ,l_m\) under the \(\varSigma _{\textsf {Bool} }\)-connectives, and \({\mathfrak {b}}\) is its truth value determined by \({\mathfrak {b}}_1,\ldots ,{\mathfrak {b}}_m\) and the truth tables. Given a set X of terms, \(\textsf {basis} _{\textsf {Bool} }(X)\) contains all subformulæ of formulæ in X by closedness (see Definition 2), and all disjunctions of subformulæ in X for lemma learning.
Theorem 2
Module \({\mathcal {I}}_{\textsf {Bool} }^\textsf {eval} \) is leading-theory-complete for all leading theories.
Proof
Let J be a plausible Boolean assignment that \({\mathcal {I}}_{\textsf {Bool} }^\textsf {eval}\) cannot expand. Since all formulæ in \(G_{\textsf {prop} }(J)\) are relevant to \(\textsf {Bool} \), J assigns them values by Part (2) of Lemma 1. This has two consequences: first,  by Corollary 1; second, J determines a unique
by Corollary 1; second, J determines a unique  -model \({\mathcal {M}}\) such that \({{\mathcal {M}}}\models J\). We show that J is leading-theory-compatible with \(\textsf {Bool} \) sharing G(J). Let \({{\mathcal {T}}}_1\) be a leading theory. Since J is a Boolean assignment, \(J_{{\mathcal {T}}_1} = J\). For all \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model \({\mathcal {M}}_1\) such that
-model \({\mathcal {M}}\) such that \({{\mathcal {M}}}\models J\). We show that J is leading-theory-compatible with \(\textsf {Bool} \) sharing G(J). Let \({{\mathcal {T}}}_1\) be a leading theory. Since J is a Boolean assignment, \(J_{{\mathcal {T}}_1} = J\). For all \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model \({\mathcal {M}}_1\) such that  and \({\mathcal {M}}_1\models J\), we have that \(\vert {\textsf {prop} ^{\mathcal {M}}} \vert = \vert {\textsf {prop} ^{{\mathcal {M}}_1}} \vert = 2\), and for all terms l and p in \(G_\textsf {prop} (J)\), \({\mathcal {M}}(l) = {\mathcal {M}}(p)\) if and only if \({\mathcal {M}}_1(l) = {\mathcal {M}}_1(p)\), since this happens if and only if l and p are assigned the same value in J. \(\square \)
and \({\mathcal {M}}_1\models J\), we have that \(\vert {\textsf {prop} ^{\mathcal {M}}} \vert = \vert {\textsf {prop} ^{{\mathcal {M}}_1}} \vert = 2\), and for all terms l and p in \(G_\textsf {prop} (J)\), \({\mathcal {M}}(l) = {\mathcal {M}}(p)\) if and only if \({\mathcal {M}}_1(l) = {\mathcal {M}}_1(p)\), since this happens if and only if l and p are assigned the same value in J. \(\square \)
Let \({\mathcal {I}}_{\textsf {Bool} }\) be the module that adds to \({\mathcal {I}}_{\textsf {Bool} }^\textsf {eval}\) rules for negation elimination, conjunction elimination, and unit propagation as in CDCL:
where \(1\le j, i\le m\). Then by Lemma 2 we have
Corollary 2
Module \({\mathcal {I}}_{\textsf {Bool} }\) is leading-theory-complete for all leading theories.
4.2 The Theory of Equality
For the theory of equality EUF, with signature \(\varSigma _{\textsf {EUF} } = (S,{\,\simeq _{S}\,}\cup F)\), the extension \(\textsf {EUF} ^+\) may either be trivial or add a countably infinite set of values for each sort in \(S\backslash \{\textsf {prop} \}\) and no axioms. A minimal module \({\mathcal {I}}_{\textsf {EUF} }^m\) complements the equality inference rules (see Fig. 3) with an inference rule
for all \(f\in F\), that fires when the trail violates a congruence axiom of equality. In case of non-trivial extension, the equality inference rules are the only rules that make use of first-order assignments, and values are employed as labels of congruence classes of terms. For example, the first-order assignment
and the Boolean assignment
represent the same four congruence classes. The first-order assignment is an optimization, because it encodes equalities and disequalities between terms without listing them explicitly, whereas a Boolean assignment requires \({m \atopwithdelims ()2}\) hence \(O(m^2)\) literals for m terms in the worst case.
The local basis \(\textsf {basis} _{\textsf {EUF} }\) has to ensure that all formulæ that may be needed to reason about equality are available. Given a set X of terms, by closedness \(\textsf {basis} _{\textsf {EUF} }(X)\) contains all equalities between subterms of terms in X of a sort s other than \(\textsf {prop} \). Then \(\textsf {basis} _{\textsf {EUF} }\) adds the following equalities between formulae: the formula \(\top \), and all equalities \(l{\,\simeq _{\textsf {prop} }\,}l^\prime \), such that either (i) l and \(l^\prime \) are formulæ in X with the same root symbol \(f\in F\), or (ii) X contains terms \(f(t_1,\ldots ,t_m,l,u_1,\ldots ,u_m)\) and \(f(t^\prime _1,\ldots ,t^\prime _m,l^\prime ,u^\prime _1,\ldots ,u^\prime _m)\) with \(f\in F\). We prove completeness assuming the non-trivial \(\textsf {EUF} ^+\): the proof rests on showing that if \({\mathcal {I}}_{\textsf {EUF} }^m\) cannot expand an assignment, all equalities are determined.
Theorem 3
Module \({\mathcal {I}}_{\textsf {EUF} }^m\) is leading-theory-complete for all leading theories.
Proof
Let \({\mathcal {T}}_{1}\) be a leading theory, with signature \(\varSigma _{1}\) and extension \({\mathcal {T}}_{1}^{+}\), and J a plausible \(\textsf {EUF} \)-assignment that \({\mathcal {I}}_{\textsf {EUF} }^m\) cannot expand. We show that J is leading-theory-compatible with \(\textsf {EUF} \) sharing G(J). We begin by observing that every formula \(l\in G_\textsf {prop} (J)\) is relevant to \(\textsf {EUF} \), and therefore J assigns a value to l by Part (2) of Lemma 1 (†). For s other than \(\textsf {prop} \), every term \(u\in G_s(J)\) is relevant to \(\textsf {EUF} \), as \(\textsf {EUF} ^{+}\) has (infinitely many) values for such sorts. Moreover, the only \(\textsf {EUF} \)-inferences using first-order assignments are equality inferences, and therefore J assigns a value to every such term u by Part (3) of Lemma 1 (‡). It follows that  by Corollary 1. Let \({\mathcal {M}}_1\) be a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that
by Corollary 1. Let \({\mathcal {M}}_1\) be a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that  and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). We build an \({\textsf {EUF} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}\) with
and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). We build an \({\textsf {EUF} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}\) with  that fulfills the requirements for leading-theory-compatibility (see Definition 5). First, \({\mathcal {M}}\) interprets the sorts in S as \({\mathcal {M}}_1\) does. This suffices for Part (ii) of Definition 5. Second, \({\mathcal {M}}\) interprets every variable
that fulfills the requirements for leading-theory-compatibility (see Definition 5). First, \({\mathcal {M}}\) interprets the sorts in S as \({\mathcal {M}}_1\) does. This suffices for Part (ii) of Definition 5. Second, \({\mathcal {M}}\) interprets every variable  as \({\mathcal {M}}_1(t)\), every EUF-value \({\mathfrak {c}}\) such that \((t{\leftarrow }_{{}}{\mathfrak {c}}) \in J\) as \({\mathcal {M}}_1(t)\), and every other EUF-value arbitrarily. The interpretation of EUF-values is well-defined, because if \(\{t{\leftarrow }_{{}}{\mathfrak {c}}, u{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq J\) then \((t\simeq u)\in J_{{\mathcal {T}}_{1}}\), by definition of \({\mathcal {T}}_{1}\)-view and because \({\mathcal {T}}_{1}\) has all the sorts, so that \({\mathcal {M}}_1(t) = {\mathcal {M}}_1(u)\) since \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). Third and last, \({\mathcal {M}}\) interprets every symbol \(f{{:}}(s_1{\times }\cdots {\times }s_m){\rightarrow }s\) in F as follows: for all elements \(e_1\in s_1^{{\mathcal {M}}_1}\ldots e_m\in s_m^{{\mathcal {M}}_1}\), if G(J) contains no term \(f(t_1,\ldots ,t_m)\) such that \({\mathcal {M}}_1(t_1)=e_1,\ldots ,{\mathcal {M}}_1(t_m)=e_m\), then \(f^{\mathcal {M}}(e_1,\ldots ,e_m)\) is an arbitrary element in \(s^{{\mathcal {M}}_1}\); otherwise, \(f^{\mathcal {M}}(e_1,\ldots ,e_m)\) is \({\mathcal {M}}_1(f(t_1,\ldots ,t_m))\). Note that \(f^{\mathcal {M}}\) is well-defined: indeed, if there is in G(J) another term \(f(u_1,\ldots ,u_m)\) such that \({\mathcal {M}}_1(u_1)=e_1,\ldots ,{\mathcal {M}}_1(u_m)=e_m\), then by (†) and (‡), J assigns values to \(t_1,\ldots ,t_m,u_1,\ldots ,u_m, f(t_1,\ldots ,t_m)\), and \(f(u_1,\ldots ,u_m)\). Also, J contains assignments \((t_i{\,\simeq _{}\,}u_i){\leftarrow }_{{}}{\mathfrak {b}}_i\), for \({1\le i\le m}\), and \((f(t_1,\ldots ,t_m){\,\simeq _{}\,}f(u_1,\ldots ,u_m)){\leftarrow }_{{}}{\mathfrak {b}}\), because otherwise an equality inference could expand it. The truth values \({\mathfrak {b}}_1,\ldots ,{\mathfrak {b}}_m\) are all \(\textsf {true}\), because \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\). The truth value \({\mathfrak {b}}\) is \(\textsf {true}\), as otherwise inference rule (2) could expand J. Since \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\), \({\mathcal {M}}_1(f(t_1,\ldots ,t_m))={\mathcal {M}}_1(f(u_1,\ldots ,u_m))\), and \(f^{\mathcal {M}}\) is well-defined. This completes the construction of \({\mathcal {M}}\). For Part (i) of Definition 5, we need to show that for all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\), we have \({\mathcal {M}}(t)={\mathcal {M}}_1(t)={\mathfrak {c}}^{\mathcal {M}}\). For Part (iii) of Definition 5, we need to show that for all \(t\in G(J)\), we have \({\mathcal {M}}(t)={\mathcal {M}}_1(t)\). Both claims are proved by a straightforward induction on the structure of terms. \(\square \)
as \({\mathcal {M}}_1(t)\), every EUF-value \({\mathfrak {c}}\) such that \((t{\leftarrow }_{{}}{\mathfrak {c}}) \in J\) as \({\mathcal {M}}_1(t)\), and every other EUF-value arbitrarily. The interpretation of EUF-values is well-defined, because if \(\{t{\leftarrow }_{{}}{\mathfrak {c}}, u{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq J\) then \((t\simeq u)\in J_{{\mathcal {T}}_{1}}\), by definition of \({\mathcal {T}}_{1}\)-view and because \({\mathcal {T}}_{1}\) has all the sorts, so that \({\mathcal {M}}_1(t) = {\mathcal {M}}_1(u)\) since \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). Third and last, \({\mathcal {M}}\) interprets every symbol \(f{{:}}(s_1{\times }\cdots {\times }s_m){\rightarrow }s\) in F as follows: for all elements \(e_1\in s_1^{{\mathcal {M}}_1}\ldots e_m\in s_m^{{\mathcal {M}}_1}\), if G(J) contains no term \(f(t_1,\ldots ,t_m)\) such that \({\mathcal {M}}_1(t_1)=e_1,\ldots ,{\mathcal {M}}_1(t_m)=e_m\), then \(f^{\mathcal {M}}(e_1,\ldots ,e_m)\) is an arbitrary element in \(s^{{\mathcal {M}}_1}\); otherwise, \(f^{\mathcal {M}}(e_1,\ldots ,e_m)\) is \({\mathcal {M}}_1(f(t_1,\ldots ,t_m))\). Note that \(f^{\mathcal {M}}\) is well-defined: indeed, if there is in G(J) another term \(f(u_1,\ldots ,u_m)\) such that \({\mathcal {M}}_1(u_1)=e_1,\ldots ,{\mathcal {M}}_1(u_m)=e_m\), then by (†) and (‡), J assigns values to \(t_1,\ldots ,t_m,u_1,\ldots ,u_m, f(t_1,\ldots ,t_m)\), and \(f(u_1,\ldots ,u_m)\). Also, J contains assignments \((t_i{\,\simeq _{}\,}u_i){\leftarrow }_{{}}{\mathfrak {b}}_i\), for \({1\le i\le m}\), and \((f(t_1,\ldots ,t_m){\,\simeq _{}\,}f(u_1,\ldots ,u_m)){\leftarrow }_{{}}{\mathfrak {b}}\), because otherwise an equality inference could expand it. The truth values \({\mathfrak {b}}_1,\ldots ,{\mathfrak {b}}_m\) are all \(\textsf {true}\), because \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\). The truth value \({\mathfrak {b}}\) is \(\textsf {true}\), as otherwise inference rule (2) could expand J. Since \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\), \({\mathcal {M}}_1(f(t_1,\ldots ,t_m))={\mathcal {M}}_1(f(u_1,\ldots ,u_m))\), and \(f^{\mathcal {M}}\) is well-defined. This completes the construction of \({\mathcal {M}}\). For Part (i) of Definition 5, we need to show that for all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\), we have \({\mathcal {M}}(t)={\mathcal {M}}_1(t)={\mathfrak {c}}^{\mathcal {M}}\). For Part (iii) of Definition 5, we need to show that for all \(t\in G(J)\), we have \({\mathcal {M}}(t)={\mathcal {M}}_1(t)\). Both claims are proved by a straightforward induction on the structure of terms. \(\square \)
If \(\textsf {EUF} ^+\) is trivial, \({\mathcal {I}}_{\textsf {EUF} }^m\) is still leading-theory complete. The proof follows the same pattern: it is simpler as there are no \(\textsf {EUF} \)-values and no first-order assignments, and the key point is that the assignment gives a value to \(t{\,\simeq _{s}\,}u\) for all terms t and u of sort \(s\in S\backslash \{\textsf {prop} \}\). Let \({\mathcal {I}}_{\textsf {EUF} }\) be the module obtained by adding to \({\mathcal {I}}_{\textsf {EUF} }^m\) inference rules that propagate consequences of assignments on the trail, according to the congruence axioms of equality for all \(f\in F\):
Corollary 3
Module \({\mathcal {I}}_{\textsf {EUF} }\) is leading-theory-complete for all leading theories.
4.3 The Theory of Arrays
The theory of arrays \(\textsf {Arr} \) features sorts for arrays, indices, and values, and function symbols to select and store array elements. Given a set of basic sorts that includes \(\textsf {prop} \), let \(\Rightarrow \) be the array sort constructor, so that  is the sort of arrays with indices of sort I and values of sort V. We use a, b, c, and d for variables of an
is the sort of arrays with indices of sort I and values of sort V. We use a, b, c, and d for variables of an  sort, u and v for variables of sort V, and i, j, and k for variables of sort I. In signature \(\varSigma _{\textsf {Arr} } = (S,F)\), the set of sorts S is the free closure of the set of basic sorts with respect to \(\Rightarrow \), and the set of symbols F is
sort, u and v for variables of sort V, and i, j, and k for variables of sort I. In signature \(\varSigma _{\textsf {Arr} } = (S,F)\), the set of sorts S is the free closure of the set of basic sorts with respect to \(\Rightarrow \), and the set of symbols F is

Sort subscripts can be omitted when clear, and \(\textsf {store}_{}(a,i,v)\) and \(\textsf {select}_{}(a,i)\) may be abbreviated as\({a}[{i}]{:=\ }{v}\) and \({a}[{i}]\). The symbol \(\textsf {diff}_{}\) is the Skolem function symbol in the clausal form of the \(\rightarrow \) direction of the extensionality axiom \(\forall a\ \forall b\ ((\forall i\ {a}[{i}] {\,\simeq _{}\,}{b}[{i}]) \leftrightarrow a{\,\simeq _{}\,}b)\): the function \(\textsf {diff}_{}\) maps two arrays to an index, called witness, where they differ. Similar to EUF, the extension \(\textsf {Arr} ^+\) may either be trivial, or add a countably infinite set of values for each sort in \(S\backslash \{\textsf {prop} \}\) and no axioms. Module \({\mathcal {I}}_{\textsf {Arr} }\) augments the equality inference rules of Fig. 3 with inference rules that apply when the trail violates an array axiom. Rules (3)–(5) detect violations of the congruence axioms for the \(\varSigma _{\textsf {Arr} }\)-symbols:
Violations of the select-over-store axioms
are detected by rules (6) and (7) of \({\mathcal {I}}_{\textsf {Arr} }\):
The last inference rule builds into \({\mathcal {I}}_{\textsf {Arr} }\) the extensionality axiom:
Most \(\textsf {Arr} \)-satisfiability procedures replace every disequality between arrays with a disequality between their elements at the witness index in a preprocessing phase (see [9, Sect. 6 and 7] for more background and references). Rule (8) is the only rule of \({\mathcal {I}}_{\textsf {Arr} }\) that produces new terms. Similar to \({\mathcal {I}}_{\textsf {EUF} }\), \({\mathcal {I}}_{\textsf {Arr} }\) reasons about \(\textsf {Arr} \)-values, if present, by the equality inference rules, treating \(\textsf {Arr} \)-values as labels of equivalence classes.
For the local basis, for all sets X of terms, \(\textsf {basis} _{\textsf {Arr} }(X)\) is the smallest closed set Y such that \(X\subseteq Y\), \(\top \in Y\), and:
-
1.
For all terms \(l_1\) and \(l_2\) of sort \(\textsf {prop} \) that occur as subterms of terms in Y with \(\textsf {select}_{}\), \(\textsf {store}_{}\), or \(\textsf {diff}_{}\) as root symbol, \((l_1{\,\simeq _{\textsf {prop} }\,}l_2)\in Y\);
-
2.
For all terms \(t, u\in Y\) of an array sort, \({t}[{\textsf {diff}_{}(t,u)}]\in Y\) and \({u}[{\textsf {diff}_{}(t,u)}]\in Y\).
Clause (1) adds equalities between formulæ that may be needed and whose presence is not already guaranteed by closedness of local bases. Clause (2) adds the terms that may be generated by rule (8); it preserves finiteness, because \(\textsf {diff}_{}\) produces terms of an index sort which is structurally smaller, in terms of the array sort constructor \(\Rightarrow \), than the array sort of its arguments.
As arrays represent functions that can be updated, a model can interpret an array as an updatable function and an array sort as a set of updatable functions. Given generic sets \({\mathcal {U}}\) and \({\mathcal {V}}\), let \({\mathcal {V}}^{{\mathcal {U}}}\) denote the set of functions from \({\mathcal {U}}\) to \({\mathcal {V}}\). A set \({\mathcal {W}}\subseteq {\mathcal {V}}^{{\mathcal {U}}}\) is an updatable function set from \({\mathcal {U}}\) to \({\mathcal {V}}\), if every function obtained by a finite number of updates to a function in \({\mathcal {W}}\) is in \({\mathcal {W}}\). As done for \(\textsf {EUF} \), we prove completeness assuming a non-trivial extension.
Theorem 4
Module \({\mathcal {I}}_{\textsf {Arr} }\) is leading-theory-complete for all leading theories \({\mathcal {T}}_{1}\) such that for all \({\mathcal {T}}_{1}\)-models \({\mathcal {M}}_1\) and array sorts  of \(\varSigma _{\textsf {Arr} }\), there is an updatable function set X from \(I^{{\mathcal {M}}_1}\) to \(V^{{\mathcal {M}}_1}\) such that
of \(\varSigma _{\textsf {Arr} }\), there is an updatable function set X from \(I^{{\mathcal {M}}_1}\) to \(V^{{\mathcal {M}}_1}\) such that  .
.
Proof
Let J be a plausible \(\textsf {Arr} \)-assignment that \({\mathcal {I}}_{\textsf {Arr} }\) cannot expand. We show that J is leading-theory-compatible with \(\textsf {Arr} \) sharing G(J). By the same reasoning at the beginning of the proof of Theorem 3, J assigns values to all terms in G(J) (\(\dag \)), and  by Corollary 1. Let \({\mathcal {T}}_{1}\) be a leading theory that satisfies the hypothesis, \(\varSigma _{1}\) its signature, \({\mathcal {T}}_{1}^{+}\) its extension, and \({\mathcal {M}}_1\) a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that
by Corollary 1. Let \({\mathcal {T}}_{1}\) be a leading theory that satisfies the hypothesis, \(\varSigma _{1}\) its signature, \({\mathcal {T}}_{1}^{+}\) its extension, and \({\mathcal {M}}_1\) a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that  and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). For all array sorts
and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). For all array sorts  of \(\varSigma _{\textsf {Arr} }\), let X be the updatable function set from \(I^{{\mathcal {M}}_1}\) to \(V^{{\mathcal {M}}_1}\) such that
of \(\varSigma _{\textsf {Arr} }\), let X be the updatable function set from \(I^{{\mathcal {M}}_1}\) to \(V^{{\mathcal {M}}_1}\) such that  . We organize the proof in two parts.
. We organize the proof in two parts.
-
1.
Definition of a bijective function
 :
:We pick an updatable function \(f_0\in X\) that will be used as default in the sequel. Then, we begin by defining the restriction \(\phi _Y\) of \(\phi \) to the finite subset
 consisting of those elements a such that \({\mathcal {M}}_1(t) = a\) for some term \(t\in G(J)\). For all \(a\in Y\), let \({\mathcal {R}}_a\subseteq I^{{\mathcal {M}}_1}{\times }V^{{\mathcal {M}}_1}\) be the relation defined by the following set of pairs: $$\begin{aligned} \begin{array}{c} \{({\mathcal {M}}_1(i),{\mathcal {M}}_1({t}[{i}])) \mid {{t}[{i}]}\in G(J),\ {\mathcal {M}}_1(t) = a\}\ \cup \\ \{({\mathcal {M}}_1(i),{\mathcal {M}}_1(u)) \mid {{t}[{i}]{:=\ }{u}}\in G(J),\ {\mathcal {M}}_1({t}[{i}]{:=\ }{u}) = a\}\ \cup \\ \{({\mathcal {M}}_1(i),{\mathcal {M}}_1({t}[{i}])) \mid {{t}[{k}]{:=\ }{u}}\in G(J),\ {\mathcal {M}}_1({t}[{k}]{:=\ }{u}){=}a,\ {\mathcal {M}}_1(i)\ne {\mathcal {M}}_1(k)\}. \end{array} \end{aligned}$$
consisting of those elements a such that \({\mathcal {M}}_1(t) = a\) for some term \(t\in G(J)\). For all \(a\in Y\), let \({\mathcal {R}}_a\subseteq I^{{\mathcal {M}}_1}{\times }V^{{\mathcal {M}}_1}\) be the relation defined by the following set of pairs: $$\begin{aligned} \begin{array}{c} \{({\mathcal {M}}_1(i),{\mathcal {M}}_1({t}[{i}])) \mid {{t}[{i}]}\in G(J),\ {\mathcal {M}}_1(t) = a\}\ \cup \\ \{({\mathcal {M}}_1(i),{\mathcal {M}}_1(u)) \mid {{t}[{i}]{:=\ }{u}}\in G(J),\ {\mathcal {M}}_1({t}[{i}]{:=\ }{u}) = a\}\ \cup \\ \{({\mathcal {M}}_1(i),{\mathcal {M}}_1({t}[{i}])) \mid {{t}[{k}]{:=\ }{u}}\in G(J),\ {\mathcal {M}}_1({t}[{k}]{:=\ }{u}){=}a,\ {\mathcal {M}}_1(i)\ne {\mathcal {M}}_1(k)\}. \end{array} \end{aligned}$$In other words, \({\mathcal {R}}_a\) is the set of index-value pairs dictated by those terms in G(J) where either \(\textsf {select}_{}\) is applied to an array term that \({{\mathcal {M}}_1}\) interprets as a or the application of \(\textsf {store}_{}\) forms an array term that \({{\mathcal {M}}_1}\) interprets as a. Since G(J) is finite, \({\mathcal {R}}_a\) is finite. Also, \({\mathcal {R}}_a\) is a partial function \({\mathcal {R}}_a :I^{{\mathcal {M}}_1} \rightarrow V^{{\mathcal {M}}_1}\), because otherwise \({\mathcal {I}}_{\textsf {Arr} }\) could expand J by rules (6)–(7). Let \(\phi _Y(a)\) be the total function that is identical to \({\mathcal {R}}_a\) where \({\mathcal {R}}_a\) is defined, and maps every \(e\in I^{{\mathcal {M}}_1}\) where \({\mathcal {R}}_a\) is undefined to \(f_0(e)\in V^{{\mathcal {M}}_1}\). Since \({\mathcal {R}}_a\) is finite, \(\phi _Y(a)\) differs from \(f_0\) by finitely many updates, and therefore \(\phi _Y(a)\in X\).
Next, we show that \(\phi _Y\) is injective. By way of contradiction, suppose that there are two elements \(a, a^\prime \in Y\) such that \(a\ne a^\prime \) and \(\phi _Y(a) = \phi _Y(a^\prime )\). Since \(a, a^\prime \in Y\), it is \(a = {\mathcal {M}}_1(t)\) and \(a^\prime = {\mathcal {M}}_1(t^\prime )\) for some terms \(t,t^\prime \in G(J)\). This means that \({\mathcal {M}}_1\models t{\,\not \simeq _{}\,}t^\prime \). By (†), J assigns values to t and \(t^\prime \), and therefore it also assigns a truth value \({\mathfrak {b}}\) to \(t{\,\simeq _{}\,}t^\prime \), because otherwise an equality inference could expand it. Also, \(((t{\,\simeq _{}\,}t^\prime ){\leftarrow }_{{}}{\mathfrak {b}})\in J_{{\mathcal {T}}_{1}}\) by definition of theory view. Since \({\mathcal {M}}_1\models t{\,\not \simeq _{}\,}t^\prime \) and \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\), \({\mathfrak {b}}\) must be \(\textsf {false}\), or, equivalently, \((t{\,\not \simeq _{}\,}t^\prime )\in J\). Therefore, also \({t}[{\textsf {diff}_{}(t,t^\prime )}]{\,\not \simeq _{}\,}{t^\prime }[{\textsf {diff}_{}(t,t^\prime )}] \in J\), because otherwise \({\mathcal {I}}_{\textsf {Arr} }\) could expand J by rule (8). As before, \(({t}[{\textsf {diff}_{}(t,t^\prime )}]{\,\not \simeq _{}\,}{t^\prime }[{\textsf {diff}_{}(t,t^\prime )}]) \in J_{{\mathcal {T}}_{1}}\). Since \({\mathcal {M}}_1\models J_{{\mathcal {T}}_{1}}\), it follows that \({\mathcal {M}}_1({t}[{\textsf {diff}_{}(t,t^\prime )}])\ne {\mathcal {M}}_1({t^\prime }[{\textsf {diff}_{}(t,t^\prime )}])\). By definition of \(\phi _Y(a)\) for a generic a, we have:
$$\begin{aligned} \begin{array}{c} \phi _Y(a)({\mathcal {M}}_1(\textsf {diff}_{}(t,t^\prime )))={\mathcal {M}}_1({t}[{\textsf {diff}_{}(t,t^\prime )}])\\ \phi _Y(a^\prime )({\mathcal {M}}_1(\textsf {diff}_{}(t,t^\prime )))= {\mathcal {M}}_1({t^\prime }[{\textsf {diff}_{}(t,t^\prime )}]). \end{array} \end{aligned}$$Since the two right-hand sides are different, the two left-hand sides are also different, so that \(\phi _Y(a)\ne \phi _Y(a^\prime )\), a contradiction.
Given that \(\phi _Y\) is injective, we can extend \(\phi _Y\) to the sought-after bijective function \(\phi \), by taking as pre-images of the elements of X that are not images of elements of Y other elements of
 and there are enough distinct such elements as
and there are enough distinct such elements as  .
. -
2.
Construction of an \({\textsf {Arr} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}\) with
 :
:The first part of the definition of \({\mathcal {M}}\) follows the same pattern as in the proof of Theorem 3: \({\mathcal {M}}\) interprets all sorts in S, all variables
 , and all \(\textsf {Arr} \)-values \({\mathfrak {c}}\) such that \((t{\leftarrow }_{{}}{\mathfrak {c}}) \in J\), as \({\mathcal {M}}_1\) does, and all other \(\textsf {Arr} \)-values arbitrary. The point on sorts suffices for Part (ii) of Definition 5. Then, for all array sorts
, and all \(\textsf {Arr} \)-values \({\mathfrak {c}}\) such that \((t{\leftarrow }_{{}}{\mathfrak {c}}) \in J\), as \({\mathcal {M}}_1\) does, and all other \(\textsf {Arr} \)-values arbitrary. The point on sorts suffices for Part (ii) of Definition 5. Then, for all array sorts  , \({\mathcal {M}}\) interprets the \(\textsf {select}_{}\), \(\textsf {store}_{}\) and \(\textsf {diff}_{}\) symbols as follows:
, \({\mathcal {M}}\) interprets the \(\textsf {select}_{}\), \(\textsf {store}_{}\) and \(\textsf {diff}_{}\) symbols as follows:-
For all array-index pairs
 , let
, let  ;
; -
For all array-index-value triples
 , let \(f\in X\) be the function mapping e to v and every other \(e^\prime \in I^{\mathcal {M}}\) to \(\phi (a)(e^\prime )\in V^{\mathcal {M}}\); then
, let \(f\in X\) be the function mapping e to v and every other \(e^\prime \in I^{\mathcal {M}}\) to \(\phi (a)(e^\prime )\in V^{\mathcal {M}}\); then  ;
; -
For all pairs
 with \(a\ne a^\prime \),
with \(a\ne a^\prime \),  such that \(\phi (a)(e)\ne \phi (a^\prime )(e)\), and
such that \(\phi (a)(e)\ne \phi (a^\prime )(e)\), and  is an arbitrary element of \(I^{\mathcal {M}}\).
is an arbitrary element of \(I^{\mathcal {M}}\).
By construction, \({\mathcal {M}}\) satisfies the \(\textsf {Arr} \)-axioms and it is an
 -model. Parts (i) and (iii) of Definition 5 follow by induction on the term structure. \(\square \)
-model. Parts (i) and (iii) of Definition 5 follow by induction on the term structure. \(\square \) -
The same property holds for the trivial \(\textsf {Arr} ^+\) with an almost identical proof, except that non-Boolean terms in G(J) are not assigned values. Rules obtained from rules (3)–(7) by removing the last premise and adding its flip as conclusion can be added to \({\mathcal {I}}_{\textsf {Arr} }\), preserving leading-theory-completeness by Lemma 2.
4.4 Linear Rational Arithmetic
Theory \(\textsf {LRA} \) has signature \(\varSigma _{\textsf {LRA} }\) with sorts \(S_\textsf {LRA} =\{\textsf {prop} ,\textsf {Q}\}\) and set of symbols \(F_\textsf {LRA} \) with equality symbols \({\,\simeq _{\{\textsf {prop} ,\textsf {Q}\}}\,}\), the constant \(1{{:}}\textsf {Q}\), the symbol \(+{{:}}(\textsf {Q}{\times }\textsf {Q}){\rightarrow }\textsf {Q}\) for addition, the predicates \(<,\le {{:}}(\textsf {Q}{\times }\textsf {Q}){\rightarrow }\textsf {prop} \) for the orderings, and the collection of unary function symbols \(\{c{\cdot }{{:}}\textsf {Q}{\rightarrow }\textsf {Q}\mid c\in {\mathbb {Q}}\}\), indexed by the set \({\mathbb {Q}}\) of the rational numbers, for multiplication by constants. The extension \(\textsf {LRA} ^{+}\) adds constants for all rational numbers, namely \(\varSigma _{\textsf {LRA} }^{+} = (\{\textsf {prop} ,\textsf {Q}\}, F_\textsf {LRA} \cup \{{\tilde{q}}{{:}}\textsf {Q}\mid q\in {\mathbb {Q}}\})\) with axioms \(\tilde{q}{\,\simeq _{\textsf {Q}}\,} q{\cdot } 1\) for all \(q\in {\mathbb {Q}}\).
The Fourier-Motzkin (FM) algorithm [41, 43, 52] determines the satisfiability of a set of linear inequalities over the reals, by applying variable elimination until either it generates a contradiction, in the form of a constraint \(0\le \tilde{q}\) with negative \(\tilde{q}\), in which case the algorithm returns unsatisfiable, or it eliminates all variables, in which case the algorithm returns satisfiable.
Variable elimination works as follows: select a variable x; if x appears only with positive, or negative, coefficients, remove all constraints where x appears; otherwise, compute all linear combinations of constraints \(t_1{+}c_1{\cdot }x {\le } u_1\) and \(t_2{-}c_2{\cdot }x {\le } u_2\) where x appears with positive and negative coefficient, respectively, generating the constraint \(c_2{\cdot }t_1{+}c_1{\cdot }t_2 {\le } c_2{\cdot }u_1{+}c_1{\cdot }u_2\) (if a premise is a strict inequality, the result is also strict). Alternatively, the constraints where x appears with positive coefficient are rearranged into upper bounds \(x\le t\), those where x appears with negative coefficient are rearranged into lower bounds \(u\le x\), and the computation of all linear combinations is replaced by that of all transitive closures, concatenating \(u\le x\) and \(x\le t\) to generate \(u\le t\) (if a premise is strict, the result is also).
Since a linear combination eliminating x recalls a propositional resolution inference eliminating the propositional variable of the literals resolved upon, a single linear combination, or transitive closure step, is known as Fourier-Motzkin (FM) resolution. A variable x appearing only with one sign parallels a pure literal in a set of clauses, and the elimination of all constraints where x occurs reminds one of the pure literal rule that eliminates, or deems satisfied, all clauses where a pure literal occurs [18]. The FM-algorithm resembles the level-saturation strategy for resolution: select a propositional variable l, add all resolvents generated by resolving upon l, remove all clauses where l appears, and repeat, until either the empty clause arises or the set is emptied.
Given m constraints in n variables the FM-algorithm generates \({m^{2^n}}\over {4^n}\) constraints in the worst case (e.g., [41]), whereas the simplex algorithm (e.g., [41, 52]) is exponential in the worst case [39], but polynomial in practice [54]. Thus, most \(\textsf {LRA} \)-satisfiability procedures adopt a modern version of the simplex algorithm that deals also with strict inequalities [26]. However, conflict-driven \(\textsf {LRA} \)-satisfiability procedures [21, 40, 46] apply FM-resolution only to explain \(\textsf {LRA} \)-conflicts, just like the CDCL procedure applies resolution only to explain Boolean conflicts [44, 45]. These procedures stand to the FM-algorithm like CDCL stands to level-saturation by resolution. Similar to MCSAT [35], CDSAT embeds a conflict-driven \(\textsf {LRA} \)-satisfiability procedure and applies FM-resolution only to solve conflicts. A difference between CDSAT and MCSAT in this regard is that the \(\textsf {Deduce}\) rule of CDSAT covers both propagation and conflict explanation, allowing CDSAT to apply FM-resolution more liberally. Therefore, we consider an \({\mathcal {I}}_{\textsf {LRA} }\) module that features FM-resolution:
where \(t_1\), \(t_2\), and \(t_3\) are terms of sort \(\textsf {Q}\), \(\lessdot _1,\lessdot _2,\lessdot _3 \in \{<,\le \}\), and \(\lessdot _3\) is < if and only if either \(\lessdot _1\) or \(\lessdot _2\) is <. Since FM-resolution concatenates inequalities, \({\mathcal {I}}_{\textsf {LRA} }\) has equality elimination rules to replace an equality by inequalities:
and positivization rules to handle flipped inequalities based on the totality of the ordering on \({\mathbb {Q}}\):
Let \(t_0,\ldots ,t_m\) be terms of sort \(\textsf {Q}\), and l a formula whose normal form is in the closure of \(t_1,\ldots ,t_m\) with respect to the symbols of \(F_\textsf {LRA} \). Module \({\mathcal {I}}_{\textsf {LRA} }\) also has an evaluation rule to evaluate the truth value of l when values for \(t_1,\ldots ,t_m\) are available on the trail:
For example, \((z{\leftarrow }_{{}}1)\vdash _{\textsf {LRA} } (w{+}2{\,\simeq _{\textsf {Q}}\,}w{+}z){\leftarrow }_{{}}\textsf {false}\) is an evaluation inference, which does not need a value for w, because the normal form of \(w{+}2{\,\simeq _{\textsf {Q}}\,}w{+}z\) is \({-z} + 2 {\,\simeq _{\textsf {Q}}\,} 0\). Let x be a free \(\varSigma _{\textsf {LRA} }\)-variable of sort \(\textsf {Q}\) that does not occur free in \(t_0\), \(t_1\), and \(t_2\). The last rule of \({\mathcal {I}}_{\textsf {LRA} }\), beside the equality rules of Fig. 3, is disequality elimination, which detects a situation where there is no value for x:
FM-resolution and disequality elimination apply also to formulæ reducible to the form of their premises, as in \(y{-}x {<} 0,\ 3{\cdot }x {<} 5\vdash _{\textsf {LRA} } y {<} \frac{5}{3}\) for FM-resolution.
The FM-algorithm bundles in one step all FM-resolutions on one variable, eliminating it altogether; as there are finitely many variables, the algorithm terminates. However, other strategies for applying FM-resolution may generate infinitely many terms as shown in Fig. 4: the never-halting series alternates FM-resolutions on a variable x with FM-resolutions on another variable y.
In CDSAT, the FM-algorithm can be emulated with \({\mathcal {I}}_{\textsf {LRA} }\)-inferences, as a series of \(\textsf {Deduce}\) transitions applied with a level-saturation search plan. The local basis can be set to those terms that are newly generated by the algorithm, in finite numbers, so that termination follows. This search plan thus provides a decision procedure for satisfiability, but it is not conflict-driven and is as inefficient as the FM-algorithm. Other search plans may be more interesting, but may raise termination issues: were it not for the finite global basis of CDSAT that forces termination, the infinite series of Fig. 4 could also be emulated in CDSAT, for instance as a never-ending search phase that never generates any conflict. While a conflict-driven search plan would not apply \(\textsf {Deduce}\) in this manner, this infinite series may ensue also if \(\textsf {Deduce}\) only explains conflicts, as detailed in the following example.
Example 7
Consider the set \(R = \{l_0:-2{\cdot }x-y {<} 0, \ l_1:x+y {<} 0,\ l_2:{x}{<}{-1}\}\) of Fig. 4. Suppose that \(\textsf {Decide}\) tries \(y{\leftarrow }_{{}}0\). The LRA-procedure sees LRA-conflict \(\{-2{\cdot }x{-}y< 0,\ x < {-1},\ y{\leftarrow }_{{}}0\}\) and explains it by the FM-resolution inference \(\{{-y}< 2{\cdot }x,\ 2{\cdot }x< {-2}\}\vdash _{\textsf {LRA} } {-y} < {-2}\), so that \(\textsf {Deduce}\) places \(l_3:{-y} < {-2}\) on the trail. Literal \(l_3\) is a late propagation, as it has level 0, but it comes after the first decision. The evaluation inference \(y{\leftarrow }_{{}}0\vdash _{\textsf {LRA} } \overline{{-y}{<}{-2}}\) reveals conflict \(\{y{\leftarrow }_{{}}0,\ {-y} < {-2}\}\) on the trail. Since its level is 1, \(\textsf {ConflictSolve}\) fires, and \(\textsf {UndoClear}\) solves the conflict by undoing \(y{\leftarrow }_{{}}0\). If \(\textsf {Decide}\) tries next \(x{\leftarrow }_{{}}{-2}\), the LRA-procedure detects LRA-conflict \(\{x+y< 0,\ {-y} < {-2},\ x{\leftarrow }_{{}}{-2}\}\) and explains it by the FM-resolution inference \(\{x< {-y},\ {-y}< {-2}\}\vdash _{\textsf {LRA} } x < {-2}\), so that \(\textsf {Deduce}\) puts \(l_4:x < {-2}\) on the trail. The evaluation inference \(x{\leftarrow }_{{}}{-2}\vdash _{\textsf {LRA} } \overline{{x}{<}{-2}}\) exposes conflict \(\{x{\leftarrow }_{{}}{-2},\ x < {-2}\}\) on the trail. Since its level is 1, \(\textsf {ConflictSolve}\) applies, and \(\textsf {UndoClear}\) solves the conflict by retracting \(x{\leftarrow }_{{}}{-2}\). A subsequent \(\textsf {Decide}\) with \(y{\leftarrow }_{{}}3\) causes LRA-conflict \(\{-2{\cdot }x-y {<} 0,\ x {<} {-2},\ y{\leftarrow }_{{}}3\}\), that \(\textsf {Deduce}\) explains by the FM-resolution \(\{{-y} {<} 2{\cdot }x,\ {2{\cdot }x}{<}{-4}\}\vdash _{\textsf {LRA} } {-y}{<}{-4}\), generating \(l_5:{-y} < {-4}\). The evaluation inference \(y{\leftarrow }_{{}}3\vdash _{\textsf {LRA} } \overline{{-y}{<}{-4}}\) gets conflict \(\{y{\leftarrow }_{{}}3,\ {-y} < {-4}\}\) on the trail, and the same \(\textsf {ConflictSolve}\) \(\textsf {UndoClear}\) pair of transitions undoes \(y{\leftarrow }_{{}}3\). Again, a \(\textsf {Decide}\) with \(x{\leftarrow }_{{}}{-3}\) leads to LRA-conflict \(\{x+y< 0,\ {-y} < {-4},\ x{\leftarrow }_{{}}{-3}\}\), explained by \(\textsf {Deduce}\) with the FM-resolution \(\{x< {-y},\ {-y}{<}{-4}\}\vdash _{\textsf {LRA} } {x}{<}{-4}\), so that \(l_6:x {<} {-4}\) is added to the trail. Evaluation inference \(x{\leftarrow }_{{}}{-3}\vdash _{\textsf {LRA} } \overline{{x}{<}{-4}}\) unveils conflict \(\{x{\leftarrow }_{{}}{-3},\ {x}{<}{-4}\}\) on the trail, so that \(\textsf {ConflictSolve}\) and \(\textsf {UndoClear}\) apply, repealing \(x{\leftarrow }_{{}}{-3}\). The last FM-resolution in Fig. 4 may respond to a \(\textsf {Decide}\) with \(y{\leftarrow }_{{}}5\), so that LRA-conflict \(\{-2{\cdot }x-y< 0,\ x < {-4},\ y{\leftarrow }_{{}}5\}\) is explained by \(\textsf {Deduce}\) with FM-resolution \(\{{-y} {<} 2{\cdot }x,\ {2{\cdot }x}{<}{-8}\}\vdash _{\textsf {LRA} } {-y}{<}{-8}\), adding \(l_7:{-y} {<} {-8}\) to the trail. The evaluation inference \(y{\leftarrow }_{{}}5\vdash _{\textsf {LRA} } \overline{{-y}{<}{-8}}\) shows conflict \(\{y{\leftarrow }_{{}}5,\ {-y}{<}{-8}\}\) on the trail, so that \(\textsf {ConflictSolve}\) applies and \(\textsf {UndoClear}\) removes \(y{\leftarrow }_{{}}5\).
A well-known solution to this problem assumes a total ordering \(\prec _{\textsf {LRA} }\) on \(\varSigma _{\textsf {LRA} }\)-variables of sort \(\textsf {Q}\) and restricts FM-resolution by requiring that the resolved variable x is \(\prec _{\textsf {LRA} }\)-maximum in both premises [11, 21, 35, 40, 46].
Example 8
Assuming \(y\prec _{\textsf {LRA} }x\), the first FM-resolution step in Fig. 4, namely \(\{{-y} {<} 2{\cdot }x,\ 2{\cdot }x {<} {-2}\}\vdash _{\textsf {LRA} } {-y} {<} {-2}\), still applies, as it eliminates the \(\prec _{\textsf {LRA} }\)-maximum variable x, and generates \(l_3:{-y} < {-2}\). The second FM-resolution step of the diverging series, namely \(\{x {<} {-y},\ {-y} {<} {-2}\}\vdash _{\textsf {LRA} } x {<} {-2}\), is barred, because y is not the \(\prec _{\textsf {LRA} }\)-maximum variable in the premises. Thus, all CDSAT-derivations embedding that diverging series of FM-resolution inferences are excluded. Multiple CDSAT-derivations discover that R is \(\textsf {LRA} \)-unsatisfiable. One that does it by mere theory propagations at level 0 begins with \(\textsf {Deduce}\) placing \(l_3\) on the trail. Another \(\textsf {Deduce}\) applies FM-resolution to compute linear combination \(l_0 + 2 l_1\) as \(\{{-y} {<} 2{\cdot }x,\ 2{\cdot }x {<} {-2}{\cdot }y\}\vdash _{\textsf {LRA} } {-y} {<} {-2}{\cdot }y\), adding the normal form \(l_4:y < 0\) of \({-y} < {-2}{\cdot }y\) to the trail. A third \(\textsf {Deduce}\) with FM-resolution inference \(\{2 {<} y,\ y {<} 0\}\vdash _{\textsf {LRA} } 2 {<} 0\), computing linear combination \({-l_3} + l_4\), expands the trail with \(l_5:2 {<} 0\). The evaluation step \(\emptyset \vdash _{\textsf {LRA} } \overline{2 < 0}\) leads to a \(\textsf {Fail}\) transition as \(2 {<} 0\) has level 0.
In CDSAT, termination is ensured by the finiteness of the global basis \({\mathcal {B}}\) which restricts \(\textsf {Deduce}\). For completeness, \({\mathcal {B}}\) must be stable, requiring in particular that \(\textsf {basis} _{\textsf {LRA} }({\mathcal {B}})\subseteq {{\mathcal {B}}}\) for the local basis \(\textsf {basis} _{\textsf {LRA} }\). Thus, \(\textsf {basis} _{\textsf {LRA} }\) must be limited so as to never introduce infinitely many terms, which is obtained by incorporating the restriction to FM-resolution as follows. For all sets X of terms, \(\textsf {basis} _{\textsf {LRA} }(X)\) is the smallest closed set Y such that \(X\subseteq Y\), \(\top \in Y\), and, for all terms \(t_1\) and \(t_2\) of sort \(\textsf {Q}\):
-
1.
If \(t_1{\,\simeq _{\textsf {Q}}\,}t_2\in Y\) then \(t_1\le t_2\in Y\) and \(t_2\le t_1\in Y\);
-
2.
If \((t_1 < t_2)\in Y\) then \((t_2\le t_1)\in Y\), and if \((t_1\le t_2)\in Y\) then \((t_2 < t_1)\in Y\);
-
3.
If \((t_1 \lessdot _1 x)\in Y\) and \((x \lessdot _2 t_2)\in Y\), then \((t_1 \lessdot _3 t_2)\in Y\), where \(\lessdot _1,\lessdot _2,\lessdot _3 \in \{<,\le \}\), \(\lessdot _3\) is < if and only if either \(\lessdot _1\) or \(\lessdot _2\) is <, and x is the \(\prec _{\textsf {LRA} }\)-maximum variable in both
 and
and  .
.
Clauses (1) and (2) add the terms that may be generated by the equality elimination and positivization rules, respectively, which do not challenge finiteness. Clause (3) adds the terms that may be inferred by FM-resolution, and it preserves finiteness thanks to the \(\prec _{\textsf {LRA} }\)-based restriction. The side-condition of \(\textsf {Deduce}\) (see Fig. 1) ensures that the evaluation rule evaluates a formula in \({\mathcal {B}}\).
For \({\mathcal {I}}_{\textsf {LRA} }\) to be complete with FM-resolution thus restricted, it suffices to add the following inference rule, named detection of an empty solution space:
where \(y_1,\ldots ,y_m\) are \(\varSigma _{\textsf {LRA} }\)-variables of sort \(\textsf {Q}\), E is an \(\textsf {LRA} \)-assignment such that for all x in  , \(x\prec _{\textsf {LRA} }y_i\) or \(x = y_i\) for some i, \(1\,{\le }\,i\,{\le }\,m\), and \(\{y_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,y_m{\leftarrow }_{{}}\tilde{q_m}\}\uplus E\) is unsatisfiable. Alternatively, and in practice, since \(\textsf {Deduce}\) applies FM-resolution to explain \(\textsf {LRA} \)-conflicts typically due to decisions on rational variables, one may adopt a search plan that selects rational variables for decisions in \(\prec _{\textsf {LRA} }\)-increasing order. We call such a search plan sensible. An \(\textsf {LRA} \)-assignment J generated by a sensible search plan is also termed sensible and has the following property: for all variables
, \(x\prec _{\textsf {LRA} }y_i\) or \(x = y_i\) for some i, \(1\,{\le }\,i\,{\le }\,m\), and \(\{y_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,y_m{\leftarrow }_{{}}\tilde{q_m}\}\uplus E\) is unsatisfiable. Alternatively, and in practice, since \(\textsf {Deduce}\) applies FM-resolution to explain \(\textsf {LRA} \)-conflicts typically due to decisions on rational variables, one may adopt a search plan that selects rational variables for decisions in \(\prec _{\textsf {LRA} }\)-increasing order. We call such a search plan sensible. An \(\textsf {LRA} \)-assignment J generated by a sensible search plan is also termed sensible and has the following property: for all variables  , if \(x\prec _{\textsf {LRA} }y\) and J assigns a value to y, then J assigns a value to x.
, if \(x\prec _{\textsf {LRA} }y\) and J assigns a value to y, then J assigns a value to x.
Toward completeness, since \({\mathcal {I}}_{\textsf {LRA} }\) does not fulfill Condition (ii) of Part (3) of Lemma 1, we prove another lemma. Preliminarily we observe that the evaluation rule of \({\mathcal {I}}_{\textsf {LRA} }\) subsumes the equality inference rules that take as premises first-order assignments (the first two in Fig. 3), and therefore we can assume that evaluation and detection of an empty solution space are the only rules of \({\mathcal {I}}_{\textsf {LRA} }\) that deal with first-order assignments. Also, the only sort of \(\textsf {LRA} \) other than \(\textsf {prop} \) is \(\textsf {Q}\), and all terms in \(G_{\textsf {Q}}(J)\) are relevant to \(\textsf {LRA} \) in an \(\textsf {LRA} \)-assignment J. Given \(\textsf {LRA} \)-assignment J and variable  , a unit constraint [35] about x in J is a singleton Boolean assignment \(L\in J\) where only x is unassigned: J assigns a value to all y,
, a unit constraint [35] about x in J is a singleton Boolean assignment \(L\in J\) where only x is unassigned: J assigns a value to all y,  and \(y\ne x\).
and \(y\ne x\).
Lemma 3
If module \({\mathcal {I}}_{\textsf {LRA} }\) cannot expand a plausible \(\textsf {LRA} \)-assignment J, then J assigns values to all terms in \(G_{\textsf {Q}}(J)\).
Proof
As a preliminary remark, all Boolean assignments in J concern terms of the form \(t_1\le t_2\), \(t_1 < t_2\), or \({t_1{\,\not \simeq _{\textsf {Q}}\,} t_2}\), because otherwise an equality elimination or positivization inference rule could expand J. We begin by showing that J assigns values to all variables in  . By way of contradiction, assume this is not the case, and let x be the \(\prec _{\textsf {LRA} }\)-smallest variable to which J does not assign a value. If J is sensible, for all variables
. By way of contradiction, assume this is not the case, and let x be the \(\prec _{\textsf {LRA} }\)-smallest variable to which J does not assign a value. If J is sensible, for all variables  such that \(y\ne x\), if J assigns a value to y then \(y\prec _{\textsf {LRA} }x\) (†). No \(\textsf {LRA} \)-assignment \(x{\leftarrow }_{{}}{\tilde{q}}\) is acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J (‡), because otherwise \({\mathcal {I}}_{\textsf {LRA} }\) could expand J by a decision. Property (‡) implies that for all values \({\tilde{q}}\) there exist \(L\in J\) and \(J^\prime \subseteq J\) such that \(J^\prime \cup \{x{\leftarrow }_{{}}{\tilde{q}}\}\vdash _{\textsf {LRA} } \overline{L}\). This means that the space of possible solutions for x is empty: we distinguish three cases.
such that \(y\ne x\), if J assigns a value to y then \(y\prec _{\textsf {LRA} }x\) (†). No \(\textsf {LRA} \)-assignment \(x{\leftarrow }_{{}}{\tilde{q}}\) is acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J (‡), because otherwise \({\mathcal {I}}_{\textsf {LRA} }\) could expand J by a decision. Property (‡) implies that for all values \({\tilde{q}}\) there exist \(L\in J\) and \(J^\prime \subseteq J\) such that \(J^\prime \cup \{x{\leftarrow }_{{}}{\tilde{q}}\}\vdash _{\textsf {LRA} } \overline{L}\). This means that the space of possible solutions for x is empty: we distinguish three cases.
-
1.
For variable x the lower bound is greater than the upper bound:
\(E=\{t_1\le x,\ x\le t_2,\ t_1{\leftarrow }_{{}}{\tilde{q}}_1,\ t_2{\leftarrow }_{{}}{\tilde{q}}_2\}\subseteq J\) and \({\tilde{q}}_2 < {\tilde{q}}_1\); every assignment \(x{\leftarrow }_{{}}{\tilde{q}}\) triggers an evaluation inference contradicting either \(t_1\le x\) or \(x\le t_2\) or both. It follows that \(t_1\le x\) and \(x\le t_2\) are unit constraints about x in J, because the evaluation rule determines the value of a Boolean term when all its rational subterms are assigned. If x is the \(\prec _{\textsf {LRA} }\)-maximum variable in
 , the FM-resolution inference \(\{t_1\le x,\ x\le t_2\}\vdash _{\textsf {LRA} } t_1\le t_2\) is enabled. If J is sensible, this is guaranteed by (†). Otherwise, if \(y_1,\ldots y_m\) are the variables other than x in
, the FM-resolution inference \(\{t_1\le x,\ x\le t_2\}\vdash _{\textsf {LRA} } t_1\le t_2\) is enabled. If J is sensible, this is guaranteed by (†). Otherwise, if \(y_1,\ldots y_m\) are the variables other than x in  , \(x\prec _{\textsf {LRA} }y_i\) for some i, \(1\,{\le }\,i\,{\le }\,m\). Since \(t_1\le x\) and \(x\le t_2\) are unit constraints about x in J, \(\{y_1{\leftarrow }_{{}}{\tilde{q}}_3,\ldots ,y_m{\leftarrow }_{{}}{\tilde{q}}_{3+k}\}\subseteq J\) (\(3+k=m\)). As \(\{y_1{\leftarrow }_{{}}{\tilde{q}}_3,\ldots ,y_m{\leftarrow }_{{}}{\tilde{q}}_{3+k}\}\uplus E\) is unsatisfiable, an inference by the detection of an empty solution space rule is enabled.
, \(x\prec _{\textsf {LRA} }y_i\) for some i, \(1\,{\le }\,i\,{\le }\,m\). Since \(t_1\le x\) and \(x\le t_2\) are unit constraints about x in J, \(\{y_1{\leftarrow }_{{}}{\tilde{q}}_3,\ldots ,y_m{\leftarrow }_{{}}{\tilde{q}}_{3+k}\}\subseteq J\) (\(3+k=m\)). As \(\{y_1{\leftarrow }_{{}}{\tilde{q}}_3,\ldots ,y_m{\leftarrow }_{{}}{\tilde{q}}_{3+k}\}\uplus E\) is unsatisfiable, an inference by the detection of an empty solution space rule is enabled. -
2.
For variable x the lower bound and the upper bound are equal, but one of them is strict: either \(E=\{t_1 < x,\ x\le t_2,\ t_1{\leftarrow }_{{}}{\tilde{q}},\ t_2{\leftarrow }_{{}}{\tilde{q}}\}\subseteq J\) or \(E=\{t_1 \le x,\ x < t_2,\ t_1{\leftarrow }_{{}}{\tilde{q}},\ t_2{\leftarrow }_{{}}{\tilde{q}}\}\subseteq J\). The reasoning is the same as in Case (1) except that the enabled instance of FM-resolution is either \(\{t_1< x,\ x\le t_2\}\vdash _{\textsf {LRA} } t_1 < t_2\) or \(\{t_1 \le x,\ x< t_2\}\vdash _{\textsf {LRA} } t_1 < t_2\).
-
3.
The lower bound and the upper bound for x are equal, and neither is strict, but a disequality excludes the only possible value: \(\{t_1 \le x,\ x\le t_2,\ t_1 \simeq t_0,\ t_2 \simeq t_0,\ x\not \simeq t_0\}\subseteq J\), so that a disequality elimination is enabled.
In all three cases an inference is enabled, contradicting the hypothesis. Thus, J assigns values to all variables in  . We complete the proof by showing that J assigns values to all non-variable terms \(t\in G_{\textsf {Q}}(J)\). Since J assigns values to all variables \(x_1,\ldots ,x_r\) in t (i.e., \(\{x_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,x_r{\leftarrow }_{{}}\tilde{q_r}\}\subseteq J\)), these assignments dictates a value \({\tilde{q}}\) for t. If \(t{\leftarrow }_{{}}{\tilde{q}}\) is acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J, \({\mathcal {I}}_{\textsf {LRA} }\) can expand J deciding \(t{\leftarrow }_{{}}{\tilde{q}}\), a contradiction. If \(t{\leftarrow }_{{}}{\tilde{q}}\) is not acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J, it means that \(t{\leftarrow }_{{}}{\tilde{q}}\) enables an evaluation step generating \(\overline{L}\) for some \(L\in J\); then also \(\{x_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,x_r{\leftarrow }_{{}}\tilde{q_r}\}\) enables an evaluation inference generating \(\overline{L}\), and \({\mathcal {I}}_{\textsf {LRA} }\) can expand J, again a contradiction. \(\square \)
. We complete the proof by showing that J assigns values to all non-variable terms \(t\in G_{\textsf {Q}}(J)\). Since J assigns values to all variables \(x_1,\ldots ,x_r\) in t (i.e., \(\{x_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,x_r{\leftarrow }_{{}}\tilde{q_r}\}\subseteq J\)), these assignments dictates a value \({\tilde{q}}\) for t. If \(t{\leftarrow }_{{}}{\tilde{q}}\) is acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J, \({\mathcal {I}}_{\textsf {LRA} }\) can expand J deciding \(t{\leftarrow }_{{}}{\tilde{q}}\), a contradiction. If \(t{\leftarrow }_{{}}{\tilde{q}}\) is not acceptable for \({\mathcal {I}}_{\textsf {LRA} }\) in J, it means that \(t{\leftarrow }_{{}}{\tilde{q}}\) enables an evaluation step generating \(\overline{L}\) for some \(L\in J\); then also \(\{x_1{\leftarrow }_{{}}\tilde{q_1},\ldots ,x_r{\leftarrow }_{{}}\tilde{q_r}\}\) enables an evaluation inference generating \(\overline{L}\), and \({\mathcal {I}}_{\textsf {LRA} }\) can expand J, again a contradiction. \(\square \)
The above lemma applies to any plausible \(\textsf {LRA} \)-assignment J, without requiring that J is sensible: if J is sensible, the rule for detection of an empty solution space plays no role in the proof of the lemma, whereas it does if J is not sensible (cf. Case (1) in the proof). It follows that if the CDSAT search plan is sensible, and therefore all generated assignments are sensible, the rule for detection of an empty solution space is unnecessary.
Theorem 5
Module \({\mathcal {I}}_{\textsf {LRA} }\) is leading-theory-complete for all leading theories whose models interpret \(\textsf {Q}\) as an infinite set.
Proof
Let J be a plausible \(\textsf {LRA} \)-assignment that \({\mathcal {I}}_{\textsf {LRA} }\) cannot expand. We show that J is leading-theory-compatible with \(\textsf {LRA} \) sharing G(J). Assignment J gives values to all terms in \(G_{\textsf {prop} }(J)\) by Part (2) of Lemma 1 and to all terms in \(G_{\textsf {Q}}(J)\) by Lemma 3 (†). Since \(S_\textsf {LRA} =\{\textsf {prop} ,\textsf {Q}\}\), \(G(J)=G_{\textsf {prop} }(J)\uplus G_{\textsf {Q}}(J)\), and  by Corollary 1. Let \({{\mathcal {T}}}_1\) be a leading theory, and \({\mathcal {M}}_1\) a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that
by Corollary 1. Let \({{\mathcal {T}}}_1\) be a leading theory, and \({\mathcal {M}}_1\) a \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that  , \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\), and \(|\textsf {Q}^{{\mathcal {M}}_1}|\) is infinite. We define an \({\textsf {LRA} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}\) with
, \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\), and \(|\textsf {Q}^{{\mathcal {M}}_1}|\) is infinite. We define an \({\textsf {LRA} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}\) with  , and we show that it satisfies Definition 5. \({\mathcal {M}}\) interprets \(\textsf {Q}\) as \({\mathbb {Q}}\), every symbol in \(\varSigma _{\textsf {LRA} }^+\) in the standard way (e.g., \({\tilde{q}}\) as q), and every \(\textsf {Q}\)-sorted \(\varSigma _{\textsf {LRA} }\)-variable
, and we show that it satisfies Definition 5. \({\mathcal {M}}\) interprets \(\textsf {Q}\) as \({\mathbb {Q}}\), every symbol in \(\varSigma _{\textsf {LRA} }^+\) in the standard way (e.g., \({\tilde{q}}\) as q), and every \(\textsf {Q}\)-sorted \(\varSigma _{\textsf {LRA} }\)-variable  as \({\tilde{q}}\) for \((x{\leftarrow }_{{}}{\tilde{q}})\in J\). For Part (i) of Definition 5, we show that \({\mathcal {M}}\models J\). For all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\), there are three cases: t is either a \(\varSigma _{\textsf {LRA} }\)-variable, or a formula, or a non-variable term of sort \(\textsf {Q}\). If t is a \(\varSigma _{\textsf {LRA} }\)-variable, then \({\mathcal {M}}(t) = {\mathfrak {c}}^{\mathcal {M}}\) by construction of \({\mathcal {M}}\). Otherwise, J assigns values to all \(\textsf {Q}\)-sorted subterms of t by (†). If t is a formula and \({\mathcal {M}}(t) \ne {\mathfrak {c}}^{\mathcal {M}}\), then \({\mathcal {I}}_{\textsf {LRA} }\) can expand J with an evaluation inference deriving \(\overline{t{\leftarrow }_{{}}{\mathfrak {c}}}\). If t is a non-variable term of sort \(\textsf {Q}\) and \({\mathcal {M}}(t) \ne {\mathfrak {c}}^{\mathcal {M}}\), then \({\mathcal {I}}_{\textsf {LRA} }\) can expand J with an evaluation inference deriving \({t{\,\not \simeq _{\textsf {Q}}\,}t}\). Both conclusions contradict the hypothesis that \({\mathcal {I}}_{\textsf {LRA} }\) cannot expand J, and therefore \({\mathcal {M}}(t) = {\mathfrak {c}}^{\mathcal {M}}\) holds. For Part (ii) of Definition 5, \(\textsf {Q}^{\mathcal {M}}\) is countably infinite. If \(\textsf {Q}^{{\mathcal {M}}_1}\) is countably infinite, we are done. Otherwise, \(|\textsf {Q}^{{\mathcal {M}}_1}|\) is some larger infinite cardinality: \(|\textsf {Q}^{{\mathcal {M}}_1}| > |\textsf {Q}^{\mathcal {M}}|\). Since \(\varSigma _{\textsf {LRA} }^+\) is countable, by the Löwenheim-Skolem theorem, there exists another \({\textsf {LRA} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}^\prime \) such that \(|\textsf {Q}^{{\mathcal {M}}^\prime }| = |\textsf {Q}^{{\mathcal {M}}_1}|\) and \({\mathcal {M}}^\prime \) agrees with \({\mathcal {M}}\) on everything else. For Part (iii) of Definition 5, we observe that \(J\subseteq J_{{\mathcal {T}}_1}\) by the definition of theory view, since J is an \(\textsf {LRA} \)-assignment and \({\mathcal {T}}_1\) has the sorts of \(\textsf {LRA} \), so that \(\textsf {LRA} \)-values are also \({\mathcal {T}}_1\)-values. Thus, \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\) implies \({\mathcal {M}}_1\models J\). For all \(t,t^\prime \in G_{\textsf {prop} }(J)\), \({\mathcal {M}}_1\models J\) and \({\mathcal {M}}\models J\) suffice for \({\mathcal {M}}(t)={\mathcal {M}}(t^\prime )\) if and only if \({\mathcal {M}}_1(t)={\mathcal {M}}_1(t^\prime )\). For all \(t,t^\prime \in G_{\textsf {Q}}(J)\), J assigns a truth value to \(t{\,\simeq _{\textsf {Q}}\,}t^\prime \), because if this were not the case, J could be expanded by an equality inference, since J gives values to t and \(t^\prime \) by (†). Thus, \({\mathcal {M}}_1\models J\) and \({\mathcal {M}}\models J\) imply \({\mathcal {M}}(t)={\mathcal {M}}(t^\prime )\) if and only if \((t{\,\simeq _{\textsf {Q}}\,}t^\prime )\in J\) if and only if \({\mathcal {M}}_1(t)={\mathcal {M}}_1(t^\prime )\).
as \({\tilde{q}}\) for \((x{\leftarrow }_{{}}{\tilde{q}})\in J\). For Part (i) of Definition 5, we show that \({\mathcal {M}}\models J\). For all \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\), there are three cases: t is either a \(\varSigma _{\textsf {LRA} }\)-variable, or a formula, or a non-variable term of sort \(\textsf {Q}\). If t is a \(\varSigma _{\textsf {LRA} }\)-variable, then \({\mathcal {M}}(t) = {\mathfrak {c}}^{\mathcal {M}}\) by construction of \({\mathcal {M}}\). Otherwise, J assigns values to all \(\textsf {Q}\)-sorted subterms of t by (†). If t is a formula and \({\mathcal {M}}(t) \ne {\mathfrak {c}}^{\mathcal {M}}\), then \({\mathcal {I}}_{\textsf {LRA} }\) can expand J with an evaluation inference deriving \(\overline{t{\leftarrow }_{{}}{\mathfrak {c}}}\). If t is a non-variable term of sort \(\textsf {Q}\) and \({\mathcal {M}}(t) \ne {\mathfrak {c}}^{\mathcal {M}}\), then \({\mathcal {I}}_{\textsf {LRA} }\) can expand J with an evaluation inference deriving \({t{\,\not \simeq _{\textsf {Q}}\,}t}\). Both conclusions contradict the hypothesis that \({\mathcal {I}}_{\textsf {LRA} }\) cannot expand J, and therefore \({\mathcal {M}}(t) = {\mathfrak {c}}^{\mathcal {M}}\) holds. For Part (ii) of Definition 5, \(\textsf {Q}^{\mathcal {M}}\) is countably infinite. If \(\textsf {Q}^{{\mathcal {M}}_1}\) is countably infinite, we are done. Otherwise, \(|\textsf {Q}^{{\mathcal {M}}_1}|\) is some larger infinite cardinality: \(|\textsf {Q}^{{\mathcal {M}}_1}| > |\textsf {Q}^{\mathcal {M}}|\). Since \(\varSigma _{\textsf {LRA} }^+\) is countable, by the Löwenheim-Skolem theorem, there exists another \({\textsf {LRA} ^+}[{\mathcal {V}}_{}]\)-model \({\mathcal {M}}^\prime \) such that \(|\textsf {Q}^{{\mathcal {M}}^\prime }| = |\textsf {Q}^{{\mathcal {M}}_1}|\) and \({\mathcal {M}}^\prime \) agrees with \({\mathcal {M}}\) on everything else. For Part (iii) of Definition 5, we observe that \(J\subseteq J_{{\mathcal {T}}_1}\) by the definition of theory view, since J is an \(\textsf {LRA} \)-assignment and \({\mathcal {T}}_1\) has the sorts of \(\textsf {LRA} \), so that \(\textsf {LRA} \)-values are also \({\mathcal {T}}_1\)-values. Thus, \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\) implies \({\mathcal {M}}_1\models J\). For all \(t,t^\prime \in G_{\textsf {prop} }(J)\), \({\mathcal {M}}_1\models J\) and \({\mathcal {M}}\models J\) suffice for \({\mathcal {M}}(t)={\mathcal {M}}(t^\prime )\) if and only if \({\mathcal {M}}_1(t)={\mathcal {M}}_1(t^\prime )\). For all \(t,t^\prime \in G_{\textsf {Q}}(J)\), J assigns a truth value to \(t{\,\simeq _{\textsf {Q}}\,}t^\prime \), because if this were not the case, J could be expanded by an equality inference, since J gives values to t and \(t^\prime \) by (†). Thus, \({\mathcal {M}}_1\models J\) and \({\mathcal {M}}\models J\) imply \({\mathcal {M}}(t)={\mathcal {M}}(t^\prime )\) if and only if \((t{\,\simeq _{\textsf {Q}}\,}t^\prime )\in J\) if and only if \({\mathcal {M}}_1(t)={\mathcal {M}}_1(t^\prime )\).
\(\square \)
A module \({\mathcal {I}}\) is unit-constraint complete [35] for sort s of its theory \({\mathcal {T}}\), if for all trails \(\varGamma \) and unassigned variables x of sort s for which \(\varGamma \) contains a unit constraint, module \({\mathcal {I}}\) offers either an acceptable assignment \(x{\leftarrow }_{{}}{\mathfrak {c}}\) or an inference revealing a conflict. The above results show that \({\mathcal {I}}_{\textsf {LRA} }\) is unit-constraint complete for \(\textsf {Q}\). In general, unit-constraint completeness is subsumed by the CDSAT completeness requirements on theory modules.
4.5 Generic Theories: Stable Infiniteness and Beyond
We consider first a generic theory \({{\mathcal {T}}}\) with signature \(\varSigma =(S,F)\) that can be part of a combination by equality sharing (e.g., [42, 48, 49]): (i) there exists a decision procedure for the \({{\mathcal {T}}}\)-satisfiability of conjunctions, or, equivalently, sets of \({{\mathcal {T}}}\)-literals; and (ii) \({{\mathcal {T}}}\) is stably infinite (every \({{\mathcal {T}}}\)-satisfiable \(\varSigma \)-formula has a \({{\mathcal {T}}}\)-model with countably infinite domains for all sorts in \(S\setminus \{\textsf {prop} \}\)). In equality sharing the decision procedures cooperate by exchanging equalities between shared variables toward building an arrangement, namely a satisfiable set of sorted equalities and disequalities telling whether any two variables of the same sort are equal (e.g., [9, Sect. 3] for more background). CDSAT handles \({{\mathcal {T}}}\) with a black-box theory module \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\). The extension \({{\mathcal {T}}}^+\) either is trivial or adds a countably infinite set of values for each sort \(s{\in } S{\setminus }\{\textsf {prop} \}\) and no axioms. Module \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) includes the equality inference rules and a black-box inference rule
where \(l_1,\ldots ,l_m\) are \(\varSigma \)-formulæ (\(\varSigma \)-atoms as \(\varSigma \) has no connectives). A black-box inference \(J\vdash _{\mathcal {T}} \bot \) applies if the set of literals defined by the Boolean assignment J, namely \(C_J = \{l\ \vert \ (l{\leftarrow }_{{}}\textsf {true}) \in J\}\cup \{\lnot l\ \vert \ (l{\leftarrow }_{{}}\textsf {false}) \in J\}\), is found \({\mathcal {T}}\)-unsatisfiable by the \({{\mathcal {T}}}\)-satisfiability procedure. If \({{\mathcal {T}}}^+\) is non-trivial, the only rules of \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) that may use first-order \({\mathcal {T}}\)-assignments are the equality inference rules, and \({{\mathcal {T}}}\)-values act as labels of congruence classes of terms. The local basis only adds \(\top \): for all sets X of terms, \(\textsf {basis} _{\mathcal {T}}(X) = X\cup \{\top \}\). Indeed, in equality sharing, no new terms introduced by non-trivial inferences are shared.
Theorem 6
Module \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) is leading-theory-complete for all leading theories whose models interpret all sorts other than \(\textsf {prop} \) as countably infinite sets.
Proof
Let J be a plausible \({{\mathcal {T}}}\)-assignment that \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) cannot expand. We show that J is leading-theory-compatible with \({{\mathcal {T}}}\) sharing G(J) (see Definition 5). Let \({\mathcal {T}}_{1}\) be a leading theory satisfying the hypothesis, \(\varSigma _{1}\) its signature, \({\mathcal {T}}_{1}^{+}\) its extension, and \({\mathcal {M}}_1\) any \({{\mathcal {T}}_{1}^{+}}[{\mathcal {V}}_{1}]\)-model such that  and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). We distinguish two cases depending on the choice of \({{\mathcal {T}}}^+\).
and \({\mathcal {M}}_1 \models J_{{\mathcal {T}}_{1}}\). We distinguish two cases depending on the choice of \({{\mathcal {T}}}^+\).
-
1.
Trivial \({{\mathcal {T}}}^+\): all terms \(l\in G_\textsf {prop} (J)\) including all equalities \(t{\,\simeq _{s}\,}u\) for \(t,u\in G_s(J)\) of sort \(s\in S\setminus \{\textsf {prop} \}\) are relevant to \({{\mathcal {T}}}\), so that J assigns them values by Part (2) of Lemma 1 (\(\dag \)), and
 by Corollary 1. \(C_J\) is \({{\mathcal {T}}}\)-satisfiable, because otherwise \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) could expand J with a black-box inference. Thus, there exists a \({\mathcal {T}}\)-model \({{\mathcal {M}}}^\prime \) of \(C_J\). Since \({{\mathcal {T}}}^+\) is trivial, it suffices to interpret the Boolean values as themselves to get from \({{\mathcal {M}}}^\prime \) a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\), with
by Corollary 1. \(C_J\) is \({{\mathcal {T}}}\)-satisfiable, because otherwise \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) could expand J with a black-box inference. Thus, there exists a \({\mathcal {T}}\)-model \({{\mathcal {M}}}^\prime \) of \(C_J\). Since \({{\mathcal {T}}}^+\) is trivial, it suffices to interpret the Boolean values as themselves to get from \({{\mathcal {M}}}^\prime \) a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\), with  , such that \({\mathcal {M}} \models J\), fulfilling Part (i) of Definition 5. For Part (ii), since \({\mathcal {T}}\) is stably infinite, we let \({\mathcal {M}}\) interpret every sort in \(S\setminus \{\textsf {prop} \}\) as a countably infinite set, thus agreeing with \({\mathcal {M}}_1\). For Part (iii), \(J\subseteq J_{{\mathcal {T}}_1}\) by definition of theory view, so that \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\) implies \({\mathcal {M}}_1\models J\). For all terms \(t,u\in G_\textsf {prop} (J)\), J gives them values by (\(\dag \)), \({\mathcal {M}}(t)={\mathcal {M}}(u)\) if and only if \(\{t{\leftarrow }_{{}}{\mathfrak {b}},\ u{\leftarrow }_{{}}{\mathfrak {b}}\}\subseteq J\) since \({\mathcal {M}}\models J\), and \({\mathcal {M}}_1(t)={\mathcal {M}}_1(u)\) if and only if \(\{t{\leftarrow }_{{}}{\mathfrak {b}},\ u{\leftarrow }_{{}}{\mathfrak {b}}\}\subseteq J\) since \({\mathcal {M}}_1\models J\), so that \({\mathcal {M}}\) and \({\mathcal {M}}_1\) agree. For all terms \(t,u\in G_s(J)\) with \(s\in S\setminus \{\textsf {prop} \}\), J gives a value to \(t{\,\simeq _{s}\,}u\) by (\(\dag \)), \({\mathcal {M}}(t)={\mathcal {M}}(u)\) if and only if \((t{\,\simeq _{s}\,}u)\in J\) since \({\mathcal {M}}\models J\), \({\mathcal {M}}_1(t)={\mathcal {M}}_1(u)\) if and only if \((t{\,\simeq _{s}\,}u)\in J\) since \({\mathcal {M}}_1\models J\), so that \({\mathcal {M}}\) and \(M_1\) agree.
, such that \({\mathcal {M}} \models J\), fulfilling Part (i) of Definition 5. For Part (ii), since \({\mathcal {T}}\) is stably infinite, we let \({\mathcal {M}}\) interpret every sort in \(S\setminus \{\textsf {prop} \}\) as a countably infinite set, thus agreeing with \({\mathcal {M}}_1\). For Part (iii), \(J\subseteq J_{{\mathcal {T}}_1}\) by definition of theory view, so that \({\mathcal {M}}_1\models J_{{\mathcal {T}}_1}\) implies \({\mathcal {M}}_1\models J\). For all terms \(t,u\in G_\textsf {prop} (J)\), J gives them values by (\(\dag \)), \({\mathcal {M}}(t)={\mathcal {M}}(u)\) if and only if \(\{t{\leftarrow }_{{}}{\mathfrak {b}},\ u{\leftarrow }_{{}}{\mathfrak {b}}\}\subseteq J\) since \({\mathcal {M}}\models J\), and \({\mathcal {M}}_1(t)={\mathcal {M}}_1(u)\) if and only if \(\{t{\leftarrow }_{{}}{\mathfrak {b}},\ u{\leftarrow }_{{}}{\mathfrak {b}}\}\subseteq J\) since \({\mathcal {M}}_1\models J\), so that \({\mathcal {M}}\) and \({\mathcal {M}}_1\) agree. For all terms \(t,u\in G_s(J)\) with \(s\in S\setminus \{\textsf {prop} \}\), J gives a value to \(t{\,\simeq _{s}\,}u\) by (\(\dag \)), \({\mathcal {M}}(t)={\mathcal {M}}(u)\) if and only if \((t{\,\simeq _{s}\,}u)\in J\) since \({\mathcal {M}}\models J\), \({\mathcal {M}}_1(t)={\mathcal {M}}_1(u)\) if and only if \((t{\,\simeq _{s}\,}u)\in J\) since \({\mathcal {M}}_1\models J\), so that \({\mathcal {M}}\) and \(M_1\) agree. -
2.
Non-trivial \({{\mathcal {T}}}^+\): by the same reasoning in the proof of Theorem 3, assignment J gives values to all terms in G(J) (†), and
 by Corollary 1. Also, J assigns a truth value to \(t{\,\simeq _{s}\,}u\) for all \(t,u\in G_s(J)\) of sort \(s\in S\setminus \{\textsf {prop} \}\) (‡), because otherwise \({\mathcal {I}}_{}\) could expand J with an equality inference, since J assigns values to t and u by (†) and \((t{\,\simeq _{s}\,}u)\in \textsf {basis} _{\mathcal {T}}(J)\) by closedness of the local basis. As in Case (1), the set \(C_J\) has a \({\mathcal {T}}\)-model \({{\mathcal {M}}}^\prime \). We show how to get from \({{\mathcal {M}}}^\prime \) a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\), with
by Corollary 1. Also, J assigns a truth value to \(t{\,\simeq _{s}\,}u\) for all \(t,u\in G_s(J)\) of sort \(s\in S\setminus \{\textsf {prop} \}\) (‡), because otherwise \({\mathcal {I}}_{}\) could expand J with an equality inference, since J assigns values to t and u by (†) and \((t{\,\simeq _{s}\,}u)\in \textsf {basis} _{\mathcal {T}}(J)\) by closedness of the local basis. As in Case (1), the set \(C_J\) has a \({\mathcal {T}}\)-model \({{\mathcal {M}}}^\prime \). We show how to get from \({{\mathcal {M}}}^\prime \) a \({{\mathcal {T}}^+}[{\mathcal {V}}^{}]\)-model \({\mathcal {M}}\), with  , such that \({\mathcal {M}} \models J\). Let \({\mathcal {M}}\) interpret the sorts in S, the symbols in F, and the \(\varSigma \)-variables as \({{\mathcal {M}}}^\prime \) does. The Boolean values are interpreted as themselves. For a non-Boolean \({\mathcal {T}}^+\)-value \({\mathfrak {c}}\) of sort s, either it is never used in J or there is some assignment \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\). In the first case we let \({\mathcal {M}}\) interpret \({\mathfrak {c}}\) arbitrarily in \(s^{\mathcal {M}}\). In the second case t appears in equalities in J by (‡), hence t appears in \(C_J\), and we define \({\mathfrak {c}}^{\mathcal {M}}\) as \({{\mathcal {M}}}^\prime (t)\). The interpretation of \({\mathcal {T}}^+\)-values is well-defined, because if \(\{t_1{\leftarrow }_{{}}{\mathfrak {c}},\ t_2{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq J\), then \((t_1{\,\simeq _{s}\,}t_2)\in J\) by (‡) and \((t_1{\,\simeq _{s}\,}t_2)\in C_J\), so that \({{\mathcal {M}}}^\prime (t_1) = {{\mathcal {M}}}^\prime (t_2)\). By construction, \({\mathcal {M}} \models J\), and the rest of the proof is the same as in Case (1). \(\square \)
, such that \({\mathcal {M}} \models J\). Let \({\mathcal {M}}\) interpret the sorts in S, the symbols in F, and the \(\varSigma \)-variables as \({{\mathcal {M}}}^\prime \) does. The Boolean values are interpreted as themselves. For a non-Boolean \({\mathcal {T}}^+\)-value \({\mathfrak {c}}\) of sort s, either it is never used in J or there is some assignment \((t{\leftarrow }_{{}}{\mathfrak {c}})\in J\). In the first case we let \({\mathcal {M}}\) interpret \({\mathfrak {c}}\) arbitrarily in \(s^{\mathcal {M}}\). In the second case t appears in equalities in J by (‡), hence t appears in \(C_J\), and we define \({\mathfrak {c}}^{\mathcal {M}}\) as \({{\mathcal {M}}}^\prime (t)\). The interpretation of \({\mathcal {T}}^+\)-values is well-defined, because if \(\{t_1{\leftarrow }_{{}}{\mathfrak {c}},\ t_2{\leftarrow }_{{}}{\mathfrak {c}}\}\subseteq J\), then \((t_1{\,\simeq _{s}\,}t_2)\in J\) by (‡) and \((t_1{\,\simeq _{s}\,}t_2)\in C_J\), so that \({{\mathcal {M}}}^\prime (t_1) = {{\mathcal {M}}}^\prime (t_2)\). By construction, \({\mathcal {M}} \models J\), and the rest of the proof is the same as in Case (1). \(\square \)
This theorem shows that the equality-sharing method is a special case of the CDSAT framework. Indeed, when the \({{\mathcal {T}}}\)-module cannot expand a \({{\mathcal {T}}}\)-assignment J (the \({{\mathcal {T}}}\)-view of the trail) it follows that: (1) there exists a \({{\mathcal {T}}}\)-model endorsing J, and (2) J determines the truth value of all equalities, hence it defines an arrangement of shared variables. If this is the case for all theories in \({\mathcal {T}}_{\infty }\), an endorsing \({\mathcal {T}}_{\infty }\)-model also exists, by the CDSAT completeness theorem [11, Theorem 4]. This remark applies also to model-based theory combination [23], which is a way to implement equality sharing and relies on equality sharing for completeness. Theorem 6 still holds if the black-box rule is restricted to apply only to \({{\mathcal {T}}}\)-unsatisfiable cores or minimal \({{\mathcal {T}}}\)-unsatisfiable assignments, where it suffices to remove an element to make the assignment \({{\mathcal {T}}}\)-satisfiable.
We describe next how CDSAT also handles a generic non-stably infinite theory \({{\mathcal {T}}}\) with signature \(\varSigma = (S,F)\). Suppose \({{\mathcal {T}}}\) is stably infinite for the sorts in \(S\setminus \{\textsf {prop} ,s_1,\ldots ,s_k\}\), whereas all \({\mathcal {T}}\)-models interpret sorts \(s_1,\ldots ,s_k\) as sets of fixed finite cardinalities \(m_1,\ldots ,m_k\), respectively. The proof of Theorem 6 can be adapted to prove the following.
Theorem 7
Module \({\mathcal {I}}_{{\mathcal {T}}}^{\textsf {bb} }\) is leading-theory-complete for all leading theories whose models interpret all sorts in \(S\setminus \{\textsf {prop} ,s_1,\ldots ,s_k\}\) as countably infinite sets and \(s_1,\ldots ,s_k\) as sets of cardinality \(m_1,\ldots ,m_k\), respectively.
For example, \({{\mathcal {T}}}\) could be a theory of bitvectors of different lengths, where for all l, \(1\le l\le k\), \(s_l\) is the sort bv[l] of bitvectors of length l and \(m_l=2^l\). Theorem 7 does not need k to be finite: for bitvectors, l could range over all nonzero natural numbers. Thus, the cardinality constraints in \({{\mathcal {T}}}\) affect the choice of the leading theory \({{\mathcal {T}}}_1\), for which \(S_1 = S_\infty \). If the leading theory can be picked so that all theory modules involved in the combination are leading-theory complete, the cardinality constraints in \({\mathcal {T}}\) are imposed to the other theories sharing \(\{s_1,\ldots ,s_k\}\) or a subset thereof. More generally, different theories in the union \({\mathcal {T}}_{\infty }\) may pose cardinality requirements on a shared sort s, and the leading theory \({{\mathcal {T}}}_1\) acts as an aggregator of such requirements (see [11, Examples 9 and 10]). Once chosen, the leading theory \({{\mathcal {T}}}_1\) needs a theory module \({\mathcal {I}}_{1}\) that can be used in CDSAT and that enforces the cardinality constraints.
We illustrate this point for an at-most-m cardinality constraint on sort s, given an integer \(m{>}0\). The constraint can be expressed by the sentence \(\forall x_0,\ldots ,\forall x_m.\ \bigvee _{0\le i\ne k\le m} x_i {\,\simeq _{s}\,} x_k\), for \(x_0,\ldots , x_m\) distinct variables of sort s, which could be an axiom or a theorem of one of the non-leading theories in \({\mathcal {T}}_{\infty }\), or an axiom of the leading theory \({{\mathcal {T}}}_1\), resulting from aggregating cardinality constraints from non-leading theories in \({\mathcal {T}}_{\infty }\). For instance, if \({\mathcal {T}}_{2}\) entails the at-most-\(m_1\) cardinality constraint on s and \({\mathcal {T}}_{3}\) entails the at-most-\(m_2\) cardinality constraint on s, the leading theory \({{\mathcal {T}}}_1\) is picked so that its models satisfy the at-most-\(\textsf {min}(m_1,m_2)\) cardinality constraint. Then, theory module \({\mathcal {I}}_{1}\) for \({{\mathcal {T}}}_1\) includes the at-most-m inference rule:
where \(u_0,\ldots u_m\) are any \(m+1\) distinct terms of sort s. If \({{\mathcal {T}}}_1^+\) is non-trivial with values for sort s, the at-most-m inference rule can be abbreviated as \(u_0{\leftarrow }_{{}}{\mathfrak {c}}_0,\ldots , u_m{\leftarrow }_{{}}{\mathfrak {c}}_m \vdash _{{{\mathcal {T}}}_1} \bot ,\) for \({\mathfrak {c}}_0,\ldots , {\mathfrak {c}}_m\) any distinct \(m{+}1\) \({{\mathcal {T}}}_1\)-values of sort s. If both \({{\mathcal {T}}}\) and the leading theory \({{\mathcal {T}}}_1\) have non-trivial extensions, \({{\mathcal {T}}}^+\) and \({{\mathcal {T}}}_1^+\) use different sets of constant symbols to name s-sorted elements, and the construction of a \({\mathcal {T}}_{\infty }\)-model for an assignment J that cannot be expanded establishes a bijection between the s-sorted \({{\mathcal {T}}}\)-values that appear in J and the s-sorted \({{\mathcal {T}}}_1\)-values that appear in J (see [11, Sect. 9.3, Theorem 4]). A module with an at-most-m inference rule satisfies a lemma that complements Lemma 1.
Lemma 4
If a \({\mathcal {T}}\)-module \({\mathcal {I}}_{}\) with the at-most-m inference rule for sort s cannot expand a plausible \({{\mathcal {T}}}\)-assignment J, the relation \({\simeq _{s}^{J}}\) is an equivalence with at most m equivalence classes.
Proof
By definition of \({\simeq _{s}^{J}}\) (see the text in Sect. 4 preceding Lemma 1), for all \(t_1, t_2 \in G_s(J)\), \({t_1} {\simeq _{s}^{J}} {t_2}\) if and only if \((t_1{\,\simeq _{s}\,}t_2)\in J\). By Part (1) of Lemma 1 the relation \({\simeq _{s}^{J}}\) is an equivalence. If \({\simeq _{s}^{J}}\) had \(m {+} 1\) equivalence classes, J would contain an instance of the premises of the at-most-m inference rule for sort s, and \({\mathcal {I}}_{}\) could expand J, a contradiction. \(\square \)
This lemma suffices to obtain the following theorem that says how to build a leading theory and its module to enforce the at-most cardinality constraint coming from the theories in \({\mathcal {T}}_{\infty }\). Given a theory \({\mathcal {T}}_{1}\), let \({\mathcal {T}}_{1}^{s{\le }m}\) be \({\mathcal {T}}_{1}\) plus the at-most-m cardinality constraint on sort s as additional axiom. Given a theory module \({\mathcal {I}}_{}\), let \({\mathcal {I}}_{}^{s{\le }m}\) be \({\mathcal {I}}_{}\) plus the at-most-m inference rule on sort s.
Theorem 8
If \({\mathcal {I}}_{1}\) is sound and complete for theory \({\mathcal {T}}_{1}\), then \({\mathcal {I}}_{1}^{s{\le }m}\) is sound and complete for theory \({\mathcal {T}}_{1}^{s{\le }m}\).
Once the enforcement of cardinality constraints is handled by the leading theory module, it is not necessary to handle them in other modules.
Theorem 9
Given a theory \({\mathcal {T}}_{}\) with signature \(\varSigma =(S,F)\) and a leading theory \({\mathcal {T}}_{1}\) that entails the at-most-m constraint on sort \(s\in S\), a \({\mathcal {T}}_{}\)-module \({\mathcal {I}}_{}\) is leading-theory complete if and only if \({\mathcal {I}}_{}^{s{\le }m}\) is leading-theory complete.
Proof
The (\(\Rightarrow \)) direction holds by Lemma 2. The (\(\Leftarrow \)) direction holds because whenever the at-most-m inference rule of \({\mathcal {I}}_{}^{s{\le }m}\) can be applied to expand an assignment J, there can be no \({\mathcal {T}}_{1}\)-model endorsing \(J_{{\mathcal {T}}_1}\) so that leading-theory compatibility is vacuously true. \(\square \)
In summary, the completeness of a leading theory module with the appropriate at-most rules ensures that cardinality constraints on shared sorts are satisfied; and all theories sharing those sorts concur on their cardinalities by leading-theory-completeness of their modules.
5 Global Basis Construction
Termination of CDSAT requires the global basis \({\mathcal {B}}\) to be finite and closed, and completeness requires it to be stable (see Theorem 1). The meaning of stability of \({\mathcal {B}}\) (for all k, \(1\,{\le }\,k\,{\le }\,n\), \(\textsf {basis} _{k}({\mathcal {B}})\subseteq {\mathcal {B}}\)) is that the global basis “contains” the local bases \(\textsf {basis} _{1},\ldots ,\textsf {basis} _{n}\) associated to the theory modules \({\mathcal {I}}_{1},\ldots ,{\mathcal {I}}_{n}\) for theories \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\): for all sets X of terms, if \(X\subseteq {\mathcal {B}}\) then for all k, \(1\,{\le }\,k\,{\le }\,n\), \(\textsf {basis} _{k}(X)\subseteq \textsf {basis} _{k}({\mathcal {B}})\) by monotonicity (see Definition 2) and \(\textsf {basis} _{k}(X)\subseteq {\mathcal {B}}\) by stability. Thus, for all input assignments H, if H is in \({\mathcal {B}}\), or, equivalently, \(G(H)\subseteq {\mathcal {B}}\), no \({\mathcal {I}}_{k}\)-inference can take us outside of \({\mathcal {B}}\). In this section we show how to build a stable global basis from local ones.
The existence of a finite stable global basis does not necessarily follow from that of local bases. Given input assignment H and \(X_0{=}G(H)\), a module \({\mathcal {I}}_{k}\) may introduce a term \(u_0\) in \(Y_0{=}\textsf {basis} _{k}(X_0)\), which prompts \({\mathcal {I}}_{j}\) to introduce a term \(t_1\) in \(X_1{=}\textsf {basis} _{j}(\textsf {basis} _{k}(X_0))\), which in turns prompts \({\mathcal {I}}_{k}\) to introduce a term \(u_1\) in \(Y_1{=}\textsf {basis} _{k}(\textsf {basis} _{j}(\textsf {basis} _{k}(X_0)))\), and so on. In other words, even if all these sets are finite, \(\bigcup _{m\ge 0}X_m\) may be infinite, where \(X_{m+1}{=}\textsf {basis} _{j}(\textsf {basis} _{k}(X_m))\). The aim is to find sufficient conditions on local bases to avoid such cyclic behavior. Since the problem arises from a cyclic alternation, the point is whether it is possible to permute local bases, relating \(\textsf {basis} _{j}(\textsf {basis} _{k}(X))\) and \(\textsf {basis} _{k}(\textsf {basis} _{j}(X))\). To this end, we introduce the following notions.
Definition 7
(Production and consumption of a sort) Let \(\textsf {basis} _{}\) be a basis for theory \({\mathcal {T}}_{}\) with signature \(\varSigma _{}=(S,F)\). For all sorts \(s\in S\), \(\textsf {basis} _{}\) produces sort s if for some closed set of terms X and term t of sort s, \(t\in \textsf {basis} _{}(X) \setminus X\); \(\textsf {basis} _{}\) consumes sort s if for some closed set of terms X and term t of sort s, \(\textsf {basis} _{}(X\uplus \{t\}) \not \subseteq \ \Downarrow (\textsf {basis} _{}(X)\uplus \{t\})\), where t is either a \(\varSigma _{}\)-variable or an equality whose strict subterms are in X.
In plain words, \(\textsf {basis} _{}\) produces sort s if its application to a closed set X yields some term t of sort s which is not in X and does not arise from the closure of X, since X is already closed; \(\textsf {basis} _{}\) consumes sort s if its application to \(X\uplus \{t\}\), where t is a term of sort s, yields some term u which is not in \(\Downarrow (\textsf {basis} _{}(X)\uplus \{t\})\), where \(\textsf {basis} _{}\) is applied to X only. The restrictions on what term t can be depend on what suffices for forthcoming Lemma 5.
Example 9
Most local bases produce \(\textsf {prop} \), as they add \(\top \); \(\textsf {basis} _{\textsf {Bool} }\) produces and consumes \(\textsf {prop} \), as it forms clauses for lemma learning; \(\textsf {basis} _{\textsf {EUF} }\) only produces \(\textsf {prop} \) by adding equalities and does not consume any sort. For \(\textsf {Arr} \), \(\textsf {basis} _{\textsf {Arr} }\) produces all sorts in \(\varSigma _{\textsf {Arr} }\) and consumes all array sorts: given array terms t and u of sort  , \(\textsf {basis} _{\textsf {Arr} }\) consumes
, \(\textsf {basis} _{\textsf {Arr} }\) consumes  and produces sorts I and V, by introducing terms \(\textsf {diff}_{}(t,u)\), \({t}[{\textsf {diff}_{}(t,u)}]\), and \({u}[{\textsf {diff}_{}(t,u)}]\); it produces also array sorts, because arrays can be values or indices, as there can be arrays of arrays and array-indexed arrays. For \(\textsf {LRA} \), \(\textsf {basis} _{\textsf {LRA} }\) produces sorts \(\textsf {prop} \) and \(\textsf {Q}\) and only consumes \(\textsf {Q}\), where \(\textsf {Q}\) is produced when polynomials are reduced to normal form. For example, the FM-resolution \(y{-}x {<} 0,\ 3{\cdot }x {<} 5\vdash _{\textsf {LRA} } y {<} \frac{5}{3}\) produces \(\textsf {prop} \) by introducing \(y {<} \frac{5}{3}\) and \(\textsf {Q}\) by introducing \(\frac{5}{3}\). The bases of \({\mathcal {I}}_{\textsf {bb} }\) and \({\mathcal {I}}_{\textsf {bb} }^m\) only produce \(\textsf {prop} \) and do not consume any sort.
and produces sorts I and V, by introducing terms \(\textsf {diff}_{}(t,u)\), \({t}[{\textsf {diff}_{}(t,u)}]\), and \({u}[{\textsf {diff}_{}(t,u)}]\); it produces also array sorts, because arrays can be values or indices, as there can be arrays of arrays and array-indexed arrays. For \(\textsf {LRA} \), \(\textsf {basis} _{\textsf {LRA} }\) produces sorts \(\textsf {prop} \) and \(\textsf {Q}\) and only consumes \(\textsf {Q}\), where \(\textsf {Q}\) is produced when polynomials are reduced to normal form. For example, the FM-resolution \(y{-}x {<} 0,\ 3{\cdot }x {<} 5\vdash _{\textsf {LRA} } y {<} \frac{5}{3}\) produces \(\textsf {prop} \) by introducing \(y {<} \frac{5}{3}\) and \(\textsf {Q}\) by introducing \(\frac{5}{3}\). The bases of \({\mathcal {I}}_{\textsf {bb} }\) and \({\mathcal {I}}_{\textsf {bb} }^m\) only produce \(\textsf {prop} \) and do not consume any sort.
The next move is to define a theory ordering on the theories that captures producer-consumer dependencies between their local bases: for all k, j such that \(1\le k\ne j\le n\), let \({\mathcal {T}}_{k}\prec {\mathcal {T}}_{j}\) if there exists a sort s that \(\textsf {basis} _{k}\) produces and \(\textsf {basis} _{j}\) consumes. By the contrapositive, if \({\mathcal {T}}_{k}\not \prec {\mathcal {T}}_{j}\), then \(\textsf {basis} _{j}\) is independent of \(\textsf {basis} _{k}\), hence \(\textsf {basis} _{j}(\textsf {basis} _{k}(X))\subseteq \textsf {basis} _{k}(\textsf {basis} _{j}(X))\) for all X. Intuitively, if \(\prec \) is acyclic, the cyclic behavior described above cannot happen. Formally, if \(\prec \) is acyclic, the listing of the theories and a basis for \({\mathcal {T}}_{\infty }\) can be defined accordingly: for all k and j, \(1{\le } k {<} j{\le } n\), if \({\mathcal {T}}_{k}\prec {\mathcal {T}}_{j}\) then \(k < j\), and for all sets X of terms, \(\textsf {basis} _{\infty }(X) = \textsf {basis} _{n}(\ldots \textsf {basis} _{1}(X))\). The next lemma shows that under these hypotheses local bases can be permuted.
Lemma 5
If \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\) are disjoint theories with an acyclic ordering \(\prec \), then for all k and j, \(1{\le } k {<} j{\le } n\), and for all finite closed sets X of terms: (1) For all \(\unlhd \)-closed sets Y of terms such that \(X {\subseteq } Y {\subseteq } \textsf {basis} _{j}(X)\), it holds that \(\textsf {basis} _{k}(Y)\ \subseteq \ \Downarrow (\textsf {basis} _{k}(X)\cup Y)\); and (2) \(\textsf {basis} _{k}(\textsf {basis} _{j}(X))\subseteq \textsf {basis} _{j}(\textsf {basis} _{k}(X))\).
Proof
First, \(k < j\) implies \(j \not < k\), hence \({\mathcal {T}}_{j}\not \prec {\mathcal {T}}_{k}\), so that no sort produced by \(\textsf {basis} _{j}\) is consumed by \(\textsf {basis} _{k}\).
-
1.
The proof is by induction on the (finite) cardinality of \(Y\backslash X\), denoted \(\vert Y\backslash X\vert \). For the base case, if \(\vert Y\backslash X\vert = 0\) (i.e., \(Y=X\)), the claim is trivially true. For the induction hypothesis, let the claim be true for any such Y with \(\vert Y\backslash X\vert = q \ge 0\). For the induction step, let \(\vert Y\backslash X\vert = q+1\) and t be a term of largest size (symbol count) in \(Y\backslash X\). By hypothesis, t is in \(\textsf {basis} _{j}(X)\). Since the theories are disjoint, t is either \(\varSigma _{j}\)-foreign, or \(\varSigma _{k}\)-foreign, or an equality. By the last property of a basis in Definition 2, t being in \({\mathcal {V}}_{\infty }\) is the only way that it can be \(\varSigma _{j}\)-foreign, in which case it is also \(\varSigma _{k}\)-foreign. Therefore, it is either \(\varSigma _{k}\)-foreign or an equality. By \(\unlhd \)-closedness of Y, all strict subterms of t are in \(Y\backslash \{t\}\), hence in \(\Downarrow (Y\backslash \{t\})\). Since \(t\in (\textsf {basis} _{j}(X) \setminus X)\), the sort s of t is produced by \(\textsf {basis} _{j}\). Last, \(\textsf {basis} _{k}\) does not consume s, because \(\textsf {basis} _{k}\) does not depend on \(\textsf {basis} _{j}\), as \(k < j\) by hypothesis. By Definition 7 applied to \(\textsf {basis} _{k}\) and the closed set \(\Downarrow (Y\backslash \{t\})\), we get
$$\begin{aligned} \textsf {basis} _{k}(\Downarrow (Y\backslash \{t\})\cup \{t\})\quad \subseteq \quad \Downarrow (\textsf {basis} _{k}(\Downarrow (Y\backslash \{t\}))\cup \{t\})\ (\dag ). \end{aligned}$$Next, we observe that \(X\subseteq {(Y\backslash \{t\})}\), since \(X\subseteq Y\) and \(t\in Y \setminus X\), and \(Y\backslash \{t\}\) is \(\unlhd \)-closed: indeed, if it were \(t\lhd u\) for some term \(u \in Y\), then either \(u\in X\), in which case \(t\in X\), because X is closed, or \(u\in Y\backslash X\), in which case t would not be a term of greatest size in \(Y\backslash X\). Therefore, we can apply the induction hypothesis to \(Y\backslash \{t\}\) and get
$$\begin{aligned} \textsf {basis} _{k}(Y\backslash \{t\})\ \subseteq \ \Downarrow (\textsf {basis} _{k}(X)\cup (Y\backslash \{t\}))\ (\ddag ). \end{aligned}$$Then the claim is established as follows:
$$\begin{aligned} \begin{array}{llll} \textsf {basis} _{k}(Y) &{} = &{} \textsf {basis} _{k}((Y\backslash \{t\})\cup \{t\})\\ &{}\subseteq &{} \textsf {basis} _{k}(\Downarrow (Y\backslash \{t\})\cup \{t\}) &{}\text{ by } \text{ monotonicity } \text{ of } \textsf {basis} _{k}\\ &{}\subseteq &{} \Downarrow (\textsf {basis} _{k}(\Downarrow (Y\backslash \{t\}))\cup \{t\}) &{}\text{ by } (\dag )\\ &{} = &{} \Downarrow (\textsf {basis} _{k}(Y\backslash \{t\})\cup \{t\}) &{}\text{ by } \text{ closedness } \text{ of } \textsf {basis} _{k}\\ &{}\subseteq &{} \Downarrow (\Downarrow (\textsf {basis} _{k}(X)\cup (Y\backslash \{t\}))\cup \{t\}) &{}\text{ by } (\ddag )\\ &{}\subseteq &{} \Downarrow \Downarrow (\textsf {basis} _{k}(X)\cup (Y\backslash \{t\})\cup \{t\})\\ &{}= &{} \Downarrow (\textsf {basis} _{k}(X)\cup Y) &{}\text{ by } \text{ idempotence } \text{ of } \Downarrow . \end{array} \end{aligned}$$ -
2.
The second claim is derived as follows:
$$\begin{aligned} \begin{array}{llll} \textsf {basis} _{k}(\textsf {basis} _{j}(X)) &{}\subseteq &{} \Downarrow (\textsf {basis} _{k}(X)\cup \textsf {basis} _{j}(X)) &{}\text{ by } \text{ Claim } \text{1 }\\ &{}\subseteq &{} \Downarrow (\textsf {basis} _{j}(\textsf {basis} _{k}(X))\cup \textsf {basis} _{j}(X)) &{}\text{ by } \text{ extensiveness }\\ &{}= &{} \Downarrow (\textsf {basis} _{j}(\textsf {basis} _{k}(X))) &{}\text{ as } X\subseteq \textsf {basis} _{k}(X)\\ &{}&{}\text{ and } \text{ by } \text{ monotonicity } \text{ of } \textsf {basis} _{j}&{}\\ &{}= &{} \textsf {basis} _{j}(\textsf {basis} _{k}(X)) &{}\text{ by } \text{ closedness. } \end{array} \end{aligned}$$
\(\square \)
Next, we use Lemma 5 to show that \(\textsf {basis} _{\infty }(X)\) is stable.
Lemma 6
If \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\) are disjoint theories with an acyclic ordering that defines \(\textsf {basis} _{\infty }\), then for all k, \(1\,{\le }\,k\,{\le }\,n\), \(\textsf {basis} _{k}(\textsf {basis} _{\infty }(X)) {=} \textsf {basis} _{\infty }(X)\) for all finite sets X of terms.
Proof
We prove a more general property, namely that \(\forall j\), \(1\le k\le j\le n\), we have \(\textsf {basis} _{k}(\textsf {basis} _{j}(\ldots \textsf {basis} _{1}(X))) = \textsf {basis} _{j}(\ldots \textsf {basis} _{1}(X))\). The \(\supseteq \)-direction holds by extensiveness of \(\textsf {basis} _{k}\). For the \(\subseteq \)-direction, the proof is by induction on j. For the base case, if \(j{=}k\), the claim holds by idempotence. For the induction hypothesis, let the claim be true for j. For the induction step, we prove the claim for \(j{+}1\). Let Z stand for \(\textsf {basis} _{j}(\ldots \textsf {basis} _{1}(X))\). Since \(k< j{+}1\) and Z is closed by closedness of the bases, \(\textsf {basis} _{k}(\textsf {basis} _{j+1}(Z))\subseteq \textsf {basis} _{j+1}(\textsf {basis} _{k}(Z))\) holds by Lemma 5. Then, \(\textsf {basis} _{k}(Z)\subseteq Z\) holds by induction hypothesis, and \(\textsf {basis} _{j+1}(\textsf {basis} _{k}(Z))\subseteq \textsf {basis} _{j+1}(Z)\) follows by monotonicity of \(\textsf {basis} _{j+1}\). \(\square \)
Theorem 10
Given disjoint theories \({\mathcal {T}}_{1},\ldots ,{\mathcal {T}}_{n}\) with modules \({\mathcal {I}}_{1},\ldots ,{\mathcal {I}}_{n}\) and local bases \(\textsf {basis} _{1},\ldots ,\textsf {basis} _{n}\) such that the theory ordering is acyclic, if \(\textsf {basis} _{\infty }\) is defined based on the theory ordering, then for all input assignments H, the set \({\mathcal {B}} {=} \textsf {basis} _{\infty }(G(H))\) is a finite stable global basis.
Proof
The function \(\textsf {basis} _{\infty }\) is a basis for the union theory \({\mathcal {T}}_{\infty }\) according to Definition 2, as it inherits the properties of local bases. Thus, \({\mathcal {B}}\) is finite, as G(H) is finite, and it is stable by Lemma 6. \(\square \)
For example, \(\textsf {basis} _{\textsf {Bool} }(\textsf {basis} _{{\mathcal {I}}_{}}(\textsf {basis} _{\textsf {EUF} }(\textsf {basis} _{\textsf {LRA} }(\textsf {basis} _{\textsf {Arr} }(G)(H)))))\), where \({\mathcal {I}}_{}\) is a black-box module for a generic theory \({\mathcal {T}}\), is a global basis for the union of theories \(\textsf {Bool} \), \({\mathcal {T}}\), \(\textsf {LRA} \), \(\textsf {EUF} \), and \(\textsf {Arr} \), given an input assignment H. The next section opens the part of the article devoted to proof generation in CDSAT.
6 Proof Reconstruction: Proof-Carrying CDSAT
When a derivation terminates detecting unsatisfiability, it is desirable to return a proof. Proof reconstruction is the activity of extracting a proof from the final state of the derivation, provided that the final state contains enough information. In this section we instrument CDSAT for proof reconstruction.
6.1 Theory Proofs
Because CDSAT combines theory modules, proof reconstruction in CDSAT requires that all theory modules produce proofs. Therefore, we assume that each theory module is equipped with a proof annotation system that annotates theory inferences with theory proofs:

states that module \({\mathcal {I}}_{k}\) infers L from J with theory proof \(j_k\). A theory proof from \({\mathcal {I}}_{k}\) is called \({\mathcal {T}}_{k}\)-proof. Theory proofs, hence CDSAT proofs, may refer to singleton assignments by means of identifiers. A \({\mathcal {T}}_{}\)-assignment with identifiers is a set of triples \({}^{a}{(t{\leftarrow }_{{}}{\mathfrak {c}})}\), where a is the identifier of \(t{\leftarrow }_{{}}{\mathfrak {c}}\). From now on all assignments are assignments with identifiers, the trail contains a \({\mathcal {T}}_{\infty }\)-assignment with identifiers, and the subset relation between assignments take identifiers into account. For example, \({\mathcal {I}}_{\textsf {Bool} }\)-inference (1) from Sect. 3.2 can be annotated with a theory proof denoted \(\textsf {UP}(a,\{a_1,\ldots ,a_n\})\), as follows:

where UP stands for unit propagation, and \(a_1,\ldots ,a_n\) are the identifiers of the assignments in \(H^\prime \). Annotated \({\mathcal {I}}_{\textsf {LRA} }\)-inferences include instances of Fourier-Motzkin resolution and of the evaluation rule:

Equality inferences are annotated with theory proofs as shown in Fig. 5. Assuming J is \({}^{a_1}{(t_1{\,\simeq _{}\,}u_1)},\ldots ,{}^{a_m}{(t_m{\,\simeq _{}\,}u_m)}\), an instance of annotated \({\mathcal {I}}_{\textsf {EUF} }\)-inference is:

where \(\textsf {Cong}\) stands for congruence.
If an assignment appears on the trail, its identifier in any theory proof is the same as its identifier on the trail: for a \(\textsf {Deduce}\) transition supported by a theory inference  , the assignments in J appear on the trail \(\varGamma \), and their identifiers in \(j_k\) are the same as in \(\varGamma \). Since identifiers are mere names, theory proof annotations are stable under their permutations: any permutation \(\pi \) of identifiers transforms a theory proof \(j_k\) into a theory proof \(\pi (j_k)\), such that, if
, the assignments in J appear on the trail \(\varGamma \), and their identifiers in \(j_k\) are the same as in \(\varGamma \). Since identifiers are mere names, theory proof annotations are stable under their permutations: any permutation \(\pi \) of identifiers transforms a theory proof \(j_k\) into a theory proof \(\pi (j_k)\), such that, if  then
then

For example, if  , with \(\pi (1) = 4\) and \(\pi (4) = 1\), it is also
, with \(\pi (1) = 4\) and \(\pi (4) = 1\), it is also  . The assumption that theory modules have proof annotation systems is not a restriction, as the proof annotation system can be a trivial one that uses a dummy theory proof for all theory inferences. The resulting theory proofs convey no information, which is acceptable if they are not required to offer more.
. The assumption that theory modules have proof annotation systems is not a restriction, as the proof annotation system can be a trivial one that uses a dummy theory proof for all theory inferences. The resulting theory proofs convey no information, which is acceptable if they are not required to offer more.
6.2 Proof Terms, Proof System, and Invariants for CDSAT
In order to enable CDSAT to compose theory proofs into CDSAT proofs, we will equip the CDSAT transition system with the capability of building proof terms. These proof terms keep track of soundness invariants that ensure that transitions do not change the problem, so that invariant-preserving transition rules are sound. The CDSAT soundness invariants are:
-
1.
For all justified assignments
 on the trail, \(H_0 \cup H\models A\), and
on the trail, \(H_0 \cup H\models A\), and -
2.
For all conflict states
 , \(H_0 \cup E\models \bot \),
, \(H_0 \cup E\models \bot \),
where \(H_0\) is the input, or initial, assignment. A proof term is either a deduction proof term recording why a justified assignment is on the trail to enforce (1), or a conflict proof term recording why a conflict is a conflict to enforce (2). The two kinds of proof terms are defined mutually recursively as follows.
Definition 8
(CDSAT proof terms) A CDSAT proof term is
-
Either a deduction proof term
 ,
, -
Or a conflict proof term
 , where:
, where:
(i) in, lem, cfl, and res, abbreviating initial, lemma, conflict, and resolve, respectively, are the CDSAT proof constructors; (ii) A is a singleton assignment, \(j_k\) is a \({\mathcal {T}}_{k}\)-proof for some k, \(1\,{\le }\,k\,{\le }\,n\), H is a Boolean assignment with identifiers, a is the identifier of a singleton Boolean conflicting assignment in  , and the identifier of A in \(\textsf {res}(j,{}^{a}{A}.c)\); and (iii) the dot notation means that \(\textsf {res}(j,{}^{a}{A}.c)\) binds \(a\) in \(c\) and \(\textsf {lem}(H.c)\) binds the identifiers of H in \(c\).
, and the identifier of A in \(\textsf {res}(j,{}^{a}{A}.c)\); and (iii) the dot notation means that \(\textsf {res}(j,{}^{a}{A}.c)\) binds \(a\) in \(c\) and \(\textsf {lem}(H.c)\) binds the identifiers of H in \(c\).
The CDSAT proof terms come with the CDSAT proof system in Fig. 6. Its first three rules establish the derivability of judgments of the form  . Proof term \(\textsf {in}(A)\) witnesses the fact that an initial assignment A holds. The second rule coerces a theory proof \(j_k\) into a CDSAT deduction proof term. The third rule says that, whenever there is a conflict including a Boolean assignment H, a clausal form of H is a lemma entailed by the rest of the conflict. The proof term \(\textsf {lem}(H.c)\) carries H to record which part of the conflict became a lemma. If identifiers of assignments in H occur in \(c\), such occurrences are bound in \(\textsf {lem}(H.c)\). The last two rules establish the derivability of judgments of the form
. Proof term \(\textsf {in}(A)\) witnesses the fact that an initial assignment A holds. The second rule coerces a theory proof \(j_k\) into a CDSAT deduction proof term. The third rule says that, whenever there is a conflict including a Boolean assignment H, a clausal form of H is a lemma entailed by the rest of the conflict. The proof term \(\textsf {lem}(H.c)\) carries H to record which part of the conflict became a lemma. If identifiers of assignments in H occur in \(c\), such occurrences are bound in \(\textsf {lem}(H.c)\). The last two rules establish the derivability of judgments of the form  . Proof term
. Proof term  witnesses the conflict between the conclusion L of a theory inference, whose theory proof is coerced into a CDSAT deduction proof term, and its flip \(\overline{L}\) (with identifier \(a\)). Proof term \(\textsf {res}(j,{}^{a}{A}.c)\) is the only construct that combines two subproofs, connecting the conclusion A of the left premise with the hypothesis \({}^{a}{A}\) of the right premise: the proof of A from H is plugged as a subproof in the proof of \(\bot \) from \(E\uplus \{{}^{a}{A}\}\) to get a proof of \(\bot \) from \(E\cup H\). Any occurrence of \(a\) in \(c\) is bound in \(\textsf {res}(j,{}^{a}{A}.c)\). The following theorem connects provability in the CDSAT proof system with endorsement, showing the soundness of the CDSAT proof system.
witnesses the conflict between the conclusion L of a theory inference, whose theory proof is coerced into a CDSAT deduction proof term, and its flip \(\overline{L}\) (with identifier \(a\)). Proof term \(\textsf {res}(j,{}^{a}{A}.c)\) is the only construct that combines two subproofs, connecting the conclusion A of the left premise with the hypothesis \({}^{a}{A}\) of the right premise: the proof of A from H is plugged as a subproof in the proof of \(\bot \) from \(E\uplus \{{}^{a}{A}\}\) to get a proof of \(\bot \) from \(E\cup H\). Any occurrence of \(a\) in \(c\) is bound in \(\textsf {res}(j,{}^{a}{A}.c)\). The following theorem connects provability in the CDSAT proof system with endorsement, showing the soundness of the CDSAT proof system.
Theorem 11
If  , then \(H_0\cup H\models A\); if
, then \(H_0\cup H\models A\); if  , then \(H_0\cup E\models \bot \).
, then \(H_0\cup E\models \bot \).
Proof
The proof is by structural induction. The base case covers in and coercion: if  has the form
has the form  , then A is initial, which means that \(A\in H_0\) and \(H_0\models A\); if
, then A is initial, which means that \(A\in H_0\) and \(H_0\models A\); if  has the form
has the form  , then
, then  and by soundness of theory inferences \(J\models L\), hence \(H_0\cup J\models L\). The induction step covers lem, cfl, and res. If
and by soundness of theory inferences \(J\models L\), hence \(H_0\cup J\models L\). The induction step covers lem, cfl, and res. If  has the form
has the form  , then
, then  , by induction hypothesis \(H_0\cup E\uplus H\models \bot \), hence \(H_0\cup E\models L\) as L is a clausal form of H. If
, by induction hypothesis \(H_0\cup E\uplus H\models \bot \), hence \(H_0\cup E\models L\) as L is a clausal form of H. If  has the form
has the form  , then
, then  , by induction hypothesis \(H_0\cup J\models L\), hence \(H_0\cup J\cup \{{}^{a}{\overline{L}}\}\models \bot \). If
, by induction hypothesis \(H_0\cup J\models L\), hence \(H_0\cup J\cup \{{}^{a}{\overline{L}}\}\models \bot \). If  has the form
has the form  , then
, then  and
and  ; by induction hypothesis \(H_0\cup H\models A\) and \(H_0\cup E\uplus \{A\}\models \bot \), hence \(H_0\cup E\cup H\models \bot \). \(\square \)
; by induction hypothesis \(H_0\cup H\models A\) and \(H_0\cup E\uplus \{A\}\models \bot \), hence \(H_0\cup E\cup H\models \bot \). \(\square \)
6.3 The Proof-Carrying CDSAT Transition System
In the proof-carrying CDSAT transition system (see Fig. 7), justified assignments are decorated with deduction proof terms, and conflict states are triples of the form  , where \(c\) is a conflict proof term. A justified assignment
, where \(c\) is a conflict proof term. A justified assignment  carries a deduction proof term \(j\) such that
carries a deduction proof term \(j\) such that  . Initial assignments have the form
. Initial assignments have the form  where the deduction proof term presents the initial assignment as a premise of the proof.
where the deduction proof term presents the initial assignment as a premise of the proof.
Comparing Figs. 1 and 7, \(\textsf {Decide}\) is unchanged as a decision does not carry a proof term; \(\textsf {Deduce}\) is modified as the supporting theory inference  is annotated with a theory proof that the added justified assignment
is annotated with a theory proof that the added justified assignment  carries with itself. In Fig. 1 the choice between \(\textsf {Fail}\) and \(\textsf {ConflictSolve}\) depends on the level of the conflict, whereas in Fig. 7 it depends on the outcome of the conflict resolution phase, because proof-carrying CDSAT fires \(\textsf {Fail}\) and returns
carries with itself. In Fig. 1 the choice between \(\textsf {Fail}\) and \(\textsf {ConflictSolve}\) depends on the level of the conflict, whereas in Fig. 7 it depends on the outcome of the conflict resolution phase, because proof-carrying CDSAT fires \(\textsf {Fail}\) and returns  , if it can return a proof of unsatisfiability. If the outcome of the conflict resolution phase is a trail, the conflict was solved and \(\textsf {ConflictSolve}\) applies; if it is a state
, if it can return a proof of unsatisfiability. If the outcome of the conflict resolution phase is a trail, the conflict was solved and \(\textsf {ConflictSolve}\) applies; if it is a state  , the system is still in conflict state, but there is no conflict to solve. The system concludes that the input assignment is \({\mathcal {T}}_{\infty }^+\)-unsatisfiable and that proof term \(c\) encodes the discovered proof of unsatisfiability: \(\textsf {Fail}\) applies and the derivation terminates in state
, the system is still in conflict state, but there is no conflict to solve. The system concludes that the input assignment is \({\mathcal {T}}_{\infty }^+\)-unsatisfiable and that proof term \(c\) encodes the discovered proof of unsatisfiability: \(\textsf {Fail}\) applies and the derivation terminates in state  returning proof term \(c\). It is simple to show that the conflict state rules of proof-carrying CDSAT reduce a conflict state
returning proof term \(c\). It is simple to show that the conflict state rules of proof-carrying CDSAT reduce a conflict state  , where \(E\ne \emptyset \), to one of the form
, where \(E\ne \emptyset \), to one of the form  if and only if \(\textsf {level}_{\varGamma }(E) = 0\); and that they solve the conflict producing some trail \(\varGamma ^\prime \) different from \(\varGamma \) if and only if \(\textsf {level}_{\varGamma }(E) > 0\).
if and only if \(\textsf {level}_{\varGamma }(E) = 0\); and that they solve the conflict producing some trail \(\varGamma ^\prime \) different from \(\varGamma \) if and only if \(\textsf {level}_{\varGamma }(E) > 0\).
Continuing with the conflict state rules, \(\textsf {UndoClear}\) and \(\textsf {UndoDecide}\) are unchanged. Proof-carrying \(\textsf {LearnBackjump}\) generates the proof term \(\textsf {lem}(H.c)\), recording that the learned lemma L is a clausal form of H, and turning the conflict proof term \(c\) that represents a proof of unsatisfiability of \(E\uplus H\) into a deduction proof term that represents a proof of L from E. The main rule for proof reconstruction is proof-carrying \(\textsf {Resolve}\), which combines proof term \(c\), witnessing the unsatisfiability of the conflict, with proof term \(j\) witnessing that one of the assignments in the conflict, named A, follows from prior assignments: A is retained in the proof term \(\textsf {res}(j,{}^{a}{A}.c)\). By applying this mechanism, proof-carrying CDSAT connects a proof of why a conflict E follows from \(H_0\) with a proof of why E is unsatisfiable, and generates a proof of unsatisfiability of \(H_0\). The following theorem shows that proof-carrying CDSAT maintains provability invariants connecting the operations of the transition system with provability in the CDSAT proof system.
Theorem 12
For all proof-carrying CDSAT-derivations
-
If a trail containing
 is generated, then
is generated, then  ;
; -
If a conflict state
 is reached, then
is reached, then  .
.
Proof
The two claims are proved simultaneously by induction on the number of transition steps yielding the justified assignment or the conflict state, respectively. The base case covers input justified assignments, justified assignments placed on the trail by \(\textsf {Deduce}\), and conflict states of the form  . A justified assignment
. A justified assignment  is on the trail because A is initial:
is on the trail because A is initial:  follows by the in rule of the CDSAT proof system. For a justified assignment
follows by the in rule of the CDSAT proof system. For a justified assignment  placed on the trail by \(\textsf {Deduce}\),
placed on the trail by \(\textsf {Deduce}\),  , hence
, hence  by coercion. For a conflict state of the form
by coercion. For a conflict state of the form  , we have
, we have  , hence
, hence  by the cfl rule. The inductive step covers a justified assignment placed on the trail by \(\textsf {LearnBackjump}\) and conflict states generated by \(\textsf {Resolve}\). For a justified assignment
by the cfl rule. The inductive step covers a justified assignment placed on the trail by \(\textsf {LearnBackjump}\) and conflict states generated by \(\textsf {Resolve}\). For a justified assignment  , by induction hypothesis
, by induction hypothesis  , and L is a clausal form of H, so that
, and L is a clausal form of H, so that  by the lem rule. For a conflict state of the form
by the lem rule. For a conflict state of the form  , by induction hypothesis
, by induction hypothesis  , and
, and  , so that
, so that  by the res rule. \(\square \)
by the res rule. \(\square \)
Theorems 11 and 12 together show that proof-carrying CDSAT builds a trace of proof terms in such a way to keep track of the CDSAT soundness invariants through the provability invariants. The next example expands Fig. 2 into a full derivation by proof-carrying CDSAT. For the sake of readability, we omit identifiers and we abuse the formalism by building proof terms made of assignments rather than their identifiers.
Example 10
Assume that the input assignment for the example in Fig. 2 is \(\{\lnot l_4 \vee l_5,\ \lnot l_2 \vee \lnot l_4 \vee \lnot l_5,\ l_2 \vee (z{\,\simeq _{}\,}y),\ x{\not \le }0 \vee l_2,\ x{\not \le }0 \vee l_4,\ f(z){\leftarrow }_{{}}\textsf {blue},\ f(y){\leftarrow }_{{}}\textsf {red}\}\), where \(l_2\) is \(y{\ge } 0\), \(l_4\) is \({x{+}y{>}0}\), and \(x{\not \le }0\) abbreviates \(\lnot (x {\le } 0)\). The initial trail \(\varGamma _0\) contains these assignments. The derivation proceeds as in Fig. 2 with decisions  ,
,  ,
,  ,
,  , and propagation
, and propagation  , but here we assume that \(A_1\) is
, but here we assume that \(A_1\) is  . Let \(\varGamma _1\) be the trail up to this point. The first conflict state is
. Let \(\varGamma _1\) be the trail up to this point. The first conflict state is  with conflict proof term
with conflict proof term

that registers the conflict between \(l_5\) and \(\lnot l_5\), the latter derived by Unit Propagation from \(\lnot l_2 {\vee } \lnot l_4 {\vee } \lnot l_5\), \(l_2\), and \(l_4\). The \(\textsf {Resolve}\) step from Fig. 2 replaces \(l_5\) in the conflict by its justification \(\{\lnot l_4{\vee }l_5,\ l_4\}\), yielding conflict state  . The associated conflict proof term is
. The associated conflict proof term is

which plugs on top of the leaf \(l_5\) of \(c_1\) its theory proof \(\textsf {UP}(\lnot l_4{\vee }l_5,\{l_4\})\). Let \(\textsf {LearnBackjump}\) solve the conflict as in Example 1 by placing on the trail

with deduction proof term \(j_1 {=} \textsf {lem}(\{l_2,l_4\}.c_2)\) recording that conflict proof \(c_2\) showed that the learned lemma \(\lnot l_2{\vee }\lnot l_4\) is inferred from \(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\) and \(\lnot l_4{\vee }l_5\). Proceeding as in Example 6, a \(\textsf {Deduce}\) step adds  , with deduction proof term
, with deduction proof term  . Suppose that the derivation continues with a \(\textsf {Deduce}\) step encapsulating the LRA evaluation inference
. Suppose that the derivation continues with a \(\textsf {Deduce}\) step encapsulating the LRA evaluation inference

with deduction proof term  . The resulting trail \(\varGamma _2\) contains the initial assignments followed by
. The resulting trail \(\varGamma _2\) contains the initial assignments followed by

At this stage, the \(\textsf {LRA} \)-procedure detects the \(\textsf {LRA} \)-conflict \(\{l_2,\overline{l_4},\overline{x{\le }0}\}\) and explains it by the FM-resolution inference

mirrored in CDSAT proof system as the inference

(see the cfl rule in Fig. 6) with conflict proof term

The conflict state is  . A \(\textsf {Resolve}\) step replaces \(\overline{l_4}\) by its justification \(\{\lnot l_2 {\vee } \lnot l_4,\ l_2\}\), producing conflict state
. A \(\textsf {Resolve}\) step replaces \(\overline{l_4}\) by its justification \(\{\lnot l_2 {\vee } \lnot l_4,\ l_2\}\), producing conflict state  with conflict proof term \(c_4 = \textsf {res}(j_2,{}^{ }{\overline{l_4}}.c_3)\) that expands upward leaf \(\overline{l_4}\) of \(c_3\) with its proof \(j_2\). The system exits from this conflict by a \(\textsf {LearnBackjump}\) transition that jumps back to level 1 and learns lemma \((x{\le }0){\vee }\lnot l_2\) with deduction proof term \(j_4 = \textsf {lem}(\{\overline{x{\le }0},l_2\}.c_4)\). The resulting trail \(\varGamma _3\) contains the initial assignments followed by
with conflict proof term \(c_4 = \textsf {res}(j_2,{}^{ }{\overline{l_4}}.c_3)\) that expands upward leaf \(\overline{l_4}\) of \(c_3\) with its proof \(j_2\). The system exits from this conflict by a \(\textsf {LearnBackjump}\) transition that jumps back to level 1 and learns lemma \((x{\le }0){\vee }\lnot l_2\) with deduction proof term \(j_4 = \textsf {lem}(\{\overline{x{\le }0},l_2\}.c_4)\). The resulting trail \(\varGamma _3\) contains the initial assignments followed by

With the last lemma the system has learned that if \(y\ge 0\) (\(l_2\)) implies \(\overline{x{+}y{>}0}\) (\(\lnot l_4\)), then \(y\ge 0\) implies \(x{\le }0\). Next, \(\textsf {Deduce}\) expands \(\varGamma _3\) with the assignments

carrying proof terms  and
and  . A \(\textsf {Deduce}\) step for EUF inference
. A \(\textsf {Deduce}\) step for EUF inference  further adds
further adds

where \(j_7 = \textsf {neq}(f(z){\leftarrow }_{{}}\textsf {blue}, f(y){\leftarrow }_{{}}\textsf {red})\). Let \(\varGamma _4\) be the resulting trail. At this point \(\textsf {ConflictSolve}\) fires, as the EUF inference  leads to conflict state
leads to conflict state  , with conflict proof term
, with conflict proof term

A \(\textsf {Resolve}\) step yields conflict state  , with conflict proof term \(c_6 = \textsf {res}(j_6,{}^{ }{(z{\,\simeq _{}\,}y)}.c_5)\) that expands upward leaf \(z{\,\simeq _{}\,}y\) of \(c_5\) with its proof \(j_6\). Similarly, another \(\textsf {Resolve}\) step produces conflict state
, with conflict proof term \(c_6 = \textsf {res}(j_6,{}^{ }{(z{\,\simeq _{}\,}y)}.c_5)\) that expands upward leaf \(z{\,\simeq _{}\,}y\) of \(c_5\) with its proof \(j_6\). Similarly, another \(\textsf {Resolve}\) step produces conflict state

with conflict proof term \(c_7 = \textsf {res}(j_5,{}^{ }{\overline{l_2}}.c_6)\) that expands upward leaf \(\overline{l_2}\) of \(c_6\) with its proof \(j_5\). The conflict is solved by a \(\textsf {LearnBackjump}\) transition that jumps back to level 0 and learns \(x{\le }0\) as

with deduction proof term \(j_8 = \textsf {lem}(\{\overline{x{\le }0}\}.c_7)\). As a byproduct, decision \(A_1\) is gone, and the resulting trail \(\varGamma _5\) contains the initial assignments, the learned lemmas, namely \(\lnot l_2 \vee \lnot l_4\), \(x{\le }0 \vee l_2\), and \(x{\le }0\), and the level 0 propagation \(f(z){\,\not \simeq _{}\,}f(y)\). Lemma \(x{\le }0\) enables \(\textsf {Deduce}\) to perform two unit propagations involving input clauses:

with  and
and  . Let \(\varGamma _6\) be \(\varGamma _5\) thus expanded. At this point the conflict in
. Let \(\varGamma _6\) be \(\varGamma _5\) thus expanded. At this point the conflict in  is at level 0. Conflict proof term
is at level 0. Conflict proof term  records the conflict between \(l_4\) and \(\lnot l_4\), the latter derived by Unit Propagation from \(\lnot l_2 \vee \lnot l_4\) and \(l_2\). While CDSAT would halt, proof-carrying CDSAT performs the series of \(\textsf {Resolve}\) steps in Fig. 8. When \(\textsf {Resolve}\) replaces a justified assignment by its justification, the proof term evolves as seen before. When \(\textsf {Resolve}\) removes an initial assignment from the conflict, the corresponding leaf in the associated proof term gets surrounded by the in constructor to mark it as a leaf of the final proof. When the conflict is empty, \(\textsf {Fail}\) fires returning
records the conflict between \(l_4\) and \(\lnot l_4\), the latter derived by Unit Propagation from \(\lnot l_2 \vee \lnot l_4\) and \(l_2\). While CDSAT would halt, proof-carrying CDSAT performs the series of \(\textsf {Resolve}\) steps in Fig. 8. When \(\textsf {Resolve}\) replaces a justified assignment by its justification, the proof term evolves as seen before. When \(\textsf {Resolve}\) removes an initial assignment from the conflict, the corresponding leaf in the associated proof term gets surrounded by the in constructor to mark it as a leaf of the final proof. When the conflict is empty, \(\textsf {Fail}\) fires returning  .
.
Conflicts and conflicts proof terms produced by the final series of steps in Example 10
This example shows how lemma learning avoids repeating work: if conflict \(\{\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5,\ l_2,\ l_4,\ \lnot l_4{\vee }l_5\}\) is solved by \(\textsf {Backjump}\) (see Example 3), rather than \(\textsf {LearnBackjump}\) (see Examples 1 and 10), trail \(\varGamma _1\) of Example 10 would be expanded with

where \(j_{11} = \textsf {lem}(\{l_4\}.c_2)\). Conflict \(\{\lnot l_2{\vee }\lnot l_4,l_2,l_4\}\) would not be detected as in Example 10, and more steps would be necessary to discover it. Such steps would build another proof of \(\lnot l_2\vee \lnot l_4\), possibly identical to the first forgotten one. Furthermore, lemmas can be reused and may appear multiple times in the final proof term. Lemma \(\lnot l_2{\vee }\lnot l_4\) is used twice in Example 10, and it occurs twice in \(c_{13}-c_{21}\): once in \(c_8\), and once in \(c_{12}\), because \(c_{12}\) contains \(j_4\), which contains \(c_4\), which contains \(j_2\), where \(\lnot l_2{\vee }\lnot l_4\) appears. Also, deduction proof terms referring to first-order decisions do not appear in the final proof term: an inspection of \(c_{21}\) shows that \(j_{3}\) is absent. The reason is that first-order decisions play a role in finding models, not proofs. An easy optimization avoids constructing deduction proof terms involving first-order decisions.
7 Proof Reconstruction: From Proof Terms to Proofs
The motivation for using the proof-carrying CDSAT system is the ability to justify the unsatisfiability of an input with a proof. When CDSAT concludes  , the proof term \(c\) and its associated derivation of
, the proof term \(c\) and its associated derivation of  can be considered as a proof of unsatisfiability of the input, following Theorem 11. If need be, the rules of Fig. 6 can be used for proof checking. If another proof format is preferred, \(c\) indicates how a proof in that format can be reconstructed, having CDSAT traced in \(c\) how a contradiction was reached from a logical point of view. Indeed, a deduction proof term \(j\) with
can be considered as a proof of unsatisfiability of the input, following Theorem 11. If need be, the rules of Fig. 6 can be used for proof checking. If another proof format is preferred, \(c\) indicates how a proof in that format can be reconstructed, having CDSAT traced in \(c\) how a contradiction was reached from a logical point of view. Indeed, a deduction proof term \(j\) with  (resp. a conflict proof term \(c\) with
(resp. a conflict proof term \(c\) with  ) can be decoded into, or can be seen as denoting, a proof of \(H_0\cup H\models A\) (resp. \(H_0\cup E\models \bot \)) in the format of choice.
) can be decoded into, or can be seen as denoting, a proof of \(H_0\cup H\models A\) (resp. \(H_0\cup E\models \bot \)) in the format of choice.
A first option is to decode proof terms into proofs after CDSAT halts, in a post-processing phase. A second option consists of identifying first the proof operations corresponding to the rules of Fig. 6 in the target proof format and then reading the proof-carrying CDSAT system as manipulating directly the proofs denoted by proof terms such as \(\textsf {in}(A)\),  , \(\textsf {lem}(H.c)\),
, \(\textsf {lem}(H.c)\),  , and \(\textsf {res}(j,{}^{a}{A}.c)\). In other words, a CDSAT-based solver would build in memory not the proof terms, but the proofs themselves. Of course, the execution of the above-mentioned proof operations during a CDSAT derivation may increase its runtime. In any case, proof-carrying CDSAT is modular in the way theory proofs are handled, reconstructed, and checked. In Sect. 7.1 we exemplify proof reconstruction by showing how CDSAT proof terms can be turned into resolution-style proof trees. In Sect. 7.2 we discuss yet another alternative consisting of applying to CDSAT the LCF approach to proofs.
, and \(\textsf {res}(j,{}^{a}{A}.c)\). In other words, a CDSAT-based solver would build in memory not the proof terms, but the proofs themselves. Of course, the execution of the above-mentioned proof operations during a CDSAT derivation may increase its runtime. In any case, proof-carrying CDSAT is modular in the way theory proofs are handled, reconstructed, and checked. In Sect. 7.1 we exemplify proof reconstruction by showing how CDSAT proof terms can be turned into resolution-style proof trees. In Sect. 7.2 we discuss yet another alternative consisting of applying to CDSAT the LCF approach to proofs.
7.1 Proof Format Based on Resolution
A resolution proof is usually represented as a resolution proof tree with nodes labeled by clauses. However, CDSAT views logical connectives as interpreted symbols of theory \(\textsf {Bool} \), treats formulæ as terms of sort \(\textsf {prop} \), allows assignments such as \((l_1{\vee }l_2){\leftarrow }_{{}}\textsf {false}\), and does not assume that the input is a set of clauses. Therefore, we distinguish between object-level clauses of the form \(l_1{\vee }\cdots {\vee }l_m\), where the \(l_i\)’s are terms of sort \(\textsf {prop} \) and \(\vee \) is the symbol for disjunction in \(\varSigma _{\textsf {Bool} }\), and CDSAT clauses written \(L_1\,||\,\cdots \,||\,L_m\), where the \(L_i\)’s are singleton Boolean assignments and \(\,||\,\) is a meta-level symbol for disjunction. Reconstructed proofs will use object-level clauses for input clauses and CDSAT clauses for generated clauses. Since in CDSAT there are first-order assignments, we introduce guarded CDSAT clauses of the form \(H\rightarrow C\), where H is a set of first-order assignments, which can be empty, and C is a CDSAT clause. When there is no ambiguity, we use clause for CDSAT clause and guarded clause for guarded CDSAT clause. The reconstruction of a resolution proof from a CDSAT proof term yields a CDSAT resolution proof.
Definition 9
(CDSAT Resolution Proof) A CDSAT resolution proof is represented as a binary tree such that:
-
1.
A leaf is labeled with either an input singleton assignment, or a guarded clause that is a theory lemma;
-
2.
An internal node n is labeled with a guarded clause and has children \(n_1\) and \(n_2\) if its label can be inferred from those of \(n_1\) and \(n_2\) by one of the following inference rules:

where L and A are input singleton assignments labeling leaves.
Theory lemmas are treated as leaves, because theory proofs involve inference rules other than resolution. Since CDSAT treats propositional logic as a theory, there are also theory lemmas for \(\textsf {Bool} \) or \(\textsf {Bool} \)-lemmas. If \(L_0\) is a clausal form of \(\{L_1,\ldots ,L_m\}\) (see Definition 1), the following clauses are \(\textsf {Bool} \)-lemmas:
Indeed, \(\overline{L}_0\,||\,\overline{L_1} \,||\,\cdots \,||\,\overline{L_m}\) and \(L_0\,||\,{L_i}\), \(1{\le }i{\le }m\), are tautologies, since \(L_0\) is a clausal form of \(\{L_1,\ldots ,L_m\}\), hence they can label leaves. The first \(\textsf {Bool} \)-lemma allows one to transform the object-level clause to which \(L_0\) assigns \(\textsf {true}\) into a CDSAT clause:

Conversely, the other lemmas allow one to turn a CDSAT clause \(\overline{L_1} \,||\,\cdots \,||\,\overline{L_m}\) into an object-level clause:

These transformations can be synthesized into derivable inference rules:

that involve \(\textsf {Bool} \)-lemmas only if \(m\ge 2\), because if \(m=1\), \(L_0\) is simply \(\overline{L_1}\). An assignment H can be partitioned as \(H_\textsf {FO} \uplus \{L_1,\ldots ,L_n\}\), where \(H_\textsf {FO}\) contains all the singleton first-order assignments in H, and \(L_1,\ldots ,L_n\) are all the singleton Boolean assignments in H. Let \(H_\textsf {clause}\) be the clause \(\overline{L_1}\,||\,\cdots \,||\,\overline{L_n}\), that is, \(H_\textsf {clause}\) is a clausal form of \(\{L_1,\ldots ,L_n\}\) (see Definition 1) written as a CDSAT clause. Then CDSAT proof terms are transformed into CDSAT resolution proofs by turning:
-
a deduction proof term
 into a leaf labeled A;
into a leaf labeled A; -
a deduction proof term
 of any other form into a proof of \(H_\textsf {FO}\rightarrow H_\textsf {clause}\,||\,L\); and
of any other form into a proof of \(H_\textsf {FO}\rightarrow H_\textsf {clause}\,||\,L\); and -
a conflict proof term
 into a proof of \(H_\textsf {FO}\rightarrow H_\textsf {clause}\).
into a proof of \(H_\textsf {FO}\rightarrow H_\textsf {clause}\).
The application of this transformation to a proof term is denoted by surrounding the proof term with \(\llbracket \) and \(\rrbracket \). The definition of this transformation is inductive and is given in Fig. 9, which should be read together with Fig. 6. The first, second, and third cases in Fig. 9 are base cases that yield leaves according to Case (1) in Definition 9. The remaining cases are inductive cases, where the recursive application of the transformation is represented as a subproof with the transformed proof term as premise and the result of the transformation as consequence. The rule for \(\textsf {res}\) in Fig. 6 is articulated into three rules in Fig. 9 distinguishing among Unit Resolution, First-order Assignment Elimination, and Binary Resolution according to Case (2) in Definition 9.
For instance, consider the transformation of a deduction proof term and a conflict proof term that encapsulate a unit propagation, where K is a clausal form of \(H\ =\ H^\prime \uplus \{L\}\) as in inference (1) from Sect. 3.2:

where \(a_1,\ldots ,a_n\) are the identifiers of the elements of \(H^\prime \). Both transformations yield the \(\textsf {Bool} \)-lemma
by applying the second and the fourth rules in Fig. 9, respectively.
Since a CDSAT answer of the form  means
means  , the resolution proof reconstructed from c is a refutation, as its conclusion is the empty clause \(\emptyset \rightarrow \emptyset \). Since first-order decisions do not appear in proofs, first-order assignments may appear in proofs only if they belong to the initial assignment of an SMA problem. If the input problem is an SMT problem, and therefore contains no first-order assignments, the reconstructed proof involves only singleton Boolean assignments labeling leaves and guarded clauses of the form \(\emptyset \rightarrow C\) labeling leaves or internal nodes. In other words, the reconstructed proof is a resolution refutation in the standard sense, with leaves labeled by input assignments or theory lemmas. On the other hand, \(\textsf {Bool} \)-lemmas are a non-standard feature that also enables the sharing of resolution proofs. For instance, in the refutation of Example 10, the conflict proof term \(c_{19} = \textsf {res}(j_1,{}^{ }{\lnot l_2{\vee }\lnot l_4}.c_{18})\) (see Fig. 8), with \(j_1 = \textsf {lem}(\{{}^{ }{l_2},{}^{ }{l_4}\}.c_2)\), yields
, the resolution proof reconstructed from c is a refutation, as its conclusion is the empty clause \(\emptyset \rightarrow \emptyset \). Since first-order decisions do not appear in proofs, first-order assignments may appear in proofs only if they belong to the initial assignment of an SMA problem. If the input problem is an SMT problem, and therefore contains no first-order assignments, the reconstructed proof involves only singleton Boolean assignments labeling leaves and guarded clauses of the form \(\emptyset \rightarrow C\) labeling leaves or internal nodes. In other words, the reconstructed proof is a resolution refutation in the standard sense, with leaves labeled by input assignments or theory lemmas. On the other hand, \(\textsf {Bool} \)-lemmas are a non-standard feature that also enables the sharing of resolution proofs. For instance, in the refutation of Example 10, the conflict proof term \(c_{19} = \textsf {res}(j_1,{}^{ }{\lnot l_2{\vee }\lnot l_4}.c_{18})\) (see Fig. 8), with \(j_1 = \textsf {lem}(\{{}^{ }{l_2},{}^{ }{l_4}\}.c_2)\), yields  , where \(L_1\) is \(\lnot l_4{\vee }l_5\) and \(L_2\) is \(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\). The resolution proof reconstructed from \(c_{19}\) is:
, where \(L_1\) is \(\lnot l_4{\vee }l_5\) and \(L_2\) is \(\lnot l_2{\vee }\lnot l_4{\vee }\lnot l_5\). The resolution proof reconstructed from \(c_{19}\) is:

In the proof reconstructed from \(c_{21}\), CDSAT clause \(\emptyset \rightarrow \overline{L_1}{\,||\,}\overline{L_2}\) resolves with initial assignments \(L_1\) and \(L_2\) to yield \(\emptyset \rightarrow \emptyset \). The double occurrence of \(\lnot l_2{\vee }\lnot l_4\) in \(c_{18}\) (see Example 10), means that the resolution proof  has two leaves labeled by the same \(\textsf {Bool} \)-lemma
has two leaves labeled by the same \(\textsf {Bool} \)-lemma
An alternative refutation can be obtained by replacing those two leaves with the subproof translating \({c_2}\), and replacing \(\overline{(\lnot l_2{\vee }\lnot l_4)}\) by \(\overline{L_1}{\,||\,}\overline{L_2}\) in all nodes underneath. This avoids the explicit conversions between the object-level clause \(\lnot l_2{\vee }\lnot l_4\) and the CDSAT clause \(\overline{l_2}{\,||\,}\overline{l_4}\). However, in this alternative proof, the subtree for \({c_2}\) is duplicated. Such duplications are customary in resolution proof trees where there is only one kind of clauses. By distinguishing between object-level clauses and CDSAT clauses, and using the former for input clauses and the latter for generated clauses, CDSAT natively supports the sharing of subproofs that one obtains by replacing trees with directed acyclic graphs.
7.2 An LCF Architecture for CDSAT
Another example of proof format is the “dummy” one, where proofs do not contain any information other than what they are supposed to be the proofs of:
-
1.
A deduction proof for proof term \(j\) with
 is the pair \(\langle H,L\rangle \), and
is the pair \(\langle H,L\rangle \), and -
2.
A conflict proof for proof term \(c\) with
 is H.
is H.
Although this proof format does not allow any proof checking, the trustworthiness of a reasoner producing such proofs can still be established by the LCF programming abstraction [30, 47]. This approach uses a type theorem , whose constructed inhabitants are provable formulæ. Actually, this type is defined as an alias for the type formula of formulæ, but this is known only to a fixed and well-identified piece of code, called the LCF kernel. This kernel hides the definition of theorem to the outside world and exports a range of kernel primitives to manipulate inhabitants of type theorem in a safe and provably correct way. For instance, assuming that \(\Rightarrow \) denotes implication, a primitive

takes as arguments two inhabitants F and G of type theorem, checks that F is of the form \(G\Rightarrow R\), and returns R as an inhabitant of theorem. The kernel can export a primitive that reveals that an inhabitant of theorem is a formula, but not one that casts any inhabitant of formula into type theorem. Thus, the existence of an inhabitant F of theorem witnesses the fact that F is provable, as an inhabitant only results from a series of correct manipulations by the kernel primitives: if the kernel code is trusted, then F can be trusted to be a theorem, while no proof has ever been constructed in memory. CDSAT is well-suited for the LCF approach: given a type assign for assignments and single_assign for singleton assignments, a trusted kernel defines types

hides their definitions to the outside world and exports a range of primitives corresponding to the proof term constructs.
The signature in Fig. 10 lists hidden-type definitions and exported primitives. The primitives check that the conditions of the rules in Fig. 6 are met: in checks that its argument is one of the initial assignments; lem takes as arguments a conflict E and an assignment H, checks that H is Boolean and included in E, computes a clausal form L of H, and produces the deduction \(\langle E\backslash H,L\rangle \), where \(\backslash \) is set subtraction. Primitive res takes a deduction \(\langle H,A\rangle \) and a conflict, checks that A occurs in the conflict, and returns the conflict where A is replaced by H. Primitives coerc and cfl take as arguments a \({\mathcal {T}}_{k}\)-proof, \(1\,{\le }\,k\,{\le }\,n\), given as an inhabitant of ’k theory_proof, a type parameterized by k. Their first argument is a handler for theory \({\mathcal {T}}_{k}\), whose type ’k theory_handler is parameterized by a matching k, as implemented for example by a generalized algebraic datatype [19, 55]. The handler allows the primitives to check that \({\mathcal {T}}_{k}\) is one of the combined theories before coercing the \({\mathcal {T}}_{k}\)-proof, trusted to be correct, into a deduction or a conflict. Proof-carrying CDSAT can be programmed on top of this kernel, so that, when it halts with answer  , the proof term \(c\) is an inhabitant of type conflict. The reveal primitive applied to \(c\) will return the empty assignment. Although no proof has been constructed in memory, the answer is correct by construction.
, the proof term \(c\) is an inhabitant of type conflict. The reveal primitive applied to \(c\) will return the empty assignment. Although no proof has been constructed in memory, the answer is correct by construction.
8 Discussion
Conflict-driven satisfiability procedures work by building partial assignments, detecting conflicts when the assignment falsifies the input formula, and performing conflict-driven inferences to explain conflicts and reorient the search. In prior work [11], we presented CDSAT as a conflict-driven combination framework for disjoint theories and proved its soundness, termination, and completeness. The present article has extended the theoretical foundations of CDSAT in three main directions, namely lemma learning, properties of theory modules (i.e., the theory inference systems that CDSAT orchestrates), and proof generation.
We generalized the lemma learning capability of CDSAT, in such a way that new clauses can be formed and learned during backjumping from a conflict, and the destination level of backjumping can be chosen according to different heuristics, including learn and restart. Soundness, termination, and completeness of CDSAT are preserved.
We proved that the theory modules listed in [11] for the Boolean theory, equality, arrays with extensionality, and linear rational arithmetic, as well as generic black-box modules for stably infinite and non-stably infinite theories, are complete with respect to all suitable leading theories in a union of theories, and admit finite local bases. We also showed how to get a finite global basis for the union of the theories from finite local bases for the individual theories. These results mean that the assumptions for the termination and completeness of CDSAT can indeed be satisfied, complementing our previous general results [11]. By including black-box modules for stably infinite theories CDSAT subsumes the equality-sharing method for theory combination [42, 48, 49], also known as Nelson-Oppen scheme, including model-based theory combination [23]. By handling also non-stably infinite theories, CDSAT goes beyond equality sharing (see [9] for a survey of other approaches to this issue).
We presented a proof-carrying CDSAT transition system that constructs and carries proof terms, so that a proof can be reconstructed when CDSAT discovers that the input problem is unsatisfiable. CDSAT proof terms can be rendered in a number of proof formats, and the resulting proofs checked by a trusted checker, or shown to be correct by construction in LCF style. A translation to resolution-style proofs is illustrated as example.
Research on CDSAT as a new paradigm for theory combination has just begun, and there are many directions for future work. A main objective is an implementation of CDSAT, either in the form of a CDSAT-based prototype (e.g., [6, 14]) or by extending the implementation of MCSAT in the Yices SMT solver [25]. An implementation can be used for exploring and evaluating different search plans and proof formats, the latter in connection with the objective of efficient proof checking. The design of a CDSAT search plan involves both global issues about reasoning in the theory union and local issues about reasoning in each theory. At the local level, each theory search plan is in charge of detecting the applicability of inferences and the acceptability of decisions. At the global level, the search plan decides which CDSAT transition rule to apply next, coordinates the theory modules, prioritizing them with respect to both decisions and deductions, and controls lemma learning.
CDSAT proofs may be extended to account for preprocessing and inprocessing techniques (e.g., [2, 38]), evaluating the cost of proof generation and proof checking (e.g., [2, 3]), and studying proof formats to reduce it (e.g., [22]). At the foundational level, we may investigate empowering CDSAT to handle unions of non-disjoint theories (e.g., [20, 28]), or formulæ with quantifiers, considering model-based conflict-driven instantiation (e.g., [4, 51]), or integrations with first-order logic modules (e.g., [13, 15]).
Notes
This proof works also if relevance (see Sect. 3.1) of term u is weakened to \(u\in {\mathcal {B}}\), which allows CDSAT to decide the value of u even if \(u\not \in G(\varGamma )\).
References
Armand, M., Faure, G., Grégoire, B., Keller, C., Théry, L., Werner, B.: A modular integration of SAT/SMT solvers to Coq through proof witnesses. In: Jouannaud, J.P., Shao, Z. (eds.) Proceedings of the 1st International Conference on Certified Programs and Proofs (CPP), pp. 135–150. Springer (2011)
Barbosa, H., Blanchette, J.C., Fleury, M., Fontaine, P.: Scalable fine-grained proofs for formula processing. J. Autom. Reason. 64(3), 485–550 (2020)
Bjørner, N., de Moura, L.: Proofs and refutations, and Z3. In: Rudnick, P., Sutcliffe, G., Konev, B., Schmidt, R.A., Schulz, S. (eds.) Proc. 7th International Workshop on Implementation of Logics (IWIL), CEUR Workshop Proc., vol. 418, pp. 123–132 (2008)
Bjørner, N., Janota, M.: Playing with quantified satisfaction. In: Fehnker, A., McIver, A., Sutcliffe, G., Voronkov, A. (eds.) Proceedings of the 20th International Conference on Logic for Programming, Artificial Intelligence, and Reasoning (LPAR)—Short Papers, EPiC Series in Computing, vol. 35, pp. 15–27. EasyChair (2015)
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.), Proceedings of the 23rd International Conference on Automated Deduction (CADE), Lecture Notes in Artificial Intelligence, vol. 6803, pp. 116–130. Springer (2011)
Bobot, F., Graham-Lengrand, S., Marre, B., Bury, G.: Centralizing equality reasoning in MCSAT. In: D’Silva, V., Dimitrova, R. (eds.), Proceedings of the 16th Workshop on Satisfiability Modulo Theories (SMT) (2018)
Böhme, S., Weber, T.: Fast LCF-style proof reconstruction for Z3. In: Kaufmann, M., Paulson, L.C. (eds.), Proceedings of the 1st International Conference on Interactive Theorem Proving (ITP), Lecture Notes in Computer Science, vol. 6172, pp. 179–194. Springer (2010)
Bonacina, M.P.: On conflict-driven reasoning. In: Shankar, N., Dutertre, B. (eds.), Proceedings of the 6th Workshop on Automated Formal Methods (AFM), Kalpa Publications, vol. 5, pp. 31–49. EasyChair (2018)
Bonacina, M.P., Fontaine, P., Ringeissen, C., Tinelli, C.: Theory combination: beyond equality sharing. In: Lutz, C., Sattler, U., Tinelli, C., Turhan, A.Y. (eds.) Description Logic, Theory Combination, and All That: Essays Dedicated to Franz Baader, Lecture Notes in Artificial Intelligence, vol. 11560, pp. 57–89. Springer (2019)
Bonacina, M.P., Graham-Lengrand, S., Shankar, N.: Proofs in conflict-driven theory combination. In: Andronick, J., Felty, A. (eds.), Proceedings of the 7th ACM International Conference on Certified Programs and Proofs (CPP), pp. 186–200. ACM Press (2018)
Bonacina, M.P., Graham-Lengrand, S., Shankar, N.: Conflict-driven satisfiability for theory combination: transition system and completeness. J. Autom. Reason. 64(3), 579–609 (2020)
Bonacina, M.P., Johansson, M.: Interpolation systems for ground proofs in automated deduction: a survey. J. Autom. Reason. 54(4), 353–390 (2015)
Bonacina, M.P., Lynch, C.A., de Moura, L.: On deciding satisfiability by theorem proving with speculative inferences. J. Autom. Reason. 47(2), 161–189 (2011)
Bonacina, M.P., Mazzi, G.: The Eos SMT/SMA-solver: a preliminary report. In: Sharygina, N., Hendrix, J. (eds.), Proceedings of the 17th Workshop on Satisfiability Modulo Theories (SMT) (2019). http://smt2019.galois.com/proceedings.html
Bonacina, M.P., Plaisted, D.A.: Semantically-guided goal-sensitive reasoning: inference system and completeness. J. Autom. Reason. 59(2), 165–218 (2017)
Brauße, F., Korovin, K., Korovina, M., Müller, N.: A CDCL-style calculus for solving non-linear constraints. In: Herzig, A., Popescu, A. (eds.), Proceedings of the 12th International Symposium on Frontiers of Combining Systems (FroCoS), Lecture Notes in Artificial Intelligence, vol. 11715, pp. 131–148. Springer (2019)
Bromberger, M., Sturm, T., Weidenbach, C.: Linear integer arithmetic revisited. In: Felty, A.P., Middeldorp, A. (eds.), Proceedings of the 25th International Conference on Automated Deduction (CADE), Lecture Notes in Artificial Intelligence, vol. 9195, pp. 623–637. Springer (2015)
Chang, C.L., Lee, R.C.T.: Symbolic Logic and Mechanical Theorem Proving. Academic Press, Cambridge (1973)
Cheney, J., Hinze, R.: First-Class Phantom Types. Tech. Rep. CUCIS TR2003-1901, Cornell University, Ithaca, NY, USA (2003)
Chocron, P., Fontaine, P., Ringeissen, C.: Politeness and combination methods for theories with bridging functions. J. Autom. Reason. 64(1), 97–134 (2020)
Cotton, S.: Natural domain SMT: a preliminary assessment. In: Chatterjee, K., Henzinger, T.A. (eds.), Proceedings of the 8th International Conference on Formal Modeling and Analysis of Timed Systems (FORMATS), Lecture Notes in Computer Science, vol. 6246, pp. 77–91. Springer (2010)
Cruz-Felipe, L., Heule, M., Hunt Jr., W., Kaufmann, M., Schneider-Kamp, P.: Efficient certified RAT verification. In: de Moura, L. (ed.), Proceedings of the 26th International Conference on Automated Deduction (CADE), Lecture Notes in Artificial Intelligence, vol. 10395, pp. 220–236. Springer (2017)
de Moura, L., Bjørner, N.: Model-based theory combination. In: Krstić, S., Oliveras, A. (eds.), Proceedings of the 5th Workshop on Satisfiability Modulo Theories (SMT 2007), Electronic Notes in Theoretical Computer Science, vol. 198(2), pp. 37–49. Elsevier (2008)
de Moura, L., Jovanović, D.: A model-constructing satisfiability calculus. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.), Proceedings of the 14th Internatinal Conference on Verification, Model Checking and Abstract Interpretation (VMCAI), Lecture Notes in Computer Science, vol. 7737, pp. 1–12. Springer (2013)
Dutertre, B.: Yices 2.2. In: A. Biere, R. Bloem (eds.), Proceedings of the 26th International Conference on Computer Aided Verification (CAV), Lecture Notes in Computer Science, vol. 8559, pp. 737–744. Springer (2014)
Dutertre, B., de Moura, L.: A fast linear-arithmetic solver for DPLL(T). In: Ball, T., Jones, R.B. (eds.), Proceedings of the 18th International Conference on Computer Aided Verification (CAV), Lecture Notes in Computer Science, vol. 4144, pp. 81–94. Springer (2006)
Fontaine, P., Marion, J.Y., Merz, S., Nieto, L.P., Tiu, A.: Expressiveness + automation + soundness: towards combining SMT solvers and interactive proof assistants. In: Hermanns, H., Palsberg, J. (eds.), Proceedings of the 12th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS), Lecture Notes in Computer Science, vol. 3920, pp. 167–181. Springer (2006)
Ghilardi, S., Nicolini, E., Zucchelli, D.: A comprehensive combination framework. ACM Trans. Comput. Log. 9(2), 1–54 (2008)
Goldberg, E.Y., Novikov, Y.: Verification of proofs of unsatisfiability for CNF formulas. In: Proceedings of the Conference on Design Automation and Test in Europe (DATE), pp. 10886–10891. IEEE (2003)
Gordon, M., Milner, R., Wadsworth, C.: Edinburgh LCF: A Mechanized Logic of Computation. Lecture Notes in Computer Science, vol. 78. Springer (1979)
Graham-Lengrand, S., Jovanović, D., Dutertre, B.: Solving bitvectors with MCSAT: explanations from bits and pieces. In: Peltier, N., Sofronie-Stokkermans, V. (eds.), Proceedings of the 10th International Joint Conference on Automated Reasoning (IJCAR), Lecture Notes in Artificial Intelligence, vol. 12166, pp. 103–121. Springer (2020)
Heule, M., Hunt Jr., W., Wetzler, N.: Verifying resolutions with extended refutation. In: Bonacina, M.P. (ed.), Proceedings of the 24th International Conference on Automated Deduction (CADE), Lecture Notes in Artificial Intelligence, vol. 7898, pp. 345–359. Springer (2013)
Järvisalo, M., Heule, M., Biere, A.: Inprocessing rules. In: Gramlich, B., Miller, D., Sattler, U. (eds.), Proceedings of the 6th International Joint Conference on Automated Reasoning (IJCAR), Lecture Notes in Artificial Intelligence, vol. 7364, pp. 355–370. Springer (2012)
Jovanović, D.: Solving nonlinear integer arithmetic with MCSAT. In: Bouajjani, A., Monniaux, D. (eds.) Proceedings of the 18th International Conference on Verification, Model Checking and Abstract Interpretation (VMCAI), Lecture Notes in Computer Science, vol. 10145, pp. 330–346. Springer (2017)
Jovanović, D., Barrett, C., de Moura, L.: The design and implementation of the model-constructing satisfiability calculus. In: Jobstman, B., Ray, S. (eds.), Proceedings of the 13th International Conference on Formal Methods in Computer Aided Design (FMCAD). ACM and IEEE (2013)
Jovanović, D., de Moura, L.: Cutting to the chase: solving linear integer arithmetic. J. Autom. Reason. 51, 79–108 (2013)
Jovanović, D., de Moura, L.: Solving non-linear arithmetic. In: Gramlich, B., Miller, D., Sattler, U. (eds.), Proceedings of the 6th International Joint Conference on Automated Reasoning (IJCAR), Lecture Notes in Artificial Intelligence, vol. 7364, pp. 339–354. Springer (2012)
Katz, G., Barrett, C.W., Tinelli, C., Reynolds, A., Hadarean, L.: Lazy proofs for DPLL(T)-based SMT solvers. In: Piskac, R., Talupur, M. (eds.), Proceedings of the 16th International Conference on Formal Methods in Computer-Aided Design (FMCAD), pp. 93–100. ACM and IEEE (2016)
Klee, V., Minty, G.J.: How good is the simplex algorithm? In: O. Shisha (ed.) Inequalities—III, pp. 159–175. Academic Press (1972)
Korovin, K., Tsiskaridze, N., Voronkov, A.: Conflict resolution. In: I.P. Gent (ed.), Proceedings of the 15th International Conference on Principles and Practice of Constraint Programming (CP), Lecture Notes in Computer Science, vol. 5732, pp. 509–523. Springer (2009)
Kroening, D., Strichman, O.: Decision Procedures—An Algorithmic Point of View. Texts in Theoretical Computer Science. Springer (2008)
Krstić, S., Goel, A.: Architecting solvers for SAT modulo theories: Nelson-Oppen with DPLL. In: F. Wolter (ed.), Proceedings of the 6th International Symposium on Frontiers of Combining Systems (FroCoS), Lecture Notes in Artificial Intelligence, vol. 4720, pp. 1–27. Springer (2007)
Lassez, J.L., Maher, M.J.: On Fourier’s algorithm for linear arithmetic constraints. J. Autom. Reason. 9, 373–379 (1992)
Marques Silva, J., Lynce, I., Malik, S.: Conflict-driven clause learning SAT solvers. In: Biere, A., Heule, M., Van Maaren, H., Walsh, T. (eds.) Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, vol. 185, pp. 131–153. IOS Press (2009)
Marques Silva, J.P., Sakallah, K.A.: GRASP: a search algorithm for propositional satisfiability. IEEE Trans. Comput. 48(5), 506–521 (1999)
McMillan, K.L., Kuehlmann, A., Sagiv, M.: Generalizing DPLL to richer logics. In: Bouajjani, A., Maler, O. (eds.), Proceedings of the 21st International Conference on Computer Aided Verification (CAV), Lecture Notes in Computer Science, vol. 5643, pp. 462–476. Springer (2009)
Milner, R.: LCF: a way of doing proofs with a machine. In: Becvár, J. (ed.) Proceedings of the 8th International Symposium on Mathematical Foundations of Computer Science (MFCS), Lecture Notes in Computer Science, vol. 74, pp. 146–159. Springer (1979)
Nelson, G.: Combining satisfiability procedures by equality sharing. In: Bledsoe, W.W., Loveland, D.W. (eds.) Automatic Theorem Proving: After 25 Years, pp. 201–211. American Mathematical Society (1983)
Nelson, G., Oppen, D.C.: Simplification by cooperating decision procedures. ACM Trans. Prog. Lang. Syst. 1(2), 245–257 (1979)
Nieuwenhuis, R., Oliveras, A., Tinelli, C.: Solving SAT and SAT modulo theories: from an abstract Davis-Putnam-Logemann-Loveland procedure to DPLL(T). J. ACM 53(6), 937–977 (2006)
Reynolds, A., Tinelli, C., de Moura, L.: Finding conflicting instances of quantified formulas in SMT. In: Claessen, K., Kuncak, V. (eds.) Proceedings of the 14th Conference on Formal Methods in Computer Aided Design (FMCAD). ACM and IEEE (2014)
Schrijver, A.: Theory of Linear and Integer Programming. Interscience Series in Discrete Mathematics and Optimization. Wiley (1998)
Shankar, N.: Trust and automation in verification tools. In: Cha, S.S., Choi, J.Y., Kim, M., Lee, I., Viswanathan, M. (eds.) Proceedings of the 6th International Symposium on Automated Technology for Verification and Analysis (ATVA), Lecture Notes in Computer Science, vol. 5311, pp. 4–17. Springer (2008)
Spielman, D.A., Teng, S.H.: Smoothed analysis of algorithms: why the simplex algorithm normally takes polynomial time. In: Proceedings of the 33rd Annual ACM Symp. on the Theory of Computing (STOC), pp. 296–305. ACM Press (2001). Long version available at arXiv:cs/0111050v7 [cs.DS] 9 Oct. 2003
Xi, H., Chen, C., Chen, G.: Guarded recursive datatype constructors. In: Aiken, A., Morrisett, G. (eds.) Proceedings of the 30th SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), pp. 224–235. ACM Press (2003)
Zeljić, A., Wintersteiger, C.M., Rümmer, P.: Deciding bit-vector formulas with mcSAT. In: Creignou, N., Le Berre, D. (eds.) Proceedings of the 19th International Conference on Theory and Applications of Satisfiability Testing (SAT), Lecture Notes in Computer Science, vol. 9710, pp. 249–266. Springer (2016)
Zhang, L., Malik, S.: Validating SAT solvers using an independent resolution-based checker: practical implementations and other applications. In: Proceedings of the Conference on Design Automation and Test in Europe (DATE), pp. 10880–10885. IEEE (2003)
Acknowledgements
This work was started when the first author was visiting the Computer Science Laboratory of SRI International, whose support is greatly appreciated, and completed while the first author was participating in a program at the Simons Institute for the Theory of Computing. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of NSF, DARPA, or the US Government.
Funding
Open access funding provided by Università degli Studi di Verona within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was funded in part by NSF Grants 1528153 and CNS-0917375, by DARPA under Agreement Number FA8750-16-C-0043, and by grant “Ricerca di base 2017” of the Università degli Studi di Verona.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonacina, M.P., Graham-Lengrand, S. & Shankar, N. Conflict-Driven Satisfiability for Theory Combination: Lemmas, Modules, and Proofs. J Autom Reasoning 66, 43–91 (2022). https://doi.org/10.1007/s10817-021-09606-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-021-09606-y



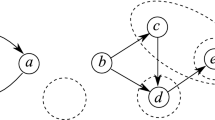


 (no introduction of foreign terms).
(no introduction of foreign terms).
 , the input problem is unsatisfiable;
, the input problem is unsatisfiable; such that no transition rule applies, there exists a
such that no transition rule applies, there exists a  :
: consisting of those elements a such that
consisting of those elements a such that  and there are enough distinct such elements as
and there are enough distinct such elements as  .
. :
: , and all
, and all  ,
,  , let
, let  ;
; , let
, let  ;
; with
with  such that
such that  is an arbitrary element of
is an arbitrary element of  -model. Parts (i) and (iii) of Definition
-model. Parts (i) and (iii) of Definition 
 and
and  .
. , the FM-resolution inference
, the FM-resolution inference  ,
,  by Corollary
by Corollary  , such that
, such that  by Corollary
by Corollary  , such that
, such that 
 on the trail,
on the trail,  ,
,  ,
, , where:
, where:

 is generated, then
is generated, then  ;
; is reached, then
is reached, then  .
.

 into a leaf labeled A;
into a leaf labeled A; of any other form into a proof of
of any other form into a proof of  into a proof of
into a proof of 
 is the pair
is the pair  is H.
is H.