Abstract
A recent literature has studied bunching at notches in tax systems; but work on the implications of bunching for welfare has been limited. We consider a setting where there are discrete changes in the enforcement of tax compliance at certain levels of reported income, creating notches that can lead to bunching. We find that greater levels of bunching can be associated with greater tax efficiency. A simulation exercise demonstrates that notches with greater bunching can be associated with higher welfare than notches with less bunching, and that a tax system with bunching at a notch can generate higher overall social welfare than a revenue-equivalent no-evasion linear tax.

Similar content being viewed by others
Notes
A large recent literature has discussed the empirical and theoretical importance of tax evasion and tax enforcement, with work covering topics such as measuring tax evasion (e.g., Artavanis et al. 2016), the efficacy of efforts to encourage compliance (Meiselman 2018), and understanding the costs of evasion (Litina and Palivos 2016); see Alm (2018) for a survey.
Aside from matching the models used in some prior studies (so that the results here can be directly compared), the use of quasilinear preferences in (1) has several benefits: it features money-metric utility, it equates compensated and uncompensated elasticities, and it makes the main derivations transparent. But it is not critical for the main point of the paper and, in the Appendix, the main result is derived for general preferences.
See section 2C of Saez’s paper for his model. Seaz’s model, as well as the analysis motivated by his model in the Appendix, takes third-party reported income as given, but assumes one can vary the reporting of other (called “informal” by Saez) earnings.
Also related are changes in enforcement based on changes in the use of presumptive taxes or the use of particular tax regimes at certain levels of reported income; Agostini (2016) gives some examples.
Similar intuition comes from inspecting first-order condition of (11) with respect to \(l_r\), which is \(-tw - z_{l_r} = 0\). For \(l_r<l^n\) the function \(z_{l_r} =-tw+F_{lr}\) so that the left-hand side of this first-order condition is always positive. For \(l_r>l^n\) the condition becomes \(-tw=0\), so that the left hand side is always negative. The optimal choice of \(l_r\) is thus at the notch.
More precisely, suppose that the government introduced a tax kink so that for \(wl_r \ge wl^n\) the tax rate became \(t^n>t\). Based on Eq. (16), an interior solution for \(l_r\) means that, in the pre-tax-kink setting, \(-tw-g_{l_r}=-tw+g_l>0\) when \(l_r=l^n\). For a sufficiently high post-kink tax rate—specifically, for \(t^n \ge g_l(l-l^n)/w\)—it will be possible to (all else equal) induce this person to report income at the notch.
Moreover, even if we specified a particular functional form for \(\Psi (l,\alpha )\), the relationship between \(\alpha\) and the optimal choices of l and \(l_r\) would still depend on the (unspecified) cost-of-evasion function g.
In Appendix “Moving onto the notch: an example” section we consider an example where individuals initially reporting income above the notch respond to an increase in the tax rate by bunching. Individual utility falls by more when a notch necessitates bunching after a tax increase, but in this case the presence of the notch yields greater social welfare. The intuition here can thus extend to the case of such switchers. Moreover, the numerical simulations in Sect. 2 also allow for switching in reported income above, below, or onto the notch.
Similar intuition can also apply to situations with tax evasion and expenditure decisions; Hungerman (2014) considers such a case.
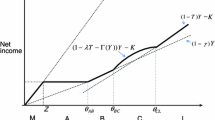
Both l and \(l_r\) are chosen together; in this figure different values of real income \(l>l_r\) are depicted for a given value of reported income \(l_r\).
Weighting the penalty function by \(\phi\) complicates the analysis but does not change the intuition.
We thus allow endogenous responses to changes in t (outside of the braces) and allow individuals to reach corner solutions in taxable income (ie bunch at the notch), but maintain the assumption that small tax changes do not induce individuals to start or stop bunching in taxable income. Below we consider a simulation that allows agents to change their labor supply across the notch as tax rates change.
Real-world estimates of \(\theta _t^n\) could generate meaningful changes in the optimal tax condition in (25). Best et al. (2015) show that low-rate firms in their data display double the density they should near a kink (apparently through evasion), with roughly 25% of firms locating near the kink. See panel B of their Figure 3, and row 2 of Table 2. If \(\theta _t^n = .25\), (25) would consequently be 1/(1-.25) =1.33 times larger in size than in a no-evasion case where \(\theta _t^n=0\). They find even larger bunching behavior for some other types of firms.
References
Agostini, C. (2016). Small firms and presumptive tax regimes in Chile: Tax avoidance and equity. Working paper.
Alm, J. (2018). What motivates tax compliance? Economic Surveys, 33, 353–388.
Almunia, M., & Lopez-Rodriguez, D. (2018). Under the radar: The effects of monitoring firms on tax compliance. American Economic Journal: Economic Policy, 10, 1–38.
Artavanis, N., Morse, A., & Tsoutsoura, M. (2016). Measuring income tax evasion using bank credit: Evidence from Greece. The Quarterly Journal of Economics, 131, 739–798.
Best, M., Brockmeyer, A., Kleven, H., Spinnewijn, J., & Waseem, M. (2015). Production versus revenue efficiency with limited tax capacity: Theory and evidence from Pakistan. Journal of Political Economy, 123, 1311–1355.
Bigio, S., & Zilberman, E. (2011). Optimal self-employment income tax enforcement. Journal of Public Economics, 95, 1021–1035.
Blinder, A., & Harvey, R. (1985). Notches. The American Economic Review, 75, 736–747.
Carrillo, P., Pomeranz, D., & Singhal, M. (2017). Dodging the taxman: Firm misreporting and limits to tax enforcement. American Economic Journal: Applied Economics, 9, 144–64.
Chetty, R. (2009). Is the taxable income elasticity sufficient to calculate deadweight loss? The implications of evasion and avoidance. American Economic Journal: Economic Policy, 1, 31–52.
Feldstein, M. (1999). Tax avoidance and the deadweight loss of the income tax. Review of Economics and Statistics, 81, 674–80.
Frey, B. (1997). A constitution for knaves crowds out civic virtues. The Economic Journal, 107, 1043–1053.
Gruber, J., & Saez, E. (2002). The elasticity of taxable income: Evidence and implications. Journal of Public Economics, 84, 1–32.
Hungerman, D. (2014). Public goods, hidden income, and tax evasion: Some nonstandard results from the warm-glow model. Journal of Development Economics, 109, 188–202.
Hungerman, D., & Wilhelm, M. (2021). Impure impact giving: Theory and evidence. Journal of Political Economy, 129, 1553–1614.
Keen, M., & Slemrod, J. (2017). Optimal tax administration. Journal of Public Economics, 152, 133–42.
Kleven, H. (2016). Bunching. Annual Review of Economics, 8, 435–64.
Kleven, H., & Waseem, M. (2013). Using notches to uncover optimization frictions and structural elasticities: Theory and evidence from Pakistan. Quarterly Journal of Economics, 128, 669–723.
Litina, A., & Palivos, T. (2016). Corruption, tax evasion, and social values. Journal of Economic Behavior & Organization, 124, 164–177.
Lockwood, B. (2020). Malas notches. International Tax and Public Finance, 27, 779–804.
Luttmer, E. F. P., & Singhal, M. (2014). Tax morale. Journal of Economic Perspectives, 28, 149–68.
Meiselman, B. (2018). Ghostbusting in Detroit: Evidence on nonfilers from a controlled field experiment. Journal of Public Economics, 158, 180–193.
Mirrlees, J. A. (1971). An exploration in the theory of optimum income taxation. The Review of Economic Studies, 38, 175–208.
National Taxpayer Advocate. (2017). Annual report to congress, Vol. 1.
Reinganum, J., & Wilde, L. (1985). Income tax compliance in a principal-agent framework. Journal of Public Economics, 26, 1–18.
Saez, E. (2001). Using elasticities to derive optimal income tax rates. Review of Economic Studies, 68, 205–29.
Saez, E. (2010). Do taxpayers bunch at kink points? American Economic Journal: Economic Policy, 2, 180–212.
Sallee, J., & Slemrod, J. (2012). Car notches: Strategic automaker responses to fuel economy policy. Journal of Public Economics, 96, 981–999.
Slemrod, J. (2013). Buenas notches: Lines and notches in tax system design. eJournal of Tax Research, 11, 259–283.
Acknowledgements
Thanks to the editor and anonymous referees for helpuful suggestions. Thanks also to Teja Konduri and especially to Vivek Moorthy for excellent research assistance.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declares that he has no relevant or material interests that relate to the research described in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 General preferences
Here, we derive the main result from (2.2) for general preferences. The agent maximizes
where \(\tau\) is a lump sum tax that will be used to derive comparative statics. This yields the first-order conditions:
Consider a change in the lump sum tax rate \(\tau\) in a world with no evasion. In this case the first-order condition in (27) still holds, with the function z set to zero. Taking the derivative of (28), we have:
Gathering terms,
Now consider a case with \(l_r^{*}=l^n\), where again by assumption the individual is at a notch so that (28) does not hold and \(z=0\). Differentiating (27) with respect to t, we have:
And solving for \(l_t\) yields:
and so for a change in the tax rate \(d\tau =wl^n dt\) the two effects will be the same. Thus, we once again have that a change in the proportional tax rate t produces no change in \(l_r^{*}\), and elicits the same effect on \(l^{*}\) as does an appropriately sized lump sum tax \(\tau\).
1.2 Derivation for the Saez model
Here we will show that it is possible to have efficient taxation in a model akin to the one used in Section 2.C in Saez (2010). That model differs from the model used in this study in four ways. First, he assumes linear preferences. Second, he introduces fixed costs of both reporting earned income, denoted \(q_A\), and of reporting earned income different from actual earned income, denoted \(q_M\). Third, he assumes earnings do not respond to taxes. Fourth, he assumes that the tax function is single peaked.
In Saez’s notation, total earnings (which are perfectly inelastic) are \(w+y\), where w is formal earnings that cannot be evaded, and y is informal earnings that can be evaded. The individual chooses \(\hat{y}\) to report; w is assumed fixed. The individual faces a tax function \(-T(w+\hat{y})\) which is single peaked. We will suppose that this tax function is differentiable in a parameter t, so that the function is \(T(w+\hat{y}, t).\) Otherwise, we would not have a parameter to optimize over for social welfare. The individual maximizes:
(cf. equation 7 in Saez). The only optimal choices would be to report no informal income, to truthfully report, or to report so that one is at the peak. (Saez proves this.) Suppose we are at the peak so that the first-order condition holds:
The welfare function is:
As in the text, assume that a change in the parameter t does not induce any “switching,” for example between choosing the be at the peak versus choosing to report all (or no) informal income. Then the derivative of (35) is:
where the first two terms cancel and the last term is zero by (34). Thus, the model again shows that under evasion, the marginal welfare cost of a change in the tax system must be zero. Note here that the result is obtained not just for a linear tax rate, but for a more general change in parameters in the face of a nonlinear (but single peaked) tax system.
The result is worth a second thought, however, as one might observe that in the above solution there is a discontinuity in the cost of evasion, but this discontinuity occurs away from the optimal choice of evasion. Here, and unlike in the main analysis in the paper, evasion is determined by a first-order condition rather than by an enforcement notch. The difference comes from Saez’s strong assumption that actual labor supply is perfectly inelastic: in Saez’s model it is actual labor supply that is at a “corner” solution (in that no interior first-order condition characterizes it), while reported labor supply is determined by an interior solution that, due to single peaked taxes, sets the marginal tax rate to zero. Saez’s assumption of a nonlinear tax system with linear preferences is also the reverse of what is done in the paper, although any combination of the two that admits a convex solution characterized by a first-order condition independent of a tax rate could suffice. Aside from highlighting the overlooked importance of enforcement notches, and enforcement more generally in discussions of taxation and welfare, a benefit of the model used in the main text of this paper is that it allows taxation to be distortionary in labor supply, whereas by assumption that channel is shut down in Saez’s model. In the Saez model, if reported income equals true income, then the tax system has no effect (since true income is by assumption fixed) and if reported income is zero, then the tax system creates no deadweight loss but also creates no revenue. Indeed, in Saez’s model, which was not intended for serious consideration of efficiency issues, if \(q_A=0\) then there will never be deadweight loss from taxation. But both models highlight how a corner solution in one choice variable and an interior solution in the other can facilitate an efficient tax system that nonetheless manages to raise revenue.
1.3 Proof of Proposition 1
The first-order conditions are
For part A, \(g_l = -g_{l_r}\) and \(z_l= -z_{l_r}\). This last equality becomes \(z_l = t w - g_l\) using (38). Plugging this into (37) produces the solution for \(l^{*}\) in (17). Replacing \(-g_{l_r}\) with \(g_l\) and taking its inverse leads to the solution for \(l_r^{*}\). For part B, the solution for \(l_r^{*}\) is the same as in A noting \(z_{l_r}=0\). Plugging (38) into (37) produces the solution for \(l^{*}\). For part C, \(l_r^{*}\) is given and \(l^{*}\) follows directly from (37). Multiply both sides of each solution by w for the expressions in the proposition.
1.4 Proof of Proposition 2
Differentiating (21) with respect to t yields:
The above expression consists of three summations, each taken over different values of \(\alpha\). For each of the three summations, we can write the general expression:
where the superscript \(i \in \{u,n,a\}\) determines whether the summation in question is for individuals under, at, or above the notch. The expression in (40) simplifies to
The evaluation of Eq. (41) depends upon whether the sum in question is for individuals reporting income under, at, or above the notch. For those under the notch, where \(l_r^{*}<l^n\), the optimal solutions are given by (17) (where one could write \(\psi ^{-1}(w(1-t))\) as \(\psi ^{-1}(w(1-t),\alpha )\)). By the first order condition for (14), for this group \(z_{l_r}=-tw-g_{l_r}=-tw+g_l\), and \(z_l = -z_{l_r}\) and finally \(g_l = -g_{l_r}\). Then (41) becomes:
For those at the notch, \(z=0\) and by (19) we have \(\frac{\mathrm{d} l^{*}}{\mathrm{d} t}=\frac{\mathrm{d} l_r^{*}}{\mathrm{d} t}=0\) so that the summation equals zero. For those reporting income above the notch, \(z=0\) and the first-order condition becomes \(tw=g_{l_r}\). Plugging these results in for all individuals yields:
Lastly, while each of the above summations resembles an expected value, as noted above the PMFs \(h^u\) and \(h^a\) do not sum to unity. Re-scaling them to sum to unity (ie, multiplying by \({\mathcal {G}}(l^n)-\beta\) over \({\mathcal {G}}(l^n)-\beta\), for the first summation) allows us to express (43) as:
which matches the proposition.
1.5 Moving onto the notch: an example
Consider a taxpayer strictly above the notch, so that \(z(l^{*}, l_r^{*}, t) = 0\). The initial tax rate is t and let \(w=1\). Let the cost of evasion be quadratic, \(g(l-l_r)= \frac{1}{2}(l-l_r)^2\), and suppose labor effort is isoelastic with unit elasticity of supply e so that \(\Psi =\frac{1}{1+e}l^{(1+1/e)} =\frac{1}{2}l^2\). The individual solves:
The first-order conditions are \(1-l+l_r-l = 0\) and \(-t + l - l_r = 0\). Combining yields \(l^{*} = 1-t\) and \(l_r^{*} = 1-2 t\). Assume an interior optimal choice for \(l_r^{*}\), so that \(t<1/2\). Of course, if the tax rate increases, labor supply and reported income both fall, but reported income falls by more. Using the first-order conditions (noting \(l-l_r = t\)), the value function is
Now introduce a notch \(l^n\). For an individual who bunches, \(l_r^{*} = l^n\) and the first-order condition for l in (45) becomes \(l^{*} = \frac{1}{2}(1+l^n)\). A bunching individual desires labor income above the notch and reported income below the notch; the first will hold if \(l^n < 1\) and the second if \(1-2t<l^n\). The value function now is:
It can be shown that (47) > (49); this is omitted for brevity but logically it must be true, else the individual optimized wrong.
Consider then an individual initially at an interior solution who faces an increase in taxes from t to \(\bar{t} > t\). We will compare a purely-interior case to a case where a notch is present and the change results in “switching,” i.e. bunching at the notch. From the above it follows that the individual facing the notch who must bunch will be worse off than if they were not constrained at the notch. But how will social welfare compare between the two cases?
Begin with the purely-interior case. Social welfare is: \(V(l^{*}, l_r^{*}, t) + tl_r^{*} = y+1/2-t^2\). With the higher tax rate, this is simply \(y+1/2-\bar{t}\,^2\). Next, if the notch is present and the tax increase induces a person to bunch, initial welfare is the same as before, and after the tax rate change welfare is \(V(l^{*}, l^n, \bar{t}) + tl^n = y+1/4+l^n/2-(l^n)^2 /4\).
A tax rate that induces bunching onto notch \(l^n\) will thus have higher social welfare than in the no-notch case if (and only if):
The left-hand side is increasing in \(l^n\) for \(l^n<1\). Since \(l^n>1-2\bar{t}\), the left hand side must then be greater than what is obtained by substituting \(1-2\bar{t}\) for \(l^n\):
The equality follows from routine algebra but again logically must be true—if the notch were set to the initial level of reported income, social welfare will be the same as before. Thus for “switchers”, individual utility falls by more if a notch necessitates bunching after a tax increase, but the presence of the notch yields greater social welfare.
1.6 Optimal taxation and proof of Proposition 3
Consider first the proposition. Social welfare is given by
where
This matches the social welfare function in Sect. 2.3 used to derive Eq. (22), with an additional term \(\phi t w l_r^{*}\) for each individual. Using Eq. (22), then, the first derivative of (52) can be written:
where the first row is from (22). The second row can be written \(\phi \left( \bar{\text {TI}}+t{E}[\frac{\mathrm{d}TI}{\mathrm{d}t}] \right)\), where \(\bar{\text {TI}}=\sum \nolimits _{i\in \{u,n,a\}}\sum \nolimits _{\alpha }{}(wl_r^{*})h^i (\alpha )\) represents the sum and mean of taxable income for all individuals since the total population is of size unity. Using this, setting (54) to zero, and denoting \({\mathcal {G}}(w l^n)\) as \({\mathcal {G}}\), we have:
Define mean elasticities thusly:
And define income shares as:
Then the first-order condition in (55) can be written as
yielding:
which matches Eq. (24) in the proposition.
Equation (25), that \(\frac{t^{*}}{1-t^{*}} =\frac{\phi }{ e(1-\theta _t^n)(1+\phi )}\), follows. First, by construction
so that setting \(\mu =0\) in Eq. (24) leads to \(\frac{t^{*}}{1-t^{*}}=\frac{\phi }{ e\theta _t^u+e\theta _t^a+\phi \varepsilon _t}=\frac{\phi }{ e(1-\theta _t^n)+\phi \varepsilon _t}\).
Next, we show that \(\varepsilon _t = e (1-\theta _n^n)\), and the result follows. This can be seen given:
Plugging this in for \(\varepsilon _t\) yields the result.
Rights and permissions
About this article
Cite this article
Hungerman, D. Tax evasion, efficiency, and bunching in the presence of enforcement notches. Int Tax Public Finance 30, 43–68 (2023). https://doi.org/10.1007/s10797-021-09710-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10797-021-09710-0