1 Introduction

It is well-known that the speed of a test particle, freely falling towards the event horizon of a black hole in Schwarzschild spacetime tends to the value of the speed of light in a vacuum, c, when measured by observers positioned outside the horizon. This result is independent of the initial conditions (see e.g Landau and Lifshitz [1]). An appealing feature of this result is that it may be interpreted as a manifestation of energy conservation (see also Sect. 2 below). A special case of this is free fall from infinity—then one finds coincidence with the classical approximation, i.e. the Newtonian escape velocity, from a spherical object of mass M, is \(v = \sqrt{2M/r}\) (see e.g. [2]). The Schwarzschild spacetime geometry is described by the metric

$$\begin{aligned} d \tau ^2= g_{ tt} dt^2- g_{ tt}^{-1} dr^2 - r^2 d \theta ^2 - r^2 \sin ^2 \theta d \phi ^2 \end{aligned}$$
(1)

where \(g_{ tt} = 1 - \frac{r_S}{r}\), \(r_S = 2M\), M denotes the mass of the source of the gravitational field and we have used normalized units where \(c=G=1\). This metric reveals a (geometric) singularity, an event horizon at \(r_S\). This can be avoided by the use of other coordinate systems. One of these is the Gulstrand–Painleve approach, where the coordinate time t is substituted by the proper time of the observer radially infalling from infinity, \(t_{inf}\). The resulting metric is singularity free,

$$\begin{aligned} d \tau ^2 = g_{ tt} d{t_{inf}}^2 - 2\sqrt{\frac{2M}{r}} dt_{inf} dr - dr^2-r^2 \, d\theta ^2-r^2\sin ^2\theta \, d\phi ^2 \end{aligned}$$
(2)

Generalization of this approach has led to an interesting perspective that has inspired laboratory analogues of black holes [3,4,5]. It has been claimed that a black hole space-time resembles a river flowing toward a waterfall: the closer to the waterfall the faster it flows. At some point, the point of no return, it exceeds a critical value of the speed, such that nothing can propagate upstream. As shown by Hamilton and Lisle [2] an interpretation of a space radially flowing inward at the Newtonian escape velocity could be applied to the case of a Schwarzschild black hole. The point of no return represents the horizon of the black hole: the value of the escape velocity reaches, and inside the horizon, exceeds c. In pioneering work, Unruh [6] suggested a condensed matter realization of such a strong gravitational field: in fluids there might exist acoustic horizons separating sub- and supersonic flows. Such a horizon would play the role of the event horizon of black holes. Recently, experimental creation of horizons were reported in a variety of systems: microcavity polaritons [3], water channels [7], atomic Bose–Einstein condensates [8, 9], and others [4, 5]. Outside the horizon, all of the “fish” (an analogy for both massive and massless objects), can make their way against the flow but inside the horizon everything is carried toward the ultimate fate, i.e. the central singularity [2]. In this context one can ask how does the speed of the radially infalling test particle change inside the horizon? One might reasonably expect that it would further increase inside the horizon as it fell through. However the critical question of how speed is measured in such circumstances arises. But, as explained elsewhere in extended discussions [10,11,12,13,14,15], the speed of the test particle crossing the horizon and measured within a moving frame of reference, which also simultaneously crosses the horizon, remains smaller than c. Although some aspects of the problem of the interpretation of the value of the speed of a freely falling test particle outside, [1, 15] and on the horizon have been discussed and presented in a series of papers [11,12,13,14] it appears that the particular context of this phenomenon remains worthy of greater clarification. It should be noted that the problem of the speeds inside the horizon presented by Hamilton [10] dealt with a somewhat different perspective from that considered here and test bodies crossing the horizon were not considered.

The aim of this paper is to discuss speeds of radially infalling test particles as measured inside (but also on and outside) the horizon in a consistent manner. We propose to consider two distinct classes of observers who may carry out a measurement on the speed of an infalling test particle, linking the outcomes of measurements inside the black hole to observations outside the horizon. One of these observers, located within an infalling system, would measure, by recording incoming signals from a static source located outside the horizon, the rate of change of their redshift, and relate this rate to a notional speed; the other is an observer residing “at rest” inside the horizon: the counterpart of the static observer outside the horizon. It is interesting to note that even though the results of these two observers seem to be contradictory, nonetheless the final conclusion turns out to be self-consistent, albeit unexpected. We shall consider a spherically symmetric, static spacetime (Eq. 1) but in a later section other kinds of black holes, where two types of horizons exist, will be discussed. The paper is organized as follows. In the following section some basic principles and results regarding free fall in Schwarzschild spacetime are recapitulated and the frequency ratio-speed correlation outside the horizon is derived. In Sect. 3 the frequency ratio inside the horizon is determined by means of Kruskal–Szekeres coordinates and the speed as measured by a so-called T-observer is found leading to the frequency ratio-speed (anti)correlation inside the horizon. The discussion is generalized in Sect. 4: the speed of the test particle in other kinds of black holes where outer and inner horizons are present is briefly analyzed. In the final section, a discussion and concluding remarks are presented.

2 Outside the horizon: frequency ratio-speed correlation

In radial free fall (RF) of a test particle, its velocity vector has two non-vanishing components

$$\begin{aligned} u_{ RF} = u^t \partial _t + u^r \partial _r \end{aligned}$$
(3)

that are found from the normalization condition

$$\begin{aligned} u^2 =u^{\alpha }u_{\alpha } \equiv g_{\alpha \beta } u^{\alpha } u^{\beta } = 1 \end{aligned}$$
(4)

and energy conservation

$$\begin{aligned} u_t&= g_{ tt}u^t = \varepsilon \end{aligned}$$
(5a)
$$\begin{aligned} u^r&=-\sqrt{ \varepsilon ^2 -g_{ tt}} \end{aligned}$$
(5b)

where \(\varepsilon \) denotes energy per unit mass; \(\varepsilon = \sqrt{g_{ tt}(r_0)}\) for the test particle starting at \(r_0\). A static observer, located at r, whose four-velocity vector has only a non-vanishing t-component (t-observer, t-o),

$$\begin{aligned} u_{t\hbox {-}o} = u^t \partial _t = g_{ tt}^{-1/2} \partial _t, \end{aligned}$$

measures the speed V of the test object RF through [13, 15],

$$\begin{aligned} u^{\alpha }_{t\hbox {-}o} u_{RF,\alpha } = g_{\alpha \beta } u^{\alpha }_{\mathrm{t-o}}u^{\beta }_{ RF} = \frac{1}{\sqrt{1-V^2}} \end{aligned}$$
(6)

and finds

$$\begin{aligned} V^2 = \frac{\varepsilon ^2 - g_{ tt}(r)}{\varepsilon ^2} . \end{aligned}$$
(7)

In the case of free fall from infinity \(\varepsilon = 1\) and \(V^2 = \frac{2M}{r}\) is the Newtonian escape velocity. In the general case, the speed (7) steadily increases and its value approaches the value of the speed of light in a vacuum

$$\begin{aligned} g_{ tt}(r) \rightarrow 0 \Rightarrow V^2 \rightarrow 1 \end{aligned}$$

as the test particle approaches the horizon, \(r\rightarrow r_S\).

One can imagine that an observer located in RF’s frame of reference exchanges electromagnetic signals with an observer arranged at a starting point \(r_0\), hereafter called the Mother Station (MS). These signals follow radial null geodesics, characterized by a tangential four vector \(k = k^{\alpha }\partial _{\alpha }\), \(k^{\alpha } = \frac{dx^{\alpha }}{d\sigma }\), forming by definition a null vector

$$\begin{aligned} g_{\alpha \beta }k^{\alpha } k^{\beta } = 0 \end{aligned}$$
(8)

where \(\sigma \) is an auxiliary parameter of such a light-like (photon) world-line. The components of k are given as:

$$\begin{aligned} k^t = \frac{\omega _{\infty }}{g_{ tt}},\;\; k^r = {\mp } \omega _{\infty } \end{aligned}$$
(9)

with the \({\mp }\) sign corresponding to incoming and outgoing rays. The frequency measured by observer O characterized by velocity vector \(u_O\) is:

$$\begin{aligned} \omega _O = g_{\alpha \beta }u^{\alpha }_O k^{\beta }. \end{aligned}$$
(10)

Applying (10) one finds that RF (r-receiver), records MS’s (s-sender) signals as redshifted according to (see Fig. 1)

$$\begin{aligned} \frac{\omega ^r_{ RF}}{\omega ^{s}_{MS}} = \frac{1}{1+\sqrt{\frac{\varepsilon ^2 - g_{ tt}(r)}{\varepsilon ^2}} }\equiv \frac{1}{1+V}. \end{aligned}$$
(11)

MS records RF’s signals as critically redshifted

$$\begin{aligned} \frac{\omega ^{r}_{MS}}{\omega ^s_{ RF}} = 1-V. \end{aligned}$$
(12)
Fig. 1
figure 1

Monotonic and continuous change of the frequency ratio \( \frac{\omega ^{r}_{ RF}}{\omega ^s_{MS}}\) outside and inside the horizon for \(\varepsilon = 1\), fall from infinity. The vertical line represents the horizon located at \(r_S = 2\) (distance expressed in M)

Full size image

The results (11) and (12) manifest a combination of distinct effects: gravitational contributions and kinematic effects related to the motion of RF [16]. Their characteristic features are: the form and the limiting value of the frequency ratio - speed correlation. When the falling system approaches the black hole horizon,

  • the frequency redshift recorded by RF tends to 1 / 2,

  • the frequency redshift recorded at the MS tends to zero.

What would the frequency shift be inside horizon? This question, irrelevant from the point of view of MS, is relevant from RF’s perspective, who will continue to receive signals from MS even after crossing the horizon.

To consider this one can use a coordinate system that is non-singular at the horizon (unlike Schwarzschild coordinates), namely Kruskal–Szekeres coordinates.

3 Inside the horizon: frequency ratio-speed (anti)correlation

In order to carry out a frequency measurement inside the horizon one transforms radial incoming geodesics, time-like, (5) and light-like (9), from Schwarzschild coordinates into the Kruskal–Szekeres coordinate system (see “Appendix”). Using Eq. (A.6) one obtains the following expressions for RF’s velocity components:

$$\begin{aligned} u^v&= \frac{4M}{K(u^2-v^2)} \left( u\varepsilon - v\sqrt{\varepsilon ^2 - \frac{K(u^2 - v^2)}{16M^2}} \right) , \end{aligned}$$
(13a)
$$\begin{aligned} u^u&= \frac{4M}{K(u^2-v^2)} \left( v\varepsilon - u\sqrt{\varepsilon ^2 - \frac{K(u^2 - v^2)}{16M^2}} \right) , \end{aligned}$$
(13b)

[c.f. Eq.  (5)], and expressions for the wave vector components [cf. Eq. (9)]

$$\begin{aligned} k^v = \frac{4M \omega _{\infty }}{K(u+v)} = - k^u. \end{aligned}$$
(14)

It should be emphasized that the wave vector components, (14) and the velocity vector components, Eq. (13) behave smoothly in the horizon’s vicinity, \(u=v\) (see “Appendix”). Hence the frequency ratio of signals emitted by the MS and recorded by RF is given as follows

$$\begin{aligned} \frac{\omega ^r_{ RF}}{\omega ^{s}_{MS}} = \frac{1}{1+\sqrt{1-\frac{K(u^2-v^2)}{16M^2 \varepsilon ^2 }}}. \end{aligned}$$
(15)

This result turns out to be a well-defined function both outside, \(r>r_S\) (\(u>v\)) and inside, \(r< r_S\) (\(u<v\)) the horizon.

Outside the horizon formula (15) reproduces the result obtained within the Schwarzschild coordinates, Eq. (11): the frequency redshift of the incoming light from the Mother Station tends, from above, to 1 / 2 as the speed of the infalling observer, RF tends to the speed of light. Then it takes the value 1 / 2 on the horizon and decreases further to zero inside the horizon. Hence, an outside-horizon property of the frequency shift, namely a monotonic decrease, is preserved also inside the horizon.

What about the other side of this relation, the linearity of the inverse frequency shift and the speed of RF, inside the horizon? It seems to be a matter of speculation requiring verification. On the contrary, anybody who would measure the speed of a test particle, by definition, has to find a value smaller than 1. One can ask: what is the speed of RF as measured by observers residing inside the horizon? There is a special class of such observers who play a role similar to the static observers outside the horizon, t-o. Those observers inside the horizon, labeled here as T-o are characterized by a velocity vector whose non-vanishing components are [17, 18]

$$\begin{aligned} \begin{aligned} u^v&= \frac{v}{\sqrt{K(v^2 - u^2)}},\\ u^u&= \frac{u}{\sqrt{K(v^2 - u^2)}}. \end{aligned} \end{aligned}$$
(16)

As underlined elsewhere various observations made by T-o, inside the horizon, may resemble those made by t-o, outside the horizon. Nevertheless, t-o and T-o differ in a fundamental manner: while the former ones must be supported in position since they are static observers, the latter must follow a geodesic trajectory.

The perception by T-o of the speed \(\tilde{V} \) of a test particle coming through the horizon and passing by follows from [c.f. Eq. (6)]

$$\begin{aligned} u^{\alpha }_{T\hbox {-}o} u_{RF, \alpha } = \frac{1}{\sqrt{1-\tilde{V} ^2}} = \sqrt{\frac{ \varepsilon ^2 +\frac{K(v^2 - u^2)}{16M^2} }{ \frac{K(v^2 - u^2)}{16M^2} }}. \end{aligned}$$
(17)

Hence, the speed of the test particle as measured by the T-observer inside the horizon is expressed as:

$$\begin{aligned} \tilde{V} ^2 = \frac{\varepsilon ^2}{ \varepsilon ^2 + \frac{K(v^2 - u^2)}{16M^2} } \end{aligned}$$
(18)

i.e. it takes an inverse form to the one measured by a t-observer located outside the horizon [c.f. Eq. (7)]. The meaning of result (18) is the following: from the point of view of a T-observer, the speed of a radially infalling test particle that crosses the horizon \(u=v\) and heads towards the ultimate singularity, decreases from the value of the speed of light to zero, as \(K\xrightarrow {r\rightarrow 0} \infty \). The speed of the test particle radially infalling as measured by t-observers outside the horizon and by T-observers is illustrated in Fig. 2.

Fig. 2
figure 2

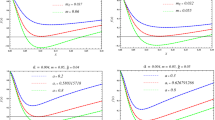
Values of squared speeds \(V^2\) measured by t-o (outside the horizon) and \(\tilde{V}^2\) measured by T-o (inside the horizon) for different test particles in a Schwarzschild metric. The red curve corresponds to \(\varepsilon =1\) (\(\tilde{V}^2 = r/r_{S}\)), the green curve to \(\varepsilon =0.5\) and the blue one to \(\varepsilon =0.2\). The vertical line represents the horizon located at \(r_S = 2\) (distance expressed in M)

Full size image

4 Speed between the outer and inner horizons

The three other kinds of black holes, charged (Reissner–Nordstrom, R-N), rotating (Kerr), and both charged and rotating (Kerr–Newman, K-N), apart from the event (outer) horizon, possess an inner horizon too. In such a case one can ask both for the status of observers at rest between the horizons and their measurements of the speeds of a test particle. In order to accomplish this task, one can make the following remark.

The considerations above concerning the interior of the Schwarzschild black hole were carried out employing singularity-free Kruskal–Szekeres coordinates. But the outcomes of these analyses can be reproduced when Schwarzschild coordinates are applied inside the horizon. However, one must remember then that for \(r<r_{S}, g_{ tt} = \left( 1-\frac{r_{S}}{r} \right) < 0\): a time-like Killing vector is converted into a space-like one. Then t- and r- coordinates interchange their roles: r plays the role of the temporal coordinate and t plays the role of a spatial coordinate. One can apply this in a discussion of the speeds between the horizons.

The R-N metric of the isotropic, static, charged black hole is

$$\begin{aligned} d \tau ^2= g_{ tt} dt^2- g_{ tt}^{-1} dr^2 - r^2 d \theta ^2 - r^2 \sin ^2 \theta d \phi ^2 , \end{aligned}$$
(19)

where

$$\begin{aligned} g_{ tt} = 1 - \frac{r_S}{r}+\frac{Q^2}{r^2}. \end{aligned}$$
(20)

There exist outer “\(+\)” and inner “−” horizons that are determined as zeros of \(g_{ tt}\)

$$\begin{aligned} r_{\pm }^{RN} = \frac{1}{2} \left( r_{S} \pm \sqrt{r_S^2 - 4Q^2} \right) , \end{aligned}$$
(21)

Q denotes the charge (\(Q<M\)). Time-independence of the metric tensor results in energy conservation for \(r>r_+\) and in consequence the velocity vector of the radially infalling test particle takes the form (3), (5) also in this case:

$$\begin{aligned} u_{ RF} = \frac{\varepsilon }{g_{ tt}} \partial _t - \sqrt{\varepsilon ^2 - g_{ tt}} \partial _r. \end{aligned}$$
(22)

A representative t-o of a class of observers at rest above the horizon \(r_1 > r_+\)

$$\begin{aligned} U_{t\hbox {-}o} = \frac{1}{\sqrt{g_{ tt}(r_1)}} \partial _t, \end{aligned}$$
(23)

measures the speed of the test particle RF and finds the same result as in the case of Schwarzschild space-time: its value

$$\begin{aligned} V^2 (r_1) = \frac{\varepsilon ^2 - g_{ tt}(r_1)}{\varepsilon ^2} \end{aligned}$$
(24)

tends to the value of the speed of light in a vacuum, as \(r_1 \rightarrow r_+\). The counterpart of this class of observers, arranged between the horizons, \(r_-<r<r_+\) includes T-observers,

$$\begin{aligned} U_{T\hbox {-}o} = -\sqrt{-g_{ tt}(r)} \partial _r. \end{aligned}$$
(25)

Measuring the speed \(\tilde{V}\) of the test particle (22) between the two horizons, T-o finds

$$\begin{aligned} {\tilde{V} }^2(r) = \frac{\varepsilon ^2}{\varepsilon ^2-g_{ tt}(r)}. \end{aligned}$$
(26)
Fig. 3
figure 3

Values of squared speeds \(V^2\) measured by t-o (above the outer horizon) and \(\tilde{V}^2\) measured by T-o (between the horizons) for different test particles in the R-N metric for parameter \(Q^2=0.8 M\). The red curve corresponds to \(\varepsilon =1\), the green to \(\varepsilon =0.5\) and the blue to \(\varepsilon =0.2\) . Vertical lines represent horizons located at \(r=\frac{2}{5}, 1\frac{3}{5} \) (distance expressed in M) and the dashed line represents the point \(r^{RN}_{m} = 0.64\) of the minimal value of the squared speed \(\tilde{V}^2\) [see Eq. (27)]

Full size image

This speed, whose value tends to 1 at the outer horizon, decreases to a minimal value (a non-universal feature, depending on the initial conditions, i.e. on \(\varepsilon \)) that is reached at

$$\begin{aligned} r^{RN}_{m} = \frac{2Q^2}{r_S} < \frac{1}{2} r_S \end{aligned}$$
(27)

and then starts to increase towards the value 1 at the inner horizon.

Plots of the velocity of different test particles in the R-N metric measured outside the outer horizon by t-o and between the horizons by T-o are presented in Fig. 3.

In the case of rotating black holes, uncharged and charged, represented by Kerr and Kerr–Newman space-times respectively, the situation above the horizon is specific due to the presence of the ergosphere: there are no observers at rest inside the ergosphere. One can consider then a special case of a test particle falling along an axis of symmetry. In such a case the line element and the metric are represented as follows:

$$\begin{aligned} d \tau ^2= & {} g_{ tt} dt^2 - \left( g_{ tt} \right) ^{-1} dr^2, \end{aligned}$$
(28)
$$\begin{aligned} g_{ tt}= & {} \frac{\Delta }{\rho ^2}, \end{aligned}$$
(29)

where \(\rho ^2 = r^2+\alpha ^2, \Delta = r^2 - r r_S + \alpha ^2 + Q^2\), \(\alpha \) is proportional to angular momentum, and \(Q=0\) represents Kerr spacetime. The outer and inner horizons are defined as

$$\begin{aligned} r_{\pm }^{KN} = \frac{1}{2} \left( r_S \pm \sqrt{r_S^2- 4\left( \alpha ^2 + Q^2 \right) } \right) . \end{aligned}$$
(30)

In this case the results are the same as those derived for the R-N metric Eqs. (22–27), with \(g_{ tt}\) substituted by (29). The speed of the test particle (24) increases as it falls in towards the outer horizon (30): its value tends to 1 with respect to resting observers outside the horizon, t-o (23). Between horizons its speed with respect T-o (24) first decreases to a minimal value, reached at

$$\begin{aligned} r_{m}^{KN} = \left( \frac{Q^2}{r_S} + \sqrt{ \left( \frac{Q^2}{r_S} \right) ^2 +\alpha ^2 } \right) < \frac{1}{2}r_{S}. \end{aligned}$$
(31)

and then increases to 1 when approaching the inner horizon.

One can conclude then that the speed of the radially infalling test particle crossing the region between the outer and inner horizons of the black hole reveals a universal behavior: its value decreases to a minimal value reached at some specific instant Eqs. (27), (31) and then increases to 1 when approaching the inner horizon.

5 Discussion

Signals coming from the Mother Station, recorded in a radially falling frame in Schwarzschild spacetime reveal a simple form of frequency redshift,

$$\begin{aligned} \left( \frac{\omega ^r_{ RF}}{\omega ^{s}_{MS}} \right) ^{-1} = 1+V, \end{aligned}$$
(32)

This implies that when an RF frame approaches the horizon the frequency ratio \(\frac{\omega ^r_{MS}}{\omega ^{s}_{ RF}}\) decreases to the characteristic limiting value 1 / 2. It might be used then as a tool for marking the horizon: the RF observer crosses the horizon when the frequency ratio hits the value 1 / 2. Inside the horizon the frequency ratio continues to decrease towards zero at the ultimate singularity. It might appear as if the speed of the test particle reaches the value of the speed of light at the instant of crossing the horizon and continues to increase further indefinitely as \(r \rightarrow 0\). This seems to comply with a river model interpretation [2,3,4,5].

However, measurement of the speed \(\tilde{V}\) of the test particle performed inside the horizon by the T-observer, the counterpart of the t-observer above the horizon, provides a different outcome. Namely, the T-observers whose specific property in common is that they reside inside (or between) the horizon(s) and their geodesics

$$\begin{aligned} U_{T\hbox {-}o} = \frac{A}{g_{ tt}} \partial _t - \sqrt{A^2 - g_{ tt}} \partial _{r} \Big |_{A=0} = - \sqrt{-g_{ tt}} \partial _r \end{aligned}$$
(33)

are of conserved (zero) momentum, \(A=0\) determine the speed of RF inside horizon \(\tilde{V}\) as monotonically decreasing from a limiting value of 1 (at the horizon) towards the opposite limit 0 at the ultimate singularity. Then an inverse frequency ratio-inverse speed correlation

$$\begin{aligned} \left( \frac{\omega _{ RF}}{\omega _{MS}} \right) ^{-1} = 1+\tilde{V}^{-1} \end{aligned}$$
(34)

is found inside the horizon.

There are two specific aspects of this result. The first is that speeds outside the horizon, \(V = \sqrt{\frac{\varepsilon ^2 - g_{ tt}}{\varepsilon ^2}}\) and inside the horizon, \(\tilde{V}= \sqrt{\frac{\varepsilon ^2}{\varepsilon ^2 - g_{ tt}}}\) are determined inversely. This is a common property for a both black hole with a single horizon (Schwarzschild spacetime) and for black holes with two horizons, an outer and inner one. The explanation of this, in a sense, universal relation is as follows. The Killing vector, which is time-like outside the horizon becomes space-like inside the horizon. In Schwarzschild spacetime this is manifested by the interchange of the roles of the coordinates t and r. Indeed, as indicated by Doran et al. [18] a line element inside the horizon of the (empty) Schwarzschild spacetime is

$$\begin{aligned} d \tau ^2= \left( \frac{r_S}{T} - 1 \right) ^{-1} dT^2- \left( \frac{r_S}{T} - 1 \right) dR^2 - T^2 \left( d\theta ^2+r^2 \sin ^2\theta d \phi ^2 \right) . \end{aligned}$$
(35)

That is \(r \rightarrow T\) and \(t\rightarrow R\). The speed of the radially infalling test particle, regarded as the ratio “distance”/“time”, is therefore inversely related in the exterior and interior of the horizon. This is also the case for other kinds of spherically symmetric and static black holes and the case of axial motion for rotating black holes.

The other specific feature of these considerations is the diverse behavior of the speed inside the horizon. It is found to monotonically decrease from its (asymptotic) value 1 at the horizon to zero at the ultimate singularity in the case of Schwarzschild spacetime. In other cases, non-monotonic behavior is found: it tends to the value 1 at both outer and inner horizons and takes its minimal value at the instant \(r_m\) corresponding to the maximal value of \(\left| g_{ tt}(r) \right| \). This property seems to be worthy of more extended discussion. We will start from the case of a Schwarzschild black hole finding it illuminating in other cases as well. The space inside the horizon [see Eq. (35)], is a dynamically changing [19], cylindrical-like (see e.g. [20]) analogue of a cosmological situation [18]. It is homogeneous along its (cylindrical) axis - that is, the t-coordinate. It was argued by Doran et al. [18] that there is an expansion in such a cosmology along this direction; one also can find a contraction taking place perpendicularly to this direction [21]. Hence, one would expect, and actually one does find, such an anisotropic cosmology to be accompanied by an appropriate Doppler-like frequency shifts: a redshift for an expansion along the t-direction and a blue shift for the contraction occurring perpendicularly to this axis. Thus the observed monotonic decrease of the speed of a test particle inside the horizon reflects the (monotonic) expansion of the interior of the Schwarzschild black hole along the t-direction.

In the case of an R-N black hole, the spacetime between the outer and inner horizons, initially \(r_{m}<r <r_{+}^{RN}\) expands, then the expansion stops, \(r = r_m\) and contraction follows, \(r_{-}^{RN}<r <r_{m}\). This might be illustrated with an appropriate Doppler-like frequency shift [21]. And this is mimicked by the behaviour of the speed of a test particle: initially it decreases, reaching a minimal value at \(r = r_m\) and then increases (asymptotically) to 1 as r tends to the inner horizon, \(r_{-}^{RN}\). The same phenomenon take place in the case of axial motion of a test particle between the horizons of rotating black holes.

Let us underline the main outcome of these considerations. In the radial infall of a test particle in Schwarzschild spacetime, its speed as measured by static observers outside the horizon, t-observers and resting inside the horizon, T-observers is given by inverse expressions for t- and T- due to the interchange of the roles of radial and temporal coordinates. The decreasing value of the speed inside the horizon is a result of expansion of the horizon’s interior (the region within the black hole) along the direction of homogeneity, the t-direction. This claim is confirmed when observing radial fall within Reissner–Nordstrom spacetime or a fall along the symmetry axis for Kerr and Kerr–Newman spacetimes. In those cases, where an internal horizon has been developed, the dynamics of the interior (along the t-direction) is such that final contraction follows an initial expansion and the speed reveals the same behaviour: a final increase follows its initial decrease.