Analysis of the failure at notches and cavities in quasi-brittle media using the Thick Level Set damage model and comparison with the coupled criterion

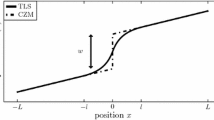
Abstract

The failure of quasi-brittle specimen weakened by sharp or blunted notches and cavities is analyzed under quasi-static loading. The load at failure is obtained with the Thick Level Set (TLS) damage modeling. In this model, the damage gradient is bounded implying that the minimal distance between a point where damage 0 (sound material) to 1 (fully damaged) is an imposed characteristic length in the model. This length plays an important role on the damage evolution and on the failure load. The paper shows that the TLS predictions are relevant. A comparison with the coupled criterion (CC) of Leguillon (2002) is given. A good agreement is obtained for cavities and V-notches provided that the characteristic length of Irwin is small compared to the notch depth (condition for the applicability of the CC criterion). A comparison with failure loads obtained experimentally is also given. In the numerical simulations, uniform stresses are imposed at infinity using a new finite element mapping technique (Cloirec 2005).

Appendices

Appendix A: Details on the softening function and damage profile used in the TLS numerical simulations

The TLS model considered is given by:

$$\begin{aligned} g(d)&= 2 \sqrt{1-d} \end{aligned}$$

(61)

$$\begin{aligned} \tilde{h}(d, \lambda _\mathrm {c})&= \frac{d}{(\sqrt{1-d} + \lambda _\mathrm {c}(1 - \sqrt{1-d})^2)^2} \end{aligned}$$

(62)

where $\lambda _\mathrm {c}$ is a dimensionless parameter defined as the ratio between the TLS thickness ($2 l_\mathrm {c}$) and the cohesive zone length:

$$\begin{aligned} \lambda _\mathrm {c}=\frac{2 l_\mathrm {c}}{E w_\mathrm {c}/ \sigma _\mathrm {c}} \end{aligned}$$

(63)

The above choice (61) corresponds to a linear cohesive relation [already considered in Gómez et al. (2015)]. Indeed, inserting g(d) into (27), we get:

$$\begin{aligned} \sigma&= \sigma _\mathrm {c}\sqrt{1-d} \sqrt{\frac{\tilde{h}(d)}{d}} \end{aligned}$$

(64)

$$\begin{aligned} w&= \frac{2\sigma _\mathrm {c}l_\mathrm {c}}{E} (1 - \sqrt{1-d})^2 \sqrt{\frac{\tilde{h}(d)}{d}} \end{aligned}$$

(65)

Eliminating d in the above yields:

$$\begin{aligned} \frac{\sigma }{\sigma _\mathrm {c}} = 1 - \frac{w}{w_\mathrm {c}} \end{aligned}$$

(66)

The toughness is given by:

$$\begin{aligned} G_{\mathrm {c}}= \frac{1}{2} \sigma _\mathrm {c}w_\mathrm {c}\end{aligned}$$

(67)

The following data for PMMA are used:

$$\begin{aligned} E= & {} 3500~\mathrm{MPa}, \nu = 0.3, \sigma _c = 70~\mathrm{MPa}, \nonumber \\ Gc= & {} 3.5 \; 10^{-4}~\mathrm{MPa~m} \end{aligned}$$

(68)

This implies:

$$\begin{aligned} l_\mathrm {ch}= & {} 2.5\times 10^{-4}~\mathrm{m},~w_\mathrm {c}= 2 G_{\mathrm {c}}/ \sigma _\mathrm {c}= 10^{-5}~\mathrm{m}, \nonumber \\ l_\mathrm {c}= & {} \frac{E w_\mathrm {c}}{2 \sigma _\mathrm {c}} \lambda _\mathrm {c}= 2.5\times 10^{-4}~\lambda _\mathrm {c}~\mathrm{m} \end{aligned}$$

(69)

Regarding the choice for $\lambda _\mathrm {c}$, it needs to be less or equal to 0.5 (Gómez et al. 2015) otherwise the convexity requirement of $\tilde{h}$ is not satisfied. We consider:

$$\begin{aligned} \lambda _\mathrm {c}= 0.2 \end{aligned}$$

(70)

leading to

$$\begin{aligned} l_\mathrm {c}= 5\times 10^{-5} \end{aligned}$$

(71)

Note that for a more general cohesive law

$$\begin{aligned} f_\mathrm {coh} \left( \frac{\sigma }{\sigma _\mathrm {c}}, \frac{w}{w_\mathrm {c}} \right) =0 \end{aligned}$$

the function $\tilde{h}(d, \lambda _\mathrm {c})$ is obtained as the solution to the equation

$$\begin{aligned} f_\mathrm {coh} \left( \sqrt{1-d} \sqrt{\frac{\tilde{h}(d, \lambda _\mathrm {c})}{d}} , \lambda _\mathrm {c}(1 - \sqrt{1-d})^2 \sqrt{\frac{\tilde{h}(d, \lambda _\mathrm {c})}{d}} \right) = 0. \end{aligned}$$

Conditions (7) imply some restrictions on the choice of $f_\mathrm {coh}$ and $\lambda _\mathrm {c}$.

Table 2 Data to compute the generalized stress intensity factor at a single edge notch in an infinite medium

Fig. 22

$A^{\star }$ (Diamond) and $\lambda$ (Triangle) function of the opening angle $\omega$

Appendix B: Generalized stress intensity factor for an edge notch in an infinite medium

The generalized stress intensity factor k at the tip of a notch with depth a in an infinite medium subjected to a prescribed tension $\sigma _\infty$ is given by:

$$\begin{aligned} k = \kappa \sigma _{\infty } a^{1-\lambda } \end{aligned}$$

(72)

where the parameter $\kappa$ is given in Table 2 one has to keep in mind the normalization proposed in Sect. 2.1. For the crack ($\omega =0$) with the usual normalization of the mode I eigenvector, it gives $\kappa ^\prime =1.119$ to be compared to the coefficient 1.122 proposed by Tada et al. (2000).

Appendix C: Data for the coupled criterion—cases of sharp and blunted V-notch

The scalar $\lambda$ is the root of the equation:

$$\begin{aligned} \sin (\lambda \beta ) + \lambda \sin \beta = 0, \quad \beta = 2 \pi - \omega \end{aligned}$$

(73)

whereas values of $A^{\star }$ derive from an asymptotic procedure carried out with respect to the small crack extension length $l_{\mathrm {CC}}$ (Leguillon 2002). The values found in this reference are made dimensionless multiplying by $E/(1-\nu ^2)$. Moreover, keep in mind again the normalization of the eigenvector in Sect. 4.1 (Fig. 22).

Fig. 23

$B^{\star }$ and $\lambda$ function of the dimensionless length $\zeta$

Fig. 24

$C^{\star }$ and $\lambda$ function of the dimensionless length $\zeta$

Table 3 Influence of the opening angle $\omega$ on the singularity strength at a V-notch in mode I and coefficient $A^{\star }$ computed for a Poisson ratio $\nu =0.3$

Similarly $B^{\star }$ and $C^{\star }$ derive from an asymptotic procedure but carried out with respect to the notch root radius $\rho$. The $B^{\star }$ and $C^{\star }$ coefficients were computed for a Young modulus $E= 2300~\mathrm{MPa}$ and a Poisson ratio $\nu =0.3$ and then multiplied by $E/(1-\nu ^2)$. As $A^{\star }$, they are functions of $\omega$ and in addition they depend also on the dimensionless crack length $\zeta =l_{\mathrm {CC}}/\rho$ which plays the role of a parameter in the model involving both lengths $\rho$ and $l_{\mathrm {CC}}$. It is illustrated in Figs. 23 and 24. Attention is drawn to the fact that $C^{\star }$ only slightly deviates from 1 except for small values of $\zeta$. This later case corresponds to large root radii compared to the crack length at initiation. At the limit it falls outside the scope of the asymptotic expansion used here which assumes that the two small parameters $\rho$ and $l_{\mathrm {CC}}$ are of the same order of magnitude. A different procedure has to be employed (Tables 3, 4, 5, 6, 7).

Table 4 Variations of the coefficients $B^{\star }$ and $C^{\star }$ for a blunted V-notch for different opening angles $\omega$

Table 5 Variations of the coefficients $B^{\star }$ and $C^{\star }$ for a blunted V-notch for different opening angles $\omega$

Table 6 Variations of the coefficients $\tilde{B}^{\star }$ and $\tilde{C}^{\star }$ as functions of ratio $\left( \frac{\rho }{l_{ch}} \right)$, for a blunted V-notch with different opening angles $\omega$

Table 7 Variations of the coefficients $\tilde{B}^{\star }$ and $\tilde{C}^{\star }$ as functions of ratio $\left( \frac{\rho }{l_{ch}} \right)$, for a blunted V-notch with different opening angles $\omega$

Fig. 25

$B^{{\star }\mathrm {t}}$ and $C^{{\star }\mathrm {t}}$ function of the dimensionless length $\zeta$

Fig. 26

$B^{{\star }\mathrm {p}}$ and $C^{{\star }\mathrm {p}}$ function of the dimensionless length $\zeta$

Table 8 $B^{{\star }\mathrm {t}}$ and, $C^{{\star }\mathrm {t}}$ as functions of the dimensionless length $\zeta$ for a cavity

Table 9 $B^{{\star }\mathrm {p}}$ and $C^{{\star }\mathrm {p}}$ as functions of the dimensionless length $\zeta$ for a cavity in compression p for compression. One can note a small inaccuracy in the penultimate line since $B^{{\star }\mathrm {p}}$ cannot be negative

Table 10 Variations of the coefficients $\tilde{B}^{{\star }\mathrm {t}/\mathrm {p}}$ and $\tilde{C}^{{\star }\mathrm {t}/\mathrm {p}}$ as functions of the dimensionless ratio $\frac{\rho }{l_{ch}}$ for a cavity under tension

Appendix D: Data for the coupled criterion—cavity

See Figs. 25, 26 and Tables 8, 9, 10.