Closing a mental account: the realization effect for gains and losses

Abstract

How do risk attitudes change after experiencing gains or losses? For the case of losses, Imas (Am Econ Rev 106:2086–2109, 2016) shows that subsequent risk-taking behavior depends on whether these losses have been realized or not. After a realized loss, individuals’ risk-taking decreases, whereas it increases after an unrealized (paper) loss. He refers to this asymmetry as the realization effect. In this study, we derive theoretical predictions for risk-taking after paper and realized gains, and for investment opportunities with different skewness. We experimentally test these predictions and, at the same time, replicate Imas’ original study. Independent of a prior gain or loss, we show that subsequent risk-taking is higher when outcomes remain unrealized. However, we find no evidence of a realization effect for non-positively skewed lotteries. While the first result suggests that the effect is more general, the second result reveals its boundary conditions.

1 Introduction

Many risky endeavors, be it a night at the casino or an investment in a stock, involve instances in which individuals must decide whether to continue, to abandon, or to double down on a previous decision. They often view such episodes in isolation, even though normative theory suggests integrating them into a broader perspective of total wealth. They instead engage in mental accounting (Thaler 1985, 1999), which refers to a cognitive process to categorize outcomes by their source or purpose. Prior outcomes within a mental account, perceived as a gain or a loss, obtain special relevance for this account and affect subsequent risk-taking (Thaler and Johnson 1990).

The direction of this influence has been subject to a long-standing debate. After losses, many studies find that individuals become more risk-seeking (Coval and Shumway 2005; Weber and Zuchel 2005; Langer and Weber 2008; Andrade and Iyer 2009), while others report they become more risk-averse (Massa and Simonov 2005; Shiv et al. 2005; Frino et al. 2008). Similarly, after gains, investors will either exhibit more risk-seeking behavior (Thaler and Johnson 1990; Weber and Zuchel 2005; Suhonen and Saastamoinen 2018) or more risk-averse behavior (Kahneman and Tversky 1979; Clark 2002; Coval and Shumway 2005).

Existing theory can account for these different reactions by a variety of models or arguments. On the one hand, risk-seeking behavior after a prior loss and risk-averse behavior after a prior gain are often explained by prospect theory (Kahneman and Tversky 1979). After a loss, the relevant part of the prospect theory value function to evaluate further outcomes is convex, which implies risk-seeking behavior. In contrast, a prior gain will situate a person in the gain domain for which the value function is concave, which implies risk-averse behavior.

On the other hand, more risk-seeking behavior after gains and more risk-averse behavior after losses can be motivated by the house money effect (Thaler and Johnson 1990) and the hedonic editing hypothesis (Thaler 1985). The house money effect describes a situation in which prior gains can be used to wager in subsequent gambles. People find it easier to part with money not coming from their own pocket. In addition, hedonic editing allows them to offset future losses against earlier gains. For losses, it is argued that they become more painful when they follow on the heels of prior losses (Barberis et al. 2001).

A unifying framework to resolve the conflicting evidence has been recently proposed by Imas (2016). It builds on the distinction between realized and unrealized outcomes, whereby a realization is defined “as an event in which money or another medium of value is transferred between accounts” (Imas 2016, p. 2091). He argues that individuals behave differently depending on whether a loss is realized or whether it is still unrealized (a paper loss). Experimentally, he replicates prior findings that participants become more risk-averse after a realized loss, while they become more risk-seeking after a paper loss. He labels the difference in risk-taking between paper and realized losses the “realization effect” and explains its occurrence with cumulative prospect theory (Tversky and Kahneman 1992) and choice bracketing (Read et al. 1999; Rabin and Weizsäcker 2009), an idea directly related to mental accounting.

The proposed framework sheds light on why both, risk-averse as well as risk-seeking behavior, can be observed after the same prior outcome. However, drawing general conclusions from realization for subsequent risk-taking requires some caution. First, Imas’s (2016) theoretical and experimental elaboration focuses exclusively on losses, and second, it tests the realization effect for an investment opportunity with a positively skewed distribution of outcomes. We argue that the literature is still in need of empirical and theoretical clarification about how prior outcomes—losses as well as gains—affect subsequent risk-taking, and in particular, under which conditions a distinction between paper and realized outcomes leads to differential risk-taking behavior. In this study, we contribute to this goal by examining two major research questions: (1) Does the realization effect exist for gains as well? (2) Does the realization effect depend on the skewness of the underlying investment opportunity?

To this end, we derive theoretical predictions for risk-taking behavior after gains and investment opportunities with positive skewness, no skewness, and negative skewness. We model loss-averse investors who open a mental account at the beginning of an investment episode and close it upon realization. Paper gains and losses alter the balance of the mental account and can thereby affect risk-taking. Paper gains act as a cushion against future losses and thus invite higher risk-taking, which is absent after gains are realized. We thus predict a realization effect for gains. Skewness comes into play mainly via the size of potential gains and losses relative to the account balance. With non-positive skewness, losses become less probable but larger. They threaten to exceed the paper gain cushion, attenuating the realization effect after gains. Likewise, after paper losses, more probable but smaller gains take away the potential to break even, which is a major motivation for higher risk-taking after losses. We thus predict a smaller or absent realization effect for non-positively skewed lotteries.

We conduct three well-powered experiments to test these predictions. In the first experiment, we replicate the main experiment by Imas (2016) using an identical design, which examines a series of positively skewed investment opportunities. The importance of replication for scientific progress in economics has been highlighted recently (Maniadis et al. 2014; Camerer et al. 2016; Christensen and Miguel 2018). At the same time, the experiment allows us to address the first research question about a realization effect for gains. Not only is risk-taking after gains arguably as important as after losses, but it shares a similar conflict in previous empirical results and theory. If there is evidence for a realization effect in the gain domain as we predict, the proposed framework would have broader implications than those already suggested for the loss domain.

To answer the second research question, we analyze in two further experiments boundary conditions for the realization effect. In particular, we depart from positively skewed lotteries used so far and examine how symmetric or negatively skewed lotteries affect risk-taking behavior after paper and realized outcomes. Not only does positive skewness encourage risk-seeking behavior as it is often associated with gambling (e.g., lotteries or casinos), but the underlying distributions of most financial investment opportunities (e.g., stocks or funds investments) are less or not at all positively skewed. In order to establish the validity of the realization effect for these settings, it is essential to confirm whether the effect is indeed reduced as theory predicts.

The first experiment, which replicates study one by Imas (2016), involves a sequence of four positively skewed lotteries, each of which represents the throw of a die. One lucky number (out of six) wins seven times the stake invested in the lottery, while the stake is lost for all other outcomes. Up to EUR 2.00 can be invested in each lottery. After the third lottery, previous earnings are either paid out to participants or remain unrealized, which defines the two treatments in the experiment (realization treatment and paper treatment). The relevant comparison then is what participants do in the fourth and final lottery depending on realization. We use a larger sample size (N = 203) than the original study to ensure sufficient statistical power and to be able to examine outcome histories that occur less frequently.

We first confirm that participants take less risk after a realized loss compared to a paper loss. However, the difference of 16 cents in average invested amounts between treatments is smaller than in the original experiment (38 cents), and the realization effect is not statistically significant. While we confirm a decrease in risk-taking in the realization treatment, we cannot corroborate an increase in risk-taking in the paper treatment. Standard replication measures show that the replication is at least partially successful.

Exploiting observations in which participants have obtained a gain at the time of realization, we find a similar investment pattern as for losses. Participants take significantly less risk after a realized gain than after a paper gain. The realization effect is larger for gains than for losses with a difference of 22 cents in average investment between treatments. In the paper treatment, participants seem to gamble with the house’s money, while in the realization treatment, they have closed the mental account and regard gains from the lottery as their personal money. Given the consistent direction of the realization effect for gains and losses, we test for the realization effect unconditional of a particular outcome history. The results show a positive and strongly significant realization effect ($p<.01$) in the full sample.

In addition to our own experimental data, we analyze data from the original study by Imas (2016) with respect to gains.¹ Although limited in the number of observations, the realization effect for gains is strong and consistent with our results. Thus, we find evidence for a realization effect for gains in two independent samples. Moreover, pooling the data from both studies, we find a positive and strongly significant realization effect ($p<0.001$) for gains and losses. To test for the theoretical relation between the realization effect after gains and the house money effect, we examine the invested amounts after a paper gain. In almost all cases, participants do not invest more than what they have gained in the lotteries. This implies that they gamble with the house’s money, but do not touch their initial experimental endowment.

In experiments two and three, we examine how other distributions of outcomes affect risk-taking behavior after paper and realized gains and losses. We keep the basic experimental setup but change the probability of gains. Instead of a positively skewed lottery, participants invest in a symmetric or negatively skewed lottery, respectively. By construction this also increases the heterogeneity of outcome histories prior to realization. We find neither in the symmetric lottery nor in the negatively skewed lottery a statistically significant realization effect for gains or losses (total sample size N = 304). In contrast to the positively skewed environment in the first study, participants tend to invest similarly after a paper outcome and a realized outcome. This finding is in line with theoretical work by Barberis (2012) and Imas (2016) in which individuals form contingent plans over a sequence of lotteries.

Fig. 1

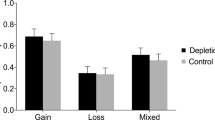
The realization effect across all experiment. The figure displays average changes in risk-taking after paper and realized outcomes unconditional of the prior outcome history, and split by loss and gain for positively skewed, symmetric, and negatively skewed lotteries. The error bars show 90%-confidence intervals. (Color figure online)

The results across all experiments suggest boundary conditions for the realization effect. Figure 1 depicts the magnitude of the realization effect we find, conditional on the outcome history as well as the skewness of the investment opportunity. Increased risk taking after paper gains and losses requires positive skewness, while decreased risk-taking after realized gains and losses does not. The absence of the realization effect for non-positively skewed lotteries is thus primarily driven by an absence of increased risk-taking after paper outcomes. This includes the absence of loss chasing, which seems to be limited to positive skewness environments.

The remainder of the paper is organized as follows. In Sect. 2, we derive theoretical predictions for the experiments, in particular for risk-taking behavior after gains and lotteries with different skewness, and review the prior literature. Section 3 presents the experimental design and the main results. A final section concludes.

2 Theory and literature

To understand the behavior of participants in the experiments, we build on the model by Barberis et al. (2001). In addition to standard consumption-based utility, they consider utility derived directly from the fluctuations of financial wealth. In particular, agents react to gains and losses from their risky assets, which makes the model suitable for the analysis of behavior after gains and losses. Prior theory used to motivate the realization effect does not generate clear predictions for risk-taking behavior after gains. We introduce two departures from the main model in Barberis et al. (2001), which are the distinction between paper outcomes and realized outcomes, and a different value function after losses. The first is a natural extension to accommodate the treatment of paper and realized outcomes, the second takes into account the empirically observed behavior in the loss domain.

2.1 Basic framework

The full utility specification in Barberis et al. (2001) includes utility from consumption $u(C_t)$ and utility derived from fluctuation of financial wealth $v(X_t,B_t,Z_t)$. We concentrate on the latter as it represents the important part of evaluating risk-taking behavior after gains and losses. $X_t$ is the gain or loss a participant experiences in lottery t.²$B_t$ is the bet size a participant selects for lottery t. And $Z_t$ is a mental account, which reflects whether a participant perceives himself up or down in the game. Mental accounting describes the cognitive processes people use to organize and evaluate their financial activities (Thaler 1985, 1999). A key implication is that people do not consider money across different mental accounts as perfect substitutes, but rather categorize money based on its origin or purpose and assign it to separate accounts. Outcomes within a mental account are evaluated jointly, whereas outcomes in different mental accounts are evaluated separately (Thaler 1999).

The three variables $X_t$, $B_t$, and $Z_t$, jointly determine the utility derived from fluctuations of financial wealth. A difference to the more general model arises from the fact that only part of a participant’s endowment is invested in the risky lottery. Still, $B_t$ can be interpreted as a participant’s risky asset holdings. The outcome of lottery t is $X_t=R_tB_t-B_t$ with gross return $R_t$. We abstract from a risk-free rate, as no return is paid on money not invested in the lottery. If a participant loses in the lottery, then $X_t=-B_t$. If a participant wins, then $X_t=(x-1)B_t$ with $x>1$ as the multiple that is applied to a winning bet. The lottery will thus either generate a loss or a gain. Besides these potential outcomes, participants take their prior gains and losses into account. $Z_t$ is the mental account, which reflects prior outcomes:

$$\begin{aligned} Z_t=\sum _{\tau =1}^tX_{\tau -1} \end{aligned}$$

(1)

While Barberis et al. (2001) leave open what exactly this mental account (or “historical benchmark”) is, in our context, we will assume that it is the sum of prior gains and losses. A participant can thus be in the gain domain ($Z_t>0$), in the loss domain ($Z_t<0$), or at break-even ($Z_t=0$). In particular, $Z_1=0$ as no lottery has yet been played. In this situation, utility from changes in financial wealth is described by:

$$\begin{aligned} v(X_t,B_t,0) = {\left\{ \begin{array}{ll} X_t &{} \quad \text {for}\,X_t \ge 0 \\ \lambda X_t &{} \quad \text {for}\,X_t < 0 \end{array}\right. } \end{aligned}$$

(2)

The parameter $\lambda >1$ captures loss aversion. We further assume that realizing a gain or a loss resets the benchmark to zero as the mental account is closed. The intuition is that when a stock is sold, the proceeds are mentally transferred from the account investment to consumption. Paper losses may consequently not be regarded as final and possess the potential to rebound (Shefrin and Statman 1985). The idea that realization affects decision making has been tested in an experimental asset market (Weber and Camerer 1998). When stocks are automatically sold after each period, the disposition effect is significantly reduced. The automatic selling procedure closes existing mental accounts, and stocks are no longer charged by prior experiences of gains or losses.³ This means that after realizing lottery outcomes, a participant is effectively in the same decision situation as before entering the first lottery:

H1:

After a gain or a loss is realized, risk-taking behavior will be similar as in a decision without prior history.

Barberis and Xiong (2009) study the implications of realized and paper outcomes as well. In two alternative models, they define prospect theory preferences either over total gains and losses or realized gains and losses. They discover that the model based on realized outcomes predicts the disposition effect more reliably.

2.2 Behavior after gains

One main idea of the model is that prior gains serve as a cushion against losses that are felt less severely as long as they do not exceed prior gains. This is consistent with the “house money effect,” predicting that people take more risk in the presence of a prior gain (Thaler and Johnson 1990). When offered a risky lottery, individuals evaluate prior paper gains (house money) and the risky prospect jointly within the same mental account. Since the house money is integrated with future outcomes, losses can be offset and are perceived as less painful than usual.⁴ Formally, losses up to the level of prior gains are not subject to loss aversion:

$$\begin{aligned} v(X_t,B_t,Z_t) = {\left\{ \begin{array}{ll} X_t &{} \quad \text {for}\,X_t \ge -Z_t \\ \lambda (X_t+Z_t) - Z_t &{} \quad \text {for}\,X_t < -Z_t \end{array}\right. } \end{aligned}$$

(3)

This means that losses up to $Z_t$ are evaluated at the gentler rate of 1 instead of $\lambda$. Accordingly, a paper gain reduces loss aversion when compared to a realized gain. This is particularly true for small bet sizes $B_t<Z_t$, which do not jeopardize the whole gain cushion. Realization closes the respective mental account for prior gains and triggers the internalization of house money. Prior gains are no longer available to offset potential losses. Without integration, individuals evaluate a risky lottery separately from the previous gain and do not use the gentler rate of 1 instead of $\lambda$ anymore. This reasoning is also graphically illustrated in Panel A of Fig. 2. We hypothesize:

H2:

After a paper gain people are more prone to take risks than after a realized gain.

H2a:

They avoid bet sizes that run the risk to lose more than the sum of prior gains.

Fig. 2

Risk-taking after paper and realized outcomes. The figure illustrates risk-taking after gains in Panel A and after losses in Panel B depending on realization. For illustrative purposes, only two rounds of a lottery are displayed, and outcomes are either on paper (left diagrams) or realized after the first round (right diagrams). Each diagram plots the round of the lottery on the x-axis and the earnings on the y-axis. Endowments are the same in t = 0, which then adjust depending on the outcome of the first lottery in t = 1. In round two, the chosen investment $B_2$ determines the potential earnings indicated by the horizontal bars. Color coding shows whether outcomes are evaluated as gains (green) or losses (red). Whether an outcome is evaluated as a gain or loss depends on the mental account and its reference point. For example, in the left diagram of Panel A, the paper gain from the first lottery enters a newly opened mental account shown in yellow. Outcomes in round two are evaluated against this previous gain which offsets potential losses. The right diagram of Panel A shows the same situation when instead the gain is realized. The respective mental account is closed, the previous gain is internalized, and the reference point shifts to the new wealth level. In round two, there is no cushion against a potential loss which is indicated in red. (Color figure online)

Hypothesis 2 may shed light on seemingly contradictory results in the empirical literature: Less risk taking after a prior gain versus more risk taking after a prior gain. While the house money effect predicts a higher propensity to gamble after a prior gain than before (or after a loss), the disposition effect describes the opposite behavior. Investors show a tendency to sell winning stocks too early and to keep losing stocks too long (Shefrin and Statman 1985; Odean 1998; Weber and Camerer 1998). Intuitively, the trading behavior behind the disposition effect is in line with prospect theory (Kahneman and Tversky 1979). A winning stock moves an investor into the gain domain of the prospect theory value function. As the value function is assumed to be concave for gains, it implies risk-averse behavior and a higher likelihood of selling the stock.

Further tests are similarly inconclusive for risk taking after gains. Weber and Zuchel (2005) show in lottery experiments that participants become more risk-seeking after a gain, while Franken et al. (2006) find in a gambling task that previous gains lead to less risk-taking. Clark (2002) does not find evidence in either direction following gains in a public goods experiment. However, bettors on the horse track take more risk after a previous gain (Suhonen and Saastamoinen 2018), as do novice investors in the stock market (Hsu and Chow 2013). Recently, Lippi et al. (2018) support this finding by showing that clients of an Italian bank engage in more risk-seeking behavior after unrealized gains. However, Coval and Shumway (2005) analyze the trading behavior of futures traders and find that traders with gains in the morning take less risky positions in the afternoon. In a similar setting, Frino et al. (2008) report the opposite result.

2.3 Behavior after losses

When a mental account is in the red, i.e., a participant has experienced an overall loss, then the outcomes of a lottery are evaluated in the following way:

$$\begin{aligned} v(X_t,B_t,Z_t) = {\left\{ \begin{array}{ll} -\lambda Z_t + (X_t+Z_t) &{} \quad \text {for}\,X_t \ge -Z_t \\ \lambda X_t &{} \quad \text {for}\,X_t < -Z_t \end{array}\right. } \end{aligned}$$

(4)

The expression represents the mirror image of the situation after gains and again reflects the idea of an open mental account in which a loss is not final. Gains that make up for prior losses are particularly attractive and are valued at a rate of $\lambda$. Barberis et al. (2001) assume that losses on the heels of prior losses are more painful than usual and let loss aversion rise in $Z_t$. However, the results by Imas (2016) for paper losses question this idea, as people take more risk after a series of losses. The traditional view inspired by prospect theory also favors higher risk-taking after losses (Kahneman and Tversky 1979). While the channel in prospect theory is higher risk tolerance, in the piecewise linear (risk-neutral) utility function used here, it could manifest in a decreasing loss aversion parameter (consistent with a learning effect documented by Merkle 2019). We thus depart from the assumption of higher loss aversion after a prior loss and instead propose a constant loss aversion parameter. The extent of loss chasing will depend on how people’s preferences react to prior losses.

When offered a risky lottery, individuals evaluate prior paper losses and the risky lottery jointly within the same mental account. They thus evaluate further losses at the same rate as gains reducing these losses. By contrast, realization closes the respective mental account, internalizes the prior losses, and resets the reference point to $Z_t=0$ (see also Panel B of Fig. 2). Note that Eqs. 3 and 4 simplify to Eq. 2 in this case. We thus expect participants to take more risk when confronted with a paper loss (mental account still open) than with a realized loss (mental account closed):

H3:

After a paper loss people are more prone to take risks than after a realized loss.

H3a:

They favor bet sizes that give them the opportunity to break even.

For risk-taking after losses similarly inconclusive empirical evidence as for gains has been found. There is strong empirical support for an increase in risk-taking after experiencing a loss, which has been demonstrated in the lab (Gneezy and Potters 1997; Weber and Zuchel 2005; Langer and Weber 2008; Andrade and Iyer 2009) as well as in the field (Coval and Shumway 2005; Meier et al. 2020). Such loss chasing has been identified as a source for gambling problems (Zhang and Clark 2020), and might be driven by impulsive action (Verbruggen et al. 2017). On the other hand, several studies report a decrease in risk-taking after losses (Massa and Simonov 2005; Shiv et al. 2005; Frino et al. 2008). Imas (2016) points out how the different results can be reconciled by distinguishing paper losses and realized losses (in line with H3). The presented findings almost exclusively rely on positively skewed gambles, for other skewness environments, there is hardly any evidence (see also Nielsen 2019).

Hypothesis 3a does not follow directly from the introduced theory, as gains are treated equally up to the point where they exceed prior losses ($X_t>-Z_t$). However, already Thaler and Johnson (1990) report such a break-even effect. Moreover, there is evidence that finally realizing an outcome is associated with an immediate burst of utility (Barberis and Xiong 2012; Frydman et al. 2014). Such realization utility implies that agents also care about the level of $Z_t$, in particular when they anticipate that the respective mental account will be closed. In the experiment, the final lottery represents the last opportunity to influence cumulative outcomes $Z_T$ which are automatically realized at the end of the experiment. Lotteries that allow changing the sign of $Z_T$ should be especially attractive. A sufficiently large multiplier x, as found in positively skewed lotteries, usually allows to break even. Depending on accumulated losses, it might not even be necessary to increase risk.

2.4 The realization effect and skewness

In our model, a positively skewed lottery is prone to the realization effect as it offers a high potential gain and limited loss. In the gain domain, the cushion provided by $Z_t$ will be able to absorb most of a possible loss and induce risk-taking unless the mental account is closed. In the loss domain, the lottery almost always offers the chance to break even, as the multiplier x applied on the bet $B_t$ is sufficiently high. This also induces risk-taking, which is why a strong realization effect can be expected for positively skewed lotteries independent of the prior outcome.

In contrast, symmetric and negatively skewed lotteries are characterized by a lower but more probable gain and a higher but less probable loss. A reasonable assumption is that probabilities and payoffs of the lotteries are altered simultaneously so that their expected payoff remains (about) constant.⁵ It is then more likely that previous gains cannot completely cushion a potential loss, which might deter people from risk-taking. Figure 2 illustrates this by the size of the mental account balance $Z_2$ in period two relative to the bet size $B_2$ in period two. The smaller account balance $Z_2$ after an initial gain only allows for smaller bets if people do not want to risk their endowment. We predict no reaction to skewness for risk-taking behavior after realized gains, as it is independent of prior history (see H1). Consequently, the realization effect should be reduced.

In the loss domain, symmetric or negatively skewed lotteries offer less potential to break even. Initial losses ($-\,Z_2$) are larger relative to potential gains $xB_2$. However, it is still possible to recoup prior losses at least partly, making the lottery somewhat more attractive than after losses are realized and mental accounts are closed.

H4:

The realization effect is reduced or absent for symmetric and negatively skewed lotteries.

Previous empirical studies have shown in various domains that skewness influences risk-taking and that positively skewed lotteries tempt individuals to engage in more risk-taking. For example, individual investors have a preference for lottery-type stocks, characterized by low prices, high volatility, and large positive skewness (Kumar 2009). Further evidence for positive skewness-loving investment behavior comes from horse race betting and state lotteries (Golec and Tamarkin 1998; Garrett and Sobel 1999). This is in line with Grossman and Eckel (2015), who find increased risk-taking in an experimental study with positively skewed lotteries. While most of the literature on dynamic risk-taking concentrates on positively skewed lotteries, there are many situations in every-day decision making in which outcome distributions are less or not at all positively skewed. For example, investors in the stock market or corporate managers usually face less lottery-like investment opportunities. Given this gap in the literature on risk-taking for non-positively skewed lotteries, the second objective of this study is to investigate whether the realization effect can be generalized to symmetric and negatively skewed lotteries.

Our model is broadly consistent with the theory provided by Imas (2016). The common prediction is that risk-taking after a paper loss is higher than a) before a paper loss and b) after a realized loss. However, we explicitly model a mental account (represented by $Z_t$), while Imas (2016) invokes a mere shift in the reference point. This difference becomes apparent when deriving predictions for the gain domain. An agent with a paper gain might take less risk in his model compared to an agent with a realized loss or no history.⁶ As this defies, for example, the presence of a house money effect, we find this approach not appealing for understanding behavior after gains.

In the main model by Imas (2016), the proof for the general existence of a realization effect after losses relies on features of a positively skewed lottery. The effect is not necessarily absent for symmetric or negatively skewed lotteries, but in these cases depends on preferences (e.g., the degree of loss aversion). Similar to our model, a reduced aggregate realization effect can be expected in a population with heterogeneous preferences. Both models rely on myopic decision makers, who take only the next round of a lottery into account. An alternative is allowing for people to make contingent plans on their investments after gains and losses (e.g., Barberis 2012). Contingent plans may alter the existing skewness of asset returns, for example, make them more positively skewed by planning to cut losses. In Online Appendix A, we discuss such models in more detail.

3 Experimental design and results

The design of the experiments is based on Imas (2016), who studies a version of the investment lottery by Gneezy and Potters (1997). Participants receive a total endowment which can be invested over several rounds in the same lottery. In each round, participants can invest a maximum amount E in the lottery, which is a constant fraction of the total endowment. They thus decide on their lottery investment ($B_t$) and how much they want to invest risk-free ($E-B_t$). For simplicity, the risk-free investment provides no interest. With probability p, the lottery returns the invested amount times a multiple x, with probability $1-p$ the investment is lost. A participant can thus either make a gain of $(x-1)B_t$ or a loss of $-\,B_t$. The expected payoff in each round is:

$$\begin{aligned} p\cdot (xB_t+E-B_t)+(1-p)\cdot (E-B_t)=E+(px-1)B_t. \end{aligned}$$

(5)

Lotteries are structured in such a way that $px>1$, which means that the lottery has a positive expected payoff, and the expected payoff increases in the bet size $B_t$. Otherwise, the lottery would be unattractive to risk-averse participants. After the investment decision is made, the outcome of the lottery is determined and revealed to participants. In the following round, the same lottery is played again. Importantly, investment possibilities in later rounds do not depend on prior payoffs as the maximum investment E is a constant fraction of the total endowment.

The total number of lottery rounds in all experiments is four. In the realization treatment, participants invest over three rounds, and outcomes are realized at the end of the third round. After this, an additional lottery takes place. In the paper treatment, all four rounds are played consecutively, and there is no special significance of the turn between the third and final round. However, to keep information between treatments constant, participants in both treatments are informed about their earnings on the screen at the end of the third round. The main analysis thus relies on the risk-taking behavior in the final round, as the first three rounds are identical between treatments.

3.1 Experiment 1

3.1.1 Design and participants

In the first experiment, we replicate the original design by Imas (2016). In each round, participants decided how much to invest in a positively skewed lottery. The lottery succeeded with a probability of 1/6 and paid seven times the invested amount, or it failed with a probability of 5/6 and the invested amount was lost. Considering this experimental design, the conditions under which the realization effect occurs turn out to be arguably restrictive. Imas (2016) focuses his attention on sequences of prior losses, excluding all histories involving a gain.⁷ In addition, the nature of the lotteries is such that participants bet on the throw of a six-sided die and win (sevenfold) if their predetermined “lucky number” comes up. This results in a positively skewed lottery. In the first experiment, we extend the analysis to the gain domain, while in experiments two and three, we introduce different types of skewness.

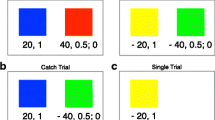
Participants were randomly assigned to either a realization treatment or a paper treatment as described above. After entering the laboratory, each participant received an envelope which contained the endowment of EUR 8.00. The instructions asked participants to count the money (see Online Appendix B for the experimental instructions). The lotteries were framed in terms of the throw of a six-sided die and always proceeded in the same way. First, each participant was randomly assigned a success number between 1 and 6, which was displayed on the computer screen. Then participants decided how much to invest in the lottery up to a maximum of EUR 2.00. As soon as all participants had entered the amount, the experimenter rolled a large die in front of the room. All participants received the opportunity to check whether the die was fair. If the success number matched the rolled number, the participant won the lottery and obtained seven times the invested amount (plus the amount invested risk-free). If the success number did not match the rolled number, the participant lost the invested amount and kept the amount not invested. For the next round, a new success number was assigned. As in the original experiment, all results of the die roll were written on a board in front of the room.

In the realization treatment, outcomes were realized at the end of the third round. Participants who lost money by that time took the lost amount out of the envelope and handed it back to the experimenter. Participants who won received additional money from the experimenter. After this, participants made one last investment decision in a final round and were paid accordingly. In the paper treatment, outcomes were not realized at the end of the third round. Outcomes were merely communicated on the screen as in the realization treatment, but no physical transfer of money took place.⁸ At the end of round four, all outcomes were realized for both groups. As in the original experiment, the time between rounds was normalized across treatments. Consistent with hypotheses H2 and H3, we predict that participants in the paper treatment (after gains and losses) will invest more in the final lottery than participants in the realization treatment.

Experiment one was programmed in z-Tree (Fischbacher 2007) and conducted in the Mannheim Experimental Laboratory (mLab). We selected a sample size of $N>200$ participants to obtain statistical power of at least 90% to detect an effect of the size of the original realization effect at the 5% significance level (Camerer et al. 2016). We recruited 203 people via ORSEE (Greiner 2015) from a university-wide subject pool to participate in a study on decision making. Participants were on average 23 years old, and the number of female ($n=108$) and male ($n=95$) participants was relatively similar (see Table 1).

Table 1 Summary statistics of experiment participants

3.1.2 Replication results

We first examine the replication of the realization effect for losses. The analysis centers on the change of investment between rounds three and four, as realization takes place before round four. To test for the realization effect, we are mainly interested in three comparisons: The difference in the change of investment between the paper and realization treatment (between-treatment comparison) and the change of investment for each treatment separately (within-treatment comparisons). Panel A of Table 2 shows the amounts invested in the lottery for participants who have a total loss by the end of round three, which means that they lost in each of the first three rounds.⁹ Investments do not differ significantly across treatments over the first three rounds. In the final round, participants in the paper treatment invest slightly more, while participants in the realization treatment invest less. This pattern is consistent with a realization effect as stated in hypothesis H3, which predicts a positive difference in differences ($\text {DiD}=0.16$, $t(113)=1.58$, $p=0.12$).

Table 2 Risk-taking in the positively skewed lottery

However, compared to results of study one by Imas (2016) ($\text {DiD}=0.38$, $t(51)=3.19$, $p<0.01$), our data show a less pronounced effect with respect to economic and statistical significance. The found effect size is 42% of the original effect size, which is smaller than the mean replicated effect size of 66% reported by Camerer et al. (2016) in a large-scale study on the replicability of laboratory experiments in economics. To further assess replicability, we apply confidence intervals and a meta-analysis they propose as standard measures. The original effect size is outside, but close to the upper bound of the 95% confidence interval of the replicated effect size $[-0.04, 0.34]$.

Interestingly, when focusing on the investment behavior within treatment, the realization effect we find is primarily driven by a decrease in risk-taking in the realization treatment ($-\,0.12$, $t(57)=1.64$, $p=0.11$), while the effect in the original data is primarily driven by an increase in risk-taking in the paper treatment. We can confirm that participants tend to take less risk after a realized loss, but we cannot replicate that participants increase risk-taking after a paper loss (0.04, $t(56)=0.57$, $p=0.57$). The magnitude of the decrease in risk-taking after a realized loss in the original study ($-\,0.15$) is well inside the 95% confidence interval in the replication $[-0.25, 0.02]$. However, the increase in risk-taking after a paper loss in the original study (0.23) is not compatible at the 95% confidence level with the replication $[-0.09, 0.17]$.

In other words, we do not find loss chasing in the paper treatment, which ultimately explains the overall less pronounced realization effect for losses as compared to Imas (2016). One reason for the non-robust results after paper losses might be that the positively skewed lottery offers participants the chance to break even without necessarily having to increase risk-taking. Whether or not some participants still increase their risk-taking will depend on their prospect theory preference parameters.¹⁰

When comparing the invested amount in round four to the invested amount in round one, we find that participants are more risk-averse after a realized loss than without any prior outcome ($-\,0.22$, $t(57)=2.49$, $p=0.02$). This is inconsistent with hypothesis H1, but in line with the idea of Barberis et al. (2001), who argue that individuals become more sensitive to future losses after a previous loss. In general, the changes in risk-taking between rounds three and four are not particularly large when compared to the changes observed for earlier rounds (see Online Appendix D). We find some significant results for earlier rounds across all three experiments, but we cannot identify a systematic pattern behind these changes. Significance occurs mostly between round one and round two, which suggests that participants try out the lottery first before making considerable adjustments to their bet size. Importantly, by round three, risk-taking behavior is very similar between treatments.

As a further test for replication, we pool our data with the original data by Imas (2016). Thus, we are able to obtain a meta-analytic estimate of the effect (Camerer et al. 2016). In the pooled data we obtain a strongly significant realization effect after losses ($\text {DiD}=0.24$, $t(165)=3.10$, $p<0.01$). We conclude that the evidence on the outcome of the replication is mixed. We find a weaker but directionally consistent realization effect after losses.

3.1.3 Results for gains

Next, we examine participants with a gain at the end of the third round. Given the considerable upside potential of the lottery, most participants who succeeded in at least one lottery faced positive net earnings at the end of the third round. The overall sample of 203 participants splits into 115 participants with a loss by the end of round 3 analyzed above, 71 participants with a gain by the end of round three, and 17 participants who have zero net earnings by the end of round three (due to not investing in the lottery at all). Of the 71 participants with a gain, 65 won the lottery once, and 6 won twice.¹¹

Panel B of Table 2 shows the invested amounts for these participants. In most cases, changes in investment in rounds one to three do not differ significantly across treatments.¹² Consistent with Hypothesis H2, the change in risk-taking between rounds three and four is significantly different between the paper and the realization treatment ($\text {DiD}=0.22$, $t(69)= 2.16$, $p=0.03$). This realization effect for gains is somewhat larger than the replicated effect for losses. Within treatment, participants in the paper treatment take significantly more risk (0.13, $t(34)=1.75$, $p=0.09$), while participants in the realization treatment take less risk ($-\,0.09$, $t(35) = 1.27$, $p=0.21$), yet statistically insignificant. However, in line with hypothesis H1, individuals invest similarly after a realized gain compared to the case of no prior outcome. The difference between the invested amount in round one and round four after a realized gain is insignificant (0.06, $t(35)=0.61$, $p=0.54$).

To back-up this finding, we turn again to the original data by Imas (2016), which has not been analyzed with regard to risk-taking after gains. As before, we only use observations of participants with a gain at the end of round three. Despite the relatively small sample size (N = 24), we nevertheless find evidence for a realization effect after gains in his data. As shown in Table 3, participants take more risk in the paper treatment than the realization treatment considering changes between rounds three and four. Consistent with the results from our experiment, the realization effect is positive and statistically significant ($\text {DiD}=0.55$, $t(22) = 2.29$, $p = 0.03$). Within treatment, participants take more risk after a paper gain (0.47, $t(8) = 1.99$, $p = 0.08$) and tend to take less risk after a realized gain ($-\,0.08$, $t(14) = 0.67$, $p = 0.51$).

Table 3 Risk-taking after gains in Imas (2016), Study 1

When we pool the data from both studies, we find a strong realization effect for gains ($\text {DiD}=0.29$, $t(93)=2.96$, $p<0.01$). We thus find experimental evidence for a realization effect for gains in two independent samples. The studies were conducted with student populations from different universities, in different countries, and at different points in time. While the p-value in both samples is similar ($p=0.03$), the combined evidence provides far stronger support to hypothesis H2.

Irrespective of whether the prior outcome is a gain or loss, risk-taking is thus higher when outcomes remain unrealized. This finding allows us to analyze the existence and strength of the effect independent of the sign of the prior outcome. Therefore, we run OLS regressions for the entire sample with the change in invested amount between rounds three and four as the dependent variable. We include a treatment indicator taking a value of one for the realization treatment. Table 4 shows in column (1) the results of the baseline regression. We observe a strong realization effect, with those in the realization treatment taking significantly less risk. Unsurprisingly, the economic magnitude is in between those estimated for gains and losses separately. The positive constant provides evidence for an increase in risk-taking in the paper treatment. Controlling for gains and losses after round three by a gain indicator (gain = 1) does not affect the main result (column 2). Interacting the treatment and gain variables allows us to test whether the realization effect is stronger after previous gains or losses. The negative but insignificant coefficient of the interaction term hints at a stronger realization effect after gains.

Table 4 The realization effect for gains and losses

We run the same regressions on the data from Imas’s (2016) study 1. Columns (4) to (6) in Table 4 display the results. A strong realization effect also exists in his data independent of prior gains and losses. The effect in his data is even more pronounced in economic magnitude than in our data. The combined effect independent of the prior outcome in the pooled data is ($\text {DiD}=0.25$, $t(283)=4.38$, $p<0.001$).

A relevant assumption about the realization effect is that people are less loss averse for money they keep in the mental account for house money (paper gains) than for their own money that they keep in a different mental account (realized gains). This assumption has testable implications for the amount people are willing to bet (hypothesis H2a). We predict that participants avoid bet sizes that run the risk losing more than the sum of prior gains. Since participants can invest up to EUR 2.00 in each round and lose at a maximum their invested amount, the subsample of interest are participants who have earnings between EUR 8.00 and EUR 10.00 after round three (i.e., gains between EUR 0 and EUR 2). If mental accounting is important, participants are expected not to invest more than their current paper gains (house money) in round four. Figure 3 plots the earnings after round three against the invested amount in round four. The maximum invested amount of participants in this subsample was EUR 1.00. All dots above the line represent participants who invest less than their house money in round four, which restricts their potential losses to less than their previous gains. Dots below the line represent participants who risk to lose more than their prior gains. Consistent with hypothesis H2a, 11 out of 12 participants invest less or exactly as much money as they previously gained.

Fig. 3

Testing the mental accounting assumption. The figure plots the earnings by the end of round three against the investment in round four for each participant who has earnings between EUR 8.00 and EUR 10.00 by the end of round three. Participants with earnings below EUR 8.00 are excluded as they made a loss and participants with earnings above EUR 10.00 are excluded as they cannot lose more than what they previously gained (given than the investment per round cannot exceed EUR 2.00 which also presents the highest possible loss per round). All dots above the diagonal line represent participants who invest less than what they previously gained, and all dots below the diagonal line represent participants who invest more than what they previously gained. (Color figrue online)

Essential for the realization effect is that the used realization mechanism is effective in closing a mental account. We tested an alternative realization mechanism in two versions of an online experiment, one of which is an identical replication of the online study in Imas (2016). As a physical transfer of money is not feasible online, participants in the realization treatment initiate a transfer of money between accounts by typing the command “closed.” We successfully replicate the realization effect using this alternative realization mechanism in the original design by Imas (2016) but discover that the effect is rather fragile when modestly changing the design. We find that the framing of how the last round is related to the preceding three matters for whether risk-taking increases or decreases in the realization treatment of the online experiment.¹³ We conclude that in an online environment, proper realization is more difficult to achieve, and mental accounts may remain open using the described procedure. Complete results are reported in Online Appendix E.

3.2 Experiment 2 and 3

3.2.1 Design and participants

Experiment two and three address the question of whether the realization effect depends on the skewness of the underlying investment opportunity. We take the same experimental design as in experiment one except for the investment opportunity, which we change to either a symmetric (experiment two) or a negatively skewed lottery (experiment three). In line with hypothesis H4, we predict a reduced or absent realization effect in these settings.

Participants were again endowed with EUR 8.00 at the beginning of the experiment and could invest up to EUR 2.00 in each of four subsequent lottery rounds. In experiment two (symmetric lottery), participants could invest in a lottery that succeeded with a probability of 1/2 and paid 2.33 times the invested amount. With a probability of 1/2, the lottery failed and the invested amount was lost. Instead of one success number for the role of the die, participants received three success numbers. In experiment three (negative skewness), participants could invest in a lottery which succeeded with a probability of 5/6 and paid 1.4 times the invested amount or failed with a probability of 1/6. Instead of a success number, they received one failure number.

The multiplier for the gain case was adjusted to keep the expected payoff of each lottery equal to the expected payoff of the lottery in experiment one. While the objective of experiment three was to create a mirror image of the original positively skewed lottery, a complete reversal of gains and losses was infeasible as losses cannot exceed the endowment (by laboratory rules). Instead of a sevenfold loss, we thus have to restrict the loss to the invested amount. Still, participants are expected to experience many small gains and occasionally (relatively) large losses.

As before, participants were randomly assigned to either a realization treatment, in which outcomes were realized by the end of the third round or a paper treatment. The procedure in the two treatments was the same as in experiment one. Both experiments were conducted in the Mannheim Experimental Laboratory (mLab) and the AWI Experimental Laboratory at the University of Heidelberg.¹⁴ We recruited 304 participants in total, 95 of them were assigned to experiment two and 209 to experiment three. A smaller sample size was required in experiment two as a symmetric lottery generates sufficient observations for gains and losses more easily. The demographics of participants in experiments two and three are similar to those in experiment one (see Table 1).

3.2.2 Results of experiment 2 (symmetric lottery)

We first analyze the investment behavior of participants who accumulate a loss by the end of round three. Panel A of Table 5 presents the invested amounts for these participants. Investments do not differ significantly across treatments in the first three rounds. Comparing the changes in investment between rounds three and four across treatments, the realization effect points in the expected direction ($DiD = 0.08$, $t(35) = 0.54$, $p=0.59$), but is small and statistically insignificant. When analyzing the invested amounts within each treatment, we find that participants who have a paper loss by the end of round three do not increase their investment (0.00), and participants who have a realized loss tend to slightly decrease their investment ($-\,0.08$, $t(14) = 0.73$, $p=0.48$). Participants thus seem not to invest differently after a paper or a realized loss. In particular, we do not observe more risk-taking after paper losses.

Panel B of Table 5 shows the invested amounts of participants with an accumulated gain by the end of round three. Similar to losses, the realization effect cannot be observed in the symmetric lottery setting ($DiD = -0.03$, $t(55)=0.18$, $p=0.86$) for gains. The change in investment between rounds three and four in the paper treatment ($-\,0.11$, $t(26)=0.69$, $p=0.50$) and the realization treatment ($-\,0.08$, $t(29)=0.89$, $p=0.38$) points in the same direction. After a paper as well as a realized gain, participants tend to invest similarly. Consistent with hypothesis H4, we find no evidence for a realization effect after gains or losses when the investment opportunity is symmetric.

Table 5 Risk-taking in the symmetric lottery

Looking at investments on participant level, we find that 53% of the participants do not change their invested amount between rounds three and four (fairly independent of treatment). Any overall effect would thus have to rely on a subset of participants to make strong changes in their investments. We also find that the absence of the realization effect does not depend on the round(s) in which participants win in the lottery.

Finally, we test whether participants in the paper treatment do not increase their investment after a loss because their losses are too high to break even in the final lottery. In contrast, the positively skewed lottery always allowed to break even. We split the sample of participants with accumulated losses into those who have earnings by the end of round three that are smaller than EUR 5.34 and those who have earnings between EUR 5.34 and EUR 8.00 (the highest possible gain in the final lottery is $2.33*2 - 2 =$ EUR 2.66). Despite the resulting small sample size, we find that participants with paper losses tend to invest differently depending on whether break-even is possible or not. Those who cannot break even tend to decrease the invested amount in round four by on average EUR 0.38, whereas participants who can break even tend to increase the invested amount by EUR 0.11. That people favor bet sizes that allow them to break even is consistent with hypothesis H3a. However, given the small sample size of participants with a paper loss (N = 22), the effect remains insignificant and has to be interpreted with caution.

3.2.3 Results of experiment 3 (negatively skewed lottery)

We again start by examining the investment behavior of participants who accumulated a loss by the end of round three. Most of these participants lost only once but remained in the loss domain. Panel A of Table 6 shows the investments in all rounds for these participants by treatment. Levels and changes in investment between rounds do not differ significantly across treatments. Considering the difference of the changes in investment from round three to round four across treatments, the realization effect points in the expected direction ($DiD = 0.05$, $t(68) = 0.36$, $p=0.72$), but is small and statistically insignificant. Participants in both treatments react similarly to a loss by slightly reducing their investments ($-\,0.04$, $t(31)=0.45$, $p=0.66$ and $-\,0.09$, $t(37)=1.17$, $p=0.25$).

The investments for participants with gains by the end of round three are displayed in Panel B of Table 6. As for losses, we do not find a significant realization effect for gains in this setting. Participants do not invest differently after a paper and a realized gain (0.00 and 0.00). In fact, the investments on average do not change at all between round three and round four. Results change very little if we restrict the sample to those participants who experience three successes in a row (N = 121). In line with hypothesis H4, we do not find evidence for a realization effect when participants invest in a negatively skewed lottery. This supports theoretical predictions that the realization effect depends on the positive skewness of the lottery.

Table 6 Risk-taking in the negatively skewed lottery

4 Conclusion

In this paper, we examine whether and under which conditions a distinction between realized and unrealized prior outcomes leads to differential subsequent risk-taking. We formalize our thoughts in a model of mental accounts that people use to keep track of their paper gains and losses. A mental account is closed when an investment episode ends and outcomes are realized. For losses, recent experimental evidence finds that individuals take less risk after a realized loss and more risk after a paper loss, which is referred to as the realization effect. It is tempting to conclude from this result that realization per se has a strong effect on subsequent behavior. We first ask whether—as our theory predicts—the finding generalizes to the gain domain, i.e., whether a realization effect can also be observed after gains. Second, we identify positive skewness as a necessary condition to observe the realization effect. As such, our results show that conclusions about the universality of the realization effect have to be drawn with some caution.

The main objectives and findings from our study can be summarized as follows: We replicate the result by Imas (2016) for losses, extend the analysis to gains and test the boundary conditions of the effect with respect to the skewness of the investment opportunity. Using the same experimental setting and a larger sample size than the original study, we show that the realization effect also exists for gains. We thus show that the framework of realization is independent of the sign of prior outcomes as it holds not only for losses but also for gains. However, at the same time, the effect turns out to be sensitive to changes in the skewness of the underlying investment opportunity. We do not find differential risk-taking after paper and realized outcomes for non-positively skewed lotteries. This finding documents the importance of learning more about the conditions under which the effect arises and informs judgments about its external validity.

The results confirm theoretical predictions that a realization effect mostly occurs in positively skewed lotteries. The analysis of risk-taking in non-positively skewed lotteries, in particular, in negatively skewed lotteries has received less attention in the literature. One recent exception is contemporaneous work by Nielsen (2019), who examines risk-taking under negatively skewed outcome distributions for realized and unrealized losses. Using a different realization mechanism and a different investment task in which individuals can choose the skewness of their preferred option, she finds no realization effect for negatively skewed outcomes. Her finding is in line with our results and further supports the conclusion that the realization of outcomes does not always induce differences in risk-taking compared to settings in which outcomes remain unrealized.