Cash flow prediction: MLP and LSTM compared to ARIMA and Prophet

Abstract

Cash flow prediction is important. It can help increase returns and improve the allocation of capital in healthy, mature firms as well as prevent fast-growing firms, or firms in distress, from running out of cash. In this paper, we predict accounts receivable cash flows employing methods applicable to companies with many customers and many transactions such as e-commerce companies, retailers, airlines and public transportation firms with sales in multiple regions and countries. We first discuss “classic” forecasting techniques such as ARIMA and Facebook's™ Prophet before moving on to neural networks with multi-layered perceptrons and, finally, long short-term memory networks, that are particularly useful for time series forecasting but were until now not used for cash flows. Our evaluation demonstrates this range of methods to be of increasing sophistication, flexibility and accuracy. We also introduce a new performance measure, interest opportunity cost, that incorporates interest rates and the cost of capital to optimize the models in a financially meaningful, money-saving, way.

Appendix: The methods in more detail

The following notation will be used:

f::

model function

$y_{{\mathrm{t}}}$::

cash flow at time t, ${\hat{y}}_{{\mathrm{t}}}$ when forecasted

$\varvec{y}_{{\text {t}}-1}$::

vector of cash flow observations $[y_{{\text {t}}-1}, \ldots ,y_{{\text {t}}-{\text {n}}}]$

$r_{{\mathrm{i}}}, \phi _{{\mathrm{i}}}, \theta _{{\mathrm{i}}}$::

model parameters to be estimated

n::

length of time series used in model

p, d, q::

parameters for ARIMA

$c, \delta$::

constants to be estimated

$\epsilon _{{\mathrm{t}}}$::

error term for prediction of $y_{{\mathrm{t}}}$

L::

lag operator, e.g. $L^{\mathrm{d}}y_{{\mathrm{t}}} = y_{\text {t-d}}$

$\varvec{hol}$::

user provided set or vector of holidays for the firm.

1.1 Weighted moving average

The weighted moving average model is of type ${\hat{y}}_{{\mathrm{t}}} = f(\varvec{y}_{{\text {t}}-1})$:

$${\hat{y}}_{{\mathrm{t}}} = \sum \limits_ {i=1} ^{n}r_{{\mathrm{i}}}y_{\text {t-i}}\text {, with } \sum\limits _{i=1} ^{n}r_{{\mathrm{i}}} = 1$$

(3)

The model parameters $r_{{\mathrm{i}}}$ can be manually set without use of a cost function, with recent values usually given more weight than older ones. They can also be estimated using a linear regression (MSE). In order to pick up a linear trend, one could adapt the formula to:

$${\hat{y}}_{{\mathrm{t}}} = c + \sum\limits_{i=1}^{n}r_{{\mathrm{i}}}y_{{\text {t}}-{\text {i}}}$$

(4)

Relaxing the constraint $\sum\nolimits_{i=1}^{n}r_{{\mathrm{i}}} = 1$ would allow for an exponential trend. Setting all $r_{{\mathrm{i}}} = 1/n$ would yield a non-weighted moving average. It is obviously not possible to take into account any information other than past observations of the variable to be predicted.

1.2 ARIMA

The Auto-Regressive Integrated Moving Average (ARIMA) [8, 9] method uses a higher level of univariate models of the type ${\hat{y}}_{{\mathrm{t}}} = f(\varvec{y}_{{\text {t}}-1})$. The model, in a convenient notation ARIMA(p, d, q), is given by:

$$\left( 1- \sum _{\begin{array}{c} i=1 \end{array}}^{p}\phi _{{\mathrm{i}}}L_{{\mathrm{i}}}\right) (1-L)^{\mathrm{d}}y_{{\mathrm{t}}} = \delta + \left( 1+ \sum _{\begin{array}{c} i=1 \end{array}}^{q}\theta _{{\mathrm{i}}}L_{{\mathrm{i}}}\right) \epsilon _{{\mathrm{t}}}$$

(5)

in which $\phi _{{\mathrm{i}}}$ and $\theta _{{\mathrm{i}}}$ are the parameters of the Auto-Regressive (AR) and Moving Average (MA) parts of the model, respectively.

In a first Integration (I) step, the method aims to remove trends and, as such, make the time series stationary. This is done by differencing, a technique whereby the values of consecutive observations are subtracted and possibly complemented by using logarithms to stabilize the variations. E.g. For $d=2$, a second-degree difference or a difference of differences:

$$(1-L)^{\text {d}}y_{\text {t}} = y_{\text {t}}-2y_{{\text {t}}-1}+y_{\text {t}-2} = (y_{\text {t}}-y_{{\text {t}}-1})-(y_{{\text {t}}-1}-y_{\text {t}-2})$$

(6)

The general equation for the AR and MA parts can be written as:

$$y_{\text {t}}= \delta + \phi _{1}y_{{\text {t}}-1} + \phi _{2}y_{\text {t}-2} + \cdots + \phi _{\text {p}}y_{\text {t}-\text{p}} + \theta _{1}\epsilon _{{\text {t}}-1} + \theta _{2}\epsilon _{\text {t}-2} + \cdots + \theta _{\text {p}}\epsilon _{\text {t}-\text{q}}+ \epsilon _{\text {t}}$$

(7)

This is for the case $d=0$. For other cases, substitute $y_{{\mathrm{t}}}$ for $(1-L)^{\mathrm{d}}y_{{\mathrm{t}}}$). Upon closer inspection, ARIMA (n, 0, 0) equals the Weighted Moving Average method described above. Its parameters can be determined using a linear regression, implicitly assuming an MSE cost function. If, however, the MA part of ARIMA is used and $q>0$, then the error terms $\epsilon$ enter the equation. Since they are the difference between the forecasts and true values, the general forecasting equations are no longer linear, and iterative techniques are to be used to find solutions. To determine the parameters p, d, and q, a grid search can be conducted, and the best performing combination withheld for prediction.

1.3 Prophet

Detailing Facebook™ Prophet’s exact inner workings would exceed the scope of this paper. However, an additive regression underpins the method, completed by the extraction of a linear or logistic growth trend, Fourier series, the use of dummy variables and a list of holidays. In our use case, Prophet is based on a model of type ${\hat{y}}_{{\mathrm{t}}} = f(\varvec{y}_{{\text {t}}-1}, \varvec{hol}$).

1.4 Multi-layer perceptrons

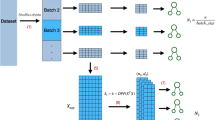
The basic building block of a neural network is the node. Nodes are connected by links, albeit in a more orderly fashion than neurons in the brain. A weight $w_{{\mathrm{i}}}$ is attributed to each of n links as a measure of its strength and sign. Figure 7 illustrates how the value of a node $a_{{\mathrm{out}}}$ is computed by first calculating the weighted sum of its inputs and then applying a non-linear activation function g to it:

$$a_{{\mathrm{out}}} = g(b+ \sum _{i=1}^{n}w_{{\mathrm{i}}}a_{{\mathrm{i}}})$$

(8)

Fig. 7

Calculating the output value $a_{{\mathrm{out}}}$ of a node, as a linear combination of its inputs $a_{{\mathrm{i}}}$ to which a bias b is added before the activation function g is applied

To facilitate further reading, we introduce the most important additional notation used:

$\varvec{y}$::

dependent variable: vector of cash flow observations, ${\hat{\varvec{y}}}$ when forecasted

$\varvec{x}$::

independent variable: vector of cash flow observations and other inputs if any

$\varPsi ^{\mathrm{j}}$::

represents the function (weighted sum) for each node at layer j

$\circ$::

operator for a composition of functions

$g_{{\mathrm{j}}}$::

activation function for layer j

$\varvec{W}_{{\mathrm{j}}}$::

jth layer’s weight matrix containing weights for the layer’s nodes (= model parameters to estimated)

$\varvec{b}_{{\mathrm{j}}}$::

vector of biases for layer j

J::

cost function yielding a scalar

$\varTheta$::

parameter space containing all weights and biases for all nodes

$\varvec{a}_{{\mathrm{j}}}$::

vector of node outputs values from previous layer $j-1$.

Information in feed forward networks or perceptrons only flows in one direction—from input to output. The nodes in these networks are usually organized in layers, without links between the nodes within a layer, such that a node only receives information from (some of) the nodes in the preceding layer. A multi-layer, or deep feed forward network, is also called a multi-layer perceptron (MLP). It consists of one or more hidden layers between the input and output layers.

MLPs, as all neural networks are used to estimate the true, unknown function that explains the output $\varvec{y}$ in function of the inputs $\varvec{x}$ [11]. This involves optimizing the parameters $\varTheta {}$, so that the function $f(\varvec{x};\varTheta )$ approximates this true function. After an input is fed to a neural network, information will start flowing through it, known as forward propagation, finally producing values for the nodes in the output layer. These values are then used to compute the scalar cost function $J(\varTheta )$. Mathematically, we can describe MLP as a model:

$$\begin{aligned}&{\hat{\varvec{y}}}=f(\varvec{x}) = (\varPsi ^{\mathrm{m}}\circ \varPsi ^{\mathrm{m}-1}\circ \varPsi ^{\mathrm{m}-2}\circ \cdots \circ \varPsi ^{1})(\varvec{x}) \nonumber \\ & \varPsi ^{\mathrm{j}}(\varvec{a}_{{\mathrm{j}}}) = g_{{\mathrm{j}}}(\varvec{W}_{{\mathrm{j}}}^{\mathrm{T}}.\varvec{a}_{{\mathrm{j}}}+\varvec{b}_{{\mathrm{j}}}) \text {, with }\varvec{a}_{1} = \varvec{x} \nonumber \\ &{\text {minimizing the cost function: }}\, \underset{\varTheta }{\arg \min } J(|{\hat{\varvec{y}}} -\varvec{y}|,\varTheta ) \end{aligned}$$

(9)

Training the neural network implies finding the parameters $\varTheta$ that minimize the cost function $J(\varTheta$). This is commonly achieved by a backpropagation algorithm [12] that computes the gradient of $J(\varTheta )$ with respect to all weights in the neural network. Another algorithm, for example SGD (stochastic gradient descent) or adam (adaptive moment estimation) [21], will then utilize these gradients to adjust all parameters $\Theta$. Once that is done, a new set of inputs is run through the network, and the entire learning cycle repeats itself until a pre-determined stopping criterion is satisfied.

Compared to the classical models above, MLPs are models of the more generic type ${\hat{\varvec{y}}}=f(\varvec{x})$ in which the vector $\varvec{x}$ can include all possible quantifiable variables, amongst which, but not limited to: $\varvec{y}_{{\text {t}}-1}, \varvec{hol}$, etc. If we were to build a model to forecast the cash inflow based on the previous day’s cash inflow and the holiday status of that day, the model would be: ${\hat{y}}_{{\mathrm{t}}}=f(y_{{\text {t}}-1}, hol_{{\text {t}}-1})$. If, however, we wanted to input multi-variate time series into an MLP model (2-dimensional input), we would have had to flatten the input into a one-dimensional vector. The above example, thus, becomes ${\hat{y}}_{{\mathrm{t}}}=f(y_{{\text {t}}-1}, hol_{{\text {t}}-1}, \ldots , y_{\text {t-k-1}}, hol_{\text {t-k-1}})$ for a k-day time series. We used this technique when evaluating MLPs for cash flow forecasting. Our output vector of length 1 corresponds to one node in the last layer.

1.5 Recurrent neural networks with a focus on LSTM

An MLP considers only one event at a time and assumes all inputs to be temporarily independent of each other.⁶ This assumption, however, is invalid in many real-world situations: In speech, every word in a sentence is related to one another, while data in time series, such as cash flows, is also related to past data. Recurrent neural networks (RNNs) are designed to handle these dependencies; hence, they are widely used in speech recognition, translation, image captioning, video-to-text, question answering, time series forecasting, etc. We propose some additional notation for this section:

$\varvec{Y}$::

matrix with (time) series of dependent variables, ${\hat{\varvec{Y}}}$ when forecasted

$\varvec{X}$::

matrix with (time) series of independent variables: cash flow observations and other inputs if any

$f_{{h}}$::

function that computes the hidden state of a RNN’s node

$h_{{\mathrm{t}}}$::

hidden state of a RNN cell at timestep t

$\varvec{a}_{{\mathrm{t}}}$::

vector of node outputs values from previous layer at timestep t

$\sigma$::

sigmoid function.

At any time step, an RNN node will remember past information by having a hidden state $h_{{\mathrm{t}}}$ that is a function of the hidden state of the previous time step $h_{{\text {t}}-1}$ and the current input $\varvec{a}_{{\mathrm{t}}}$ (that equals $\varvec{x}_{{\mathrm{t}}}$ if the node is in the first hidden layer that acts upon the model’s inputs):

$$h_{{\mathrm{t}}}= f_{h}(h_{{\text {t}}-1}, \varvec{a}_{{\mathrm{t}}})$$

(10)

RNNs allow for sequences in the output, input, or both, whereas MLPs are only capable of handling fixed-length vectors as input and output. For this paper, however, we chose to only output a one-step time sequence with one variable, i.e. a 1x1 matrix.

RNNs, thus, belong to the ${\hat{\varvec{Y}}}=f(\varvec{X})$ class of models, in which $\varvec{Y}$ and $\varvec{X}$ are matrices. The general mathematical description is similar to that of MLPs, however both inputs and outputs have an added dimension to allow for different time instances:

$$\begin{aligned}&{\hat{\varvec{Y}}}=f(\varvec{X}) = ( \varPsi ^{\mathrm{m}}\circ \varPsi ^{\mathrm{m}-1}\circ \varPsi ^{\mathrm{m}-2}\circ \cdots \circ \varPsi ^{1})(\varvec{X}) \nonumber \\&\quad \text {minimizing the cost function: } \underset{\varTheta }{\arg \min } J(|{\hat{\varvec{Y}}} -\varvec{Y}|,\varTheta )\end{aligned}$$

(11)

RNNs can be difficult to train: the backpropagation algorithm must be adapted to backpropagate through time as well, which can lead to vanishing or exploding gradients problems. We will not elaborate on those here. By making a more sophisticated function $f_{{\mathrm{h}}}$ for the hidden state, Long Short-Term Memory models (LSTMs) [13] were created. They suffer less from the aforementioned problems and are capable of learning long-term dependencies. Data scientists use LSTMs more than any other type of RNNs. Figure 8 provides a schematic overview of an LSTM node’s inner workings. The formulas for an LSTM memory cell demonstrate their high complexity compared to MLP cells.⁷ Fortunately, these formulas are usually integrated in the deep learning software packages and need not concern users:

Fig. 8

A glance at the inner workings of an LSTM node. Information is forward-propagated through the node from input $\varvec{a}_{{\mathrm{t}}}$ to output $\varvec{h}_{{\mathrm{t}}}$ as well as passed to a subsequent instance of the node in time (from $\varvec{h}_{{\text {t}}-1}$ and $\varvec{c}_{{\text {t}}-1}$ to $\varvec{h}_{{\mathrm{t}}}$ and $\varvec{c}_{{\mathrm{t}}}$ respectively)

$$\begin{aligned} \varvec{ i}_{{\mathrm{t}}}&= \sigma (\varvec{W}_{{\mathrm{i}}}\varvec{h}_{{\text {t}}-1}+\varvec{V}_{{\mathrm{i}}}\varvec{a}_{{\mathrm{t}}}+\varvec{b}_{{\mathrm{i}}})\text {: input gate} \nonumber \\ \varvec{f}_{{\mathrm{t}}}&= \sigma (\varvec{W}_{{\mathrm{f}}}\varvec{h}_{{\text {t}}-1}+\varvec{V}_{{\mathrm{f}}}\varvec{a}_{{\mathrm{t}}}+\varvec{b}_{{\mathrm{f}}})\text {: forget gate} \nonumber \\ \varvec{o}_{{\mathrm{t}}}&= \sigma (\varvec{W}_{{\mathrm{o}}}\varvec{h}_{{\text {t}}-1}+\varvec{V}_{0}\varvec{a}_{{\mathrm{t}}}+\varvec{b}_{{\mathrm{o}}}) \text {: output gate} \nonumber \\ \varvec{g}_{{\mathrm{t}}}&= \text {tanh}(\varvec{W}_{{\mathrm{g}}}\varvec{h}_{{\text {t}}-1}+\varvec{V}_{{\mathrm{g}}}\varvec{a}_{{\mathrm{t}}}+\varvec{b}_{{\mathrm{g}}}) \text {: internal hidden state}\nonumber \\ \varvec{c}_{{\mathrm{t}}}&= (\varvec{c}_{{\text {t}}-1} \otimes \varvec{f}_{{\mathrm{t}}}) \oplus (\varvec{g}_{{\mathrm{t}}}\otimes \varvec{i}_{{\mathrm{t}}}) \text {: memory cell} \nonumber \\ \varvec{h}_{{\mathrm{t}}}&= \text {tanh}(\varvec{c}_{{\mathrm{t}}} \otimes \varvec{o}_{{\mathrm{t}}})\text {: hidden state} \end{aligned}$$

(12)