Modelling the two-way coupling of tidal sand waves and benthic organisms: a linear stability approach

Abstract

We use a linear stability approach to develop a process-based morphodynamic model including a two-way coupling between tidal sand wave dynamics and benthic organisms. With this model we are able to study both the effect of benthic organisms on the hydro- and sediment dynamics, and the effect of spatial and temporal environmental variations on the distribution of these organisms. Specifically, we include two coupling processes: the effect of the biomass of the organisms on the bottom slip parameter, and the effect of shear stress variations on the biological carrying capacity. We discuss the differences and similarities between the methodology used in this work and that from ‘traditional’ (morphodynamics only) stability modelling studies. Here, we end up with a $2\times 2$ linear eigenvalue problem, which leads to two distinct eigenmodes for each topographic wave number. These eigenmodes control the growth and migration properties of both sand waves and benthic organisms (biomass). Apart from hydrodynamic forcing, the biomass also grows autonomously, which results in a changing fastest growing mode (FGM, i.e. the preferred wavelength) over time. As a result, in contrast to ‘traditional’ stability modelling studies, the FGM for a certain model outcome does not necessarily have to be dominant in the field. Therefore, we also analysed the temporal evolution of an initial bed hump (without perturbing biomass) and of an initial biomass hump (without perturbing topography). It turns out that these local disturbances may trigger the combined growth of sand waves and spatially varying biomass patterns. Moreover, the results reveal that the autonomous benthic growth significantly influences the growth rate of sand waves. Finally, we show that biomass maxima tend to concentrate in the region around the trough and lee side slope of sand waves, which corresponds to observations in the field.

1 Introduction

In large parts of tide-dominated sandy shelf seas, such as the North Sea, rhythmic bed patterns can be observed [53]. Amongst the various types of marine bed forms, tidal sand waves (Fig. 1a) are often the most relevant type to investigate from an engineering point of view, due to their dimensions and dynamic behaviour. Typical heights are on the order of several meters, with wavelengths of 100–1000 m. Migration rates can be up to 10 m per year [45], and they form on a time scale of decades [26]. Moreover, these shallow coastal seas form the habitat for numerous different benthic communities, within which large spatial and temporal variations are observed. These variations are often related to geomorphological patterns of various dimensions [1, 42, 44, 46]. In particular, Damveld et al. [17] found that benthic organisms (benthos) occurred in much higher densities in sand wave troughs compared to the crests. Additionally, previous studies have shown that benthos in turn may significantly affect the local hydro- and sediment dynamics, and thereby the morphological development [29, 55].

Fig. 1

a Sand wave field in the North Sea (data from Royal Dutch Navy), where the colours denote the bed level relative to the mean sea level (m). b Example of a biostabiliser: adult sea urchin (E. cordatum). Photograph from first author

Knowledge of tidal sand waves is of practical interest, as they tend to endanger a broad range of applications for coastal shelf seas [26, 28, 32, 39]. For instance, migrating sand waves may form obstacles for shipping and infrastructure (e.g. oil and gas platforms, cables and wind farms). Also, due to an increased pressure on the coastal environment [54], as well as the increased awareness towards ecological sustainability, knowledge about the interaction of morphological processes with benthic species is gaining importance [2].

The presence of benthic species in coastal areas has been extensively studied [30, and references therein]. Although benthic species may influence the sediment dynamics in many ways, they are commonly classified in two functional groups, namely stabilisers and destabilisers [55]. For example, the sea urchin Echinocardium cordatum (see Fig. 1b) is able to stabilise the bed by reworking the top sediment layer [27]. In addition, benthic species that protrude from the bed into the water column (e.g. the tube-building worm Lanice conchilega [19, 37]) may affect water motion as well [22]. Nevertheless, this general classification makes it possible to capture the complex interactions among biology and hydro- and sediment dynamics in mathematical models [8, 34].

Various aspects regarding sand wave formation have been studied for over 2 decades using process-based morphodynamic models [4]. Many of these model studies involve a method called linear stability analysis [20], where the stability of a sandy seabed, subject to tidal motion, is analysed. For a symmetrical tide, while only incorporating bed load sediment transport, Hulscher [24] used this method to explain the formation of tidal sand waves. She showed that small bed perturbations distort the tidal flow in such a way that small tide-averaged vertical recirculation cells appear in the water column. The presence of these cells results in a near-bed flow from trough to crest, which in turn induces a net transport of sediments in the same direction. On the other hand, gravitational effects favour sediment transport in a down-slope direction. It is the competition between these two processes that eventually leads to sand wave growth or decay. The typical result of this method is a set of modes with either a positive or a negative growth rate, where the mode with the largest positive growth rate is termed the fastest growing mode (FGM). The FGM is characterised by a wavelength, an orientation and a growth and migration rate (the latter being zero in case of symmetrical forcing). Other studies have shown that the properties of the FGM are comparable to those of sand waves observed in the field [25, 52].

Other model studies have extended the approach of Hulscher [24] and identified additional processes affecting the initial growth of sand waves. For instance, migration due to wind [14, 31] and tidal asymmetry [5], suspended sediment transport and turbulence formulation [6, 7], varying grain sizes [49] and sand scarcity [36]. Moreover, it has been shown that the presence of benthic organisms can influence the initial growth of sand waves [10]. In addition, other researchers used non-linear models to investigate equilibrium sand wave shapes [33, 43, 47], storm effects [13], the role of turbulence [11] and suspended sediment [12].

Whereas the majority of the idealised model studies into morphological features only consider the morphological evolution of the bed, some studies included a coupling between bed topography and multiple grain size fractions in order to explain observed phase differences between them [21, 41, 50, 51]. Moreover, for riverine environments a similar approach has been used, here focussing on the coupling between vegetation and morphodynamics [3, 16]. In these latter studies, a coupled model has been successfully employed to explain bar formation patterns in rivers.

Although previous research has provided evidence of two-way interactions between benthos and coastal morphology, present modelling tools are lacking the ability to investigate these effects. In this paper we use a linear stability approach to develop a fully two-way coupled model to study the feedbacks between sand waves and benthic organisms. In particular, we include the effects of benthos on the bottom roughness; and benthic habitat variations are represented through the biological carrying capacity. The main purpose of this work is to determine whether disturbances in the spatial distribution of benthic organisms may trigger the development of phase-related bed patterns, and vice versa. To this end, we show that the outcome of the two-way coupled methodology is essentially different from that of ‘traditional’ (uncoupled) stability methods. Moreover, we zoom in on the effect of the interaction among three different time scales (hydrodynamical, morphological and biological) within the coupled system.

This paper is organised as follows. The coupled biogeomorphological model is presented in Sect. 2. Next, the solution method, involving a scaling procedure and a linear stability analysis, is given in Sect. 3. In Sect. 4 the results are given, followed by the discussion and conclusions, presented in Sects. 5 and 6, respectively.

2 Model formulation

2.1 Geometry

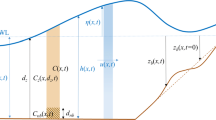
We consider a tidal wave of angular frequency $\sigma ^*$ and horizontal velocity amplitude $U^*$ in a shallow sea of average depth $H^*$, propagating over a sandy bottom with small undulations (see Fig. 2). Additionally, the bed is the habitat of various benthic organisms, described by the benthic biomass $\phi ^*(x^*,t^*)$. To represent the coupled biogeomorphological system, we define a Cartesian coordinate system $\left( x^*,z^*\right)$ with the $x^*$ coordinate pointing horizontally and the $z^*$ coordinate pointing upward. The free surface level is denoted by $z^* = \zeta ^* (x^*,t^*)$, with $z^* =0$ as the undisturbed water level. The sea bed is located at $z^* =-H^*+h^*(x^*,t^*)$, with bottom topography $h^*$. The spatial average of $h^*$ equals zero. Furthermore, $u^*(x^*, z^*, t^*)$ and $w^*(x^*, z^*, t^*)$ denote the flow velocities in horizontal and vertical direction, respectively. Finally, the asterisk * denotes unscaled variables.

Fig. 2

Side view of the bed and water column in the direction of the tidal current, illustrating the coordinate system, free surface level $\zeta ^*$, average depth $H^*$, bed topography $h^*$ and biomass density $\phi ^*$ (symbolically denoted by the green dots)

2.2 Hydrodynamics

Flow and bottom development are described by the shallow water equations, flow and sediment continuity equations, supplemented with appropriate boundary conditions. Turbulence is represented by a constant vertical eddy viscosity with regard to time and space and a partial slip condition at the bottom. Following the 2DV approach, we choose to ignore Coriolis forces, which have been shown to be negligible on the spatial scale of sand waves [24]. The model equations read

$$\begin{aligned}&\frac{\partial u^*}{\partial x^*}+\frac{\partial w^*}{\partial z^*}=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u^*}{\partial t^*}+u^*\frac{\partial u^*}{\partial x^*}+w^*\frac{\partial u^*}{\partial z^*}=-F^*-g^*\dfrac{\partial \tilde{\zeta }^*}{\partial x^*}+A_\text {v}^*\dfrac{\partial ^2u^*}{\partial z^{*2}}. \end{aligned}$$

(2)

Here, $u^*$ and $w^*$ represent the fluid velocity in horizontal and vertical dimension, respectively, $g^*$ the gravitational acceleration and $A_\text {v}^*$ the vertical eddy viscosity. Following Campmans et al. [14], we express the water level gradient term as a superposition of a (spatially uniform) tidal forcing $F^*$ and the water level gradient due to variations in topography only $(g^*\partial \tilde{\zeta }^*/\partial x^* )$.

The boundary conditions at the free surface and bottom read

$$\begin{aligned} w^*&=\dfrac{\partial \zeta ^*}{\partial t^*}+u^*\dfrac{\partial \zeta ^*}{\partial x^*}, \quad \dfrac{\partial u^*}{\partial z^*}=0&\text {at } z^*=\zeta ^*, \end{aligned}$$

(3)

$$\begin{aligned} w^*&=\dfrac{\partial h^*}{\partial t^*}+u^*\dfrac{\partial h^*}{\partial x^*}, \quad \dfrac{\tau ^*}{\rho ^*}\equiv A_\text {v}^*\dfrac{\partial u^*}{\partial z^*}=f_\text {slip}S^*u^*&\text {at } z^*=-H^*+h^*, \end{aligned}$$

(4)

respectively. Here, $\tau ^*$ is the bed shear stress, $\rho ^*$ the water density, $S^*$ a slip parameter and $f_\text {slip}$ a dimensionless coupling coefficient which expresses the effect of biomass on the slip parameter, to be further specified in Sect. 2.6.

2.3 Sediment transport

In this model we limit ourselves to bed load transport, since it is assumed to be the prevailing transport in tide-dominated sandy seas where sand waves occur. The transport of bed load sediment is described by the following general equation:

$$\begin{aligned} q^*=\alpha ^*\left( \left| \tau ^*\right| -\tau _\text {c}^*\right) ^{\nicefrac {3}{2}}\left( \frac{\tau ^*}{\left| \tau ^*\right| } -\lambda ^* \frac{\partial h^*}{\partial x^*}\right) {{\mathscr {H}}}\left( \left| \tau ^*\right| -\tau _\text {c}^*\right) . \end{aligned}$$

(5)

Here, $q^*$ is the bed load transport, $\alpha ^*$ a bed load coefficient, $\tau _\text {c}^*$ the critical bed shear stress according to Shields (depending on the sediment diameter $d^*$), $\lambda ^*$ a slope correction factor and ${\mathscr {H}}\left( \cdot \right)$ the Heaviside function, equating one for a positive argument and zero otherwise.

2.4 Bottom evolution

The bed evolution is governed by the sediment continuity equation (Exner equation), which reads

$$\begin{aligned} \left( 1-p\right) \frac{\partial h^*}{\partial t^*}=-\frac{\partial q^*}{\partial x^*}, \end{aligned}$$

(6)

with $p=0.4$ the volume fraction of voids in the bed. This equation simply states that converging (diverging) sediment transport will lead to a rising (falling) bed profile.

2.5 Biomass evolution

Fig. 3

Evolution of benthic biomass, described by a logistic growth profile (solid lines) and a carrying capacity (dashed lines). The black lines denote the flat bottom case, where the grey lines represent an arbitrary response to local variations in shear stress. The black dot indicates the inflection point of the black line, representing the transition point between increasing and reducing growth. Parameters values according to Table 1, and the initial biomass is $\phi ^*|_{t^*=0}=0.05\phi ^*_\text {eq}$

Analogous to Bärenbold et al. [3], we describe benthic biomass by a combination of logistic growth (see Fig. 3) and biological dispersal, according to

$$\begin{aligned} \frac{\partial {\phi }^*}{\partial {t}^*}={\alpha _\text {g}^*}{\phi ^*}\left( f_\text {eq}\phi _\text {eq}^*-{\phi }^*\right) +{D^*}\frac{\partial ^2\phi ^*}{\partial x^{*2}}. \end{aligned}$$

(7)

Here, ${\alpha _\text {g}}^*$ is the logistic growth parameter, ${\phi }_\text {eq}^*$ the undisturbed (in case of a flat bed) carrying capacity and ${D^*}$ the biological dispersal parameter (note that this is a diffusion coefficient from a mathematical perspective) which controls the spatial spreading of biomass. Furthermore, the actual carrying capacity is modelled as the undisturbed carrying capacity multiplied by a dimensionless coupling coefficient $f_\text {eq}$ (see Sect. 2.6).

2.6 Coupling coefficients

The two-way coupling between benthic biomass and sand wave morphology is represented through the coefficients influencing the slip parameter $\left( f_\text {slip}\right)$ and carrying capacity $\left( f_\text {eq} \right)$, which are specified in more detail below. In general, $f_\text {slip}$ represents the effect of benthic organisms on morphological processes, whereas the opposite holds for $f_\text {eq}$.

$f_{\mathrm {slip}}$:

In this work we focus on species that protrude out of the bed (e.g. L. conchilega). They influence the water motion by increasing the bottom roughness through their tubes [22, 35] or created mounds [23]. As defined in Eq. (4), bottom roughness is represented by the bottom slip parameter. To describe the behaviour of these species, we define $f_\text {slip}$ (see Fig. 4a) by an exponentially decreasing function of biomass

$$\begin{aligned} f_\text {slip}=\frac{S_\text {bio}^*}{S^*} = \left( 1-\mu _\text {slip}\right) \exp \left( -\kappa _\text {slip}^*\phi ^*\right) +\mu _\text {slip}, \end{aligned}$$

(8)

with $S_\text {bio}^*$ as the actual slip parameter, $\mu _\text {slip} = S_\text {bio,max}^*/S^*$ as the ratio between the highest possible bottom slip parameter due to benthic biomass $S_\text {bio,max}^*$ and the abiotic bottom slip parameter $S^*$, and $\kappa _\text {slip}^*$ as the rate of increase due to an increasing biomass density.

$f_{\mathrm {eq} }$:

In order to represent the influence of morphological processes on the benthic biomass, we let the carrying capacity be a function of the bottom shear stress. It is widely accepted that the bottom shear stress is a suitable predictor for the distribution of benthic organisms (e.g., de Jong et al. [18]). Therefore, the correction factor for the carrying capacity in Eq. (7) is written as

$$\begin{aligned} f_\text {eq}=\frac{\phi _\text {eq,bio}^*}{\phi _\text {eq}^*} = {\left( \tau ^*_\text {ref}-\left| \tau ^*\right| \right) }\kappa ^*_\text {eq}+1, \end{aligned}$$

(9)

where $\phi ^*_\text {eq,bio}$is the actual carrying capacity, $\kappa _\text {eq}^*$ is the rate of change due to an increasing density of biomass and $\tau ^*_\text {ref}$ is a reference value for the critical shear stress. Our choice for this linear function (see Fig. 4c) is justified by the fact that only the derivative of $f_\text {eq}$ in $\tau ^*_\text {ref}$ matters in the linear stability analysis.

Fig. 4

Example relations for the coupling coefficients for a slip parameter as in Eq. (8) and b carrying capacity as in Eq. (9). Parameter values are as indicated as in Table 1

Table 1 Overview of the model parameters and their values used in this work

3 Solution method

3.1 Outline

First we will present a scaling procedure, after which we describe the forcing. Next, we introduce the linear stability analysis, in which the basic and perturbed state solutions are given. Finally, we describe the individual process contributions.

3.2 Scaling procedure

In order to scale the model equations, we introduce the dimensionless coordinates (x, z, t) and quantities $(u, w, h, \zeta , \tau , q, \phi )$ according to

$$\begin{aligned} \left. \begin{array}{ll} x^*=l^*_\text {sw}{x},&{} z^*=H^*z\\ t^*=\frac{t}{\sigma ^*}={t_\text {long}}T_\text {long}^*\\ \\ h^*=H^*h,&{}\tilde{\zeta }^*=\frac{U^{*2}}{g^*}\zeta \\ u^*=U^*u,&{} w^*=\frac{U^*H^*}{l^*_\text {sw}}w\\ \tau ^*=\rho ^*U^*H^*\sigma ^*\tau ,&{} q^*=\alpha ^*\left( \rho ^*U^*H^*\sigma ^*\right) ^{\nicefrac {3}{2}} q\\ {\phi }^* = {\phi }_\text {eq}^*{\phi } \end{array}\right\} , \end{aligned}$$

(10)

in which $l^*_\text {sw}$ is the topographic length scale, which is in the order of the wavelength of sand waves. Furthermore, we use two different time coordinates t and $t_\text {long}$, such that two time scales are identified, i.e. the tidal time scale $1/\sigma ^*$ and a yet to be determined biogeomorphological time scale $T^*_\text {long}$. The biogeomorphological time scale is given by

$$\begin{aligned} T_\text {long}^* = \text {min}{\left( T_\text {m}^*,T_\text {b}^*\right) }, \end{aligned}$$

(11)

which equals the shortest of the time scales $T_\text {m}^*$ and $T_\text {b}^*$, associated with morphology and biomass, respectively.

As a result of the chosen scaling, the non-dimensional version of the hydrodynamic model equations [Eqs. (1), (2)] are as follows:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\partial u}{\partial t}+ru\frac{\partial u}{\partial x}+w\frac{\partial u}{\partial z}=-F-r\dfrac{\partial \zeta }{\partial x}+A_\text {v}\dfrac{\partial ^2u}{\partial z^{2}}, \end{aligned}$$

(13)

where $r=U^*/\left( l^*_\text {sw}\sigma ^*\right)$ is the Keulegan–Carpenter number, $F=F^*/(U^*\sigma ^*)$ is the non-dimensional forcing term and $A_{\mathrm {v}}=A_{\mathrm {v}}^*/(H^{*2}\sigma ^*)$ is the non-dimensional eddy viscosity term.

The scaled, non-dimensional counterparts of the boundary conditions at the free surface [Eq. (3)] read

$$\begin{aligned} w=0, \quad \dfrac{\partial u}{\partial z}=0 \quad \text {at } z=0, \end{aligned}$$

(14)

where we have used that $\text {Fr}^2 \ll 1$ and ${\text {Fr}^2}/{r} \ll 1$, with the Froude number $\text {Fr} = U^*/\sqrt{g^*H^*}$. Hence, the vertical velocity becomes zero at the top boundary and the free surface boundary condition is evaluated at $z=0$, i.e. the rigid lid approximation. At the bottom boundary, the scaled, non-dimensional version of the boundary conditions [Eq. (4)] are

$$\begin{aligned} w=u\dfrac{\partial h}{\partial x}, \quad \tau \equiv A_\text {v}\dfrac{\partial u}{\partial z}=f_\text {slip}Su \quad \text {at } z=-1+h. \end{aligned}$$

(15)

Here, $S=S^*/\left( \sigma ^*H^*\right)$ is the non-dimensional slip parameter and we assume the biogeomorphological time scale to be long, such that $\partial h/\partial t$ is negligible. The bed load transport equation [Eq. (5)] in scaled, non-dimensional form reads

$$\begin{aligned} q=\left( \left| \tau \right| -\tau _\text {c}\right) ^{\nicefrac {3}{2}}\left( \frac{\tau }{\left| \tau \right| } -\lambda \frac{\partial h}{\partial x}\right) {\mathscr {H}}{\left( \left| \tau \right| -\tau _\text {c}\right) }, \end{aligned}$$

(16)

where $\lambda = \lambda ^* H^*/l^*_\text {sw}$ is the scaled bed slope coefficient. The scaled, non-dimensional version of the bed evolution equation [Eq. (6)] reads

$$\begin{aligned} \frac{\partial h}{\partial t_\text {long}}=-\nu _\text {m}\frac{\partial \left\langle q\right\rangle _\text {tide}}{\partial x}. \end{aligned}$$

(17)

Here we identify the non-dimensional parameter $\nu _\text {m} = T^*_\text {long}/T^*_\text {m}$. Moreover, we have used that the tidal time scale is much smaller than the biogeomorphological time scale, so that only the tide-averaged bed load transport, denoted by $\left\langle \cdot \right\rangle _\text {tide}$, effectively contributes to the bed evolution. The resulting morphological time scale, using parameters from Table 1, is given by

$$\begin{aligned} T^*_\text {m}=\frac{(1-p)H^*l^*_\text {sw}}{\alpha ^*\left( \rho ^*U^*H^*\sigma ^*\right) ^{\nicefrac {3}{2}} } \approx 6\,\hbox {year}. \end{aligned}$$

(18)

Next, the biomass evolution equation [Eq. (7)] is cast in scaled, non-dimensional form, leading to

$$\begin{aligned} \frac{\partial {\phi }}{\partial {t_\text {long}}}=\left\langle {\nu }_\text {b,g}{\phi }\left( f_\text {eq}-{\phi }\right) +{\nu }_\text {b,D}\frac{\partial ^2{\phi }}{\partial {x}^2}\right\rangle _\text {tide}, \end{aligned}$$

(19)

where we have introduced the non-dimensional parameters ${\nu }_\text {b,g}= T_\text {long}^*/ {T}_\text {b,g}^*$ and $\nu _\text {b,D}= T_\text {long}^*/ T_\text {b,D}^*$. As a result, we identify two biological time scales, the biological-growth time scale ${T}_\text {b,g}^*$ and the biological-dispersal time scale ${T}_\text {b,D}^*$

$$\begin{aligned} {T}_\text {b,g}^* = \frac{1}{{\alpha _\text {g}^*}{\phi }_\text {eq}^* }, \quad {T}_\text {b,D}^* = \frac{1}{{D^*k^{*2}}}. \end{aligned}$$

(20)

The actual biological time scale is defined as the shortest of the two, i.e.

$$\begin{aligned} {T}_\text {b}^* = \min {\left( {T}_\text {b,g}^*,{T}_\text {b,D}^* \right) }. \end{aligned}$$

(21)

Typical values for ${\phi }_\text {eq}^*$ and ${\alpha }_\text {g}^*$ are on the order of $1\hbox { kg m}^{-1}$ and $0.5\hbox { m kg}^{-1}\,\hbox {year}^{-1}$, respectively (see Table 1), and so the biological(-growth) time scale becomes $T_\text {b,g}^* \approx 2\hbox { year}.$ The resulting biological time scale is thus much larger than the hydrodynamic (tidal) time scale. Similar to morphodynamics, it is therefore appropriate to calculate the evolution of biomass on a tide-averaged scale.

Finally, we repeat the coefficients which control the two-way coupling between sand waves and benthic organisms [Eqs. (8), (9)], now expressed in terms of dimensionless quantities:

$$\begin{aligned} f_\text {slip}&= \left( 1-\mu _\text {slip}\right) \exp \left( -\kappa _\text {slip}\phi \right) +\mu _\text {slip}, \end{aligned}$$

(22)

$$\begin{aligned} f_\text {eq}&= \left( \tau _\text {ref}-\left<\left| \tau \right| \right>_\text {tide} \right) \kappa _\text {eq}+1, \end{aligned}$$

(23)

with $\kappa _\text {eq} = \kappa _\text {eq}^*\rho ^*U^*H^*\sigma ^*$ and $\kappa _\text {slip} = \kappa _\text {slip}^*\phi _\text {eq}^*$ as the scaled coupling parameters.

3.3 Forcing

In our model we recognise two different length scales: (1) the topographic length scale $(l^*_\text {sw} \approx 0.5\hbox { km} )$ and (2) the length scale of the tidal wave $( l^*_\text {tw} \approx 400\hbox { km} )$. Since the tidal length scale is much larger than the topographic length scale, we consider the tidal wave to be spatially uniform. Hence, we describe the forcing in Eq. (13) by the following truncated temporal Fourier series:

$$\begin{aligned} F{\left( t\right) }=\sum _{m=-M}^{M}\hat{F}_m e^{imt}. \end{aligned}$$

(24)

Here, M is the number of tidal constituents, which in turn are represented by the complex amplitudes of the Fourier components $\hat{F}_m = \overline{\hat{F}_{-m}}$. The actual forcing is hence real-valued and chosen such that—in the case of a flat bed—a prescribed depth-averaged flow is attained. In the results shown in this paper, $M = 8$ and has been chosen based on numerical experiments, such that the contribution of harmonics $\pm \left( M+1\right)$ to the solution are negligible. This value is determined by the inclusion of the critical shear stress in the sediment transport formulation.

3.4 Linear stability analysis

We will evaluate the coupled system using a linear stability approach, where we investigate the stability of a flat bed and a spatially uniform distribution of biomass, subject to tidal motion and biological growth. To this end, we analyse the response of the so called basic state to small-amplitude sinusoidal perturbations (perturbed state), where the initial state of the system is defined as

$$\begin{aligned} \left. h^*\right| _{t^*=0}&=\left. h_0^*\right| _{t^*=0}+\tilde{h}^{*\text {init}}\cos {\left( k^*x^*\right) }, \end{aligned}$$

(25)

$$\begin{aligned} \left. \phi ^*\right| _{t^*=0}&=\left. \phi _0^*\right| _{t^*=0}+\tilde{\phi }^{*\text {init}}\cos {\left( k^*x^*+\theta \right) }. \end{aligned}$$

(26)

Here, $\tilde{h}^{*\text {init}}$ and $\tilde{\phi }^{*\text {init}}$ are the initial real-valued perturbation amplitudes for topography and biomass, respectively, $\theta$ a possible phase shift between topography and biomass, and $h_0^*$ and $\phi _0^*$ are the initial bed profile and biomass distribution in the basic state, respectively. Since the basic state always represents a uniform flat bed—opposed to the biomass distribution which is uniform, but non-zero—we write $h_0^*=0$. Moreover, it is required that $\tilde{\phi }^{*\text {init}} < \phi _0^*$ to ensure that $\phi ^*$ does not become negative, which would physically not be valid.

In scaled, non-dimensional form, Eqs. (25) and (26) read

$$\begin{aligned} \left. h\right| _{t_\text {long}=0}&= {\left. \epsilon h_1\right| _{t_\text {long}=0}}= \left. \epsilon \tilde{h}_1^{\text {init}}\cos {\left( kx\right) },\right. \end{aligned}$$

(27)

$$\begin{aligned} \left. \phi \right| _{t_\text {long}=0}&=\left. \phi _0\right| _{t_\text {long}=0}+ {\left. \epsilon \phi _1\right| _{t_\text {long}=0}}=\left. \phi _0\right| _{t_\text {long}=0}+ \left. \epsilon \tilde{\phi }_1^{\text {init}}\cos {\left( kx + \theta \right) },\right. \end{aligned}$$

(28)

with $k=l^*_\text {sw}k^*$ as the scaled, dimensionless wave number, $\phi _0$ as the basic benthic biomass, $h_1$ and $\phi _1$, and $\tilde{h}_1^{\text {init}}=\epsilon _\text {m}/\epsilon$ and $\tilde{\phi }_1^{\text {init}}=\epsilon _\text {b}/\epsilon$, as the perturbed bed level and benthic biomass with their initial amplitudes, respectively. Furthermore, $\epsilon$ is the largest of two small expansion parameters $\epsilon _\text {m}$ and $\epsilon _\text {b}$, defined as

$$\begin{aligned} \epsilon = \text {max}{\left( \epsilon _\text {m},\epsilon _\text {b}\right) } \ll 1, \quad \epsilon _\text {m}=\frac{\tilde{h}^{*\text {init}}}{H^*}, \quad \epsilon _\text {b}= \frac{\tilde{\phi }^{*\text {init}}}{\phi _\text {eq}^*}. \end{aligned}$$

(29)

Given that $\epsilon$ is small, the unknowns of the coupled system $\psi = \left( h, \phi , u, w, \tau , q, f_\text {slip}, f_\text {eq}\right)$ are expanded in a power series of the form

$$\begin{aligned} \psi = \psi _0+\epsilon \psi _1+{\mathscr {O}}{ \bigl (\epsilon ^2 \bigr )}, \end{aligned}$$

(30)

where $\psi _0$ and $\psi _1$ denote the basic and perturbed state, respectively. Furthermore, the perturbed unknown is written as a spatial Fourier mode

$$\begin{aligned} \psi _1 = \frac{1}{2}\breve{\psi }_1 \exp \left( ikx\right) +c.c.,\qquad \breve{\psi }_1 = \breve{\psi }_1^\text {h}\breve{{h}}_1+ \breve{\psi }_1^\phi \breve{\phi }_1, \end{aligned}$$

(31)

with a possible complex amplitude $\breve{\psi }_1$ and the complex conjugate c.c. . Here we further distinguish between contributions proportional to the complex amplitudes $\breve{h}_1$ and $\breve{\phi }_1$, respectively.

3.5 Basic state

The basic state describes the solution of the system obtained over a flat bed. For the sake of brevity, the solution to the basic flow problem is given in "Flow solution" of “Appendix 1”. Furthermore, the basic bed load sediment transport solution is given in “Sediment transport" of “Appendix 1”, and the basic coupling coefficients are described in “Coupling coefficients" of “Appendix 1”.

Finally, in the basic state there are no spatial variations in sediment transport, hence the bed evolution equals zero and the flat bed remains flat. However, as can be seen in “Biomass evolution" of “Appendix 1”, the basic benthic biomass does increase (spatially uniform) due to autonomous logistic growth.

3.6 Perturbed state

The solution to the perturbed flow problem, bed load sediment transport and coupling coefficients at order $\epsilon ^1$ are described in “Appendix 2”, respectively. Finally, the evolution of the perturbed bed, as well as biomass, are given by

$$\begin{aligned} \frac{\partial h_1}{\partial t_\text {long}}&=-\nu _\text {m}\frac{\partial \left\langle q_{1} \right\rangle _\text {tide}}{\partial x}, \end{aligned}$$

(32)

$$\begin{aligned} \dfrac{\partial \phi _1}{\partial t_\text {long}}&=\left\langle \nu _\text {b,g}\left[ \phi _1\left( 1-2\phi _0\right) +f_{\text {eq},1}\phi _0 \right] +\nu _\text {b,D} \frac{\partial ^2\phi _1}{\partial x^2}\right\rangle _\text {tide}. \end{aligned}$$

(33)

Given the dependencies due to the two-way coupling, we write (in terms of complex amplitudes) Eqs. (32) and (33) in matrix form

$$\begin{aligned} \frac{\partial }{\partial t_\text {long}} \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix} = \begin{bmatrix} \omega ^{\text {h}}_{{h}_1}&\omega ^\phi _{{h}_1} \\ \omega ^{\text {h}}_{\phi _1}&\omega ^\phi _{\phi _1} \end{bmatrix} \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix}. \end{aligned}$$

(34)

Here, $\omega ^{\text {h}}_{{h}_1},\ \omega ^\phi _{{h}_1},\ \omega ^{\text {h}}_{\phi _1}\ \text {and}\ \omega ^\phi _{\phi _1}$ denote the topographic and biological contributions to bed and biomass perturbations, respectively, based on the (second) definition in Eq. (31). These contributions will be further specified in Sect. 4.1.

4 Results

First, we present and analyse the obtained linear eigenvalue problem and its properties, which consists of two distinct eigenmodes. Then we will describe a reference case, where no coupling is present. The results of the coupled system follows after that, for both symmetrical and asymmetrical forcing. Finally, we show bed and biomass evolution in case of an initial hump of either topography (without perturbing biomass), or biomass (without perturbing topography).

An important note for the following results is that we differentiate between fixed and variable values for the benthic basic state. As an evolving benthic basic state complicates the interpretation of the results, in Sects. 4.1–4.4 we first describe the results for a fixed basic biomass. Second, in Sect. 4.5 we focus on the effect of the temporal evolution of the benthic basic state.

4.1 Linear eigenvalue problem

From Eq. (34), the solution is obtained by looking for complex eigenvalues $\varGamma$ according to

$$\begin{aligned} \frac{\partial }{\partial t_\text {long}} \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix} = \varGamma \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix}, \end{aligned}$$

(35)

to be further analysed in Sect. 4.2. Consequently, the system of equations is given by the following linear eigenvalue problem for the (complex) amplitudes of the sand wave profile $\breve{h}_1$ and benthic biomass $\breve{\phi }_1$:

$$\begin{aligned} \begin{bmatrix} \omega _\text {flow,abiotic} + \omega _\text {slope}&\quad \omega _\text {flow,biotic} \\ \omega _{\text {eq,abiotic}}&\quad \omega _\text {eq,biotic}+\omega _\text {logistic} + \omega _{\text {dispersal}} \end{bmatrix} \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix} = \varGamma \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix}, \end{aligned}$$

(36)

Here we have further specified the contributions $\omega ^{\text {h}}_{{h}_1},\ \omega ^\phi _{{{h}}_1},$$\omega ^{\text {h}}_{\phi _1}\ \text {and}\ \omega ^\phi _{\phi _1}$, as presented in Eq. (34). These specified contributions are given in “Appendix 3”.

4.2 Solution properties

Assuming fixed $\varGamma$-values (due to a fixed benthic basic state), it turns out that the (complex) amplitudes of bed and biomass perturbations in Eq. (36) are given by

$$\begin{aligned} \begin{bmatrix} \breve{h}_1\\ \breve{\phi }_1 \end{bmatrix} = C_1\begin{bmatrix} \chi ^\text {h}_{1}\\ \chi ^\phi _{1} \end{bmatrix} \exp \left( \varGamma _1t_\text {long}\right) +C_2\begin{bmatrix} \chi ^\text {h}_{2}\\ \chi ^\phi _{2} \end{bmatrix} \exp {\left( \varGamma _2t_\text {long}\right) }, \end{aligned}$$

(37)

where $C_1, C_2$ are constants which are found through the initial perturbation amplitudes as defined in Eqs. (27) and (28). Furthermore, $\vec {\chi }_{1}, \vec {\chi }_{2}$ and $\varGamma _1, \varGamma _2$ are the associated eigenvectors and eigenvalues of the solution, respectively. From Eq. (37), it follows that the real part of $\varGamma$ controls the growth rate $\gamma$ of the perturbations in bottom topography and benthic biomass, while the imaginary part is associated to the migration rate $c_\text {mig}$, according to

$$\begin{aligned} \varGamma =\gamma -ikc_{\text {mig}}. \end{aligned}$$

(38)

The eigenmode with the largest growth rate will eventually dominate the linear dynamics (again given fixed $\varGamma$-values), similar to the FGM as used in uncoupled systems (e.g., Hulscher [24]).

In order to determine the relative contribution of each eigenmode to either morphology or biology, we define $\varTheta ^{\phi }_j$ as the the complex amplitude ratio of the biomass perturbations $\chi ^\phi _j$ with respect to the bed perturbations $\chi ^\text {h}_j$ and reads

$$\begin{aligned} \varTheta ^{\phi }_j={1}/{\varTheta ^\text {h}_j}=\frac{\chi ^\phi _j}{\chi ^\text {h}_j}\qquad \left( j=1,2\right) . \end{aligned}$$

(39)

It follows that the moduli $\bigl |\varTheta ^{\phi }_j\bigr |$ describe the relative amplitude ratio of the biomass perturbations with respect to the bed topography perturbations, and $\bigl |\varTheta ^\text {h}_j\bigr |$ its inverse. In the following results, we use both definitions such that their ratio falls within the range $0\leqslant \bigl |\varTheta \bigr | \leqslant 1$.

Next, the phase difference between biomass and bed topography perturbations $\theta ^{\phi }_j$ is given by

$$\begin{aligned} \theta ^{\phi }_j=-\theta ^{\text {h}}_j ={{\,{\mathrm{atan2}}\,}}{\left( {\varTheta ^{\phi }_{j\text {,im}}},{\varTheta ^{\phi }_{j\text {,re}}}\right) } \qquad \left( j=1,2\right) , \end{aligned}$$

(40)

where the additional subscripts im and re denote the imaginary and real parts, respectively.

From now on, the model results for a mode (with the wave number $k^*$) are given in dimensional output, furthermore characterised by a wavelength $L^*$, growth rate $\gamma ^*$ and migration rate $c_\text {mig}^*$ according to

$$\begin{aligned} L^* = \frac{2\pi }{k^*},\quad \gamma ^* = \frac{\gamma }{T^*_\text {long}}, \quad c_\text {mig}^*=\frac{c_\text {mig}}{T^*_\text {long}k^*}. \end{aligned}$$

(41)

4.3 Reference case: no coupling

Fig. 5

Reference case (no coupling, symmetrical forcing) for a benthic basic state of a$\phi ^*_0=0.25\ \hbox {kg m}^{-1}$ and b$\phi ^*_0=0.75\ \hbox {kg m}^{-1}$. The solid and dashed-dotted lines denote growth rates for the (real-valued) ‘morphological’ and ‘biological’ eigenmodes, respectively. Both (real-valued) eigenvectors are given for the FGM (black dots), but are valid for all $k^*$

In order to better interpret the outcome of this methodology, we first present a reference case with a fixed benthic basic state of $\phi ^*_0=0.25\ \hbox {kg m}^{-1}$ (Fig. 5a) and $\phi ^*_0=0.75\ \hbox {kg m}^{-1}$ (Fig. 5b), corresponding to the increasing and reducing growth regions of the logistic growth profile (Fig. 3), respectively. Here the coupling coefficients $f_\text {eq}$ and $f_\text {slip}$ are set to 1, such that $\omega _\text {flow,biotic}$ and $\omega _\text {eq,abiotic}$ turn out to be zero. The resulting evolution equations [see Eq. (36)] are thus characterised by a diagonal matrix, and hence, no coupling.

This is plotted in Fig. 5, where for the two resulting eigenvalues $\varGamma _1, \varGamma _2$ the growth rate is given as a function of the wave number. As can be seen from the corresponding eigenvectors $\vec {\chi }_1,\vec {\chi }_2$, the solid line corresponds to topography, while the dashed-dotted line corresponds to biomass. From now on—whenever applicable—we will therefore refer to these eigenmodes as the ‘morphological’ and ‘biological’ eigenmode, respectively. However, as we will see further on, this distinction is not always justified.

Interestingly, around $k^*=0\ \hbox { m}^{-1}$ we observe non-zero growth rates for the ‘biological’ eigenmode, unlike the ‘morphological’ eigenmode, which has a tendency towards zero growth. Indeed, we see in Eq. (77) that the logistic growth contribution does not depend on the wave number, such that there is no damping effect.

For larger values of the benthic basic state, the growth rate of the ‘biological’ eigenmode uniformly decreases, which again can be ascribed to the logistic growth contribution. Moreover, for the ‘biological’ eigenmode we see a tendency towards lower growth rates for larger wave numbers (smaller wavelengths) due to the biological dispersal effect.

4.4 Interpretation of the two-way coupled system

4.4.1 Symmetrical forcing

Fig. 6

Model outcome in case of a two-way coupling with a the eigenvalues and their associated, b eigenvectors (both real-valued), c moduli and d phase shifts. This case uses a symmetrical tidal forcing and a benthic basic state of $\phi ^*_0 = 0.75\ \hbox {kg m}^{-1}$, other parameters are as indicated in Table 1. The black dots in a denote both eigenvectors for the FGM. Note that in c the solid black and grey lines are each others inverse $\big (\varTheta _1^\phi =1/\varTheta _1^\text {h}\big )$, such that the modulus $\varTheta _1$ does not exceed 1

To facilitate interpretation of the solution of the fully two-way coupled model, we first focus on a symmetrical forcing, with a (fixed) benthic basic state of $\phi ^*_0=0.75\ \hbox {kg m}^{-1}$.

The result for this case is plotted in Fig. 6, where the (real-valued) eigenvalues and associated eigenvectors, moduli and phase shifts are presented. Figure 6a shows the growth rate of the two eigenmodes. The FGM for this case is denoted by the black dots, which corresponds to the highest growth rate of $\varGamma _1$.

Also, in Fig. 6a the eigenvectors $\vec {\chi }_1,\vec {\chi }_2$ associated to the FGM are shown, which correspond to the result illustrated in Fig. 6b. Here, the solid lines, related to $\varGamma _1$, clearly show that this eigenvalue influences both bed topography as well as benthic biomass. Unlike the first eigenvector, $\vec {\chi }_2$ has only a minor influence on the topographic perturbations. This becomes more clear in Fig. 6c, where the moduli are given. Here, an amplitude ratio of value one indicates that the contribution of the eigenvector to the amplitude is equal for both topography as well as biomass, and that an amplitude ratio close to zero indicates that either bed or biomass is dominant. Based on these results $\varGamma _2$ can thus be referred to as the eigenvalue of the ‘biological’ eigenmode, whereas $\varGamma _1$ can be ascribed to the ‘mixed’ eigenmode.

Finally, Fig. 6d shows the phase shift between the amplitudes of topography and biomass. Here we see that for both the dominant ‘mixed’ eigenmode and the ‘biological’ eigenmode the crests are shifted $180^{\circ }$. Thus, the resulting perturbations turn out to grow in anti-phase.

Fig. 7

Model result for a symmetrical forcing and a benthic basic state of $\phi ^*_0 = 0.25\ \hbox {kg m}^{-1}$ with the a real and b imaginary parts of the eigenvalues and their associated c moduli and d phase shifts. The imaginary part of the eigenvalue is associated to the migration rate $c^*_\text {mig}$. Note the difference in y-axis in a compared to Fig. 6

Next, we will focus again on a symmetrical forcing, but now for $\phi ^*_0=0.25\ \hbox {kg m}^{-1}$. The corresponding model results are plotted in Fig. 7, where panel (b) now shows the imaginary part of the eigenvalues, presented as the migration rate. Furthermore, the modulus $\varTheta _2^\text {h}$ (Fig. 7c) shows that the relative topography amplitude is larger in this case, such that it is not justified any more to refer to this eigenmode as the ‘biological’ eigenmode.

A striking difference between this case and the previous one is that in Fig. 7 three distinct ranges for the wave number $k^*$ can be observed.

$\varGamma _1 < \varGamma _2$:

The first is for small wave numbers where $\varGamma _2$ is dominant. Here it stands out that the $180^{\circ }$ phase shift, which was present in Fig. 6d, is not visible any more. It turns out that for the range of modes where the eigenvalue of the ‘mixed’ eigenmode dominates the ‘biological’, no phase shift occurs. However, this behaviour can only be observed when the morphological amplitude of the ‘biological’ eigenmode is small compared to the amplitude of the biomass, i.e. when the modulus $\varTheta _2^\text {h}$ is close to zero.

$\varGamma _1 > \varGamma _2$:

Second, in the part where $\varGamma _1$ is dominant, both eigenmodes show a phase shift of $180^{\circ }$, similar to what was observed in Fig. 6d.

$\varGamma _1 = \overline{\varGamma _2}$:

The third range we observe is where both eigenmodes show the exact same growth rates, while their imaginary parts are non-zero. The latter results in migration rates for this range of modes, which might seem counter-intuitive for a symmetrical forcing. Moreover, from the moduli we see that the amplitude ratio for both eigenvalues is equal as well. It turns out that the eigenvectors for this situation (not shown here) are each other’s complex conjugate. Consequently, it follows that in this particular region of wave numbers, the perturbations can be interpreted as two identical travelling waves migrating in opposite direction, such that both topography and biomass behave like a standing wave. Furthermore, the phase difference between the two standing waves (bed and biomass) ranges between $0^{\circ }$ and $180^{\circ }$. As pointed out in Sect. 4.3, these results only hold for a specific moment in time, since the benthic basic state is fixed. It is thus possible that this standing wave will not fully develop in the field, as this behaviour can only be observed in case of increasing biological growth $(\phi ^*_0 <0.5\ \hbox {kg m}^{-1}$, see Fig. 3). This type of behaviour is also observed in other morphodynamic stability studies, as will be further discussed in Sect. 5.

4.4.2 Asymmetrical forcing

We will now focus on the effects of an asymmetrical forcing, specifically due to the presence of a residual current. In the results below, an $M_0$ residual current of $0.01\hbox { m s}^{-1}$ has been superimposed upon the $M_2$ tidal forcing. Compared to the symmetrical reference case (Fig. 5a) the growth rates of both sand waves and biomass are hardly influenced by the residual current (not shown here). Furthermore, the ‘morphological’ eigenmode shows an increasing positive migration rate for an increasing wave number (whereas the ‘biological’ eigenmode shows no migration at all, also not shown here).

Figure 8 shows the results for the full two-way coupling and a benthic basic state of $\phi ^*_0=0.25\ \hbox {kg m}^{-1}$. Compared to the uncoupled result described above, the migration rates show an overall increase for the first eigenmode, while a small migration in opposite direction can be observed for the second. In addition, we see that, compared to the reference case, for the first eigenmode the growth rate increases and the FGM shifts towards a shorter wavelength, in opposition to $\varGamma _2$, which is hardly influenced.

Moreover, we see that in the region where $\varGamma _1$ is almost equal to $\varGamma _2$, both eigenmodes tend to show the same behaviour as in the symmetrical case (Fig. 7). However, due to the asymmetrical forcing, no pure standing wave can be observed. This is best visible in Fig. 8b, c, where for this region of modes the migration rates are not each others inverse and the moduli are not equal. It appears that for an increasing residual current strength (not shown here), this behaviour is becoming increasingly less apparent.

Fig. 8

Results for the two-way coupled model, with an $M_0$ residual current strength of $0.01\hbox { m s}^{-1}$ and a benthic basic state of $\phi ^*_0=0.25\ \hbox {kg m}^{-1}$, other parameters are as indicated as in Table 1. In a the real parts of the eigenvalues (with the black dot denoting the FGM) which correspond to the growth rate, in b the imaginary parts which correspond to the migration rate, and their associated c moduli and d phase shifts

When looking at the phase shifts between the amplitudes of the eigenmodes (Fig. 8d), we see that in particular in the region where $\varGamma _1$ is dominant, the phase shifts change compared to symmetrical case (Fig. 7d). For the dominant (‘mixed’) eigenmode, it thus follows that the crests of the biomass perturbations are concentrated on the stoss side of the topography perturbations. If we increase the residual current even further (not shown here) we observe that this eigenmode has a tendency towards a phase shift of around $-\,90^{\circ }$.

4.5 Hump evolution: initial value problem

As already pointed out, the autonomous evolution of the benthic basic state has been neglected in the previous results. However, we have seen that the resulting eigenmodes vary for different stages of the biomass evolution. In order to study this behaviour, here we will consider, after Roos and Hulscher [40], the evolution of an initial hump over time, while allowing for autonomous biomass growth. This hump can either be a topography or biomass perturbation, without perturbing the other. The initial state of the system is represented by a Gaussian hump centered around the middle of a domain with length $D^*$, according to either one of the two following initial profiles for $\phi ^*$ and $h^*$

$$\begin{aligned} \phi ^*&=\phi _0^*& \& \quad \ h^* = h_\text {gaus}^*\exp \left( -\left[ \frac{x^*-\frac{D^*}{2}}{\delta ^*}\right] ^2\right) = \sum _{n=0}^{N}h^*_n\exp \left( in k^*_\text {min}x^*\right) , \end{aligned}$$

(42)

$$\begin{aligned} h^*&= 0& \& \quad \ \phi ^* = \phi _0^* +\phi _\text {gaus}^*\exp \left( -\left[ \frac{x^*-\frac{D^*}{2}}{\delta ^*}\right] ^2\right) = \phi _0^*+ \sum _{n=0}^{N}\phi ^*_n\exp \left( in k^*_\text {min}x^*\right) . \end{aligned}$$

(43)

Here, $h^*_\text {gaus}$ and $\phi ^*_\text {gaus}$ are the height of the initial topography and biomass hump, respectively and $\delta ^*$ is the half-width of the initial hump. Furthermore, both the topography and biomass hump are written as truncated Fourier series in space, with $h^*_n$ and $\phi ^*_n$ as their complex amplitudes, respectively and $k^*_\text {min}=\frac{2\pi }{D^*}$ as the smallest wave number which fits in the domain. In the cases presented below, $N=128$ is found to be sufficient to obtain an accurate representation.

In the following cases, we use a discrete time step of $\varDelta t^*= 0.1\ \hbox { year}$ to determine the temporal evolution of the perturbations according to Eq. (37). To account for the evolving benthic basic state, on each time step we (i) update the eigenmodes $\varGamma _1, \varGamma _2$ (and associated eigenvectors), and (ii) update the eigenmode decomposition according to the definitions in Eqs. (42) and (43).

Fig. 9

Temporal evolution of topography and biomass in case of a local disturbance, represented by a Gaussian hump [Eqs. (42), (43)]. The upper panels a, b show the result for an initial biomass hump with $\phi ^*_\text {gaus}=0.05\ \hbox {kg m}^{-1}$ and $\delta ^* = 100\ \hbox {m}$, and an initially flat bed. The lower panels c, d show the results for an initial topography hump with $h^*_\text {gaus}=0.05\ \hbox {m}$ and $\delta ^* = 100\ \hbox {m}$, and an initially spatially uniform biomass $\left( \left. \phi _0^*\right| _{t^*=0} = 0.1\ \hbox {kg m}^{-1} \right)$. The dashed dotted lines indicate the initial humps, and each shade of grey indicates a time step of $1\ \hbox {year}$

4.5.1 Topography versus biomass hump

Figure 9 presents the time evolution of the seabed and biomass given an initial hump on a domain of $D^* = 10\ \hbox { km}$, where each line indicates a time step of 1 year. In (a, b) we see the results for an initial biomass hump with $\phi ^*_\text {gaus}=0.05\ \hbox {kg m}^{-1}$ and $\delta ^* = 100\ \hbox {m}$, without an initial bed perturbation. The lower panels (c, d) show the results in case of an initial topography hump with $h^*_\text {gaus}=0.05\ \hbox {m}$ and $\delta ^* = 100\ \hbox {m}$, without an initial biomass perturbation. It is clearly visible that a biomass disturbance triggers sand wave growth, and vice versa. Moreover, in case of an initial bed perturbation, we see an anti-phase between topography and biomass developing, which becomes more distinct over time. However, for an initial biomass perturbation, both profiles develop in phase. This corresponds with the ‘small’ wave number range in Fig. 7, where the ‘biological’ eigenmode is dominant. It turns out that this behaviour always occurs when the benthic basic state is below the inflection point (see Fig. 3), regardless of the dimensions of the initial biomass hump.

Fig. 10

Similar to Fig. 9c, d, but now for different values of the logistic growth rate. In a, b the results for fast biomass growth $\bigl( \alpha _\text {g}^* = 1\ \hbox {m kg}^{-1}\hbox {year}^{-1}\bigr)$, and in c, d the results for slow biomass growth $\bigl( \alpha _\text {g}^* = 0.1\ \hbox {m kg}^{-1}\hbox {year}^{-1}\big)$

4.5.2 Logistic growth rate

Up till now, we have presented our cases for a single value of the logistic benthic growth $\alpha _\text {g}^*$. In Fig. 10 the effect of a varying $\alpha ^*_\text {g}$ is shown in case of an initial biomass hump. For a large logistic growth rate (Fig. 10a, b), we see indeed that the benthic basic state develops more quickly than in the previous case (Fig. 9b). The transition from an in phase to an in anti-phase development after the inflection point has passed also clearly stands out. The opposite holds for a slow logistic growth (Fig. 10d), where the biomass hump hardly evolves over time. Moreover, we see that the growth rate of the topography is significantly affected by a changing logistic growth. Also the preferred wavelength of the coupled system is slightly affected (not shown here), albeit much less than the growth rate.

Fig. 11

Evolution of topography and biomass in case of a superimposed residual current velocity of $U^*_{M_0} =0.01\ \hbox {m s}^{-1}$ in the positive $x^*$-direction. The results are given for an initial biomass hump (dashed-dotted line) with $\phi ^*_\text {gaus}=0.03\ \hbox {kg m}^{-1}$ and $\delta ^* = 50\ \hbox {m}$, and a flat bed. Each shade of grey indicates a time step of $1\ \hbox {year}$. The lower panels c, d show the tracked crest and trough positions of the above topography and biomass evolution, respectively. The dashed lines indicate the troughs, whereas the solid lines indicate the crests

4.5.3 Residual current

Here we show the topography and biomass evolution given an asymmetrical forcing. Similar as in Fig. 8, a residual current is superimposed upon the $M_2$ tidal constituent (in the positive $x^*$-direction). Figure 11 presents the results for this case, where in panels (a, b) the temporal evolution of a biomass hump ($\phi ^*_\text {gaus}=0.03\ \hbox {kg m}^{-1}$ and $\delta ^* = 50\ \hbox {m}$) and a flat bed is shown. Due to the imposed residual current, patterns of migration now appear for both topography and biomass. Remarkably, we see that the biomass hump initially migrates in a negative $x^*$-direction. This becomes more clear from Fig. 11d, where the position of the biomass crests and troughs are tracked over time. The negative migration of this peak even increases near the inflection point $\left( \phi _0^*= 0.5\ \hbox {kg m}^{-1} \right)$. Moreover, the developing biomass trough shows a similar negative migration trend. The downstream crest, however, is migrating in the direction of the residual current. The different migration directions are also visible for the bed evolution, where in Fig. 11c its crest and trough development are tracked. It appears that for both bed and biomass evolution, this behaviour continues until a stable (positive) migration and phase difference is established.

Fig. 12

In a the bed (black line) and biomass (grey line) profile after $t^* = 8\ \hbox {year}$ for a residual current strength of $U^*_{M_0}=0.05\ \hbox {m s}^{-1}$. The two dots indicate the location of the biomass crest with respect to the topography profile. In b the phase difference of biomass w.r.t. topography $\left( \theta ^\phi \right)$ after $t^* = 8\ \hbox {year}$ as a function of the residual current strength $U^*_{M_0}$. Here, the dot refers to the case presented in a

Although not distinctly visible from Fig. 11, the preferred phase difference between biomass and topography in this situation is slightly less than $180^{\circ }$. For an increasing residual current strength, this phase difference decreases even more. To illustrate this, we present in Fig. 12a the bed and biomass profile after $8\ \hbox {year}$ in case of a residual current strength of $U^*_{M_0} =0.05\ \hbox {kg m}^{-1}$. It can be clearly seen that the biomass crests are now concentrated on the lee side of the developing sand waves. Additionally, in Fig. 12b the phase difference between biomass and topography $\left( \theta ^\phi \right)$ is plotted as a function of the residual current strength. It shows that for an increasing residual velocity, the phase shift gradually decreases and tends towards a value of $90^{\circ }$.

5 Discussion

5.1 Comparison to ‘traditional’ stability analysis

In ‘traditional’ stability modelling studies (i.e. morphodynamics only, uncoupled), it is common to unravel the individual contributions to the growth and migrations rates (e.g., Campmans et al. [14]). Also for the two-way coupled model presented in this work, these contributions can be specified (as in “Appendix 3”). However, within the current methodology the interpretation of these contributions is somewhat different, since the resulting system of equations forms a $2\times 2$ eigenvalue problem [Eq. (36)], leading to two distinct complex growth rates. As a result, the growth (and migration) rate does not depend proportionally on its associated entries any more. For instance, a change of a certain individual contribution related to bed perturbations $\big (\omega ^{\text {h}}_{{h}_1},\ \omega ^\phi _{{{h}}_1}\big )$ does not solely affect the associated topography growth rate—as is the case for ‘traditional’ stability analysis—but now also that of biomass. Consequently, to fully understand the magnitude of these contributions, the resulting eigenvectors of the eigenvalue problem have to be taken into account as well. These eigenvectors describe the relative contribution of the entries to the associated growth rates. We would like to stress that our approach still implies a linear problem, and thus can be analytically solved by means of linear algebra.

In a study into current-generated sorted bed forms, van Oyen et al. [50] found that the resulting eigenmodes could be assigned to either roughness or topography. In our model, we observe that the eigenmodes can be related to either biomass or topography, but only to a certain extent. It turns out that the classification of these eigenmodes is bound by a certain range of parameter settings. Particularly for smaller values of the benthic basic state, both eigenmodes have the tendency to influence both perturbations (here referred to as the ‘mixed’ eigenmode). However, using this classification still contributes to our general understanding of the system, such that we can effectively use this methodology for a systematic process analysis.

5.2 Autonomous benthic growth and the role of the biological time scale

In contrast to ‘traditional’ stability analysis, the FGM for a given parameter setting does not have to be the eventual mode (wavelength) observed in the field. The role of the autonomous benthic growth here is crucial; as the resulting eigenmodes are only valid for a certain moment in time, the FGM (and its properties) may vary due to an evolving biomass. In particular, the largest effect of the autonomous benthic growth on the perturbations enters the system through the logistic growth contribution ($\omega _\text {logistic}$). It appears that this contribution leads to positive growth rates for the ‘biological’ eigenmode if the benthic basic state is below the inflection point of the logistic growth profile (Fig. 3), while the opposite holds for values larger than the inflection point. Moreover, we can conclude from the moduli that if the benthic basic state is above the inflection point, the growth rate of the topography perturbation is almost solely determined by the ‘mixed’ eigenmode, whereas for values lower than the inflection point, both eigenmodes influence the topographical growth rate. On the other hand, the biomass growth is determined by both eigenmodes regardless the benthic basic state. Furthermore, the results showed that the growth rate of the ‘biological’ mode is almost spatially uniform (equal for all $k^*$), whereas the ‘mixed’ mode shows a distinct FGM. As a consequence, the ‘mixed’ mode is mainly responsible for the eventually occurring wavelength in the field.

Although we gain much insight from the cases where $\phi ^*_0$ is fixed, one should continue to study the temporal behaviour of the system to fully understand the outcome. Imposing a hump (biomass or topography, without perturbing the other) shows us that only a small disturbance may trigger growth of rhythmic patterns of both sand waves and biomass. It appears that the biological time scale is an important factor for the initial evolution of the coupled system. If the biological time scale were much shorter than the morphological time scale, it would be justified to only look at the FGM for the situation of fully developed biomass $( \phi ^*_0=1\ \hbox {kg m}^{-1})$. Conversely, if both time scales were of the same order, the FGM would constantly be subject to change. Important to note here is that a slow biological growth does not only affect the biomass evolution, but also the initial growth of the topographic perturbations. Although linear stability models are not able to describe finite-amplitude behaviour of sand waves, non-linear models, used for this particular purpose, determine the FGM (preferred wavelength) to bypass the initial growth stage, and hence, speed up computational time [47]. If biological processes would be included in these non-linear models, it should thus be noted that the FGM might vary over time.

From the results it follows that phase shifts of various magnitudes may occur between the crests of bed and biomass perturbations. In particular for the cases where the benthic basic state is fixed, rich behaviour is visible with regard to phase shifts. In the situation where a topography hump is imposed, an anti-phase develops between bed and biomass. Remarkably, when a biomass hump is imposed, this phase difference only starts to evolve after the autonomous biomass evolution has passed the inflection point of logistic growth. Moreover, for an increasing residual current strength, the phase difference decreases and the biomass crests are concentrated on the lee side of the sand waves $\left( \theta ^\phi = 90^{\circ }{-}180^{\circ }\right)$. This contrasts the result from Fig. 8, where an opposite (i.e. negative) phase shift is present for the dominant ‘mixed’ eigenmode. Indeed, from the crest and trough development in Fig. 11 it can be seen that before both perturbations have developed a steady phase difference, crests and troughs may show negative migration rates, resulting in phase shifts that significantly differ from the eventual phase difference. Again, this emphasizes the importance of taking into account the evolving basic state, rather than only looking at a fixed value for $\phi ^*_0$.

For a limited range of modes, and given that the benthic basic state is below the inflection point, we showed that standing waves for both sand waves and biomass can occur. In this case both eigenmodes are each others complex conjugate, each displaying migration in opposite direction. The temporal evolution of the superimposed bed and biomass patterns would thus be oscillatory, hence a standing wave. This type of behaviour is observed in other morphodynamic stability studies as well [38, 48]. The latter showed that for waves approaching the coast perpendicularly, surf zone patterns may behave as standing waves. Moreover, they showed that for oblique wave incidence this behaviour vanishes. These findings correspond to our results where complex conjugate eigenmodes only occur for symmetrical tidal forcing. Considering that under field conditions a pure symmetrical tide does not occur—and taking into account the evolution of the benthic basic state—it is highly unlikely that this standing wave pattern will develop in nature.

5.3 Comparison to field data

Our model shows that the biomass of benthic organisms and sand waves develop in anti-phase (or close to), which is supported by observations in the field. Baptist et al. [1], and more recently, Damveld et al. [17] observed that organisms living on top of the seabed as well as within, occur much more frequently in sand waves troughs compared to the crests. Moreover, preliminary results from a recent field campaign show that various abiotic parameters, which are good predictors for the occurrence of benthic organisms, such as silt content and permeability, also show phase related patterns over sand waves [15]. This study showed that silt content, for example, is much higher in the sand wave troughs, but also on the lee slope, compared to the crests and stoss slope of the sand wave. Although other processes influence the habitat of benthic organisms as well, the observed patterns from this field study generally agree with the phase differences presented in this work.

To enable further comparison of our model results to field observations, the next step is to gather more information about local environmental and biological conditions. We are particularly interested in the biomass values over sand wave fields. In addition, data from different locations enables us to quantitatively relate these biological parameters to the wavelengths and growth and migration rates of the local bed forms. Furthermore, the parametrisations used in this model need to be fitted to more realistic parameter settings, although information on the effect of benthic organisms on the hydrodynamic and morphological processes in subtidal areas is scarce. Nevertheless, Borsje et al. [9] already proposed several biological parametrisations, which could serve as a starting point for future work. For instance, this two-way coupled model allows for the inclusion of a biologically influenced critical shear stress. Finally, in order to be flexible towards the available experimental data, we would like to point out that our modelling approach is not restricted to the use biomass as an indicator for benthic organisms, but that other indicators can be used as well (e.g., abundance, biodiversity).

6 Conclusions and outlook

In this paper we developed a fully two-way coupled model between sand waves and benthic organisms. With this model we are able to systematically investigate the processes that are leading to the formation of sand waves and the spatial and temporal distribution of benthos over these bed forms. Although the parametrisations used for the two-way coupling were not yet fitted to local environmental data, we showed that a local biomass disturbance leads to the growth of sand waves, and vice versa. Furthermore, we observed that phase shifts may occur between sand waves and biomass perturbations, similar to field observations. For a symmetrical forcing, we observed that they are in anti-phase. Furthermore, a residual current leads to a phase shift where the biomass maxima are concentrated on the lee slope of the sand waves.

This is the first study including the two-way coupling between sand waves and benthic organisms in a process-based morphodynamic model. In doing so, we recognised that the methodology of this work differs from ‘traditional’ morphodynamic stability modelling studies. Here, we ended up with a linear eigenvalue problem that eventually results in two distinct eigenmodes, instead of one eigenmode for the ‘traditional’ stability analysis. Moreover, the benthic basic state displays autonomous growth, such that the temporal evolution of the bed and biomass profile has to be taken into account to fully understand the results of this methodology. Also, the growth of this benthic basic state plays an important role in this study, as its stage relative to the inflection point of the logistic growth determines whether the eigenmodes can be related to either biology, morphology, or both. Also, if the benthic basic stage is below the inflection point an in-phase pattern may initially develop. This is especially relevant in case of slow biological growth, i.e. a long biological time scale. Finally, we have shown that the biological time scale significantly influences the morphological evolution. For slow biological growth, sand waves also tend to develop on a slower rate, in contrast to a fast biological growth.

A next step is to investigate these processes using parametrisations which are better fitted to experimental data. A sensitivity analysis into a realistic biological parameter range would then give insight in their influence on the model results. Using these insights, this model can eventually be used for predicting the formation properties of tidal sand waves combined with biological evolution in shallow sandy seas.

Appendices

Appendix 1: Basic state

1.1 Flow solution

In the case of a flat bed, no spatial variations are present, and the basic flow is characterised by the absence of vertical velocities near the bed. Thus, based on continuity, we conclude that $w_0 = 0$ in the entire water column. The basic flow problem can then be written as

$$\begin{aligned} \frac{\partial u_0}{\partial t}=-F+A_\text {v}\dfrac{\partial ^2u_0}{\partial z^{2}}. \end{aligned}$$

(44)

The boundary conditions at the free surface and at the bed read

$$\begin{aligned}&\dfrac{\partial u_0}{\partial z}=0 \quad \text {at } z=0, \end{aligned}$$

(45)

$$\begin{aligned}&A_\text {v}\dfrac{\partial u_0}{\partial z}=f_\text {slip,0}Su_0 \quad \text {at } z=-\,1. \end{aligned}$$

(46)

Similar to the forcing [Eq. (24)], the horizontal basic flow can be described using a temporal Fourier series

$$\begin{aligned} u_0=\sum _{m=-M}^{M}\hat{u}_{0,m} e^{imt}, \end{aligned}$$

(47)

with complex Fourier coefficients $\hat{u}_{0,m}$. This leads to the following differential equation for the basic state flow problem:

$$\begin{aligned} im\hat{u}_{0,m}=&-\hat{F}_m+A_\text {v}\frac{\text {d}^2\hat{u}_{0,m}}{\text {d} z^{2}}, \end{aligned}$$

(48)

which can be solved for an expression for $\hat{u}_{0,m}$:

$$\begin{aligned} \hat{u}_{0,m}&= \frac{\hat{F_{m}}}{2A_\text {v}}\left[ z^2-1+\frac{2A_\text {v}}{f_{\text {slip},0}S}\right] \qquad&\text {for } m= 0, \end{aligned}$$

(49)

$$\begin{aligned} \hat{u}_{0,m}&=\frac{i\hat{F_{m}}}{m}\left[ 1-\frac{f_{\text {slip},0}S\cosh \left( \xi z\right) }{A_\text {v}\xi \sinh \left( \xi \right) +f_{\text {slip},0}S\cosh \left( \xi \right) }\right] \qquad&\text {for } m\ne 0, \end{aligned}$$

(50)

with $\xi = \sqrt{\frac{im}{A_\text {v}}}$. Finally, the basic shear stress is given by

$$\begin{aligned} \tau _0=A_\text {v}\frac{\partial u_0}{\partial z} \quad \text {at } z=-\,1, \end{aligned}$$

(51)

1.2 Sediment transport

In the basic state, the sediment flux for $\left| \tau _0\right| >\tau _\text {c}$ reads

$$\begin{aligned} q_{0}=\left( \left| \tau _0\right| -\tau _\text {c}\right) ^{\nicefrac {3}{2}}\frac{\tau _0}{\left| \tau _0\right| }. \end{aligned}$$

(52)

1.3 Coupling coefficients

The basic coupling coefficients read

$$\begin{aligned} f_\text {eq,0}&=1, \end{aligned}$$

(53)

$$\begin{aligned} f_\text {slip,0}&= \left( 1-\mu _\text {slip}\right) \exp \left( -\kappa _\text {slip}\phi _0\right) +\mu _\text {slip}. \end{aligned}$$

(54)

In Eq. (53) we have used that the evolution of biomass can be calculated on a tide-averaged scale. Moreover, there is no spatial dependency in shear stress, hence we obtain $\tau _\text {ref,0} = \left<\left| \tau _0\right| \right>_\text {tide}$.

1.4 Biomass evolution

The basic biomass satisfies a logistic equation without a dispersal term, i.e.

$$\begin{aligned} \dfrac{\partial \phi _0}{\partial t_\text {long}}=\nu _\text {b,g}\phi _0{\left( 1-\phi _0\right) }. \end{aligned}$$

(55)

The solution to Eq. (55) is found to be

$$\begin{aligned} \phi _0(t_\text {long}) = \dfrac{1}{\exp \left( -\nu _\text {b,g} t_\text {long}\right) \left[ \left( \phi _{0,0}\right) ^{-1}-1\right] +1}, \end{aligned}$$

(56)

where $\phi _{0,0}$ denotes the basic biomass at $t_\text {long}=0$.

Appendix 2: Perturbed state

1.1 Flow solution

The perturbed flow problem is written as

$$\begin{aligned}&\frac{\partial u_1}{\partial x}+\frac{\partial w_1}{\partial z}=0, \end{aligned}$$

(57)

$$\begin{aligned}&\frac{\partial u_1}{\partial t}+r\left( u_0\frac{\partial u_1}{\partial x}+w_1\frac{\partial u_0}{\partial z}\right) =-r\dfrac{\partial \zeta _1}{\partial x}+A_\text {v}\dfrac{\partial ^2u_1}{\partial z^{2}}, \end{aligned}$$

(58)

with boundary conditions at the free surface

$$\begin{aligned} {w}_{1}=0, \quad \dfrac{\partial {u}_{1}}{\partial z}=0 \qquad \text {at } z=0, \end{aligned}$$

(59)

and at the bed

$$\begin{aligned}&{w}_{1}={u}_{0}\dfrac{\partial h_1}{\partial x}&\text {at } z=-1, \end{aligned}$$

(60)

$$\begin{aligned}&A_\text {v}\left( \frac{\partial {u}_{1}}{\partial z}+{h}_1\frac{\partial ^2 {u}_{0}}{\partial z^2}\right) ={f}_{\text {slip},0}S\left( {u}_{1}+{h}_1\frac{\partial {u}_{0}}{\partial z}\right) +{f}_{\text {slip},1}S{u}_{0}&\text {at} z=-\,1. \end{aligned}$$

(61)

Using Eq. (31), the complex amplitudes $\breve{\psi }_1$ are described as a truncated Fourier series in time, and is given by

$$\begin{aligned} \breve{\psi }\left( t \right) =\sum _{m=-M}^{M}\hat{\psi }_{1,m} e^{imt}. \end{aligned}$$

(62)

This leads to the following differential equation for the flow problem per temporal component:

$$\begin{aligned}&i\hat{u}_{1,m}+\frac{\text {d} \hat{w}_{1,m}}{\text {d} z}=0,\end{aligned}$$

(63)

$$\begin{aligned}&im\hat{u}_{1,m}+r\sum _{n=-M}^{M}\left[ i\hat{u}_{0,n}\hat{u}_{1,m-n}+\hat{w}_{1,n}\frac{\text {d} \hat{u}_{0,m-n}}{\text {d} z}\right] =-ir\hat{\zeta }_{1,m}+A_\text {v}\frac{\text {d}^2\hat{u}_{1,m}}{\text {d} z^2}. \end{aligned}$$

(64)

The boundary conditions at the free surface read

$$\begin{aligned} \hat{w}_{1,m}=0, \quad \dfrac{\text {d} \hat{u}_{1,m}}{\text {d} z}=0 \quad \text {at } z=0, \end{aligned}$$

(65)

and the boundary conditions at the bed are given by

$$\begin{aligned}&\hat{w}_{1,m}=i\breve{h}_1\hat{u}_{0,m}&\text {at } z=-\,1,\end{aligned}$$

(66)

$$\begin{aligned}&A_\text {v}\left( \frac{\text {d} \hat{u}_{1,m}}{\text {d} z}+\breve{h}_1\frac{\text {d}^2 \hat{u}_{0,m}}{\text {d} z^2}\right) =\breve{f}_{\text {slip},0}S\left( \hat{u}_{1,m}+\breve{h}_1\frac{\text {d} \hat{u}_{0,m}}{\text {d} z}\right) +\breve{f}_{\text {slip},1}S\hat{u}_{0,m}&\text {at } z=-\,1. \end{aligned}$$

(67)

Similar to Campmans et al. [14], we solve this system of ordinary differential equations using a shooting method in combination with the $4\text {th}$ order Runge–Kutta numerical integration. Finally, the perturbed bed shear stress reads

$$\begin{aligned} {\tau }_1=A_\text {v}\left( \frac{\partial u_1}{\partial z}+h_1\frac{\partial ^2u_0}{\partial z^2}\right) \quad \text {at } z=-\,1. \end{aligned}$$

(68)

1.2 Sediment transport

The perturbed sediment transport equation for $\left| \tau _0\right| >\tau _\text {c}$ is given by

$$\begin{aligned} q_{1}= \beta \sqrt{ \left| \tau _0\right| -\tau _\text {c} }\left( \tau _1-\frac{\tau _0}{\left| \tau _0\right| }\tau _\text {c}\right) -\lambda \frac{\partial h_1}{\partial x}\left( \left| \tau _0\right| -\tau _\text {c}\right) ^{\nicefrac {3}{2}}. \end{aligned}$$

(69)

1.3 Coupling coefficients

The perturbed coupling coefficients read

$$\begin{aligned} f_\text {eq,1}&=-\left\langle \kappa _\text {eq} \frac{\tau _1\tau _0}{\left| \tau _0\right| } \right\rangle _\text {tide}, \end{aligned}$$

(70)

$$\begin{aligned} f_\text {slip,1}&= \left( \mu _\text {slip}-1\right) \kappa _\text {slip}\phi _1\exp {\left( -\kappa _\text {slip}\phi _0\right) }. \end{aligned}$$

(71)

Appendix 3: Individual contributions to the eigenvalue problem

The contributions $\omega ^{\text {h}}_{{h}_1},\ \omega ^\phi _{{{h}}_1},$$\omega ^{\text {h}}_{\phi _1}\ \text {and}\ \omega ^\phi _{\phi _1}$ [as presented in Eq. (34), and further specified in Eq. (36)] are given below. The topographic contributions related to bottom evolution $\bigl (\omega ^{\text {h}}_{{h}_1}\bigr )$ are

$$\begin{aligned}&\omega _{\text {flow,abiotic}}={-ik\nu _\text {m}}\frac{3}{2}\left\langle \sqrt{\left| \tau _0\right| -f_{\text {crit},0}\tau _\text {c}}\breve{\tau }^{{\text {h}}}_1\right\rangle _\text {tide}, \end{aligned}$$

(72)

$$\begin{aligned}&\omega _{\text {slope}}=-k^2\nu _\text {m}\lambda \left\langle \left( \left| \tau _0\right| -f_{\text {crit},0}\tau _\text {c}\right) ^{\nicefrac {3}{2}}\right\rangle _\text {tide}, \end{aligned}$$

(73)

where $\omega _{\text {flow,abiotic}}$ is the abiotic contribution due to the perturbed flow and $\omega _{\text {slope}}$ is the slope effect contribution. Furthermore, the biological contributions related to bottom evolution $\bigl ( \omega ^{\phi }_{{h}_1} \bigr )$ are

$$\begin{aligned} \omega _{\text {flow,biotic}}&={-ik\nu _\text {m}}\frac{3}{2}\left\langle \sqrt{\left| \tau _0\right| -f_{\text {crit},0}\tau _\text {c} }\breve{\tau }^{{\phi }}_1\right\rangle _\text {tide}, \end{aligned}$$

(74)

Here, $\omega _\text {flow,biotic}$ is the biotic contribution due to the perturbed flow. Next, the topographic contribution related to the evolution of biomass $\bigl (\omega ^{\text {h}}_{\phi _1}\bigr )$ is

$$\begin{aligned} \omega _{\text {eq,abiotic}}&={-\nu _\text {b,g}}\phi _0\left\langle \breve{f}^{{\text {h}}}_{\text {eq},1}\right\rangle _\text {tide} \end{aligned}$$

(75)

with $\omega _{\text {eq,abiotic}}$ as the contribution related to the abiotic influenced carrying capacity. Finally, the biological contributions related to the evolution of biomass $\bigl (\omega ^{\phi }_{\phi _1}\bigr )$ are

$$\begin{aligned} \omega _{\text {eq,biotic}}&={-\nu _\text {b,g}}\phi _0\left\langle \breve{f}^{{\phi }}_{\text {eq},1}\right\rangle _\text {tide}, \end{aligned}$$

(76)

$$\begin{aligned} \omega _{\text {logistic}}&=\nu _\text {b,g}\left( 1-2\phi _0\right) , \end{aligned}$$

(77)

$$\begin{aligned} \omega _{\text {dispersal}}&= -k^2\nu _\text {b,D}. \end{aligned}$$

(78)

Here, $\omega _\text {eq,biotic}$ is the contribution related to the biotic influenced carrying capacity, $\omega _{\text {logistic}}$ is the contribution due to the perturbed logistic growth and $\omega _{\text {dispersal}}$ is the biological dispersal effect.