Optimal Delineation of Ambulatory Holter ECG Events via False-Alarm Bounded Segmentation of a Wavelet-Based Principal Components Analyzed Decision Statistic

Abstract

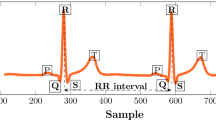
The aim of this study is to develop and describe a new ambulatory holter electrocardiogram (ECG) events detection-delineation algorithm with the major focus on the bounded false-alarm probability (FAP) segmentation of an information-optimized decision statistic. After implementation of appropriate preprocessing methods to the discrete wavelet transform (DWT) of the original ECG data, a uniform length sliding window is applied to the obtained signal and in each slid, six feature vectors namely as summation of the nonlinearly amplified Hilbert transform, summation of absolute first order differentiation, summation of absolute second order differentiation, curve length, area and variance of the excerpted segment are calculated to construct a newly proposed principal components analyzed geometric index (PCAGI) by application of a linear orthonormal projection. In the next step, the α-level Neyman-Pearson classifier (which is a FAP controlled tester) is implemented to detect and delineate QRS complexes. The presented method was applied to MIT-BIH Arrhythmia Database, QT Database, and T-Wave Alternans Database and as a result, the average values of sensitivity and positive predictivity Se = 99.96% and P+ = 99.96% are obtained for the detection of QRS complexes, with the average maximum delineation error of 5.7, 3.8 and 6.1 m for P-wave, QRS complex and T-wave, respectively. Also, the proposed method was applied to DAY general hospital high resolution holter data (more than 1,500,000 beats including Bundle Branch Blocks-BBB, Premature Ventricular Complex-PVC and Premature Atrial Complex-PAC) and average values of Se = 99.98% and P+ = 99.97% are obtained for QRS detection. In summary, marginal performance improvement of ECG events detection-delineation process in a widespread values of signal to noise ratio (SNR), reliable robustness against strong noise, artifacts and probable severe arrhythmia(s) of high resolution holter data and the processing speed 155,000 samples/s can be mentioned as important merits and capabilities of the proposed algorithm.

Appendix

Discrete Wavelet Transform Using à Trous Method

Generally, it can be stated that the wavelet transform is a quasi-convolution of the hypothetical signal x(t) and the wavelet function ψ(t) with the dilation parameter a and translation parameter b, as follows

$$ W_{{a^{x} }} (b) = {\frac{1}{\sqrt a }}\int\limits_{ - \infty }^{ + \infty } {x(t)\psi \left( {{{(t - b)} \mathord{\left/ {\vphantom {{(t - b)} a}} \right. \kern-\nulldelimiterspace} a}} \right)dt,\;a > 0} $$

(33)

The parameter a can be used to adjust the wideness of the basis function and therefore the transform can be adjusted in temporal resolutions. Suppose that the function $Y_{{a^{x} }} (b)$ is obtained based on a quasi-convolution of signal x(t) and function θ(t), as follows

$$ Y_{{a^{x} }} (b) = \int\limits_{ - \infty }^{ + \infty } {x(t)\theta \left( {{{(t - b)} \mathord{\left/ {\vphantom {{(t - b)} a}} \right. \kern-\nulldelimiterspace} a}} \right)dt} $$

(34)

If the derivative of $Y_{{a^{x} }} (b)$ is calculated relative to b, then

$$ {\frac{{\partial Y_{{a^{x} }} (b)}}{\partial b}} = - \frac{1}{a}\int\limits_{ - \infty }^{ + \infty } {x(t)\theta^{\prime}\left( {{{(t - b)} \mathord{\left/ {\vphantom {{(t - b)} a}} \right. \kern-\nulldelimiterspace} a}} \right)} dt $$

(35)

On the other hand, if ψ(t) is the derivative of a smoothing function θ(t), i.e. ψ(t) = θ′(t), then

$$ W_{{a^{x} }} (b) = -\frac{1}{\sqrt a} \frac{\partial Y_{a^{x}} (b)}{\partial b} $$

(36)

Accordingly, it can be concluded that wavelet transform at the scale a is proportional to the quasi-convolution derivative of the signal x(t) and the smoothing function θ(t). Therefore, if wavelet transform of the signal crosses of zero, it will be an indicative of local extremum(s) existence in the smoothed signal and the absolute maximum value of the wavelet transform in different scales represents a maximum slope in the filtered signal. Thus, useful information can be obtained using wavelet transform in different scales.

In Eq. 33, for dilation parameter “a” and translation parameter “b”, the values a = q ^k and $b = q^{k} lT$ can be used in which q is the discretization parameter, l is a positive constant, k is the discrete scale power and T is the sampling period. By substituting the new values of the parameters “a” and “b” into Eq. 33, the following result is obtained

$$ \psi_{k,l} (t) = q^{ - k/2} \psi (q^{ - k} t - lT);k,l \in Z^{ + } $$

(37)

The scale index k determines the width of wavelet function, while the parameter l provides translation of the wavelet function.If the scale factor a and the translation parameter b are chosen as q = 2 i.e., a = 2 ^k and b = 2^k l, the dyadic wavelet with the following basis function will be resulted (Martinez et al. 2004)

$$ \psi_{k,l} (t) = 2^{ - k/2} \psi (2^{ - k} t - lT);k,l \in Z^{ + } $$

(38)

To implement the à trous wavelet transform algorithm, filters H(z) and G(z) should be used according to the block diagram represented in Fig. 14a (Martinez et al. 2004). According to this block diagram, each smoothing function (SMF) is obtained by sequential low-pass filtering (convolving with G(z) filters), while after high-pass filtering of a SMF (convolving with H(z) filters), the corresponding DWT at appropriate scale is generated. In order to decompose the input signal x(t) into different frequency passbands, according to the block diagram of Fig. 14b, sequential high-pass low-pass filtering including down-sampling should be implemented. The filter outputs x _H (t) and x _L (t) can be obtained by convolving the input signal x(t) with corresponding high-pass and low-pass FIRs and contributing the down-sampling as

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {x_{L} (t) = \sum\limits_{k = - \infty }^{k = + \infty } {g(k)x(2t - k)} } \\ {x_{H} (t) = \sum\limits_{k = - \infty }^{k = + \infty } {h(k)x(2t - k)} } \\ \end{array} } \right. \hfill \\ t = 0,1, \ldots ,N - 1 \hfill \\ \end{gathered} $$

(39)

On the other hand, to reconstruct the transformed signal, the obtained signals x _H (t) and x _L (t) should be first be up-sampled by following simple operation

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {x_{L}^{*} (2t) = x_{L} (t)} & , & {x_{L}^{*} (2t + 1) = 0} \\ {x_{H}^{*} (2t) = x_{H} (t)} & , & {x_{H}^{*} (2t + 1) = 0} \\ \end{array} } \right. \hfill \\ t = 0,1, \ldots ,N - 1 \hfill \\ \end{gathered} $$

(40)

If the FIR lengths of the H(z) and G(z) filters are represented by L _H and L _G , respectively, then the reconstructing high-pass and low-pass filters are obtained as

$$ \left\{ \begin{gathered} g^{*} (t) = g(L_{G} - 1 - t) \hfill \\ h^{*} (t) = h(L_{H} - 1 - t) \hfill \\ \end{gathered} \right. $$

(41)

Fig. 14

FIR filter-bank implementation to generate discrete wavelet dyadic scales and smoothing functions transform based on à trous algorithm. a one-step generation of detail coefficient scales and reconstruction of the input signal, b four-step implementation of DWT for extraction of dyadic scales

Then the reconstructed signal x _R (t) is obtained by superposition of the up-sampled signals convolution with their appropriately flipped FIR filters as follow

$$ x_{R} (t) = \sum\limits_{k = - \infty }^{k = + \infty } {h^{*} (k)x_{H}^{*} (t - k)} + \sum\limits_{k = - \infty }^{k = + \infty } {g^{*} (k)x_{G}^{*} (t - k)} $$

(42)

For a prototype wavelet ψ(t) with the following quadratic spline Fourier transform,

$$ {\varvec{\Uppsi}}(\Upomega ) = j\Upomega \left( {{\frac{{\sin ({\Upomega \mathord{\left/ {\vphantom {\Upomega 4}} \right. \kern-\nulldelimiterspace} 4})}}{{{\Upomega \mathord{\left/ {\vphantom {\Upomega 4}} \right. \kern-\nulldelimiterspace} 4}}}}} \right)^{4} $$

(43)

the transfer functions H(z) and G(z) can be obtained from the following equation

$$ \begin{aligned} H(e^{j\omega } ) & =\,& e^{{{{j\omega } \mathord{\left/ {\vphantom {{j\omega } 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {\cos ({\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2})} \right)^{3} \\ G(e^{j\omega } ) & =\,& 4je^{{{{j\omega } \mathord{\left/ {\vphantom {{j\omega } 2}} \right. \kern-\nulldelimiterspace} 2}}} \left( {\sin ({\omega \mathord{\left/ {\vphantom {\omega 2}} \right. \kern-\nulldelimiterspace} 2})} \right) \\ \end{aligned} $$

(44)

and therefore,

$$ \begin{aligned} h[n] & =\,& \left( {{1 \mathord{\left/ {\vphantom {1 8}} \right. \kern-\nulldelimiterspace} 8}} \right)\{ \delta [n + 2] + 3\delta [n + 1] + 3\delta [n] + \delta [n - 1]\} \\ g[n] & =\,& 2\{ \delta [n + 1] - \delta [n]\} \\ \end{aligned} $$

(45)

It should be noted that for frequency contents of up to 50 Hz, the à trous algorithm can be used in different sampling frequencies. Therefore, one of the most prominent advantages of the à trous algorithm is the approximate independency of its results from sampling frequency. This is because of the main frequency contents of the ECG signal concentrate on the range less than 20 Hz (Martinez et al. 2004; Ghaffari et al. (2009c). After examination of various databases with different sampling frequencies (range between 136–10 kHz), it has been concluded that in low sampling frequencies (less than 750 Hz), scales 2^λ (λ = 1,2,…,5) are usable while for sampling frequencies more than 1,000 Hz, scales 2^λ (λ = 1,2,…,8) contain profitable information that can be used for the purpose of wave detection, delineation and classification.

In Fig. 15, several dyadic scales obtained via application of à trous DWT to an arbitrary holter record belonging to the DAY general hospital database are illustrated. As it can be seen, by increment of the dyadic dilation parameter 2^λ, the high-frequency fluctuations of the transform induced by measurement noises are diminished. The pseudo code associated with Eqs. 33–45 can be written in Matlab format as follows

Fig. 15

Illustration of several DWT dyadic scales 2^λ obtained from application of a trous filter bank to an arbitrary record of high-resolution holter data for a λ = 1, b λ = 2, c λ = 3, d λ = 4, e λ = 5, f λ = 6, g λ = 7, h λ = 8