A fast numerical solution for the first kind boundary integral equation for the Helmholtz equation

Abstract

The main purpose of this paper is to develop a fast numerical method for solving the first kind boundary integral equation, arising from the two-dimensional interior Dirichlet boundary value problem for the Helmholtz equation with a smooth boundary. This method leads to a fully discrete linear system with a sparse coefficient matrix. We observe that it requires a nearly linear computational cost to produce and then solve this system, and the corresponding approximate solution obtained by this proposed method preserves the optimal convergence order. One numerical example demonstrates the efficiency and accuracy of the proposed method.

1 Introduction

In this paper, we establish a fast numerical solution for the first kind boundary integral equation, induced from a single layer approach for solving the interior Dirichlet problem for the Helmholtz equation

$$ \triangle U(P)+\kappa^2 U(P)=0,\ \ \ P \in\ D,$$

(1.1)

satisfying the boundary condition

$$ U(P)=h(P), \quad P\in S:=\partial D,$$

(1.2)

where D is a bounded, simply connected open region in ℝ² with a smooth boundary S. We seek a solution $U\in C^{2}(D)\cap C(\bar{D})$ for the boundary value problem (1.1)–(1.2). κ in (1.1) is a given positive constant, and the function h in (1.2) is assumed to be given and continuous on the boundary S. As shown in [1, 2, 5, 20, 21], if the transfinite diameter C _S of the boundary S is not equal to 1, then −κ ² is not the eigenvalue of the Laplace operator, and then the boundary value problem (1.1)–(1.2) has a unique solution, otherwise, this boundary value problem can be rescaled to another Dirichlet problem for the Helmholtz equation, with the curve whose transfinite diameter is not 1. Hence, in this paper, without loss of generality, we assume that the boundary value problem (1.1)–(1.2) has a unique solution.

Among all methods for solving the two-dimensional Dirichlet boundary value problem for the Helmholtz equation with a smooth boundary, the boundary integral equation method is one of the most fundamental treatments. As shown in [17], the single layer method to the solution of the Dirichlet problem for the Helmholtz equation leads to a first kind boundary integral equation. This integral equation can be split into three parts. The first part in the kernel is a logarithmic term with a constant coefficient, and the second smooth part are familiar with the integral equation arising from the single layer approach to the Dirichlet problem for the Laplace equation, and the third part in the kernel function is a product of a logarithmic singular function and a smooth function, which requires our special attention.

For this arising boundary integral equation, various numerical methods have been developed in the literature. In [17], a fully discrete Fourier-Galerkin method is proposed. In [1, 5, 20, 21], the quadrature method and the modified quadrature method are considered. In [22, 23], the qualocation method has been developed as a new approximation, which tries to combine the advantage of the Galerkin method and the collocation method into a new scheme.

All these numerical methods enjoy nice convergence properties but at the same time suffer from having large computational costs due to the density of the coefficient matrix of the discrete linear system. To overcome this shortcoming, in [6], a fast truncated Fourier-Galerkin method is presented for solving the singular boundary integral equations, which are induced from the two-dimensional interior Dirichlet and Neumann boundary value problem for Laplace equation with a smooth boundary. This fast truncated Fourier-Galerkin method preserves the optimal order of the approximate solution, and leads to a semi-discrete linear system with a sparse coefficient matrix. In [14], they continue the theme of [6] and obtain a fast fully discrete Fourier-Galerkin method. This method generates a fully discrete sparse linear system with a nearly linear computational complexity, and preserves the optimal order of the approximate solution. In [24], following the ideas coming from [6, 14], a fast fully discrete Fourier-Galerkin method is used for solving first-kind logarithmic-kernel integral equation, induced from the two-dimensional Dirichlet problem for the Laplace equation on open arcs. In this paper, we shall continue the work of [6, 14, 24] and develop a fast numerical solution for the first kind boundary integral equation, arising from the interior Dirichlet problem for Helmholtz equation.

We organize this paper as follows. In Sect. 2, we introduce some notations and review the boundary integral equation method for solving (1.1)–(1.2). For the linear system produced by the Fourier-Galerkin method, we propose the matrix truncation strategy in Sect. 3.6. This truncation strategy leads to a semi-discrete linear system with a sparse coefficient matrix. Moreover, we give a few necessary technical results so as to analyze this truncation algorithm. In Sect. 4, we construct an efficient numerical integration scheme to compute all nonzero entries in the semi-discrete sparse linear system produced in last section. This scheme combining the matrix truncation strategy leads to a fully discrete sparse linear system. We prove that it requires a nearly linear computational cost to generate this fully discrete sparse linear system. In Sect. 5, the stability of this linear system and the convergence of this approximate solution are considered. We establish that this fully discrete linear system has a unique solution, and the approximate solution produced by this proposed method remains the optimal convergence order. Moreover, a precondition for the compressed coefficient matrix is proposed to obtain a preconditioned matrix having a uniformly bounded spectral condition number. In Sect. 6, the numerical example is presented to show the efficiency and accuracy of this method. In Sect. 7, we give a conclusion.

2 The Fourier-Galerkin method for solving singular boundary integral equations

In this section, as shown in [17], we first review the boundary integral equation reformulation of the boundary value problem (1.1)–(1.2) by a single-layer approach, and then describe the Fourier-Galerkin method for solving this arising boundary integral equation.

Let ℤ:={…,−1,0,1,…}, ℕ:={1,2,…,},ℕ₀:=ℕ∪{0}, $\mathbb{Z}_{n}^{+}:=\{1,2,\ldots,n\}$ and $\mathbb{Z}_{n}:=\mathbb{Z}_{n}^{+}\cup\{0\}$ for each n∈ℕ. We introduce the Bessel function J ₀(z), the Neumann function N ₀(z) and the Hankel function $H_{0}^{(1)}(z)$ as follows

$$J_0(z):=\sum_{n\in\mathbb{N}_0}\frac{(-1)^n}{(n!)^2}\biggl(\frac{z}{2} \biggr)^{2n},$$

and

$$N_0(z):=\frac{2}{\pi}\biggl(\log\frac{z}{2}+c_{\mathrm{Euler}}\biggr)J_0(z)+\frac{2}{\pi}\sum_{n\in\mathbb{N}} \biggl(\sum_{l\in\mathbb{Z}_n^+}\frac{1}{l} \biggr)\frac{(-1)^{n+1}}{(n!)^2}\biggl(\frac{z}{2} \biggr)^{2n},$$

and

$$H_0^{(1)}(z):=J_0(z)+iN_0(z),$$

in which c _Euler:=0.57721… and i is the imaginary unit.

Let

$$\varPsi(Q_1,Q_2):=\frac{i}{4}H_0^{(1)}\bigl(\kappa|Q_1-Q_2|\bigr),\ Q_1\not=Q_2,$$

be the fundamental solution to the Helmholtz equation (1.1). Using a single-layer potential method, the solution U of the boundary value problem (1.1)–(1.2) is expressed in the form

$$ U(P):=\int_S\varPsi(P,Q)\phi(Q)ds_Q, \quad P\in D,$$

(2.1)

where ds _Q denotes the differential of the line element along S with respect to Q.

In (2.1), letting P tend to a point on the boundary S, and using the boundary condition (1.2), we obtain a first kind boundary integral equation

$$ \int_S\varPsi(P,Q)\phi(Q)ds_Q=h(P), \quad P\in S.$$

(2.2)

If the function ϕ on the boundary S is the solution for the first kind boundary integral equation (2.2), then the single-layer representation (2.1) gives the solution U of the boundary value problem (1.1)–(1.2).

In order to give the operator form of (2.2), we let I:=[0,2π] and introduce a parameterization

$$\mathbf{x}(t):=\bigl(x_1(t),x_2(t)\bigr), \quad t\in I,$$

for the boundary S. We assume that each component of x is in $C_{2\pi}^{\infty}(I)$, the space of 2π-periodic functions in C ^∞(I). Choosing P:=x(t) and Q:=x(s), then (2.2) becomes

$$ \int_I\varPsi\bigl(\mathbf{x}(t), \mathbf{x}(s) \bigr)u(s)ds=f(t), \quad t\in I,$$

(2.3)

where u(s):=ϕ(x(s))|x′(s)| and f(t):=h(x(t)).

Let r(s,t):=|x(s)−x(t)|, and we have that

$$\varPsi\bigl(\mathbf{x}(t), \mathbf{x}(s)\bigr):=\frac{i}{4}H_0^{(1)}\bigl(\kappa r(s,t)\bigr).$$

Likewise, in [17], we decompose the kernel function $\frac{i}{4}H_{0}^{(1)}(\kappa r(s,t))$ into three parts. For this we let

$$a(s,t):=\frac{1}{2\pi}\log\biggl(\frac{4}{e}\sin^2\frac{s-t}{2}\biggr),$$

and

$$ b(s,t):=\frac{i}{4}H_0^{(1)} \bigl(\kappa r(s,t)\bigr)-a(s,t)J_0 \bigl(\kappa r(s,t) \bigr),$$

(2.4)

and

with

$$ c^*(s,t):=\left\{ \begin{array}{l@{\quad}l}\frac{J_0(\kappa r(s,t))-1}{\sin^2\frac{s-t}{2}},&s-t\not=2m\pi,\ m\in\mathbb{Z},\\-\kappa^2|\mathbf{x}^\prime(t)|^2, &\mbox{others}.\end{array}\right.$$

(2.5)

If the curve S and its parameterization x(t),t∈I are smooth, so is the function c ^∗ in (2.5). Now we define three integral operators , and defined by the following equations

Using these notations, we rewrite (2.3) in the operator form

(2.6)

In order to study (2.6), we need an appropriate space of functions. For ψ∈L ²(I), we denote its l-th Fourier coefficient by

where

$$e_l(t):=\frac{1}{\sqrt{2\pi}}e^{ilt},\quad t\in I.$$

Following [1, 16, 17], we denote by H ^p(I)(p≥0) the Sobolev space of functions ψ∈L ²(I) with the property

The inner product of space H ^p(I)(p≥0) is defined by

and the corresponding norm is given by $\|\psi\|_{p}:=(\psi,\psi)_{p}^{\frac{1}{2}}$.

For any ψ∈H ⁰(I) having the following expression

applying the result (7.2.24) in [1] we have

(2.7)

which implies that operator is a bijective mapping from H ⁰(I) onto H ¹(I).

By the smoothness of the boundary S, it follows from Theorem 3.1 in [17] that and are two compact integral operators from H ⁰(I) to H ¹(I) and is an isomorphism.

Next we describe the Fourier-Galerkin method for solving (2.6). For each n∈ℕ we define a finite-dimensional subspace sequence

$$X_n:=\operatorname{span}\bigl\{e_l: |l|\in \mathbb{Z}_n\bigr\}.$$

Let be the orthogonal projection operator from space H ⁰(I) to X _n . By Theorem 8.2 in [16], for all ω∈H ^μ+ν(I) with μ,ν≥0, we have

(2.8)

The Fourier-Galerkin method for solving (2.6) is to seek a solution

$$ u_n(s):=\sum_{|l|\in\mathbb{Z}_n}a_le_l(s)\in X_n,$$

(2.9)

satisfying

(2.10)

By (2.7), the operator has the Fourier basis functions as its eigenfunctions, which implies . Hence, (2.10) has the form

(2.11)

Letting and , (2.11) is rewritten as

(2.12)

The related stability and convergence results regarding the Fourier-Galerkin method can be obtained by the result in Chap. 7.3.3 in [1].

Theorem 2.1

Suppose that (2.6) has a unique solution u, then there exist a positive integer n ₀ and a positive constant ς such that for n≥n ₀ and for any w∈X _n ,

(2.13)

and

Moreover, if the solution u to (2.6) belongs to space H ^q(I) with q>0, then we have

$$ \|u-{u}_n\|_0\leq\frac{1}{\varsigma}\|u\|_{q}n^{-q}.$$

At the end of this section, we present the matrix form of (2.12). For this purpose we use the notation $\mathbf {v}:=[v_{k}, v_{-k}, k\in\mathbb{Z}_{n}^{+}]^{T}\in\mathbb{C}^{2n}$ to denote the vector [v ₁,v ₋₁,…,v _n ,v _−n ]^T and v:=[v _k ,v _−k ,k∈ℤ _n ]^T∈ℂ²ⁿ⁺¹ by [v ₀,v ₁,v ₋₁,…,v _n ,v _−n ]^T. For m ₁,m ₂∈ℤ, we let

and then set

For k,l∈ℕ, set

and we define matrix A ^∗ of order 2n

$$\mathbf{A}^*:=\bigl[\mathbf{A}_{k,l},\ k,l\in\mathbb{Z}_n^+\bigr].$$

Using these matrix notations, we denote matrix A by

$$\mathbf{A}:=\left( \begin{array}{c@{\quad}c}\mathbf{A}^\prime&\mathbf{A}^{\prime\prime}\\\mathbf{A}^{\prime\prime\prime}&\mathbf{A}^*\end{array}\right).$$

Clearly, the formula (2.7) produces that

$$\mathbf{A}:=\operatorname{diag} \biggl(-1,-1,-1,-\frac{1}{2},-\frac{1}{2},\ldots, -\frac{1}{n},-\frac{1}{n} \biggr).$$

Likewise, for m ₁,m ₂∈ℤ, setting

(2.14)

and

(2.15)

we can define matrix B and matrix C and their corresponding blocks. We let

and then denote the coefficient vector in the approximate solution (2.9) by

$$\mathbf{u}:=[a_l, a_{-l}: l\in\mathbb{Z}_n]^T.$$

Using these matrix and vector notations, (2.10) has the matrix form

$$ (\mathbf{A}+\mathbf{B}+\mathbf{C})\mathbf {u}=\mathbf{f}.$$

(2.16)

The Fourier-Galerkin numerical method for solving (2.6) is equivalent to solve the linear system (2.16). Due to the density of matrix B and matrix C, we observe that storing this linear system requires of computational complexity, and then generating its fully discrete form needs number of multiplications by the fast Fourier transform, and at last, solving the fully discrete linear system of (2.16) requires number of multiplications. Moreover, the spectral condition number of the coefficient matrix A+B+C is . When the order n is large, the computational cost for solving (2.16) is huge at the sane time the linear system (2.16) is extremely ill-posed. Hence, it is of great importance to develop a fast and stable algorithm for solving (2.16).

The issues about the fast and stable algorithm includes: (1) Can the dense coefficient matrix A+B+C be replaced by a sparse one so as to yield a semi-discrete sparse linear system? (2) Can the semi-discrete sparse linear system be fully discretized with a quasi-linear computational cost? (3) Can the fully discrete sparse linear system be solved efficiently and steadily while the approximate solution remains the optimal convergence order? We are going to answer these three questions in the next three sections, respectively.

3 The matrix truncation strategy and its analysis

In this section, we first compress these two full matrices B and C into two sparse ones by using two different matrix truncation strategies, and then analyze these two truncation strategies.

For the dense matrix B, since the kernel function b is smooth, we use the hyperbolic cross approximate method in [6, 14, 15, 19] to compress matrix B into a sparse matrix $\tilde{\mathbf{B}}$ without loss of critical information encoded in the matrix. Specifically, we introduce an index set $\mathbb{L}_{n}^{\mathbf{B}}:=[(m_{1},m_{2})\in{\mathbb{Z}_{n}^{*}}^{2}:|m_{1}m_{2}|\leq n]$, where ${\mathbb{Z}_{n}^{*}}^{2}:=[(k_{1},k_{2}):|k_{1}|,|k_{2}|\in\mathbb{Z}_{n}]$, and then define matrix $\tilde{\mathbf{B}}$ by preserving the entry in B for $(m_{1},m_{2})\in\mathbb {L}_{n}^{\mathbf{B}}$ and replacing others by zeros.

If we use the symbol to denote the number of the nonzero entries for any matrix G, then Theorem 3.1 in [6] shows that is .

For the matrix C, since the kernel function c is not smooth, we are going to develop another matrix truncation strategy different form that of matrix B. Similarly, we first introduce an index collection ${\mathbb{L}_{n}^{\mathbf{C}}}$ given by

$${\mathbb{L}_n^\mathbf{C}}:=\bigl[(m_1,m_2)\in{\mathbb{Z}_n^*}^2: \bigl|(m_1-m_2)m_2\bigr|\leq n \log_2 n\bigr],$$

and then define matrix $\tilde{\mathbf{C}}$ by preserving the entry in matrix C for $(m_{1},m_{2})\in{\mathbb{L}_{n}^{\mathbf{C}}}$ and replacing others by zeros.

In the next theorem we show that the matrix $\tilde{\mathbf{C}}$ is a sparse matrix. To this end, we denote by the cardinality for any set S.

Theorem 3.1

For each n∈ℕ, we have that is .

Proof

Noting the fact that , as a result, we only need to estimate the latter. Let

Clearly,

$${\mathbb{L}_n^\mathbf{C}}=\mathbb{J}_n^\prime \cup\mathbb{J}_n^{\prime\prime},\qquad \mathbb{J}_n^\prime \cap\mathbb{J}_n^{\prime\prime}=\emptyset,$$

which implies that

(3.1)

A direct estimation produces that

(3.2)

On the other hand, we have that

which combining the fact that yields that

(3.3)

A direct combination of (3.1)–(3.3) leads to the desired result. □

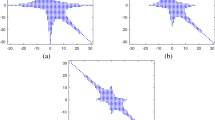
Figure 1 shows the sparsity of matrix $\tilde{\mathbf{B}}$ and matrix $\tilde{\mathbf{C}}$.

Fig. 1

(a) The sparse matrix $\tilde{\mathbf{B}}$ of order 1025 and (b) The sparse matrix $\tilde{\mathbf{C}}$ of order 1025

Let and be the linear operators such that their matrix representations under the Fourier basis X _n are ${\tilde{\mathbf{B}}}$ and $\tilde{\mathbf{C}}$, respectively. Below we give the estimations of and . To this end, we let H ^μ,ν(I ²),μ,ν≥0 denote the Sobolev space of functions ψ∈L ²(I ²) with the norm

The next result concerns the difference .

Lemma 3.1

Suppose that the kernel function b∈H ^q+1,q+1(I ²), then there holds

(3.4)

for w∈H ^ν(I) with ν:=0 or q.

Proof

By Lemma 4.4 in [6], we obtain that

which and the fact that ∥w∥₀≤∥w∥ _q lead to the desired conclusion. □

Next we consider the difference between and . For this purpose, let

$$ \alpha_j:=\left\{ \begin{array}{l@{\quad}l}0,& j=0,\\-\frac{1}{8}, & j=\pm1,\\\frac{1}{2|j|(j^2-1)}, & \mbox{others},\end{array}\right.$$

(3.5)

and we present a few technical results.

Lemma 3.2

Assume that the function c ^∗∈L ²(I ²), then every entry in (2.15) can be rewritten as

(3.6)

Proof

Since c ^∗∈L ²(I ²), then its Fourier expansion has the following form

Substituting the right hand side of the equation above into (2.15) with $\bar{e}_{m_{1}}e_{j_{1}}=\frac{1}{\sqrt{2\pi}}\bar{e}_{m_{1}-j_{1}}$ and $\bar{e}_{m_{2}}e_{j_{2}}=\frac{1}{\sqrt{2\pi}}\bar{e}_{m_{2}-j_{2}}$ yields

(3.7)

Again substituting the result (3.12) in [17],

$$\int_{I}\sin^2\frac{s-t}{2}a(s,t)\bar{e}_{m_1-j_1}(t)dt=\alpha_{m_1-j_1}\bar{e}_{m_1-j_1}(s),\quad s\in I,$$

into the right hand side of (3.7) confirms (3.6). □

Remark 3.1

By changing the variable of integration in (3.7), can also be expressed as

(3.8)

The next lemma gives three fundamental inequalities.

Lemma 3.3

For k,l∈ℤ, there holds

(3.9)

(3.10)

A combination of (3.5) and (3.9) yields that

$$ |\alpha_{k+l}| \bigl(1+k^2 \bigr)\leq2\bigl(1+l^2 \bigr).$$

(3.11)

Proof

The equalities (3.9), (3.10) hold and the equality (3.11) holds for the case |k+l|≤1, obviously. Hence, it only requires us to prove (3.11) for the case |k+l|≥2. In fact, by the definition (3.5), we have that

which combining (3.9) and the next inequality for |k+l|≥2

$$\frac{|k+1|((k+l)^2-1)}{(k+l)^2+1}\geq1,$$

produces that

$$\frac{2(1+l^2)}{|\alpha_{k+l}|}\geq4+k^2\geq1+k^2.$$

This completes the proof of this Lemma. □

For a vector v:=[v _k ,v _−k :k∈ℤ _n ]^T, we use the notation ∥v∥ to denote its spectral norm and then use $\mathbf{v}_{\mu}:=[(1+k^{2})^{\frac{\mu}{2}}v_{k}, (1+k^{2})^{\frac{\mu}{2}}v_{-k}:k\in\mathbb{Z}_{n}]^{T}$ to denote a weighted vector for a nonnegative constant μ.

Lemma 3.4

Suppose that there exist a sequence $\beta_{m_{1},m_{2},j}$ and a positive constant θ independent of m ₁∈ℤ such that for some nonnegative constant μ,

$$ \sum_{j\in\mathbb{Z}}\sum _{m_2\in\mathbb{Z}} \bigl(1+ (m_2-m_1-j)^2 \bigr)^{\mu+1} \bigl(1+j^2\bigr)^{\mu+1}| \beta_{m_1,m_2,j}|^2\leq \theta^2,$$

(3.12)

then there holds for any two vectors v,w∈ℂ²ⁿ⁺¹ and for ν:=0 or μ,

(3.13)

Proof

Associated with the sequence $\beta_{m_{1},m_{2},j}$, we let

$$g_{m_1,m_2,j}:= \bigl(1+(m_2-m_1-j)^{2}\bigr)^{\frac{\mu+1}{2}}\bigl(1+j^2\bigr)^{\frac {\mu+1}{2}}|\beta_{m_1,m_2,j}||\alpha_{m_1+j}|^{\frac{1}{2}},$$

and associated with the vectors v and w, we define

$$h_{m_1,m_2,j}:=\frac{|\alpha_{m_1+j}|^{\frac{1}{2}}(1+m_1^2)^{\frac{1}{2}}|(1+m_1^2)^{\frac{1}{2}}v_{m_1}||(1+{m_2}^2)^{\frac{\nu}{2}}w_{m_2}|}{(1+{m_2}^2)^{\frac{\nu}{2}} (1+(m_2-m_1-j)^{2} )^{\frac{\mu +1}{2}}(1+j^2)^{\frac{\mu+1}{2}}}.$$

We denote by the left hand side of (3.13), that is,

Using the Cauchy-Schwarz inequality to the right hand side of the above equation yields

(3.14)

On one hand, employing the inequality

$$ \sum_{m_1\in\mathbb{Z}}|\alpha_{m_1+j}|\leq1,$$

(3.15)

with the hypothesis (3.12) produces that

$$ \sum_{j\in\mathbb{Z}}\sum _{(m_1,m_2)\in{\mathbb{Z}_n^*}^2\backslash{\mathbb{L}_n^\mathbf {C}}}g_{m_1,m_2,j}^2\leq \theta^2.$$

(3.16)

On the other hand, using (3.9) with k:=m ₂−m ₁ and l:=j yields

$$\bigl(1+(m_2-m_1-j)^{2} \bigr)\bigl(1+j^2\bigr)\geq1+\frac{(m_2-m_1)^{2}}{4},$$

which combining $(m_{1},m_{2})\in{\mathbb{Z}_{n}^{*}}^{2}\backslash{\mathbb{L}_{n}^{\mathbf{C}}}$ obtains that

$$ \bigl(1+m_2^2 \bigr)^{-\nu}\bigl(1+(m_2-m_1-j)^{2} \bigr)^{-{\mu}}\bigl(1+j^2 \bigr)^{-{\mu}}\leq4^{\mu}n^{-2\nu}\log_2^{-2\mu}n.$$

(3.17)

Using (3.10) with k:=m ₂−m ₁ and l:=j yields that

$$ \sum_{j\in\mathbb{Z}}\frac{1}{1+(m_2-m_1-j)^2}\leq4.$$

(3.18)

Employing (3.11) with k:=m ₁ and l:=j produces that

$$ |\alpha_{m_1+j}| \bigl(1+m_1^2\bigr) \leq2 \bigl(1+j^2 \bigr).\ $$

(3.19)

A combination of (3.18) and (3.19) obtains that

$$ \sum_{j\in\mathbb{Z}}\frac{|\alpha _{m_1+j}|(1+m_1^2)}{(1+j^2)(1+(m_2-m_1-j)^2)}\leq8.$$

(3.20)

Hence, a direct consequence of (3.17) and (3.20) concludes that

$$\sum_{j\in\mathbb{Z}}\sum_{(m_1,m_2)\in{\mathbb {Z}_n^*}^2\backslash{\mathbb{L}_n^\mathbf{C}}}h_{m_1,m_2,j}^2\leq4^\mu8 \|\mathbf{v}_1\|^2\|\mathbf{w}_\nu\|^2 n^{-2\nu}\log_2^{-2\mu}n,$$

which and (3.14), (3.16) yield the desired conclusion (3.13). □

The following result concerns the difference between two matrices C and $\tilde{\mathbf{C}}$.

Lemma 3.5

Assume that there exist a positive constant σ and some nonnegative constant μ,

(3.21)

then for any two arbitrary vectors v,w∈ℂ²ⁿ⁺¹ and for ν:=0 or μ, there holds

$$ \bigl|{\mathbf{v}_{2}}^T(\mathbf{C}-\tilde{\mathbf{C}})\mathbf{w}\bigr|\leq{2^{\mu}} \sigma\|\mathbf{w}_\nu \|\|\mathbf{v}_1\| n^{-\nu}\log_2^{-\mu}n.$$

(3.22)

Proof

We first observe that

which combining (3.6) yields that

Hence, using the condition (3.21) and the estimation (3.13) with confirms that

$$\bigl\vert{\mathbf{v}_{2}}^T(\mathbf{C}-\tilde{\mathbf{C}})\mathbf{w}\bigr\vert\leq(2\pi)^{-1}{2^{\mu}8^{1/2}}\sigma\|\mathbf{w}_\nu\|\|\mathbf{v}_1\| n^{-\nu}\log_2^{-2\mu}n.$$

This with $\frac{\sqrt{8}}{2\pi}<1$ yields the desired conclusion. □

Now we give the difference between and .

Lemma 3.6

Suppose that the function c ^∗∈H ^q+1,q+1(I ²), then for each w∈H ^ν(I) with ν:=0 or q, there holds

(3.23)

Proof

By the definition of norm, we have that

For v∈H ¹(I) and w∈H ⁰(I), we express their orthogonal projections onto X _n as

(3.24)

Two coefficient vectors in (3.24) are denoted by v:=[v _k ,v _−k :k∈ℤ _n ]^T and w:=[w _k ,w _−k :k∈ℤ _n ]^T, respectively. Obviously,

$$ \|\mathbf{v}_{1}\|\leq\|v\|_{1},\qquad \|{ \bf w}_{\nu}\|\leq\|w\|_\nu.$$

(3.25)

From (3.24) and the definition of the operators and , we obtain that

A combination of (3.22) and (3.25) with σ:=∥c ^∗∥ _q+1,q+1, μ:=q leads to the desired estimation (3.23). □

Replacing B and C in (2.16) by $\tilde{\mathbf{B}}$ and $\tilde{\mathbf{C}}$, respectively leads to a truncated linear system

$$ (\mathbf{A}+\tilde{\mathbf{B}}+\tilde{\mathbf{C}})\tilde{\mathbf{u}}=\mathbf{f},$$

(3.26)

with the unknown solution vector $\tilde{\mathbf{u}}:=[\tilde {a}_{l},\tilde{a}_{-l}: l\in\mathbb{Z}_{n}]^{T}$. Because the coefficient matrix $\mathbf{A}+\tilde{\mathbf{B}}+\tilde{\mathbf{C}}$ has number of nonzero entries, solving (3.26) is a fast semi-discrete algorithm.

4 The numerical integration scheme and its analysis

The numerical implementation of the fast method (3.26) requires an efficient computation of the nonzero elements in this linear system. We observe that , and are oscillatory integrals. To treat these oscillatory integrals, we adopt the product integration method so the integrals of the oscillatory factors are evaluated exactly. For recent development of numerical integration of oscillatory integrals, see [10–13, 18, 20]. With the product integration method, we can obtain sufficient precision to ensure that the approximate solution has the optimal convergence order. Specifically, we are going to use three appropriate functions to replace b, c ^∗ and f, respectively, so that it requires a quasi-linear computational cost to generate the fully discrete forms of $\tilde{\mathbf{B}}$, $\tilde{\mathbf{C}}$ and f and the approximate solution preserves the optimal order.

In the next three subsections we are going to present and analyze the efficient numerical integration algorithm for computing all nonzero entries in $\tilde{\mathbf{B}}$, $\tilde{\mathbf{C}}$ and f, respectively. Accordingly, we use the notation ⌊x⌋ to denote the largest integer not more than x.

4.1 The numerical integration scheme for matrix $\tilde{\mathbf{B}}$

In this section, we first present the Boolean approximate function of the function b. This idea comes from [3, 4, 8]. To this end, for any two-dimensional continuous function g∈C(I ²) and for M _k ∈ℕ and $|j_{k}|\in\mathbb{Z}_{M_{k}}$, k=1,2, we set

and then let

As shown in [4], let r:=⌊log₂ n⌋+1, and we define the two-dimensional Boolean approximate function of b by

(4.1)

A direct computation for yields that

(4.2)

where $\delta_{l_{1},l_{2}}$ is defined by

$$\delta_{l_1,l_2}:=\left\{ \begin{array}{l@{\quad}l}1,& l_1=l_2,\\0,& l_1\not= l_2.\end{array}\right.$$

We let $\hat{\mathbf{B}}$ denote the matrix $\tilde{\mathbf{B}}$ with being replaced by for $(m_{1},m_{2})\in\mathbb{L}_{n}^{\mathbf{B}}$. Now we describe the algorithm for generating the fully discrete matrix $\hat{\mathbf{B}}$.

Algorithm 4.1

Choosing r:=⌊log₂ n⌋+1 for n∈ℕ.

Step 1::

Computing $b(\frac{2\pi j_{1}}{2^{j+1}}, \frac{2\pi j_{2}}{2^{r+2-j}})$ for $j_{1}\in\mathbb{Z}_{2^{j+1}-1},j_{2}\in\mathbb{Z}_{2^{r+2-j}-1}$, $j\in\mathbb{Z}_{r}^{+}$.

Step 2::

Computing $b(\frac{2\pi j_{1}}{2^{j+1}}, \frac{2\pi j_{2}}{2^{r+1-j}})$ for $j_{1}\in\mathbb{Z}_{2^{j+1}-1},j_{2}\in\mathbb{Z}_{2^{r+1-j}-1}$, $j\in\mathbb{Z}_{r-1}^{+}$.

Step 3::

For $j\in\mathbb{Z}_{r}^{+}$, computing for $j_{1}\in\mathbb{Z}_{2^{j+1}-1}, j_{2}\in\mathbb{Z}_{2^{r+2-j}-1}$ by the two-dimensional fast Fourier transform.

Step 4::

For $j\in\mathbb{Z}_{r-1}^{+}$, computing for $j_{1}\in\mathbb{Z}_{2^{j+1}-1}, j_{2}\in\mathbb{Z}_{2^{r+1-j}-1}$ by the two-dimensional fast Fourier transform.

Step 5::

Computing for all $(m_{1},m_{2})\in\mathbb{L}_{n}^{\mathbf{B}}$, according to the formula (4.2).

The next theorem concerns on the computational cost used in generating $\hat{\mathbf{B}}$.

Theorem 4.1

For (s,t)∈I ², if the number of multiplications used in computing b(s,t) is , then the number of multiplications for computing all nonzero entry in $\tilde{\mathbf{B}}$ is .

Proof

The number of multiplications used in Step 1 and Step 2 is . Step 3 and Step 4, by FFT method, require number of multiplications. In Step 5, a direct observation infers that the number of multiplications is . In view of the total number of multiplications used in Algorithm 4.1 equaling to the sum of that used in each step, we obtain the desired result. □

Let be the linear operator such that its matrix representation under the Fourier basis X _n is ${\hat{\mathbf{B}}}$. The next step is to give a few technical results so as to show the difference between and .

Lemma 4.1

Suppose that the kernel function $b\in{H}^{q_{1}, q_{1}}(I^{2})$ such that q ₁>q+3/2, then there exists a positive integer n ₀ such that when n≥n ₀ and for any two arbitrary vectors v,w∈ℂ²ⁿ⁺¹,

$$ \bigl|{\mathbf{v}}_{2}^T(\tilde{\mathbf{B}}-\hat{\mathbf{B}})\mathbf{w}\bigr|\leq\|b\|_{q_1,q_1} \|\mathbf{w}\|\|\mathbf{v}_1\| n^{-q}.$$

(4.3)

Proof

A direct expansion of $\mathbf{v}_{2}^{T}(\tilde{\mathbf{B}}-\hat{\mathbf{B}})\mathbf{w}$ yields that

Employing Cauchy-Schwartz inequality to the right hand side of the above equation, we have

(4.4)

Applying Theorem 8 in [4], there exists a positive constant ς ₁ such that for $b\in H^{q_{1},q_{1}}(I^{2})$,

(4.5)

which yields that

(4.6)

Together with (4.6) and the inequality $1+m_{1}^{2}\leq2 n^{2}$ for |m ₁|∈ℤ _n , the inequality (4.4) infers that

$$\bigl|{\mathbf{v}}_{2}^T(\tilde{\mathbf{B}}-\hat{\mathbf{B}})\mathbf{w}\bigr|\leq\sqrt{2}\varsigma_1\|b\|_{q_1, q_1}\|\mathbf{v}_1\| \|{ \bf w}\| \biggl( \sum_{(k,l)\in\mathbb {L}_n^\mathbf{B}}n^{-2q_1+2}\log_2^2 n \biggr)^{\frac{1}{2}}.$$

Since

there exists a positive constant ς ₂ such that

(4.7)

Because −q ₁+q+3/2<0, we obtain that $n^{-q_{1}+q+3/2}\log_{2}^{3/2}n\rightarrow0$ as n→∞, and then there exists a positive constant n ₀ such that n≥n ₀, the value $\varsigma_{2} n^{-q_{1}+q+3/2}\log_{2}^{3/2}n$ is bounded by 1. Substituting the above estimate into the right hand side of (4.7) leads to (4.3). □

Similar to the proof of Lemma 3.6, using Lemma 4.1 leads to

Lemma 4.2

Suppose that the function $b\in{H}^{q_{1},q_{1}}(I^{2})$, then there exists a positive integer n ₀ such that when n≥n ₀ and for any w∈H ⁰(I),

(4.8)

4.2 The numerical integration scheme for matrix $\tilde{\mathbf{C}}$

Similar as in Sect. 4.1, using to denote the Boolean approximate function of c ^∗, we let

(4.9)

and then set

$$ \hat{c}(s,t):=\sin^2\frac{s-t}{2}a(s,t)\hat{c}^*(s,t).$$

(4.10)

A simple computation for by (3.5) yields that

(4.11)

where

$$\mathbb{M}_{(m_1,m_2,n)}:= \bigl\{j\in\mathbb{Z}: (m_1-m_2-j,-j)\in\mathbb{L}_n^\mathbf{B} \bigr\}.$$

We let $\hat{\mathbf{C}}$ denote the matrix $\tilde{\mathbf{C}}$ with being replaced by for $(m_{1},m_{2})\in{\mathbb{L}_{n}^{\mathbf{C}}}$. Now we describe the algorithm for computing all nonzero entries in matrix $\tilde{\mathbf{C}}$.

Algorithm 4.2

Choosing r:=⌊log₂ n⌋+1 for n∈ℕ.

Step 1::

For $(m_{1},m_{2})\in\mathbb{L}_{n}^{\mathbf{B}}$, computing by Algorithm 4.1.

Step 2::

Computing for all $(m_{1},m_{2})\in{\mathbb{L}_{n}^{\mathbf{C}}}$, according to the formula (4.11).

The next result considers the computational cost for generating $\hat{\mathbf{C}}$.

Theorem 4.2

For (s,t)∈I ², if the number of multiplications used in computing c ^∗(s,t) is , then the number of multiplications for computing all nonzero entries in $\tilde{\mathbf{C}}$ is .

Proof

Noting that the computational cost of Step 1 is by Theorem 4.1, it only requires to estimate the cost of Step 2 in Algorithm 4.2. Consequently, let p:=m ₁−m ₂, and we define an index set $\mathbb{M}_{p,n}$ as

$$\mathbb{M}_{p,n}:=\left\{ \begin{array}{l@{\quad}l}\mathbb{Z}_{p_2} \backslash\mathbb{Z}_{p_1}, & p^2-4n\leq0,\\\{\mathbb{Z}_{p_1} \backslash\mathbb{Z}_{p_3}\}\cup \{\mathbb{Z}_{p_2} \backslash\mathbb{Z}_{p_4}\}, & p^2-4n>0,\end{array}\right.$$

where

$$p_1:= \biggl\lfloor\frac{p-\sqrt{p^2+4n}}{2} \biggr\rfloor-1,\qquad p_2:= \biggl\lfloor\frac{p+\sqrt{p^2+4n}}{2} \biggr\rfloor+1,$$

and

$$p_3:= \biggl\lfloor\frac{p-\sqrt{p^2-4n}}{2} \biggr\rfloor-1,\qquad p_4:= \biggl\lfloor\frac{p+\sqrt{p^2-4n}}{2} \biggr\rfloor+1.$$

Thus we write of (4.11) as

where

$$\lambda(p):=\min\biggl\{ n, \biggl\lfloor\frac{n\log_2n}{\max\{1,|p|\}} \biggr\rfloor\biggr \}.$$

Clearly, for p ²−4n≤0, otherwise, . Let

and we infer that the number of multiplications finishing Step 2 by the FFT method is not more than

which yields the desired conclusion. □

Next we concern on the estimation . For this we set

(4.12)

By Theorem 1 in [15], there exists a positive constant τ ₁ such that for $c^{*}\in H^{q_{1}, q_{1}}(I^{2})$,

$$ \bigl\|c^*-\tilde{c}^*\bigr\|_{0,0}\leq\tau_1\bigl\|c^*\bigr\|_{q_1, q_1}n^{-q_1}.$$

(4.13)

Again using Theorem 8 in [4], combining (4.9) and (4.12) with (4.5) yields that there exists a positive constant τ ₂ such that

(4.14)

A combination of (4.13) and (4.14) yields that

$$ \bigl\|c^*-\hat{c}^*\bigr\|_{0,0}\leq(\tau_1+\tau_2)\bigl\|c^*\bigr\|_{q_1,q_1}n^{-q_1}.$$

(4.15)

Lemma 4.3

Suppose that the function $c^{*}\in{H}^{q_{1}, q_{1}}(I^{2})$, then there exists a positive constant τ such that

(4.16)

Proof

By the definition, the difference between and is written as

Using Cauchy-Schwartz inequality to the right hand side of the equation above with letting

$$\tau_3:= \biggl(\int_{I^2}\sin^4\frac{s-t}{2}a^2(s,t)dsdt \biggr)^{1/2},$$

produces that

Clearly, τ ₃<+∞. Substituting the estimate (4.15) into the right hand side of the equation above with τ:=(τ ₁+τ ₂)τ ₃ leads to the desired conclusion. □

We denote by the linear operator such that its matrix representation under the Fourier basis X _n is ${\hat{\mathbf {C}}}$ and then estimate the difference between and .

Lemma 4.4

Suppose that the function $c^{*}\in{H}^{q_{1},q_{1}}(I^{2})$, then there exists a positive integer n ₀ such that when n≥n ₀, for any two arbitrary vectors v,w∈ℂ²ⁿ⁺¹,

$$ \bigl|{\mathbf{v}}_{2}^T(\tilde{\mathbf{C}}-\hat{\mathbf{C}})\mathbf{w}\bigr|\leq\bigl\|c^*\bigr\|_{q_1, q_1} \|\mathbf{w}\|\|\mathbf{v}_1\| n^{-q}.$$

Hence, we also have that for w∈H ⁰(I),

(4.17)

Proof

Combining Lemma 4.3, a similar proof of Lemmas 4.1 and 4.2 yields the desired conclusion. □

4.3 The numerical integration scheme for vector f

We first consider the right hand side vector f in (3.26). For |m ₁|∈ℤ _n , we define $\tilde{f}_{m_{1}}$ by,

$$\tilde{f}_{m_1}:=\frac{\pi}{n}\sum_{j\in\mathbb{Z}_{2n-1}}f\biggl(\frac {\pi j}{n}\biggr)\bar{e}_{m_1}\biggl(\frac{\pi j}{n}\biggr),$$

and then let

$$\hat{f}_n(t):=\sum_{|m_1|\in\mathbb{Z}_n}\tilde{f}_{m_1}e_{m_1}(t).$$

Clearly, we have that for |m ₁|∈ℤ _n , . Now we use $\hat{f}_{m_{1}}$ to approximate ${f}_{m_{1}}$ and let

$$\hat{\mathbf{f}}:=[\tilde{f}_k,\tilde{f}_{-k},k\in \mathbb{Z}_n]^T.$$

A standard argument in [1, 9] shows that obtaining $\hat{\mathbf{f}}$ requires number of computational cost by the fast Fourier transform method and there exists a positive constant ε such that for f∈H ^q+1(I) with q>0,

$$ \|f_n-\hat{f}_n\|_1\leq\varepsilon\|f\|_{q+1} n^{-q}.$$

(4.18)

By replacing the matrices $\tilde{\mathbf{B}}, \tilde{\mathbf{C}}$ and f in (3.26) by the fully discrete matrices $\hat{\mathbf{B}}, \hat{\mathbf{C}}$ and $\hat{\mathbf{f}}$, a fully discrete truncated linear system is obtained

$$ (\mathbf{A}+\hat{\mathbf{B}}+\hat{\mathbf{C}})\hat{\mathbf{u}}=\hat{ \bf f},$$

(4.19)

with the unknown solution vector $\hat{\mathbf{u}}:=[\hat{a}_{l},\hat {a}_{-l}: l\in\mathbb{Z}_{n}]^{T}$.

From the analysis above we observe that generating the linear system (4.19) requires the number of of multiplications. Moreover, solving this linear system requires number of multiplications by the multilevel augmentation method proposed in [7]. Hence, it is a fast fully discrete algorithm.

5 The analysis of the proposed fast method

In this section, we first present the stability of the approximate operator .

Lemma 5.1

Suppose that the kernel function $b\in{H}^{q_{1},q_{1}}(I^{2})$, then there exists a positive integer n ₀ such that for n≥n ₀ and for any w∈H ⁰(I),

(5.1)

Proof

Using the triangle inequality we have that

which combining (2.3) and (4.8) with $H^{q_{1},q_{1}}(I^{2}) \subseteq H^{q+1,q+1}(I^{2})$ yields the desired conclusion. □

Lemma 5.2

Suppose that the function $c^{*}\in{H}^{q_{1},q_{1}}(I^{2})$, then there exist a positive integer n ₀ and a positive constant γ such that when n≥n ₀ and for w∈H ^ν(I) with ν:=0 or q,

(5.2)

Proof

This result is a consequence of Lemma 3.6 and Lemma 4.4. □

Theorem 5.1

Suppose that the functions $b,c^{*}\in{H}^{q_{1}, q_{1}}(I^{2})$, then there exists a positive integer n ₀ such that n≥n ₀ and for any w∈X _n

(5.3)

where ς is given in (2.13).

Proof

By the hypothesis on the function b, using (5.1) and the fact that lim _n→∞ n ^−q=0, we conclude that there exists a positive integer n ₁ such that for all n≥n ₁ and for all w∈X _n ,

(5.4)

As mentioned in the above, a consequence of (5.2) leads to the fact that there exists a positive integer n ₂ such that when n≥n ₂ and for w∈X _n ,

(5.5)

When n≥n ₀:=max{n ₁,n ₂}, these two estimates (5.4) and (5.5) combining with (2.13) yield that

proving the desired conclusion. □

This theorem shows that when n≥n ₀, (4.19) has a unique solution. Clearly, the linear system (4.19) is equivalent to the operator form:

(5.6)

where

$$\hat{u}_n(s)=\sum_{|l|\in \mathbb{Z}_{n}}\hat{a}_le_{l}(s), \quad s\in I.$$

Next we establish the convergence order of the approximate solution $\hat{u}_{n}$.

Theorem 5.2

Suppose the conditions in Theorem 5.1 hold, f∈H ^q+1(I), then there exist a positive constant η and a positive integer n ₀ such that for n≥n ₀,

$$\|u-\hat{u}_n\|_0\leq\eta\|u\|_qn^{-q}.$$

Proof

By the triangle inequality we have that

(5.7)

Using (2.8) with ω:=u,μ:=q,ν:=0 obtains that the first term on the right hand side of (5.7) is bounded by ∥u∥ _q n ^−q. Therefore, it requires us to give an estimate of the second term on the right hand side of (5.7). Using Theorem 5.1 there exists a positive integer n ₀ such that n≥n ₀,

(5.8)

On the other hand, employing operator to both sides of (2.6) and using ${f}_{n}:=\hat{f}_{n}+{f}_{n}-\hat{f}_{n}$ yield that

(5.9)

Combining (5.9) and (4.19) shows that

(5.10)

A direct computation using (5.10) confirms the equation

Together with (2.8), (4.18), (4.8), (4.17) and (5.3) using the triangle inequality for the equation above shows that there exist a positive constant η ₁ and a positive integer n ₀ such that when n≥n ₀,

(5.11)

Hence, there exists a positive constant η such that

$$\eta_1\|u\|_q n^{-q} +\varepsilon\|f\|_{q+1}n^{-q}\leq\eta\|u\|_qn^{-q},$$

which and (5.11) lead to the desired conclusion. □

Theorem 5.2 illustrates that the proposed method preserves the optimal order of convergence.

In the remainder of this section, we consider a precondition of the coefficient matrix of the linear system (4.19) so that the resulting matrix has a uniformly bounded spectral condition number. For this purpose, we introduce a lemma.

Lemma 5.3

Suppose that the conditions in Theorem 5.1 hold, then there exist two positive constants θ ₁ and θ ₂ and a positive integer n ₀ such that when n≥n ₀ and for w∈X _n ,

(5.12)

Proof

By Theorem 5.1 we observe that the left hand side of the inequality (5.12) holds with θ ₁:=ς/2. The left issue is to prove the right hand side of this inequality. By using the triangle inequality, there holds

(5.13)

Noting that is bounded. With the definition of operators and , there exist a positive constant ξ and a positive integer n ₁ such that for n≥n ₁ and w∈X _n ,

(5.14)

Again by (5.1) and (5.2) there exists a positive integer n ₂ such that n≥n ₂,

(5.15)

Substituting these two estimates (5.14) and (5.15) into the right hand side of (5.13) leads to the desired result (5.12) with θ ₂:=ξ+1 and n≥n ₀:=max{n ₁,n ₂}. □

Now we define a diagonal matrix D by

$$\mathbf{D}:=\operatorname{diag} \bigl(1,2^{\frac{1}{2}},2^{\frac{1}{2}},\ldots ,\bigl(1+n^2\bigr)^\frac{1}{2},\bigl(1+n^2\bigr)^\frac{1}{2} \bigr),$$

which will be used as a preconditioner for the coefficient matrix $(\mathbf{A}+\hat{\mathbf{B}}+\hat{\mathbf{C}})$. To this end, we let

$$\mathbf{E}:=\mathbf{D}(\mathbf{A}+\hat{\mathbf{B}}+\hat{\mathbf{C}}).$$

Clearly, (4.19) is rewritten as

$$\mathbf{E}\hat{\mathbf{u}}=\mathbf{D}\hat{\mathbf{f}}.$$

Below we prove that matrix E enjoys a uniformly bounded spectral condition number. For this purpose, we use the symbol $\operatorname{cond}(\bf G)$ to denote the spectral condition number for any inverse square matrix G.

Theorem 5.3

Suppose that the conditions in Theorem 5.2 hold, then there exists a positive integer n ₀ such that when n≥n ₀, the spectral condition number of matrix E is uniformly bounded, that is

$$ \operatorname{cond}(\mathbf{E})\leq\theta_2/\theta_1.$$

(5.16)

Proof

This proof is similar to that of Theorem 4.2 in [13]. For any w:=[w _l ,w _−l :l∈ℤ _n ]^T, we let

Clearly, v∈X _n . Let , and we have that

$$\mathbf{v}=(\mathbf{A}+\hat{\mathbf{B}}+\mathbf{C})\mathbf{w},$$

that is,

$$\mathbf{D}\mathbf{v}=\mathbf{E}\mathbf{w},$$

which yields

(5.17)

A combination of (5.12) and (5.17) with the fact ∥w∥₀=∥w∥ leads to the estimate (5.16). □

6 Numerical examples

In this section, we shall adopt the conventional method and the proposed method respectively to compute one numerical example and then show that our proposed method is better than the conventional method.

In the conventional method, the fully discrete form of B is obtained by using the two-dimensional fast Fourier transform algorithm. For the matrix C, we first use the two-dimensional fast Fourier transform algorithm to compute for $(m_{1},m_{2})\in{\mathbb{Z}_{n}^{*}}^{2}$, and then obtain the fully discrete form of matrix C by using (3.8) and the fast Fourier transform method. In our proposed method, we obtain the matrix $\hat{\mathbf{B}}$ and matrix $\hat{\mathbf{C}}$ by Algorithm 4.1 and Algorithm 4.2 respectively.

All computer programs are compiled by Matlab language and run on a personal computer with a 2.01 GHz celeron CPU and 1 G memory. We solve the fully discrete linear system by the multilevel augmentation method. We use the notations CT₁ and CT₂ to denote the computing time (measured in seconds), spent in generating the fully discrete form of matrix B and C in the conventional method and that of $\tilde{\mathbf{B}}$ and $\tilde{\mathbf{C}}$ in the proposed method, respectively. We use CT₃ to denote the time (measured in seconds) spent in solving the linear system (2.16) and (4.19), respectively.

Example

Consider solving the boundary value problem (1.1)–(1.2). Assume the boundary S has a parametrization x(t):=(2cost,sint), t∈I. We choose the boundary function h in (1.2) so that the exact solution for the boundary value problem (1.1)–(1.2) is U(P):=N ₀(2|P−P ₀|), P∈D, where P ₀:=(4,0). Let $\hat{u}_{n}$ be the solution by solving (5.6), and we define the corresponding approximate solution $\hat{U}_{n}$ for the boundary value problem (1.1)–(1.2) by

$$\hat{U}_n(x,y):=\frac{i}{4}\int_IH_0^{(1)}\bigl(2 \bigl((x-2\cos t)^2+(y-2\sin t)^2\bigr)^{1/2} \bigr)\hat{u}_n(t)dt, \quad (x,y)\in D.$$

We define the error function δ(x,y) as follows

$$\delta(x,y):=\bigl\vert U(x,y)-\hat{U}_n(x,y)\bigr\vert,\qquad P:=(x,y)\in D.$$

The numerical results for this example obtained by using the conventional method and the proposed method are given in Tables 1 and 2, respectively, where δ _k :=δ(P _k ) at the points $P_{k}:=p_{k}(\cos\frac{\pi}{4}, \sin\frac{\pi}{4}), k=1,2,3$, where p ₁:=0,p ₂:=0.25 and p ₃:=0.5 and the values of $\hat{U}_{k}$ at points P _k are computed by the trapezoid quadrature formula. Figure 2 illustrates that our proposed method is more efficient than the conventional method.

Fig. 2

Computation times CT of conventional and proposed methods

Table 1 Results of the conventional method for Example 2 for κ:=2

Table 2 Results of the proposed method for Example 2 for κ:=2

7 Conclusion

The proposed method is superior to the conventional numerical method for solving the first kind boundary integral equation, reformulations of boundary value problems of the two-dimensional Helmholtz equation with a smooth boundary. Moreover, this method may be used to solve other boundary value problems.