1 Introduction

Various emergency events occur frequently all over the world, which have resulted in enormous property losses and negative effects on social stability and public security [1,2,3]. For example, the 2019 Super Typhoon Lekima disaster caused direct economic losses of about 52 billion yuan in China. The Australian bushfires in 2019 destroyed more than 1.4 thousand homes, killed over a billion animals, and burned about 15 million acres of land. The coronavirus disease 2019 (COVID-19) has spread to over 200 countries and more than 4 million people have unfortunately died by July, 2021. The COVID-19 epidemic seriously restricted the development of social economy and threaten the stability of society [4]. As an effective tool to reduce the adverse effects of emergencies, emergency decision making (EDM) plays a crucial role in public management and social interaction. One of the significant characters of the emergency response is timeliness, which means that the rescue teams are asked for taking effective actions during a short time [5, 6]. In the process of dealing with an emergency event, inadequate decision information and tight time pressure make it difficult for decision makers to make a reasonable and efficient choice under an unpredictable decision environment [7, 8]. Consequently, it is of great significance to develop systematic and reliable EDM methods for determining the optimal response to an emergency event to minimize economic losses and casualties [1, 9, 10].

In EDM, the information on emergency alternatives is usually uncertain due to strong time constraints and intricate emergency circumstances, especially in the early stages [11, 12]. Normally, decision makers tend to use linguistic terms to express their opinions because of time pressure and lack of data [13,14,15]. Therefore, Herrera and Martínez [16] suggested the use of natural language for the management of uncertainty and proposed the concept of 2-tuple linguistic method. Due to its accuracy and simplicity, the 2-tuple linguistic method has been applied to many fields [17,18,19,20], and various extended forms have been developed for improving linguistic solving processes [21,22,23]. Besides, some studies have deal with the personalized individual semantics issue (i.e., words mean different things to different people) based on the 2-tuple linguistic model [24,25,26]. Recently, the notion of 2-tuple spherical linguistic sets (TSLTSs) was introduced by Abdullah et al. [27] as an integration of the 2-tuple linguistic method and spherical fuzzy sets [28]. The 2-tuple spherical linguistic method, which is characterized by linguistic positive, neutral, and negative membership grades, can effectively avoid any loss of information which formerly occurred during linguistic information processing. It is more flexible and realistic because both numerical and linguistic information are taken into consideration [29]. Taking the advantages of the 2-tuple linguistic variables, the TSLTSs can effectively avoid information loss and distortion in the processing of linguistic information. Therefore, the TSLTSs are applied here to handle vague and uncertain evaluation information on emergency events provided by decision makers.

Generally, the selection of the optimal response to an emergency event can be treated as a multiple criteria decision making (MCDM) problem since many contradict and even conflict criteria are involved in the EDM process [30, 31]. Thus, MCDM methods are useful and effective tools for handling EDM problems [14, 32, 33]. To capturing and quantifying decision makers’ psychological behaviours, such as regretful and joyful emotions, the regret theory was introduced by Loomes and Sugden [34]. Since then, the regret theory has been combined with many MCDM methods for better decision making, which include the preference ranking organization method for enrichment evaluation (PROMETHEE) [35], the TODIM (an acronym in Portuguese for interactive MCDM) [36], and the multi-attributive border approximation area comparison (MABAC) [37]. In addition, the evaluation based on the distance from the average solution (EDAS) method, put forward by Ghorabaee et al. [38], is a new MCDM method. The EDAS method applies the average solution in the appraisal of alternatives and calculates the positive distance and negative distance of each alternative from the average solution. The optimal alternative is defined with higher values of positive distances and lower values of negative distances. When compared with other MCDM methods, the EDAS method is more suitable for solving problems with conflicting criteria, because it only needs to calculate the expected function from the average solution [39, 40]. Owing to these benefits, the EDAS has been applied to address a lot of real-world decision-making issues, such as inventory management [41], sustainable operational performance analysis [42], renewable energy investment assessment [43], and quality function deployment [44]. Keeping the advantages of the two decision making techniques, it is of great significance to realize an integration of the regret theory and the EDAS method for determining the priorities of emergency alternatives in EDM.

Against the analysis above, the aim of this paper is to develop a regret theory-EDAS method within the environment of TSLTSs for handling EDM problems. First, the TSLTSs are employed to manage decision makers’ vague and uncertain evaluation information on emergency alternatives. Second, the criteria importance through inter-criteria correlation (CRITIC) method is adopted for the determination of objective criteria weights. Third, an integrated approach combining regret theory with the EDAS method is proposed for ranking emergency alternatives and determining the optimal one for EDM. At last, an empirical example of COVID-19 as well as a comparative analysis with existing EDM methods are presented for justifying effectiveness and superiority of our proposed regret theory-EDAS method.

The remainder of this paper is arranged as follows. In Sect. 2, the basic concepts regarding the TSLTSs and regret theory are presented. In Sect. 3, the framework of the integrated regret theory-EDAS method is introduced for solving EDM problems. Section 4 presents a practical example and a comparative performance for validating the proposed new EDM model. Section 5 ends this paper with conclusions and directions for future research.

2 Literature review

Over the past decades, a variety of MCDM methods have been applied for the prioritization of emergency alternatives in EDM. For example, Yu and Lai [45] proposed a distance-based model to address multi-criteria group EDM problems. Ju and Wang [46] presented a method of incorporating Dempster-Shafer theory/analytic hierarchy process (AHP) with technique for order preference by similarity to an ideal solution (TOPSIS) to evaluate an emergency alternative selection problem with incomplete information. Ju et al. [47] put forward a framework combining analytic network process (ANP) method, decision-making trial and evaluation laboratory (DEMATEL) technique, and 2-tuple linguistic TOPSIS method for emergency alternative evaluation and selection. In [48], a discrete conflict-eliminating model was developed for EDM, in which the simple additive weighting (SAW) method was used to determine the best emergency alternative. Besides, Liu et al. [49] introduced a method based on cumulative prospect theory for risk decision making considering decision makers’ psychological behavior in emergency response. Xu et al. [50] suggested a large group method for risk dynamic EDM based on the cumulative prospect theory. Wang et al. [51] gave a prospect theory-based interval dynamic reference point method to solve the emergency alternative evaluation and selection problem, and Wang et al. [30] proposed an EDM method based on prospect theory to include experts’ psychological behavior in the group decision process. In [52], an EDM approach using the prospect theory and linear programing model was designed for different emergency situations.

Recently, more and more researchers combined fuzzy theories with MCDM methods to handle the ambiguity and uncertainty data in emergency problems. For instance, the 2-dimension uncertain linguistic variables were integrated with prospect theory and VIKOR (VIsekriterijumska optimizacija i KOm-promisno Resenje) for EDM in [14]. The interval-valued Pythagorean fuzzy linguistic variables were used to extend prospect theory for dynamic EDM in [12]. Three EDM algorithms for interval-valued fuzzy soft sets based on weighted distance-based approximation (WDBA), combinative distance-based assessment (CODAS), and similarity measure were proposed in [53]. Sun and Ma [31] combined the soft fuzzy rough sets with TOPSIS method to evaluate emergency plans for unconventional emergency events. Ashraf and Abdullah [54] proposed an integrated methodology using spherical fuzzy sets, TOPSIS and grey relational analysis (GRA) methods for dealing with EDM problems. An EDM model based on the Pythagorean probabilistic hesitant fuzzy sets and EDAS method was established by Batool et al. [2]. A dynamic reference point method with the probabilistic linguistic information based on regret theory was presented by Xue et al. [7] for public health EDM. Additionally, the hesitant fuzzy linguistic TODIM [1], the picture fuzzy axiomatic design technique [55], and the Pythagorean fuzzy TOPSIS [11] were proposed to tackle the uncertainty in various EDM problems.

The literature review above shows that existing studies on EDM have made significant contributions to emergency management under complicated and uncertain decision environment. On the one hand, different fuzzy theories have been employed to capture and depict the fuzziness and vagueness of emergency evaluations collected from decision makers. Although these fuzzy methods have some desirable properties in handling uncertain decision making information, there still exist situations where complex assessments cannot be depicted adequately and information loss in the processing process cannot be solved well. On the other hand, many MCDM methods have been utilized or extended to handle different kinds of emergency events. To the best of our knowledge, however, the EDAS, as a powerful and straightforward MCDM method, has not been combined with regret theory for tackling EDM problems. To bridge these gaps, the aim of this paper is to propose a new technique by integrating regret theory with the EDAS method for EDM under the 2-tuple spherical linguistic environment. In addition, the CRITIC technique is extended and utilized to determine the weights of criteria objectively based on the evaluation information on emergency events.

3 Preliminaries

3.1 2-Tuple spherical linguistic term sets

The TSLTSs were introduced by Abdullah et al. [27] to deal with uncertain and vague information in MCDM problems.

Definition 1 [27]

Let \(S=\{s_1,s_2,\cdots,s_\tau\}\) be a linguistic term set with odd cardinality, then a TSLTS on the universe discourse \({\mathbb{R}}\), R, is in the form of

$$R=\left\{\langle {s}_{\mu \left(r\right)},{s}_{\eta \left(r\right)},{s}_{v\left(r\right)}\rangle |r\in {\mathbb{R}}\right\},$$
(1)

where \({s}_{\mu \left(r\right)},{s}_{\eta \left(r\right)},{s}_{v\left(r\right)}\in S\) represent the positive membership, neutral membership and negative membership degrees of r to R, respectively, satisfying the condition that \(3\le {\mu }^{2}\left(r\right)+{\eta }^{2}\left(r\right)+{v}^{2}\left(r\right)\le {\left(\tau +1\right)}^{2}\). The degree of refusal membership of the element r to the set R is denoted as \({s}_{\pi \left(r\right)}={s}_{\sqrt{{\left(\tau +1\right)}^{2}-{\mu \left(r\right)}^{2}-{\eta \left(r\right)}^{2}+{v\left(r\right)}^{2}}}\).

For convenience, \(\tilde{r }=\langle \left({s}_{\mu },\ddot{a}\right),\left({s}_{\eta },\ddot{e}\right),\left({s}_{v},\ddot{u}\right)\rangle\) is named as a 2-tuple spherical linguistic number (TSLN), where \(\left({s}_{\mu },\ddot{a}\right),\left({s}_{\eta },\ddot{e}\right),\left({s}_{v},\ddot{u}\right)\) are three 2-tuple linguistic terms and \(\ddot{a},\ddot{e},\ddot{u}\in \left[-0.5\right.,\left.0.5\right)\).

Definition 2 [27]

Let \(S=\{s_1,s_2,\cdots,s_\tau\}\) be a linguistic term set, \(\tilde{r }=\langle \left({s}_{\mu },\ddot{a}\right),\left({s}_{\eta },\ddot{e}\right),\left({s}_{v},\ddot{u}\right)\rangle\) be a TSLN and \(\alpha ,\beta ,\gamma \in \left[1,\tau \right]\) be three numbers representing the results of a symbolic aggregation operation. Considering that \(\langle \alpha ,\beta ,\gamma \rangle\) conveys the equivalent information to \(\tilde{r }\), they can be transformed with each other by

$$\Delta :\left[1,\tau \right]\to S\times \left[-0.5\right.,\left.0.5\right),\left\{\begin{array}{l}\Delta \left(\alpha \right)=\left\{\begin{array}{l}{s}_{\mu },\mu =\mathrm{round}\left(\alpha \right);\\ \ddot{a}=\alpha -\mu ,\ddot{a}\in \left[0.5\right.,\left.0.5\right)\end{array}\right.\\ \Delta \left(\beta \right)=\left\{\begin{array}{l}{s}_{\eta },\eta =\mathrm{round}\left(\beta \right);\\ \ddot{e}=\beta -\eta ,\ddot{e}\in \left[0.5\right.,\left.0.5\right)\end{array}\right.\\ \Delta \left(\gamma \right)=\left\{\begin{array}{l}{s}_{\upsilon },\upsilon =\mathrm{round}\left(\gamma \right);\\ \ddot{u}=\gamma -\upsilon ,\ddot{u}\in \left[0.5\right.,\left.0.5\right)\end{array}\right.\end{array}\right.,$$
(2)
$${\Delta }^{-1}:S\times \left[-0.5\right..\left.0.5\right)\to \left[1,\tau \right],\left\{\begin{array}{c}{\Delta }^{-1}\left({s}_{\mu },\ddot{a}\right)=\ddot{a}+\mu =\alpha \\ {\Delta }^{-1}\left({s}_{\eta },\ddot{e}\right)=\ddot{e}+\eta =\beta \\ {\Delta }^{-1}\left({s}_{\upsilon },\ddot{u}\right)=\ddot{u}+\upsilon =\gamma \end{array}\right..$$
(3)

Definition 3 [27]

Suppose that \(\tilde{r }=\langle \left({s}_{\mu },\ddot{a}\right),\left({s}_{\eta },\ddot{e}\right),\left({s}_{v},\ddot{u}\right)\rangle\) is a TSLN, then its score function is calculated by

$$Sc\left(\tilde{r }\right)=\Delta \sqrt{\frac{{\tau }^{2}+{\Delta }^{-1}\left({s}_{{\mu }^{2}},\ddot{a}\right)-{\Delta }^{-1}\left({s}_{{\eta }^{2}},\ddot{e}\right)-{\Delta }^{-1}\left({s}_{{\upsilon }^{2}},\ddot{u}\right)}{{3}^{2}}},$$
(4)

and its accuracy function is calculated by

$$Ac\left(\tilde{r }\right)=\Delta \sqrt{\frac{{\Delta }^{-1}\left({s}_{{\mu }^{2}},\ddot{a}\right)+{\Delta }^{-1}\left({s}_{{\eta }^{2}},\ddot{e}\right)+{\Delta }^{-1}\left({s}_{{\upsilon }^{2}},\ddot{u}\right)}{{3}^{2}}}.$$
(5)

Definition 4 [27]

Let \({\tilde{r }}_{1}=\langle \left({{s}_{\mu }}_{1},{\ddot{a}}_{1}\right),\left({{s}_{\eta }}_{1},{\ddot{e}}_{1}\right),\left({{s}_{v}}_{1},\ddot{{u}_{1}}\right)\rangle\) and \({\tilde{r }}_{2}=\langle \left({{s}_{\mu }}_{2},{\ddot{a}}_{2}\right),\left({{s}_{\eta }}_{2},{\ddot{e}}_{2}\right),\left({{s}_{v}}_{2},\ddot{{u}_{2}}\right)\rangle\) be two TSLNs. Suppose that λ is a real number and \(\lambda >0\), then the operational laws of TSLNs are given below:

  1. (1)

    \({\tilde{r }}_{1}\oplus {\tilde{r }}_{2}=\Bigg\langle \begin{array}{c}\sqrt{\Delta \left({\tau }^{2}\left(\frac{{\Delta }^{-1}\left({S}_{{\mu }_{1}^{2}},{\ddot{a}}_{1}\right)}{{\tau }^{2}}+\frac{{\Delta }^{-1}\left({S}_{{\mu }_{2}^{2}},{\ddot{a}}_{2}\right)}{{\tau }^{2}}-\frac{{\Delta }^{-1}\left({S}_{{\mu }_{1}^{2}},{\ddot{a}}_{1}\right)}{{\tau }^{2}}\frac{{\Delta }^{-1}\left({S}_{{\mu }_{2}^{2}},{\ddot{a}}_{2}\right)}{{\tau }^{2}}\right)\right),}\\ \Delta \left(\tau \left(\frac{{\Delta }^{-1}\left({S}_{{\eta }_{1}},{\ddot{e}}_{1}\right)}{\tau }\frac{{\Delta }^{-1}\left({S}_{{\eta }_{2}},{\ddot{e}}_{2}\right)}{\tau }\right)\right),\Delta \left(\tau \left(\frac{{\Delta }^{-1}\left({S}_{{v}_{1}},{\ddot{u}}_{1}\right)}{\tau }\frac{{\Delta }^{-1}\left({S}_{{v}_{2}},{\ddot{u}}_{2}\right)}{\tau }\right)\right)\end{array}\Bigg\rangle ;\)  

  2. (2)

    \({\tilde{r }}_{1}\otimes {\tilde{r }}_{2}=\Bigg\langle \begin{array}{c}\Delta \left(\tau \left(\frac{{\Delta }^{-1}\left({S}_{{\mu }_{1}},{\ddot{a}}_{1}\right)}{\tau }\frac{{\Delta }^{-1}\left({S}_{{\mu }_{2}},{\ddot{a}}_{2}\right)}{\tau }\right)\right),\\ \sqrt{\Delta \left({\tau }^{2}\left(\frac{{\Delta }^{-1}\left({S}_{{\eta }_{1}^{2}},{\ddot{e}}_{1}\right)}{{\tau }^{2}}+\frac{{\Delta }^{-1}\left({S}_{{\eta }_{2}^{2}},{\ddot{e}}_{2}\right)}{{\tau }^{2}}-\frac{{\Delta }^{-1}\left({S}_{{\eta }_{1}^{2}},{\ddot{e}}_{1}\right)}{{\tau }^{2}}\frac{{\Delta }^{-1}\left({S}_{{\eta }_{2}^{2}},{\ddot{e}}_{2}\right)}{{\tau }^{2}}\right)\right),}\\ \sqrt{\Delta \left({\tau }^{2}\left(\frac{{\Delta }^{-1}\left({S}_{{\upsilon }_{1}^{2}},{\ddot{u}}_{1}\right)}{{\tau }^{2}}+\frac{{\Delta }^{-1}\left({S}_{{\upsilon }_{2}^{2}},{\ddot{u}}_{2}\right)}{{\tau }^{2}}-\frac{{\Delta }^{-1}\left({S}_{{\upsilon }_{1}^{2}},{\ddot{u}}_{1}\right)}{{\tau }^{2}}\frac{{\Delta }^{-1}\left({S}_{{\upsilon }_{2}^{2}},{\ddot{u}}_{2}\right)}{{\tau }^{2}}\right)\right)}\end{array}\Bigg\rangle ;\)  

  3. (3)

    \(\begin{array}{l}\lambda {\tilde{r }}_{1}=\Bigg\langle \sqrt{\Delta \left({\tau }^{2}\left(1-{\left(\frac{{\Delta }^{-1}\left({S}_{{\mu }_{1}^{2}},{\ddot{a}}_{1}\right)}{{\tau }^{2}}\right)}^{\lambda }\right)\right)},\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({{s}_{\eta }}_{1},{\ddot{e}}_{1}\right)}{\tau }\right)}^{\lambda }\right),\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({{s}_{v}}_{1},{\ddot{u}}_{1}\right)}{\tau }\right)}^{\lambda }\right)\Bigg\rangle ;\end{array}\)  

  4. (4)

    \({\tilde{r }}_{1}^{\lambda }=\Bigg\langle \begin{array}{c}\Delta \left(\tau {\left(\frac{{\Delta }^{-1}\left({S}_{{\mu }_{1}},{\ddot{a}}_{1}\right)}{\tau }\right)}^{\lambda }\right),\sqrt{\Delta \left({\tau }^{2}\left(1-{\left(1-\frac{{\Delta }^{-1}\left({S}_{{\eta }_{1}^{2}},{\ddot{e}}_{1}\right)}{{\tau }^{2}}\right)}^{\lambda }\right)\right)}\\ ,\sqrt{\Delta \left({\tau }^{2}\left(1-{\left(1-\frac{{\Delta }^{-1}\left({S}_{{v}_{1}^{2}},{\ddot{u}}_{1}\right)}{{\tau }^{2}}\right)}^{\lambda }\right)\right)}\end{array}\Bigg\rangle ;\)  

  5. (5)

    \({\tilde{r }}_{1}^{C}=\langle \left({S}_{{v}_{1}},{\ddot{u}}_{1}\right),\left({S}_{{\eta }_{1}},{\ddot{e}}_{1}\right),\left({S}_{{\mu }_{1}},{\ddot{a}}_{1}\right)\rangle .\)

Definition 5 [27]

Let \({\tilde{r }}_{1}=\langle \left({s}_{{\mu }_{1}},{\ddot{a}}_{1}\right),\left({s}_{{\eta }_{1}},{\ddot{e}}_{1}\right),\left({s}_{{v}_{1}},{\ddot{u}}_{1}\right)\rangle\) and \({\tilde{r }}_{2}=\langle \left({s}_{{\mu }_{2}},{\ddot{a}}_{2}\right),\left({s}_{{\eta }_{2}},{\ddot{e}}_{2}\right),\left({s}_{{v}_{2}},{\ddot{u}}_{2}\right)\rangle\) be any two TSLNs, then

  1. (1)

    If \(Sc\left({\tilde{r }}_{1}\right)>Sc\left({\tilde{r }}_{2}\right)\), then \({\tilde{r }}_{1}\) is bigger than \({\tilde{r }}_{2}\), denoted as \({\tilde{r }}_{1}>{\tilde{r }}_{2}\);

  2. (2)

    If \(Sc\left({\tilde{r }}_{1}\right)=Sc\left({\tilde{r }}_{2}\right)\), then

    1. (a)

      If \(Ac\left({\tilde{r }}_{1}\right)<Ac\left({\tilde{r }}_{2}\right)\), then \({\tilde{r }}_{1}\) is bigger than \({\tilde{r }}_{2}\), denoted as \({\tilde{r }}_{1}<{\tilde{r }}_{2}\);

    2. (b)

      If \(Ac\left({\tilde{r }}_{1}\right)=Ac\left({\tilde{r }}_{2}\right)\), then \({\tilde{r }}_{1}\) is equivalent to \({\tilde{r }}_{2}\), denoted as \({\tilde{r }}_{1}={\tilde{r }}_{2}\).

Definition 6 [27]

Suppose that \(\tilde{R }=\left\{{\tilde{r }}_{i}\right\}\left(i=\mathrm{1,2},\cdots ,n\right)\) is a collection of 2TSLNs and \({\tilde{r }}_{i}=\langle \left({s}_{{\mu }_{i}},{\ddot{a}}_{i}\right),\left({s}_{{\eta }_{i}},{\ddot{e}}_{i}\right),\left({s}_{{v}_{i}},{\ddot{u}}_{i}\right)\rangle\). The weight of \({\tilde{r }}_{i}\) is represented as \({w}_{i}\), which satisfies the condition that \({w}_{i}\in \left[\mathrm{0,1}\right]\left(i=\mathrm{1,2},\cdots ,n\right)\) and \({\sum }_{i=1}^{n}{w}_{i}\). Then the 2-tuple spherical linguistic weighted average (TSLWA) operator is defined as:

$$\begin{array}{l}{TSLWA}_{w}\left({\tilde{r }}_{1},{\tilde{r }}_{2},\dots ,{\tilde{r }}_{n}\right)=\bigoplus\limits_{i=1}^{n}\left({w}_{i}{\tilde{r }}_{i}\right)=\\\Bigg\langle \begin{array}{c}\sqrt{\Delta \left({\tau }^{2}\left(1-\prod\limits_{i=1}^{n}{\left(1-\frac{{\Delta }^{-1}\left({s}_{{\mu }_{i}^{2}},{\ddot{a}}_{i}\right)}{{\tau }^{2}}\right)}^{{w}_{i}}\right)\right)},\\ \Delta \left(\tau \prod\limits_{i=1}^{n}{\left(\frac{{\Delta }^{-1}\left({s}_{{\eta }_{i}},{\ddot{e}}_{i}\right)}{\tau }\right)}^{{w}_{i}},\Delta \left(\tau \prod\limits_{i=1}^{n}{\left(\frac{{\Delta }^{-1}\left({s}_{{v}_{i}},{\ddot{u}}_{i}\right)}{\tau }\right)}^{{w}_{i}}\right)\right)\end{array}\Bigg\rangle .\end{array}$$
(6)

Definition 7

Let \({\tilde{r }}_{1}\) and \({\tilde{r }}_{2}\) be two TSLNs, then the Euclidean distance between \({\tilde{r }}_{1}\) and \({\tilde{r }}_{2}\) can be calculated by

$$d\left({\tilde{r }}_{1},{\tilde{r }}_{2}\right)=\sqrt{{\left({\Delta }^{-1}\left({S}_{{\mu }_{1}},{\ddot{a}}_{1}\right)-{\Delta }^{-1}\left({S}_{{\mu }_{2}},{\ddot{a}}_{2}\right)\right)}^{2}+{\left({\Delta }^{-1}\left({S}_{{\eta }_{1}},{\ddot{e}}_{1}\right)-{\Delta }^{-1}\left({S}_{{\eta }_{2}},{\ddot{e}}_{2}\right)\right)}^{2}+{\left({\Delta }^{-1}\left({S}_{{\upsilon }_{1}},{\ddot{u}}_{1}\right)-{\Delta }^{-1}\left({S}_{{v}_{2}},{\ddot{u}}_{2}\right)\right)}^{2}}.$$
(7)

3.2 Regret theory

The regret theory [34] is a behavioural decision theory that takes people’s bounded rationality into account. When the selected alternative is worse than others, decision makers will feel regretful for the choice; on the contrary, the feeling of rejoice will naturally appears.

Definition 8 [34]

If a is the consequence of selecting alternative A, the utility value derived from A can be computed by

$$u\left(a\right)={a}^{\theta },$$
(8)

where \(\theta \left(0<\theta <1\right)\) represents decision makers’ risk aversion. When a decision maker has a higher degree of risk aversion, the value of θ should be set smaller.

Definition 9 [34]

Let \({a}_{1}\) and \({a}_{2}\) be the consequences of selecting alternatives A1 and A2, and the corresponding utility values are \(u\left({a}_{1}\right)\) and \(u\left({a}_{2}\right)\), respectively. Then the regret-rejoice value of selecting \({A}_{1}\) rather than \({A}_{2}\) is defined as:

$$r\left(a_1,a_2\right)=1-e^{-\gamma\left(u\left(a_1\right)-u\left(a_2\right)\right),}$$
(9)

where \(\gamma >0\) represents decision makers’ regret aversion. When \(u\left({a}_{1}\right)-u\left({a}_{2}\right)\le 0\), \(r\left({a}_{1},{a}_{2}\right)\) is a representative of regret value; otherwise, it denotes rejoice value.

It is necessary to note that, the value of \(\theta\) is suggested to be set as 0.88 and \(\gamma =0.3\) based on the verification of experiments [56].

Definition 10 [57]

Let \({a}_{i}\left(i=\mathrm{1,2},\cdots ,m\right)\) be the consequences of selecting \({A}_{i}\left(i=\mathrm{1,2},\cdots ,m\right)\) the overall utility value of choosing \({A}_{i}\) can be calculated by

$$v\left({a}_{i}\right)=u\left({a}_{i}\right)+r\left({a}_{i},{a}^{*}\right).$$
(10)

Here, \({a}^{*}=\underset{i=\mathrm{1,2},\cdots ,m}{\mathrm{max}}{a}_{i}\) and \(r\left({a}_{i},{a}^{*}\right)\le 0\).

4 The proposed EDM method

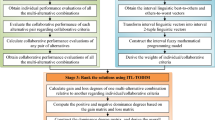
In this section, an extended regret theory-EDAS method based on TSLTSs is proposed to deal with EDM problems. The procedural steps of the proposed EDM method in the form of a flowchart are shown in Fig. 1.

Fig. 1
figure 1

Flowchart of the proposed EDM methodology

Full size image

For an EDM problem, suppose that \(A=\left\{{A}_{1},{A}_{2}\cdots ,{A}_{m}\right\}\) represents a set of emergency response alternatives, \(C=\left\{{C}_{1},{C}_{2}\cdots ,{C}_{n}\right\}\) is a set of criteria and \(DM=\left\{{DM}_{1},{DM}_{2}\cdots ,{DM}_{l}\right\}\) is a set of decision makers. Let \(\lambda =\left\{{\lambda }_{1},{\lambda }_{2},\cdots ,{\lambda }_{l}\right\}\) be the weights of decision makers, meeting the condition that \(0\le {\lambda }_{k}\le 1\left(k=\mathrm{1,2},\cdots ,l\right)\) and \({\sum }_{k=1}^{l}{\lambda }_{k}=1\). Each decision maker is requested to provide his/her evaluations over \({A}_{i}\) concerning \({C}_{j}\) in the form of TSLNs to determine the optimal emergency alternative. After that, l 2-tuple spherical linguistic evaluation matrices can be obtained, \({\tilde{E }}_{k}={\left[{\tilde{e }}_{ij}^{k}\right]}_{m\times n}\left(k=\mathrm{1,2},\cdots ,l\right)\), where the basic element \({\tilde{e }}_{ij}^{k}=\langle \left({s}_{{\mu }_{ij}}^{k},{\ddot{a}}_{ij}^{k}\right),\left({s}_{{\eta }_{ij}}^{k},{\ddot{e}}_{ij}^{k}\right),\left({s}_{{v}_{ij}}^{k},{\ddot{u}}_{ij}^{k}\right)\rangle\) are the 2-tuple spherical linguistic evaluation relating to Ai with respect to Cj provided by Dk. Next, the detailed steps of the extended regret theory-EDAS method are summarized.

Step 1: Construct the group 2-tuple spherical linguistic evaluation matrix.

By using the TSLWA operator, the individual 2-tuple spherical linguistic decision matrices \({\tilde{E }}_{k}\left(k=\mathrm{1,2},\cdots ,l\right)\) are aggregated into the group 2-tuple spherical linguistic decision matrix \(\tilde{E }={\left[{\tilde{e }}_{ij}\right]}_{m\times n}\) by

$$\begin{array}{l}{\tilde{e }}_{ij}={TSLWA}_{\lambda }\left({\tilde{e }}_{ij}^{1},{\tilde{e }}_{ij}^{2},\cdots ,{\tilde{e }}_{ij}^{l}\right)=\bigoplus\limits_{k=1}^{l}\left({\lambda }_{k}{\tilde{e }}_{ij}^{k}\right)\\\quad\:\;=\left\{\begin{array}{l}\sqrt{\Delta \left({\tau }^{2}\left(1-\prod\limits_{i=1}^{n}{\left(1-\frac{{\Delta }^{-1}\left({s}_{{\mu }_{ij}^{2}}^{k},{\ddot{a}}_{ij}^{k}\right)}{{\tau }^{2}}\right)}^{{\lambda }_{k}}\right)\right)},\\ \Delta \left(\tau \prod\limits_{i=1}^{n}{\left(\frac{{\Delta }^{-1}\left({s}_{{\eta }_{ij}}^{k},{\ddot{e}}_{ij}^{k}\right)}{\tau }\right)}^{{\lambda }_{k}}\right),\Delta \left(\tau \prod\limits_{i=1}^{n}{\left(\frac{{\Delta }^{-1}\left({s}_{{v}_{ij}}^{k},{\ddot{u}}_{ij}^{k}\right)}{\tau }\right)}^{{w}_{i}}\right)\end{array}\right\},\\\qquad\:\:\;i=\mathrm{1,2},\cdots ,m;j=\mathrm{1,2},\cdots ,n;\ k=\mathrm{1,2},\cdots ,l.\end{array}$$
(11)

Step 2: Calculate the normalized 2-tuple spherical linguistic evaluation matrix.

Based on the matrix \(\tilde{E }\), the normalized 2-tuple spherical linguistic evaluation matrix \(\overline{E }={\left[{\overline{e} }_{ij}\right]}_{m\times n}\) is obtained by

$${\overline{e} }_{ij}=\left\{\begin{array}{c}{\tilde{e }}_{ij}=\langle \left({s}_{{\mu }_{ij}},{\ddot{a}}_{ij}\right),\left({s}_{{\eta }_{ij}},{\ddot{e}}_{ij}\right),\left({s}_{{\nu }_{ij}},{\ddot{u}}_{ij}\right)\rangle, \\ {\tilde{e }}_{ij}^{C}=\langle \left({s}_{{\nu }_{ij}},{\ddot{u}}_{ij}\right),\left({s}_{{\eta }_{ij}},{\ddot{e}}_{ij}\right),\left({s}_{{\mu }_{ij}},{\ddot{a}}_{ij}\right)\rangle, \end{array}\begin{array}{c}for\ benefit\ criteria,\\ for\ cost\ criteria.\end{array}\right.$$
(12)

Step 3: Construct the correlation coefficient matrix between criteria.

The correlation coefficient matrix between criteria is denoted as \(R={\left[{r}_{{jj}^{^{\prime}}}\right]}_{m\times n}\), in which \({r}_{{jj}^{^{\prime}}}\) represents the correlation coefficient between the jth and the \({j}^{^{\prime}}\mathrm{th}\) criteria, and is calculated by

$$\begin{array}{cc}{r}_{{jj}^{^{\prime}}}=\frac{\sum\limits_{i=1}^{m}\left(Sc\left({\overline{e} }_{ij}\right)-\sum\limits_{i=1}^{m}\frac{Sc\left({\overline{e} }_{ij}\right)}{m}\right)\left(Sc\left({\overline{e} }_{{ij}^{^{\prime}}}\right)-\sum\limits_{i=1}^{m}\frac{Sc\left({\overline{e} }_{{ij}^{^{\prime}}}\right)}{m}\right)}{\sqrt{{\sum\limits_{i=1}^{m}\left(Sc\left({\overline{e} }_{ij}\right)-\sum\limits_{i=1}^{m}\frac{Sc\left({\overline{e} }_{ij}\right)}{m}\right)}^{2}}\sqrt{{\sum\limits_{i=1}^{m}\left(Sc\left({\overline{e} }_{{ij}^{^{\prime}}}\right)-\sum\limits_{i=1}^{m}\frac{Sc\left({\overline{e} }_{{ij}^{^{\prime}}}\right)}{m}\right)}^{2}}}& j,{j}^{^{\prime}}=\mathrm{1,2},\cdots ,n.\end{array}$$
(13)

Step 4: Calculate the criteria standard values.

The standard value of each criterion \({\sigma }_{j}\left(j=\mathrm{1,2},\cdots ,n\right)\) can be computed by

$$\begin{array}{cc}{\sigma }_{j}=\sqrt{\frac{{\sum }_{i=1}^{m}{\left(Sc\left({\overline{e} }_{ij}\right)-{\sum }_{i=1}^{m}Sc\left({\overline{e} }_{ij}\right)/m\right)}^{2}}{m}},& j=\mathrm{1,2},\cdots ,n.\end{array}$$
(14)

Step 5: Determine the amount of information contained in each criterion.

The amount of information of each criterion \({\sigma }_{j}\) is determined by the following formula:

$$\begin{array}{cc}{\sigma }_{j}={\sigma }_{j}{\sum }_{{j}^{^{\prime}}=1}^{n}\left(1-{r}_{{jj}^{^{\prime}}}\right),& j=\mathrm{1,2},\cdots ,n.\end{array}$$
(15)

Step 6: Calculate the relative weights of criteria.

Based on different amount of information between criteria, the weights of criteria are calculated by

$$\begin{array}{cc}{w}_{j}=\frac{{o}_{j}}{{\sum }_{j=1}^{n}{o}_{j}},& j=\mathrm{1,2},\cdots ,n.\end{array}$$
(16)

Step 7: Derive the utility matrix of emergency alternatives.

In this step, the utility matrix of emergency alternatives \(U={\left[{u}_{ij}\right]}_{m\times n}\) can be calculated by

$${u}_{ij}={\left({s}_{ij}\right)}^{\theta },$$
(17)

where \({u}_{ij}\) is the utility value of each emergency alternative \({A}_{i}\) on the criterion \({C}_{j}\), and \(\theta\) refers to the risk aversion coefficient of decision makers.

Step 8: Calculate the vector of ideal points.

The vector of ideal points is formed as \({\overline{e} }^{+}=\left({\overline{{e }_{1}}}^{+},{\overline{{e }_{2}}}^{+},\cdots ,{\overline{{e }_{n}}}^{+}\right)\), in which the ideal point of the criterion \({C}_{j}\) is calculated by

$$\begin{array}{cc}{\overline{e} }_{j}^{+}=\underset{1\le i\le m}{\mathrm{max}}\left({\overline{e} }_{ij}\right),& j=\mathrm{1,2},\cdots ,n.\end{array}$$
(18)

Step 9: Obtain the regret matrix of emergency alternatives.

Through comparing with the ideal points, the regret matrix of emergency alternatives \(T={\left[{t}_{ij}\right]}_{m\times n}\) is obtained by

$${t}_{ij}=1-{e}^{-\gamma \left({u}_{ij}-{u}_{j}^{+}\right)}$$
(19)

where \({u}_{j}^{+}\) is the utility value of the ideal point \({\overline{e} }_{j}^{+}\) and \(\gamma\) represents decision makers’ risk aversion coefficient.

Step 10: Calculate the overall utility matrix of emergency alternatives.

Based on Eq. (10), the overall utility matrix of emergency alternatives \(V={\left[{v}_{ij}\right]}_{m\times n}\) is constructed, in which

$${v}_{ij}={u}_{ij}+{t}_{ij}.$$
(20)

Step 11: Obtain the vector of average solution.

The average solution vector \({A}^{*}\) is formed as \(A^\ast=(A_1^\ast,A_2^\ast,\cdots A_n^\ast)\), in which

$${A}_{j}^{*}={\sum }_{i=1}^{m}{v}_{ij}/m.$$
(21)

Step 12: Construct the positive and the negative distance matrices from the average solution.

The positive distance matrix is denoted as \({V}^{+}={\left[{v}_{ij}^{+}\right]}_{m\times n}\) and the negative distance matrix is denoted as \({V}^{-}={\left[{v}_{ij}^{-}\right]}_{m\times n}\). Then, \({v}_{ij}^{+}\) and \({v}_{ij}^{-}\), which represent the positive and the negative distance of each alternative to the corresponding average solution are, respectively, calculated by

$${v}_{ij}^{+}=\mathrm{max}\left(0,\left({v}_{ij}-{A}_{j}^{*}\right)\right)/{A}_{j}^{*},$$
(22)
$${v}_{ij}^{-}=\mathrm{max}\left(0,\left({A}_{j}^{*}-{v}_{ij}\right)\right)/{A}_{j}^{*}.$$
(23)

Step 13: Calculate the appraisal scores of emergency alternatives.

The appraisal score of each emergency alternative \({AS}_{i}\left(i=\mathrm{1,2},\cdots ,m\right)\) is determined by

$${AS}_{i}=\frac{1}{2}\left(\frac{{\sum }_{j=1}^{n}{w}_{i}{v}_{ij}^{+}}{\underset{i=\mathrm{1,2},\cdots ,m}{\mathrm{max}}\left({\sum }_{j=1}^{n}{w}_{i}{v}_{ij}^{+}\right)}+\left(1-\frac{{\sum }_{j=1}^{n}{w}_{i}{v}_{ij}^{-}}{\underset{i=\mathrm{1,2},\cdots ,m}{\mathrm{max}}\left({\sum }_{j=1}^{n}{w}_{i}{v}_{ij}^{-}\right)}\right)\right).$$
(24)

As a result, the ranking of all emergency alternatives is derived based on the descending order of their appraisal scores \({AS}_{i}\left(i=\mathrm{1,2},\cdots ,m\right)\). Thus, the emergency response solution with the maximum \({AS}_{i}\) value can be identified for EDM.

5 Illustrative example

In this section, a practical public health emergency problem is taken as an example to illustrate the feasibility and practicability of the proposed EDM method.

5.1 Implementation and results

In December 2019, several unexplained cases of pneumonia were found in Wuhan, Hubei province, China. A COVID-19 was considered to be the cause of pneumonia, which was named as coronavirus disease 2019 later. Due to its long incubation period that lasts from 1 to 14 days, infected people with no symptoms can transmit the virus to others rapidly through droplets and close contact. By July 22, 2020, more 92 thousand people had been diagnosed in China, over 4 thousand patients unfortunately died. Among them, approximately 50 thousand people were in Wuhan, the centre of the epidemic, accounting for 81.31% of the whole patients and mortality was about 5.02%. This acute infectious disease has caused huge economic losses to industries such as catering, entertainment, retail and tourism. It is generally accepted that controlling the sources of the virus and cutting off the ways of virus transmission are fundamental solutions to prevent and control infectious diseases. Therefore, it is quite important to take timely quarantine measures and control population movement.

Based on the analysis above, for the citizens of Wuhan, four emergency response alternatives are put forward:

A1: Quarantine the infected person and observe them closely;

A2: Adopt A1 and quarantine suspected infection people and those who were recently in close contact with infected people. Besides, ordinary people are suggested to take self-protective work, such as wearing masks;

A3: Adopt A2 and strictly forbidden people to participate in public gathering activities. When going outside, people must implement protective measures, including wearing masks, taking temperature if entering public places and so on;

A4: Adopt A3 and suspend all classes and work, let all people must stay at home and confine their travel freedom.

Besides, five criteria are considered to evaluate the four emergency response alternatives: life satisfaction (C1), morality (C2), the rate of epidemic transmission (C3), economic losses (C4), and the consumption of medical supplies (C5). Among them, C1 is a benefit criterion, while the remaining four are cost criteria.

Five expert panels are invited for the given EDM and they are denoted as \(DM=\left\{{DM}_{1},{DM}_{2},{DM}_{3},{DM}_{4},{DM}_{5}\right\}\), where each expert panel is required to provide unified evaluation results. The expert panel \({DM}_{1}\) includes doctors in upper first-class hospitals, who have accumulated a wealth of clinical experience; experts in \({DM}_{2}\) refer to professionals in Centres for disease control and prevention; \({DM}_{3}\) is composed of specialists from local emergency management agency; \({DM}_{4}\) consists of government workers serving the community, and \({DM}_{5}\) contains experienced experts in the research area of EDM. Note that the importance weights of the five expert panels are assumed to be equal, i.e., \(\lambda =\left(\mathrm{0.2,0.2,0.2,0.2,0.2}\right)\). The following linguistic term set is used by the expert panels for describing emergency response alternatives:

$$S=\left\{\begin{array}{l}{s}_{1}=Very\ bad,{s}_{2}=Quite\ bad,{s}_{3}=Slightly\ bad,\\{s}_{4}=Fair,{s}_{5}=Slightly\ good,\\{s}_{6}=Quite\ good,{s}_{7}=Very\ good\end{array}\right\}.$$

At first, decision makers in each panel are requested to provide their evaluations of emergency response alternatives under the environment of TSLNs. As a result, the 2-tuple spherical linguistic matrices \({\tilde{E }}_{k}={\left[{e}_{ij}^{k}\right]}_{4\times 5}\left(k=\mathrm{1,2},\cdots ,5\right)\) obtained are presented in Table 1.

Table 1 The 2-tuple spherical linguistic matrices by the five expert panels
Full size table

In what follows, the proposed EDM approach is applied for determining the optimal response action to the given emergency event, and the detailed implementation results are presented.

Step 1: By using Eq. (11), the group 2-tuple spherical linguistic decision matrix \(\tilde{E }={\left[{\tilde{e }}_{ij}\right]}_{4\times 5}\) is constructed as shown in Table 2.

Table 2 The group 2-tuple spherical linguistic matrix
Full size table

Step 2: With Eq. (12), the normalized 2-tuple spherical evaluation matrix \(\overline{E }={\left[{\overline{e} }_{ij}\right]}_{4\times 5}\) is obtained as displayed in Table 3.

Table 3 The normalized 2-tuple spherical linguistic matrix
Full size table

Step 3: By Eq. (13), the correlation coefficient matrix between criteria \(R={\left[{r}_{{jj}^{\prime}}\right]}_{5\times 5}\) is determined as shown in Table 4.

Table 4 The correlation coefficient matrix
Full size table

Step 4: Through Eq. (14), the standard deviation values of criteria are calculated as: \({\sigma }_{1}=0.189\), \({\sigma }_{2}=0.346\), \({\sigma }_{3}=0.251\), \({\sigma }_{4}=0.290\), \({\sigma }_{5}=0.136\).

Step 5: With Eq. (15), the contained information concerning each criterion is obtained as: \({o}_{1}=0.710\), \({o}_{2}=1.852\), \({o}_{3}=1.269\), \({o}_{4}=1.008\), \({o}_{5}=0.473\).

Step 6: After utilizing Eq. (16), the criteria weights are computed as: \({w}_{1}=0.134\), \({w}_{2}=0.349\), \({w}_{3}=0.239\), \({w}_{4}=0.190\), \({w}_{5}=0.089\).

Step 7: The utility matrix of emergency alternatives \(U={\left[{u}_{ij}\right]}_{4\times 5}\) is determined by Eq. (17), and displayed in Table 5; \(\theta\) is set as 0.88.

Table 5 The utility matrix of emergency alternatives
Full size table

Step 8: By Eq. (18), the vector of ideal points is formed as \({\overline{e} }^{+}=\left(\langle \left({s}_{5},0.497\right),\left({s}_{3},0.482\right),\left({s}_{2},0.221\right)\rangle \right.\), \(\langle \left({s}_{2},0\right),\left({s}_{3},-0.298\right),\left({s}_{2},0\right)\rangle\), \(\langle \left({s}_{2},-0.484\right),\left({s}_{3},0\right),\left({s}_{3},0.242\right)\rangle\), \(\langle \left({s}_{3},-0.488\right),\left({s}_{2},0\right),\left({s}_{3},-0.163\right)\rangle\), \(\left.\langle \left({s}_{3},-0.449\right),\left({s}_{3},0.178\right),\left({s}_{3},-0.341\right)\rangle \right)\).

Step 9: Using Eq. (19), the obtained regret matrix of emergency alternatives \(T={\left[{t}_{ij}\right]}_{4\times 5}\) can be seen in Table 6; \(\gamma\) is set as 0.30.

Table 6 The regret matrix of emergency alternatives
Full size table

Step 10: The overall utility matrix of emergency alternatives \(V={\left[{v}_{ij}\right]}_{4\times 5}\) is determined via Eq. (20) and depicted in Table 7.

Table 7 The overall utility matrix of emergency alternatives
Full size table
Table 8 The positive distance average matrix
Full size table

Step 11: By Eq. (21), the average solution vector of criteria is obtained as \({A}^{*}=\left(\mathrm{2.109,1.528,1.511,1.773,1.858}\right)\).

Step 12: Based on Eqs. (22) and (23), the positive distance matrix \({V}^{+}={\left[{v}_{ij}^{+}\right]}_{4\times 5}\) and the negative distance matrix \({V}^{-}={\left[{v}_{ij}^{-}\right]}_{4\times 5}\) are determined, with the results listed in Tables 8 and 9.

Table 9 The negative distance average matrix
Full size table
Table 10 Criteria weights regarding the considered cases
Full size table

Step 13: By utilizing Eq. (24), the appraisal scores of the four considered emergency alternatives are derived as: \({AS}_{1}=0.205\), \({AS}_{2}=0.472\), \({AS}_{3}=0.810\), \({AS}_{4}=0.506\). Hence, the ranking of emergency alternatives is derived as: A3 > A4 > A2 > A1, and the emergency alternative A3 should be selected to handle the public health emergency problem in this case study.

5.2 Sensitivity analysis

In this section, a sensitivity analysis is carried out to explore the influence of criteria weights on the ranking of emergency alternatives. In the sensitivity analysis, six cases with different set of criteria weights are considered and shown in Table 10. Note that Case 0 indicates the original criteria weights calculated by the CRITIC method while other cases denote different possible situations. The ranking results of four emergency alternatives concerning the considered cases are depicted in Fig. 2.

Fig. 2
figure 2

Ranking results of emergency alternatives

Full size image

It can be seen from Fig. 2 that A3 always ranks first despite the change of criteria weights in all cases. Thus, the proposed method is relatively robust to criteria weights. However, the ranking orders of other emergency alternatives distinguish greatly with respect to different criteria weights. For example, A1 is the second most important emergency alternative in Case 1 and Case 4, when the weights of C1 or C4 is the highest. In Case 3 and Case 5, A2 is at the second position and A1 is ranked behind A2, which can be ascribed to the higher weights of C3 and C5. Meanwhile, the priority order of A4 is turned into the fourth with the increasing importance of C1, C3, C4 and C5. The significant distinction between the ranking orders reveals that criteria weights play a vital role in evaluating and ranking emergency alternatives. Determining accurate weights of decision criteria is beneficial for finding out the best plan for an EDM problem.

5.3 Comparison analysis

In this section, a comparative analysis with some existing EDM methods is conducted to further demonstrate the effectiveness of our proposed method. Four EDM methods, including the spherical fuzzy GRA (SF-GRA) [54], the interval-valued Pythagorean fuzzy prospect theory (IVPF-PT) [2], the hesitant fuzzy TODIM (HF-TODIM) [1] and the Z-uncertain probabilistic fuzzy TOPSIS (ZUPF-TOPSIS) [58], are applied to rank the emergency alternatives presented in this study. Among them, different fuzzy theories are utilized to depict uncertain EDM information and the ranking orders derived by the listed methods are displayed in Fig. 3.

Fig. 3
figure 3

Ranking results by five different EDM methods

Full size image

As can be seen from Fig. 2, the ranking result of emergency alternatives by implementing the proposed method is completely consistent with those of the IVPF-PT and the ZUPF-TOPSIS methods. In addition, A3 is determined as the optimal solution by the SF-GRA, the IVPF-PT, the ZUPF-TOPSIS and the proposed method. Therefore, the availability and effectiveness of the proposed EDM method is verified.

However, the ranking result of the SF-GRA method is slightly different from that of our proposed method. Meanwhile, significant differences exist in the priorities of emergency alternatives between the HF-TODIM method and our proposed method. According to the HF-TODIM, A2 has the highest priority and A4 has the lowest priority. But based on our proposed method, A3 is determined as the optimal alternative and A4 is the worst one. The main reasons for these discrepancies may include the following aspects: First, the basic elements of hesitant triangular fuzzy sets applied in the HF-TODIM method are exact values. The spherical fuzzy numbers used in the SF-GRA method are converted from a fixed linguistic term set and only one linguistic term can be selected by experts for evaluating emergency alternatives. In such situations, experts’ uncertain and complex assessment information cannot be reflected accurately and information loss can hardly be solved well in the computation process. Second, in the HF-TODIM method, the weight range of criteria given by experts in determining criteria weights is constructed by crisp values. Thus, the information accuracy is highly dependent on experts’ experience and the lacking experience or restricted time will always lead to inaccurate information and unreasonable criteria weights. Third, the SF-GRA method is implemented based on the precondition that decision makers are totally rational when assessing emergency alternatives. This may cause diverse sorting results in practical applications. From the perspective of the actual epidemic control process, the ranking result of our proposed method is more reasonable. For acute infectious diseases, selecting A3 as the first emergency response is more reliable and credible than others. What’s more, the solution A3 (Quarantine the infected person and observe them closely) is in line with the emergency response adopted by the local emergency management agency in the reality.

5.4 Managerial implications

Based on the findings above, the proposed EDM method in this study has some managerial implications in improving the efficiency of EDM and further advancing emergency management level in practical situations. Firstly, the proposed model is implemented under the 2-tuple spherical linguistic context, which allows decision makers to express their uncertain and complex evaluations with linguistic terms easily. In this way, our proposed EDM model serves as a flexible and effective technique to gather comprehensive evaluations on emergency alternatives in practical applications. Secondly, the CRITIC method is applied to calculate the weights of criteria objectively. In this way, the proposed model is able to determine objective criteria weights rationally based on the evaluation information on emergency alternatives directly, which facilitates the decision making process in practice. Thirdly, according to an integration of regret theory and EDAS method, the proposed model incorporates psychological characteristics of decision makers with the rational decision process, which helps to produce more reasonable and credible priority results of emergency alternatives. Therefore, the new EDM model being developed in this paper is practical and provides a systematic and scientific approach for emergency management, by which emergency alternatives can be evaluated accurately and ultimately EDM problems can be tackled effectively with minimal loss.

6 Conclusions

In this study, a new method is proposed based on an integrated regret theory-EDAS method to deal with EDM problems with the 2-tuple spherical linguistic information. In specific, the TSLTSs are used to describe decision makers’ uncertain assessment information on emergency alternatives. The regret theory and EDAS method are integrated for ranking emergency alternatives and determine the optimal response to an emergency event. An extended CRITIC method is introduced to compute criteria weights from the initial decision information directly. Finally, a real EDM example of COVID-19 is provided to demonstrate the effectiveness and practicability of our proposed method. The results showed that A3 (Quarantine the infected person and observe them closely) is the best solution to handle the emergency event considered. In comparison with the existing methods, the regret theory-EDAS method being proposed in this paper has the following advantages: (1) It can more easily to describe the vagueness and uncertainty of decision information by using the TSLTSs; (2) It is able to avoid human intervention and secondary information collection in criteria weight computation with the extended CRITIC method; (3) It can better characterize the psychological behaviours of decision makers and make reasonable decisions under emergency situations by combining regret theory and EDAS method.

However, this study has several limitans which can be addressed in the future research. First, the proposed method can only deal with the linguistic expressions given by decision makers. In many actual situations, different types of decision information may be involved because of heterogeneous features of criteria. Thus, the proposed EDM method can be extended to handle heterogeneous information in the future. Second, the proposed method is restricted to a small group of experts for evaluating emergency alternatives. As a result, the experience limitation of a small expert team may cause biased ranking results of emergency responses. In the future, it is promising to put forward an advanced method for EDM in the large group environment. Third, only one case is given in this paper to demonstrate the proposed EDM approach. This does not have statistical significance. In the future, it would be better to apply the proposed method to deal with other EDM problems to further verify its practicability and efficiency.