1 Introduction

In late December 2019, a group of patients was come up with an unknown Etiology to the hospitals having symptoms of pneumonia. Later on, the first case of novel coronavirus was reported in the city of Wuhan in Hubei province in Central China [1]. After taking a basic understanding of the virus, medical experts have given a name as severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and the name of the disease caused by this virus is coronavirus disease 2019 (COVID-19) [2]. The cases of COVID-19 pandemic are growing rapidly. Till 30th April 2020, we have 3,251,587 confirmed and 229,832 death cases throughout the world due to this hazardous pandemic, COVID-19.

In India, the first laboratory-confirmed case of COVID-19 was reported from Kerala on 30th January 2020 and as of 30th April 2020, a total of 33,931 cases and 943 deaths were reported in India [3]. To tackle this ongoing pandemic and such events in the future where the lives of millions of people are at high risk, we need a strong health care system and technology that will be the means of making a way to a panacea. Whenever such pandemic spread in a country or province it has some patterns and various mathematical models can be proposed to forecast using such technologies and mathematical theories. For example, in [4], the authors proposed a model for Malaria transmission dynamics of the anopheles mosquito and in [5] a Bifurcation analysis for malaria transmission has been developed. As we are also aware of the menacing of HIV/TB and study [6] presented the mathematical analysis of the transmission dynamics of the same. According to [7], Due to being class of β-Coronavirus, it has a spreading capability among hosts (Primary to secondary source) and that is why the magnitude of infected cases growing non-linearly. Non-linearity of any pandemic can be detected in several ways e.g. in [8] a laplacian based decomposition is used to solve the non-linear parameters in a Pine Witt disease. Similarly, in [9], a fractional version of SIRS (Susceptible - Infectious - Recovered - Susceptible) model has been developed to help, to control the syncytial virus in infants. Also, in [10], the author has used Generalized Additive Models (GAMs) to predict dengue outbreaks based on disease surveillance, meteorological and socio-economic data.

Despite several research works and their documentation, there are huge opportunities for the utilization of AI, Machine Learning, and Data Science in this field, due to the novelty of the root cause. For example, in [11]. This article author has a comprehensive discussion regarding AI applications, constraints, and pitfalls during the COVID-19 pandemic. So, there must be some prediction methods that are required to estimate the magnitude of infected cases, and masses of studies on distinct methods of forecasting are represented so far [12]. In [12, 13], authors estimate the possible number of infected cases in India using long short-term memory (LSTM). Same as in [14], the study represented virus progression and forecast using the same algorithm for Canada and compare with the United States (US) and Italy. In [15], Sujatha performed linear regression (LR), Multilayer perceptron (MLP), and Vector autoregression model (VARM) for expectation on the COVID-19 kaggle information to anticipate the epidemiological pattern of the disease and rate of COVID-2019 cases in India. In [16] author proposed machine learning models (XGBoost and Multi-Output Regressor) to predict confirmed cases over the coming 24 days in every province of South Korea with 82.4% accuracy. As we have already discussed, a study in [10], proposed to control the syncytial virus in infants, same as for China, a modified SEIR and AI prediction of the trend of the epidemic of COVID-19 has been proposed in this study [17]. Different research also takes place on the cases of India but using different methods, and autoregression integrated moving average model (ARIMA) and Richard’s model [18]. Moreover predictions, some mathematical models have also estimated the effects of lockdown and social-distancing in India in a practical scenario [19] but all these studies represented so far are based on inadequate data at the initial stage without any measurement of uncertainty. These models are developed with good accuracy but as well as the data become available, those entire algorithms will not be able to survive without a few evaluations due to the dynamic nature of pandemic escalation of the COVID-19.

So, a distribution based learning model will be more promising rather than doing point estimation. Bayesian Learning is a very well-known method of making any prediction based on our prior knowledge [20]. Many studies have been already used the Bayesian approach for prediction for many pandemics and clinical forecasting like in [21] authors have been estimated the probability of demonstrating vaccine efficacy in the declining Ebola epidemic using the Bayesian modeling approach. In this [22] chapter, the author focuses on the various utility of Bayesian Prediction and it is not only useful, but simple, exact, and coherent, and hence beautiful. Also, the study [23] illustrated a Bayesian analysis for emerging infectious diseases. Same as in [24], paper presented a Bayesian scheme for real-time estimation of the probability distribution of the effective reproduction number of the epidemic potential of emerging infectious diseases and show how to use such inferences to formulate significance tests on future epidemiological observations. Besides, a study also proposed a system, able to provide early, quantitative predictions of SARS epidemic events using a Bayesian dynamic model for influenza surveillance demonstrated [25]. So, this was the motivation behind the proposed study, the prediction of infected cases by COVID-19 which is also a SARS family virus can be formulated using Bayesian learning as a study [25] already represented for influenza surveillance. In the proposed study we are formulating Bayesian Learning Regression with a polynomial of n-degree. Furthermore, one issue occurs when working with time-series data (as COVID-19 confirmed cases) is over-fitting particularly when estimating models with large numbers of parameters over relatively short periods and the solution to the over-fitting problem, is to take a Bayesian approach (using Ridge Regularization) which allows us to impose certain priors on depended variables [26]. Another big reason we often prefer to use Bayesian methods is that it allows us to incorporate uncertainty in our parameter estimates which are particularly useful when forecasting [26].

The manuscript is organized as follows. “Method and Model” explains the methodology used to construct the model and various terminology used in the study. “ Significance of Proposed Model in COVID-19 Outbreak” describes the important advantages of such a hybrid model and also discussed our novelty of the work in the COVID-19 outbreak. After that three case studies in “Case Studies” also presented to justify our results and fruition of the model. In the last, we discussed our results, comparison with other developed models, and finding in the section “Results and Discussion” followed by the conclusion in “Conclusion”.

2 Method and model

2.1 Datasets

The datasets collected from Johns Hopkins University are used in the studies [27]. The datasets accessed on 11 May 2020. It provides several fatalities and registered patients by the end of each day. The dataset is available in the time series format with date, month, and year so that the temporal components are not neglected. A wavelet transformation [28] is applied to preserve the time-frequency components and it also mitigates the random noise in the dataset. This dataset consists of six columns (Table 1).

Table 1 Dataset Description
Full size table

The only pre-processing was required to transform the dataset. The observations recorded every day and for each day a new column added. The datasets are divided into two parts training (80%) and testing (20%) datasets.

2.2 Model formulation

One of the very basic approaches to make a prediction is another version of linear regression is Polynomial regression in which the relationship between independent and dependent variables is an n-degree polynomial. Mathematically, it can represent as follows:

$$ f(X)={\beta}_0+{\beta}_1{x}_1^1+{\beta}_2{x}_2^2+\dots +{\beta}_{n\kern0.5em }{x}_n^n+\epsilon $$
(1)

Or,

$$ f(X)={\beta}_0+\sum \limits_{i=1}^n{\beta}_i{x}_i^i+\epsilon $$
(2)

Where βiis the coefficient and ϵ the measurement error which is

$$ \epsilon \sim N\left(0,{\sigma}^2\right) $$
(3)

f(X) is our polynomial model and to develop a good model we need to tuning, βi So that following loss function with L2 Regularization (Ridge Regularization) will be as minimum as possible

$$ \beta =L\left({y}_i,{x}_i\right)=\sum \limits_{i=1}^n{\left({y}_i-f\left({x}_i\right)\right)}^2+\lambda \sum \limits_{i=1}^n{\beta}_i^2 $$
(4)

Where, the first part of the Eq. 4 is the residual sum of squares (RSS), the difference between actual value (yi) and predicted value (f(xi)) of the ith observation. λ is the regularization term, deciding how much regularize the βi.

Now, for the best fitting our aim to minimize the β by tuning coefficients, βi. According to [29], the Maximum Likelihood Estimate of β which reduces the L(yi, xi) is

$$ \hat{\boldsymbol{\beta}}={\left({\boldsymbol{x}}^{\boldsymbol{T}}\boldsymbol{x}\right)}^{-\mathbf{1}}{\boldsymbol{x}}^{\boldsymbol{T}}\boldsymbol{y} $$
(5)

Now, instead of a vector of coefficients, we have a single value \( \hat{\beta} \), in ℝp + 1 [30]. Here Bayesian Regression (BR) comes into the picture. In the BR, instead of predicting value mentioned as above, it used probabilistic distribution to estimate the value of yiand its follow the following syntax

$$ {y}_i\sim N\left({\beta}^TX,{\sigma}^2\right) $$
(6)

So,

$$ \boldsymbol{p}\left(\boldsymbol{y}\ \right|\boldsymbol{X},\boldsymbol{\beta}, {\boldsymbol{\sigma}}^{\mathbf{2}}\Big)\propto \frac{\mathbf{1}}{\sqrt[\boldsymbol{n}/\mathbf{2}]{{\boldsymbol{\sigma}}^{\mathbf{2}}}}{\boldsymbol{e}}^{-\frac{\mathbf{1}}{\mathbf{2}{\boldsymbol{\sigma}}^{\mathbf{2}}}{\left(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta } \right)}^{\boldsymbol{T}}\left(\boldsymbol{y}-\boldsymbol{X}\boldsymbol{\beta } \right)} $$
(7)

From conjugate prior distribution [20],

$$ {\left(y- X\beta \right)}^T\left(y- X\beta \right)={\left(y-X\hat{\beta}\right)}^T\left(y-X\hat{\beta}\right)-{\left(\beta -\hat{\beta}\right)}^T\left({X}^TX\right)\left(\beta -\hat{\beta}\right) $$
(8)

The Eq. 7 is re-written as

$$ p\left(y\ \right|X,\beta, {\sigma}^2\Big)\propto \frac{1}{\sqrt[\frac{n}{2}]{\sigma^2}}\mathit{\exp}\left(-\frac{v{s}^2}{2{\sigma}^2}\right){\left({\sigma}^2\right)}^{-\frac{n-v}{2}}\ \mathit{\exp}\left(-\frac{1}{2{\sigma}^2}{\left(\beta -\hat{\beta}\right)}^T\left({X}^TX\right)\left(\beta -\hat{\beta}\right)\right) $$
(9)

Where, \( v{s}^2={\left(y-X\hat{\beta}\right)}^T\left(y-X\hat{\beta}\right) \) and v = n − k, n is the number of observations, and k is the number of coefficients in vector β. This suggests a form for the prior distribution is

$$ p\left(\beta, {\sigma}^2\right)=p\left({\sigma}^2\right)p\left(\beta\ |\ {\sigma}^2\right) $$
(10)

After the formulation of the prior distribution, now we need to generate posterior distribution, which can be formulated as follow (from Eqs. 7, 9 and 10),

$$ {\displaystyle \begin{array}{c}p\left(\beta, {\sigma}^2\ |\ y,X\right)\propto p\left(y\ \right|X,\beta, {\sigma}^2\Big)\ p\left(\beta\ |\ {\sigma}^2\right)p\left({\sigma}^2\right)\\ {}p\left(\beta, {\sigma}^2\ |\ y,X\right)\propto \frac{1}{\sqrt[\frac{n}{2}]{\sigma^2}}{e}^{-\frac{1}{2{\sigma}^2}{\left(y- X\beta \right)}^T\left(y- X\beta \right)}{\left({\sigma}^2\right)}^{-\frac{n-v}{2}}\ {e}^{\left(-\frac{1}{2{\sigma}^2}{\left(\beta -{\mu}_0\right)}^T{\Lambda}_0\left(\beta -{\mu}_0\right)\right)}{\left({\sigma}^2\right)}^{-\left({a}_0-1\right)}{e}^{\left(\frac{b_0}{\sigma^2}\right)}\end{array}} $$
(11)

Where Λ0 is ridge regression [31] used to overcome the problem of multicollinearity normally occurring when the model has large numbers of parameter and it is equal to

$$ {\Lambda}_0=\mathrm{cI} $$
(12)

In Equation 12, \( \mathrm{c}=\sum \limits_{i=1}^n{\beta}_i \) and I is an identity matrix of n × n. Now, the posterior mean (μn) can be represented in the term of \( \hat{\beta} \) and prior mean μ0 and for the Bayesian learning other can be upgraded as follows

$$ {\displaystyle \begin{array}{c}{\mu}_n={\left({\mathrm{X}}^TX+{\Lambda}_0\right)}^{-1}\left({\mathrm{X}}^TX\hat{\beta}+{\Lambda}_0{\mu}_0\right)\\ {}{\Lambda}_n=\left({\mathrm{X}}^TX+{\Lambda}_0\right)\\ {}{a}_n=\left({a}_0+\frac{n}{2}\right)\\ {}{b}_n=\left({b}_0+\frac{1}{2}\left({y}^Ty+{\mu}_0^T{\Lambda}_0{\mu}_0+{\mu}_n^T{\Lambda}_n{\mu}_n\right)\right)\end{array}} $$
(13)

Now we are ready to estimate the probability of y on given conditions (m) using Bayes Theorem as

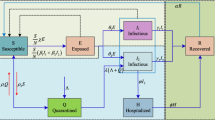
$$ p\left(y\ |\ m\right)=\frac{p\left(\beta, \sigma |m\right)p\left(y|X,\beta, \sigma, m\right)}{p\left(\beta, \sigma |y,X,m\right)} $$
(14)

Where m is the marginal likelihood and prior density, here, m is p(y| X, β, σ) (See Fig. 1).

Fig. 1
figure 1

PBRR Demonstration

Full size image

2.3 Parameter setting

There are many parameters used in the proposed model (Table 2) and a Fit-and-Score method implemented to optimize. It also implements Predict, Predict_proba, Decision_function, Transforms, and Inverse_transform if they are implemented in the estimator used. The parameters of the estimator used to apply these methods are optimized by cross-validated search over parameter settings [32]. The number of parameter settings that are tried is given by n_iter (≈100 in the proposed model). We initialize the parameters with default values and obtain the best-fitted parameters as given in the following Tables (Tables 3 and 4). The optimization of hyperparameters take place by implementing proposed model in Python.3.6 using scikit-learn [32] and used Spyder, a publically available software, a GUI to debug the code. The piece of code available as follows.

  • tol = [1e-4, 1e-3, 1e-2]

  • alpha_1 = [1e-7, 1e-6, 1e-5, 1e-4]

  • alpha_2 = [1e-7, 1e-6, 1e-5, 1e-4]

  • lambda_1 = [1e-7, 1e-6, 1e-5, 1e-4]

  • lambda_2 = [1e-7, 1e-6, 1e-5, 1e-4]

Table 2 Model Parameters
Full size table
Table 3 Initial Parameters Values of the Model
Full size table
Table 4 Best Fitted Parameters for Model
Full size table

bayesian_grid = {‘tol’: tol, ‘alpha_1’: alpha_1, ‘alpha_2’: alpha_2, ‘lambda_1’: lambda_1, ‘lambda_2’: lambda_2}.

bayesian = BayesianRidge(fit_intercept = False, normalize = True).

bayesian_search = RandomizedSearchCV(bayesian, bayesian_grid, scoring = ‘neg_mean_squared_error’, cv = 3, return_train_score = True, n_jobs = −1, n_iter = 40, verbose = 1).

bayesian_search.fit(poly_X_train_confirmed, y_train_confirmed).

bayesian_search.best_params_.

2.4 Advantages and novelty of the work

In the proposed model we have developed concepts of Bayesian inference that differ fundamentally from the traditional approach. This is completely mathematical methods in which we have successfully incorporated with prior knowledge. Instead of making predictions only, it discovers full probability distribution of the problem-domain even on a small dataset which also encounters the features of the confidence interval, risk aversity, etc. [33]. Moreover, posterior distribution makes the model to incorporate more upcoming data without storing previous data. In the current situation of the pandemic, data are not enough to make any prediction without any measurement of uncertainty. In the introduction section, we have seen many studies for COVID-19 progression with good accuracy but as well as data become available, those entire algorithms will not able to survive without a few evaluations. It will happen because of the dynamic nature of pandemic escalation. For example, if we consider our traditional regression methods (Eq. 1)

$$ f(X)={\beta}_0+{\beta}_1{x}_1^1+{\beta}_2{x}_2^2+\dots +{\beta}_{n\kern0.5em }{x}_n^n+\epsilon $$

And we can discover the best possible values for vector β by using Eq. 5,

$$ \hat{\beta}={\left({x}^Tx\right)}^{-1}{x}^Ty $$

In this case, β will be more promising on large datasets rather than small datasets (the available data of COVID-19 is not enough yet) because this method failed to quantify the certainty [34]. Here, we need to make little change with β, determine a distribution instead of a single point estimation and it is all that Bayesian Ridge Regression does in this model. Now, when β is a distribution instead of a mere number our dependent variable \( \left(\hat{y} = f(X)\right) \) also turns into stochastic and becomes a distribution too.

$$ {\beta}_0+{\beta}_1{x}_1^1+{\beta}_2{x}_2^2+\dots +{\beta}_{n\kern0.5em }{x}_n^n+\epsilon \to \hat{y\ } $$

This means that we have confidence interval in our prediction and it became necessary to encounter uncertainty in the case of COVID-19 progression forecasting when datasets are rapidly growing but not sufficient yet. Besides, in Eq. 4 of the model, we also used L2 (Ridge) regularization to makes model less prone to overfitting.

$$ \beta =L\left({y}_i,{x}_i\right)=\sum \limits_{i=1}^n{\left({y}_i-f\left({x}_i\right)\right)}^2+\lambda \sum \limits_{i=1}^n{\beta}_i^2 $$

Ridge regression is better to use when all the weights are equal sizes and the dataset has no outliers.

3 Significance of proposed model in COVID-19 outbreak

Clinical trials and diagnosis are very expensive and their outcomes are crucial to the concerned stakeholders and, hence, there is considerable pressure to optimize them. In medical treatments, clinicians and nurses very often have to make various complex and critical decisions during the diagnosis of the patients. In reality, these decisions are full of uncertainty and unpredictability. However, based on the available information, obtained from various clinical and diagnostic tests and situation of the patient, both clinicians and nurses try to reduce their uncertainty in clinical decisions and attempts to shift to the predictability of the chance of improvement in patient’s condition. In the case of the COVID-19 pandemic, the situation is the same as any other clinical trials. Many pre-planning and controlling need good prediction for the magnitude of infected cases as well as the measurement of uncertainty. One route of optimization is to make better use of all available information, and Bayesian statistics provides this opportunity. Bayesian statistics provide a formal mathematical method for combining prior information with current information at the design stage, during the conduct of the trial, and at the analysis stage. The main reason for using a Bayesian approach to COVID-19 is that it facilitates representing and taking fuller account of the uncertainties related to models and parameter values. In contrast, most decision analyses based on maximum likelihood (or least squares) estimation involve fixing the values of parameters that may, in actuality, have an important bearing on the outcome of the analysis and for which there is considerable uncertainty. One of the major benefits of the Bayesian approach is the ability to incorporate prior information.

Bayesian inference based approach is really important to conduct for COVID-19 pandemic rather than doing point estimations because it makes it possible to obtain probability density functions for model parameters and estimate the uncertainty that is important in the risk assessment analytics. In the Bayesian regression approach, we can take into account expert opinions via information prior to distribution. Other models are developed with good accuracy but as well as data become available, those entire algorithms will not able to survive without a few evaluations due to the dynamic nature of pandemic escalation of the COVID-19 but the proposed model corrects the distributions for model parameters and forecasting results using parameters distributions. This approach has always been used for pandemic and clinical forecasting due to uncertainty measurement for example in [21] Bayesian modeling approach has used to calculate vaccine efficacy in the declining Ebola epidemic and [23, 24] demonstrated a Bayesian scheme for emerging infectious diseases and show how to use such inferences to formulate significance tests on future epidemiological observations. In short, Bayesian methods have the following advantages [35] over other time-series machine learning approaches:

  • It provides an organized way of combining prior information with data, within a solid decision theoretical framework.

  • It’s an inference based learning approach based on previously available data without reliance on asymptotic approximation and such learning gives the consistency of the results with a small sample and large sample equally.

  • It is based on the likelihood principle which gives identical inferences with distinct sampling designs.

  • Interpretability of distribution of various parameters used in the model.

4 Case studies

The method of the present study is unique because the model uses prior and posterior distribution to estimate the confirmed cases. The model should not only judge by the accuracy but also on the reliability of the prediction it makes using prior and posterior knowledge fetched from the data. To test the results and get the accuracy of the model we have proposed a case study of three countries- the U.S, Spain, and Italy. We implemented the proposed model with hybridization of polynomial fitting of degree 4, 5, 6, and 7 because we have observed the best estimation are happen within this range of degrees.

4.1 Italy cases

The confirmed cases in Italy were the lowest since 13th March but the deaths remain stubbornly high, have hovered between 600 and 800 for the last few weeks (See Fig. 2).

Fig. 2
figure 2

Daily Death and New Cases in Italy

Full size image

Using PBRR, we fitted polynomials and discovered that degree-6 is the best fit for the dataset of Italy. In Fig. 3 the solid blue line demonstrating the actual confirmed cases and dashed green line represented observation calculated by the model. In Fig. 3 (a), the degree-4 PBRR is suffering from underfitting and poorly estimate the cases for the unseen days. Also, in Fig. 3 (b), the model showing overfitting and overestimate on the testing data. Fig. 3 (b), sudden decrement in the number of cases which is not a good prediction considering the ongoing situation of Italy. Fig. 3 (c), degree-6 PBRR given RMSE 418.36 with an accuracy of 91% on testing data.

Fig. 3
figure 3

Italy Cases forecasting (a) Represent degree-4, (b) degree-5, (c) degree-6, and (d) degree-7 PBRR as well

Full size image

4.2 U.S. cases

In Fig. 4 we have plotted four polynomial-curves using PBRR of different degrees and observed degree-6 is well suited the case examined using Root Mean Square Error (RMSE). We have recorded 723.75 RMSE with an accuracy of 88% after training and testing our model on the U.S. dataset. Within 60 days of the first COVID-19 positive case occurrence, the number of confirmed cases started growing exponentially. In Fig. 4 (a) 4-degree PBRR fitted but given poor performance-tested data due to overfitting on training data. Also, in Fig. 4 (b) 5-degree and (d) 7-degree PBRR fitted so well but after 100 days, it started decreasing which is not suitable for the current circumstances.

Fig. 4
figure 4

U.S. Cases forecasting (a) Represent degree-4, (b) degree-5, (c) degree-6, and (d) degree-7 PBRR as well

Full size image

4.3 Spain cases

Through our investigation on the dataset of Spain, an instant decrement is recorded on the 95th days of first case arrival. Similar to the previous we fitted four different PBRR on Spain dataset too and found that 7-degree is the best fit that not correctly estimates confirmed cases for unseen days but also tracks the decrement happen earlier (See Fig. 5). The model, in Fig. 5 (a) is underfitting that neither predicts the unseen observation nor performed well on the training dataset. The other two models (Fig. 5 (b) and (c)) are not suitable for the present ongoing. The model, in Fig. 5 (d) estimates the testing data having RMSE 624.27 with an accuracy of 90.5%.

Fig. 5
figure 5

Spain Cases forecasting (a) Represent degree-4, (b) degree-5, (c) degree-6, and (d) degree-7 PBRR as well

Full size image

In the above case studies, we have fitted and found different parameters for the predictions (Table 4). Now, we can predict for the upcoming days. So, we have predicted for 6 days and compare with the actual number of cases on those days (Table 5).

Table 5 Comparisons of Predicted and Actual Number of Cases
Full size table

5 Results and discussions

It is demanding to construct a model to predict the dynamic progression of COVID-19 situations. So many researchers are struggling to find and implementing such models with optimal parameters and unknown variables which lead them to uncertainty. PBRR model is different from all the studies published or at least discussed in the literature survey because of its nature of making an estimation. It is a complex mathematical model that more focused to discover distribution instead of making a single value linear prediction of the dependent variable and this feature makes it more promising.

As far as we have seen in all the above-mentioned case studies different polynomial based on Bayesian belief having a range of degrees between 4 and 7 best fit and enable us to forecast future infected cases of COVID-19. Instead of applying any specific country, we can also estimate the cases on the worldwide dataset. Fig. 6, demonstrates the curve fitting using the PBRR model of degree 5 on world-wide data with accuracy 89% on testing data. We also estimate the magnitude of confirmed cases in the upcoming 10 days. Applying PBRR on world-wide data is means scaling the independent variables but our model also survived in this scenario and showing the consistency of the system.

Fig. 6
figure 6

Word-Wide Cases Forecasting

Full size image

To prove the novelty and superiority of the proposed model, we have compared several models (Table 6) based on many attributes which are following-

  • Root Mean Square Error (RMSE)

  • Accuracy of Prediction

  • Prior Distribution/ Posterior Distribution (For parameters)

  • Standard Deviation of Prediction (SD)

Table 6 Models Comparisons
Full size table

After the comparison, we finally observed that the proposed model is better than other in the term of RMSE and comparable equal in term of accuracy with ARIMA and LSTM. Although, ARIMA and LSTM are giving little bit more accurate results PBRR using the prior and posterior distribution for the model parameters which is not used by any of either ARIMA or LSTM. We also experiment with Bayesian Linear Regression with using the prior and posterior distribution for the model parameters which has not given satisfactory result in the term of RMSE, accuracy, and SD. In section 2, we have already discussed the importance of the prior and posterior distribution for the model parameters.

No doubt, LSTM is a deep learning based advanced approach to forecast time series data but it also has some drawbacks compare to proposed model e.g. longer time to train, more memory, overfitting, sensitive to different random weight initializations etc. The overfitting is one of the major issues of the LSTM which has overcome in proposed model by adding ridge regularization. We have a sequential path from older past cells to the current one in LSTM hidden layers. In fact the path is now even more complicated, because it has additive and forget branches attached to it. LSTM and GRU and derivatives are able to learn a lot of longer term information but they can remember sequences of 100 s, not 1000s or 10,000 s or more as given here [40]. Moreover, RNNs are not hardware friendly. It takes a lot of resources we do not have to train these networks fast. Also it takes many resources to run these models in the cloud, the cloud is not scalable [40].

6 Conclusion

PBRR modeling not only has sufficient accuracy but also reliable than other methods. In present circumstances when thousands of people are losing their loving ones or own lives a model with more promising algorithms is needed along with good accuracy. Prediction with misconceptions may lead to a serious problem for health care professionals as well as governments. Although, PBRR is giving reliable results the reality is the forecasting of any pandemic is not only merely dependent on previous observations or time-series analytical inference. Many more important factors influence the magnitude of infection like healthcare system stability, education, awareness of people, weather, lockdown, and social-distancing, etc. Soon, the researcher may come up with different robust models that also consider these factors.