Pricing and recycling decisions of remanufacturing alliances with third-party recycling platform

Abstract

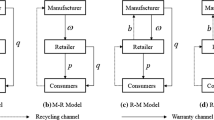
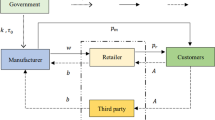
In this paper, we investigate a closed-loop supply chain where the original manufacturer plays as the channel leader and the third-party recycling platform participates in the recycling of used products. The remanufacturer produces remanufactured products through a remanufacturing license, and four different types of alliances are investigated as: the third-party recycling platform and the original manufacturer alliance, the third-party recycling platform and the remanufacturer alliance, the original manufacturer and the remanufacturer alliance, the original manufacturer and the remanufacturer and the third-party recycling platform alliance. We compare the overall benefits of different alliances and find that the alliance of the original manufacturer, the remanufacturer and the third-party recycling platform has the largest income. We set up a reasonable profit distribution mechanism under the alliance, which can make the three parties get the optimal benefit and make the whole CLSC remanufacturing alliance reach the Pareto optimum. We also compare the recycling rates across alliances and find that the recycling rate is highest in the case of the remanufacturer and the third-party recycling platform alliance, whose recycling rate is positively correlated with recycling costs. Importantly, we make a comparative analysis of the equilibrium decisions and profit distribution of the four alliance models with the participation of the third-party platform. Both the original manufacturer and the remanufacturer need to seek a third-party platform as partners, but if there are conflicts between two manufacturers, the third-party recycling platform may become a mediator between the original manufacturer and the remanufacturer in the supply chain. The results of our study will provide a theoretical basis for enterprises to choose the appropriate alliance in closed-loop supply chains.

Appendix

1.1 Appendix 1: The solving process of equilibrium decisions in different models

In order to facilitate the calculation and simplify the results, we make some parameters replacement in the calculation process, let $L_{1} = \delta - 1;\;L_{2} = k\delta ;\;L_{3} = A - B;\;L = - AB + B^{2} + 4k\delta .$

1.1.1 The solving process of model MT

It is easy to obtain the Hessian matrix of the retailer’s profit function:

$$ H_{R}^{MT} = \left[ {\begin{array}{*{20}c} { - \frac{2}{1 - \delta }} & {\frac{2}{1 - \delta }} \\ {\frac{2}{1 - \delta }} & { - \frac{2}{{\delta \left( {1 - \delta } \right)}}} \\ \end{array} } \right] $$

(A1)

For $- \frac{2}{1 - \delta } < 0$, if $\left| {H_{R}^{MT} } \right| = \frac{4}{{\delta \left( {1 - \delta } \right)}} > 0$, that is to say $0 < \delta < 1$ is satisfied. So the Hessian matrix is negatively definite, and taking the first-order derivative of ${\Pi }_{L}^{MT}$ with respect to p_N and $p_{{R_{1} }}$, we can obtain the unique optimal solution. Then we can derive the following equilibrium solution by using the reverse recursion method.

$$ \left\{ {\begin{array}{*{20}c} {p_{N} \left( {{\upomega }_{N} } \right) = \frac{{1 + {\upomega }_{N} }}{2}} \\ {p_{{R_{1} }} \left( {{\upomega }_{R1} } \right) = \frac{{\delta + {\upomega }_{{R_{1} }} }}{2}} \\ \end{array} } \right. $$

(A2)

Substituting (A1) into (2), we can obtain the Hessian matrix of (2):

$$ H_{L}^{MT} = \left[ {\begin{array}{*{20}c} {\frac{1}{ - 1 + \delta }} & { - \frac{1}{ - 1 + \delta }} & 0 \\ {\frac{1}{1 - \delta }} & { - \frac{1}{{\delta - \delta^{2} }}} & {\frac{A}{2\delta }} \\ 0 & {\frac{A}{2\delta }} & { - 2k} \\ \end{array} } \right] $$

(A3)

For $\frac{1}{ - 1 + \delta } < 0$, if $\left| {H_{L}^{MT} } \right| = - \frac{2k}{{\delta \left( {\delta - 1} \right)^{2} }} < 0$, that is to say $\frac{1}{ - 1 + \delta }{ }\left( {{ } - \frac{1}{{\delta - \delta^{2} }}{ }} \right) - \left( {\frac{1}{1 - \delta }} \right)^{2} > 0$ is satisfied. So the Hessian matrix is negatively definite, and taking the first-order derivative of ${\Pi }_{L}^{MT}$ with respect to $\upomega _{N} ,\upomega _{{R_{1} }}$ and τ, we can obtain the unique optimal solution of ${\Pi }_{L}^{MT}$ with respect to ${\upomega }_{N} ,{\upomega }_{{R_{1} }}$ and τ.

Then, we can get the following equilibrium solution by using the reverse recursion method.

$$ {\upomega }_{N}^{{MT^{*} }} = \frac{{ - 8k\delta + A^{2} \left( {1 + \delta } \right) + \left( {A^{2} - 8k\delta } \right)C_{N} - A^{2} C_{{R_{1} }} }}{{2\left( {A^{2} - 8k\delta } \right)}}, $$

(A4)

$$ {\upomega }_{{R_{1} }}^{{MT^{*} }} = \frac{{\delta \left( {A^{2} - 4k\delta - 4kC_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}, $$

(A5)

$$ {\uptau }^{{MT^{*} }} = \frac{{A\left( {\delta - C_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}. $$

(A6)

Substituting (A2) and (A3) into (A1) we can obtain

$$ p_{N}^{{MT^{*} }} = \frac{{ - 24k\delta + A^{2} \left( {3 + \delta } \right) + \left( {A^{2} - 8k\delta } \right)C_{N} - A^{2} C_{{R_{1} }} }}{{4\left( {A^{2} - 8k\delta } \right)}}, $$

(A7)

$$ p_{{R_{1} }}^{{MT^{*} }} = \frac{{\delta \left( {A^{2} - 6k\delta - 2kC_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}. $$

(A8)

Therefore, the optimal profits of the alliance and the retailer are further obtained as follows:

$$ {\Pi }_{L}^{{MT^{*} }} = \frac{{\left( {L_{1} \left( {A^{2} L_{1} + 8L_{2} } \right) + \left( {A^{2} - 8L_{2} } \right)C_{N}^{2} + 2\left( {A^{2} - 8L_{2} } \right)C_{N} \left( {L_{1} - C_{{R_{1} }} } \right) - 2A^{2} L_{1} C_{{R_{1} }} + \left( {A^{2} - 8k} \right)C_{{R_{1} }}^{2} } \right)}}{{\left( {8L_{1} \left( { - A^{2} + 8L_{2} } \right)} \right)}}, $$

(A9)

$$ {\Pi }_{r}^{{MT^{*} }} = \frac{{\left( {A^{2} L_{1} \left( {A^{2} - 16L_{2} } \right)\left( {L_{1} - 2C_{{R_{1} }} } \right) + 64L_{2}^{2} + \left( {A^{2} - 8L_{2} } \right)^{2} C_{N} \left( {2L_{1} + C_{N} - 2C_{{R_{1} }} } \right) + \left( {A^{4} - 16L_{2} \left( {A^{2} - 4k} \right)} \right)C_{{R_{1} }}^{2} } \right)}}{{ - 16L_{1} \left( {A^{2} - 8L_{2} } \right)^{2} }}, $$

(A10)

where $L_{1} = \delta - 1;{ }L_{2} = k\delta ;{ }L_{3} = A - B;{ }L = - AB + B^{2} + 4k\delta$.

1.1.2 The solving process of model RT

From assumption 4 we can see that the retailer is the follower of the game in any model, so the reaction function of the retailer is the same as 3.1, i.e.

$$ \left\{ {\begin{array}{*{20}c} {p_{N} = \frac{{1 + {\upomega }_{N} }}{2}} \\ {p_{{R_{2} }} = \frac{{\delta + {\upomega }_{{R_{2} }} }}{2}} \\ \end{array} } \right. $$

(A11)

It is easy to obtain the Hessian matrix of (11):

$$ H_{L}^{RT} = \left[ {\begin{array}{*{20}c} {\frac{1}{{\left( { - 1 + \delta } \right)\delta }}} & {\frac{A}{2\delta }} \\ {\frac{A}{2\delta }} & { - 2k} \\ \end{array} } \right] $$

(A12)

For ${ }\frac{1}{{\left( { - 1 + \delta } \right)\delta }} < 0$, if ${ } \left| {H_{L}^{RT} } \right| = \left| {\begin{array}{*{20}c} {\frac{1}{{\left( { - 1 + \delta } \right)\delta }}} & {\frac{A}{2\delta }} \\ {\frac{A}{2\delta }} & { - 2k} \\ \end{array} } \right| = \frac{{A^{2} - A^{2} \delta - 8k\delta }}{{4\delta^{2} \left( { - 1 + \delta } \right)}} > 0$, that is to say $A^{2} - A^{2} \delta - 8k\delta < 0$ is satisfied. So the Hessian matrix is negatively definite, and taking the first-order derivative of ${\Pi }_{L}^{RT}$ with respect to ${\upomega }_{{R_{2} }}$ and ${ }\tau$, we can obtain the unique optimal solution of ${\Pi }_{L}^{RT}$ with respect to ${\upomega }_{{R_{2} }}$ and ${ }\tau$.

Then, we can derive the following equilibrium solution by using the reverse recursion method.

$$ {\upomega }_{{R_{2} }} = \frac{{\delta \left( {A^{2} \left( { - 1 + \delta } \right) + 2k\left( {C_{{R_{2} }} + \delta {\upomega }_{N} } \right)} \right)}}{{A^{2} \left( { - 1 + \delta } \right) + 4k\delta }} $$

(A13)

$$ \tau = \frac{{A\left( {C_{{R_{2} }} + \delta \left( { - 2 + {\upomega }_{N} } \right)} \right)}}{{A^{2} \left( { - 1 + \delta } \right) + 4k\delta }} $$

(A14)

Similarly, since the profit function of the original manufacturer is

$$ {\Pi }_{M}^{RT} = \left( {{\upomega }_{N} - C_{N} } \right)q_{N} $$

(A15)

We have

$$ {\upomega }_{N}^{{RT^{*} }} = \frac{{\left( { - 1 + \delta } \right)\left( {A^{2} - 8k\delta } \right) + \left( {A^{2} \left( { - 1 + \delta } \right) + 8k\delta } \right)C_{N} + 4k\delta C_{{R_{2} }} }}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }} $$

(A16)

$$ {\upomega }_{{R_{2} }}^{{RT^{*} }} = \frac{{\delta \left( {\left( { - 1 + \delta } \right)\left( {A^{2} - 2k\delta } \right) + 2k\delta C_{N} + 4kC_{{R_{2} }} } \right)}}{{A^{2} \left( { - 1 + \delta } \right) - 2k\left( { - 4 + \delta } \right)\delta }} $$

(A17)

$$ {\uptau }^{{RT^{*} }} = \frac{{A\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }} $$

(A18)

$$ p_{N}^{{RT^{*} }} = \frac{{3A^{2} \left( { - 1 + \delta } \right) - 12k\left( { - 2 + \delta } \right)\delta + \left( {A^{2} \left( { - 1 + \delta } \right) + 8k\delta } \right)C_{N} + 4k\delta C_{{R_{2} }} }}{{4A^{2} \left( { - 1 + \delta } \right) - 8k\left( { - 4 + \delta } \right)\delta }} $$

(A19)

$$ p_{{R_{2} }}^{{RT^{*} }} = \frac{{\delta \left( {2A^{2} \left( { - 1 + \delta } \right) + k\left( {13 - 4\delta } \right)\delta + k\delta C_{N} + 2kC_{{R_{2} }} } \right)}}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }} $$

(A20)

Thus, we can further obtain the optimal profits of the retailer, alliance and original manufacturer as follows:

$${\Pi }_{\mathrm{r}}^{{\mathrm{RT}}^{*}}=\frac{\begin{array}{c}-(({\mathrm{L}}_{1}({\mathrm{A}}^{4}{\mathrm{L}}_{1}(1+8\delta )+16{{\mathrm{L}}_{2}\mathrm{A}}^{2}(1+(4-5\delta )\delta )+16{{\mathrm{L}}_{2}}^{2}(-4+\delta (-13+8\delta )))+\\ ({\mathrm{A}}^{4}{{\mathrm{L}}_{1}}^{2}+16{{\mathrm{L}}_{2}}^{2}(4+5\delta )+8{\mathrm{A}}^{2}{\mathrm{L}}_{2}({\mathrm{L}}_{1}(\delta +1)){\mathrm{C}}_{\mathrm{N}}^{2}+8{\mathrm{L}}_{2}{\mathrm{C}}_{{\mathrm{R}}_{2}}(({\mathrm{L}}_{1}(-4{\mathrm{L}}_{2}(2+\delta )\\ +{\mathrm{A}}^{2}(5+4\delta ))+(8k+10{\mathrm{L}}_{2}){\mathrm{C}}_{{\mathrm{R}}_{2}})+\\ 2{\mathrm{C}}_{\mathrm{N}}({\mathrm{L}}_{1}({{16\mathrm{L}}_{2}}^{2}(4-7\delta )+{\mathrm{A}}^{4}{\mathrm{L}}_{1}(3+4{\mathrm{L}}_{1})-4{\mathrm{A}}^{2}{\mathrm{L}}_{2}(4+\delta (-13+2{\mathrm{L}}_{1})))\\ +4{\mathrm{L}}_{2}(3{\mathrm{A}}^{2}{\mathrm{L}}_{1}+4{\mathrm{L}}_{2}(8+\delta )){\mathrm{C}}_{{\mathrm{R}}_{2}}))\end{array}}{16{\mathrm{L}}_{1}{({\mathrm{A}}^{2}{\mathrm{L}}_{1}-2\mathrm{k}(-4+\updelta )\updelta )}^{2}},$$

(A21)

$${\Pi }_{L}^{{RT}^{*}}=\frac{\begin{array}{c}(\delta ({A}^{4}(-1+{C}_{N}){{L}_{1}}^{2}-8{{L}_{2}}^{2}({C}_{N}-{L}_{1})(-7+{C}_{N}+\delta )-{A}^{2}{L}_{1}{L}_{2}(1+{C}_{N}^{2}+2{C}_{N}(-7+\delta )+2\delta ))+\\ {C}_{{R}_{2}}({A}^{4}(-1+B){{L}_{1}}^{2}-2{A}^{2}{L}_{1}{L}_{2}(10+{C}_{N}(-6+\delta )-\delta )-\\ 16{{L}_{2}}^{2}(-3+{C}_{N})(-2+\delta )+4k({A}^{2}{{L}_{1}}^{2}-2{L}_{2}{(-2+\delta )}^{2}){C}_{{R}_{2}}))\end{array}}{(4{L}_{1}{({A}^{2}{L}_{1}-2{L}_{2}(-4+\delta ))}^{2})},$$

(A22)

$$ {\Pi }_{M}^{{RT^{*} }} = \frac{{\begin{array}{*{20}c} {\left( {\left( {A^{2} \left( {1 + \left( {3 - 4\delta } \right)\delta } \right) + 8L_{2} \left( { - 1 + \left( { - 3 + \delta } \right)\delta } \right) + \left( {A^{2} L_{1} - 4L_{2} \left( { - 2 + \delta } \right)} \right)C_{N} - 4L_{2} C_{{R_{2} }} } \right)} \right.\left( {L_{1} \left( {A^{2} - 8L_{2} } \right) + } \right.} \\ {\left. {\left. {\left( { - A^{2} L_{1} + 4L_{2} \left( { - 2 + \delta } \right)} \right)C_{N} + 4L_{2} C_{{R_{2} }} } \right)} \right)} \\ \end{array} }}{{\left( {8L_{1} \left( {A^{2} L_{1} - 2L_{2} \left( { - 4 + \delta } \right)} \right)^{2} } \right)}}. $$

(A23)

1.1.3 The solving process of Model MR

From assumption 4 we can see that the retailer is the follower of the game in any model, so the reaction function of the retailer is the same. i.e.

$$ \left\{ {\begin{array}{*{20}c} {p_{N} = \frac{{1 + {\upomega }_{N} }}{2}} \\ {p_{{R_{3} }} = \frac{{\delta + {\upomega }_{{R_{3} }} }}{2}} \\ \end{array} } \right.. $$

(A24)

It is easy to obtain the Hessian matrix of (18):

$$ H_{L}^{MR} = \left[ {\begin{array}{*{20}c} {\frac{1}{{\left( { - 1 + \delta } \right)}}} & {\frac{1}{1 - \delta }} \\ {\frac{1}{1 - \delta }} & {\frac{1}{{\left( { - 1 + \delta } \right)\delta }}} \\ \end{array} } \right] $$

(A25)

For ${ }\frac{1}{{\left( { - 1 + \delta } \right)}} < 0$, if $\left| {H_{L}^{MR} } \right| = \frac{1}{{\left( {1 - \delta } \right)\delta }} > 0$, that is to say 0 < δ < 1 is satisfied, so the matrix is negatively definite, ${\Pi }_{L}^{MR}$ is jointly concave with respect to ${\upomega }_{N}$ and ${\upomega }_{{R_{3} }}$, and there is unique optimal solution of ${\Pi }_{L}^{MR}$ with respect to ${\upomega }_{N}$ and ${\upomega }_{{R_{3} }}$.

Then, we can derive the following equilibrium solution by using the reverse recursion method.

$$ {\upomega }_{N}^{{MR^{*} }} = \frac{{ - 4k\delta + AB\left( {1 + \delta } \right) - B^{2} \left( {1 + \delta } \right) + \left( {\left( {A - B} \right)B - 4k\delta } \right)C_{N} + b\left( { - A + B} \right)C_{{R_{3} }} }}{{2\left( {A - B} \right)B - 8k\delta }}, $$

(A26)

$$ {\upomega }_{{R_{3} }}^{{MR^{*} }} = \frac{{\delta \left( { - AB + B^{2} + 2k\delta + 2kC_{{R_{3} }} } \right)}}{{ - AB + B^{2} + 4k\delta }}, $$

(A27)

$$ \tau^{{MR^{*} }} = \frac{{\left( {B - A} \right)\left( {C_{{R_{3} }} - \delta } \right)}}{{2\left( {B - A} \right)B + 8k\delta }}, $$

(A28)

$$ p_{N}^{{MR^{*} }} = \frac{{ - 12k\delta + AB\left( {3 + \delta } \right) - B^{2} \left( {3 + \delta } \right) + \left( {\left( {A - B} \right)B - 4k\delta } \right)C_{N} + b\left( { - A + B} \right)C_{{R_{3} }} }}{{4AB - 4\left( {B^{2} + 4k\delta } \right)}}, $$

(A29)

$$ p_{{R_{3} }}^{{MR^{*} }} = \frac{{\delta \left( { - AB + B^{2} + 3k\delta + kC_{{R_{3} }} } \right)}}{{ - AB + B^{2} + 4k\delta }}. $$

(A30)

Thus, we can further obtain the following optimal profits of the retailer, third-party recycling platform and alliance.

$$ {\Pi }_{r}^{{MR^{*} }} = \frac{{\begin{array}{*{20}c} {(32L_{2}^{2} \left( {\delta - C_{{R_{3} }} } \right)\left( {L_{3} BL_{1} + \left( {L_{3} B - 8L_{2} } \right)C_{N} + \left( { - BL_{3} + 8k} \right)C_{{R_{3} }} } \right) + } \\ {\left( {L + 4L_{2} } \right)\left( {L_{1} + C_{N} - C_{{R_{3} }} } \right)(L_{3}^{2} B^{2} - L_{3} B\left( {L_{3} B + 12k} \right)\delta + 4L_{2} \left( {3L_{3} B + 8k} \right)\delta } \\ { - \left( {L + 4L_{2} } \right)LC_{N} - L_{3} B\left( {L + 8L_{2} } \right)C_{{R_{3} }} ))} \\ \end{array} }}{{16L_{1} L\left( {L + 4L_{2} } \right)^{2} }}. $$

(A31)

$$ {\Pi }_{T}^{{MR^{*} }} = \frac{{\left( {A - B} \right)^{2} k\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{4\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}, $$

(A32)

$${\Pi }_{L}^{{MR}^{*}}=\frac{\begin{array}{c}(\delta (L+4k{C}_{{R}_{3}})({L}_{1}(20{L}_{2}-12{{L}_{3}}^{2}-64{{L}_{2}}^{2}{L}_{3}B\left({L}_{1}-1\right)+256{{L}_{2}}^{3})+(L{\left(L+4{L}_{2}\right)}^{2}{C}_{N}^{2}-2L{\left(L+4{L}_{2}\right)}^{2}\\ {C}_{N}({L}_{1}-{C}_{{R}_{3}})-2{L}_{3}B{L}_{1}({{L}_{3}}^{2}{B}^{2}-12B{L}_{3}{L}_{2}+64{{L}_{2}}^{2}){C}_{{R}_{3}}+({{L}_{3}}^{2}{B}^{2}({L}_{3}B-8k)-\\ 4{L}_{3}B(3{L}_{3}B-16k){L}_{2}+64({L}_{3}B-4k){{L}_{2}}^{2}){{C}_{{R}_{3}}}^{2}))\end{array}}{8{L}_{1}L{(L+4{L}_{2})}^{3}}.$$

(A33)

1.1.4 The solving process of model MRT

The solving process is similar to that of Model MR and we omit it here.

1.2 Appendix 2: the proofs of the lemmas and propositions in this paper

Proof of Proposition 1

Taking the first-order derivatives of ${\uptau }^{{MT^{*} }}$ with respect to A and $C_{{R_{1} }}$ for model MT, we obtain $\frac{{\partial {\uptau }^{{MT^{*} }} }}{\partial A} = \frac{{\left( {A^{2} + 8k\delta } \right)\left( {C_{{R_{1} }} - \delta } \right)}}{{\left( {A^{2} - 8k\delta } \right)^{2} }} > 0$ and $\frac{{\partial {\uptau }^{{MT^{*} }} }}{{\partial C_{{R_{1} }} }} = \frac{ - A}{{A^{2} - 8k\delta }} > 0$.

Proof of Proposition 2

Taking the first-order and second-order derivatives of ${\Pi }_{L}^{{MT^{*} }}$ and ${\Pi }_{R}^{{MT^{*} }}$ with respect to $A$ for model MT, we have

$$ \frac{{\partial {\Pi }_{L}^{MT} }}{{\partial {\text{A}}}} = \frac{{2Ak\left( {\delta - C_{{R_{1} }} } \right)^{2} }}{{\left( {A^{2} - 8k\delta } \right)^{2} }} > 0, $$

(A34)

$$ \frac{{\partial^{2} {\Pi }_{L}^{MT} }}{{\partial {\text{A}}^{2} }} = - \frac{{2k\left( {3A^{2} + 8k\delta } \right)\left( {\delta - C_{{R_{1} }} } \right)^{2} }}{{\left( {A^{2} - 8k\delta } \right)^{3} }} > 0, $$

(A35)

$$ \frac{{\partial {\Pi }_{R}^{MT} }}{{\partial {\text{A}}}} = - \frac{{16Ak^{2} \delta \left( {\delta - C_{{R_{1} }} } \right)^{2} }}{{\left( {A^{2} - 8k\delta } \right)^{3} }} > 0, $$

(A36)

$$ \frac{{\partial^{2} {\Pi }_{R}^{MT} }}{{\partial {\text{A}}^{2} }} = \frac{{16k^{2} \delta \left( {5A^{2} + 8k\delta } \right)\left( {\delta - C_{{R_{1} }} } \right)^{2} }}{{\left( {A^{2} - 8k\delta } \right)^{4} }} > 0. $$

(A37)

Proof of Proposition 3

Taking the first-order derivative of $\tau^{{RT^{*} }}$ with respect to A for model RT, we derive.

$\frac{{\partial \tau^{{RT^{*} }} }}{{\partial {\text{A}}}} = - \frac{{\left( {A^{2} \left( { - 1 + \delta } \right) + 2k\left( { - 4 + \delta } \right)\delta } \right)\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{2\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\left( { - 4 + \delta } \right)\delta } \right)^{2} }}$ and ${\uptau }^{{RT^{*} }} = \frac{{A\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }}$ > 0.

Let $g\left( \delta \right)$ = $A\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)$, $\frac{dg\left( \delta \right)}{{d\delta }} = \left( { - 3 + C_{N} } \right)A$, if $- 3 + C_{N} > 0$, $g\left( \delta \right)$ increases with $\delta$, ${\text{so }}g\left( \delta \right) > g\left( 0 \right) = 2AC_{{R_{2} }} > 0$;

If $- 3 + C_{N} < 0$,${ }g\left( \delta \right)$ decreases with $\delta$, so $g\left( \delta \right) > g\left( 1 \right) = A\left( { - 3 + C_{N} + 2C_{{R_{2} }} } \right);{ } - 3 + C_{N} + 2C_{{R_{2} }} > 3\left( {C_{{R_{2} }} - 1} \right)$, at this time $\delta = 1$, according to Assumption 1, ${ }C_{{R_{2} }} > 1$; thus $g\left( \delta \right) > g\left( 1 \right) > 0$, so we have $- \left( {A^{2} \left( { - 1 + \delta } \right) + 2k\left( { - 4 + \delta } \right)\delta } \right)\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right) > 0$, which leads to $\frac{{\partial \tau^{{RT^{*} }} }}{{\partial {\text{A}}}} > 0$.

Taking the second-order derivative of $\tau^{{RT^{*} }}$ with respect to A for model RT, we derive

$$ \frac{{\partial^{2} \tau^{{RT^{*} }} }}{{\partial {\text{A}}^{2} }} = \frac{{A\left( { - 1 + \delta } \right)\left( {A^{2} \left( { - 1 + \delta } \right) + 6k\left( { - 4 + \delta } \right)\delta } \right)\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\left( { - 4 + \delta } \right)\delta } \right)^{3} }} > 0, $$

(A38)

and taking the first-order derivatives of $\tau^{{RT^{*} }}$ with respect to $C_{N} , C_{{R_{2} }} {\text{for model RT}}$, we get

$$ \frac{{\partial {\uptau }^{{RT^{*} }} }}{{\partial C_{N} }} = \frac{A\delta }{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }} > 0, $$

(A39)

$$ \frac{{\partial {\uptau }^{{RT^{*} }} }}{{\partial C_{{R_{2} }} }} = \frac{2A}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }} > 0. $$

(A40)

Thus, from $0 \le \delta \le 1$, we have $\frac{{\partial {\uptau }^{{RT^{*} }} }}{{\partial C_{{R_{2} }} }} > \frac{{\partial {\uptau }^{{RT^{*} }} }}{{\partial C_{N} }}$.

Proof of Proposition 4

Taking the first-order derivative of $\tau^{{MR^{*} }}$ with respect to A for model MR, we derive.

$$ \frac{{\partial \tau^{{MR^{*} }} }}{{\partial {\text{A}}}} = \frac{{2k\delta \left( { - \delta + C_{{R_{3} }} } \right)}}{{\left( { - AB + B^{2} + 4k\delta } \right)^{2} }} > 0. $$

(A41)

And taking the second-order derivative of $\tau^{{MR^{*} }}$ with respect to A for model MR, we get

$$ \frac{{\partial^{2} \tau^{{MR^{*} }} }}{{\partial {\text{A}}^{2} }} = - \frac{{4Bk\delta \left( { - \delta + C_{{R_{3} }} } \right)}}{{\left( {B\left( { - A + B} \right) + 4k\delta } \right)^{3} }} < 0. $$

(A42)

Proof of Proposition 5

Taking the first-order derivative of $\tau^{{RT^{*} }}$ with respect to A for model MRT, we obtain.

$$ \frac{{\partial {\uptau }^{{MRT^{*} }} }}{\partial A} = \frac{{\left( {A^{2} + 8k\delta } \right)\left( {C_{{R_{4} }} - \delta } \right)}}{{\left( {A^{2} - 8k\delta } \right)^{2} }} > 0, $$

(A43)

and from $C_{{R_{4} }} < C_{{R_{1} }}$, we have $\frac{{\partial {\uptau }^{{MRT^{*} }} }}{\partial A} < \frac{{\partial {\uptau }^{{MT^{*} }} }}{\partial A}{ };{ }$ then, taking the first-order derivative of $\tau^{{MRT^{*} }}$ with respect to $C_{{R_{4} }}$ for model MRT, we derive

$$ \frac{{\partial {\uptau }^{{MRT^{*} }} }}{{\partial C_{{R_{4} }} }} = \frac{ - A}{{A^{2} - 8k\delta }} > 0. $$

(A44)

Proof of Theorem 1

Form $\uptau ^{{MRT^{*} }} = \frac{{A\left( {\delta - C_{{R_{4} }} } \right)}}{{A^{2} - 8k\delta }}, \uptau ^{{MT^{*} }} = \frac{{A\left( {\delta - C_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}$, ${\uptau }^{{MRT^{*} }} - {\uptau }^{{MT^{*} }} = \frac{{A\left( {C_{{R_{1} }} - C_{{R_{4} }} } \right)}}{{A^{2} - 8k\delta }}$, according to Assumption 1, we have $C_{{R_{1} }} > C_{{R_{4} }}$, so ${\uptau }^{{MRT^{*} }} - {\uptau }^{{MT^{*} }} < 0$, i.e. ${\uptau }^{{MRT^{*} }} < {\uptau }^{{MT^{*} }}$.

Since ${\uptau }^{{MT^{*} }} = \frac{{A\left( {\delta - C_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}$ and ${\uptau }^{{RT^{*} }} = \frac{{A\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }}$, then,${\uptau }^{{MT^{*} }} - {\uptau }^{{RT^{*} }} = \frac{{ - A\left( {A^{2} - 8k\delta } \right)\left( {2C_{{R_{2} }} + \delta \left( { - 3 + C_{N} } \right)} \right) + 2A\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right)\left( {\delta - C_{{R_{1} }} } \right)}}{{\left( {A^{2} - 8k\delta } \right)\left( {2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta } \right)}}$. To make the recycling rate meaningful, it must be met ${ }A^{2} - 8k\delta < 0$,$2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta > 0$, thus, we can obtain $A^{2} \left( { - 1 + \delta } \right) > 2k\delta \left( { - 4 + \delta } \right)$.

From $- A\left( {A^{2} - 8k\delta } \right)\left( {2C_{{R_{2} }} + \delta \left( { - 3 + C_{N} } \right)} \right) + 2A\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right)\left( {\delta - C_{{R_{1} }} } \right) = - A\left( {A^{2} - 8k\delta } \right)\delta \left( { - 3 + C_{N} } \right) - 2A\left( {A^{2} - 8k\delta } \right)C_{{R_{2} }} + 2A\delta \left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right) - 2A\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right)C_{{R_{1} }}$, we have $- A\left( {A^{2} - 8k\delta } \right)\delta \left( { - 3 + C_{N} } \right) > 0, 2A\delta \left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right) > 0$.

Let $f\left( \delta \right) = - 2A\left( {A^{2} - 8k\delta } \right)C_{{R_{2} }} - 2A\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\delta \left( { - 4 + \delta } \right)} \right)C_{{R_{1} }}$, and $\frac{{{\text{d}}^{2} f\left( \delta \right)}}{{{\text{d}}\delta^{2} }} = 8Ak > 0,$ so $f\left( \delta \right)$ is convex with respect to $\delta$. Therefore, we can obtain $f\left( \delta \right){ }$ achieves the minimum value in $\delta^{*} = \frac{{A^{2} C_{R} + 8kC_{{R_{1} }} - 8kC_{{{\text{R}}2}} }}{{4kC_{{R_{1} }} }}{ },{ }and{ }f_{min} = f\left( {\delta^{*} } \right) = \left( { - A^{2} + \frac{{A^{4} }}{8k} + 8k} \right)C_{{R_{1} }} + \left( {A^{2} + 16k} \right)C_{R2} - \frac{{8kC_{R2}^{2} }}{{C_{{R_{1} }} }}.$

From $A^{2} - 8k\delta < 0$, $0 < \delta < 1$, we have $8k > A^{2}$; similarly, from $C_{{R_{1} }} > C_{{{\text{R}}2}}$, we have $\frac{{8kC_{{{\text{R}}2}}^{2} }}{{C_{{R_{1} }} }} < 8kC_{{{\text{R}}2}}$ and $f_{min} > 0$, thus $f\left( \delta \right) > 0$, which leads to ${\uptau }^{{MT^{*} }} < {\uptau }^{{RT^{*} }}$.

Since $\tau^{{MR^{*} }} = \frac{{\left( {B - A} \right)\left( {\delta - C_{{R_{3} }} } \right)}}{{2\left( {A - B} \right)B - 8k\delta }}$,$\uptau ^{{RT^{*} }} = \frac{{A\left( {\delta \left( { - 3 + C_{N} } \right) + 2C_{{R_{2} }} } \right)}}{{2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta }}$, if ${\uptau }^{{RT^{*} }} - \tau^{{MR^{*} }} = 0$ we can obtain a threshold value $A_{1}^{*}$($A_{1}^{*}$ is a real root of ${\uptau }^{{RT^{*} }} = \tau^{{MR^{*} }}$, and $A_{1}^{*} < B)$; besides, if $A > A_{1}^{*}$, we have ${\uptau }^{{RT^{*} }} > \tau^{{MR^{*} }}$, otherwise, ${\uptau }^{{RT^{*} }} < \tau^{{MR^{*} }}$.

From $\tau^{{MR^{*} }} = \frac{{\left( {B - A} \right)\left( {\delta - C_{{R_{3} }} } \right)}}{{2\left( {A - B} \right)B - 8k\delta }}$; ${\uptau }^{{MT^{*} }} = \frac{{A\left( {\delta - C_{{R_{1} }} } \right)}}{{A^{2} - 8k\delta }}$, if $\tau^{{MR^{*} }} - {\uptau }^{{MT^{*} }} = 0$ we can obtain another threshold value $A_{2}^{*} { }(A_{2}^{*}$ is a real value of $\tau^{{MR^{*} }} = {\uptau }^{{MT^{*} }}$, and $A_{1}^{*} < A_{2}^{*} < B){ }$; however, if $A > A_{2}^{*}$, we have ${\uptau }^{{MT^{*} }} > \tau^{{MR^{*} }}$, otherwise, ${\uptau }^{{MT^{*} }} < \tau^{{MR^{*} }}$.

Since $\tau^{{MR^{*} }} = \frac{{\left( {B - A} \right)\left( {\delta - C_{{R_{3} }} } \right)}}{{2\left( {A - B} \right)B - 8k\delta }}$; ${\uptau }^{{MRT^{*} }} = \frac{{A\left( {\delta - C_{{R_{4} }} } \right)}}{{A^{2} - 8k\delta }}$, if $\tau^{{MR^{*} }} - {\uptau }^{{MRT^{*} }} = 0$ we can obtain a threshold value $A_{3}^{*} { }(A_{3}^{*} is a real root of \tau^{{MR^{*} }} = {\uptau }^{{MRT^{*} }}$, and $A_{1}^{*} < A_{2}^{*} < A_{3}^{*} < B){ }$; but if $A > A_{3}^{*}$, we can obtain $\tau^{{MR^{*} }} < {\uptau }^{{MRT^{*} }}$, otherwise, $\tau^{{MR^{*} }} > {\uptau }^{{MRT^{*} }}$.

Proof of Theorem 2

From $p_{N}^{{MT^{*} }} - p_{N}^{{MR^{*} }} = \frac{{k\delta \left( {\left( {b - A} \right)^{2} + B^{2} } \right)\left( {C_{{R_{3} }} - C_{{R_{1} }} - \delta } \right)}}{{4\left( {A^{2} - 8k\delta } \right)\left( {4k\delta + B^{2} - AB} \right)}} > 0,$ we have $p_{N}^{{MT^{*} }} > p_{N}^{{MR^{*} }}$.

According to Assumption 1, since $C_{{R_{2} }} < C_{{R_{1} }}$, we derive $\overline{{p_{N}^{{RT^{*} }} }}$ through increasing $C_{{R_{2} }}$ to $C_{{R_{1} }}$, thus, $p_{N}^{{MT^{*} }} - p_{N}^{{RT^{*} }} > p_{N}^{{MT^{*} }} - \overline{{p_{N}^{{RT^{*} }} }} .$ Then, we compare $p_{N}^{{MT^{*} }}$ and $\overline{{p_{N}^{{RT^{*} }} }}$.

$$ p_{N}^{{MT^{*} }} - \overline{{p_{N}^{{RT^{*} }} }} = \frac{{4\left( {A^{2} \left( { - 1 + \delta } \right) - 2k\left( { - 4 + \delta } \right)\delta } \right)\left( {A^{2} \left( { - 1 + \delta } \right) + 8k\delta + \left( {A^{2} - 8k\delta } \right)C_{N} - A^{2} C_{{R_{1} }} } \right)}}{{4\left( {A^{2} - 8k\delta } \right)\left( {4A^{2} \left( { - 1 + \delta } \right) - 8k\left( { - 4 + \delta } \right)\delta } \right)}} > 0. $$

(A45)

Therefore, $p_{N}^{{MT^{*} }} - p_{N}^{{RT^{*} }} > p_{N}^{{MT^{*} }} - \overline{{p_{N}^{{RT^{*} }} }} > 0$, i.e. $p_{N}^{{MT^{*} }} - p_{N}^{{RT^{*} }} > 0.$

According to Assumption 1, from $C_{{R_{4} }} < C_{{R_{1} }}$, we have $p_{N}^{{MT^{*} }} - p_{N}^{{MRT^{*} }} = \frac{{A^{2} \left( {C_{{R_{4} }} - C_{{R_{1} }} } \right)}}{{4\left( {A^{2} - 8k\delta } \right)}} > 0$.

Proof of Theorem 3

From $p_{{R_{4} }}^{{MRT^{*} }} - p_{{R_{3} }}^{{MR^{*} }} = \frac{{\left( {A^{2} - 2AB + 2B^{2} } \right)k\delta \left( {\delta - C_{{R_{4} }} } \right)}}{{\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)}} > 0$, we have $p_{{R_{4} }}^{{MRT^{*} }} > p_{{R_{3} }}^{{MR^{*} }}$.

According to Assumption 1 and $C_{{R_{2} }} < C_{{R_{1} }}$, we derive $p_{{R_{1} }}^{{MT^{*} }} - p_{{R_{2} }}^{{RT^{*} }} > p_{N}^{{MT^{*} }} - \overline{{p_{{R_{2} }}^{{RT^{*} }} }}$ and ${ }p_{{R_{1} }}^{{MT^{*} }} - \overline{{p_{{R_{2} }}^{{RT^{*} }} }} = \frac{{\delta \left( { - A^{4} \left( { - 1 + \delta } \right) + 4k^{2} \left( {14 - 5\delta } \right)\delta^{2} + 3A^{2} k\delta \left( { - 5 + 4\delta } \right) + k\delta \left( { - \left( {A^{2} - 8k\delta } \right)C_{N} - 2\left( {A^{2} - 2k\delta } \right)C_{{R_{1} }} } \right)} \right)}}{{\left( {A^{2} - 8k\delta } \right)\left( {2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta } \right)}}$. According to Assumption 3, we have $A^{2} - 8k\delta < 0$,$2A^{2} \left( { - 1 + \delta } \right) - 4k\left( { - 4 + \delta } \right)\delta > 0$, so $\frac{{2k\delta \left( {\delta - 4} \right)}}{\delta - 1} < A^{2} \left\langle {8k\delta which leads to { }p_{{R_{1} }}^{{MT^{*} }} - \overline{{p_{{R_{2} }}^{{RT^{*} }} }} } \right\rangle 0$, thus, $p_{{R_{1} }}^{{MT^{*} }} > p_{{R_{2} }}^{{RT^{*} }}$.

According to Assumption 1, from $C_{{R_{4} }} < C_{{R_{1} }}$ and $p_{{R_{1} }}^{{MT^{*} }} - p_{{R_{4} }}^{{MRT^{*} }} = \frac{{2k\delta \left( {C_{{R_{4} }} - C_{{R_{1} }} } \right)}}{{\left( {A^{2} - 8k\delta } \right)}} > 0$, it is easy to obtain $p_{{R_{1} }}^{{MT^{*} }} > p_{{R_{4} }}^{{MRT^{*} }}$.

Proof of Theorem 4

From ${\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MT^{*} }} = \frac{{2\left( {A^{2} - 8L_{2} } \right)C_{N} \left( {C_{{R_{1} }} - C_{{R_{4} }} } \right) + 2A^{2} L_{1} \left( {C_{{R_{1} }} - C_{{R_{4} }} } \right) + \left( {A^{2} - 8k} \right)\left( {C_{{R_{1} }}^{2} - C_{{R_{4} }}^{2} } \right)}}{{8L_{1} - A^{2} + 8L_{2} }}0$, $C_{{R_{1} }} > C_{{R_{4} }}$, $L_{1} = \delta - 1$ and $L_{2} = k\delta$, we obtain $\Pi_{L}^{{MRT^{*} }} > \Pi_{L}^{{MT^{*} }}$

From ${\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MR^{*} }} = \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}$, $A^{2} - 8k\delta < 0$,$A < B$ and $3A^{2} - 2AB + 2B^{2} = 2A^{2} + B^{2} + \left( {A - B} \right)^{2} > 0,$ we can obtain $\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta \left\langle {0 ,{\text{when}} \left( {A^{2} + 2AB - 2B^{2} } \right)} \right\rangle 0$; otherwise, if $\left( {A^{2} + 2AB - 2B^{2} } \right) < 0$ and $A\left\langle {\left( {\sqrt 3 - 1} \right)B, {\text{thus}} , - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k} \right\rangle 0$. Let $T\left( A \right) = \left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta$ and $\frac{dT\left( A \right)}{{dA}} = 6A\left( {A - B} \right)B + B\left( {3A^{2} - 2{\text{AB}} + 2B^{2} } \right) - 8Ak\delta$, we obtain two real roots of $\frac{dT\left( A \right)}{{dA}} = 0{ }$: $A_{1} = \frac{{8B^{2} + 8k\delta - \sqrt { - 72B^{4} + \left( {8B^{2} - 8k\delta } \right)^{2} } }}{18B}$ and $A_{2} = \frac{{8B^{2} + 8k\delta + \sqrt { - 72B^{4} + \left( {8B^{2} - 8k\delta } \right)^{2} } }}{18B},$ where we have $- 72B^{4} + \left( {8B^{2} - 8k\delta } \right)^{2} \ge 0$, which leads to $k\delta \ge \frac{3\sqrt 2 + 4}{4}B^{2} ,{\text{ then }}\sqrt { - 72B^{4} + \left( {8B^{2} - 8k\delta } \right)^{2} } < \sqrt {\left( {8B^{2} - 8k\delta } \right)^{2} } = \left| {8B^{2} - 8k\delta } \right| = 8k\delta - 8B^{2}$. Therefore, $A_{1} > \frac{{8B^{2} + 8k\delta - \left( {8k\delta - 8B^{2} } \right)}}{18B} = \frac{8}{9}B > \left( {\sqrt 3 - 1} \right)B;$ on the other hand, from $\frac{{\partial T_{\left( A \right)}^{3} }}{{\partial A^{3} }} = 18B > 0$, we obtain the first-order derivative of $T\left( A \right)$ is convex with respect to $A$, thus $T\left( A \right)$ increases with $A$ in (0, $A_{1}$), and decreases with $A$ in $(A_{1} ,A_{2} );$ furthermore, from above we know $A_{1} > \left( {\sqrt 3 - 1} \right)B > A$, and we denote $\check{A} = \left( {\sqrt 3 - 1} \right)B$, so $T\left( A \right) <$ $T\left( {\check{A}} \right) = \left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) < 0$, which leads to ${\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MR^{*} }} > 0$.

Proof of Theorem 5

If $F = {\Pi }_{T}^{{MR^{*} }}$, we can obtain $\overline{{B^{*} }} = \frac{A}{2} - \frac{{\sqrt k \left( {\delta - C_{{R_{3} }} } \right)}}{4\sqrt F } + \frac{1}{4}\sqrt {4A^{2} - 64L_{2} + \frac{{\delta L_{2} }}{F} + \frac{{4A\sqrt k \delta^{2} }}{{\sqrt F \left( {\delta - C_{{R_{3} }} } \right)}} - \frac{{2L_{2} C_{{R_{3} }} }}{F} - \frac{{8A\sqrt k \delta C_{{R_{3} }} }}{{\sqrt F \left( {\delta - C_{{R_{3} }} } \right)}} + \frac{{kC_{{R_{3} }}^{2} }}{F} + \frac{{4A\sqrt k C_{{R_{3} }}^{2} }}{{\sqrt F \left( {\delta - C_{{R_{3} }} } \right)}}}$, $\Pi_{T}^{{MR^{*} }} - F = \frac{{\left( {A - B} \right)^{2} k\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{4\left( { - AB + B^{2} + 4k\delta } \right)^{2} }} - F,{ }$ $\frac{{\partial \left( {\Pi_{T}^{{MR^{*} }} - F} \right)}}{\partial B} = - \frac{{\left( {A - B} \right)k\left( {\left( {A - B} \right)^{2} - 4k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {\left( {A - B} \right)B - 4k\delta } \right)^{3} }}$, from the proof process of Theorem 4 we have ${ }k\delta \ge \frac{3\sqrt 2 + 4}{4}B^{2}$, so $\left( {A - B} \right)^{2} - 4k\delta \le \left( {A - B} \right)^{2} - \left( {3\sqrt 2 + 4} \right)B^{2} = A^{2} - 2AB - 3\left( {\sqrt 2 + 1} \right)B^{2} < 0$, and thus $\frac{{\partial \left( {\Pi_{T}^{{MR^{*} }} - F} \right)}}{\partial B} > 0$, which indicates that $\Pi_{T}^{{MR^{*} }} - F$ increases with $B$. When $B = \overline{{B^{*} }}$, we derive $\Pi_{T}^{{MR^{*} }} - F = 0$; when $A < B < \overline{{B^{*} }}$, we get $\Pi_{T}^{{MR^{*} }} - F < 0$; when $B > \overline{{B^{*} }}$, we have $\Pi_{T}^{{MR^{*} }} - F > 0$.

Proof of Theorem 6

According to Theorem 4, we have ${\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MR^{*} }} = \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }} > 0$, so the original manufacturer's alliance with the remanufacturer and the third party's recycling platform is more profitable than the original manufacturer's alliance with the remanufacturer.

From ${\Pi }_{R}^{{MRT^{*} }} - {\Pi }_{R}^{{MR^{*} }} = \alpha \left( {\frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }} - F} \right)$, we have when ${\Pi }_{R}^{{MRT^{*} }} - {\Pi }_{R}^{{MR^{*} }} > 0$, it must be met $F < \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}$, according to Theorem 4, to make $F$ to be meaningful, we have $F > \frac{{\left( {A - B} \right)^{2} k\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{4\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}$.

Besides, when ${\Pi }_{R}^{{MRT^{*} }} - {\Pi }_{R}^{{MR^{*} }} < 0$, it must be met $F > \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}$, since the third-party recycling platform is a follower in the game, and $F > \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}$ does not meet the actual situation. Thus there exists a set $F^{*} = \left( {\frac{{\left( {A - B} \right)^{2} k\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{4\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}, \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }}} \right)$ such that when $F \in F^{*}$, the remanufacturer’s profit in Model MRT is greater than that in Model MR.

When $F \in F^{*}$,

If ${\Pi }_{R}^{{MR^{*} }} = {\Pi }_{R}^{{RT^{*} }}$, there exists $\alpha_{1}^{*} = \frac{{{\Pi }_{L}^{{RT^{*} }} - F}}{{{\Pi }_{L}^{{MR^{*} }} }}$ such that when $\alpha \in \left( {0,\alpha_{1}^{*} } \right)$, we have ${\Pi }_{R}^{{RT^{*} }} > {\Pi }_{R}^{{MR^{*} }}$; when $\alpha \in \left( {\alpha_{1}^{*} ,1} \right)$, we have ${\Pi }_{R}^{{RT^{*} }} < {\Pi }_{R}^{{MR^{*} }}$;

If ${\Pi }_{R}^{{MRT^{*} }} = {\Pi }_{R}^{{RT^{*} }} ,{\text{ there exists }}\alpha_{2}^{*} = \frac{{{\Pi }_{L}^{{RT^{*} }} - F}}{{{\Pi }_{L}^{{MRT^{*} }} - F}}{\text{ such that when }}\alpha \in \left( {0,\alpha_{2}^{*} } \right)$, we have ${\Pi }_{R}^{{MRT^{*} }} < {\Pi }_{R}^{{RT^{*} }}$; when $\alpha \in \left( {\alpha_{2}^{*} ,1} \right)$, we have ${\Pi }_{R}^{{MRT^{*} }} > {\Pi }_{R}^{{RT^{*} }}$.

Proof of Theorem 7

From ${\Pi }_{M}^{{MRT^{*} }} - {\Pi }_{M}^{{MR^{*} }} = \left( {1 - \alpha } \right)({\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MR^{*} }} - F)$, and ${\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MR^{*} }} = \frac{{k\left( {\left( {A - B} \right)B\left( {3A^{2} - 2AB + 2B^{2} } \right) - 4\left( {A^{2} + 2AB - 2B^{2} } \right)k\delta } \right)\left( {\delta - C_{{R_{3} }} } \right)^{2} }}{{2\left( {A^{2} - 8k\delta } \right)\left( { - AB + B^{2} + 4k\delta } \right)^{2} }} > 0$. Similar to Theorem 6, we can prove that the profit of the original manufacturer in Model MRT is greater than that in Model MR.

Only when $F \in F^{*}$, the third-party recycling platform is willing to participate in the alliance.

From $\Pi_{M}^{{MRT^{*} }} - \Pi_{M}^{{MT^{*} }} = \left( {1 - \alpha } \right)\Pi_{L}^{{MRT^{*} }} - \Pi_{L}^{{MT^{*} }} + \alpha F$, we can get that $\alpha_{3}^{*} = \frac{{\Pi_{L}^{MRT*} - \Pi_{L}^{MT*} }}{{\Pi_{L}^{MRT*} - F}}$ such that when $\alpha \in \left( {0,\alpha_{3}^{*} } \right)$, we have ${\Pi }_{M}^{{MRT^{*} }} > {\Pi }_{M}^{{MT^{*} }}$; when $\alpha \in \left( {\alpha_{3}^{*} ,1} \right)$, we have ${\Pi }_{M}^{{MRT^{*} }} < {\Pi }_{M}^{{MT^{*} }}$.

From ${\Pi }_{M}^{{MRT^{*} }} - {\Pi }_{M}^{{RT^{*} }} = \left( {1 - \alpha } \right){\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{M}^{{RT^{*} }} - \left( {1 - \alpha } \right)F$, when ${\Pi }_{M}^{{MRT^{*} }} - {\Pi }_{M}^{{RT^{*} }} = \left( {1 - \alpha } \right){\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{M}^{{RT^{*} }} - \left( {1 - \alpha } \right)F = 0$, we can get $\alpha_{4}^{*} = \frac{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} - {\Pi }_{M}^{{RT^{*} }} }}{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} }}$ such that when $\alpha \in \left( {0,\alpha_{4}^{*} } \right)$, we have $\Pi_{M}^{{MRT^{*} }} > \Pi_{M}^{{RT^{*} }}$.

$\alpha_{3}^{*} = \frac{{{\Pi }_{L}^{{MRT^{*} }} - {\Pi }_{L}^{{MT^{*} }} }}{{{\Pi }_{L}^{{MRT^{*} }} - F}}$, $\alpha_{4}^{*} = \frac{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} - {\Pi }_{M}^{{RT^{*} }} }}{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} }}$, when $\alpha_{3}^{*} > \alpha_{4}^{*}$ and $\alpha \in \left( {0,\alpha_{4}^{*} } \right)$, the original manufacturer will get the maximum profit when the three parties of the closed-loop supply chain make the alliance; when $\alpha_{3}^{*} < \alpha_{4}^{*}$ and $\alpha \in \left( {0,{ }\alpha_{3}^{*} } \right)$, the original manufacturer will get the maximum profit when the three parties of the closed-loop supply chain make the alliance.

According to Theorem 6, we can obtain that when $\alpha \in \left( {\alpha_{2}^{*} ,1} \right)$ and $F \in F^{*}$, the remanufacturer will get the maximum benefit when the three parties of the closed-loop supply chain make the alliance. And $\alpha_{2}^{*} = \frac{{\Pi_{L}^{{RT^{*} }} - F^{*} }}{{\Pi_{L}^{{MRT^{*} }} - F^{*} }}$, $\alpha_{4}^{*} = \frac{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} - {\Pi }_{M}^{{RT^{*} }} }}{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} }}$, $\alpha_{4}^{*} - \alpha_{2}^{*} = \frac{{{\Pi }_{L}^{{MRT^{*} }} - \Pi_{L}^{{RT^{*} }} - {\Pi }_{M}^{{RT^{*} }} }}{{{\Pi }_{L}^{{MRT^{*} }} - F^{*} }}$, it is obvious when the three parties make the alliance, the supply chain benefit is the largest, so we have $\alpha_{4}^{*} > \alpha_{2}^{*}$. Since the original manufacturer is the leader in the game, the technology licensing rate $\alpha$ is controlled at $\alpha \in \left( {\alpha_{2}^{*} ,\alpha_{4}^{*} } \right)$ and the fixed fee paid to the third-party recycling platform is controlled at, when the three parties of the closed-loop supply chain jointly form an alliance, the original manufacturer, remanufacturer and third-party recycling platform can all get the most benefits.