A hybrid MIP-based large neighborhood search heuristic for solving the machine reassignment problem

Abstract

We present a hybrid metaheuristic approach for the machine reassignment problem, which was proposed for ROADEF/EURO Challenge 2012. The problem is a combinatorial optimization problem, which can be viewed as a highly constrained version of the multidimensional bin packing problem. Our algorithm, which took the third place in the challenge, consists of two components: a fast greedy hill climber and a large neighborhood search, which uses mixed integer programming to solve subproblems. We show that the hill climber, although simple, is an indispensable component that allows us to achieve high quality results especially for large instances of the problem. In the experimental part we analyze two subproblem selection methods used by the large neighborhood search algorithm and compare our approach with the two best entries in the competition, observing that none of the three algorithms dominates others on all available instances.

1 Introduction

Cloud computing is an emerging paradigm aimed at providing network access to computing resources including storage, processing, memory and network bandwidth (Armbrust et al. 2010; Buyya et al. 2009). Such resources are typically gathered in large-scale data centers and form a shared pool, which can serve multiple applications. Since data centers host a variety of applications with different requirements and time-varying workloads, resources should be dynamically reassigned according to demands. However, there are many constraints and criteria which make the problem of resource allocation non-trivial. For instance, due to increasing energy costs and pressure towards reducing environmental impact, one particular measure that should be optimized by a resource allocation policy is the power consumption (Beloglazov et al. 2011). Lowering the energy usage is possible by, e.g., consolidating applications on a minimal number of machines. That being said, devising an efficient data center resource allocation strategy constitutes a serious challenge.

Many optimization problems related to managing data center resources have been defined and considered in the literature recently (Song et al. 2009; Stillwell et al. 2010; Beloglazov et al. 2012). Following this trend, the subject of ROADEF/EURO 2012 Challenge¹ was proposed by Google—one of the leading cloud computing-based service providers—and concerned the machine reassignment problem. The goal of the problem is to optimize the assignment of service processes to machines with respect to a given cost function. The original assignment is part of a problem instance, but processes can be reassigned by moving them from one machine to another. Possible moves are limited by a set of hard constraints, which must be satisfied to make the assignment feasible. For example, constraints refer to the amount of consumed resources on a machine or distribution of processes belonging to the same service over multiple distinct machines.

In this paper, we propose a heuristic approach for the machine reassignment problem, which produces satisfactory results in a limited time even for large instances of the problem. The main idea behind our approach is to combine a single-state metaheuristic with Mixed Integer Programming (MIP), which is able to quickly solve small subproblems. This approach can be classified as an example of Large Neighborhood Search (LNS), in which a solution’s neighborhood (specified by a subset of processes that can be reassigned to a subset of machines) is searched (sub)optimally by mathematical programming techniques (Pisinger and Ropke 2010; Ahuja et al. 2002). Since the choice of neighborhood is often crucial to the performance of LNS, we analyze the average performance of two methods of selecting processes to be reassigned: random selection of a subset of processes, and a dedicated heuristic designed to select processes that are likely to improve the assignment cost. Moreover, we attempt to hybridize such MIP-based LNS with a fast greedy hill climber, which aims to improve the assignment by reassigning single processes independently. The experimental results demonstrate that such greedy hill climber improves the results of the whole algorithm.

A version of the algorithm presented in this paper allowed us to win the Junior category and take the third place in the general classification of ROADEF/EURO 2012 Challenge. In this paper, we further test our approach, by conducting a computational analysis to compare our algorithm on all available problem instances with the methods that took the two first places in the competition. Since we average the results over 25 algorithm runs, we claim that our results are more reliable than the results obtained in the competition finals.

2 Machine reassignment problem

The goal of the machine reassignment problem² is to find a mapping $M:{\mathcal {P}}\rightarrow {\mathcal {M}}$ which assigns each given process $p\in \mathcal {P}$ to one of the available machines $m\in {\mathcal {M}}$. The mapping $M(p_{1})=m_{1}$ denotes that process $p_{1}$ runs on machine $m_{1}$ and uses its resources. The set of resources $\mathbb {\mathfrak {\mathcal {R}}}$ is common to all machines, but each machine provides specific capacity $C(m,r)$ of the given resource $r\in {\mathcal {R}}$. Additional constraints (cnf. Sect. 2.1) are induced by splitting the set of processes ${\mathcal {P}}$ into disjoint subsets, each of which represents a service $s\in {\mathcal {S}}$.

Fig. 1

The original assignment in an exemplary instance of the machine reassignment problem. (Color figure online)

An exemplary instance of the problem and the original assignment are illustrated in Fig. 1. This particular instance consists of three processes, ${\mathcal {P}}=\{p_{1},p_{2},p_{3}\}$, four machines, ${\mathcal {M}}=\{m_{1},m_{2},m_{3},m_{4}\}$ and two kinds of resources, ${\mathcal {R}}=\{r_{1},r_{2}\}$. Grey bars associated with the processes represent their resource requirements. All processes are initially assigned to some machines, but some machines may remain without processes (here: $m_{2}$ and $m_{3}$). Figure 1 highlights the fact that part of the resources on every machine (marked with green color) is available for processes without any cost while using the rest (marked with red color) increases the cost of the assignment. Processes are partitioned into disjoint services, which may, but need not, depend on each other. In Fig. 1 a dashed arrow means that service $s_{2}$ depends on service $s_{1}$. Machines are grouped into disjoint locations and neighborhoods.

In the following, we describe all the constraints and cost parameters of the problem. Wherever possible, we refer to the instance (and the original solution) presented in Fig. 1 and a possible solution illustrated in Fig. 2.

Fig. 2

A possible reassignment of the assignment shown in Fig. 1. (Color figure online)

2.1 Constraints

2.1.1 Capacity constraints

For each resource $r\in {\mathcal {R}}$, $C(m,r)$ is the capacity of this resource on machine $m\in {\mathcal {M}}$ and $R(p,r)$ is the amount of this resource required by process $p\in {\mathcal {P}}$. The sum of requirements of all processes assigned to machine $m$ is denoted as resource usage $U(m,r)$. The capacity constraints indicate that usage $U(m,r)$ cannot exceed capacity $C(m,r)$ for any $r\in {\mathcal {R}}$ and $m\in {\mathcal {M}}$. In the considered instance, process $p_{1}$ cannot be moved from machine $m_{1}$ to machine $m_{4}$ because $R(p_{1},r_{1})+R(p_{2},r_{1})$ is higher than capacity $C(m_{4},r_{1})$.

2.1.2 Conflict constraints

Each process belongs to exactly one service $s\in {\mathcal {S}}$. Processes of a given service must be assigned to distinct machines. For this reason, in our example, processes $p_{1}$ and $p_{2}$, which belong to service $s_{1}$, cannot be assigned to the same machine.

2.1.3 Spread constraints

Each machine belongs to exactly one location $l\in {\mathcal {L}}$. Processes of a given service $s$ must be assigned to machines in a number of distinct locations. The minimum number of locations over which the service $s$ must be spread is defined by $spreadMin(s)$ for any $s\in {\mathcal {S}}$. Assuming that $spreadMin(s_{1})=2$, processes $p_{1}$ and $p_{2}$ have to be assigned to machines from different locations.

2.1.4 Dependency constraints

Each machine belongs to exactly one neighborhood $n\in {\mathcal {N}}$, which is important in the context of service dependencies. If service $s_{2}$ depends on service $s_{1}$, then in each neighborhood to which processes of service $s_{2}$ are assigned, at least one process of service $s_{1}$ must be also assigned. For example, if $service_{2}$ depends on $service_{1}$, then $p_{1}$ can be moved to $m_{2}$, but cannot be moved neither to $m_{3}$ nor to $m_{4}$.

2.1.5 Transient usage constraints

A subset of resources ${\mathcal {TR}}\subseteq {\mathcal {R}}$ is regarded as transient. It means that when a process is reassigned from one machine to another one, such resources are required on both the original and the target machine. In the considered example resource $r_{1}$ is transient (marked with hatched boxes). For this reason, when process $p_{2}$ is reassigned from machine $m_{4}$ to $m_{3}$ (see Fig. 2) this resource remains being used on $m_{4}$ (marked with hatched lines) and is also used on $m_{3}$. Due to transient usage constraints no other process can be assigned to $m_{4}$ if it requires any amount of resource $r_{1}$.

2.2 Costs

The problem aims at minimizing the total cost of an assignment which is a weighted sum of load costs, balance costs and move costs described below.

2.2.1 Load cost

For each resource $r\in {\mathcal {R}}$ and machine $m\in {\mathcal {M}}$ there is a safety capacity limit $SC(m,r)$. If resource usage $U(m,r)$ (cf. Sect. 2.1.1) is below the limit then no cost is incurred. However, if the usage exceeds the limit, the load cost is equal to $U(m,r)-SC(m,r)$. Figures 1 and 2 illustrate the safety capacity limit by dividing each resource into two parts—below the limit (green color) and over the limit (red color). Clearly, the reassignment demonstrated in Fig. 2 reduces the load cost.

2.2.2 Balance cost

The amount of unused resource $r$ on machine $m$ is denoted as $A(m,r)=C(m,r)-U(m,r)$. In some circumstances the values of $A(m,r_{1})$ and $A(m,r_{2})$ should be balanced according to a given ratio called $target$. To model each such situation, the problem definition includes a set of balance triples $\left\langle r_{1},r_{2},target\right\rangle \in {\mathcal {B}}$. If unused resources are imbalanced, a balance cost of $\max (0,target\cdot A(m,r_{1})-A(m,r_{2}))$ is incurred.

In the referred example, there is a single balance triple $b$ with ratio between resources $r_{2}$ and $r_{1}$ equal to $1$. Initially (see Fig. 1), the balance cost on machine $m_{4}$ is high, because there is a considerable amount $A(m_{4},r_{2})$ of unused resource $r_{2}$ left, while resource $r_{1}$ is fully used. Reassigning process $p_{3}$ to machine $m_{3}$ (see Fig. 2) results in improving the balance between available resources (since $A(m_{3},r_{2})\approxeq A(m_{3},r_{1})$) and reducing the balance cost.

2.2.3 Move costs

Reassigning process $p$ from its original machine $m_{1}$ to machine $m_{2}$ involves both process move cost $PMC(p)$, defined for each process $p\in \mathcal {P}$, and machine move cost $MMC(m_{1},m_{2})$ defined for each pair of machines $m_{1},m_{2}\in {\mathcal {M}}$. Additionally, a service move cost $SMC(s)$ is defined as the maximum of reassigned processes over all services $s\in {\mathcal {S}}$. The reassignment in Fig. 2 has the service move cost equal to $1$ since for each service exactly one process is reassigned.

2.2.4 Total cost

The total cost to be minimized is expressed as:

$$\begin{aligned} totalCost&=\sum _{r\in \mathcal {R}}{ weight}_{{ loadCost}}(r)\cdot { loadCost}(r)\\&\quad \, +\,\sum _{b\in \mathcal {B}}{ weight}_{{ balanceCost}}(b)\cdot { balanceCost}(b)\\&\quad \, +\,{ weight}_{{ processMoveCost}}\cdot { processMoveCost}\\&\quad \, +\,{ weight}_{{ serviceMoveCost}}\cdot { serviceMoveCost}\\&\quad \, +\,{ weight}_{{ machineMoveCost}}\cdot { machineMoveCost}. \end{aligned}$$

2.3 Lower bounds

The solution cost can be bounded from below by independently bounding its individual components.³

For any resource $r\in {\mathcal {R}}$

For any balance triple $b=\left\langle r_{1},r_{2},target\right\rangle \in {\mathcal {B}}$

$$\begin{aligned} balanceCost(b)&= \sum _{m\in {\mathcal {M}}}\max (0,target\cdot A(m,r_{1})-A(m,r_{2}))\\&\ge \max (0,target\cdot \sum _{m\in {\mathcal {M}}}A(m,r_{1}) -\sum _{m\in {\mathcal {M}}}A(m,r_{2})), \end{aligned}$$

where

$$\begin{aligned} A(m,r)=C(m,r)-U(m,r). \end{aligned}$$

Finally, for the move costs we have

$$\begin{aligned} { serviceMoveCost}&\ge 0,\\ { processMoveCost}&\ge 0,\\ { machineMoveCost}&\ge 0. \end{aligned}$$

For the majority of available instances, these inequations allow us to determine tight bounds, which will be shown in Sect. 4.

2.4 Related problems

Since the machine reassignment problem was defined only recently for a special purpose of ROADEF/EURO 2012 challenge, there is very little literature concerning it. The notable exceptions are the works of Mehta et al. (2012)—ranked second in the competition (team S38), and Gavranović et al. (2012)—ranked first (team S41). The former study compares constraint programming and mixed integer programming approaches on the basis of the challenge qualification results, while the latter presents a variable neighborhood search algorithm.

It is worth mentioning, however, that the considered problem is related to some combinatorial optimization problems studied in the past. These include multi-dimensional generalizations of classical packing problems such as multi-processor scheduling, bin packing and the knapsack problem. In contrast to canonical one-dimensional versions, in such problems the items to be packed as well as the bins are $d$-dimensional objects. Due to this characteristics they are harder to solve than their single-dimensional versions. A theoretical study of approximation algorithms for these problems can be found in the work of Chekuri and Khanna (1999).

Another group of related problems originates directly from the field of cloud computing and data center resource management. Examples of such problems include server consolidation problem (Srikantaiah et al. 2008; Speitkamp and Bichler 2010) and power aware load balancing and activity migration (Singh et al. 2008).

In this context, the machine reassignment problem can be seen as a strongly constrained version of the multi-dimensional resource allocation problem, where the number of dimensions is equal to the number of resources. Importantly, in contrast to typical resource scheduling problems (Garofalakis and Ioannidis 1996; Shen et al. 2012), there is no time dimension here—all reassignments are assumed to be done only once, at the same time moment.

3 Hybrid metaheuristic algorithm

The proposed approach is a single-state heuristic, which starts from a provided original assignment (a feasible solution). It consists of two subsequent phases. In the first phase it employs a simple hill climbing algorithm (Sect. 3.1) to quickly improve the solution. Further improvements are performed in the second phase by a MIP-based large neighborhood search (Sect. 3.2).

3.1 Greedy hill climber

The goal of a greedy hill climber is to improve a given assignment as fast as possible. For the set of instances provided in the ROADEF/EURO competition (see Sect. 4.1) it has been observed that the original solution can be substantially improved by elementary local changes. The hill climber searches the neighborhood induced by a shift move $shift(p,m)$ which reassigns process $p$ from its current machine $m_{0}$ to another machine $m_{1}\ne m_{0}$. The algorithm is deterministic and greedy—it accepts the first move which leads to a feasible solution of lower cost than the current solution. If no better solution in the neighborhood is found, the algorithm stops.

Although a straightforward implementation of such an algorithm is too slow to be practical, the structure of the problem makes it possible to apply several techniques to boost its performance. These techniques are described in the following subsections.

3.1.1 Delta evaluation

The performance bottleneck of the hill climber algorithm lies in the shift move implementation, which computes the cost of a neighbor candidate solution. An efficient way of computing it is attained with delta evaluation. Instead of calculating the solution cost from scratch, only the cost difference between neighbors is calculated. Delta evaluation allows us to achieve time complexity of a single $shift(p,m)$ operation of $O(|\mathcal {B}|+|\mathcal {R}|+dep(p)+revdep(p))$, where $dep(p)$ is the number of services dependent on the service containing process $p$ and $revdep(p)$ is the number of services on which the service containing process $p$ is dependent. For the instances provided in the competition, $|\mathcal {B}|$ is at most 1 and $|\mathcal {R}|$ is at most 12. While in the considered instances there can be as many as 50,000 service dependencies, the vast majority of services have less than 10 dependencies.

In order to make delta evaluation possible, the solution must, apart from the assignment, maintain additional data structures, which are updated on each shift move. Table 1 shows these data structures along with time required to update them after a shift move.

Table 1 Operations, time complexity and data structures used in $shift(p,m)$ implementation

3.1.2 Process potential

Another technique used to speed up the hill climber algorithm is exploring the neighborhood in the order that increases the chances of quickly finding a better solution. For this purpose, the list of processes is sorted decreasingly by their potential. Process potential measures how much the total cost of the solution would be reduced if the process did not exist. The higher the process potential, the more likely it is to reduce the cost of the solution; that is why the algorithm considers the processes with the highest potential first. The processes with zero potential are not considered at all since the solution cost cannot be reduced when moving such processes. After the processes are initially sorted, their order in the list remains fixed during consecutive iterations.

The cost of computing the process potential is $O(|\mathcal {B}|+|\mathcal {R}|)$. Process potential consists of three independent components: load cost potential, balance cost potential and move cost potential. The preliminary experiments have shown that the balance cost component of the process potential has a negligible effect on the algorithm performance and can be safely ignored (at least for the problem instances considered in this paper).

3.1.3 Iteration over processes and machines

For each process $p_{j}$ in the sorted sequence, the algorithm examines all possible moves $shift(p_{j},m_{i})$, trying to reassign the process from its current machine $m_{0}=M(p_{j})$ to any other machine $m_{i}\ne m_{0}$ except those on the tabu list (see Sect. 3.1.4). A move is accepted if it leads to a feasible solution that is better than the currently best one, and it is rejected otherwise. If the move is accepted, machine $m_{i}$ is saved as the best machine $m_{best}$, but the neighborhood search is not stopped; instead, the algorithm continues with an attempt to move process $p_{j}$ to the next machine $m_{i+1}$ by making $shift(p_{j},m_{i+1})$. Conversely, if the move is rejected, $m_{best}$ is not updated. However, there is no need to undo the move until reaching the end of machines list. As a result, process $p_{j}$ is iteratively moved to subsequent machines using the $shift$ operator even if the currently considered solution is (temporarily) infeasible or worse than the currently best one.

Finally, when all machines have been considered, process $p_{j}$ is moved back to $m_{0}$ if no better machine has been found, or to machine $m_{best}$, otherwise. This way, although we call the hill climber greedy, each considered process is moved to the (locally) best possible machine. Notice that the order of machines does not matter unless two or more machines are equally efficient for a given process.

After trying to assign process $p_{j}$ to each machine, the algorithm continues its search by attempting to move process $p_{j+1}$ (or $p_{0}$ if $p_{j}$ was the last machine in the list). The hill climber stops when no move can be accepted for any process.

3.1.4 Machines Tabu list

The hill climber algorithm maintains a tabu list that contains the machines that are ignored when looking for the best machine for any given process. Initially, the tabu list is empty. During iteration over processes, for each machine $m$ the algorithm remembers whether any process has been moved to or from this machine. If $m$ remains unchanged, then it is added to the tabu list, and thus it is not considered as a destination of any process moves. Machine $m$ stays on the list until any process is removed from it.

The motivation behind this idea is a heuristic assumption that if no process is worth moving to a machine, then only removing a process from it may change the situation. This assumption does not hold in general, since it ignores the situation in which moving a process from machine $m_{0}$ to machine $m_{1}$ ‘unblocks’ some constraints and makes it possible to move another process to machine $m_{2}$, where $m_{2}\notin \{m_{0},m_{1}\}$. However, we have found that this assumption does not make the hill climber substantially worse for the available instances, having the advantage of improving the algorithm speed performance by a factor of 2–4.

3.2 Large neighborhood search

The hill climbing phase of the algorithm described in the previous section explores a straightforward move-based neighborhood induced by the $shift(p,m)$ operation. The size of the neighborhood is polynomial with respect to the problem size, and the algorithm is capable of improving the original solution by means of lots of small changes. In contrast, the second phase of the proposed algorithm focuses on moving many processes at once and consists of a limited number of such changes. Since the size of the neighborhood grows exponentially with the number of processes and machines considered, the algorithm can be classified as a large neighborhood search (LNS) (Shaw 1998).

In LNS, exploring a neighborhood can be viewed as solving a subproblem of the original problem with a specialized procedure (Pisinger and Ropke 2010; Palpant et al. 2004). This procedure may be either a heuristic or an exact method such as mathematical programming (Bent and Hentenryck 2004). The latter variant is sometimes called a matheuristic (Boschetti et al. 2009).

Our algorithm iteratively selects a subproblem and tries to solve it to optimality. If it is computationally infeasible to find an optimal solution, a suboptimal one can be returned. The subproblem is extracted from the original problem by selecting a subset of machines $\mathcal {M}_{x}\subset \mathcal {M}$. Given the currently best solution, a mixed integer programming (MIP) solver is allowed to move any number of processes among machines in $\mathcal {M}_{x}$. The processes on machines outside $\mathcal {M}_{x}$ remain untouched. The solver respects all constraints given in the original problem, thus it always produces a feasible solution.

The acceptance criterion is greedy—the solution found by the solver is accepted only if it is better than the currently best one.

3.2.1 Selecting subproblems

The performance of LNS is largely influenced by the choice of a subproblem to be solved by the MIP solver. In our approach for the machine reassignment problem, a subproblem is defined by selecting a subset of machines $\mathcal {M}_{x}\subset \mathcal {M}$ and consists in (sub)optimally reassigning the processes assigned to these machines.

We consider two selection variants. The first variant assumes that machines for $\mathcal {M}_{x}$ are selected randomly from all machines in $\mathcal {M}$. In the second one, we try to select a subset of machines which is the most promising in terms of potential decrease in the solution cost.

We consider subsets of $\mathcal {M}$ not larger than ${ maxNumMachines}$. Among all such subsets we would like to select the one that, optimistically, allows us to obtain the biggest improvement of the solution. As considering all subsets is computationally infeasible, we fall back to a heuristic approach. To this aim, from the set $\mathcal {M}$ we consider only two machines at a time, defining their potential as

$$\begin{aligned} { potential}(m_{1},m_{2})={ optimistic}(\left\{ m_{1},m_{2}\right\} )/(1+{ used}(m_{1})+{ used}(m_{2})), \end{aligned}$$

where $optimistic({\mathcal {M}}_{x})$ is the optimistic improvement, i.e., the difference between the current solution cost and the lower bound of subproblem induced by $\mathcal {M}_{x}$. The lower bound for the subproblem is calculated in the same way as for the whole problem (cf. Sect. 2.3). The variable $used(m)$ is the number of times a machine $m$ has been selected before in some set $\mathcal {M}_{x}'$. By dividing the expression by $1+used(m_{1})+used(m_{2})$ we promote machines which have not been considered by the algorithm so far.

In order to construct the subset $\mathcal {M}_{x}$, first we take two machines $(m_{1},m_{2})$ which have the largest ${ potential}(m_{1},m_{2})$. Then, we iteratively add more machines. In each step, from all machines not yet added to $\mathcal {M}_{x}$, we add such machine $m\in \mathcal {M}$ that maximizes the formula:

$$\begin{aligned} \max _{m_{x}\in \mathcal {M}_{x}}{ potential}(m_{x},m). \end{aligned}$$

We stop adding machines when the size of $\mathcal {M}_{x}$ equals ${ maxNumMachines}$ or when the number of processes assigned to machines in $\mathcal {M}_{x}$ exceeds ${ maxNumProcesses}$.

3.2.2 Solving the subproblem

After selecting the set of machines $\mathcal {M}_{x}$ the related subproblem is modeled as a mixed integer programming problem. The model is described in detail in “Appendix 1”. In this section we only introduce its main properties.

Modeling the capacity constraints, transient usage constraints and conflict constraints is straightforward and requires linear equations only. It is harder to model spread and dependency constraints for which introducing additional variables is necessary.

The objective function is a sum of a number of nonlinear elements (maximum function). Thus, every balance and load cost that applies to machines from $\mathcal {M}_{x}$ requires introducing an additional variable to model the maximum function in a linear way. Process and machine move costs can be explicitly defined as a linear function of input variables. Finally, modeling service move costs requires both the introduction of additional variables and a nonlinear function.

We solve the resulting mixed integer programming problem with IBM CPLEX solver version 12.5. Table 2 presents the parameters of the solver. Notice that in order to provide reproducibility, the stopping criterion is not related to the computation time and it is dependent only on $NodeLim$. Thus the algorithm is deterministic.⁴

Table 2 IBM CPLEX parameters. If not specified, default values were used

3.2.3 Dynamic adaptation of subproblem size

The general guidelines for designing LNS-based algorithms (Blum et al. 2011) state that the subproblem size should be large enough to diversify the search, but, at the same time, small enough to solve it quickly and allow the algorithm to perform many iterations. For this purpose we allow the algorithm to dynamically change the subproblem size. Initially, ${ maxNumMachines}$ is set to 2 and ${ maxNumProcesses}$ to 100. If the solver reports that the subproblem has been solved optimally, the algorithm concludes that the size of the subproblem might be too small, and increases ${ maxNumMachines}$ by 0.025 and ${ maxNumProcesses}$ by 0.5. However, if the solver reports that it failed to solve the current subproblem optimally, the algorithm decreases the ${ maxNumMachines}$ by 1 and the ${ maxNumProcesses}$ by 20 (the constants were chosen experimentally). In this way, the algorithm can dynamically self-adjust to the problem instance characteristics.

3.2.4 Improving the solution by local search

If the MIP solver improves the solution by solving a given subproblem, it might be possible to quickly improve the solution of the problem further using the greedy hill climber described in Sect. 3.1. To increase efficiency, the hill climber initially considers only machines which have been changed by the solver. For this purpose, we execute it with the tabu list including all machines unchanged by the solver.

4 Experiments and results

4.1 The dataset

The organizers of the ROADEF/EURO Challenge 2012 provided two set instances, A and B, 10 instances each. Set A contains small instances and has been used for the qualification phase, while set B, containing larger instances, has been released to help teams with preparing algorithms for the final round.⁵

Table 3 summarizes the characteristics of the instances from both sets.

Table 3 The main statistics of instances used in ROADEF/EURO Challenge 2012

4.2 Performance measure

Since the solution cost is difficult to interpret and hard to compare across problem instances, for the presentation of results, we employ a measure of improvement of a solution over the original one, defined as:

$$\begin{aligned} { improvement}({ solution})=\frac{{ cost(originalSolution)}-{ cost(solution})}{{ cost(originalSolution)}}. \end{aligned}$$

Improvement can be expressed as a percentage: 0 % means no improvement over the original solution and 100 % means that the cost of the original solution has been reduced to 0.

4.3 Experimental environment

In the following experiments we allow an algorithm to run for $300$ s, since this was the time limit in ROADEF/EURO 2012 challenge. Our algorithm was implemented in Java and executed using Java 1.7.0_04 on a 64bit Linux machine with Intel Core i7 950 3.07 GHz processor and 6GB of RAM. Although the processor has four cores, the algorithm utilizes only one of them. As a mixed integer programming solver we used IBM ILOG CPLEX Optimizer 12.5.

4.4 Comparison of algorithm variants

In the first experiment we compare nine variants of our algorithm. The goal is not only to determine which variant is the best, but also to justify the presence of all components of the algorithm.

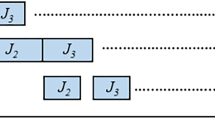
The variants are: hc, lns, lnshc, lnsr, lnsrhc, hc-lns, hc-lnsr, hc-lnshc, hc-lnsrhc. hc is the greedy hill climber algorithm described in Sect. 3.1 while lns is the large neighborhood search algorithm introduced in Sect. 3.2; lnsr is a variant of lns, in which subproblems are selected randomly instead of being selected using the optimistic improvement heuristic (cf. Sect. 3.2.1). The string hc after lns or lnsr means that after solving a subproblem, the algorithm tries to further improve the solution using the greedy hill climber as described in Sect. 3.2.4. Variants whose name start with hc- consists of two phases: first they quickly improve the solution with the greedy hill climber and then switch to some variants of large neighborhood search: either lns, lnsr, lnshc, or lnsrhc. Figure 3 illustrates these nine variants of algorithms with the emphasis on particular search phases.

Fig. 3

Flowchart illustration of the compared algorithms variants

The results for instances of set A and B of the nine algorithm’s variants are presented in Table 4. The table shows average improvements and their standard deviations expressed as percentage points. The average is obtained by running each algorithm 25 times with different random seeds. The algorithms were ordered by decreasing average improvement. The first row of each table presents upper bound of the improvement (thus lower bound of the cost) computed using the method described in Sect. 2.3. We compare the algorithms in terms of two instance sets A and B separately, since the instances in set A are much smaller than those in set B (cf. Sect. 4.1), and thus, they may reveal different characteristics of considered algorithms.

Table 4 Comparison of algorithm variants

First, let us consider the greedy hill climber (i.e., hc). Although, overall, this is the worst variant of all considered, being such a simple algorithm, it gets surprisingly good results in absolute terms. Most importantly, however, hc is fast, because it terminates as soon as it cannot make any local improvements. The low running times of hc, which are presented in Table 5, makes it a practical choice if the time to obtain a solution matters more than the solution’s quality. Observe that for all instances from set A, the algorithm finishes in less than half a second. For set B, it uses up to 60 s, but at the same time it achieves an average improvement of $62.32\,\%$, which is close to the lower bound’s improvement of $64.31\,\%$ (see Table 4).

The greedy hill climber algorithm is also a good choice for the first phase of any algorithm. This is observed for set B—all the algorithms starting with hc- are superior to their non-hc counterparts. This statement does not hold for set A, since variants lns and lnshc perform better than some hc- variants. Notice, however, that the differences between the first six algorithms for set A are minor: lns, which is second in the ranking, achieves the average improvement of $41.09\,\%$, while the sixth hc-lns obtains $40.92\,\%$.

Table 5 Average running times for the greedy hill climber, in seconds

Next, we would like to answer the question whether the optimistic improvement heuristic is a better subproblem selection method than the random one. We can see that for both instance sets, on average: (1) hc-lnshc is better than hc-lnsrhc, (2) lns is better than lnsr, iii) lnshc is better than lnsrhc. Although the results for set A indicate that hc-lnsr outperforms hc-lns, the difference between these methods is minimal. Thus, although lns does not strictly dominate over lnsr, we conclude that it is a more robust method of choosing subproblems.

The obtained results do not answer the question whether it is worth improving the solution further using the greedy hill climber after a successful solver improvement. Although hc-lnshc is on average better than hc-lns, hc-lnsr outperforms hc-lnsrhc. Moreover, lnshc and lnsrhc are worse than lns and lnsr, respectively.

Finally, let us point out that the best algorithm for both data sets is hc-lnshc. This is also the algorithm which has the largest number of best results: it is best in 6 out of 10 cases in set A and 7 out of 10 cases in set B. Note also that although the programs were executed $25$ times with random seeds the results for a given program were mostly the same or at least very similar to each other. The small variance allows to reason about statistical significance of the obtained results. On the other hand, the results concern only an arbitrary set of instances, so it is not possible to make any general statements about relative superiority of one algorithm over the other.

Although the analysis of algorithms in terms of improvements achieved in a given time limit allows for an easy comparison, it neglects algorithms dynamics. To analyze the algorithms time characteristics, we plotted the improvement in the function of time. We concentrate here on eight instances, for which the plots are the most diverse. Figure 4 shows the results for instances a1_4, a2_2, a2_3, a2_5, b_01, b_07, b_08, and b_10. Plots for other instances can be found in “Appendix 2”. Each point in a plot is an average over 25 runs of a certain algorithm; for clarity of the presentation, the standard deviations have not been shown. Notice, however, that the standard deviations reported in Table 4 are non significant. We introduce different scales for each instance to amplify the visual differences between algorithms.

Fig. 4

Comparison of algorithm variants in time. lnsr-* variants has been excluded for better readability. See “Appendix 2” for plots involving all algorithms

The observation we can make analyzing the plots concerns the comparison between hc- variants (plotted with solid lines) and other ones (plotted with dashed lines). Notice that, generally, when the algorithm starts with the greedy hill climber, it gets higher improvements more quickly. This is especially evident for large instances from set B. For these instances, but also for a2_2 to some extent, the results obtained solely by the greedy hill climber remain for some time better than the ones produced by any large neighborhood search variant. Surprisingly, for the largest b_10 instance, some large neighborhood search variants (lnshc and lns) were unable to overtake the simple hill climber even in 300 s. lns and lnshc improve the solution so slowly for the two largest instances b_10 and b_07 that they fall behind with respect to the greedy hill climber method for the whole set B (cf. Table 4).

4.5 Comparison with best ROADEF/EURO challenge algorithms

Our algorithm won the first place in the ROADEF/EURO Challenge 2012 competition in the junior category and the third place in the general classification. The winner in the general classification was team S41.⁶ while the second place went to team S38.⁷ Since both teams competed in the open source category and made their solutions publicly available, we were able to directly compare their algorithms with our approach on the same machine.⁸

Unlike the competition where each submitted program was executed only once, we executed each of the compared algorithms for all instances 25 times with different random seeds. Thus, our results may be considered as more reliable than the results of the competition. Moreover, we are able to reason about robustness of the algorithms.

In this section we compare hc-lnshc, our best variant, with the programs submitted by teams S38 and S41. The hc-lnshc algorithm is a simplified version of the algorithm submitted by us to the competition. The differences between the submitted version and hc-lnshc are twofold. First, the submitted algorithm used the greedy hill climber and large neighborhood search wrapped in a hyper-heuristic. However, in post-competition experiments we have found that this additional layer does not improve the results, while adding unnecessary complexity to the method. Second, in the submitted version the termination condition of the solver was computation time (500 ms), which makes the algorithm behave differently on computers of different speeds. As we noted in Sect. 3.2.2, the algorithm described in this paper uses a deterministic termination condition to bypass this problem.

The algorithms of teams S38 (Mehta et al. 2012) and S41 (Gavranović et al. 2012) were implemented in C and C++, respectively. We compiled the source code with gcc and g++ compilers, respectively, using standard optimizations (most notably, -O3 flag). As the competition rules allowed using two CPU cores, the program prepared by the team S41 uses two threads for computations. Both the S38 solution and our solution use only a single thread.

Table 6 contains results of the comparison in the same format as Table 4. Although for both instance sets S41 is on average the best, neither algorithm is the best on all instances. When considering all 20 instances, S41 is the best on 10 instances, whereas hc-lnshc on 7 instances and S38 on 5 instances. Notice that for most instances the differences between algorithms are minor. Exceptions include instances a2_2 and a2_3, where S41 achieves much better results than other algorithms, and a1_4, where hc-lnshc (but also S38) is significantly better than S41.

Table 6 Comparison of hc-lnshc with open source algorithms provided by the two best teams of the competition

The advantage of hc-lnshc algorithm lies in its robustness, which is noticeable in its low variance. For 17 out of 20 instances, the standard deviation error of hc-lnshc is less than 0.01 % and the source of indeterminism of hc-lnshc lies only in the time-dependent stopping criterion for the whole program (the program was terminated after 300 s). In contrast, the dispersion of results obtained by S41 is larger, especially for set A (but also b_01). The algorithm with the highest variance is S38, whose standard deviation for a2_2 exceeds 1.20 %.

Figure 5 presents the dynamics of all algorithms for 8 instances. Despite S41 being clearly the best algorithm for a2_2 and a2_3, it can be observed that for other instances, it progresses significantly slower than both S38 and hc-lnshc.

Fig. 5

Comparison of S41, S38 and hc-lnshc in time

5 Discussion

In the proposed approach for the machine reassignment problem, we do not employ a single algorithm, but instead we combine several different algorithms including local search heuristics and exact mathematical programming techniques. Interestingly, this approach follows a wider trend in solving real-world combinatorial optimization problems which is referred to as hybrid metaheuristics (Blum and Roli 2008). Such hybrid approaches are believed to benefit from synergetic exploitation of complementary strength of their components. Indeed, many works concerning non-trivial optimization problems report that hybrids are more efficient and flexible than traditional metaheuristics applied separately (Prandtstetter and Raidl 2008; Burke et al. 2010; Hu et al. 2008; Cambazard et al. 2012). In this work we confirm these observations.

According to the classification of hybrid metaheuristics proposed by Puchinger and Raidl (2005), the MIP-based LNS approach can be regarded as an integrative master–slave combination, where one algorithm acts at a higher level and manages the calls to a subordinate algorithm. Since the combination includes mathematical programming which is embedded in a metaheuristic framework, it can be also viewed as a matheuristic (Maniezzo and Voß 2009). However, in contrast to most of these previous approaches, we precede the LNS with a greedy hill climber algorithm based on a simple move-based neighborhood. For this reason our approach also resembles collaborative sequential combination of metaheuristic algorithms.

6 Conclusions

The purpose of this study was to present and analyze a hybrid metaheuristic approach for the machine reassignment problem—a hard optimization problem of practical relevance. We showed that a combination of straightforward local search heuristic and fine-tuned large neighborhood search can benefit from complementary characteristics of both constituent algorithms. In particular, the fast hill climber component turned out to be crucial for bigger instances of the problem for which exploring large neighborhoods was excessively time-consuming. On the other hand, due to a large number of constraints and dependencies defined in the problem, reassigning single processes only was often not enough to escape from local optima. In such situations, exploring much larger neighborhoods and making many process reassignments at once was indispensable for obtaining high quality results.

Although the proposed algorithm achieved third place overall in the ROADEF/EURO 2012 Challenge, the comparison with the best two entries reveals that the top three results were not substantially different. Clearly, no single best algorithm beat the other ones on all the available problem instances. The performance of considered algorithms is largely influenced by characteristics of particular instances, and to some extent, also by the seed of a random number generator. In this context, it is worth pointing out that our algorithm is the least sensitive to the randomness—the standard deviation of its average results is the smallest.

An interesting direction for future work is to investigate what kind of instances are favored by specific algorithms. We can hypothesize that combining ideas of the three algorithms in the instance-specific approach may outperform these algorithms applied separately. Taking one step further would include conducting a fitness landscape analysis (Watson et al. 2005), which could shed new light on the search space characteristics that make certain instances particularly hard to solve. This could potentially explain the differences in algorithm performances and help design more robust approaches.

Appendices

Appendix 1: Mixed integer programming model

1.1 Input of the model

The input of the model consists of five elements:

• the machine reassignment problem instance including the $originalSolution$.

• $initialSolution$—current solution to be improved by the solver (not necessarily the original one),

• $\mathcal {P}_{x}$—the set of processes that could be relocated by the solver. Additionally, $\mathcal {S}_{x}$ is the minimal set of services containing all processes from $\mathcal {P}_{x}$,

• $\mathcal {M}_{x}$—the set of machines to which the processes from $\mathcal {P}_{x}$ are allowed to be moved. To ensure feasibility of the model, $\mathcal {M}_{x}$ must include all machines to which processes from $\mathcal {P}_{x}$ are assigned.

1.2 Output

The output from the solver is a set of new assignments for every process $p\in \mathcal {P}_{x}$. Each process can be assigned to one machine $m\in \mathcal {M}_{x}$. Thus, the output consists of $|\mathcal {P}_{x}|*|\mathcal {M}_{x}|$ decision variables $x_{pm}$, where $p$ is the index of a process and $m$ is the index of a machine. $x_{pm}$ is 1 if and only if the process $p$ is assigned to machine $m$; it is 0 otherwise:

$$\begin{aligned} \forall _{p\in \mathcal {P}_{x},m\in \mathcal {M}_{x}}x_{pm}\in \{0,1\}. \end{aligned}$$

(1)

1.3 Constraints

Some constraints described in this section refer to variables $x_{pm}$ that are not considered in the model $(p\notin \mathcal {P}_{x})$. In such cases, $x_{pm}$ is a constant, which values is indicated by the $initialSolution$.

1.3.1 Basic integer programming constraints

Every process must be assigned to exactly one machine:

$$\begin{aligned} \forall _{p\in \mathcal {P}_{x}}\sum _{m\in \mathcal {M}_{x}}x_{pm}=1. \end{aligned}$$

(2)

1.3.2 Capacity constraints

The goal of the solver is to find assignments only for a small subset of processes, thus for capacity constraints we consider only machines $m\in \mathcal {M}_{x}$.

(3)

where

$$\begin{aligned} U(m,r)=\sum _{\begin{array}{c} p\in P \text{ such }\\ \text{ that } M(p)=m \end{array}}R(p,r). \end{aligned}$$

(4)

As only some machines and processes are considered by the solver, we can decompose usage $U(m,r)$ into variable and constant parts:

$$\begin{aligned} U(m,r)=U_{const}(m,r)+U_{var}(m,r), \end{aligned}$$

(5)

where

$$\begin{aligned} U_{const}(m,r)&= \sum _{\begin{array}{c} p\notin \mathcal {P}_{x} \text{ such }\\ \text{ that } M(p)=m \end{array}}R(p,r), \end{aligned}$$

(6)

$$\begin{aligned} U_{var}(m,r)&= \sum _{p\in \mathcal {P}_{x}}(R(p,r)\cdot x_{pm}). \end{aligned}$$

(7)

Thus, the set of capacity constraints

(8)

is transformed to:

(9)

where $U_{const}(m,r)$ is constant for any $m\in \mathcal {M}_{x}$, $r\in {\mathcal {R}}$.

1.3.3 Transient constraints

For transient constraint let us define transient usage $TU$ as follows:

$$\begin{aligned} TU(m,r)=\sum _{\begin{array}{c} p\in \mathcal {P} \text{ such }\\ \text{ that } M(p)=m\,\vee \, M_{0}(p)=m \end{array}}R(p,r). \end{aligned}$$

As for modeling the capacity constraints, we split $TU$ into the constant part (processes not considered in the model) and the variable part:

$$\begin{aligned} TU(m,r)=TU_{const}(m,r)+TU_{var}(m,r), \end{aligned}$$

where

$$\begin{aligned} TU_{const}(m,r)&= \sum _{\begin{array}{c} p\notin \mathcal {P}_{x} \text{ such }\\ \text{ that } M(p)=m\,\vee \, M_{0}(p)=m \end{array}}R(p,r), \\ TU_{var}(m,r)&= \sum _{p\in \mathcal {P}_{x}}(R(p,r) \cdot \max (x_{pm},x_{p_{0}m})). \end{aligned}$$

Finally, we get:

$$\begin{aligned} \forall _{m\in \mathcal {M}_{x},r\in \mathcal {R}} \sum _{p\in \mathcal {P}_{x}}(R(p,r)\cdot \max (x_{pm},x_{p_{0}m})) \le C(m,r)-TU_{const}(m,r). \end{aligned}$$

1.3.4 Conflict constraints

Conflict constraints are modeled as:

$$\begin{aligned} \forall _{s\in \mathcal {S}_{x}} \forall _{m\in \mathcal {M}_{x}}\sum _{p\in s}x_{pm}\le 1 \end{aligned}$$

(10)

1.3.5 Spread constraints

Spread constraints cannot be modeled directly. To introduce them into the model, additional variables are required. For every location $l\in L$ and every service $s\in \mathcal {S}$, we introduce a variable $y_{ls}$, which is 1 if the location $l$ in the service $s$ has at least one process, and 0 otherwise:

$$\begin{aligned}&\displaystyle \forall _{s\in \mathcal {S}_{x},l\in L}y_{ls}\in \{0,1\}, \end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle \forall _{s\in \mathcal {S}_{x}}\sum _{l\in L}y_{ls}\ge spreadMin(s). \end{aligned}$$

(12)

For $y_{ls}$ we need two additional constraints. First, if there is no process $p$ in service $s$ that is assigned to machines $m$ in location $l$, then $y_{ls}$ must be equal to $0$:

$$\begin{aligned} \forall _{s\in \mathcal {S}_{x},l\in L} \quad \sum _{p\in s,m\in l}x_{pm}-y_{ls}\ge 0. \end{aligned}$$

(13)

Second, when at least one process $p\in s$ is assigned to machine $m\in l$, $y_{ls}$ must equal $1$:

$$\begin{aligned} \forall _{s\in \mathcal {S}_{x},l\in L} \sum _{p\in s,m\in l}|P|\cdot y_{ls}-x_{pm}\ge 0, \end{aligned}$$

(14)

where $|P|$ is the number of processes.

1.3.6 Dependency constraints

Dependency constraints are modeled as:

$$\begin{aligned} \forall _{s_{1}\in \mathcal {S}}\forall _{s_{2}\in (dep(s_{1}))} \forall _{n\in N}|P|\cdot \sum _{m\in n}\sum _{q\in s_{2}}x_{qm}- \sum _{m\in n}\sum _{p\in s_{1}}x_{pm}\ge 0 \end{aligned}$$

(15)

1.4 Objective function

The objective function is a sum of five elements:

$$\begin{aligned} f(variables)=LC+BC+PMC+SMC+MMC. \end{aligned}$$

(16)

Each element of the sum will be considered separately in the following paragraphs. Notice that the modeled objective function does not take into account the costs related to processes or machines which are not part of the subproblem. Obviously, this objective function is consistent with the objective function for the whole problem.

1.4.1 Load cost

Load cost for a single resource is defined as a sum:

$$\begin{aligned} loadCost(r)=loadCostWeight(r)\cdot \sum _{m\in \mathcal {M}_{x}} \max (0,U(m,r)-SC(m,r)). \end{aligned}$$

(17)

In our model, $U(m,r)$ is replaced by Eqs. (5), (6) and (7). Since the problem is to minimize the value of the load cost, function $\max$ can be modeled by introducing an artificial variable. In general, function $\max (a,b)$ can be replaced by a variable $f$ with two constraints:

$$\begin{aligned} f\ge a, \end{aligned}$$

(18)

$$\begin{aligned} f\ge b. \end{aligned}$$

(19)

Thus, the $\max$ function from Eq. 17 can be replaced by a variable $z_{rm}$ with constants:

$$\begin{aligned}&\displaystyle \forall _{m\in \mathcal {M}_{x}}\forall _{r\in \mathcal {R}}z_{rm}\ge 0, \end{aligned}$$

(20)

$$\begin{aligned}&\displaystyle \forall _{m\in \mathcal {M}_{x}}\forall _{r\in \mathcal {R}}z_{rm} -\sum _{p\in \mathcal {P}_{x}}R(p,r)\cdot x_{pm}\ge U_{const}-SC(m,r). \end{aligned}$$

(21)

Finally, the load cost function is modeled as:

$$\begin{aligned} LC=\sum _{r\in \mathcal {R}}(loadCostWeight(r) \cdot \sum _{m\in \mathcal {M}_{x}}z_{rm}). \end{aligned}$$

(22)

Note that $z_{rm}$ variable should be an integer. However, examination of the goal function shows that the optimizer will assign the lowest possible integer value to $z_{rm}$ even if $z_{rm}$ is a continuous variable, because all parameters of the max function are integers.

1.4.2 Balance cost

A single balance cost is defined as:

$$\begin{aligned} balanceCost(b)=\sum _{m\in \mathcal {M}_{x}}\max (0,target \cdot A(m,r_{1})-A(m,r_{2})), \end{aligned}$$

(23)

where

$$\begin{aligned} A(m,r)=C(m,r)-U(m,r). \end{aligned}$$

(24)

We dispose of the $\max$ function as described in Sect. 7.4.1 Every occurrence of this $\max$ function is replaced by a variable $t_{bm}$ with constraints

$$\begin{aligned} \forall _{m\in \mathcal {M}}\forall _{b\in \mathcal {B}}t_{bm}\ge 0, \end{aligned}$$

(25)

and

$$\begin{aligned} \begin{array}{cl} \forall _{m\in \mathcal {M}_{x}}\forall _{b\in B} &{} t_{bm}+target\cdot \sum _{p\in \mathcal {P}_{x}}(x_{pm} \cdot R(p,r_{1}))-\sum _{p\in \mathcal {P}_{x}}(x_{pm}\cdot R(p,r_{2}))\\ &{} \quad \ge target\cdot (C(m,r_{1})-U_{const}(m,r_{1}))-(C(m,r_{2})-U_{const}(m,r_{2})). \end{array} \end{aligned}$$

(26)

Finally, the balance cost is modeled as:

$$\begin{aligned} BC=\sum _{b\in \mathcal {B}}\left( weightBalanceCost(b) \sum _{m\in \mathcal {M}_{x}}t_{bm}\right) . \end{aligned}$$

(27)

1.4.3 Process move cost

We model the process move cost as:

$$\begin{aligned} PMC=-procesMoveCostWeight\cdot \sum _{p\in \mathcal {P}_{x}}PMC(p) \cdot x_{pm_{0}}, \end{aligned}$$

(28)

where $x_{pm_{0}}$ refers to a variable that indicates that process $p$ was reassigned back to its original machine $m_{0}$.

1.4.4 Service move cost

To model the service move cost additional variables are required. Let us define $SMC_{s}$ as a variable which denotes the number of processes from service $s$ that are assigned to other machines than in $originalSolution$:

$$\begin{aligned} \forall _{s\in \mathcal {S}_{x}}\sum _{p\in s}x_{pm_{0}}+SMC_{s}=|s|, \end{aligned}$$

(29)

where $x_{pm_{0}}$ is defined in Sect. 7.4.3.

The total service move cost ($SMC$) is modeled with a set of constraints:

$$\begin{aligned} \forall _{s\in \mathcal {S}_{x}}SMC-serviceMoveCostWeight\cdot SMC_{s}\ge 0 \end{aligned}$$

(30)

Notice that the above constraints refer only to services containing processes that could be moved. To implement this cost correctly it is necessary to add a constraint with a constant value of service move cost for services which cannot be reassigned in this model. This can be modeled by the following set of constraints:

$$\begin{aligned} \forall _{s\notin \mathcal {S}_{x}}SMC\ge serviceMoveCostWeight\cdot SMC_{s}. \end{aligned}$$

(31)

1.4.5 Machine move cost

Machine move cost can be modeled without any additional transformations:

$$\begin{aligned} MMC=machineMoveCostWeight\cdot \sum _{p\in \mathcal {P}_{x}} \sum _{m\in \mathcal {M}_{x}}(MMC(M_{0}(p),m)\cdot x_{pm}). \end{aligned}$$

(32)

Appendix 2: Detailed results

See Figs. 6, 7 and Table 7.

Table 7 The table shows lower bounds, ‘best found’ solutions and ROADEF/EURO competition solutions in terms of improvement and absolute cost for instances from sets A and B

Fig. 6

Comparison of all algorithm variants for set A

Fig. 7

Comparison of all algorithms variants for set B