1 Introduction

Despite decades of research and development, the efficient recovery of oil from reservoir rock remains a challenging problem. Even with current improved oil recovery (IOR) methods, a significant volume of the oil typically remains behind in the reservoir (Sheng 2013). Different IOR strategies are being explored to retrieve more oil (while also minimizing the ecological footprint of the recovery process itself). Most common are methods based on water injection (Goolsby and Anderson 1964; Rausch and Beaver 1964; Hussain et al. 2013; Esmaeili and Maaref 2019), for which different strategies are followed: adding alkali, polymers, surfactants or nanoparticles, or adjusting the ion composition. The latter, also known as Smart Water Flooding (SWF) is a relatively recent technique which has been reported to give higher yields than conventional (sea) water injection, (Bernard 1967) in both sandstone (Tang and Morrow 1999; Morrow and Buckley 2011) and carbonate (Gupta et al. 2011; Yousef et al. 2011; Shehata et al. 2014; Nasralla et al. 2016, 2018) reservoirs.

However, a comprehensive understanding of how SWF works is still lacking, as evidenced by scattered results from different field studies specifically in clastics, (Bartels et al. 2019) and ongoing debates on underlying mechanisms in the scientific literature (Hao et al. 2019), in particular to carbonate reservoirs. Convergence towards a unified understanding has been hampered by the difficulty to acquire experimental data that allow straightforward analysis on the effect of changing the water flooding condition. An important reason for this deficiency is that experiments using core plugs are both time-consuming and costly. In the past decade, microfluidics has emerged as a potential alternative, offering a visualization of the retention and transport of oil and water at the micro and nano length scales pertinent to oil reservoirs (Lifton 2016; Mohammadi and Mahani 2020). In principle, both quantification of residual oil and mechanistic insights could be obtained from such visualizations, especially when combined with systematic variation of the flooding water composition. Microfluidics offers such possibilities via a flexible design of the pore space and accurate fluid control, at relatively low cost (Cao et al. 2019).

However, one major challenge associated with the microfluidic approach is the difficulty in mimicking two ideal conditions simultaneously: optical access to the pore space and a good representation of the (geo) chemical ingredients (crude oil, brine and rock). In relation to this, most micro-fluidic studies on SWF have optimized either one or the other aspect.

Various studies were undertaken with the emphasis on representing the pore structure of oil reservoirs. The first microfluidic device named reservoir on-a-chip (Gunda et al. 2011) (ROC) was fabricated with this purpose in 2011. In this 2D micromodel the connected pores were all lying in a single plane, thereby making optical access easy. It has also been realized in this study that the chip-level oil recovery trends can be correlated to the results of actual reservoir core flooding experiments. Since then, a variety of 2D micromodels have been developed, from various materials such as glass (Grate et al. 2012; Karadimitriou et al. 2012), silicon (Gunda et al. 2011; Grate et al. 2013; Song and Kovscek 2015) and polymers (Berejnov et al. 2008; Sollier et al. 2011; Ma et al. 2012; Wu et al. 2015). To better represent the fluid processes occurring in 3D porous media, so called 2.5D (Xu et al. 2017; Yu et al. 2019) and dual porosity/depth micromodels (Buchgraber et al. 2012; Yun et al. 2017) were also established. In micromodels with dimensionality higher than 2, visualization of the rock and the fluids generally requires the use of dedicated imaging techniques and/or adaptation of the materials; examples are the application of X-ray computer tomography using brines enriched in heavy metal ions (Berg et al. 2013; Reynolds et al. 2017) or the use of glass beads together with two immiscible fluids having the same refractive index in optical microscopy studies (Krummel et al. 2013; do Nascimento et al. 2019). To capture the physical aspects, the model fluids were selected to present clearly different wettability characteristics for the model rock surfaces (Lee et al. 2015).

Other studies focused more on an adequate representation of the chemistry of the rock surface. Alzahid et al. (2018) developed a method to coat sandstone and carbonate minerals on a poly(dimethylsiloxane) (PDMS) surface. They could visualize multi-phase flow phenomena such as snap-off (Roof 1970) and corner flow (Mohanty et al. 1987) that usually occur in reservoir rock. Wang et al. (2017) coated a thin layer of calcite crystals on cover glass to achieve the proper mineral-fluid contact. Yun et al. (Wonjin et al. 2020) later used this calcite coated microfluidic chip to both quickly and cost-effectively prescreen surfactant chemicals used for oil recovery tests in carbonate cores. Doyle et al. (Lee et al. 2016) developed a method to coat the inner surfaces of microchannels in situ with CaCO3, to achieve tunable porosity and geochemical properties.

Also real rock surfaces were used in microfluidic chips: Song et al. (2014) used carbonate rock to study geological processes, while Mohammadi and Mahani (2020) reported on the use of natural calcite rock. Singh et al. (2017) designed a new microfluidic test bed called “Real Rock Microfluidic Flow Cell (RR-MFC)”, wherein a 500 µm-thick North Sea reservoir rock sample was mounted inside a PDMS microfluidic channel. Gerold et al. (2018) fabricated and used a microfluidic device called “Flow On Rock Device (FORD)” by directly integrating thin sections of reservoir rock into micro-fluidics for oil recovery studies. While these microfluidic chips should offer a closer correspondence with the (geo) chemical properties in real oil reservoirs, they have not been used with water and oil as co-existing phases in three dimensions to the best of our knowledge. Also the geometry of the pore network did not always correspond closely to that of real reservoirs, which often display a ‘grainy’ 3D nature with dual porosity (Cantrell and Hagerty 1999).

This current state of know-how, where simplifications of the real porous medium in oil reservoirs have been applied along either ‘physical’ or ‘chemical’ lines, has prompted us to explore a hybrid approach, in which a close chemical representation of the rock material is combined with a corresponding 3D and double porosity aspects of the porous network. This is achieved by packing mineral particles inside a microfluidic chip. In this work, we have used synthetic calcite particles to mimic carbonate reservoirs; in this case a proper representation of the chemistry is particularly important, since the calcite can not only ad/desorb organic molecules, but is also prone to dissolution and precipitation (Buhmann and Dreybrodt 1985; Liang et al. 1996; Zuddas and Mucci 1998).

An inherent compromise with our approach is that optical accessibility is limited: water, oil and calcite all have very different refractive indices, with the consequence that any visible light impinging on the packed bed will be strongly scattered. Visualization of the spatial distribution of the three components with an optical microscope is hence restricted to a thin layer near a transparent bounding surface. This raises the question, to which depth it is still possible to obtain reliable information about the distribution of water, oil and rock phases. An additional question is, to what extent the proximity of the wall could influence the structure of the porous medium and the ensuing distributions of water and oil.

In the present work we mainly focus on addressing the first question, while we touch upon the second one. We will consider optical microscopy observations up to penetration depths, where the images get completely blurred, and use image enhancement and analysis techniques to identify the smaller depth range in which the water, oil and calcite volume fractions can still be measured. Using the image data for this depth range, we measure the amount of oil at various locations inside the packed bed, and average over it, to obtain a reliable number for the residual oil saturation. Measurement of this ROS value as a function of time (or equivalently, injected pore volumes) is then used to study the effect of changes in the waterflooding conditions. Two variations will be explored: the capillary number of the water injection, and the wettability of the calcite particles. We will show that a packed-bed microfluidic chip, combined with our image analysis method, allows to detect changes in ROS caused by changes in the waterflooding physicochemical conditions.

2 Experimental section

2.1 Materials inside microchannels

All chemicals were obtained from Sigma Aldrich. To mimic the rock material of carbonate reservoirs, CaCO3 was synthesized using only sodium carbonate (Na2CO3) and calcium chloride (CaCl2). A precursor Na2CO3 solution (100 mL, 50 mM) was adjusted from pH 11.7 to pH 10.0 by adding HCl, and then mixed with a solution of CaCl2 (100 mL, 50 mM) by gently stirring with a magnetic bar for 2 min. The resulting supersaturated solution was kept at 22 °C for 24 h to allow precipitation. The CaCO3 precipitates were then washed three times with ethanol, dried and characterized by scanning electron microscopy (JEOL JSM 5610) and confocal Raman microscopy (WiTec Alpha 300R, using a 532 nm excitation laser).

Deionized water (Millipore Synergy, conductivity: 18 MΩ cm−1, viscosity: 1.0 mPa. s) with 1.0 mM fluorescein and heavy mineral oil (viscosity ≈ 55–61 mPa. s) were used in the waterflooding experiments. At 22 °C, the oil/water interfacial tension is 46 mN/m. The DI water and oil have respective densities ρ1 = 0.998 g/cm3 and ρ2 = 0.86 g/cm3. Equilibrated formation water (eqFW), a high salinity brine containing water soluble organic components from crude oil (CRO), was prepared as described in the Supporting Information. The key physicochemical characteristics of CRO are summarized in Table S1. Formation water with a defined ionic composition (shown in Table S2) was initially prepared. Then equal parts of CRO and FW were equilibrated in the presence of few Iceland spar chip at 95 °C for a period of 48 h. After cooling to room temperature, the brine phase (eqFW) was isolated using a separating funnel and stored in sealed glass containers.

2.2 Surface characterization

The eqFW was used to modify both the inner glass wall and the calcite packed bed of the microchannel. To examine the effects of this 'aging’ treatment on the separate materials, contact angle measurements of mineral oil droplets in ambient water were measured using a goniometer (Dataphysics OCA 20L) in the captive bubble mode. Freshly cleaved Iceland spar (Ward's Science) and cover glass were examined before and after being immersed in eqFW at room temperature for 18 h. In addition, chemical analyses of calcite powders before and after aging were performed, via Fourier transform infrared (FTIR) spectroscopy with a Bruker Alpha spectrometer operated in attenuated total reflection mode. Thermogravimetric analysis (TGA) on calcite powders was performed using a NETZSCH STA 449 F3 Instrument under a nitrogen atmosphere and heating rate of 20 °C/min.

2.3 Microfluidic chip design and fabrication

A schematic illustration of the poly(dimethylsiloxane) (PDMS) microchannel is shown in Fig. 1a (see SI Fig. S1 for additional design aspects). The channel has two inlets and an outlet, each 0.8 mm in diameter. A perpendicular side port (Fig. S1) facilitates a fast fluid exchange between the different water-flooding operations. The microchannel dimensions are 8 mm (length) × 0.31 mm (width) × 55 µm (height). A barrier consisting of six equidistant pillars (40 × 40 µm2), with gaps of 11 µm in between, is incorporated to enable the generation of a packed bed. Since the spacing is larger than the particles, initially some particles will be lost. However, on sustaining the flow, a regime of ‘clogging via sieving’ (Dressaire and Sauret 2017) sets in, leading to an ongoing particle accumulation, while the solvent keeps flowing through the interstitial space. This process is enabled by the so-called ‘keystone effect’ (Nagy and Gaspar 2013). Following up on the findings by Nagy and Gaspar, we designed the gap to be two times the average particle size, to maximize the efficiency of particle retention.

Fig. 1
figure 1

a Schematic 3D illustration of the packed bed in the rectangular microchannel, gray microparticles are CaCO3. b Schematic top view (not to scale) of XY regions of interest visualized with confocal scanning laser microscopy (CLSM). The space between adjacent ROIs is 100 µm and the visualization Z depth is 25 µm. c Top view cartoon of the distributions of water (green) and oil (brown). The subsequent injection of oil and water represents a cycle, which is repeated (color figure online)

Full size image

A polydimethylsiloxane (PDMS) channel obtained from soft photolithography (Xia and Whitesides 1998) was bonded onto a 170 µm thick cover glass (Menzel-Glaser, Germany) after an oxygen plasma treatment at 60 W for 1 min. The bonded channel was put into an oven at 60 °C overnight to improve the bonding strength. Teflon tubes (1/16 in. OD X 1/32 in. ID) were connected to the inlets and outlet using 23G stainless steel couplers (0.025 inch OD × 0.013 in. ID, length: 15 mm) and Loctite EA 3430 epoxy glue. The main inlet tubing and syringe were connected via male 1/4"-28 threaded fittings and male Luer Lock adapter. The Teflon tubing from the outlet was connected to Tygon LMT-55 tubing (1.65 mm ID × 0.8 mm wall) by epoxy. The completed sealed channel was then cured for 24 h at 60 °C before use.

2.4 Filling and flushing protocols

The outlet tubing was connected to a peristaltic pump, while the main inlet was connected to a displacement pump (KD Scientific) operated with gastight glass syringes (Hamilton). The microfluidic channel was cleaned by flushing with DI water and then with ethanol for 1 min each. The packed bed was prepared by injecting the suspension of microparticles (10 µL) at a flow rate of 20 mL/min from the side port using a peristaltic pump. The calcite microparticles have an estimated mean diameter of 5.5 ± 0.6 µm (Fig. 2d). Further information can be found in Sect. 3.1. Meanwhile, the PDMS chip was kept vertical (outlet down) to ensure that the particles were homogeneously packed over the entire channel cross section. After the side port was closed, DI water was injected at a high flow rate of 200 µL/min from the main inlet to make the initially somewhat loose packing more compact. The densely packed bed was then kept horizontal in the absence of flow for 12 h at room temperature, to equalize the pressure and achieve a tight packing via the clamping effect (Gaspar et al. 2007; Kabiri et al. 2014). Finally, the packed bed was consolidated via a chemical process. First, a mixture of CaCl2 and Na2CO3 solution (2 mM each; supersaturated in CaCO3) was injected at 1.0 µL/min to saturate the packed bed. Next, intermittent injection was applied, which involved injecting the ionic mixture at 0.5 µL/min for 5 min, followed by a waiting time of 5 min. This cycle was repeated 8–10 times, after which the channel was dried at 70 °C overnight. All on-chip experiments were done at room temperature.

Fig. 2
figure 2

a, b Representative SEM image of synthesized CaCO3 microparticles. c Representative Raman spectra of synthesized and reference calcite. d Size distribution of synthesized particles, along with a normal distribution fitted to the data

Full size image

Upon completion of the packed bed, its absolute permeability was measured by injecting DI water at varying flow rates and recording the corresponding pressure drop using a pressure sensor (Elveflow microfluidic pressure sensor MPS4, resolution ± 1.2 kPa, range 100–690 kPa). The permeability was calculated using Darcy’s Law (Gunda et al. 2013) as follows:

$$K=\frac{Q\mu L}{A\Delta P},$$
(1)

where Q is the injection flow rate, µ is the viscosity of water, ∆P is the pressure drop, and A is the cross-sectional area of the channel. K is obtained by a linear fit of (Qµ/A) versus (∆P/L). The permeability of packed bed was measured to be around 220 mD (Fig. S3).

To perform waterflooding, first fluorescein-dyed water was injected at high flow rate until it reached the unlocked side port. This procedure speeds up the fluid transport without causing excessive hydraulic pressure on the packed bed. The flow rate was then lowered to 1.0 µL/min and the side port was closed, to allow a gentle saturation of the packed bed in the main channel. This ‘first water injection’, aimed at ‘priming’ the calcite packed bed, was terminated when the water reached the main outlet. Second, oil was injected in a similar way. This ‘drainage’ process was terminated when, based on visual observations with the CSLM, the oil saturation had reached So ≈ 1 without further change. Third, a ‘second water injection’ using fluorescein-dyed water was performed at a chosen capillary number (Ca). This ‘imbibition’ process was continued for a sufficiently large number of pore volumes to reach an apparent steady state, as assessed from CSLM images. Each waterflooding condition was repeated two or three times (‘cycles’ in Fig. 1c) to check repeatability of the experiment.

2.5 Image acquisition

Z stacks at 25 (X, Y) regions of interest (ROI) inside the packed bed (Fig. 1b), each covering a field of view 90 × 90 µm2 were acquired by a Visitech Infinity3 Confocal Scanning Laser Microscope (CSLM) in fluorescence mode, using a 488 nm laser, 100 × objective (oil immersion, NA = 1.49) and an ORCA Flash 2.8 camera at 2 × 2 binning. The effective pixel size was 0.135 × 0.135 µm. The middle regions of the packed beds were visualized, while the downstream regions (300–400 µm close to the pillars) were excluded to avoid end effects (Tanino et al. 2018). At each (X, Y) ROI, a series of images along the Z-direction was recorded over a range of 25 µm (in steps of 330 nm), at an exposure time of 100 ms per image. For the water and oil saturation steps, only image stacks of the end result were recorded. For the secondary water injections, Z stacks at Nxy = 25 locations were measured as a function of time. Each image stack was recorded in 10 s and a programmable XY stage was used to revisit each XY location at regular time intervals (about 5 min). Decreasing the Z range from 25 to 15 µm, would allow a cycling time of about 6Nxy seconds.

2.6 Image analysis

Image stacks along the Z-direction were first separated manually into individual (XY) images using ImageJ FIJI software developed by NIH and LOCI (Wisconsin) (Collins 2007; Schneider et al. 2012). Further data analysis was performed automatically with Matlab codes to quantify the area fraction of fluorescein-dyed water per individual image. By averaging this fraction over the different Z slices while taking into account all (X, Y) ROIs, an average water volume fraction, representative for the (optically accessible part of the) packed bed is calculated as a function of time (or equivalently, pore volume).

First a pre-processing was done to improve image quality. Given the illumination conditions in our CSLM system, the (90 × 90 µm) images showed slightly reduced intensities, (1) in the corners and (2) due to an alternating stripe pattern. After cropping 4 µm from the edges, the striping issue was mitigated by fast Fourier transforming (FFT) a representative striped image, and judiciously ‘masking out’ the responsible peaks in the FFT image. This mask in reciprocal space was applied to all images, after FFT and before the inverse transformation.

The pre-processed images were next binarized using Otsu's method (Otsu 1979), which automatically determines the optimum intensity threshold. To examine the robustness of the binarization, also slightly lower and higher intensity thresholds were explored. The area fraction of bright pixels [denoted as water area fraction (WAF)] was attributed to the presence of fluorescent water, while dark pixels could correspond to either oil or calcite. Saturating the packed bed with fluorescent water before the first exposure to oil, allowed measuring the fraction occupied by (non-fluorescent) calcite particles. By assuming this reference WAF to remain constant throughout the entire experiment, the residual oil fraction in relation to initial WAF values was estimated.

While averaging the values of WAF over different Z values, it had to be ensured that the same Z-range was analyzed for each experimental condition. Small tilt angles or vertical drifts of the micro-channel might cause the channel bottom (i.e., the internal Z = 0) at different (X, Y) locations or times, to be located at slightly different Z-positions in the (external) coordinate system of the microscope. This issue was resolved by estimating the local Z = 0 from the corresponding intensity (I(Z)) profile, where I(Z) is the average intensity of an image at depth Z within a pre-processed grayscale image stack. This I(Z) function typically shows a maximum (at Zmax ≈ 1 µm) that can be found via parabolic fitting; except for cases, where the packed bed is almost completely saturated with oil. Considering that the maximum depth resolution was about 5 µm from the channel bottom, the same Z-distance range was utilized for all (X, Y) ROIs.

3 Results and discussion

3.1 Characterization of CaCO3 particles

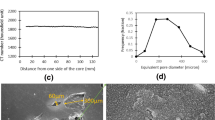
The major mineral constituents of carbonate reservoirs mostly consist of calcite and dolomite (Ahr 2011). X-ray powder diffraction (XRD) of carbonate reservoir rocks indicates that the calcite content is even up to 100% at certain depths (Al-Jaroudi et al. 2007). Therefore, calcite particles were synthesized to represent the predominant mineral constituent of carbonate reservoirs (see Sect. 2.1). Figure 2a, b shows an SEM image of the synthesized CaCO3. The particles have an estimated mean diameter of 5.5 ± 0.6 µm (Fig. 2d). The typical crystal morphology is rhombohedral, similar to the characteristic crystal habit of calcite (Dhanaraj et al. 2010). Figure 2c presents the Raman spectrum of the synthesized CaCO3 particles, with peaks observed at 1089 cm−1 (symmetric stretching CO3, ν1), 715 cm−1 (in-phase bending CO3, ν4) as well as 285 and 158 cm−1 (lattice modes). These peaks positions correspond well to the spectrum for pure calcite (Li et al. 2017; Wang et al. 2017) and confirms that our crystals do not contain other crystalline phases of CaCO3.

3.2 Characterization of the packed bed

The mechanical stability of the packed bed was examined by flushing fluorescein-dyed water at 1 µL/min (superficial velocity v≈ 1 mm/s) in the packed bed and simultaneously monitoring several (X, Y) ROIs with CSLM. The calcite particles showed no significant displacement, as evidenced by the image-time series shown in Fig. S2.

The permeability of packed bed was measured to be around 220 mD, which is within the range of that in carbonate reservoirs (Cantrell and Hagerty 1999). Using an estimated pore volume fraction of about 0.53 (measurement shown in Sect. 3.3) and the average particle size of about 5.5 µm, an approximate permeability can be calculated from the Kozeny-Carman equation for spheres (Bear 2013):

$$k \, = a^{2} \varphi^{3} /45\left( {1 - \varphi } \right)^{2} ,$$
(2)

where φ is the porosity and a = 2.75 µm the average sphere radius. This estimation provides k≈ 130 mD. The discrepancy could arise from factors such as different particle morphologies, polydispersity and possibly also the presence of the nearby glass wall (Krummel et al. 2013). In addition, the coefficient (here taken 45) also shows some variation with the type of porous medium (Tien and Ramarao 2013).

Figure 3 presents an example of a Z stack at a given (X, Y) ROI in the packed bed filled with fluorescent water. Clearly, the image contrast gets compromised as the optical penetration into the sample (i.e., the Z coordinate) is increased. This is due to the scattering of (both the incoming and outgoing) light by the calcite particles, which have an average refractive index of 1.65 (compared to 1.33 for water). Typically, the images get blurred when focusing more than a depth of 5 µm into the packed bed (Fig. 3e, f). A typical Z stack after second water injection shows a similar phenomenon (Fig. S4). Previous studies reported likewise difficulties when using CLSM to visualize the bulk of rocks materials (Yio et al. 2015). A key observation is that the packed bed exhibits both macro- and micro-porosity (the division lies around 10 µm) for various ROIs close to the glass surface. The packed bed thus reasonably represents the geometrical complexity of the pore structure in carbonate reservoirs, where micro-porosity constitutes up to 50% of the total porosity (Cantrell and Hagerty 1999; Okasha et al. 2007; Ahr 2011).

Fig. 3
figure 3

Representative Z stack in the 3D calcite packed bed immersed in fluorescently labeled water. The 2D images are shown at different depths into the channel, measured from the inner glass surface

Full size image

3.3 Measurement of (local) porosity

The image analysis procedure performed on a single (X, Y) ROI of a packed bed in fluorescent water is illustrated in Fig. 4.

Fig. 4
figure 4

Illustration of the image analysis process: a raw grayscale image. b Binarized image. c Fluorescently-dyed water (white) area fraction versus image depth. d 3D reconstruction image of a Z stack (green: water, blue: calcite) (color figure online)

Full size image

The conversion from a raw grayscale image to a binary one, as shown in Fig. 4a, b, is effective for images acquired in proximity to the glass bottom. However, the binarization becomes increasingly difficult upon deeper optical penetration into the packed bed, i.e., for larger Z. While already shown in Fig. 3, this is illustrated more quantitatively in Fig. 4c, where WAF(Z) is plotted for binarizations using slightly different intensity thresholds (ITH). In the first 5 µm from the bottom the WAF magnitudes are very similar, but for larger Z the WAF(ITH) values diverge due to image blurring. WAF(Z) curves after the second water injection show a similar trend (Fig. S5). For this reason, we have limited our measurement (and subsequent Z-averaging) of WAF(Z) to a distance ≈ 5 µm from the bottom (see Sect. 2).

Up to 5 µm, the steady decrease of WAF with Z increasing is thus reliable. It illustrates a feature which is probably intrinsic for a packed bed: the channel walls induce a heterogeneity of the particle packing density, at least at the length scale of the constituent particles. Clearly, WAF(Z) should ‘saturate’ for Z values far enough from the wall, where the structure will reach the random packing of the bulk material. Because of the geometrical wall effect, the porosity of the packed bed is thus somewhat different than near the wall. However, since the typical porosity length scale will still be comparable, we can expect that the changes in residual oil saturation, obtained by interventions in capillary number or wettability, will still be similar. Because of the slight arbitrariness of the Z integration range, the calculated oil and water saturations will depend somewhat on the upper Z limit.

Comparison between the ROIs at different (X, Y) locations (Fig. 5) reveals some heterogeneity in WAF at larger length scales; the typical lateral distance between the ROIs is 100 µm. The WAF values at Z = 0 for the different ROIs do not show any systematic dependence along the downstream direction, nor perpendicular to it, but there are small variations. This could produce a spread in occupancy between the different ROIs. Taking the average over 25 ROIs reduces the standard deviation of the average to ≈ 2.6%, which is in our case sufficiently small to measure effects of capillary number and wettability alterations.

Fig. 5
figure 5

a Spread in WAF(Z) profiles for ROIs located at 25 different (X, Y) locations in the packed bed, in the case of 100% water saturation. b Histogram of the (Z-averaged) porosity: the standard deviation is ≈ 2.6%

Full size image

3.4 Waterflooding experiments

The waterflooding conditions explored using two microfluidic chips (with the same design) are summarized in Table 1. In IOR from oil fields, the typical injection velocity typically varies between 1 and 4 ft/day; some variations exist between literature values (Gerold et al. 2018; Sarvestani et al. 2019). Since the flow rates correspond to typical capillary numbers in the range 10–6 to 10–5, (Guo et al. 2015) we have also explored this range (Table 1).

Table 1 Flow conditions in water flooding experiments
Full size table

We further investigated the effect of surface modification of the porous medium on ROS, defining the latter as the fraction of oil in the XYZ pore space for Z ≤ 5 µm (see above). After the waterflooding experiments using unaged calcite, the packed beds were injected with eqFW to displace the fluorescently labeled water, and aged for 18 h. The goal of the long equilibration time was, to allow adsorption of organic components onto the pore surfaces. Thereafter, the same injection protocols were performed, to enable optimal comparison between the results obtained with unaged and aged pore spaces.

Figure 6 summarizes the results of the waterflooding experiments. The remaining water saturation (RWS), i.e., the WAF averaged over Z-depths from 0 to ≈ 5 µm for (X, Y) ROIs, is plotted versus the number of effective pore volumes (PVeff). Here PVeff is estimated from the pore volume and the injected water volume. The (‘drainage’) stage where oil is injected to replace the water is not shown, because the water content was too low to obtain a reliable number. However, from the CSLM images it was observed that some regions on the calcite surface were still covered by a layer of water; this is shown in Supplementary Fig. S6b. The initial water saturation (IWS) (equivalent to the porosity of the packed bed) appears to be very similar (at ≈ 53%) for the two chips. This illustrates the reproducibility of the particle packing procedure.

Fig. 6
figure 6

Evolution of the remaining water saturation during waterflooding experiments. Values represent remaining water (%) for initial water injection (i.e., before first oil injection; orange) as well as for (after oil-drainage) waterflooding of packed beds, unaged (red) and aged in eqFW (blue). Waterflooding cycles: 1 = circle, 2 = triangle, 3 = square. Sample 1: a Ca = 6.3 × 10–7, b Ca = 2.1 × 10–5. Sample 2: c Ca = 6.3 × 10–6, d Ca = 2.1 × 10–5. Vertical bars present the spread among the 24–26 ROIs in the packed bed (calculated as a standard deviation) (color figure online)

Full size image

In the second injection stage, water is injected continuously, to displace oil from the packed bed. Direct CSLM images (not shown) revealed that oil was mostly displaced from the large pores. This is in agreement with previous studies (Bowden et al. 2016) and can be explained by the lower capillary pressure in those pores.

The quantitative image analysis shown in Fig. 6 reveals that generally, within a given waterflooding cycle, the RWS quickly reaches a stable value. Also generally, the differences between subsequent cycles under the same condition (capillary number, aging history) are modest. A slight exception is panel C, where the scatter is somewhat larger (for which we have no tentative explanation). Importantly, the remaining water content is significantly lower for the chip that had been aged in eqFW. For example, in Fig. 6a, the aged case (blue symbols) presents an RWS of 31.5%, whereas it was 36.5% for the unaged case (red symbols). Similar differences are found in Fig. 6b–d, and the differences between the aged and unaged cases are always bigger than the differences within these two datasets. This underlines that aging the pore space with eqFW has a significant effect on the ability of water to displace oil. Previous studies (Klimenko et al. 2020) also indicate that the endogenous crude oil species in equilibrated brines can apparently increase the oil-wetness of both quartz and calcite surfaces. Moreover, the magnitude of such effect depends strongly on oil nature and brine salinity.

The range of capillary number studied here has no noticeable effects on the RWS. This can be seen by comparing Fig. 6a (low Ca) to Fig. 6b (high Ca) and likewise for Fig. 6c, d. We emphasize here that, although our reported RWS and ROS values do not strictly correspond to the averages over the entire packed bed, very similar trends in RWS and ROS were found for differently chosen Z integration ranges.

The final Residual Oil Saturations, \(\mathrm{R}\mathrm{O}\mathrm{S}=1-(\mathrm{R}\mathrm{W}\mathrm{S}/\mathrm{I}\mathrm{W}\mathrm{S})\) for the different waterflooding experiments (highlighted in Fig. 6) are plotted in Fig. 7 versus the capillary number. We observe that the data for Ca = 2.1 × 10–5, which were measured on two different chips, correspond well. Again, we see that the capillary number does not have a clear effect on the ROS in any of the explored conditions. Previous studies also showed a weak dependence of ROS on Ca. Krummel et al. (2013) found that ROS decreases significantly for Ca larger than 2 × 10–4 but not for lower capillary numbers as used in our study (Krummel et al. 2013; Tanino et al. 2018). It is worth noting here that our findings were made at comparable capillary numbers but for smaller pore sizes and a higher (oil:water) viscosity ratio.

Fig. 7
figure 7

Average ROS for waterflooding experiments in two freshly prepared chips (triangles or squares). For each sample, capillary numbers were varied in the increasing direction, and the unaged calcite (red) was studied before the eqFW-aged calcite (blue). Error bars indicate the standard deviation of ROS measured at different locations across the channel (color figure online)

Full size image

The higher ROS values for samples aged in eqFW confirm the expectation that the intermediate aging with crude-oil equilibrated formation water makes the porous medium more oil-wet: in that case it should be more difficult to displace oil. This trend is similar to previous studies in which 2D arrays of cylindrical polymer posts were used. Here we observe a similar behavior (Lee et al. 2015; Zhao et al. 2016) but with different materials and for a 3D porous medium. This similarity of the observations further confirms that our visual observations in a packed bed close to a wall, can be used to detect the effect of wettability alteration on the fraction of residual oil.

We note here that not only the calcite particles but also the glass wall (and possibly also the PDMS) could adsorb components from the eqFW. To examine this in more detail, we exposed a glass slide and a piece of Iceland Spar calcite to a similar aging procedure, and measured the advancing and receding contact angles before and after aging. Here, the glass surface showed a 15° lower advancing contact angle (for an oil droplet in ambient water), while for the calcite substrate this contact angle remained unchanged (see Fig. S7). It is remarked here that for many substrates, contact angles provide a mixed information that can often not be disentangled: the inherent wettability of the surface material gets modulated by chemical heterogeneity and/or surface roughness. In fact, additional characterizations of the calcite particles using TGA and FTIR (see SI Fig. S8, 9 and Table S3) revealed that adsorption of organic compounds had in fact taken place during the aging step.

4 Conclusions and outlook

We demonstrated how micron-sized calcite particles can be assembled into a porous medium inside a microfluidic chip. Fluorescence based visualization of the particles, water and oil in various regions close to the transparent wall, followed by automated image analysis, allows accurate quantification of the residual oil saturation. This allows detecting the consequences of wettability alteration, as is of interest in the exploration of SWF. Compared to traditional core flooding experiments, our microfluidic approach potentially offers an attractive alternative tool for screening many fluid compositions and/or flow rates in a short time.

While our approach can already accommodate the use of other particles (e.g., crushed rock), a further development of the platform will be needed to enable measurements with crude oils and at elevated temperatures. Defining the microfluidic channels in materials with enhanced thermal and chemical resistance will be a necessary step for that. Materials which such characteristics are known and have been applied (Marre et al. 2010), while methods to coat typical wall materials with calcite have also become available recently (Wang et al. 2017). The use of crude oil may then contribute to the visualization via its auto-fluorescence.