Abstract
The coordinate time series determined with the Global Positioning System (GPS) contain annual and semi-annual periods that are routinely modeled by two periodic signals with constant amplitude and phase-lag. However, the amplitude and phase-lag of the seasonal signals vary slightly over time. Various methods have been proposed to model these variations such as Wavelet Decomposition (WD), writing the amplitude of the seasonal signal as a Chebyshev polynomial that is a function of time (CP), Singular Spectrum Analysis (SSA), and using a Kalman Filter (KF). Using synthetic time series, we investigate the ability of each method to capture the time-varying seasonal signal in time series with different noise levels. We demonstrate that the precision by which the varying seasonal signal can be estimated depends on the ratio of the variations in the seasonal signal to the noise level. For most GPS time series, this ratio is between 0.05 and 0.1. Within this range, the WD and CP have the most trouble in separating the seasonal signal from the noise. The most precise estimates of the variations are given by the SSA and KF methods. For real GPS data, SSA and KF can model 49–84 and 77–90% of the variance of the true varying seasonal signal, respectively.
Similar content being viewed by others
Introduction
Global Positioning System (GPS) position time series are used to study geophysical phenomena such as plate tectonics (Tobita 2016), post-glacial rebound (Larson and van Dam 2000), and vertical land motion at tide gauges (Teferle et al. 2009). In all these cases, one normally estimates a secular motion or velocity together with seasonal signals. These annual and semi-annual signals have amplitudes of few millimeters and are partially caused by atmospheric and hydrological loadings (van Dam et al. 2001; Tregoning et al. 2009; Bogusz and Figurski 2014), thermal expansion of ground and monuments (Yan et al. 2009; Hill et al. 2009), varying tropospheric delay (Munekane et al. 2008) or multi-path variations (King et al. 2008). Although the seasonal signals are generally modeled as having constant amplitudes and phase-lags with the parameters estimated using Weighted Least Squares (WLS), their values might vary slightly from year to year because their geophysical causes are not constant.
Noise or a so-called residuals are created when the deterministic model was removed. For the GPS position time series, the power spectrum of the noise follows a power-law behavior at the low frequencies with spectral indices varying between −2 and 0. This noise has a significant impact on the uncertainty of velocity (Zhang et al. 1997; Williams et al. 2004; Santamaría-Gómez et al. 2011; Bogusz and Kontny 2011). Moreover, if any seasonal signal or residual periodicity is not properly modeled and removed, it will move the stochastic part to much more correlated noise causing the uncertainties to be artificially overestimated (Bogusz and Klos 2016).
The time-varying seasonal signals can be studied by several methods. Chen et al. (2013) applied Singular Spectrum Analysis (SSA) to model time-varying signals in weekly GPS position time series. They cross-compared the SSA results with Kalman Filter (KF) estimates. Didova et al. (2016) used Kalman Filter (KF) to estimate time-varying trends and seasonal signals in Gravity Recovery and Climate Experiment (GRACE) and GPS data. Although the noise level may have a significant impact on the precision of the estimated seasonal signals, up until now, no special attention has been paid to its influence on the effectiveness of each method. Only recently, Xu and Yue (2015) emphasized that the seasonal signals filtered with SSA may contain an artificial signal driven by colored noise. Therefore, some of the power may be artificially removed from power spectra of the residuals, leading to imprecise estimates of the noise level. A good separation between noise and seasonal signal ensures that once the time-varying seasonal signal has been removed, the data can be processed using standard GPS time series analysis packages such as CATS (Williams 2008), est_noise (Langbein 2010) or Hector (Bos et al. 2013) to estimate the velocity and its uncertainty. The objective of this research is to perform a comparison of these various methods to estimate the time-varying seasonal signal in GPS time series while taking the noise level into account.
We discuss the Kalman Filter (KF), Singular Spectrum Analysis (SSA), Wavelet Decomposition (WD), Moving Ordinary Least Squares (MOLS), and Chebyshev polynomials (CP) approaches and compare them with the standard WLS approach which provides time-constant curves. Using the noise level derived for real GPS position time series, we create various sets of synthetic position time series with time-varying seasonal signals. Then, we estimate the seasonal signals with the KF, SSA, WD, MOLS, and CP approaches in order to determine the noise level for which the variations in the seasonal signal can be modeled precisely. Finally, we analyze real GPS position time series and predict how precisely the varying seasonal signal can be captured under real noise conditions.
GPS coordinate time series
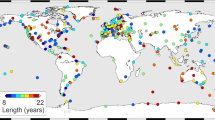
In this section, we characterize the noise level in the true GPS position time series in order to use this information to create realistic synthetic time series. We employed daily GPS time series processed at the JPL/NASA from 174 stations (Fig. 1). The time series have a time span longer than 13 years to ensure reliable estimation of the time-varying seasonal signal. Outliers were removed using the median criterion (Klos et al. 2015). Epochs of offsets were taken from the information provided by JPL. Additional offsets were estimated using the Sequential t test algorithm (Rodionov 2004) with a segment length of 100 days and a confidence level of 95%. Gaps in the data ranged between 0.1 and 11% of the entire time series. The SSA method described below requires that these missing data are filled. Therefore, gaps were interpolated with a linear interpolation which is the simplest and most often employed to interpolate any missing value.
A total of 174 GPS stations are used in this research. The color of the circles indicates standard deviation (mm) of the annual amplitudes estimated with MOLS for vertical component. Stations AUCK (Auckland, Australia) and ULAB (Ulaanbaatar, Mongolia), which we focus on in this research, are also marked
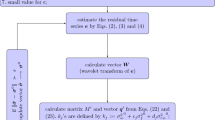
The following model was fitted to the time series:
where x 0 and v x are the initial position and velocity, respectively. a i and b i are constants for the sine and cosine term of the periodic signal of ω i angular velocity. The last term represents noise. The t 0 term is the reference epoch.
Parameters describing the initial position, velocity, seasonal signals, and combination of power-law and white noise model were estimated using Maximum Likelihood Estimation (MLE) as implemented in the Hector software (Bos et al. 2013). From the parameter estimation in Hector, we know that the uncertainties of parameters a and b are nearly equal. We used the Rice distribution to compute uncertainty of the total amplitude \( A = \sqrt {a^{2} + b^{2} } \) (Rice 1944). For the GPS position time series which we analyzed, the amplitude of the annual signal of the vertical component varied between 0.6 and 8.2 mm with a median of 2.4 mm. The minimal and maximal amplitudes of the semi-annual signal are, respectively, 0.6 and 2.7 with a median of 1.3 mm. For the vertical component, the spectral indices (κ) of a power-law process were estimated to vary between − 1.27 ± 0.08 and − 0.37 ± 0.02 with a median of − 0.68. The power-law noise amplitudes ranged between 7.39 and 21.01 mm/year− κ/4 with a median of 12.05 mm/year−κ/4. Supported and confirmed by previously published papers (Williams et al. 2004; Klos et al. 2014), this range of noise level was used to create a set of synthetic series.
To estimate the variability of the annual and semi-annual signals in the GPS coordinate time series, we first removed the velocity. Next, we split the time series into 3-year segments that are overlapping with each other with a separation of 1 year. For each segment, we estimated the annual and semi-annual signals with the constant-amplitude approach (see Eq. 1). In Fig. 1, we present the standard deviation of the annual amplitude in the vertical direction. This indicates how much the amplitudes differ from each other between the consecutive segments. The largest variations are observed in the East Europe and Asia. The mean value of the standard deviation is 0.8 mm. For about 30% of stations, this value is smaller than 0.5 mm, while for about 15% of stations it is larger than 1.0 mm. For the North and East components (not presented in the figure), the mean standard deviation is 0.4 mm.
In Fig. 2, we show the detrended vertical component of station AUCK (Australia) and ULAB (Mongolia) with the annual amplitude varying in each segment from 0.3 ± 0.1 mm to 2.6 ± 0.1 mm for AUCK and from 0.1 ± 0.1 mm to 1.1 ± 0.1 mm for ULAB. This simple exercise gives us a clear insight into the variability of the seasonal signal over time.
Methods used for modeling the time-varying seasonal signal
In the previous section, we demonstrated that for tens of GPS stations, the amplitude of the annual and semi-annual signals significantly varies over time. We will now review various methods that subtract the time-varying seasonal signal.
Moving Ordinary Least Squares: MOLS
In the previous section, we presented the Moving Ordinary Least Squares (MOLS) approach to estimate seasonal signals in 3-year segments. To generate a single time series with the varying seasonal signal, we used linear interpolation to guarantee a smooth transition between the segments. Next, we found that the difference between applying weighted or ordinary least squares, which ignores the properties of the noise, only produced sub-millimeter differences. The MOLS method is fast, easy to implement and, also, can deal with missing data and offsets.
Wavelet decomposition: WD
Wavelet Decomposition (WD) is a pyramidal algorithm that enables us to capture time-varying seasonal signal at various resolution levels. We used seventh and eighth levels of Meyer’s wavelet (Meyer 1990) to model time-varying signals with periods between 128 and 512 days, which include the annual and semi-annual periods. The Wavelet Decomposition technique can be used to extract the time-varying seasonal signal in a preprocessing step after which the residuals can be analyzed to estimate the velocity (Bogusz 2015). Although it is a promising tool to model time-changeable seasonal curves for any modulating signal (Wu et al. 2015), its main disadvantage is that it models both signal and noise between the frequency limits that define the resolution. No separation between signal and noise is performed.
Singular Spectrum Analysis: SSA
Singular Spectrum Analysis (SSA; Broomhead and King 1986; Vautard and Ghil 1989; Allen and Robertson 1996) is based on the idea to use pairs of Empirical Orthogonal Functions (EOFs) to model oscillations that change over time. SSA was introduced to GPS time series analysis by Chen et al. (2013) to model the nonlinear trend along with time-varying seasonal signal in weekly data. Zerbini et al. (2013) used SSA to analyze the inter-annual variability of different series. Recently, Xu and Yue (2015) used daily GPS vertical coordinate time series, to investigate seasonal SSA-filtered signals. Although it was not quantified, they concluded that SSA might absorb a part of the colored noise. Using a set of synthetic time series, we investigated the use of a 2-, 3- and 4-year moving window lengths to deliver the most precise results under different noise levels.
Kalman Filter: KF
The standard model, as shown in Eq. (1), was modified by Davis et al. (2012) as follows:
where a i (t) and b i (t) are now instantaneous amplitudes which are assumed to consist of a mean value plus a random walk component. The parameters x 0, v x , a i (t) and b i (t) are solved using a Kalman Filter (KF, Kalman 1960). We manually tuned the variances of the stochastic part of a i (t) and b i (t) to obtain the best fit between the estimated time-varying seasonal signal and the synthetic seasonal signal. The state vector of parameters and covariance were estimated in a forward pass and smoothed in a backward pass with a Rauch–Tung–Striebel smoother (Gelb 1974).
It must be noted that the noise term ε(t) has disappeared in (2) (compare to (1)). As a result, the power spectrum of the noise in the GPS position time series flattens for frequencies below the annual period. However, as it was shown by Didova et al. (2016), it can be modified by adding the ε(t) term in the form of a third-order autoregressive model which mimics a power-law noise. They tuned their filter so that the low frequencies were not absorbed in the stochastic part. They limited the standard deviation of the parameters a i (t) and b i (t) to the estimated standard deviation of the series by cutting the time series into segments and estimating the annual signal for each segment. It was noted that this is a complex nonconvex optimization problem and advocated the use of the likelihood function to determine the values of variances in the filter. In this research, we limited ourselves to find the optimal values of the stochastic variables of the seasonal signal in the state vector by trial and error approach. This approach is explained in the next section.
Modeling the seasonal amplitudes with polynomials: CP
Bennett (2008) assumed that the variations in the amplitude of the seasonal signals vary slowly over time. These variations in the amplitude can be estimated using n + 1 orthonormal basis functions η j (t). Thus, the following model is used:
We have implemented this model into the Hector software package. We used simple Chebyshev polynomials (CP) as basic functions for η j (t), where j indicates the degree of the polynomial, instead of orthonormal basis functions derived from the representors of amplitude deviation (Bennett 2008). For j = 0, the Chebyshev polynomial is 1, and we have the case of constant amplitudes. For j = 1, linear variations are allowed; for j = 2, a quadratic function is fitted and so on until degree n. All functions \( \eta_{j} \left( t \right)\cos \left( {\omega_{i} t} \right) \) and \( \eta_{j} \left( t \right)\sin \left( {\omega_{i} t} \right) \) were made orthogonal to each other by applying the Gram–Schmidt’s algorithm to improve numerical stability (Bennett 2008). Thus, we also created a set of orthonormal basis functions, only they are not derived from representors. We tested a set of polynomial degrees between 1 and 10 for the synthetic data set. We chose degree 4 as the most appropriate single value to model time-varying curves in both synthetic and real data for a wide range of noise values. However, also higher degrees were tested to estimate the seasonal signal under different noise levels.
Synthetic GPS time series
To test the efficiency of the various techniques mentioned in the previous section, we generated 500 synthetic time series without gaps with a length of 6000 days which makes 16.4 years (Fig. 3). We assumed a pure flicker noise (spectral index of −1) with the amplitudes between 1 and 25 mm/year0.25 which covers the range of 7–21 mm/year−κ/4 that we found in the real GPS JPL time series and is the most common noise type seen in the GPS position time series. The noise amplitude of 1 mm/year0.25 is very low, but was used to investigate how the various methods perform in an ideal situation. The annual and semi-annual signals were simulated in all time series with mean amplitudes of, respectively, 3.0 and 1.0 mm, and various phase-lags between 1 and 6 months and added to pure flicker noise. The modeled variations in the amplitude of the seasonal signal were chosen to have standard deviations of 1.0 and 0.5 mm for annual and semi-annual signals, respectively, to mimic the mean values of real time-varying signals (Fig. 2).
Example of a few synthetic time series created for different noise levels employed in this research. Top panel: a very low noise level, that is, 1 mm/year0.25. Bottom panel: a normal noise level, that is, 10 mm/year0.25, which is the most common for GPS position time series. Various colors mean the consecutive simulations
To investigate the effect that data gaps may have on the precision of each approach, we also simulated time series with missing data that varied from 4 to 16% of the total length of data, with a mean of 8%. These missing data were filled using linear interpolation.
Having estimated the seasonal signal individually for each of the data with the MOLS, CP, SSA, KF and WD methods, we removed this curve from the synthetic series. Then, residuals were analyzed with MLE assuming white plus power-law noise model to deliver the parameters of noise.
Parameters of CP, SSA, and KF
For the CP method, we tried degrees of the Chebyshev polynomial from 2 to 10. We found that for low noise levels, degrees equal to or higher than 8 produced a maximum misfit (or standard deviation) of 0.18 mm, which was slightly smaller than it was for lower degrees. For a normal noise level of 10 mm/year0.25, the opposite was true: lower degrees of CP produced smaller misfit. For a minimum degree of 2, the misfit was equal to 1.19 mm. It seems that lowering the degree is necessary to avoid the situation when the CP method starts fitting to the noise instead of fitting to the annual signal. In our analyses, we used a degree of 4, representing a mean value that can be used for a wide range of noise levels.
The performance of the SSA method is dependent on the length of the window employed to compute SSA. Chen et al. (2013) have already investigated the influence of the window length on the performance of SSA, but did not link it directly to the noise levels. We analyzed the misfit between seasonal curves simulated and estimated with 2-, 3- and 4-year windows. For the highest noise level of 25 mm/year0.25, a window length of 4 years produced a misfit between the synthetic and estimated varying seasonal signals of 1.61 mm. For a window length of 3 years, this value was equal to 1.68 mm. For a noise level of 1 mm/year0.25, for a window length of 3 years, the misfit was equal to 0.22 mm, while for a 2-year window, it was equal to 0.18 mm. We found that in the presence of higher noise levels, longer window lengths, as 4-year window, produce better results. For low noise levels, smaller windows behave better. Due to the fact that the differences in these misfits are small enough, in our analyses, we used a window length of 3 years.
As explained in the previous section, the KF method of Davis et al. (2012) differs from the one of Didova et al. (2016), as, in the former, the temporal correlated noise was omitted in the state vector. To obtain the best fit, we tried various values for the variances by which the amplitude of the seasonal signal is assumed to vary between each of the time steps. Then, we implemented both filters, but after tuning the filter of Davis et al. (2012), we could not obtain misfits lower than 0.21 and 1.15 mm for the 1 and 10 mm/year0.25 noise levels, respectively. These values are larger than the values we obtained using the filter of Didova et al. (2016). Therefore, the latter was used in this research. We ran KF with an additional third-order autoregressive model, AR(3). The coefficients for this process were estimated by fitting a third-order autoregressive model to pure synthetic flicker noise of a length of 6000 days to mimic a power-law noise. Then, they were directly employed in the KF. If the variances of the seasonal signals are too large, then the seasonal signal will start to model the noise as well. This results in a too low value for the estimated spectral index and an underestimation of the trend uncertainty.
Results for synthetic time series
The results of all the methods are summarized in Tables 1 and 2, which show the estimated trend uncertainty, the estimated spectral index of the power-law noise κ, and the estimated amplitude of the power-law noise σ. The last column, which we label as ‘misfit,’ shows the standard deviation computed between the seasonal signal estimated with a certain method and the seasonal signal which was simulated. The results of the analyses of the time series with interpolated data gaps are given within the brackets
Tables 1 and 2 also include a case when the seasonal signal was not modeled, although being present in the series (label ‘no seasonal assumed’). This generates an overestimation of the spectral index and, as a result, a too large trend uncertainty. The last row contains the actual trend error estimated using Eq. (29) of Bos et al. (2008), in case there is no seasonal signal present in the time series and trend uncertainty is generated only by the synthetic noise.
First, to examine how precisely we can retrieve time-changeability of the synthetic series, we employed MOLS. For very low noise levels, that is, for 1 mm/year0.25, the standard deviation computed for the estimated annual amplitudes was equal to 0.55 mm and for the highest noise levels, that is, for 25 mm/year0.25, the value was equal to 1.34 mm. This difference highlights that the ability of the MOLS method to separate noise from the annual signal decreases when noise levels increase. A conclusion is that a part of the noise is absorbed in the estimated annual signal.
Table 1 proves that for the case when the flicker noise amplitude is very low compared to the size of the variations in the seasonal signal, estimating a constant seasonal signal with WLS performs as expected worse than any of the methods that try to model the varying seasonal signal. Furthermore, there is a good agreement between the modeled and synthetic seasonal signals for all methods, with SSA and KF obtaining the lowest misfit values. On the other hand, Table 2 shows that when normal noise levels are employed, i.e., 10 mm/year0.25, the varying seasonal signal can no longer be estimated so precisely. At the same time, these results show that for normal noise levels, the WD absorbs a part of the noise which results in an underestimation of the spectral index. The higher the noise level, the more power is in fact absorbed by WD.
Tables 1 and 2 show that estimating a varying seasonal signal always results in lower noise amplitudes and lower spectral indices compared to estimating a constant seasonal signal. For low noise levels, it stems from the fact that the varying seasonal signal is correctly removed, eliminating the spikes in the power spectrum at the annual and semi-annual periods. For high noise levels, part of the noise in a seasonal frequency band is absorbed in the estimated varying seasonal signal. Figure 4 shows the power spectral density (PSD) plots estimated with Welch periodogram (Welch 1967) for two synthetic time series, one with a flicker noise amplitude of 1 and the other of 10 mm/year0.25, after removing the seasonal signal with various methods. For a low noise level of 1 mm/year0.25, both the CP and WLS methods give similar poor results, and the WD method appears to absorb too much of the seasonal signals for both low and normal noise levels.
PSDs of synthesized time series and residuals after applying the WLS, MOLS, WD, KF, SSA, and CP methods for two levels of noise: 1 mm/year0.25 and 10 mm/year0.25. Top panel: When the flicker noise amplitude is very low relating to the size of the variations in the seasonal signal, estimating a constant seasonal signal performs worse than any of the methods. Bottom panel: When normal noise levels are used, the varying seasonal signal can no longer be estimated so precisely, as it absorbs some part of the noise. PSD was estimated with Welch periodogram
Figure 5 presents the standard deviations of the difference between estimated and synthetic seasonal signals, labeled as a misfit, for different noise levels and methods. We also provide the empirical ratio of the estimated standard deviation of the annual signal to the noise level, i.e., standard deviation of annual signal divided by noise amplitude. As was expected, not estimating a seasonal signal gives the largest misfit. Estimating a constant seasonal signal with WLS produces misfits that are equal to the standard deviations of the estimated variations in the annual signal. SSA and KF have excellent performance for high signal-to-noise ratios in capturing the varying seasonal signal, but the precision of SSA deteriorates for higher noise levels. KF suffers from the same problem, but to a lesser extent. CP absorbs noise for high noise levels which makes it worse than WLS.
Standard deviation of the estimated varying seasonal signal minus the synthetic one (the misfit) as a function of the power-law noise amplitude in the time series. The top axis (signal-to-noise ratio) notes the corresponding ratio of standard deviation of the estimated annual amplitudes to the noise amplitude. WD and MOLS were not included for a better clarity of a plot
The mean total variance of the synthetic varying seasonal signal is equal to 5.5 mm2. At the lowest noise level of 1 mm/year0.25, the variances of the misfits are equal to 0.162 for SSA and KF, respectively, see the last column of Table 1, and thus explain 99.1–99.5% of the seasonal signal variance. At a noise level of 10 mm/year0.25, these values decrease to 84 and 90%, respectively, while for 25 mm/year0.25, these numbers are equal to 49 and 77%. Thus, not only the quality of the method determines the precision of the estimated varying seasonal signal, but also the noise level in the investigated time series.
For the highest amplitude of power-law noise, that is, 25 mm/year0.25, CP produces the largest misfit, i.e., higher than 2 mm. The WLS method, although assuming a time-constancy of the seasonal signal, performs better than CP, producing a misfit of approximately 2 mm. KF-derived seasonal curve is the closest to the original synthetic seasonal curve with a misfit of around 1 mm.
The results we presented in this section are valid also for synthetic series with gaps being filled using simple linear interpolation. As shown in Tables 1 and 2, the trend uncertainties and the misfit differ insignificantly for both sets of data.
Observed GPS position time series
We introduced the ratio of standard deviation of the annual signal to the power-law noise amplitude. We showed that this ratio provides an indication of how precisely one can estimate the varying seasonal signal using various methods; see also the top of Fig. 5. For the 174 GPS stations we described, we have plotted this ratio in Fig. 6 for the North, East, and Up components. It can be noticed that the signal-to-noise ratio is similar for all components.
For each individual station, the varying seasonal signal was estimated with SSA, KF, and CP. After subtraction of this signal from the observations, the residuals were analyzed using MLE assuming a power-law plus white noise model. Table 3 presents the mean spectral indices and power-law noise amplitudes we estimated. The average power-law noise has an amplitude of around 4 mm/yearκ/4, falling within the range of synthetic noise levels presented before. Together with the fact that the signal-to-noise ratios are similar for all components, our conclusions are also applicable to all three components. The table also shows that omitting the modeling of the varying seasonal signal leads to an overestimation of the spectral index of around 0.1 which will result in an overestimation of the trend uncertainty. The smallest uncertainties were found for WD. However, this arises from the artificial removal of some power in a frequency band we analyzed. The results of trend uncertainty and noise parameters, after WLS, MOLS, CP, KF, and SSA were applied, are similar to each other. The difference in trend uncertainty is equal to 0.03 mm/year at maximum.
According to the results we obtained for synthetic series (Fig. 5), the KF is the best to model varying seasonal signals for series characterized by a signal-to-noise ratio between 0.02 and 0.05 or power-law noise amplitude between 10 and 25 mm/year−κ/4. In our case, from a set of 174 stations analyzed in this research, the North, East, and Up components are characterized by such a ratio for 17, 12, and 34 stations (Fig. 6). KF and SSA produced similar results for 110, 108, 120 stations, with a signal-to-noise ratio between 0.05 and 0.10 or power-law noise amplitude between 5 and 10 mm/year−κ/4, KF and SSA. For any signal-to-noise ratio higher than 0.10 or power-law noise amplitude lower than 5 mm/year−κ/4, the KF, SSA, and CP behave in a similar way and all of them are applicable in this ideal case.
Figure 7 presents PSD for original series and residuals of MOLS, CP, KF, SSA, and WD for station AUCK for the vertical time series. The Up component of AUCK is characterized by spectral index κ of −0.92 and amplitude of power-law noise of 9.11 mm/year0.23. Signal-to-noise ratio is equal to 0.07 for Up. It means that KF and SSA should work similarly and will produce similar misfit between the estimated seasonal curve and real data. The CP method removes too much power from the frequency of 1 cpy, which is in very good agreement with what we showed for the synthetic dataset (Fig. 5). For amplitude of power-law noise around 10 mm/year−κ/4, the CP works much worse than KF and SSA. Also, WLS leaves some power around 1 cpy, which can be noticed as a small peak at the PSD. WD absorbs too much power between 0.8 and 3 cpy, causing the dip in the curve. The uncertainty of trend delivered from WD residuals will be the smallest from all methods applied, but is not really what we aim at. We should remove time-changeable signals, but leave the stochastic properties intact if we want to continue to use a simple power-law plus white noise model in the time series analysis.
Discussion and conclusions
Nowadays, the annual and semi-annual signals in the GPS position time series are routinely modeled using periodic signals with constant amplitudes using WLS. However, on physical grounds, it is likely that the amplitudes vary slightly over time. To estimate these signals, various methods have been developed such as WD, SSA, KF, and writing the variations in the seasonal signal as a sum of orthonormal polynomials (CP). In addition to these techniques, we also presented a new method based on Ordinary Least Squares, but applied to 3-year segments of data that are overlapping with a spacing of 1 year, which we call Moving Ordinary Least Squares (MOLS). For each segment, an annual and semi-annual signal was estimated. The main purpose of this method is to quantify the temporal variations in the annual signal. However, its performance as an estimator of the varying seasonal signal is acceptable considering its simplicity.
The performance of above-mentioned methods was investigated using 500 synthetic time series using a period of 16.4 years with pure flicker noise with amplitudes between 1 and 25 mm/year0.25, which means that noise properties delivered from real GPS position time series are covered.
Fitting Chebyshev polynomials through the amplitudes of the seasonal signal performed slightly better than the MOLS method, but we found that for higher noise levels it started to absorb power-law noise which decreased its usefulness. Lowering the degree of the Chebyshev polynomials reduced this problem to some degree.
That SSA is a good estimator of the varying seasonal signal has been demonstrated by several people (Chen et al. 2013; Klos et al. 2017). Here, we confirm these findings, but also show its performance for various noise levels in the time series. We found that in the presence of higher noise levels longer window lengths, e.g., 4-year window, produce better results. For a noise level of 25 mm/year0.25, a window length of 4 years produces a misfit between the real and estimated varying seasonal signals of 1.61 mm. While for a window length of 3 years, this value is 1.68 mm. For our synthetic time series, SSA with a window length of 3 years can model 49–84% of the variance of the true varying seasonal signal and this for most common noise levels found in real GPS data.
The KF, with a correct tuning of the variances in the filter, as described by Didova et al. (2016), was found to be the most precise method for estimating the varying seasonal signal. The addition of temporal correlated noise in the state vector was found to give superior results compared to the KF of Davis et al. (2012) who did not include this type of noise. We concur with Didova et al. (2016) that the search for the optimal values of the variances of the temporal correlated noise and the random walk part of the seasonal signal is a complex problem. However, when this task is well done, the KF is able to estimate better the varying seasonal signal at normal to high noise levels than the afore-mentioned methods. For this range of noise levels, and length of time series, it can model 77-90% of the total variance of the varying seasonal signal.
For series with power-law noise amplitude between 5 and 10 mm/year−κ/4, KF and SSA will produce similar results. For any signal with power-law noise amplitude lower than 5 mm/year−κ/4, KF, SSA, and CP will work in a similar way, and all of them are applicable in this ideal case.
SSA, KF, and CP have all been investigated in previous studies, but none emphasized the fact that their performance is dependent on the noise level in the time series that were analyzed. We demonstrated that the noise level is one of the most important factors that determine the precision of the results. The higher the noise level, the more difficult it is to extract the desired signal. Our contribution is that we have quantified this effect and our results can serve as a recommendation for future studies to estimate how much of the estimated varying seasonal model is real signal and how much is noise. This not only applies to GPS position time series, but also to other geophysical observations such as temperature and sea level time series which are also affected by power-law noise (Bos et al. 2014; Fredriksen and Rypdal 2016) and thus experience similar difficulties to separate the varying seasonal signal from the background noise.
References
Allen MR, Robertson AW (1996) Distinguishing modulated oscillations from coloured noise in multivariate datasets. Clim Dyn 12(11):775–784. https://doi.org/10.1007/s003820050142
Bennett RA (2008) Instantaneous deformation from continuous GPS: contributions from quasi-periodic loads. Geophys J Int 174(3):1052–1064. https://doi.org/10.1111/j.1365-246X.2008.03846.x
Bogusz J (2015) Geodetic aspects of GPS permanent stations non-linearity studies. Acta Geodyn Geomater 12(4):323–333. https://doi.org/10.13168/AGG.2015.0033
Bogusz J, Figurski M (2014) Annual signals observed in regional GPS networks. Acta Geodyn Geomater 11(2):125–131. https://doi.org/10.13168/AGG.2014.0003
Bogusz J, Klos A (2016) On the significance of periodic signals in noise analysis of GPS station coordinates time series. GPS Solut 20(4):655–664. https://doi.org/10.1007/s10291-015-0478-9
Bogusz J, Kontny B (2011) Estimation of sub-diurnal noise level in GPS time series. Acta Geodyn Geomater 8(3):273–281
Bos MS, Fernandes RMS, Williams SDP, Bastos L (2008) Fast error analysis of continuous GPS observations. J Geod 82(3):157–166. https://doi.org/10.1007/s00190-007-0165-x
Bos MS, Fernandes RMS, Williams SDP, Bastos L (2013) Fast error analysis of continuous GNSS observations with missing data. J Geod 87(4):351–360. https://doi.org/10.1007/s00190-012-0605-0
Bos MS, Williams SDP, Araújo IB, Bastos L (2014) The effect of temporal correlated noise on the sea level rate and acceleration uncertainty. Geophys J Int 196(3):1423–1430. https://doi.org/10.1093/gji/ggt481
Broomhead DS, King GP (1986) Extracting qualitative dynamics from experimental data. Phys Nonlinear Phenom 20(2–3):217–236. https://doi.org/10.1016/0167-2789(86)90031-X
Chen Q, van Dam T, Sneeuw N, Collilieux X, Weigelt M, Rebischung P (2013) Singular spectrum analysis for modeling seasonal signals from GPS time series. J Geodyn 72:25–35. https://doi.org/10.1016/j.jog.2013.05.005
Davis JL, Wernicke BP, Tamisiea ME (2012) On seasonal signals in geodetic time series. J Geophys Res 117(B1):B01403. https://doi.org/10.1029/2011JB008690
Didova O, Gunter B, Riva R, Klees R, Roese-Koerner L (2016) An approach for estimating time-variable rates from geodetic time series. J Geod 90(11):1207–1221. https://doi.org/10.1007/s00190-016-0918-5
Fredriksen H-B, Rypdal K (2016) Spectral characteristics of instrumental and climate model surface temperatures. J Clim 29:1253–1268. https://doi.org/10.1175/JCLI-D-15-0457.1
Gelb A (ed) (1974) Applied optimal estimation. The MIT Press, Cambridge. ISBN 0-262-57048-3
Hill EM, Davis JL, Elósegui P, Wernicke BP, Malikowski E, Niemi NA (2009) Characterization of site-specific GPS errors using a short-baseline network of braced monuments at Yucca Mountain, Southern Nevada. J Geophys Res 114(B11):B11402. https://doi.org/10.1029/2008JB006027
Kalman RE (1960) A new approach to linear filtering and prediction problems. J Basic Eng-Trans ASME 82:35–45
King MA, Watson CS, Penna NT, Clarke PJ (2008) Subdaily signals in GPS observations and their effect at semiannual and annual periods. Geophys Res Lett 35(3):L03302. https://doi.org/10.1029/2007GL032252
Klos A, Bogusz J, Figurski M, Kosek W (2014) Uncertainties of geodetic velocities from permanent GPS observations: the Sudeten case study. Acta Geodyn Geomater 11(3):201–209. https://doi.org/10.13168/AGG.2014.0005
Klos A, Bogusz J, Figurski M, Kosek W (2015) On the handling of outliers in the GNSS time series by means of the noise and probability analysis. In: Springer IAG symposium series, vol 143, 657–664. doi:https://doi.org/10.1007/1345_2015_78
Klos A, Gruszczynska M, Bos MS, Boy J-P, Bogusz J (2017) Estimates of vertical velocity errors for IGS ITRF2014 stations by applying the improved singular spectrum analysis method and environmental loading models. Pure appl Geophys. https://doi.org/10.1007/s00024-017-1494-1
Langbein J (2010) Computer algorithm for analyzing and processing borehole strainmeter data. Comput Geosci 36(5):611–619. https://doi.org/10.1016/j.cageo.2009.08.011
Larson KM, van Dam T (2000) Measuring Postglacial rebound with GPS and absolute gravity. Geophys Res Lett 27(23):3925–3928
Meyer Y (1990) Ondelettes et Opérateurs, vol I–III, Hermann, Paris, 1990
Munekane H, Kuroishi Y, Hatanaka Y, Yarai H (2008) Spurious annual vertical deformations over Japan due to mismodelling of tropospheric delays. Geophys J Int 175(3):831–836. https://doi.org/10.1111/j.1365-246X.2008.03980.x
Rice SO (1944) Mathematical analysis of random noise. Bell Syst Tech J 23(3):282–332. https://doi.org/10.1002/j.1538-7305.1944.tb00874.x
Rodionov SN (2004) A sequential algorithm for testing climate regime shifts. Geophys Res Lett 31(9):L09204. https://doi.org/10.1029/2004GL019448
Santamaría-Gómez A, Bouin M-N, Collilieux X, Wöppelmann G (2011) Correlated errors in GPS position time series: implications for velocity estimates. J Geophys Res 116(B1):1405. https://doi.org/10.1029/2010JB007701
Teferle FN, Bingley RM, Orliac EJ, Williams SDP, Woodworth PL, McLaughlin D, Baker TF, Shennan I, Milne GA, Bradley SL, Hansen DN (2009) Crustal motions in Great Britain: evidence from continuous GPS, absolute gravity and Holocene sea level data. Geophys J Int 178(1):23–46. https://doi.org/10.1111/j.1365-246X.2009.04185.x
Tobita M (2016) Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 68:41. https://doi.org/10.1186/s40623-016-0422-4
Tregoning P, Watson C, Ramillien G, McQueen H, Zhang J (2009) Detecting hydrologic deformation using GRACE and GPS. Geophys Res Lett 36(15):L15401. https://doi.org/10.1029/2009GL038718
van Dam T, Wahr J, Milly PCD, Shmakin AB, Blewitt G, Lavallée D, Larson KM (2001) Crustal displacements due to continental water loading. Geophys Res Lett 28(4):651–654. https://doi.org/10.1029/2000GL012120
Vautard R, Ghil M (1989) Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys Nonlinear Phenom 35(3):395–424
Welch PD (1967) The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans Audio Electroacoust 15(2):70–73. https://doi.org/10.1109/TAU.1967.1161901
Wessel P, Smith WHF, Scharroo R, Luis J, Wobbe F (2013) Generic mapping tools: improved version released. Eos Trans. Am Geophys Union 94(45):409–410. https://doi.org/10.1002/2013EO450001
Williams SDP (2008) CATS: GPS coordinate time series analysis software. GPS Solut 12(2):147–153. https://doi.org/10.1007/s10291-007-0086-4
Williams SDP, Bock Y, Fang P, Jamason P, Nikolaidis RM, Prawirodirdjo L, Miller M, Johnson DJ (2004) Error analysis of continuous GPS position time series. J Geophys Res 109(B3):B03412. https://doi.org/10.1029/2003JB002741
Wu H, Li K, Shi W, Clarke K, Zhang J, Li H (2015) A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut 19(4):511–523. https://doi.org/10.1007/s10291-014-0412-6
Xu C, Yue D (2015) Monte Carlo SSA to detect time-variable seasonal oscillations from GPS-derived site position time series. Tectonophysics 665:118–126. https://doi.org/10.1016/j.tecto.2015.09.029
Yan H, Chen W, Zhu Y, Zhang W, Zhong M (2009) Contributions of thermal expansion of monuments and nearby bedrock to observed GPS height changes. Geophys Res Lett 36(13):L13301. https://doi.org/10.1029/2009GL038152
Zerbini S, Raicich F, Errico M, Cappello G (2013) An EOF and SVD analysis of interannual variability of GPS coordinates, environmental parameters and space gravity data. J Geodyn 67:111–124. https://doi.org/10.1016/j.jog.2012.04.006
Zhang J, Bock Y, Johnson H, Fang P, Williams S, Genrich J, Wdowinski S, Behr J (1997) Southern California permanent GPS geodetic array: error analysis of daily position estimates and site velocities. J Geophys Res 102(B8):18035–18055. https://doi.org/10.1029/97JB01380
Acknowledgements
Anna Klos is supported by the National Science Centre, Poland, grant no. UMO-2016/23/D/ST10/00495. Machiel Simon Bos is supported by national funds through FCT in the scope of the Project IDL-FCT-UID/GEO/50019/2013 and grant number SFRH/BPD/89923/2012. JPL time series were accessed from ftp://sideshow.jpl.nasa.gov/pub/JPL_GPS_Timeseries/repro2011b/. The map was drawn in the Generic Mapping Tool (Wessel et al. 2013).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Klos, A., Bos, M.S. & Bogusz, J. Detecting time-varying seasonal signal in GPS position time series with different noise levels. GPS Solut 22, 21 (2018). https://doi.org/10.1007/s10291-017-0686-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10291-017-0686-6